Promieniowanie

synchrotronowe i jego

zastosowania (EXAFS,

XANES)

Konrad Osiecki

IS (WFiIS) gr.1.

Plan prezentacji

• trochę historii (starsze sposoby
otrzymywani promieniowani X)

• promieniowanie synchrotronowe (jak wygląda
synchrotron)

• niektóre własności promieniowania
synchrotronowego

• wigglery i ondulatory
• przykład synchrotronu (ESRF)
• zastosowanie promieniowania
synchrotronowego (EXAFS)

Troszkę historii

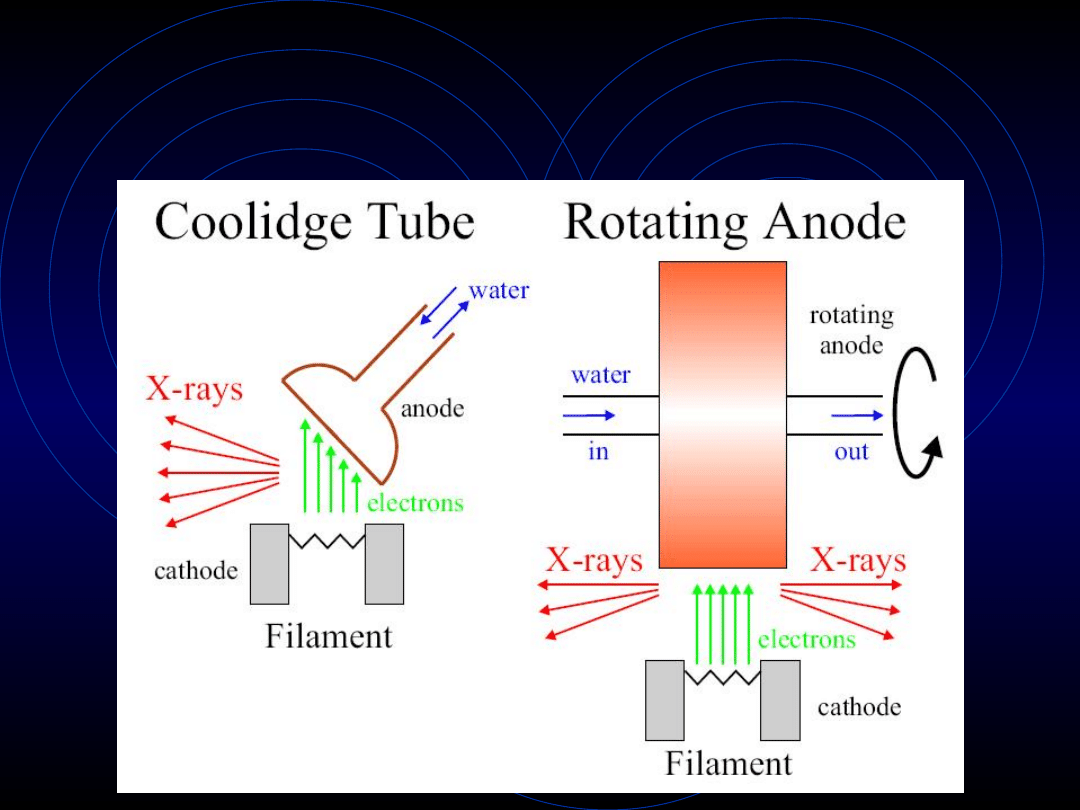
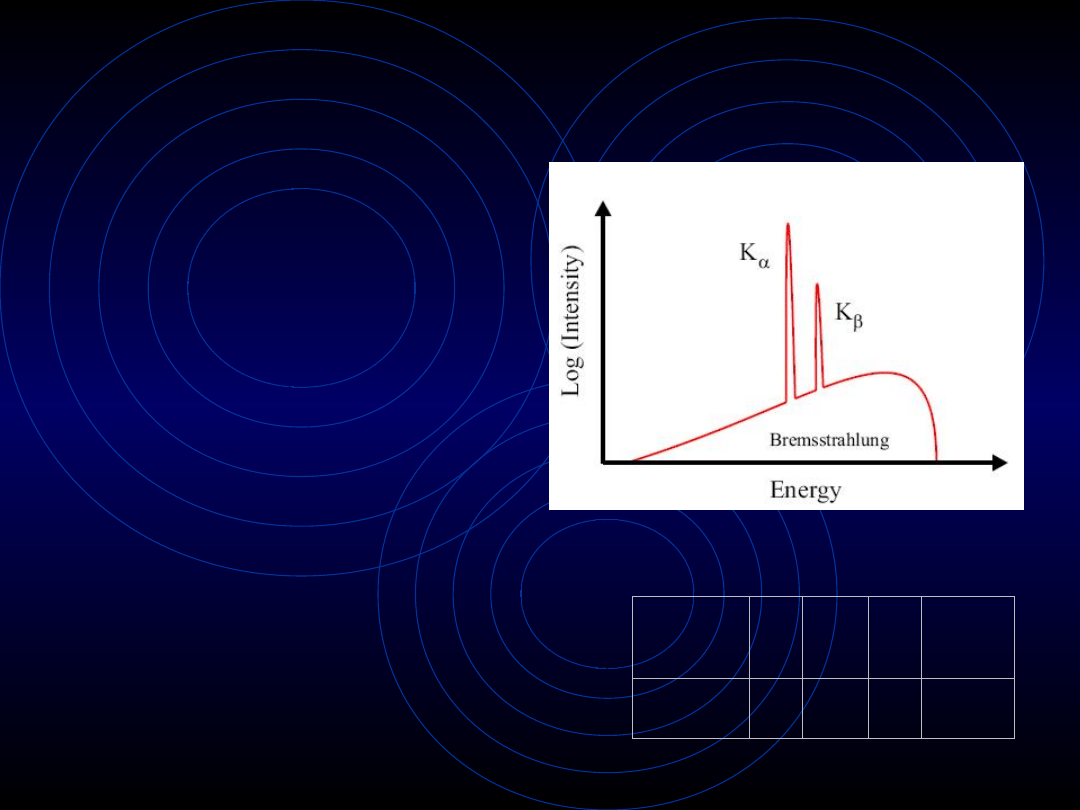
Troszkę historii – c.d.

Elektron uderza w atom i
wybija w atomie elektron
z wewnętrznej powłoki.
Elektron z któreś z
dalszych powłok zapełnia
wolne miejsce, co
produkuje promieniowanie
X o charakterystycznej
energii równej różnicy
energetycznej tych dwóch
powłok.

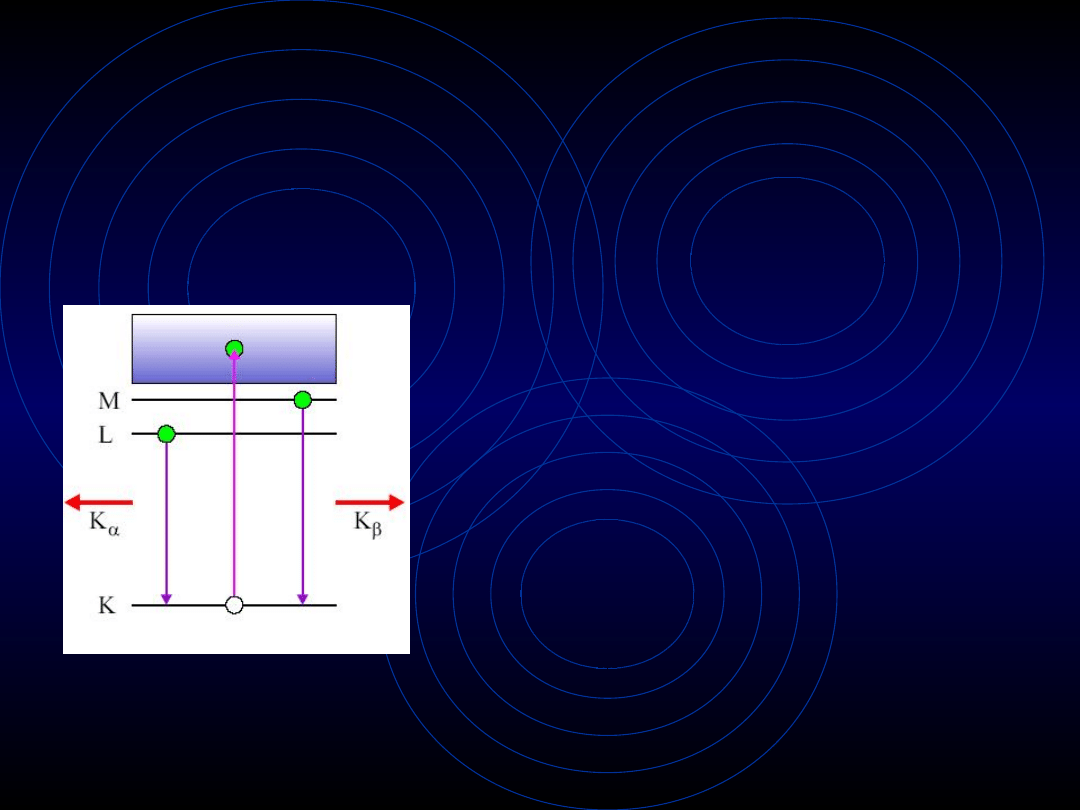
Troszkę historii – c.d.

promieniowanie K



-

promieniowanie
powstałe w wyniku
przeskoku elektronu
z powłoki L do K po
wcześniejszym
wybiciu elektronu z
powłoki K pod
wpływem działania
czynnika
zewnętrznego
(głęboka jonizacja)

Liczba
kwantowa

główna n

1 2 3

4

Symbol

powłoki

K L M

N

itd.

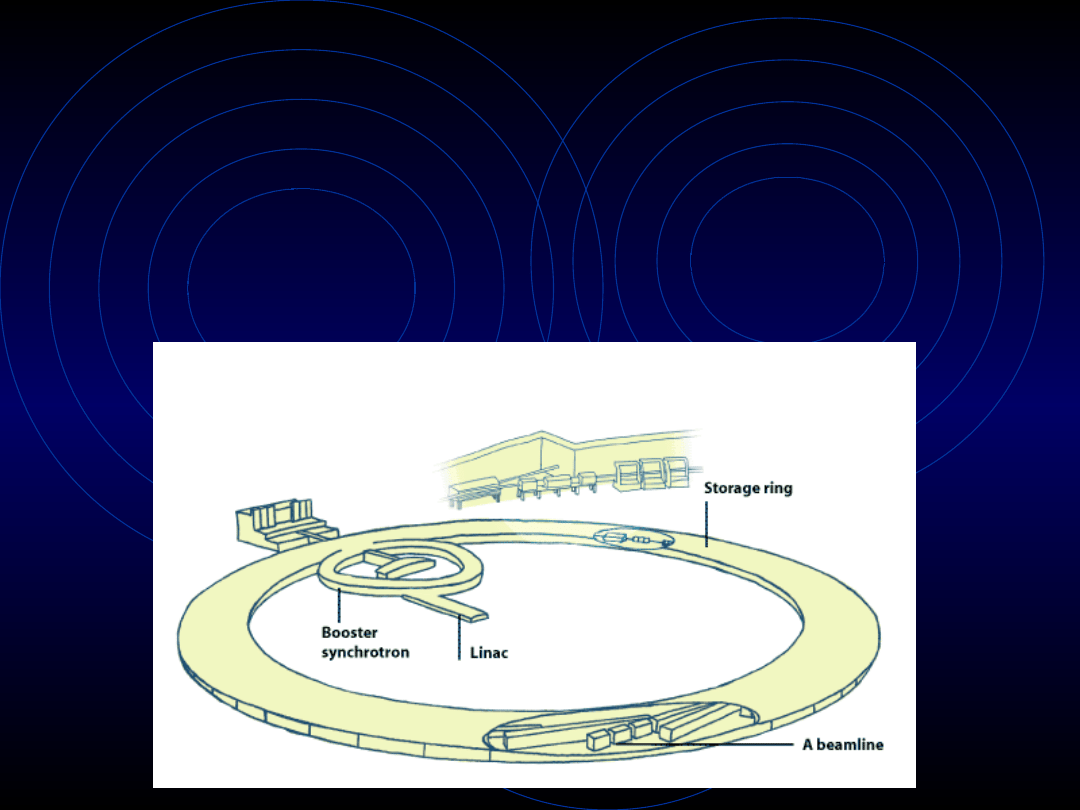
Promieniowanie
synchrotronowe

Jest to promieniowanie wysyłane przez

cząstki (elektrony lub pozytrony),
poruszające się po torze kołowym.

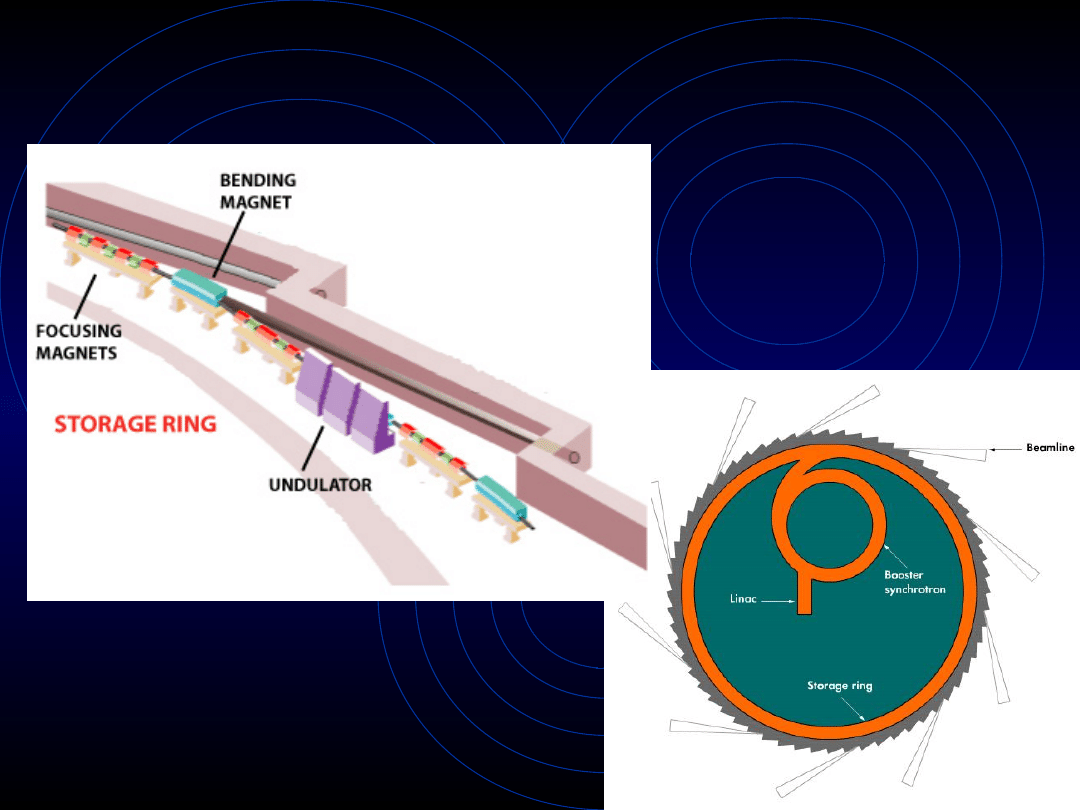
Pierścień akumulacyjny

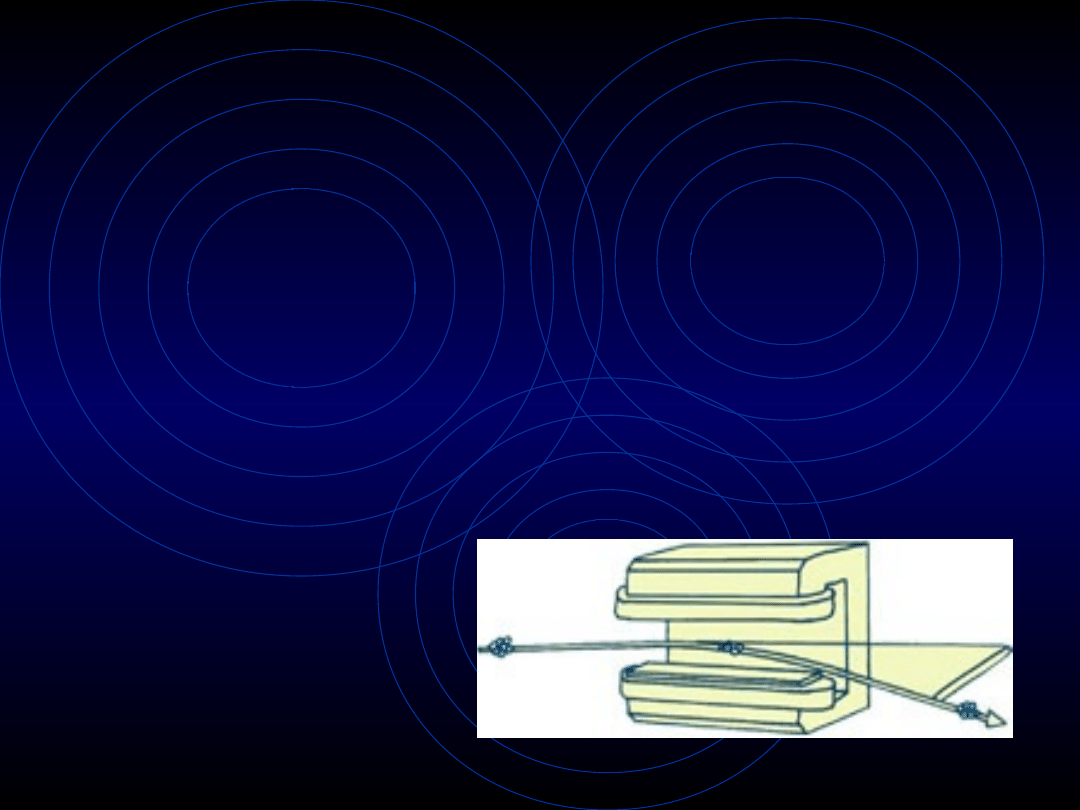
Pierścień akumulacyjny
– magnes zakrzywiający

Gdy cząstki przechodzą przez ten magnes ich
tor ruchu zostaje odchylony o kilka stopni.
Podczas odchylania (działa przyspieszenie
dośrodkowe! – zmienia się kierunek wektora
prędkości!) emitują one promieniowanie
synchrotronowe.

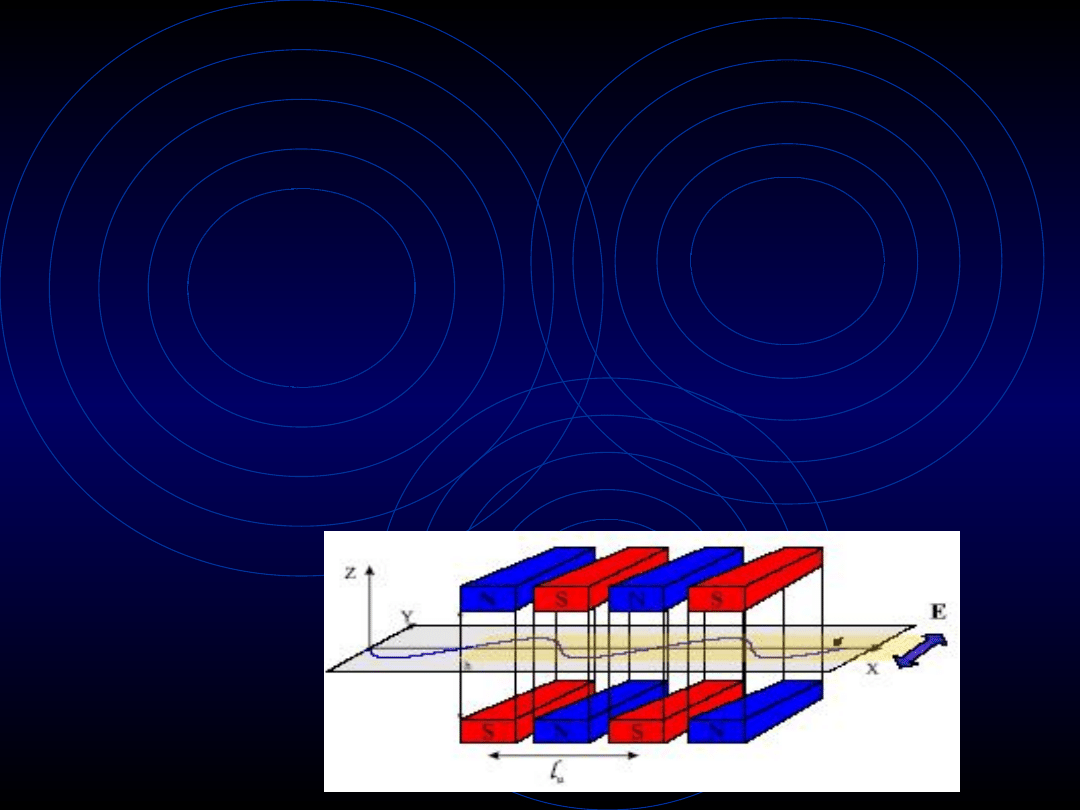
Pierścień akumulacyjny

– wigglery i ondulatory

Należą do tzw. insertion devices i powodują
harmoniczny ruch cząstek na prostych odcinkach
pierścienia dzięki zastosowaniu specjalnych
macierzy magnesów. Elektrony wprawione w ruch
znów emitują promieniowanie, a wigglery i
ondulatory pozwalają na uzyskanie pożądanych
cech tego promieniowania w znacznie większej
skali.

Pierścień akumulacyjny
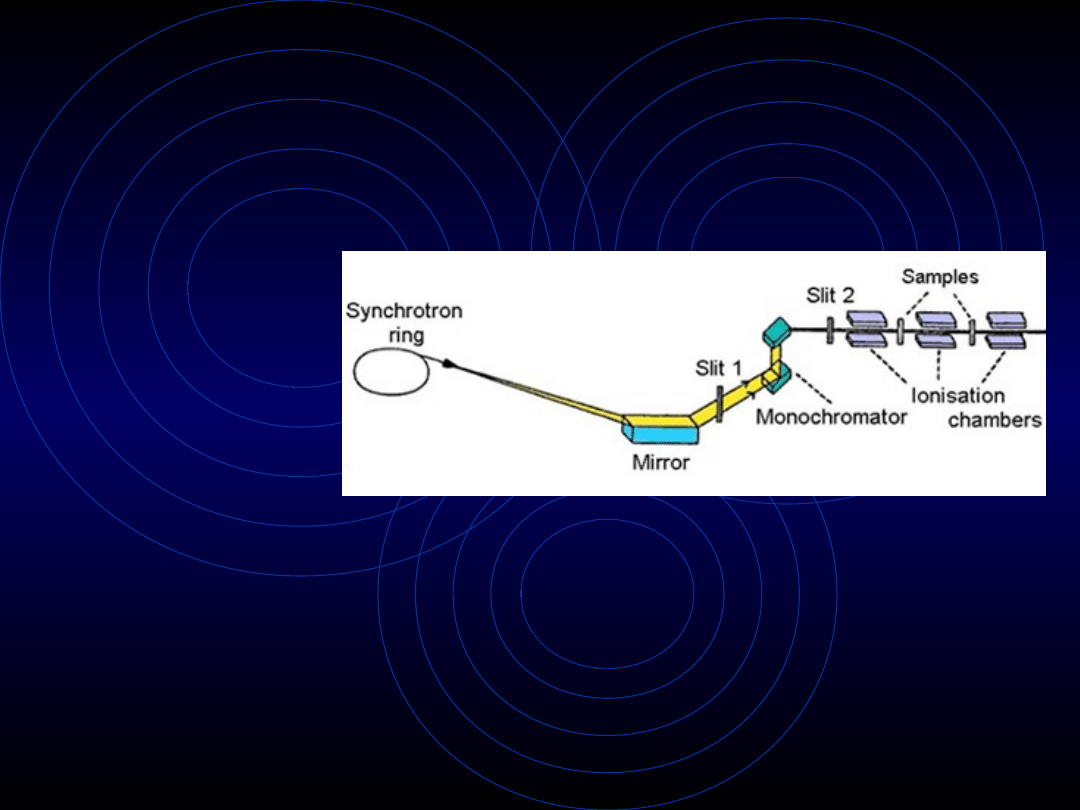
– pozostałe urządzenia

W miejscach, gdzie promieniowanie
synchrotronowe jest emitowane buduje się linie
eksperymentalne składające się z:

•

monochromatorów

– kryształ lub kilka warstw

kryształów przepuszczających falę o danej
długości lub pewien zakres fal promieniowania

•

zwierciadeł, soczewek

– służą do

maksymalnego możliwego skupienia wiązki
promieniowania monochromatycznego

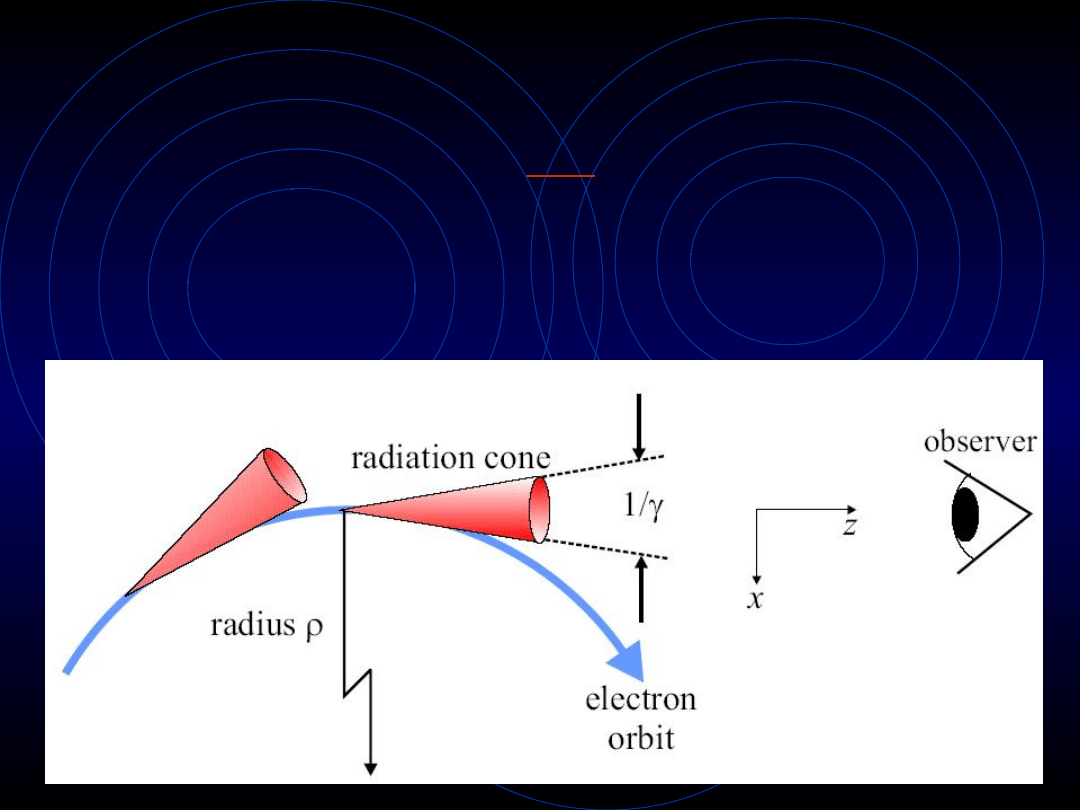
Jednym z charakterystycznych parametrów
promieniowania synchrotronowego jest kąt
otwarcia γ

-1

:

2

1

e

mc

E

g

-

=

Parametr ten z reguły wynosi ok. 0.1
miliradiana.

Efekt Dopplera

1

'

1

v
c

f

v
c

+

=

-

Dla ciał zbliżających się (do nas):

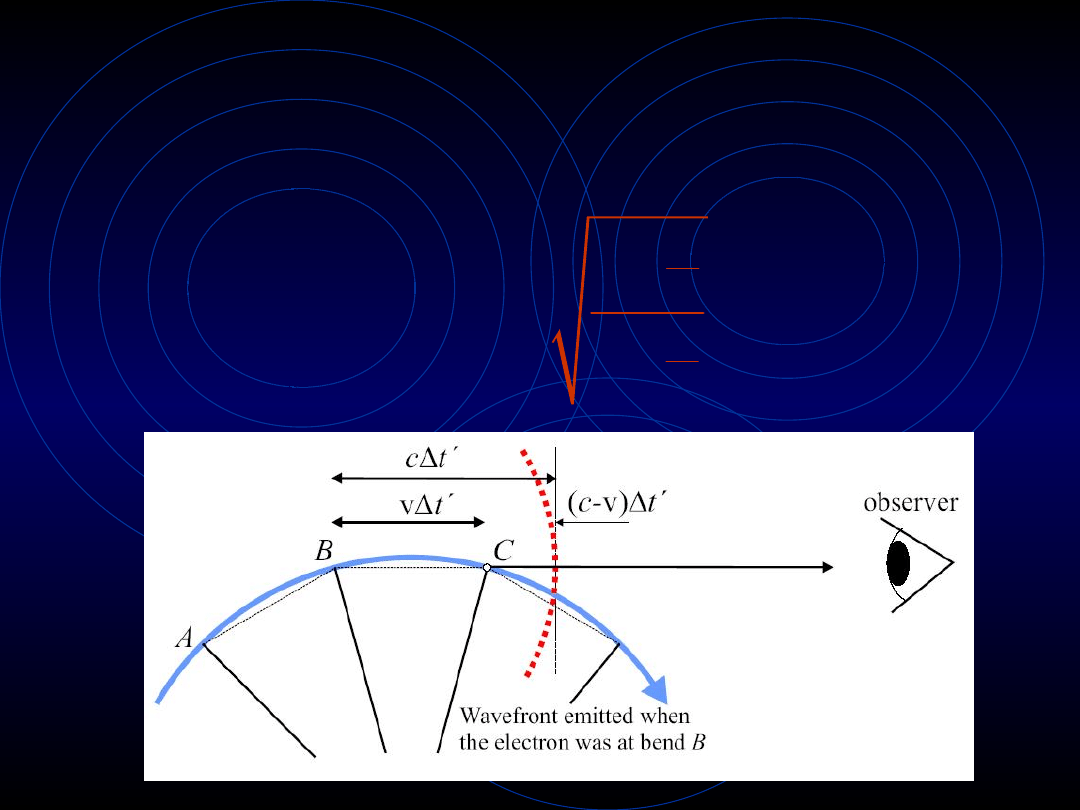
Efekt Dopplera – c.d.

Efekt Dopplera – c.d.

W pierwszym przypadku odległość wysyłanych fali:

(

)

'

c v t

-

D

Czyli obserwator zobaczy:

(

)

(

)

'

1

'

c v t

t

t

c

b

-

D

D =

= -

D

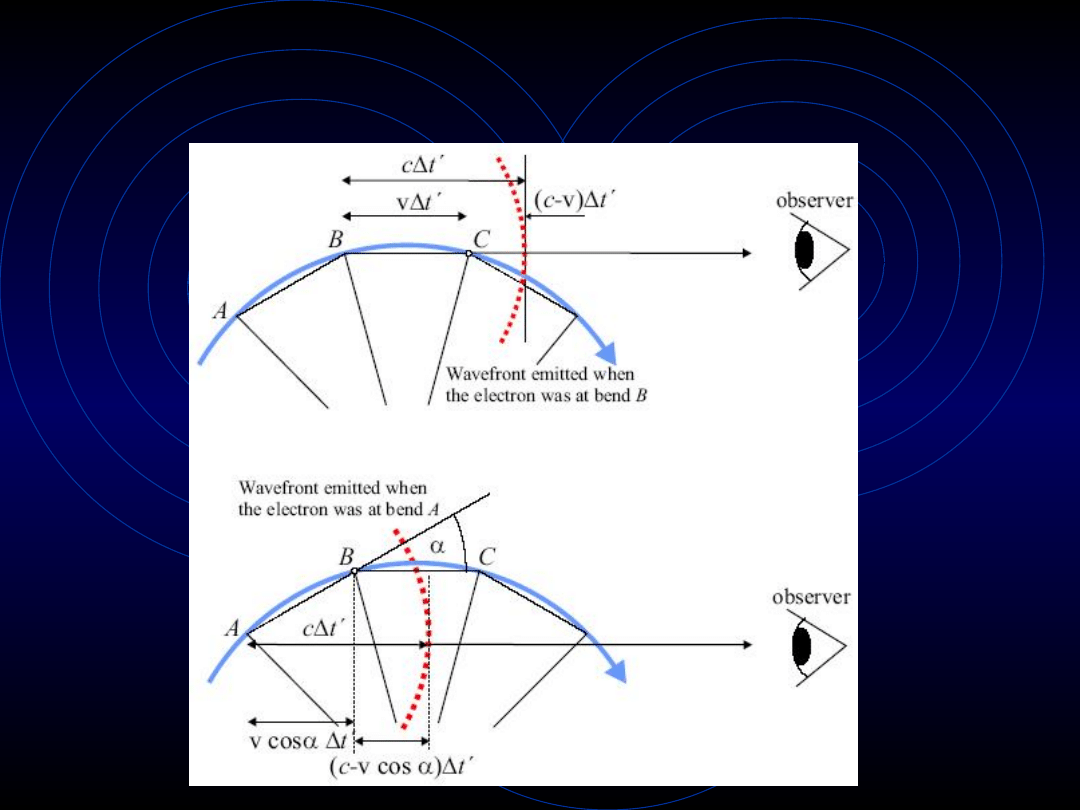
W drugim (ogólniejszym przypadku):

(

)

1

cos

'

t

t

b

a

D = -

D

To można rozpisać jako (ponieważ β i cosα są bliskie
jedności):

( )

2

2

2

2

1

1

1 1

1

'

'

2

2

2

t

t

t

ag

a

g

g

�

�

�

�

+

�

�

�

�

D � -

-

-

D �

D

�

�

�

�

�

�

�

�

�

�

�

��

�

�

�

�

�

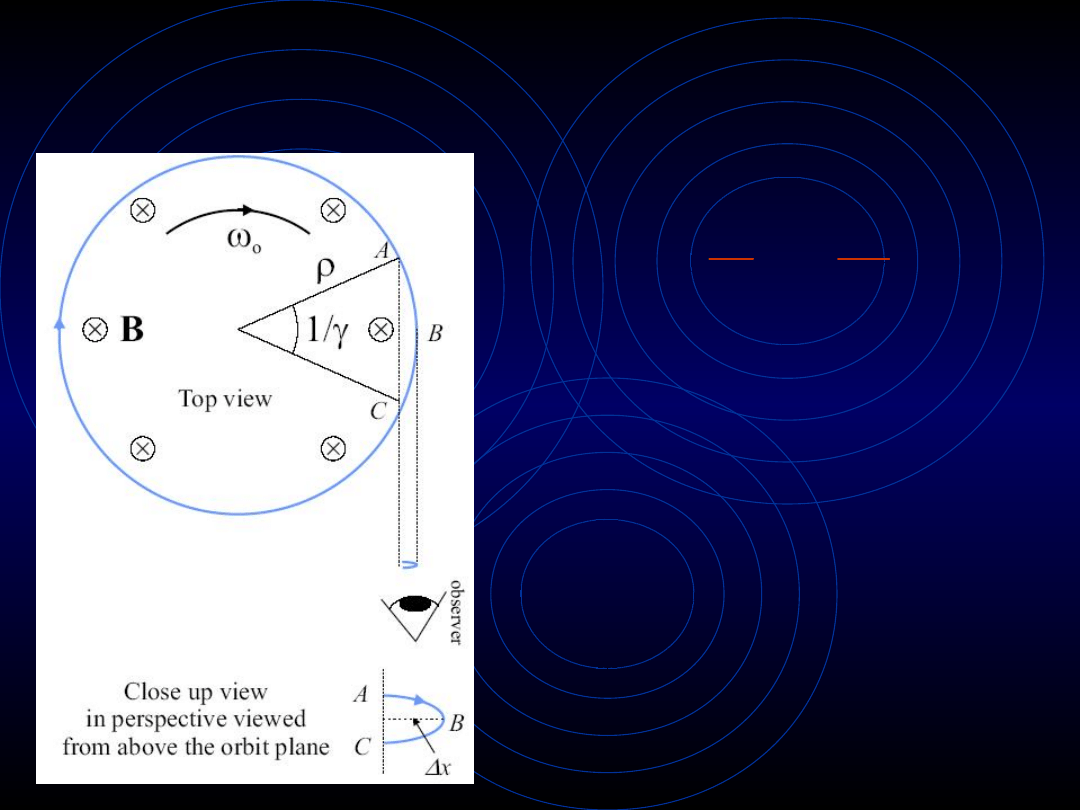
Częstotliwość

1

1

'

2

o

T

g

p

gw

-

� �

=

� �

� �

Przejście z A do C:

Ale obserwator
obserwuje czas
skrócony γ

2

krótszy,

zatem ostatecznie rząd
wielkości dla
częstotliwości
promieniowania:

3

calkowite

o

w

g w

=

3

calkowite

o

w

g w

=

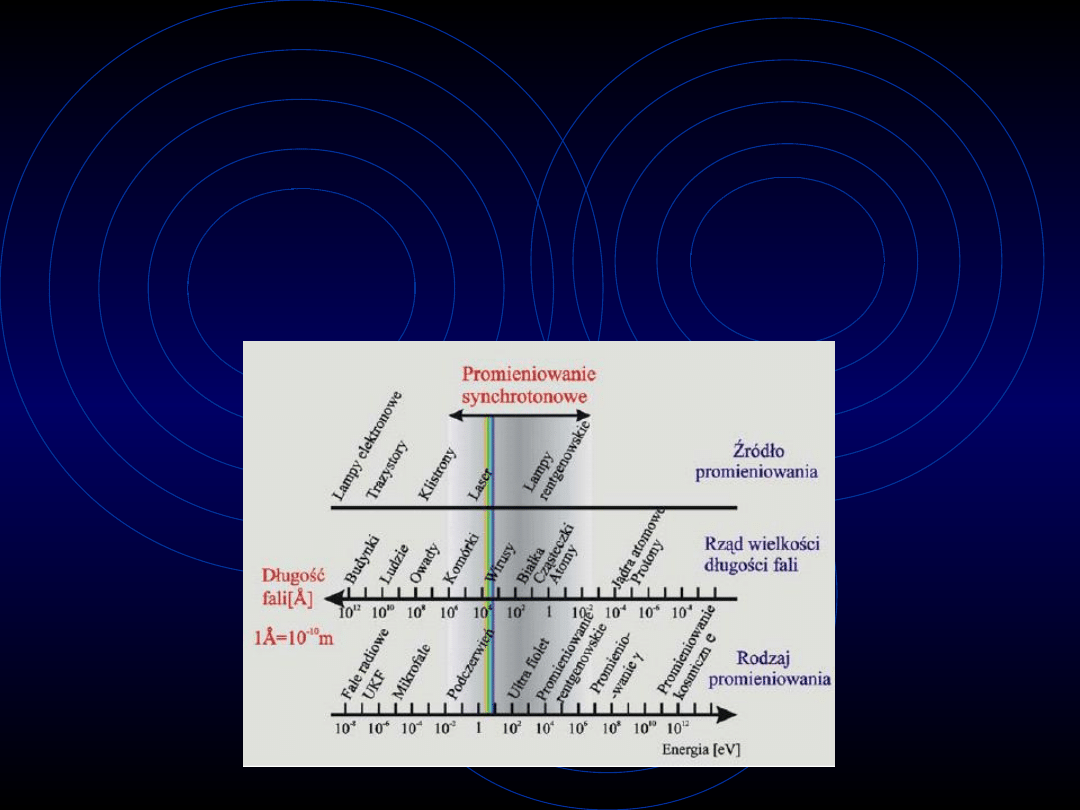
Promieniowanie synchrotronowe obejmuje
bardzo szeroki zakres widmowy: od
promieniowania podczerwonego, poprzez
obszar widzialny i ultrafiolet aż do
twardego promieniowania rentgenowskiego
(czyli fali o częstotliwości rzędu 10

18

).

Doświadczenia w synchrotronie przeprowadza
się na wielu paczkach elektronów,
wpuszczanych w równych odległościach od
siebie.

Cykl pracy jednej paczki elektronów na
pierścieniu akumulacyjnym dł. 300m wynosi
1µs. Paczka jest długości rzędu 1cm, a czas
trwania jednego impulsu jest rzędu 100ps.

Szacowana moc wypromieniowana na odcinku L
(wzdłuż drogi elektronu) wynosi:

[

]

[

] [ ] [ ] [ ]

2

2

1.266

e

P kW

E GeV B T L m I A

=

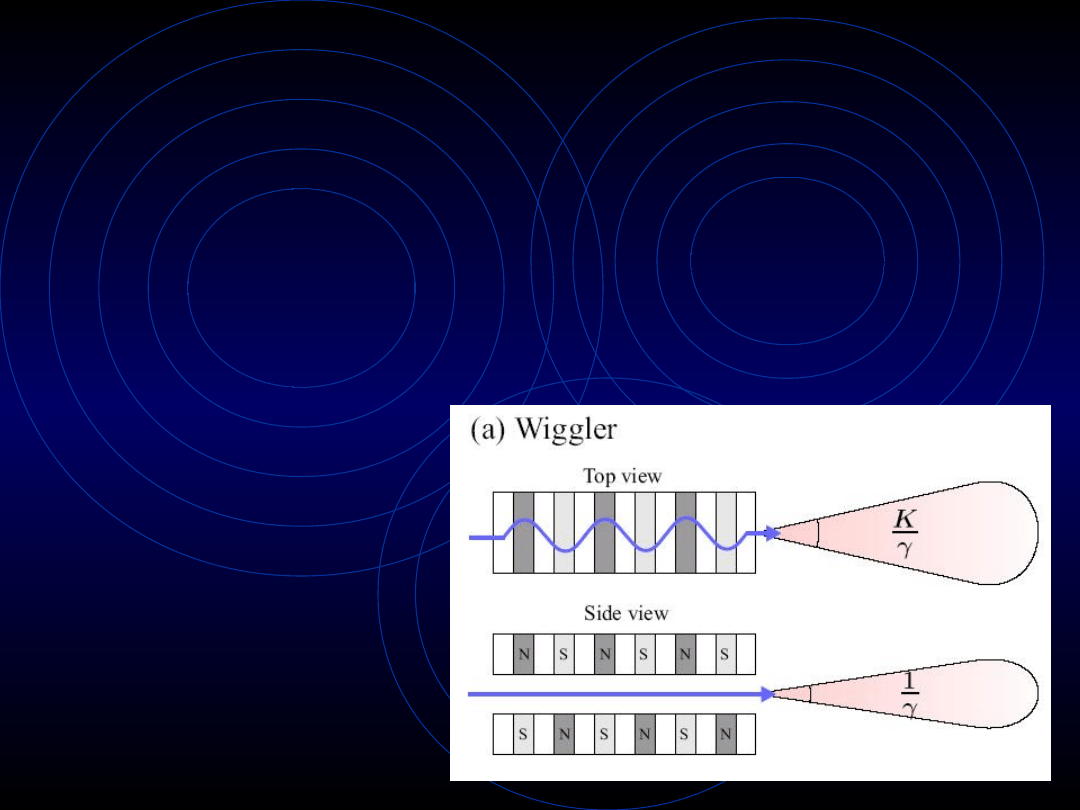
Wigglery (wigglers)

• poprawa intensywności promieniowania o czynnik
2N (N – liczba okresów)

•wypromieniowana moc:

• długość L ok. 1m
• intensywności
są dodawane

[

]

[

]

[ ] [ ] [ ]

2

2

0

0.663

e

P kW

E GeV B T L m I A

=

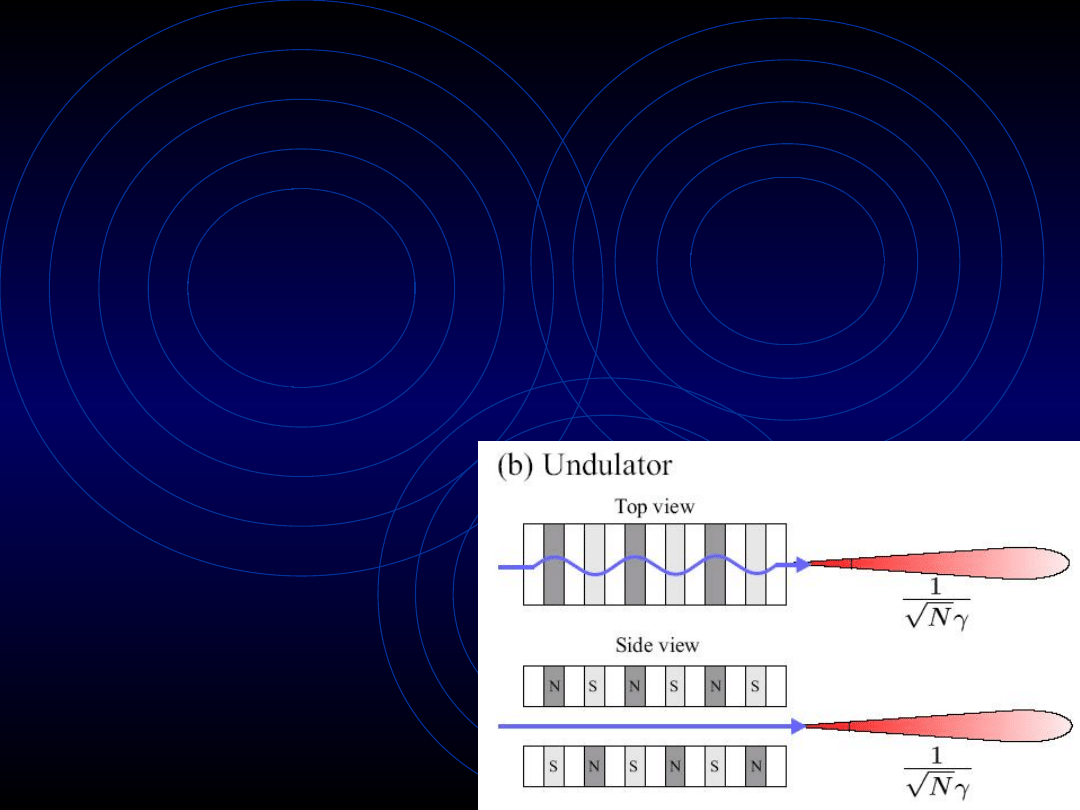
Ondulatory (undulators)

• promieniowanie z jednej oscylacji jest w fazie
z następnymi oscylacjami

• amplitudy są najpierw dodawane, suma jest
podniesiona
do kwadratu  intensywność
• amplitudy skalowalne
przez γ

-1

• sumowanie amplitud
obowiązuje dla jednej
określonej dł. Fali
 promieniowanie

(prawie) monochroma-
tyczne

Współczynnik K

[ ] [ ]

0

0

0.934

2

u

u

eB

K

cm B T

mc

l

l

p

=

=

�

• dla wigglerów wynosi ok.20-50 (tylko w
płaszczyźnie poziomej)

• dla ondulatorów wynosi ok. 1. W konsekwencji
kąt otwarcia jest skompresowany o czynnik
. N wynosi z reguły ok. 50.

1/ N

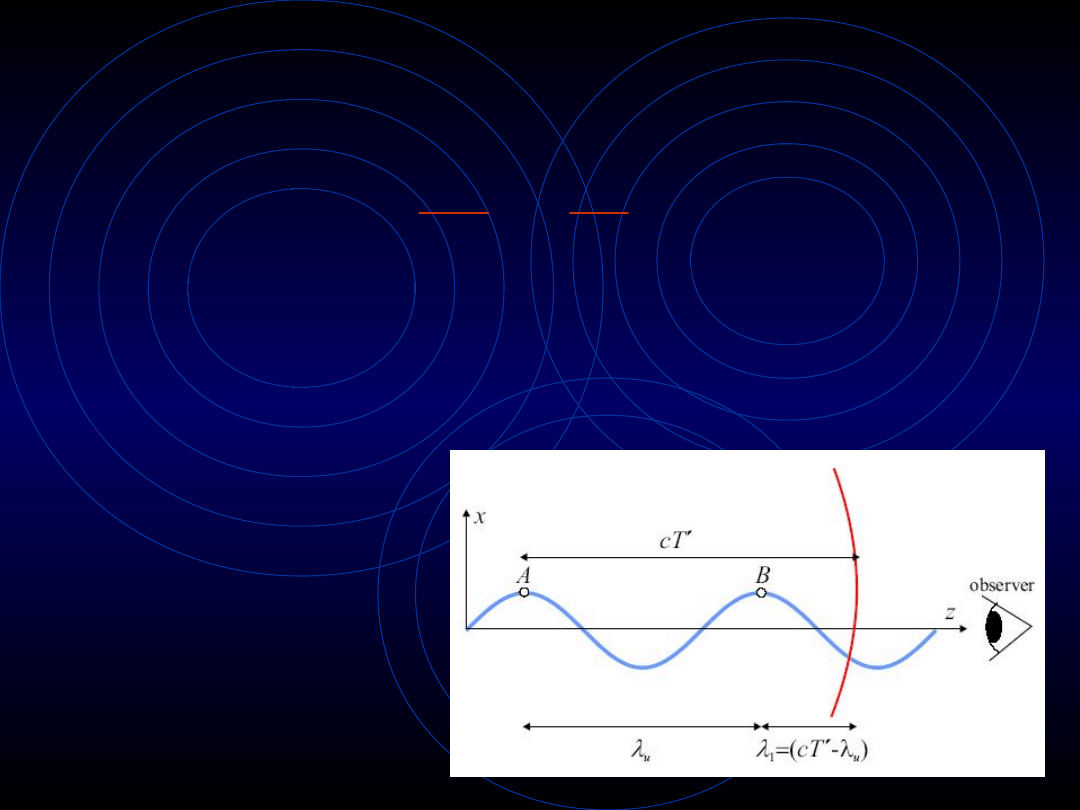
Podstawowa dł. fali – λ

1

( )

( )

2

2

1

2

1

2

2

u

K

l

l q

gq

g

�

�

=

+

+

�

�

�

�

Przy typowych wartościach γ

-2

rzędu 10

-8

oraz

λ

u

rzędu 10

-2

m λ

1

jest rzędu Angströma (10

-10

) i

dlatego mieści się w zakresie promieniowania
X.

ERSF–European Synchrotron

Radiation Facility

• znajduje się w Grenoble (Francja) – wspierane i
współdzielone przez 18 krajów Europy

• budżet – w 2004 roku wyniósł 74 mln €
• załoga – 600 ludzi
• ok. 3500 naukowców rocznie
wykonuje tu eksperymenty

• ponad 1600 podań rocznie o możliwość wykonania
eksperymentu

ESRF – Pre-injector

Preinjector

200 MeV

Repetition rate

1 Hz/10Hz

Pulse length

1000 – 2 ns

Electron current

25 – 2500 mA

Długość impulsu:
1μs lub 1ns

ESRF - Booster

ESRF - Booster

Repetition
Rate

10 Hz

Energy

6 GeV

Circumferen
ce

300 m

ERSF – Storage Ring

Energy

6.03 GeV

Max. Current

200 mA

Frequency

355 kHz

Number of bunches

1 to 992

Time between

bunches

2816 to 2.82 ns

• obwód: 844.4 m
• zadaniem jest
utrzymać energię
6 GeV uzyskanych
w boosterze

• 64 magnesy
zakrzywiające

• wiązka skupiana przez 320
kwadropolów

• 16 skecji 6-metrowych, w których można umieścić
insertion devices o długości do 5 m

• wszystkie rodzaje eksperymentów (ondulatory i
wigglery)

ERSF – Storage Ring

(u góry)panorama z inseriotn
devices (różowe)

(z boku) widok z góry na fragment
pierścienia 

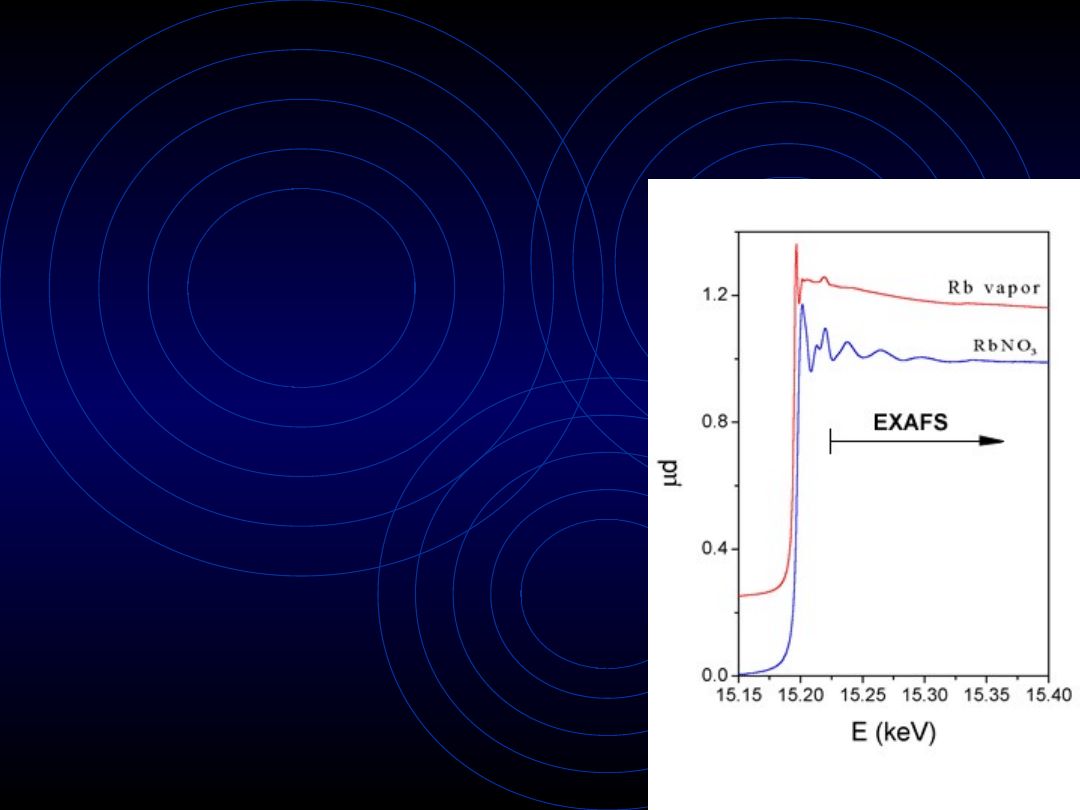
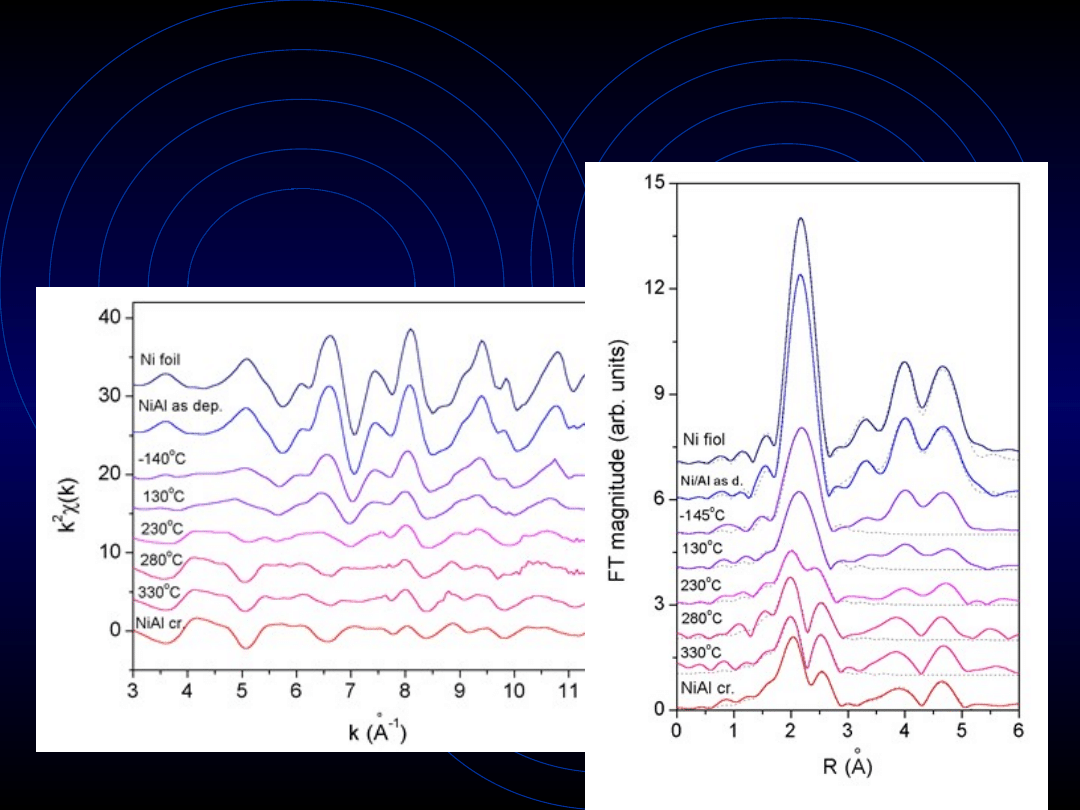
EXAFS - Extended X-Ray

Absorption Fine Structure

• Wykorzystuje proces
absorpcji
fotoelektrycznej

• linia absorpcji pokazuje
gwałtowny skok
prawdopodobieństwa wyrwania
elektronu z powłoki K

• po dostarczeniu odpowiednio
dużej energii wyrwany zostaje
elektron z powłoki K
(ucieka z atomu) i rozchodzi
się w postaci fali

EXAFS

Fotoelektron
wyzwalany
przez padający
kwant energię
kinetyczną:

K

E h

E

n

= -

Fala fotoelektronu, rozchodząc się w próbce,
napotyka sąsiednie atomy, od których się odbija.

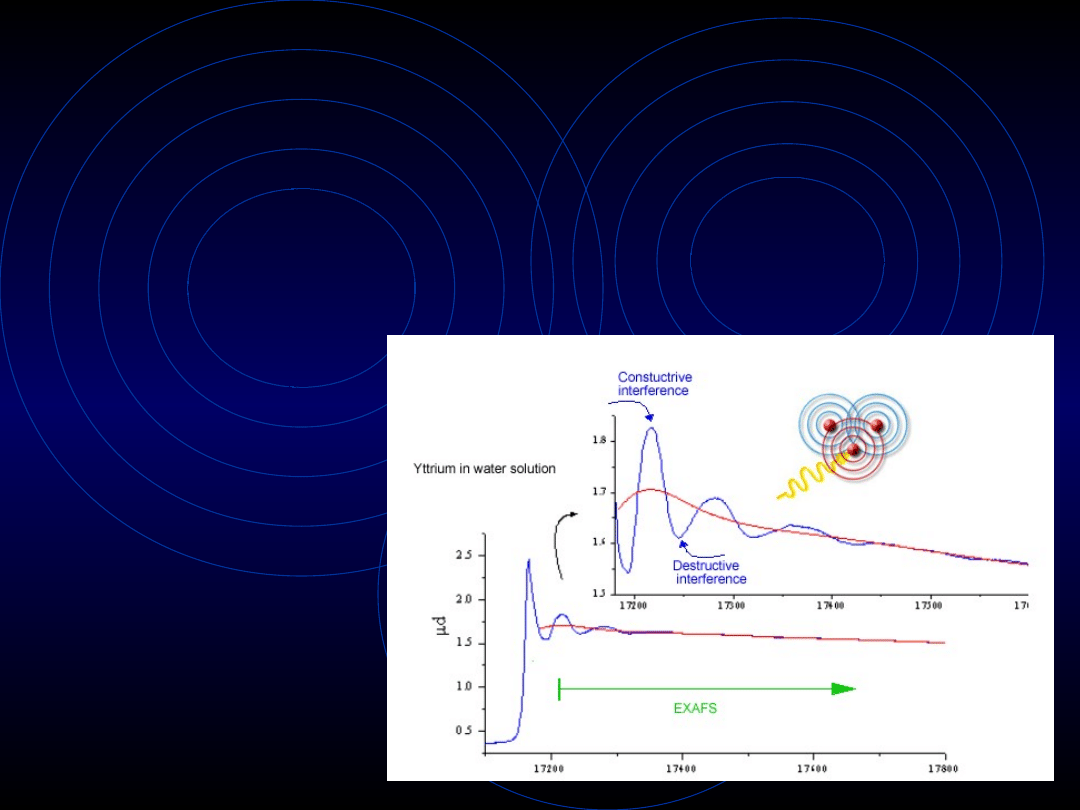
EXAFS

Odbita fala elektronu interferuje z falą
biegnącą, czego wynikiem jest albo jej
wzmocnienie, albo osłabienie (w zależności od
odległości
od sąsiadów).

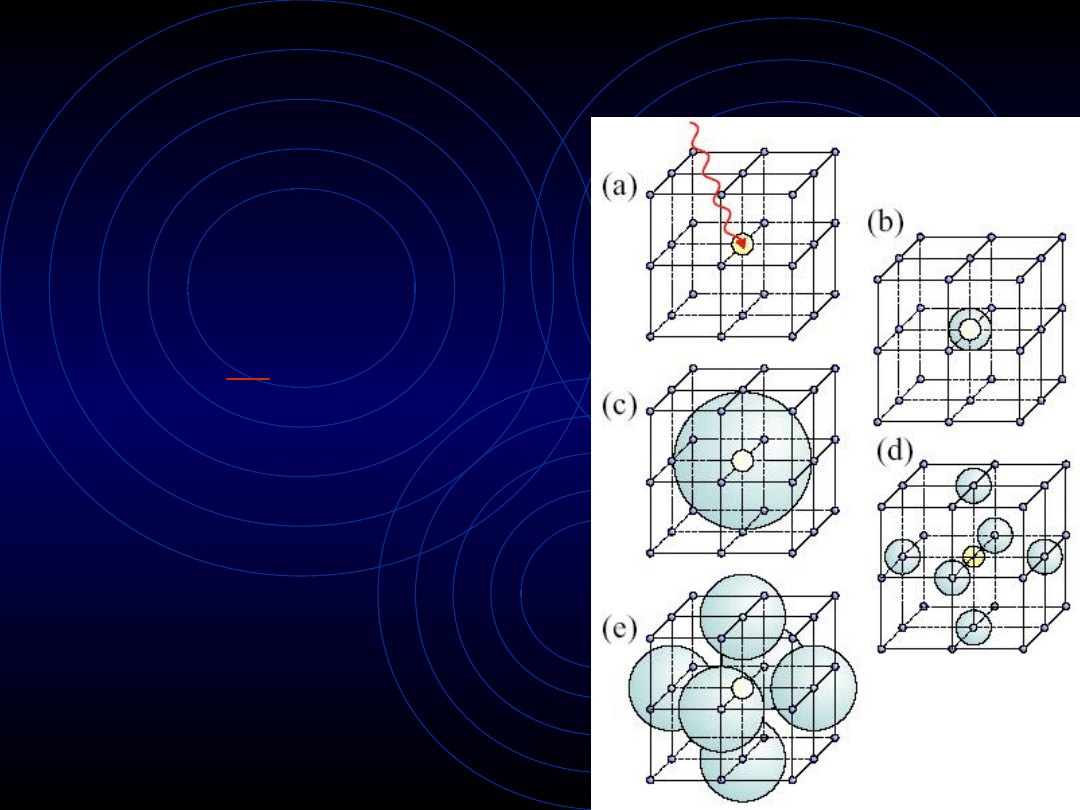
EXAFS

Transmisja:

( )

1

0

E d

I

T

e

I

m

-

= =

�

współczynnik absorpcji

μ(E)

EXAFS

Całkowity współczynnik absorpcji powyżej
krawędzi można zapisać:

( )

( )

( )

0

1

k

k

k

m

m

c

=

+

�

�

�

�

gdzie:

(

)

2

2

K

m

E

k

w-

=

h

h

i k jest liczbą falową elektronu.
Można uznać, że:

( )

0

k

m mc

D =

EXAFS

Funkcję χ(k) można przedstawić następująco:

( )

(

)

( )

2 2

2

2

2

,

sin 2

j

j

j

j

k

dR

j

j

j

j

N f k

k

e

e

kR

k

kR

s

p

c

J

-

-

-

�

�

=

+

�

�

�

2kR

j

– odzwierciedla faz padającego i rozproszonego

el.
- przesunięcie fazowe – konsekwencja
potencjału atomu centralnego i atomu
rozpraszającego falę el.

( )

k

J

EXAFS