SZCZELINY

ZMĘCZENIOWE

Mateusz

Soja

IM gr.2 sem.3

WZROST SZCZELIN

ZMĘCZENIOWYCH

Cel kryteriów pękania można także sformułować

alternatywnie - dla znanego obciążenia zewnętrznego

wyznaczyć maksymalną dopuszczalną długość

szczeliny, tzw. długość krytyczną. Inną wspólną cechą

wszystkich przedstawionych kryteriów pękania jest to,

że nie uwzględniają one sposobu, w jaki szczelina o

początkowej długości lo osiąga swoją wartość

krytyczną. Tymczasem od dawna wiadomo, że mały

defekt istniejący w elemencie konstrukcyjnym w

normalnych warunkach pracy tego urządzenia może

okazać się stabilny przez cały okres eksploatacji

elementu, zaś przy zmianie tych warunków może

okazać się niebezpieczny już po krótkim okresie

eksploatacji. Typowym przykładem może tu być zmiana

zachowania szczeliny w zależności od rodzaju

obciążenia.

Zupełnie inny jest obraz zachowania się

szczeliny przy obciążeniu stałym, a inny przy

obciążeniu zmiennym (np. cyklicznie

zmiennym). Analiza licznych katastrof

mostowych w XIX wieku wykazała, że ich

przyczyną były obciążenia cyklicznie zmienne,

których amplituda nie przekraczała połowy

dopuszczalnego obciążenia statycznego.

Decydującą rolę w powstawaniu katastrof

odgrywała tu więc nie wielkość obciążenia, ale

jego zmienność w czasie. Przykład ten

wskazuje na znaczenie w mechanice obciążeń

cyklicznie zmiennych, szczególnie groźnych

dla bezpiecznej pracy konstrukcji, bądź jej

elementów.

Mówiąc o wzroście szczeliny mamy na
myśli jej stabilne podrastanie od
długości lo do długości krytycznej lkr,
osiągnięcie której przyjmuje się za
zniszczenie elementu. W mechanice
pękania zniszczenie pod wpływem
obciążeń zmiennych określa się
terminem „zniszczenie zmęczeniowe”.

Etap początkowy to nukleacja (inicjacja)

makroszczeliny, czyli szczeliny o długości

wystarczająco dużej, aby opis jej zachowania na

gruncie mechaniki ciała odkształcalnego był

wystarczająco dokładny. Uważa się, że obciążenie

cyklicznie zmienne powoduje kumulowanie się energii

w pobliżu wewnętrznych pustek bądź wtrąceń obcych.

To z kolei prowadzi do wzrostu i łączenia się tych

mikrodefektów, aż do utworzenia po pewnej liczbie

cykli Ni makropęknięcia, określanego mianem szczeliny

zmęczeniowej. Etap drugi to etap wzrostu (propagacji)

szczeliny zmęczeniowej od długości li do długości lkr.

Okres trwania tego etapu określony jest liczbą cykli Np.

Ostatni etap to niestabilny wzrost szczeliny,

utożsamiany ze zniszczeniem zmęczeniowym.

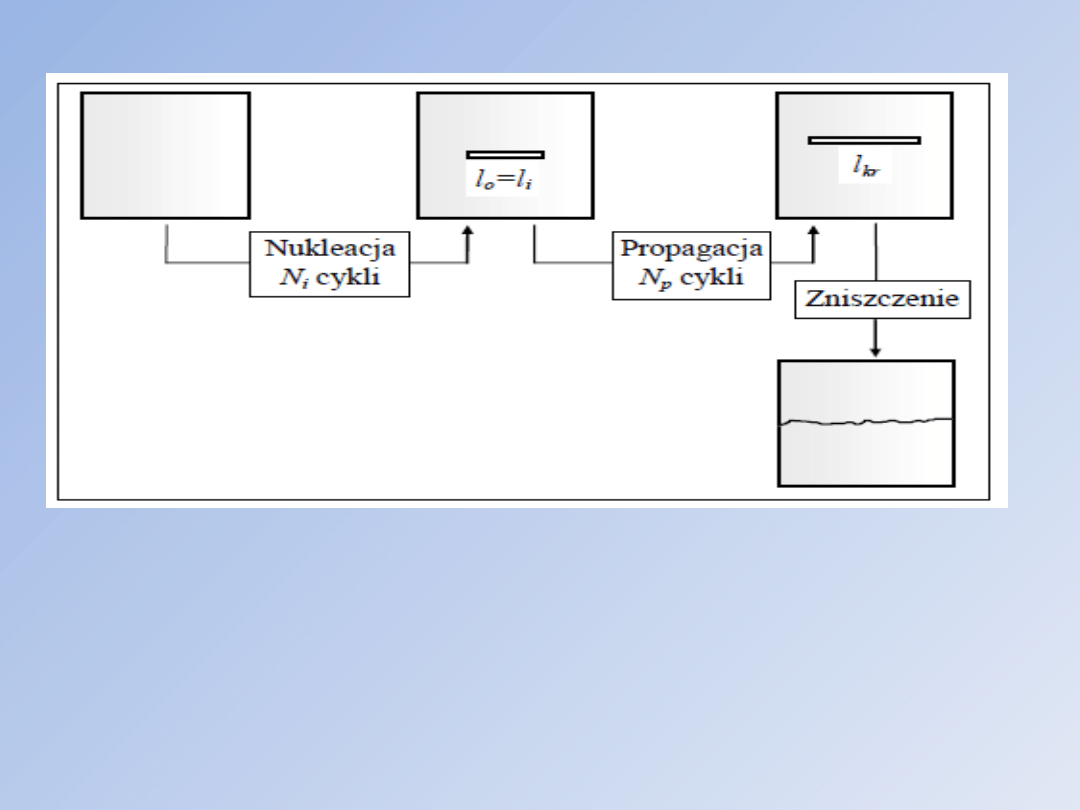
Rys. 7.1. Etapy rozwoju szczelin zmęczeniowych

Z powyższych rozważań wynika, że całkowita liczba cykli
obciążenia, jaką może bezpiecznie przenieść element
konstrukcyjny (zwana jest ona niekiedy okresem życia
elementu) jest sumą liczby cykli do inicjacji pęknięcia Ni i liczby
cykli odpowiadającej jego propagacji Np. Wartości liczbowe obu
tych wielkości zależą od wielu czynników, m.in. od rodzaju
materiału, parametrów charakteryzujących obciążenie oraz
geometrii szczeliny - trudno zatem podać
jakieś ogólne prawidłowości. Jest to tym trudniejsze, że
pierwszy etap – inicjacja szczeliny zmęczeniowej - jest wciąż
słabo poznany, tak od strony doświadczalnej, jak i teoretycznej.
W wielu jednak przypadkach przyjmuje się, że dla oceny
trwałości konstrukcji miarodajna jest faza propagacji szczeliny
zmęczeniowej - wystarcza zatem znajomość liczby cykli Np.

SZCZELINA ZMĘCZENIOWA PRZY

OBCIĄŻENIU

CYKLICZNYM O STAŁEJ AMPLITUDZIE

Rozważmy podstawowe dla praktyki inżynierskiej

zagadnienie wzrostu szczeliny przy obciążeniu

cyklicznie zmiennym o stałej amplitudzie.

Niezależnymi parametrami opisującymi naprężenia

wywołane tym obciążeniem są: naprężenie średnie

sm, amplituda naprężenia sa oraz częstotliwość w (w

celu określenia wielkości wyłącznie naprężenia

znajomość amplitudy nie jest konieczna). Możliwy jest

oczywiście inny dobór parametrów naprężeniowych –

przykładowo, mogą nimi być naprężenie maksymalne

smax i minimalne smin lub też zakres zmienności

naprężenia Ds i jeden z parametrów smax, smin, sm.

Często stosowanym parametrem jest tzw.

współczynnik asymetrii cyklu R. Może on zastąpić

jeden z wymienionych wyżej parametrów.

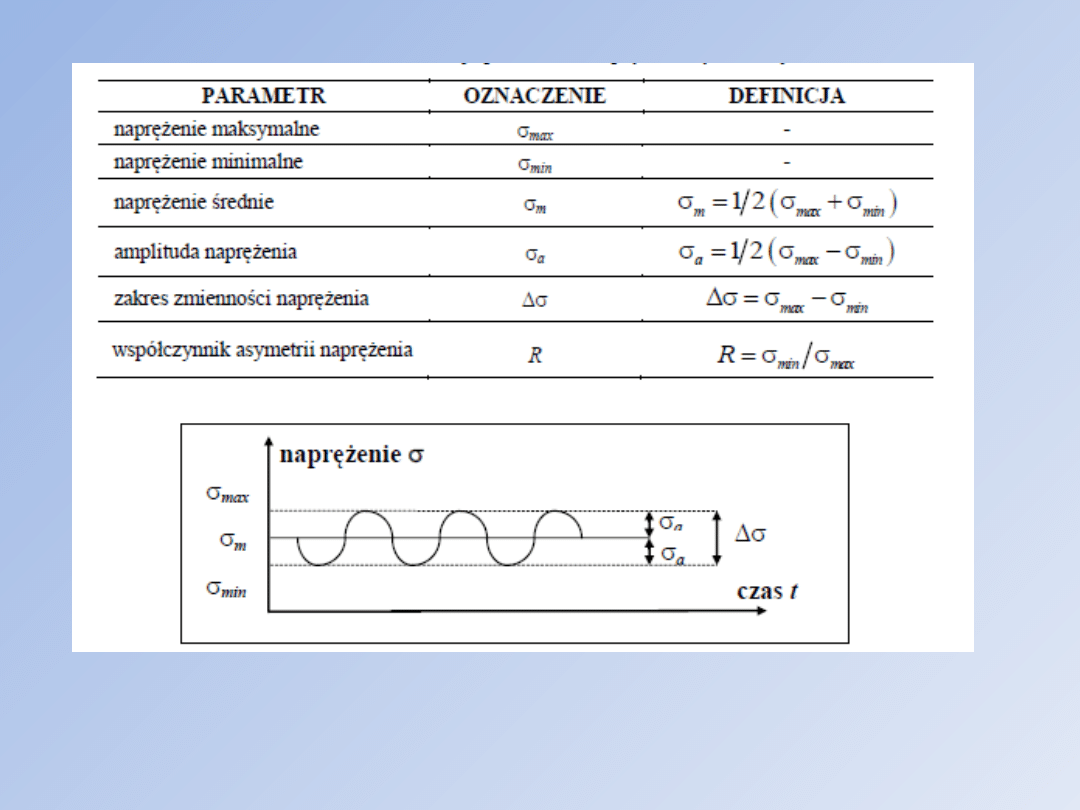
Tab. określenia i definicje parametrów naprężeń
zmęczeniowych.

Podstawowe parametry charakteryzujące wzrost szczelin zmęczeniowych.

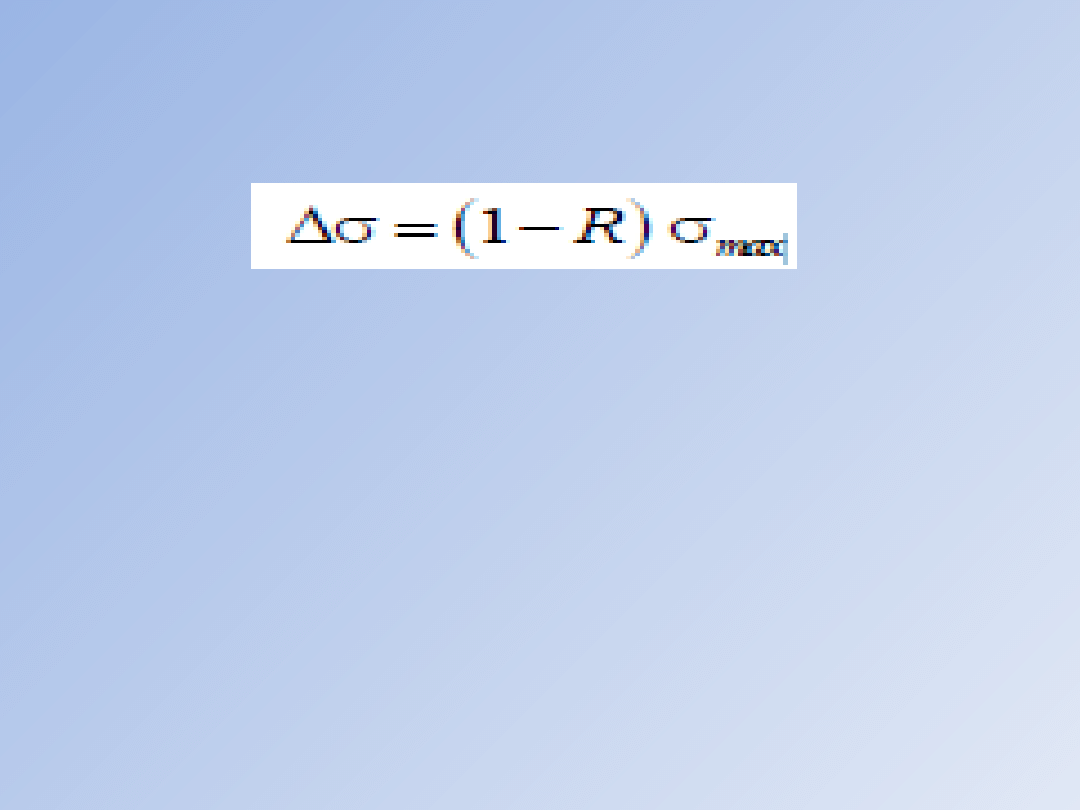
Z określeń zamieszczonych w Tab. wynika
następujący związek między parametrami
zmęczeniowymi:

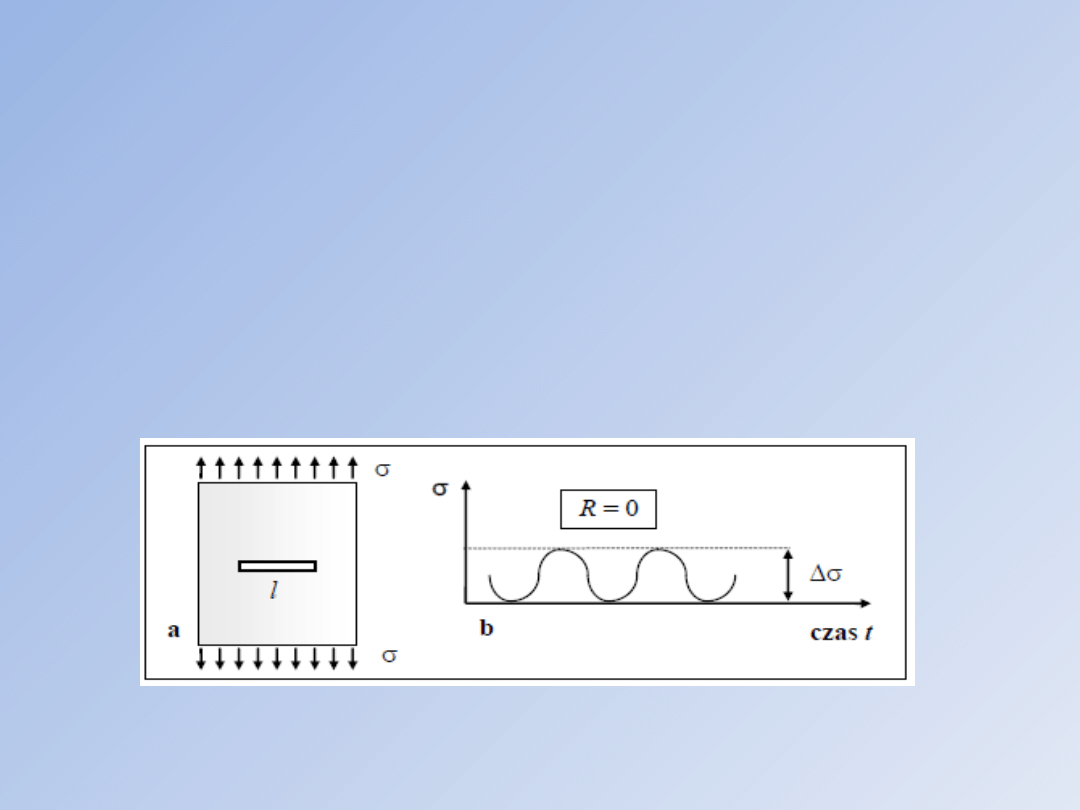
Wartość R = 0 oznacza cykl, w którym naprężenie
rośnie od wartości zerowej do wartości
maksymalnej, a następnie maleje ponownie do
zera - naprężenia nie zmieniają zatem znaku w
całym procesie obciążania elementu
konstrukcyjnego. Naprężenia zmieniające się
zgodnie z takim cyklem noszą nazwę tętniących.
Często występującym przypadkiem jest cykl o
współczynniku R = -1. W tym przypadku
naprężenia oscylują wokół naprężenia średniego
sm=0.

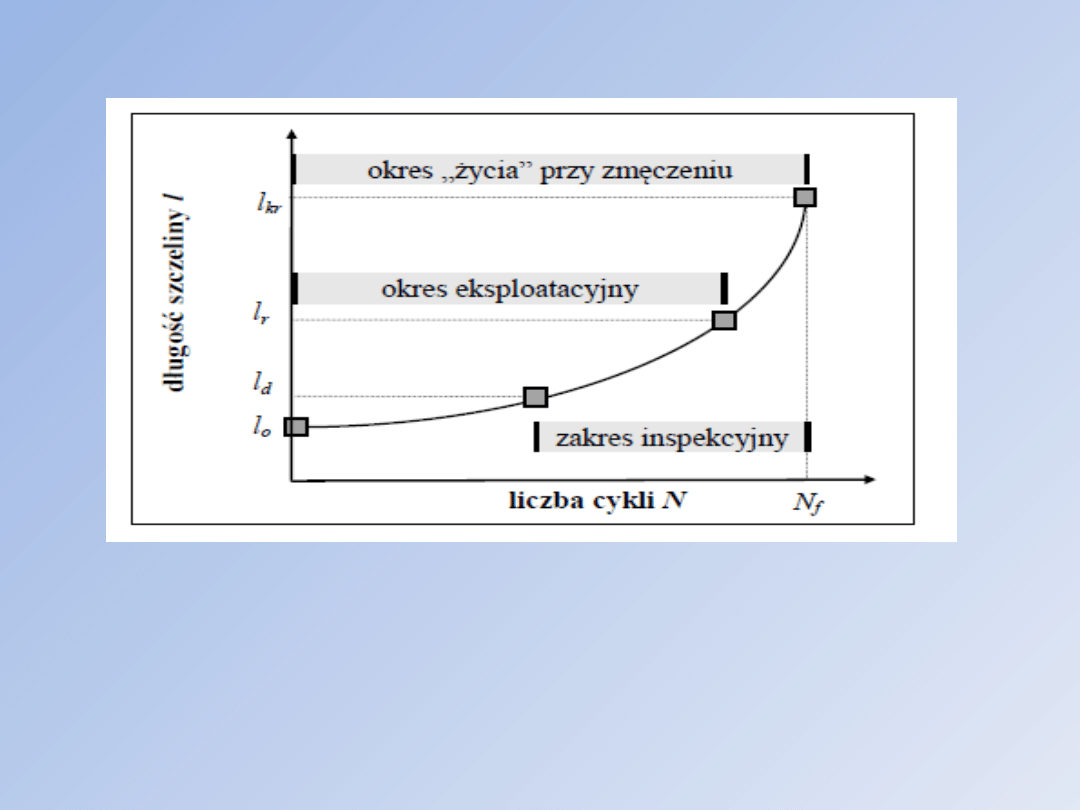
Przykładowa krzywa propagacji szczeliny zmęczeniowej (obciążenie o
stałej amplitudzie).
 

Rzeczywista początkowa długość szczeliny

oznaczona jest jako lo - musi ona być na tyle duża,

aby można do opisu zachowania szczeliny stosować

mechanikę pękania. W praktyce może się okazać, że

jest ona zbyt mała, aby można ją zidentyfikować

przy pomocy stosowanych metod i przyrządów

pomiarowych w badaniach nieniszczących.

Najmniejszą możliwą do wykrycia w ten sposób

długość szczeliny oznaczono jako ld - tę długość

będziemy rozumieć w dalszej analizie jako

początkową (ld wyznacza tzw. zakres inspekcyjny,

tzn. zakres, w którym możliwa jest doświadczalna

obserwacja szczeliny). Na skutek działającego

obciążenia zmiennego szczelina powoli podrasta od

długości początkowej aż do pewnej długości lr, kiedy

to następuje wyraźne przyspieszenie ruchu szczeliny.

Ten okres w pracy elementu ze szczeliną uważa się

za użyteczny okres eksploatacyjny.

Po osiągnięciu przez szczelinę długości
krytycznej następuje lawinowy,
niekontrolowany jej wzrost utożsamiany ze
zniszczeniem elementu - liczba cykli
odpowiadająca zniszczeniu wynosi Nf .
Wyznaczenie okresu życia elementu,
określonego liczbą cykli do zniszczenia Nf, jak
również krzywej l= l(N) stanowi
podstawowe zadanie analizy wzrostu szczeliny
przy zmęczeniu.

Krzywa prędkości wzrostu

szczeliny zmęczeniowej

Ogólnie akceptowanym poglądem jest ten, że mechanizm

wzrostu szczeliny przy obciążeniu zmiennym związany jest

z lokalnym polem naprężeń w pobliżu wierzchołka szczeliny.

Jeden z modeli wzrostu mówi, że nawet przy bardzo małych

obciążeniach, wskutek dużych koncentracji naprężeń w

okolicach wierzchołkowych ostrej szczeliny występują

odkształcenia plastyczne. Uzewnętrzniają się one w fazie

obciążania (wzrostu wartości obciążenia cyklicznego)

powstawaniem poślizgów płaszczyzn atomowych, w wyniku

których następuje powiększenie długości szczeliny oraz

stępienie (zaokrąglenie) jej wierzchołków. W fazie

odciążenia (zmniejszania wartości obciążenia cyklicznego)

zmniejsza się rozwarcie szczeliny, a wierzchołki ponownie

staja się ostre. W cyklu wzrostu obciążenia powyższy

proces rozpoczyna się od początku. Jest to proces

nieodwracalny na skutek trwałego zburzenia struktury

atomowej przy poślizgach plastycznych.

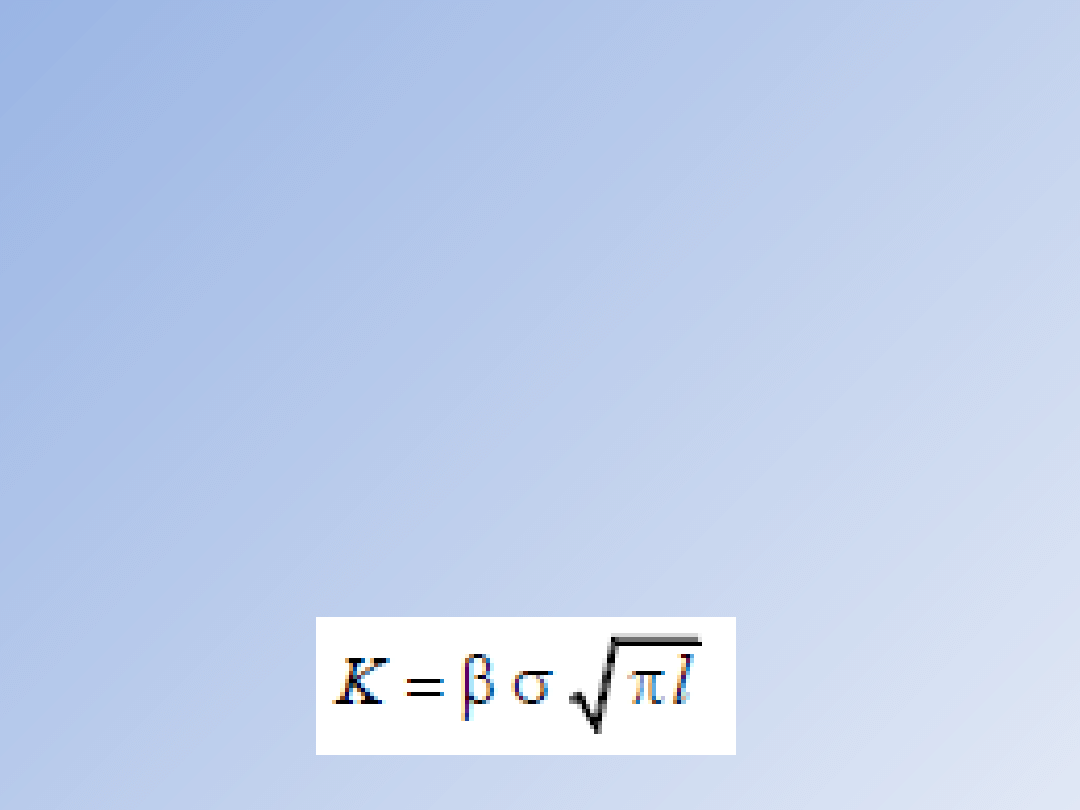
Korzystając z tego, że proces wzrostu

szczeliny zmęczeniowej związany jest z

lokalnym spiętrzeniem naprężeń - można

przyjąć za uzasadnione powiązanie wzrostu

szczeliny z wielkością współczynnika

intensywności naprężeń (WIN) K -

podstawowego parametru wykorzystywanego

w mechanice pękania, znanego dla ogromnej

ilości konfiguracji ciał, szczelin i obciążeń.

Przypomnijmy, że WIN można dla dowolnej

konfiguracji zapisać w postaci:

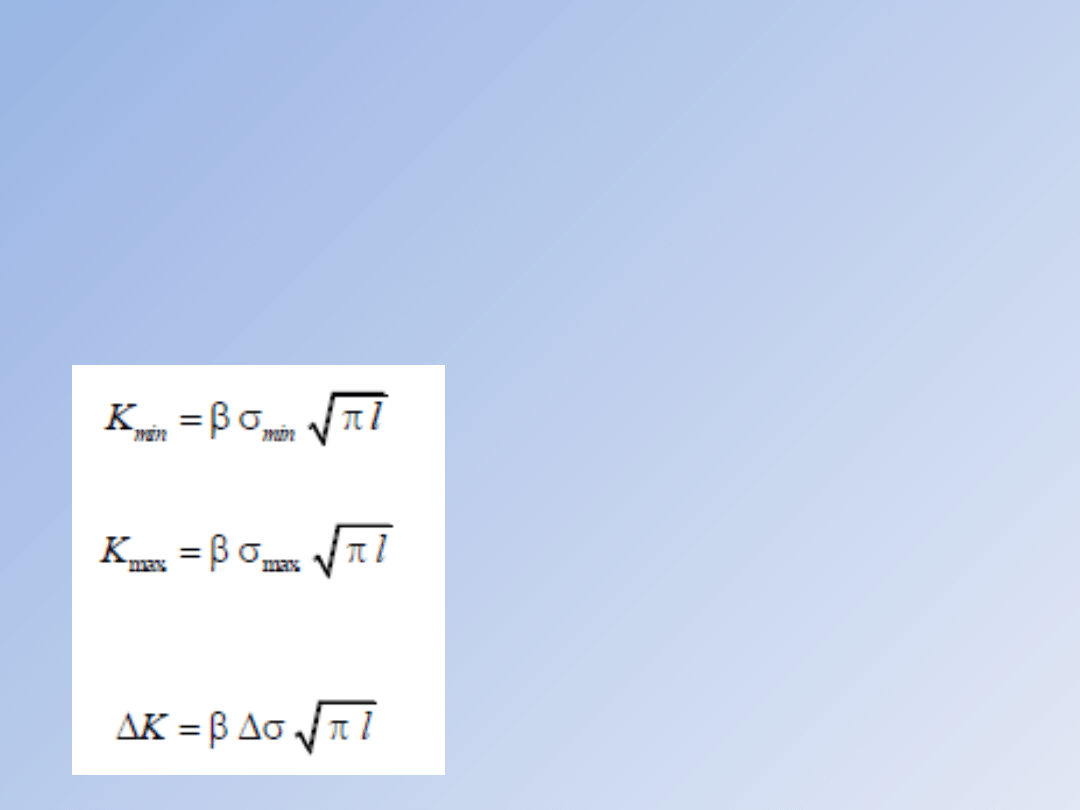
gdzie β jest współczynnikiem (liczbowym lub
funkcyjnym) związanym ze skończonymi wymiarami
ciała, zaś σ oznacza przyłożone obciążenie.
Wprowadzony poprzednio jako parametr sterujący
procesem zniszczenia zakres zmienności naprężenia
można zastąpić zakresem zmienności WIN.
Uwzględniając, że dla poszczególnego cyklu
określonego zmiennością naprężenia między σ min
a σ max zachodzą zależności:

zakres zmienności WIN wyraża się równaniem:

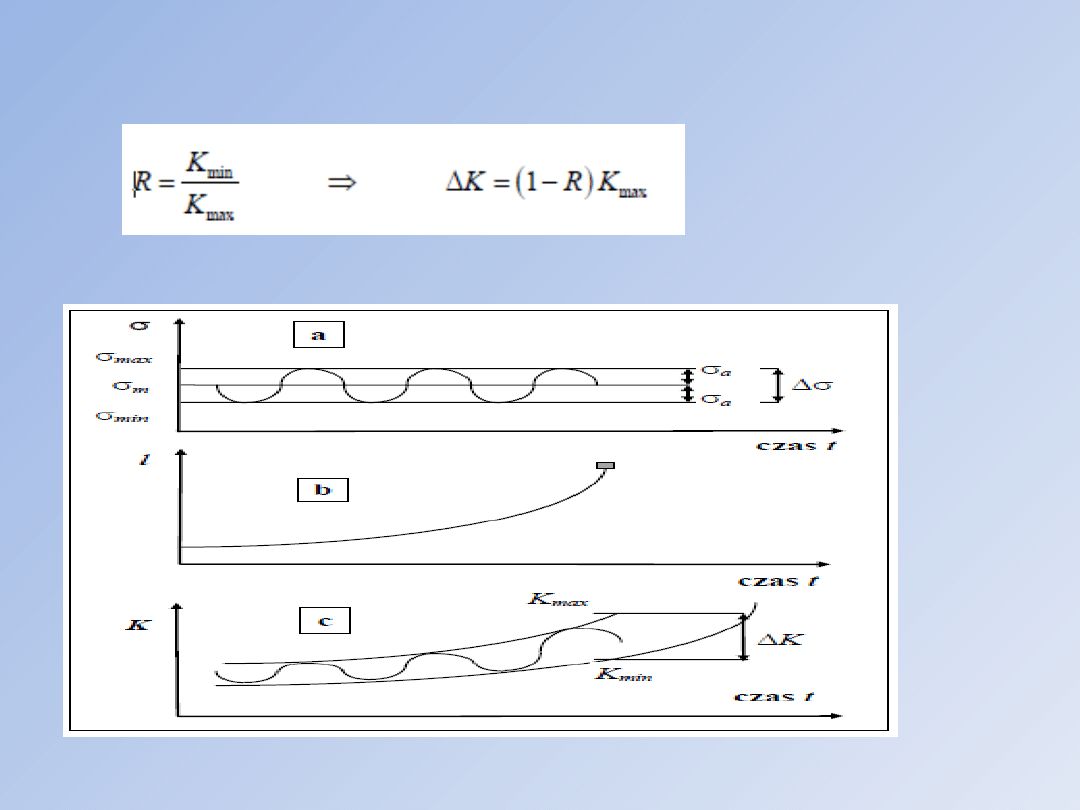
zaś współczynnik asymetrii cyklu R wynosi:

Interpretację geometryczną zakresu zmienności WIN pokazano
poniżej

Parametry stosowane w opisie wzrostu szczeliny zmęczeniowej: a) obciążenie zmienne, b) krzywa wzrostu szczeliny,
c) zakres zmienności współczynnika intensywności naprężeń

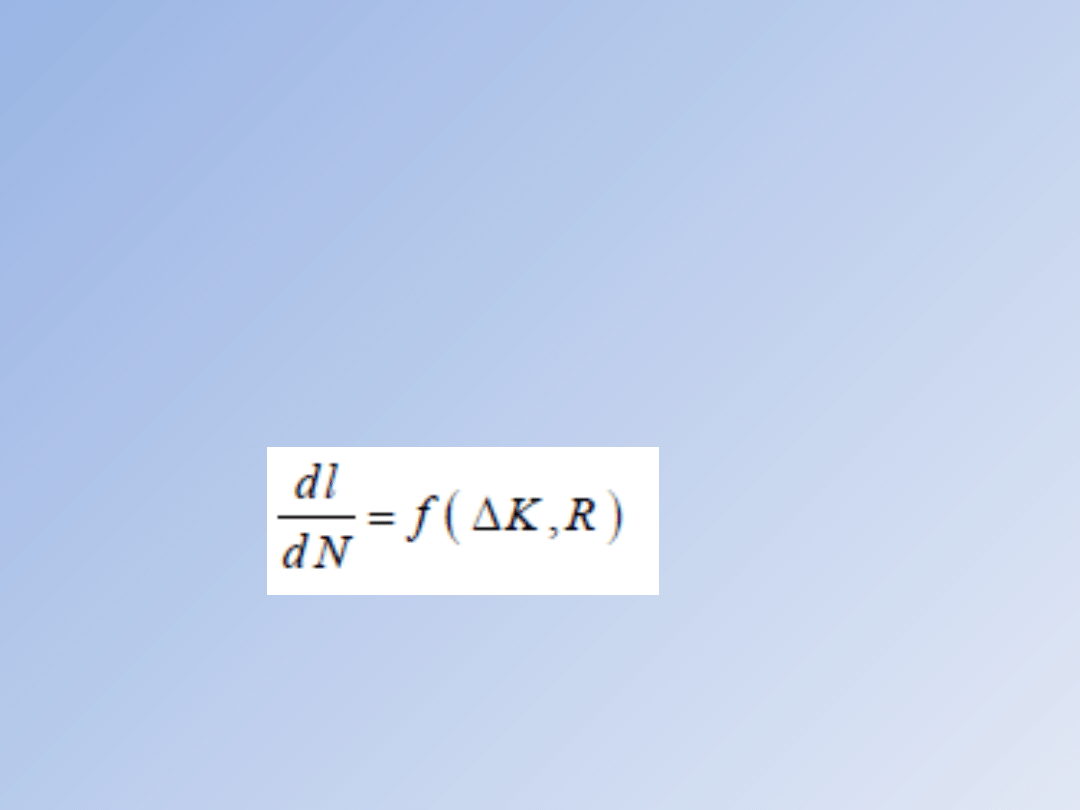
Prędkość propagacji szczeliny zmęczeniowej
definiuje się jako przyrost długości szczeliny
przypadający na jeden cykl - wyraża się ona
zatem pochodną dl / dN o wymiarze [mm/cykl].
Korzystając ze zdefiniowanych uprzednio
niezależnych parametrów sterujących
procesem zmęczenia równanie prędkości
propagacji szczeliny zmęczeniowej można
zapisać w postaci:

Można wykazać, że funkcja f jest funkcją rosnącą ze

względu na oba argumenty. Otwarte pozostaje

pytanie o postać tej funkcji. Należy wyraźnie

powiedzieć, że jak dotychczas nie udało się jej

znaleźć funkcji na drodze
teoretycznej. Jest to związane z zasadniczymi

trudnościami wynikającymi z konieczności

powiązania makroskopowych parametrów

propagacji szczeliny, tzn. DK i R, z mikroskopowymi

- zachodzącymi na poziomie płaszczyzn atomowych

procesami poślizgów, odpowiedzialnymi za

nieodwracalny wzrost szczeliny przy obciążeniu

zmęczeniowym. Pozostaje w tej sytuacji tylko droga

eksperymentalna, w oparciu o którą można pokusić

się o pewne uogólnienia prowadzące do czysto

empirycznych formuł opisujących funkcję o ogólnej

postaci wyrażonej równaniem.

W mechanice pękania do opisu wzrostu

szczelin zmęczeniowych przyjęło się
używać właśnie krzywą prędkości (a nie

krzywą wzrostu długości l(N)) choć nie
uzyskuje się jej wprost z doświadczenia,

ale poprzez przetworzenie krzywej
wzrostu. Poniżej przedstawione będą

podstawowe procedury służące

wyznaczeniu obu krzywych.

Krzywą wzrostu szczeliny zmęczeniowej uzyskuje się

podczas próby
zmęczeniowej przeprowadzonej na dowolnej próbce o

znanej wartości
współczynnika b. Z reguły jest to próbka w kształcie

płaskiej tarczy prostokątnej z krótką, ostro zakończoną

szczeliną centralną lub próbka kompaktowa. Obciążenie

zewnętrzne jest przeważnie sinusoidalnie zmienne o

stałej amplitudzie i częstotliwości. W trakcie testu

rejestrowana jest bieżąca długość szczeliny w funkcji

liczby cykli obciążenia Jest to cała informacja uzyskiwana

doświadczalnie i dopiero jej przetworzenie pozwala

określić funkcję. Procedurę tę prześledzimy na

przykładzie, który dotyczy próbki ze szczeliną centralną,

poddanej obciążeniu tętniącemu o stałej amplitudzie.

Parametry typowej próby zmęczeniowej: a) próbka testowa, b) obciążenie tętniące

Równania prędkości propagacji

szczeliny zmęczeniowej

Wszystkie te równania są czysto empirycznymi i
wynikają wyłącznie z procedur matematycznych
dopasowujących linię ciągłą o równaniu
analitycznym do dyskretnych wyników pomiarów
(z reguły wykorzystywana jest metoda
najmniejszych kwadratów). Zajmijmy się najpierw
II, liniową fazą na wykresie log (dl/dN) vs. log DK.
Dla określonego jednego współczynnika asymetrii
cyklu R, korzystając z ogólnego równania prostej
y=mp x +b, gdzie y = log(dl /dN); x = log (DK)
możemy równanie tej prostej zapisać w postaci:

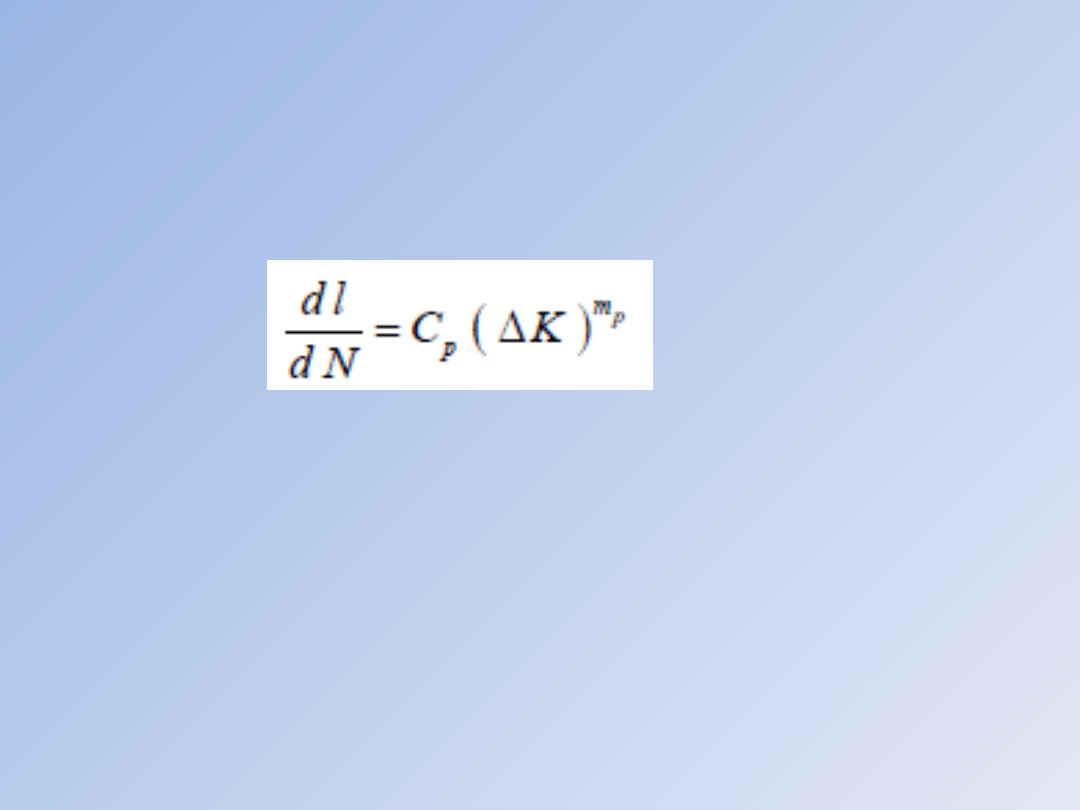
Uwzględniając własności funkcji
logarytmicznej, po prostych
przekształceniach otrzymamy
równanie w postaci:

Równanie zostało wprowadzone do literatury wspólnie przez Parisa i
Erdogana, ale znane jest powszechnie pod nazwą „równanie Parisa”. Stałe
mp i Cp wyznacza się z danych doświadczalnych - wystarcza oczywiście
znajomość dwóch punktów (DK, dl/dN ), ale lepsze efekty daje
wyznaczenie stałych z większej ilości punktów pomiarowych. Stała mp
zawiera się dla większości materiałów w zakresie 3÷5, stała Cp silniej
zależy od materiału, a co więcej zależy od jednostek w jakich prowadzone
są obliczenia. Orientacyjne wartości tych stałych dla niektórych
materiałów zestawiono w tab. Dane dotyczą cyklu o współczynniku
asymetrii R=0; prędkość propagacji szczeliny dl/dN wyrażona jest w
mm/cykl, zaś zakres zmienności DK w MPa m1/2.

Istnieją proste wzory empiryczne dla określonych
klas materiałów, które wiążą stałe m i C w równaniu
Parisa z wartościami granicy plastyczności Re i
wytrzymałości na rozciąganie Rm. Pozwalają one
określić choćby szacunkowo m i C, w przypadku gdy
zachodzi konieczność wykonania obliczeń
zmęczeniowych, a brak jest danych
doświadczalnych dotyczących materiału. Do tej
kategorii należą np. relacje odnoszące się do dużej
grupy stali, zaproponowane przez Takashimę - mają
one następujące postaci:

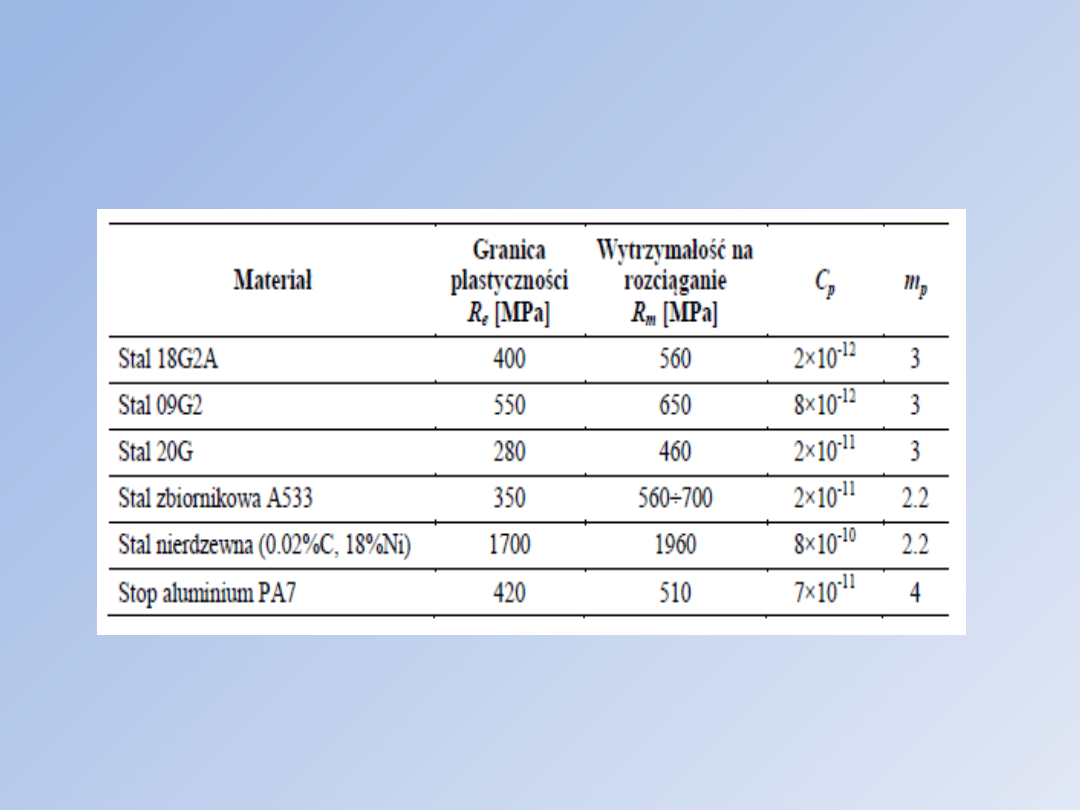
Tab. Orientacyjne wartości stałych w
równania Parisa

Rombari określił równanie, które dość precyzyjnie pozwala określić stałą
C dla
większości stali w oparciu o znaną wartość stałej m - odpowiednia
zależność ma
postać:

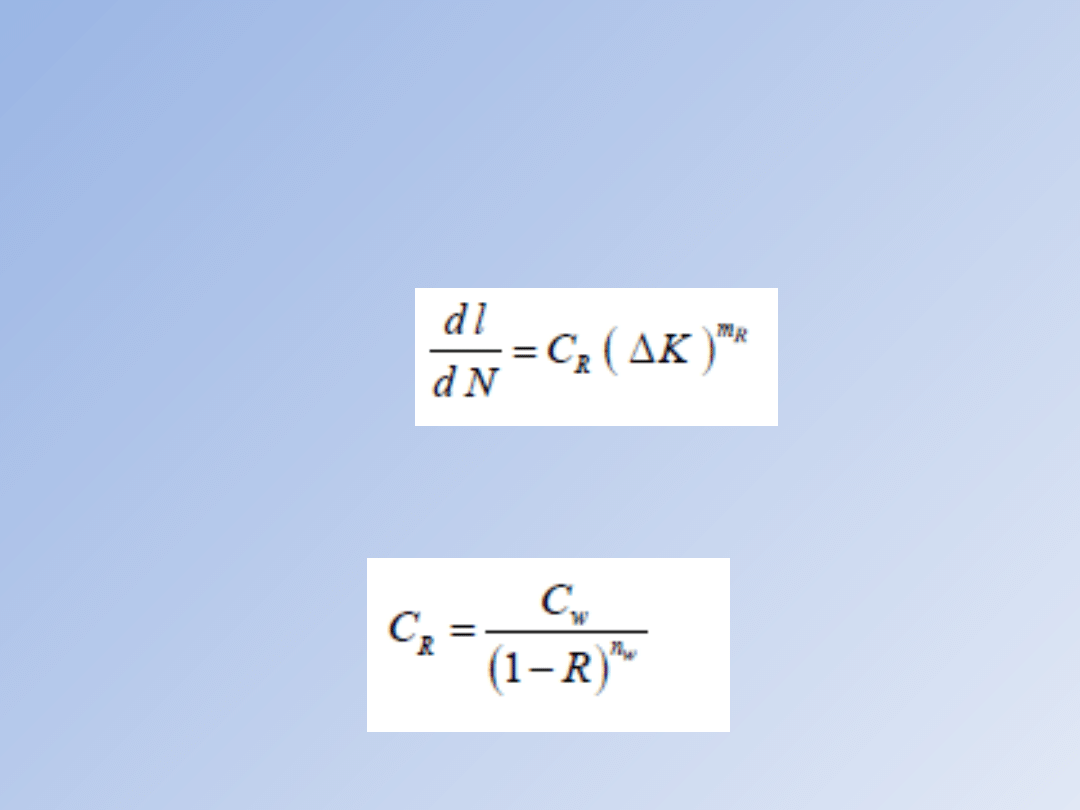
Równanie prawdziwe jest w przedziale mÎ<5, 11> oraz RÎ<0, 0.5>, przy
czym zakres zmienności DK wyrażony jest w [N mm-3/2]. Jak
wspomniano wcześniej, wykresy prędkości propagacji szczeliny dla
różnych wartości R są równoległe w liniowym ich zakresie - muszą
zatem mieć identyczne współczynniki nachylenia, czyli zarazem m, a
różne współczynniki przesunięcia, czyli C. Wynika stąd, że uogólnieniem
równania Parisa w postaci jest równanie:

Dla wielu materiałów zależność CR można z wystarczającą
dokładnością opisać
równaniem w postaci:

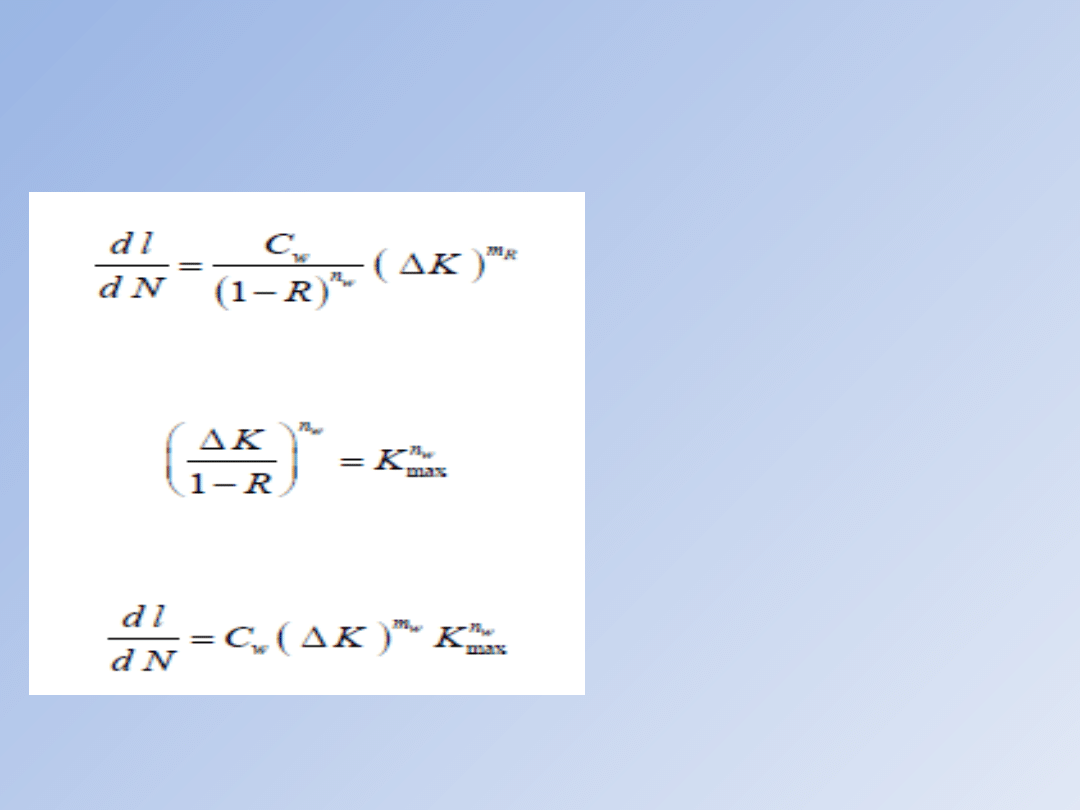
Stała Cw jest równa stałej CR dla testu o współczynniku asymetrii
R=0. Po wstawieniu otrzymujemy równanie prędkości szczeliny w
postaci:

Korzystając w równania można dokonać następującego
podstawienia:

a po dalszych przekształceniach można otrzymać
zamiast równanie:

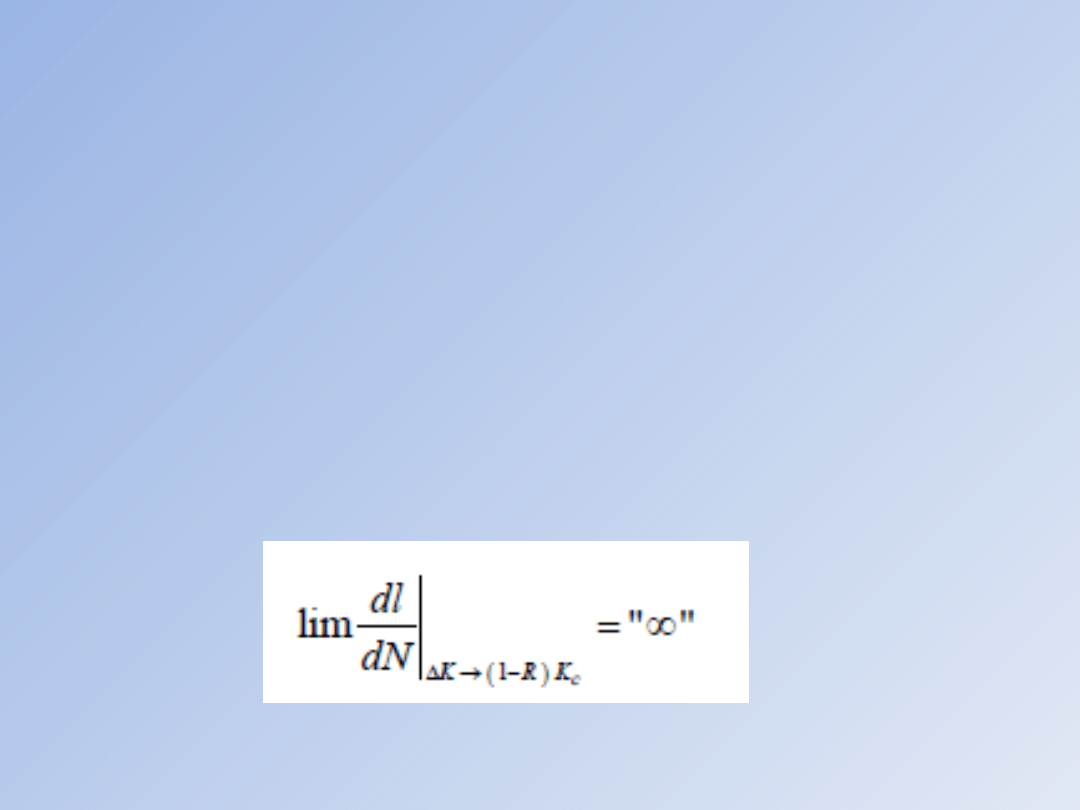
gdzie mw=mR-nw. Równanie nosi nazwę
równania Walkera. Sposób wyznaczania
stałych w tym równaniu. Zarówno równanie
Parisa, jak i jego proste rozwinięcie - równanie
Walkera odnoszą się wyłącznie do liniowego
zakresu wykresu log(dl/dN ) vs. log Δ K. Z
myślą o opisie nieliniowej, III fazy tego
wykresu, charakteryzującej się tym, że dla Δ K
= ΔKc = Kc (1-R) prędkość wzrostu szczeliny
zmierza do wartości nieskończenie dużej, tzn.:

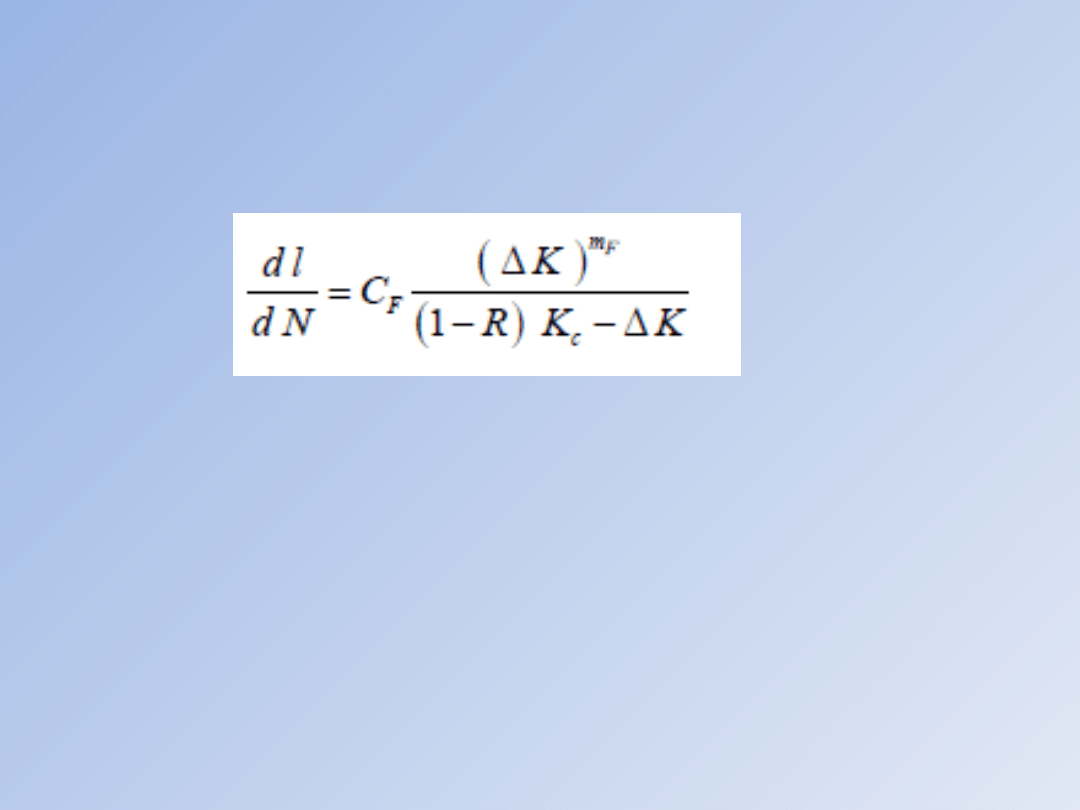
Forman i in. zaproponowali następującą adaptację

równania Parisa:

Wielkość Kc oznacza odporność na pękanie w

konkretnych warunkach obciążenia. W przypadku

braku odpowiednich danych należy wykorzystać

KIc,
pamiętając o zgłoszonych wcześniej

zastrzeżeniach co do poprawności takiego

postępowania. Równanie Formana pozwala

wyznaczyć prędkość wzrostu pęknięcia przy

dowolnym współczynniku asymetrii cyklu R.

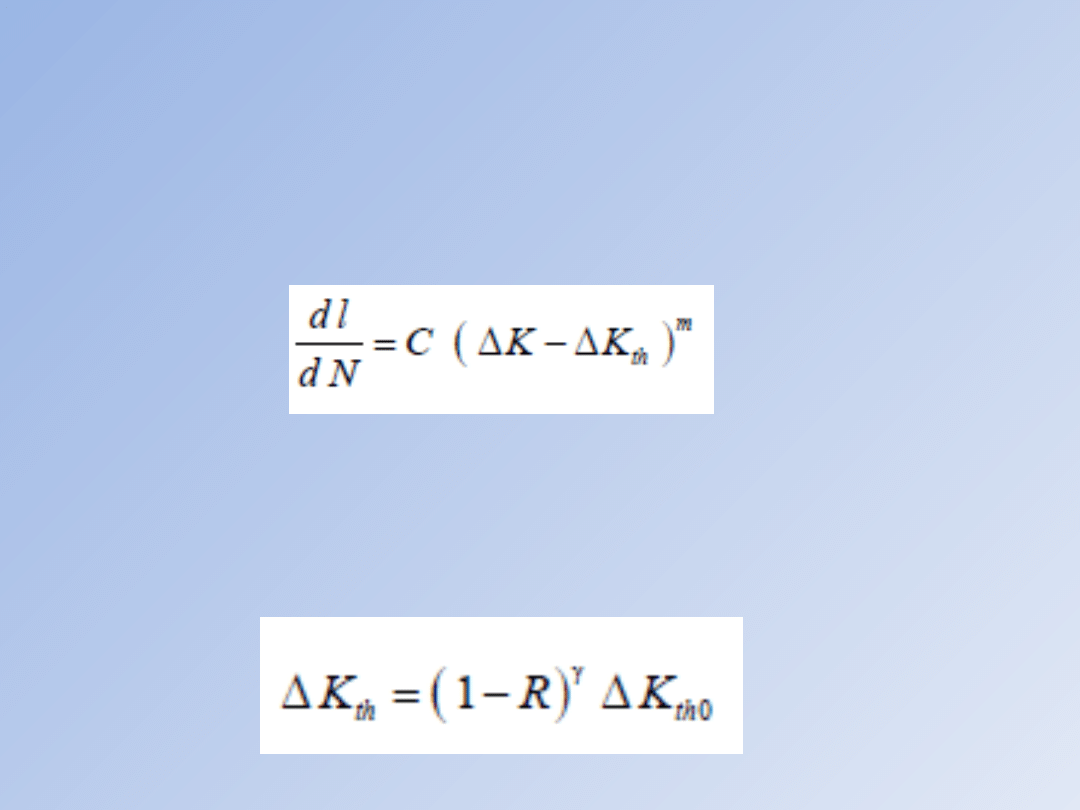
Duża grupa równań dotyczy początkowej fazy na
krzywej prędkości propagacji szczeliny. Wszystkie one
zawierają jako jeden z parametrów wartość progową
zakresu zmienności współczynnika intensywności
naprężeń Δ Kth. Donahue i in. zaproponowali relację:

Kluczowe znaczenie dla możliwości wykorzystania
tego równania ma znajomość wartości progowej Δ Kth
. Spośród bardzo dużej ilości propozycji wybierzmy te,
które stosowane są najczęściej. Należy do nich wzór
Klesnila i Lukaša w postaci:

gdzie Δ Kth0 to wartość progowa dla cyklu charakteryzującego się
współczynnikiem
R=0, zaśγjest parametrem materiałowym, zawierającym się w
zakresie 0.5÷1.0.
Za relacje dające dobre oszacowanie wartości progowej dla różnych
gatunków
stali i współczynnika asymetrii R=0 uważa się wzory
zaproponowane przez
Vosikovsky’ego, wiążące Δ Kth z granicą plastyczności Re i
wytrzymałością na
rozciąganie Rm . Mają one następujące postaci:

W przypadku cykli o współczynniku R =/=0 można korzystać z równania:

gdzie:

Bardzo dobre równanie opisujące wartość progową dla stopów
aluminium podał
Mackay, ma ono postać:

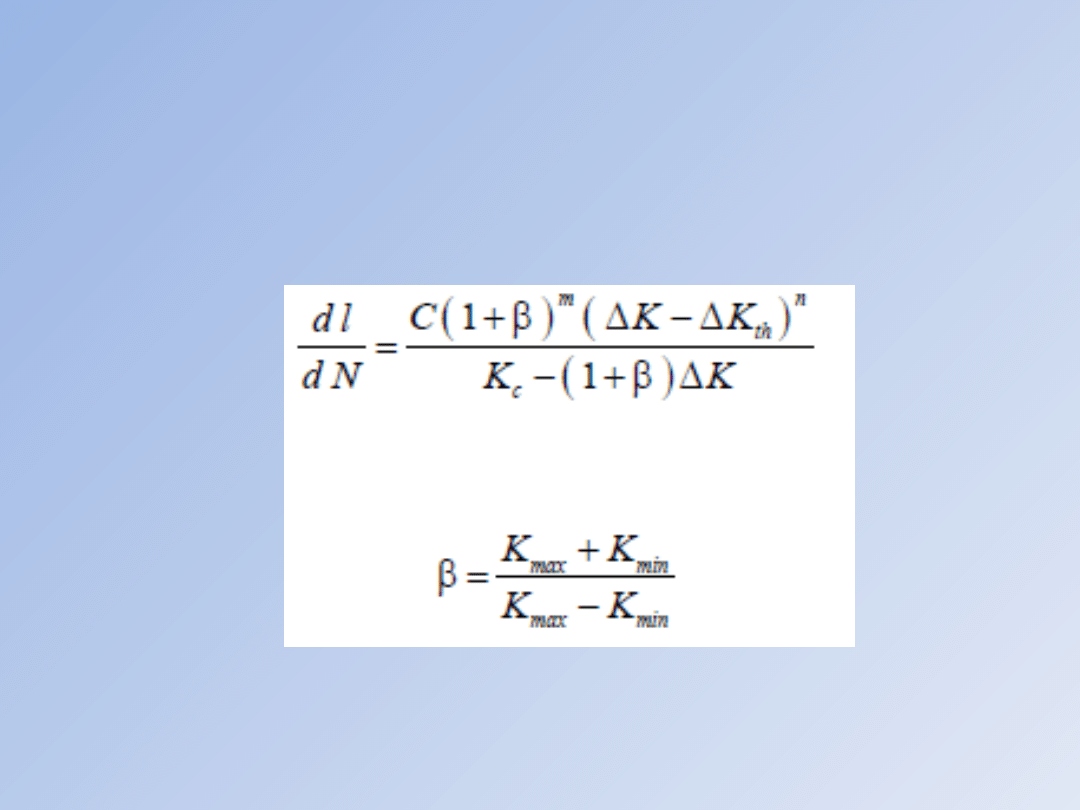
Szerszą prezentację propozycji dotyczących wyznaczania ΔKth
można znaleźć
w. Na zakończenie wspomnijmy jeszcze o tzw. uogólnionym
prawie propagacji
szczeliny zmęczeniowej, które pozwala opisać
charakterystyczny kształt krzywej
pokazanej na Rys. w całym jej zakresie. Zgodnie z propozycją
Erdogana i
Ratwani’ego prędkość propagacji szczeliny wyraża się
równaniem:

gdzie:

Zaś C, m i n są stałymi materiałowymi, które należy

wyznaczyć z danych doświadczalnych. Czynnik (1+β)m

uwzględnia wpływ naprężenia średniego i amplitudy
naprężenia (patrz Tab.) na propagację szczeliny

zmęczeniowej, czynnik [Kc-(1+β)ΔK] bierze pod uwagę

dane eksperymentalne dotyczące prędkości przy
wysokich poziomach naprężenia, zaś czynnik (ΔK –

ΔKth)n odpowiedzialny jest za opis pierwszej I fazy

wzrostu szczeliny po przekroczeniu wartości progowej

ΔKth .
Równanie dobrze pasujedo wyników doświadczalnych w

zakresie prędkości 2.5×10-7÷2.5×10-1 mm/cykl.

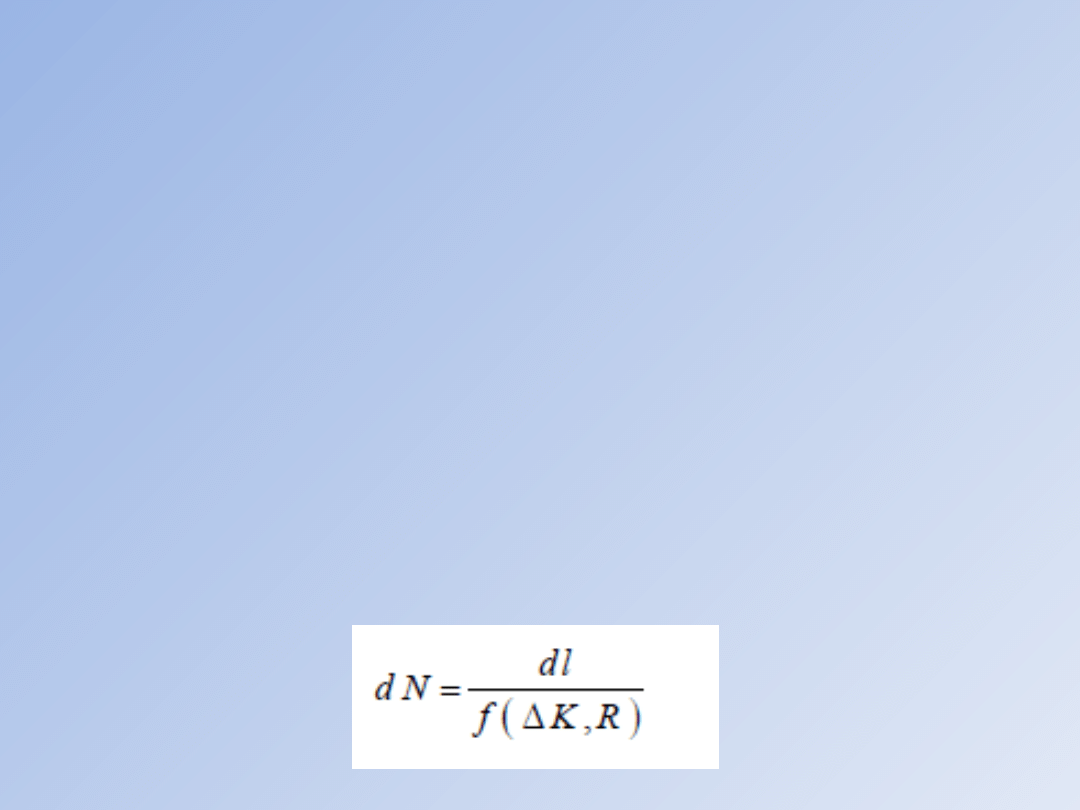
Czas życia elementu ze

szczeliną zmęczeniową

Powiedziano już uprzednio, że celem analizy zagadnienia
wzrostu szczelin zmęczeniowych jest wyznaczenie
krzywej propagacji szczeliny oraz określenie liczby cykli,
po której dochodzi do zniszczenia elementu. Liczba ta,
oznaczona symbolem Nf określa tzw. czas życia
elementu ze szczeliną zmęczeniową. przypadku
omawianych tu obciążeń cyklicznych o stałej amplitudzie
czas życia można wyznaczyć stosunkowo prosto, pod
warunkiem, że znane są parametry obciążenia oraz
postać współczynnika intensywności naprężeń, a w
zasadzie współczynnika skończonych wymiarów ciała b -
z reguły określonego funkcyjnie lub tabelarycznie. Z
równania tego wynika relacja:

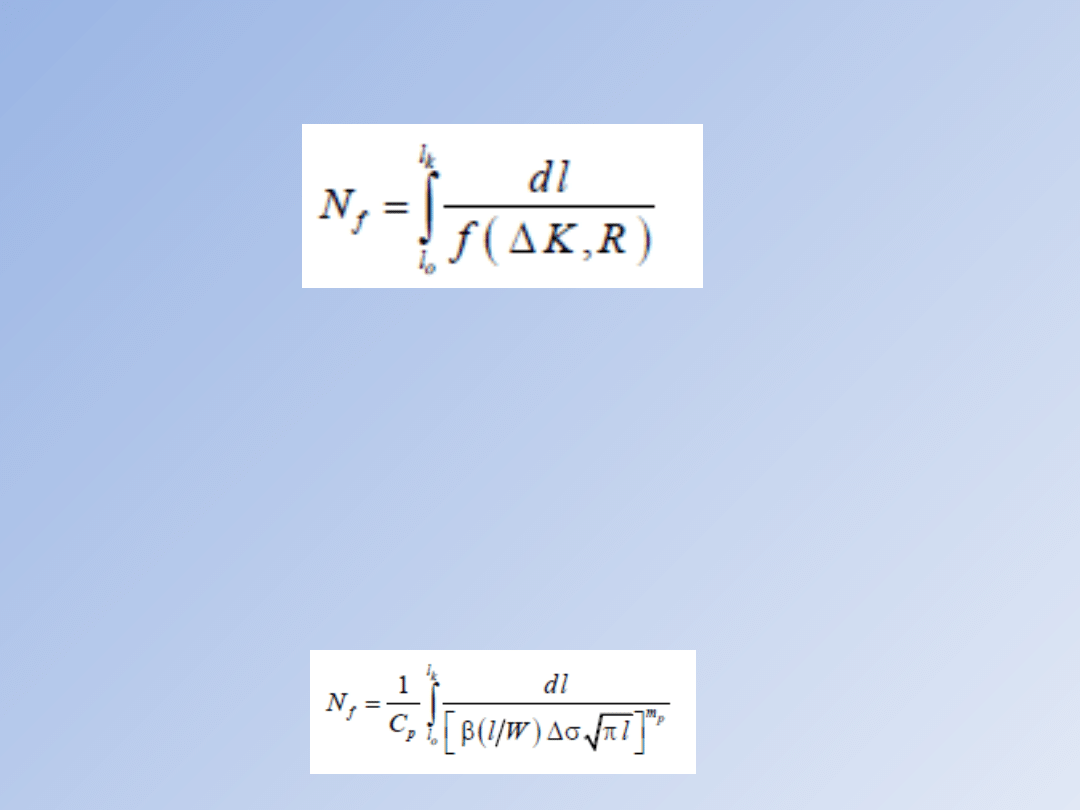
Stąd, po scałkowaniu otrzymuje się liczbę cykli do zniszczenia lub liczbę
określoną wymaganiami kontrolnymi w postaci:

gdzie: lo oznacza założoną lub stwierdzoną w elemencie długość
początkową
szczeliny, a lk długość końcową szczeliny, często utożsamianą z
długością
krytyczną lkr wyznaczaną w oparciu o jedno z kryteriów pękania.
Biorąc pod uwagę, że funkcje f(ΔK, R) mogą mieć dość kłopotliwe
obliczeniowo postacie, a także to, że tę samą uwagę można odnieść
do
współczynnika β, należy mieć świadomość występujących przy
wyznaczaniu Nf
trudności rachunkowych - z reguły konieczne jest zastosowanie
procedur
całkowania numerycznego. Stosują stosunkowo najprostsze równanie
Parisa,
z równania po uwzględnieniu, otrzymujemy:

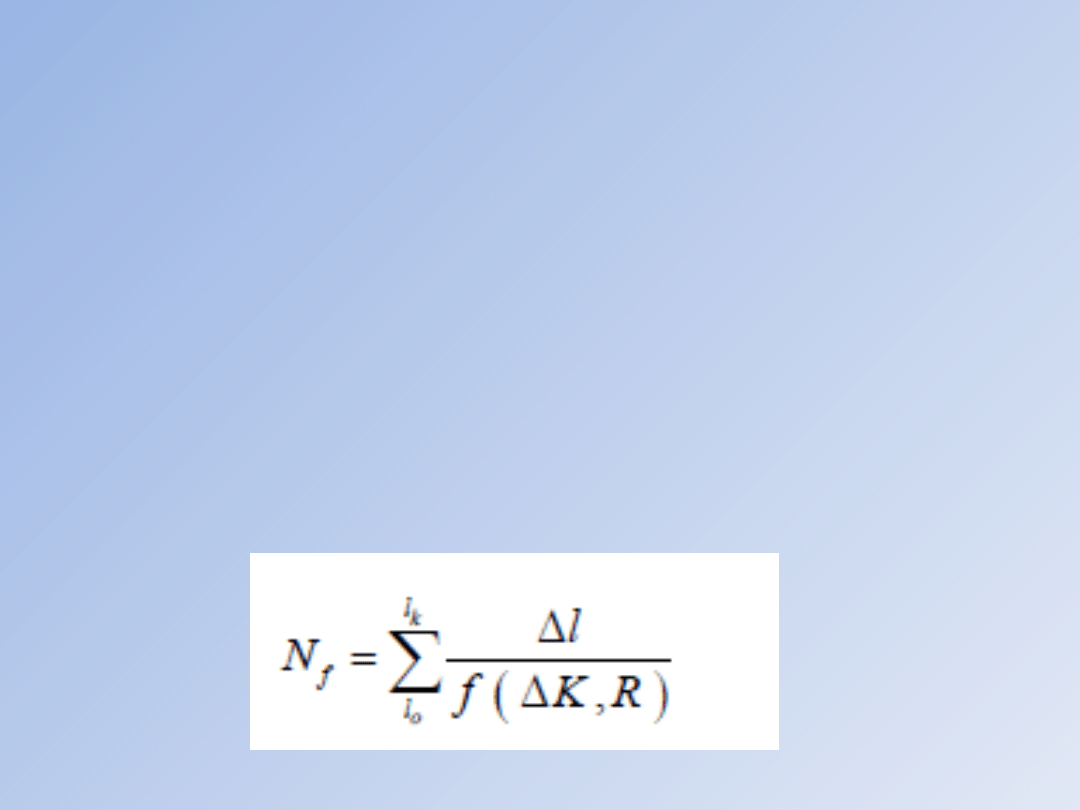
Nawet w tak elementarnym przypadku, jak

obciążenie cykliczne o stałej amplitudzie Δσ

(niezależnej od długości szczeliny) działające na

pasmo prostokątne o skończonych wymiarach ze

szczeliną centralną obliczenia w myśl równania

muszą być wykonywane numerycznie. Decyduje o

tym wielomianowa postać współczynnika β = β

(l/W). W przypadku konieczności wykonania

szybkich obliczeń, w warunkach braku

natychmiastowego dostępu do mikrokomputera z

odpowiednim oprogramowaniem, można zamiast

wzoru całkowego wykorzystać wzór przybliżony w

postaci:

Powiedzmy jednak wyraźnie -
przedstawiony tu szczegółowo przypadek
obciążeń cyklicznych o stałej
amplitudzie, jakkolwiek ważny z
praktycznego punktu widzenia,
występuje w pracy konstrukcji
inżynierskich rzadziej niż przypadek
obciążeń zmiennych o amplitudzie
zmiennej. Przypadek ten będzie
przedstawiony w poniżej

SZCZELINA ZMĘCZENIOWA PRZY

OBCIĄŻENIU

CYKLICZNYM O ZMIENNEJ AMPLITUDZIE

Przypadek obciążeń cyklicznych, w których amplituda zmienia się w pewien
określony sposób, lub też zmiany te są losowe, jest przypadkiem o dużym
znaczeniu praktycznym, gdyż takim obciążeniom podlega wiele konstrukcji, od
których wymaga się absolutnej niezawodności. Można w tym kontekście

wymienić choćby konstrukcje lotnicze, narażone przede wszystkim właśnie na

obciążenia zmęczeniowe (wibracje od silników, drgania skrzydeł itd.). Z punktu

widzenia analizy teoretycznej zagadnienie to jest znacznie bardziej złożone od

problemu zniszczenia zmęczeniowego przy stałej amplitudzie - to sprawia, że

liczba relacji opisujących to zagadnienie ilościowo, jest nieporównywalnie

mniejsza niż w tym drugim przypadku.
Doświadczenia prowadzone jeszcze w latach sześćdziesiątych wykazały, że
nawet pojedynczy cykl przeciążający (nazwijmy go popularnie „pikiem”)
występujący w obciążeniu cyklicznym o stałej amplitudzie całkowicie zmienia
przebieg krzywej l=l(N). Każdy cykl przeciążający w dowolnym widmie
(programie) obciążenia powoduje opóźnienie (niekiedy nawet zatrzymanie)
wzrostu szczeliny, w tym sensie, że prędkość wzrostu szczeliny po każdym

cyklu przeciążającym jest mniejsza niżby była dla cyklu o stałej amplitudzie.

Pokazano to na rysunku zaczerpniętym z pracy, który przedstawia
schematycznie kolejne etapy wpływu przeciążenia o wartości s2

występującego w cyklu podstawowym o amplitudzie s1 na przyrost

długości szczeliny zmęczeniowej oraz prędkość jej propagacji

Symbol Nd oznacza ten okres wzrostu szczeliny (wyrażony liczbą

cykli), w którym utrzymuje się wpływ efektu przeciążenia na

zachowanie szczeliny wywołane cyklem podstawowym. W

przypadku cykli o przeciążeniu zarówno dodatnim (rozciąganie),

jak i ujemnym (ściskanie) zjawisko opóźnienia wzrostu pęknięcia

również jest obserwowane, choć w znacznie mniejszym stopniu.

Chcąc wyjaśnić mechanizm powstawania efektu opóźnienia należy

odwołać się do analizy obszaru leżącego przed czołem

(wierzchołkiem) szczeliny. Nagłemu wzrostowi naprężenia w cyklu

przeciążającym towarzyszy powstanie przed czołem szczeliny

dużej strefy plastycznej (strefa umocnienia plastycznego). Po

odciążeniu, sprężysty materiał otaczający tę strefę staje się swego

rodzaju klamrą, powodującą powstanie w strefie plastycznej

naprężeń własnych, ściskających. Podrastająca szczelina

przekraczając granicę strefy plastycznej narażona jest na działanie

tych naprężeń ściskających - ich skutkiem jest efekt zamykania się

powierzchni szczeliny. Prędkość wzrostu szczeliny ulega zatem po

jej wejściu w strefę plastyczną zmniejszeniu - mówimy wtedy o

efekcie opóźnienia. Po opuszczeniu strefy plastycznej szczelina

ponownie się otwiera i kolejne stałe cykle obciążenia wywołują

dalszy jej wzrost.

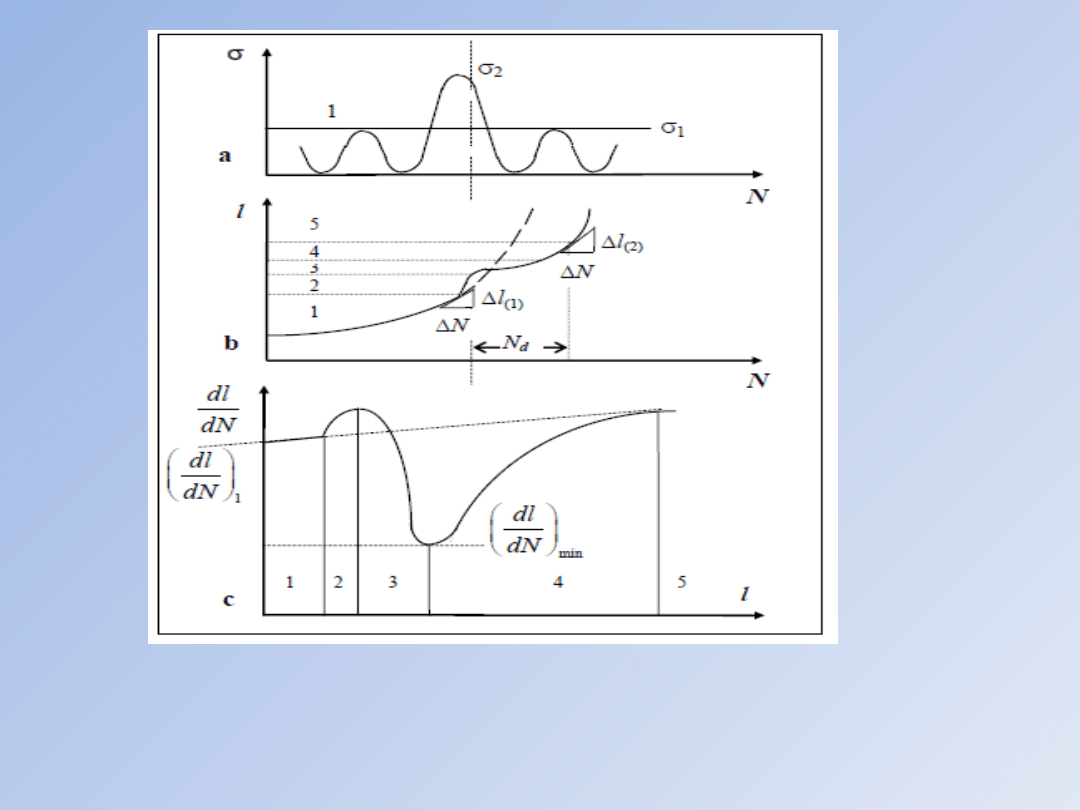
Efekt pojedynczego cyklu przeciążającego: a) naprężenie, b) krzywa wzrostu
szczeliny, c) krzywa prędkości szczeliny

Istnienie efektu opóźnienia sprawia, że wyznaczenie

czasu życia elementu konstrukcyjnego ze szczeliną,

poddanego działaniu obciążenia cyklicznego o zmiennej

amplitudzie, w oparciu o prostą procedurę polegającą na

podzieleniu widma obciążenia na sekwencje o stałej

amplitudzie, obliczeniu czasu życia elementu dla każdej

z sekwencji, a wreszcie zsumowaniu tych cząstkowych

czasów - a zatem procedury pomijającej efekt

opóźnienia - prowadzi do dolnego oszacowania

rzeczywistego okresu życia, który jest większy. Z punktu

widzenia bezpieczeństwa jest to korzystne, ale zarazem

niedoszacowanie okresu życia może być tak duże, że aż

trudne do zaakceptowania, szczególnie wówczas, gdy w

oparciu tak uzyskany wynik następuje wyłączenie

konstrukcji z eksploatacji, co wiąże się ze stratami

finansowymi. Spośród wielu modeli ilościowych

pomyślanych do obliczeń czasu życia elementów przy

obciążeniach cyklicznych o zmiennych amplitudach

wymieńmy tutaj dwa - oba chętnie i często stosowane,

przede wszystkim ze względu na swoją prostotę.

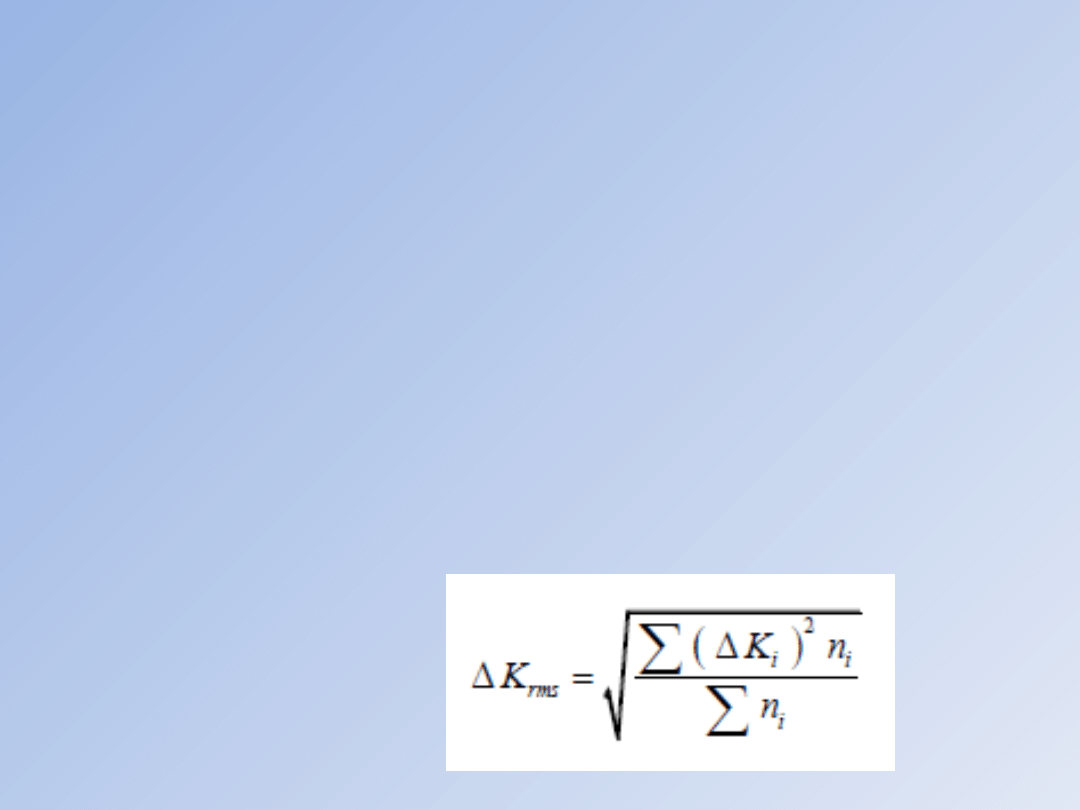
Pierwszy z nich to model zaproponowany przez

Barsoma. Może on być stosowany dla obciążeń, w

których widmie losowe przeciążenia występują często i

mieszczą się w dość wąskim paśmie zmienności. W

modelu tym przyjmuje się, że średnia prędkość wzrostu

szczeliny zmęczeniowej przy losowo zmieniającym się

obciążeniu o zmiennej amplitudzie jest w przybliżeniu

równa prędkości wzrostu szczeliny zmęczeniowej przy

obciążeniu o stałej amplitudzie. Istota modelu

sprowadza się do tego, że prędkość wzrostu pęknięcia

można nadal opisywać przy pomocy równań dla cyklu o

stałej amplitudzie - po zastąpieniu zakresu zmienności

współczynnika intensywności naprężeń ΔK tzw.

wartością skuteczną tego współczynnika ΔKrms (ang.

root-meansquare value) określoną równaniem w

postaci:

gdzie: ni oznacza liczbę amplitud obciążenia,
którym odpowiadają zakresy Dki współczynnika
intensywności naprężeń. Drugim z modeli, który
zostanie krótko omówiony jest model Wheelera,
odwołujący się bezpośrednio do mechanizmu
odpowiedzialnego za powstawanie efektu
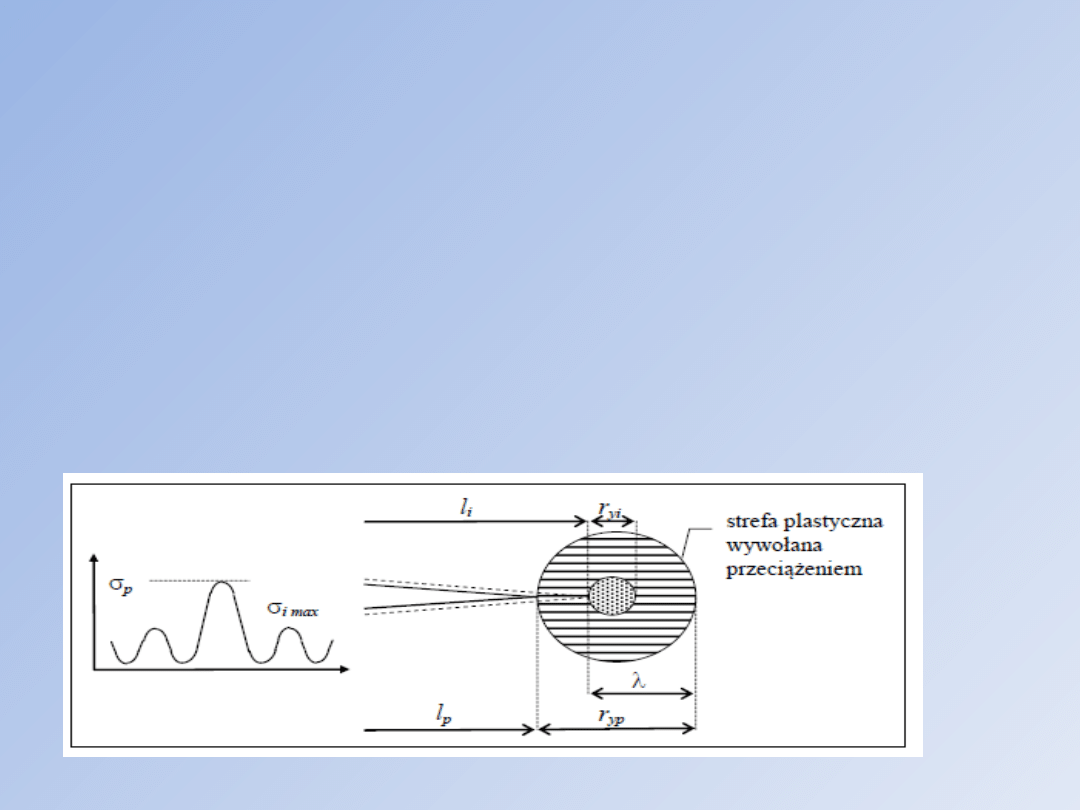
opóźnienia. Symbole użyte oznaczają: lp - długość
szczeliny w momencie przeciążenia, ryp - długość
strefy plastycznej odpowiadającej szczelinie lp, li -
długość szczeliny po przeciążeniu, ryidługość strefy
plastycznej towarzyszącej szczelinie li i obciążeniu
podstawowemu po wystąpieniu przeciążenia.

Model Wheelera opóźnienia wzrostu szczeliny zmęczeniowej.

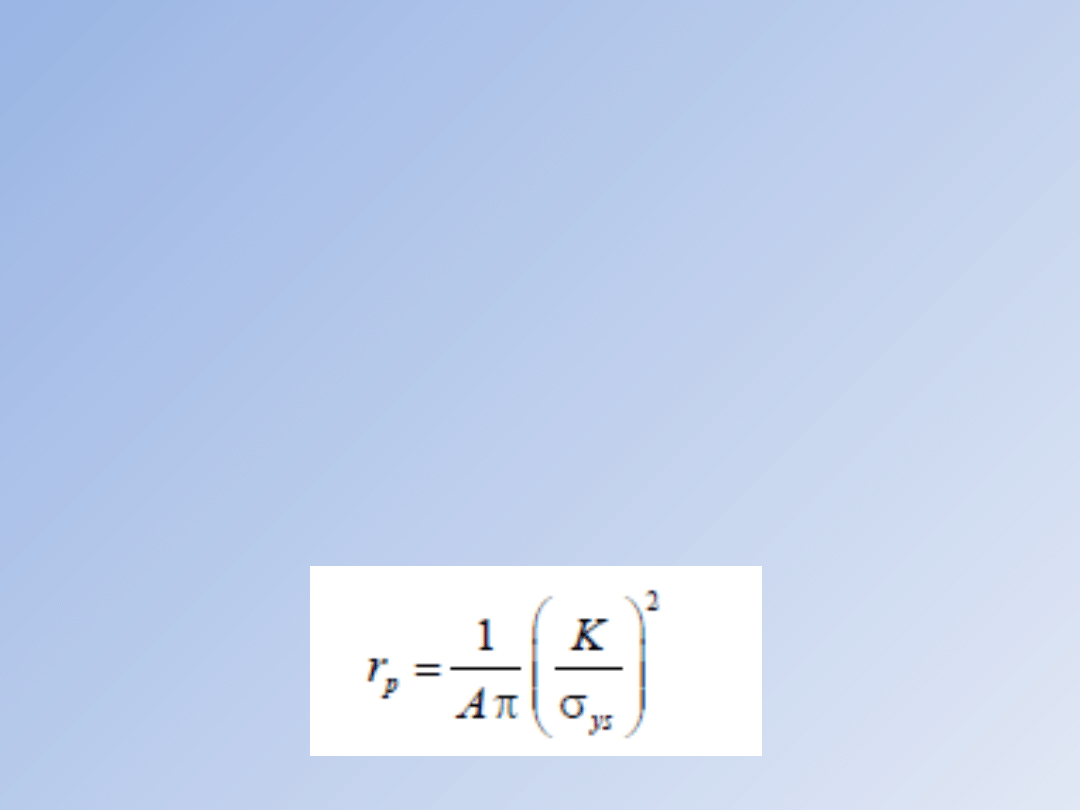
Idea tego modelu opiera się na założeniu, że cykl

przeciążenia powoduje powstanie strefy

plastycznej o takiej wielkości, że strefy

plastyczne opowiadające kolejnym cyklom

podstawowym są od niej mniejsze. Oznacza to,

że ruch szczeliny zostanie przyhamowany -

„opóźniony” - gdyż musi się ona „przebić” przez

obszar umocniony plastycznie. Załóżmy, że w

chwili, gdy długość szczeliny wynosi lp następuje

cykl przeciążający o wielkości σp, w wyniku

którego tworzy się strefa plastyczna o długości

ryp. Miarodajne oszacowanie strefy plastycznej

daje związek - oparty na modelu Irwina - który

można zapisać w postaci:

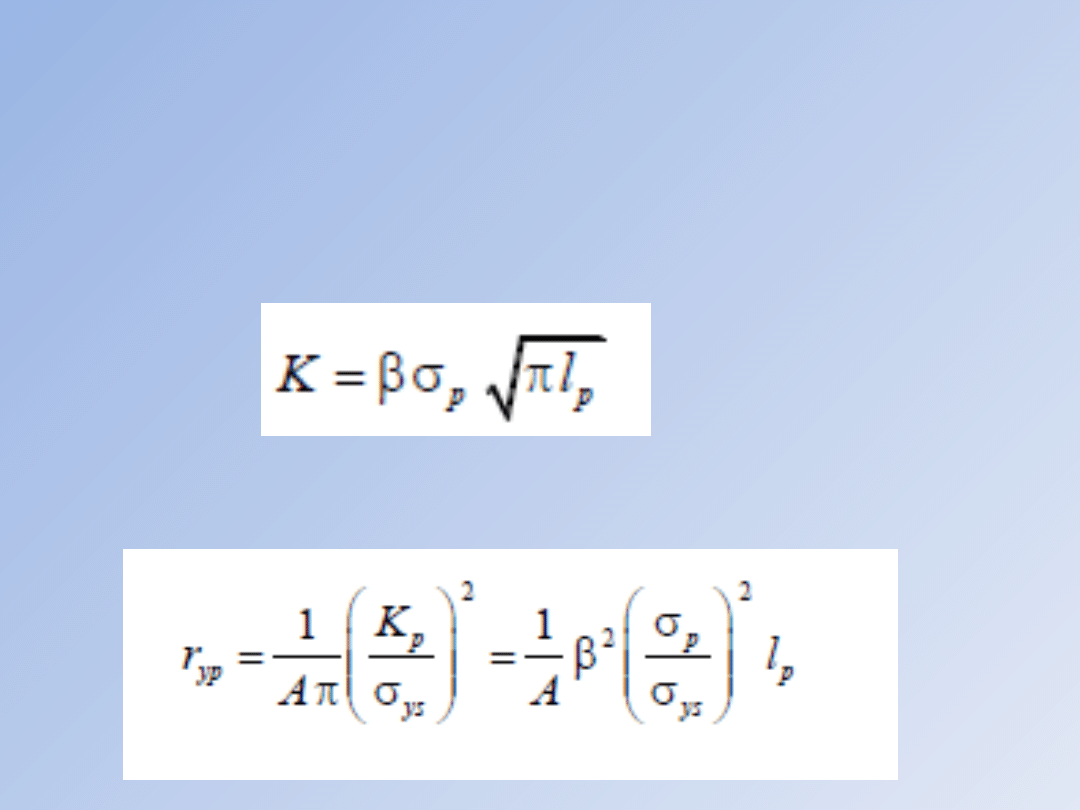
gdzie: σys przyjmuje się jako równe granicy
plastyczności, zaś A jest współczynnikiem
wynoszącym A=1 dla płaskiego stanu
naprężenia i A=3 dla płaskiego stanu
odkształcenia. Uwzględniając, że
współczynnik intensywności naprężeń ma
dla opisanej sytuacji postać:

długość strefy plastycznej przy przeciążeniu
wynosi:

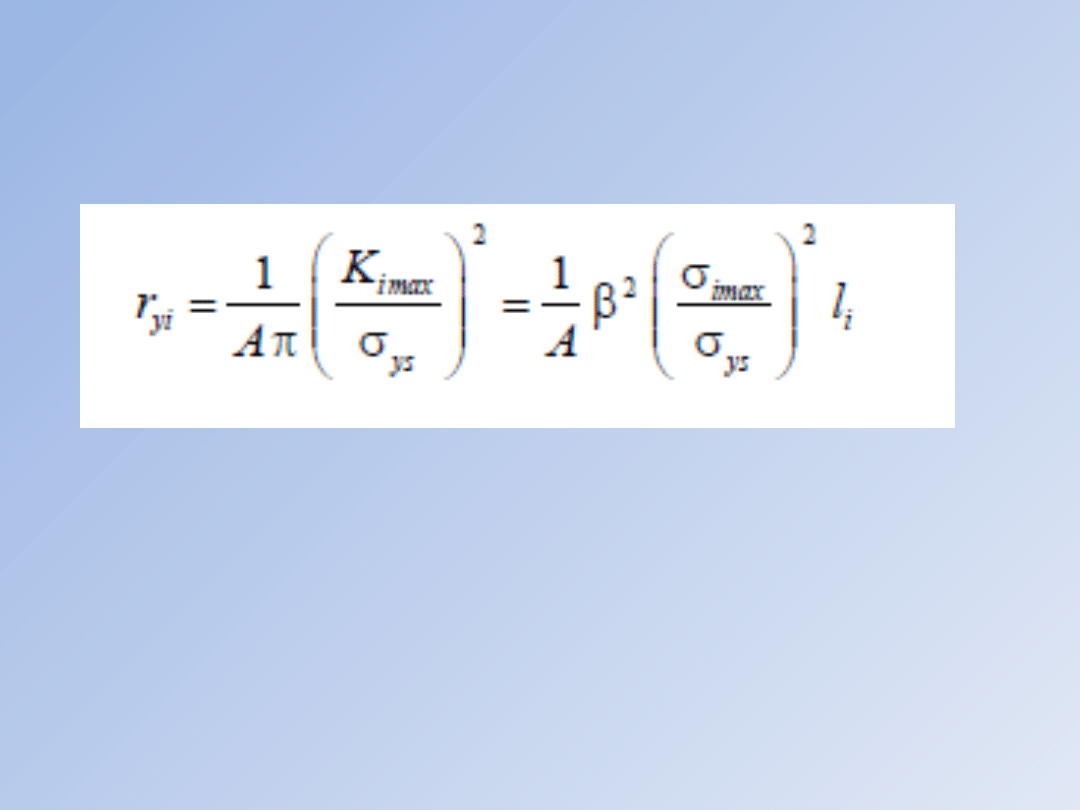
Gdy szczelina powiększy swoją długość do wartości li ,
aktualna długość strefy plastycznej będzie miała
długość:

gdzie: σimax jest maksymalnym naprężeniem w i -
tym cyklu.
Aktualna strefa plastyczna zawiera się w strefie
wywołanej przeciążeniem, która rozciąga się na
odległość λ od wierzchołka aktualnej szczeliny li.

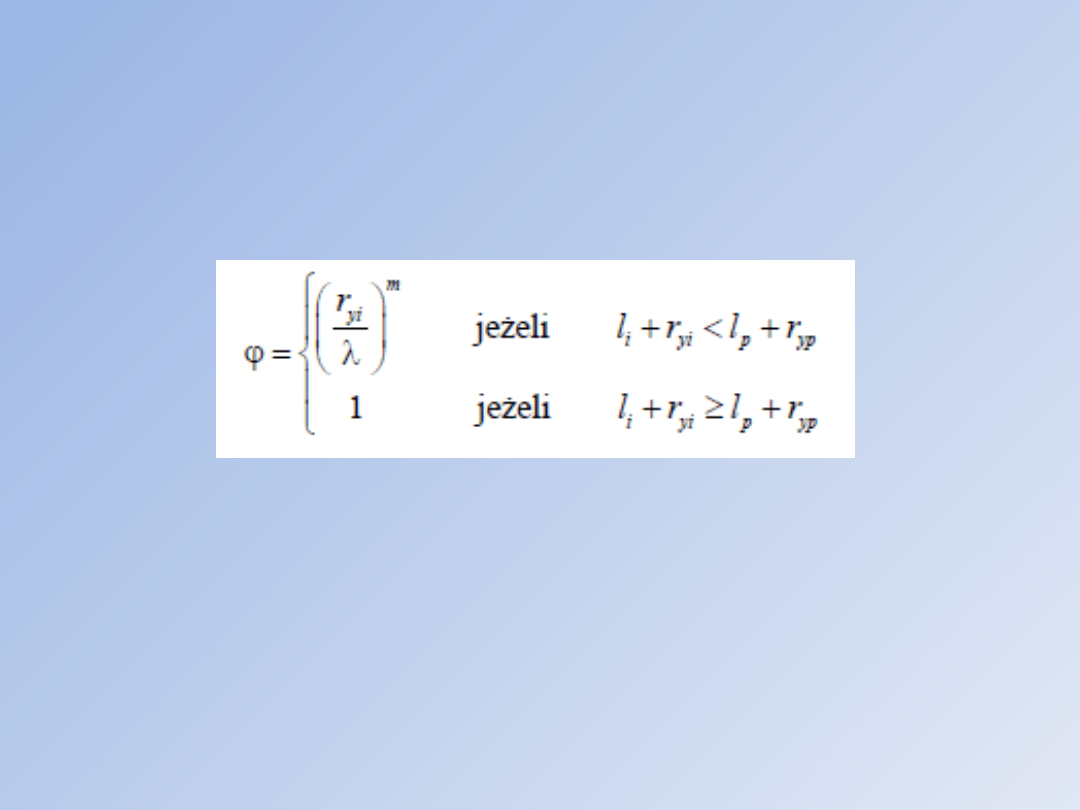
Wheeler wprowadził parametr opóźnienia φ i
powiązał go ze stosunkiem długości
aktualnej strefy plastycznej i enklawy
plastycznej utworzonej przy przeciążeniu.
Formuła określająca parametr φ ma
następującą postać:

gdzie: λ=lp+ryp-li, zaś wartość wykładnika m w
równaniu wynosi wg Wheelera: dla stali stopowej
D6AC m = 1.4, dla stopu tytanu Ti-6Al-4V m = 3.4.
Wartość φ =1 oznacza, że szczelina „przeszła”
przez strefę plastyczną wywołaną przeciążeniem,
a mówiąc inaczej można stwierdzić, że ustał wpływ
przeciążenia, a zarazem zanikł efekt opóźnienia
wzrostu szczeliny.

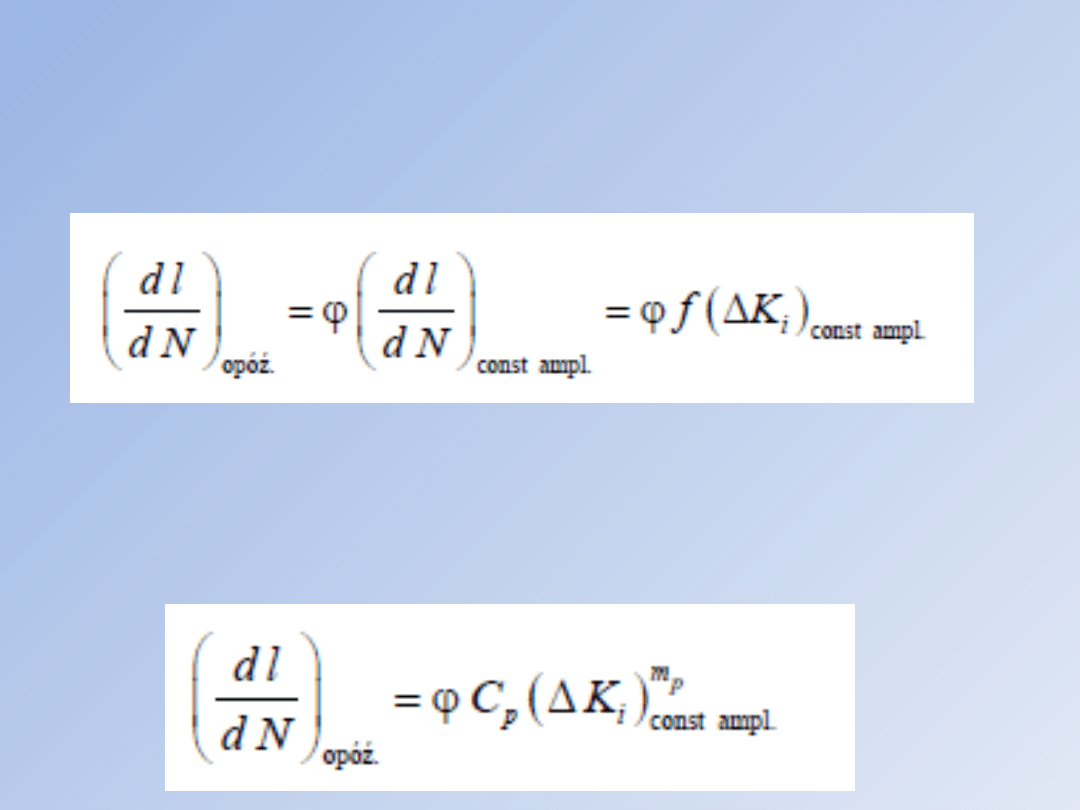
Prędkość wzrostu szczeliny zmęczeniowej przy
obciążeniu cyklicznym o zmiennej amplitudzie,
zgodnie z propozycją Wheelera wyraża się
następującym równaniem:

Równanie mówi, że prędkość wzrostu szczeliny przy zmiennej
amplitudzie można wyrazić poprzez prędkość wzrostu pęknięcia
odpowiadającą i-temu cyklowi obciążenia o zakresie zmienności
współczynnika intensywności naprężeń ΔKi. Funkcją f w równaniu
może być równanie Parisa lub inne formuły podane. W przypadku
wykorzystania równania Parisa, równanie przyjmuje postać:

WPŁYW ŚRODOWISKA NA

PROCES PĘKANIA

Od dawna wiadomo, że środowisko zewnętrzne, a w szczególności
media chemicznie agresywne w znaczący sposób przyspieszają
proces niszczenia konstrukcji inżynierskich. W obecności
środowiska agresywnego element może ulec zniszczeniu (np.
wskutek propagacji szczeliny) przy obciążeniu wywołującym
naprężenia znacznie mniejsze od wytrzymałości w normalnych
warunkach eksploatacyjnych. W kontekście zniszczenia
środowiskowego, przez które będziemy tu rozumieć podkrytyczne
(tzn. przy obciążeniu mniejszym od krytycznego) podrastanie
szczeliny, wyróżnia się trzy zasadnicze mechanizmy, a
mianowicie pękanie korozyjne, pękanie w wyniku kruchości
wodorowej (ang. hydrogen embrittlement) oraz kruchości
ciekłometalicznej (ang. liquid metal embrittlement). Mimo wielu
badań jakie wykonano dla wyjaśnienia istoty tych zjawisk, żadne
z nich nie doczekało się jak dotychczas całościowej teorii.

W badaniach doświadczalnych dotyczących oceny

podatności szczelin na propagację wywołaną procesami

korozyjnymi stosuje się dwa typy eksperymentów - badania

czasu do zniszczenia i badania prędkości wzrostu szczeliny.

W obu kategoriach badań korzysta się z próbek poddanych

działaniu stałego obciążenia (próbki w postaci beleczek

wspornikowych) lub też poddanych działaniu stałego

przemieszczenia powierzchni szczeliny, wymuszanego

poprzez zagłębianie klina w szczelinę.
Badania prowadzi się w określonym środowisku

zewnętrznym – wyniki badań mogą więc być następnie

odnoszone do takich samych lub zbliżonych warunków

środowiskowych. W przypadku prób polegających na

określaniu czasu do zniszczenia – seria próbek zawierających

szczeliny o tej samej długości początkowej, obciążana jest

różnymi co do wartości obciążeniami początkowymi, którym

odpowiadają różne początkowe współczynniki intensywności

naprężeń KIi . Każdy pojedynczy i – ty test trwa tak długo, aż

próbka ulegnie zniszczeniu. W ten sposób otrzymuje się parę

liczb (KIi , ti), gdzie ti oznacza czas do zniszczenia dla i - tej

próbki. Dzięki takiej procedurze uzyskuje się wykres

zależności czasu do zniszczenia od początkowej wartości

współczynnika intensywności naprężeń.

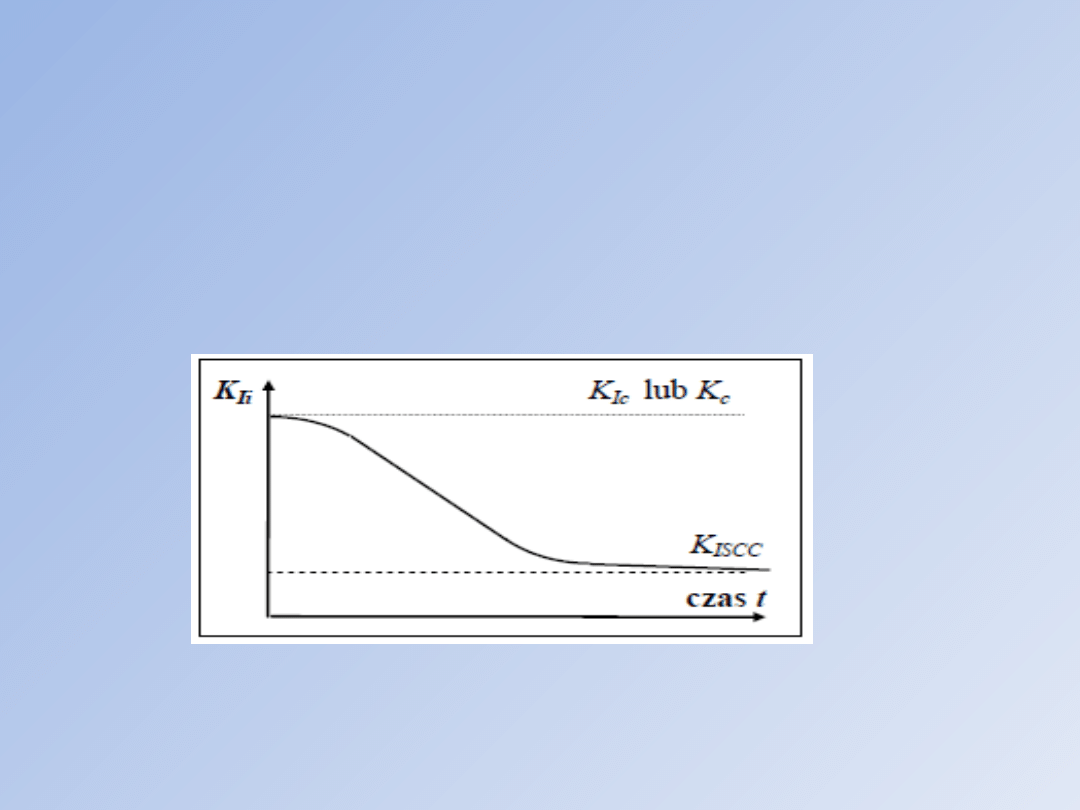
Przykład takiego wykresu pokazano na Rys. .Próbki obciążone

początkowo obciążeniem o współczynniku intensywności Kic

(odporność na kruche pękanie) lub Kc (odporność na pękanie w

konkretnych warunkach, niespełniających warunków płaskiego

stanu odkształcenia) niszczą się w momencie jego przyłożenia.

Próbki poddane działaniu obciążenia o WIN mniejszym od pewnej

wartości KISCC nie niszczą się nigdy. Wartość ta nosi nazwę

progowej - indeks „SCC” oznacza, że chodzi o pękanie wywołane

naprężeniami korozyjnymi (ang. Stress Corrosion Cracking).

Czas do zniszczenia t w funkcji początkowej wartości
współczynnika intensywności naprężeń KIi, w określonych
warunkach środowiskowych

Panuje zgodność co do tego, że wartość KISCC jest

charakterystyką tylko materiału i środowiska w

jakim się on znajduje. Wszystkie inne stany

obciążenia mieszczą się pomiędzy dwoma stanami

granicznymi, określonymi przez KIc (Kc) i KISCC.

Przypomnijmy, że obciążenie w omawianej

metodzie jest utrzymywane w trakcie trwania

próby na stałym poziomie. Jeśli uwzględnimy, że

długość szczeliny wraz z upływem czasu rośnie, to

dochodzimy do wniosku, że musi także wzrastać

bieżąca wartość współczynnika intensywności

naprężeń. Stad konkluzja, że wzrost szczeliny na

jednostkę czasu jest funkcją WIN.

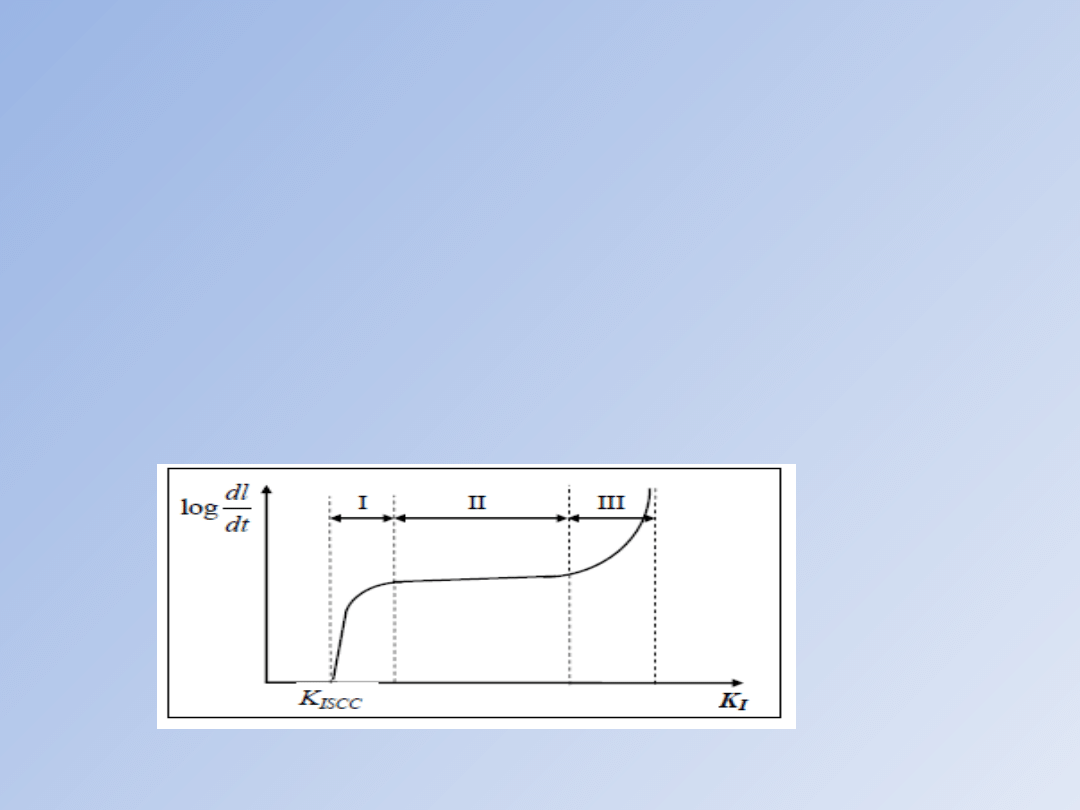
Cały zakres prędkości szczeliny można podzielić na

trzy obszary, z których I i III to obszary, w których

prędkość silnie zależy od współczynnika

intensywności naprężeń, czyli zarazem

działającego obciążenia zewnętrznego. W obszarze

II prędkość jest niemal niewrażliwa na zmiany K,

tak więc ruch szczeliny nie jest spowodowany

przyczyną mechaniczną, jaką jest obciążenie, ale

niemal wyłącznie czynnikami powiązanymi z

procesem korozji (chemicznymi, metalurgicznymi,

materiałowymi i in.)

Prędkość podkrytycznego wzrostu szczeliny korozyjnej w funkcji współczynnika
intensywności naprężeń.

Wg danych Broek’a proces korozyjnego wzrostu szczeliny,

jeżeli tylko ma miejsce (oznacza to, że musi zachodzić

warunek K ³KISCC), trwa zwykle nie dłużej niż 1000 godzin.

Jest to tak krótki okres, że z reguły fakt rozwoju pęknięcia

uchodzi uwadze w trakcie rutynowych inspekcji,

przeprowadzanych rzadziej. Doświadczenie jednoznacznie

wskazuje, że zdecydowanie lepsze skutki w przypadku

szczelin korozyjnych daje zapobieganie ich wzrostowi, aniżeli

kontrolowanie tego wzrostu (dodajmy w tym miejscu, że w

przypadku obciążeń cyklicznych okresowa kontrola

zachowania szczeliny jest z punktu widzenia bezpieczeństwa

konstrukcji w zupełności wystarczająca). Z formalnego

punktu widzenia zapobieganie rozwojowi pęknięcia w

środowisku wywołującym korozję polega na spełnieniu

warunku K<KISCC. Sposób wykorzystania tej relacji jest taki

sam jak sposób wykorzystania siłowego kryterium pękania

K<KIc w celu określenia dopuszczalnej długości szczeliny lub

dopuszczalnego obciążenia - wystarczy jedynie zamienić KIc

przez KISCC.

BIBLIOGRAFIA

• Janusz German „podstawy mechaniki

pękania” Kraków 2011,

• Janusz German „Liniowa mechanika

pękania”,

• Grzegorz Robak „Analiza rozwoju

pęknięć”.

DZIĘKUJĘ ZA UWAGĘ