1

Obiektowy system graficzny

dr inż. Henryk Olszewski

2

Ćwiczenia:
Przywrócić standardowe wartości obiektu root:

»

reset(0)

Wyświetlenie bieżącego ustawienia cechy ScreenSize obiektu
root:

»

get(0,’ScreenSize’)

Uaktywnienie układu współrzędnych o identyfikatorze id:

»

axes(id)

Operacje na obiektach graficznych -

ćwiczenia

3

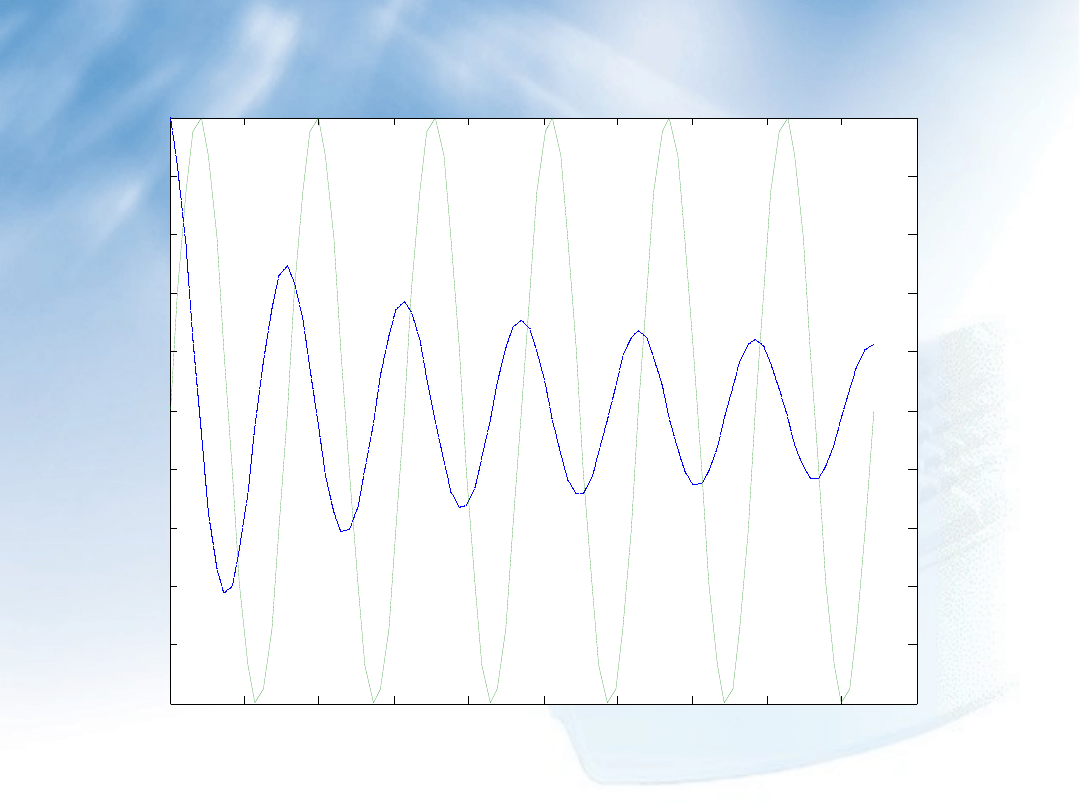
Przykład przypisania zmiennej hh2 wartości identyfikatora:

»

x=0:pi/15:6*pi;

»

hh2=plot(x,cos(2.*x)./sqrt(x+1),’:’,x,sin(x.*2));

Zmienna hh2 jest wektorem dwuelementowym i reprezentuje
wykonanie wykresu:

»

hh2

hh2=

3.0010

102.0009

Do każdego można się odwołać (poprzez nazwę zmiennej
zawierającej identyfikator obiektu), oczytać – funkcja get lub
zmienić jego właściwości – funkcja set. Nie zaleca się stosowanie
identyfikatorów w postaci liczb.

Operacje na obiektach graficznych -

ćwiczenia

4

Operacje na obiektach graficznych -

ćwiczenia

0

2

4

6

8

10

12

14

16

18

20

-1

-0.8

-0.6

-0.4

-0.2

0

0.2

0.4

0.6

0.8

1

5

Każdy obiekt graficzny posiada własną bazę danych, której pola
zwierają informacje o cechach (argumentach) tego obiektu.
Nazwy i ilość pól zależą od typu obiektu. Wartości pól
(argumenty obiektów) są określane w momencie tworzenia
obiektów.

Pobranie informacji o aktywnym oknie:

»

get(gcf)

Pobranie informacji o aktywnym układzie współrzędnych:

»

get(gca)

Pobranie informacji o aktywnym obiekcie:

»

get(gco)

Dla innych obiektów pierwszym argumentem funkcji get i set
jest identyfikator (handle).

Cechy obiektów graficznych -

ćwiczenia

6

Rezultat działania funkcji get:

»

get(hh2(1))

Color = [0 0 1]
EraseMode = normal
LineStyle = :
LineWidth = [0.5]
Marker = none
MarkerSize = [6]
MarkerEdgeColor = auto
MarkerFaceColor = none
XData = [ (1 by 91) double array]
YData = [ (1 by 91) double array]
ZData = []

Cechy obiektów graficznych -

ćwiczenia

0

2

4

6

8

10

12

14

16

18

20

-1

-0.8

-0.6

-0.4

-0.2

0

0.2

0.4

0.6

0.8

1

7

Rezultat działania funkcji get:

BeingDeleted = off

ButtonDownFcn =

Children = []

Clipping = on

CreateFcn =

DeleteFcn =

BusyAction = queue

HandleVisibility = on

HitTest = on

Interruptible = on

Parent = [101.001]

Cechy obiektów graficznych -

ćwiczenia

0

2

4

6

8

10

12

14

16

18

20

-1

-0.8

-0.6

-0.4

-0.2

0

0.2

0.4

0.6

0.8

1

8

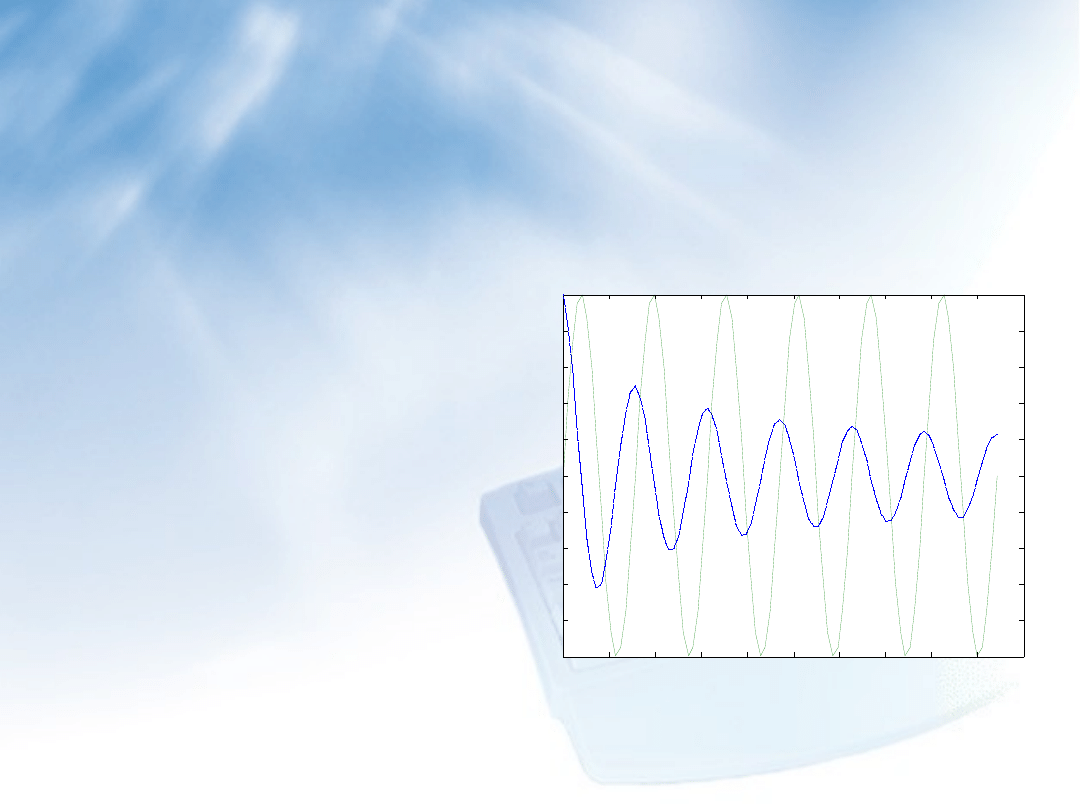
Rezultat działania funkcji get:

Selected = off

SelectionHighlight = on

Tag =

Type = line

UIContextMenu = []

UserData = []

Visible = on

Cechy obiektów graficznych -

ćwiczenia

0

2

4

6

8

10

12

14

16

18

20

-1

-0.8

-0.6

-0.4

-0.2

0

0.2

0.4

0.6

0.8

1

9

Informacje o przodku obiektu:

»

hp=get(hh2(1),’Parent’);get(hp)

Funkcja set(handle) umożliwia wyświetlenie listę wariantów

wartości cech obiektów. Bieżące wartości cech (atrybuty) są

umieszczone w nawiasach okrągłych:

»

set(hh2(1))

Color
EraseMode: [ {normal} | background | xor | none ]
LineStyle: [ {-} | -- | : | -. | none ]
LineWidth
Marker: [ + | o | * | . | x | square | diamond | v |

^

]| > | < | pentagram | hexagram | {none} ]

MarkerSize
MarkerEdgeColor: [ none | {auto} ] -or- a ColorSpec.

Cechy obiektów graficznych -

ćwiczenia

10

XData
YData
ZData

ButtonDownFcn: string -or- function handle -or- cell

array

Children
Clipping: [ {on} | off ]
CreateFcn: string -or- function handle -or- cell array
DeleteFcn: string -or- function handle -or- cell array
BusyAction: [ {queue} | cancel ]
HandleVisibility: [ {on} | callback | off ]
HitTest: [ {on} | off ]

Cechy obiektów graficznych -

ćwiczenia

11

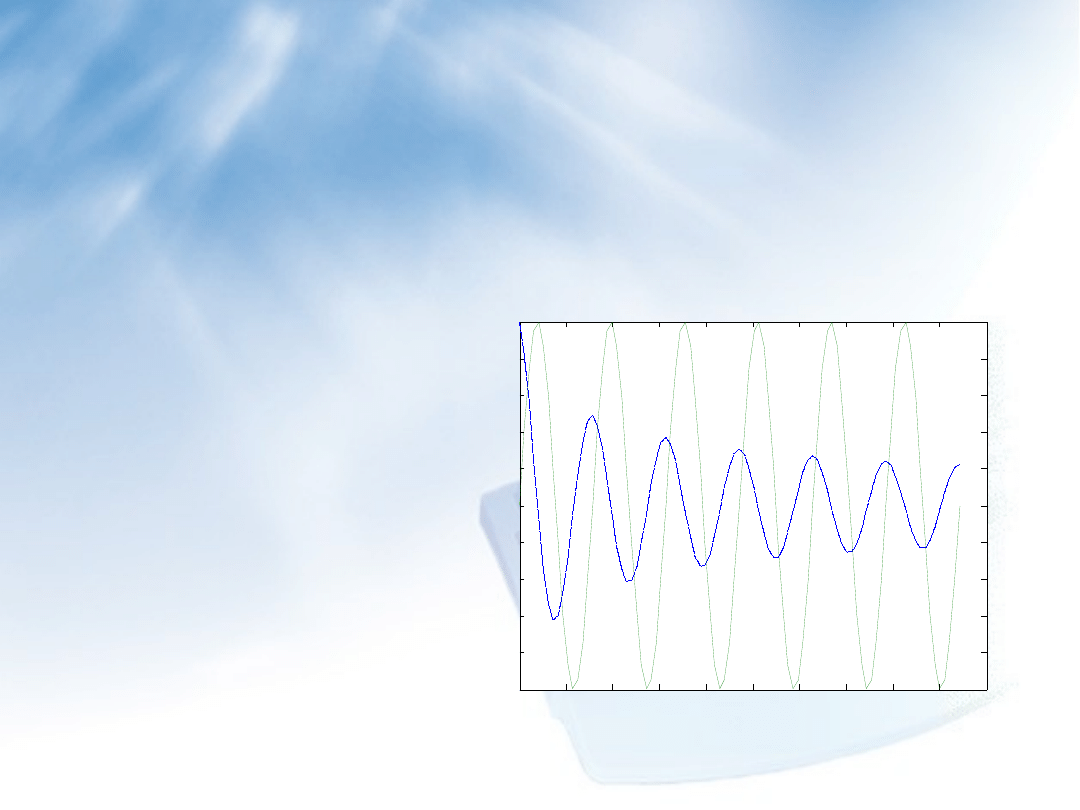
Interruptible: [ {on} | off ]

Parent

Selected: [ on | off ]

SelectionHighlight: [ {on} | off ]

Tag

UIContextMenu

UserData

Visible: [ {on} | off ]

Cechy obiektów graficznych -

ćwiczenia

0

2

4

6

8

10

12

14

16

18

20

-1

-0.8

-0.6

-0.4

-0.2

0

0.2

0.4

0.6

0.8

1

12

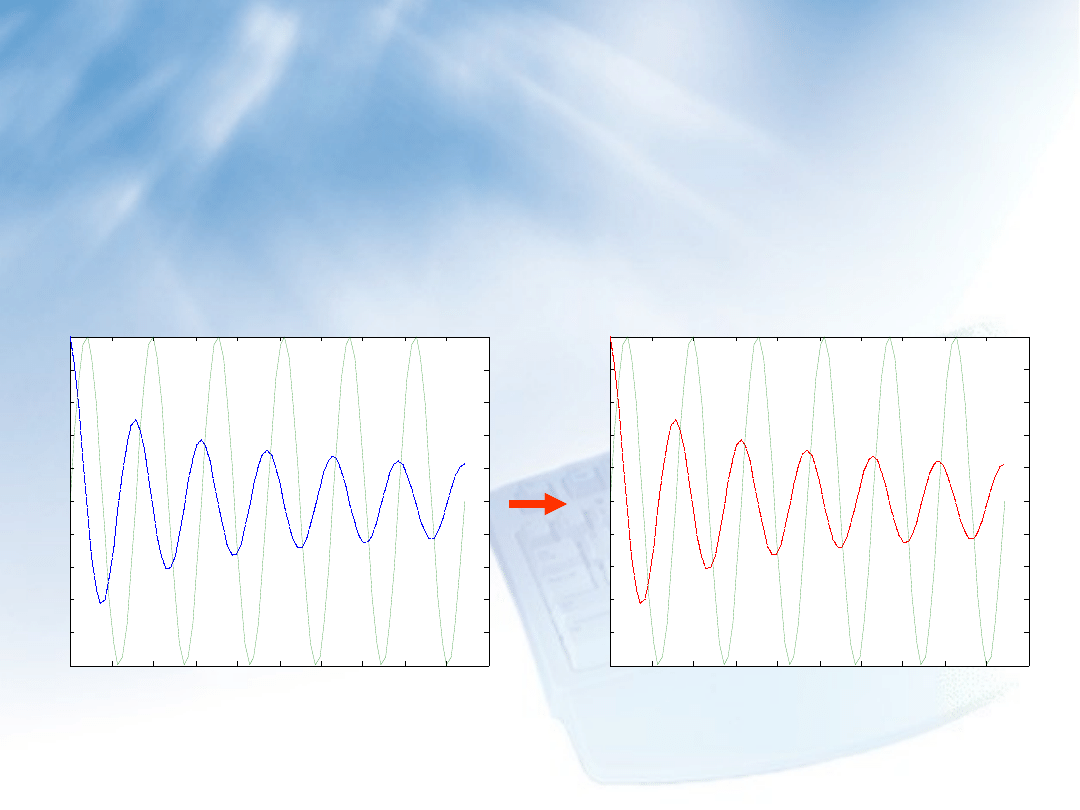
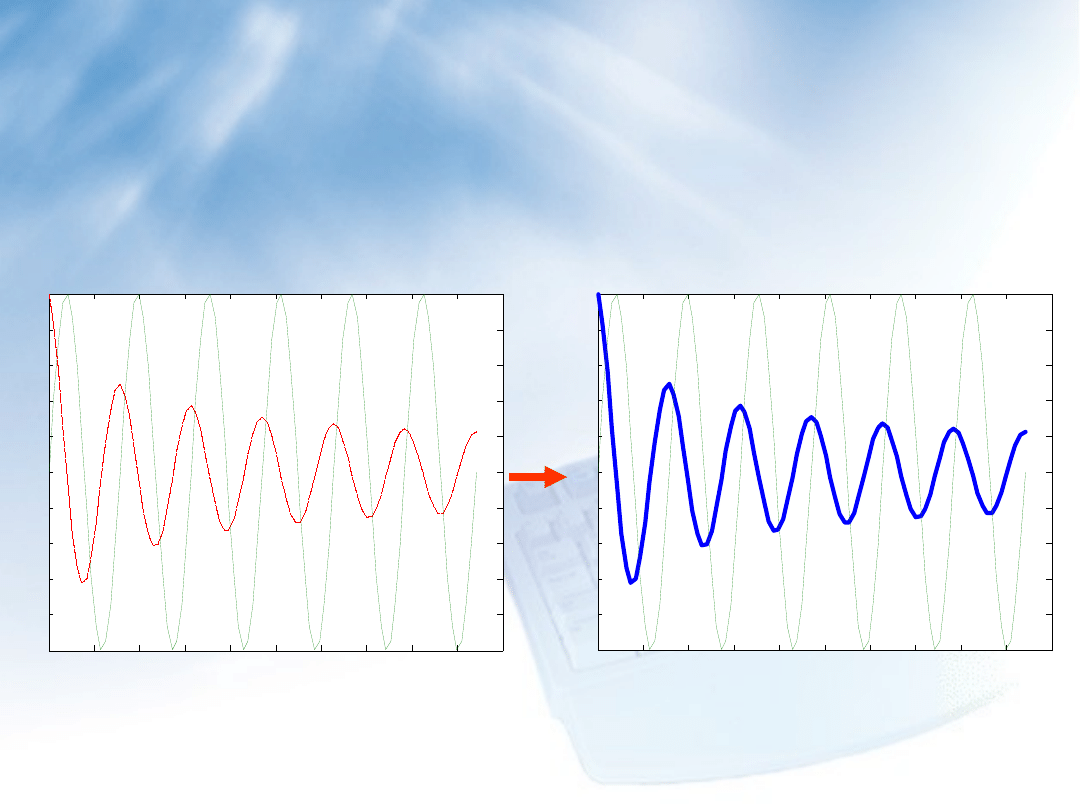
Zmiana wartości cechy dotyczącej kolorowi w obiekcie o
identyfikatorze hh2(1):

set(hh2(1),’Color’,’r’)

powoduje zmianę koloru pierwszej linii na kolor czerwony.

Cechy obiektów graficznych -

ćwiczenia

0

2

4

6

8

10

12

14

16

18

20

-1

-0.8

-0.6

-0.4

-0.2

0

0.2

0.4

0.6

0.8

1

0

2

4

6

8

10

12

14

16

18

20

-1

-0.8

-0.6

-0.4

-0.2

0

0.2

0.4

0.6

0.8

1

13

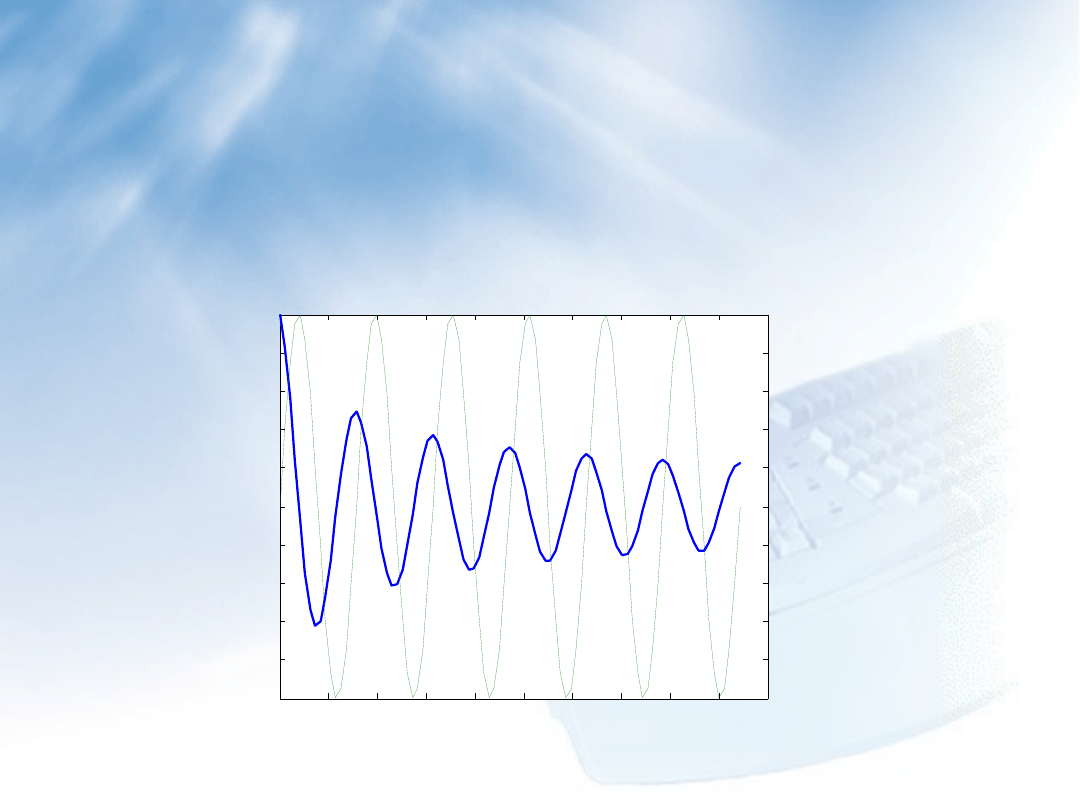
Dopuszczalna jest zmiana grupy (nieograniczonej) cech obiektów
w jednym poleceniu set:

set(hh2(1),’Color’,’b’,’LineWidth’,2)

Cechy obiektów graficznych -

ćwiczenia

0

2

4

6

8

10

12

14

16

18

20

-1

-0.8

-0.6

-0.4

-0.2

0

0.2

0.4

0.6

0.8

1

0

2

4

6

8

10

12

14

16

18

20

-1

-0.8

-0.6

-0.4

-0.2

0

0.2

0.4

0.6

0.8

1

14

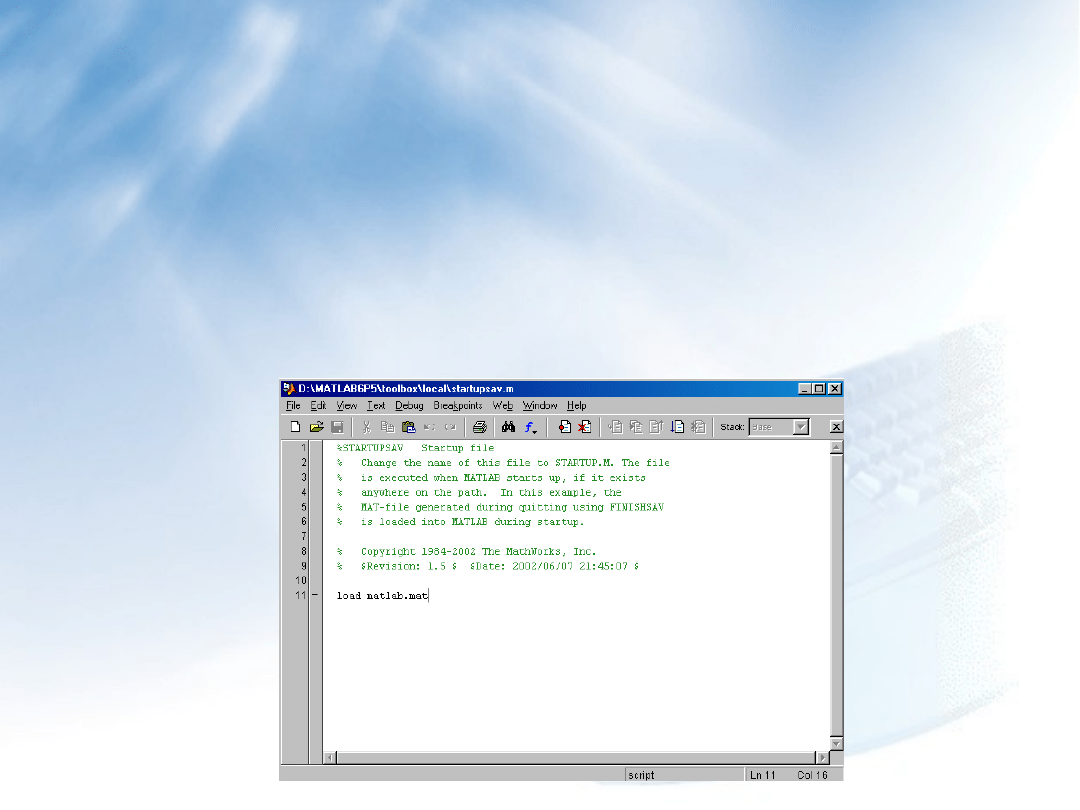
Zmiana rodzaju linii na linię ciągłą, pogrubioną:

set(hh2(1),’LineStyle’,’-’,’LineWidth’,2)

Cechy obiektów mogą być określone w momencie tworzenia
obiektów. Dalsze zmiany obiektów wymagają znajomości ich
identyfikatorów.

Cechy obiektów graficznych -

ćwiczenia

0

2

4

6

8

10

12

14

16

18

20

-1

-0.8

-0.6

-0.4

-0.2

0

0.2

0.4

0.6

0.8

1

15

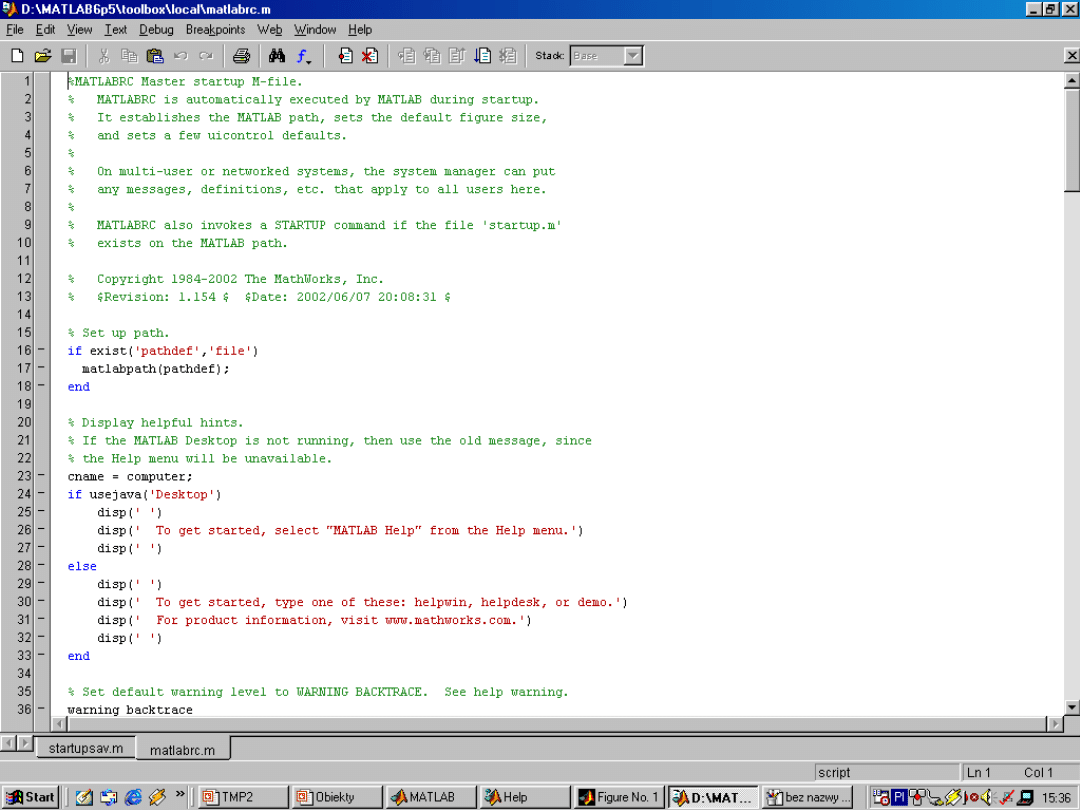
W programie MATLAB można ustawić domyślne wartości cech
obiektów graficznych:

set(hh2(1),’DefaultLineStyle’,’-’,...

’ DefaultLineWidth’,2.0)

Powyższe polecenia można zapisać w plikach konfiguracyjnych
matlabrc.m lub startup.m.

Cechy obiektów graficznych –

ćwiczenia

16

Cechy obiektów graficznych

17

Cechy obiektów graficznych

18

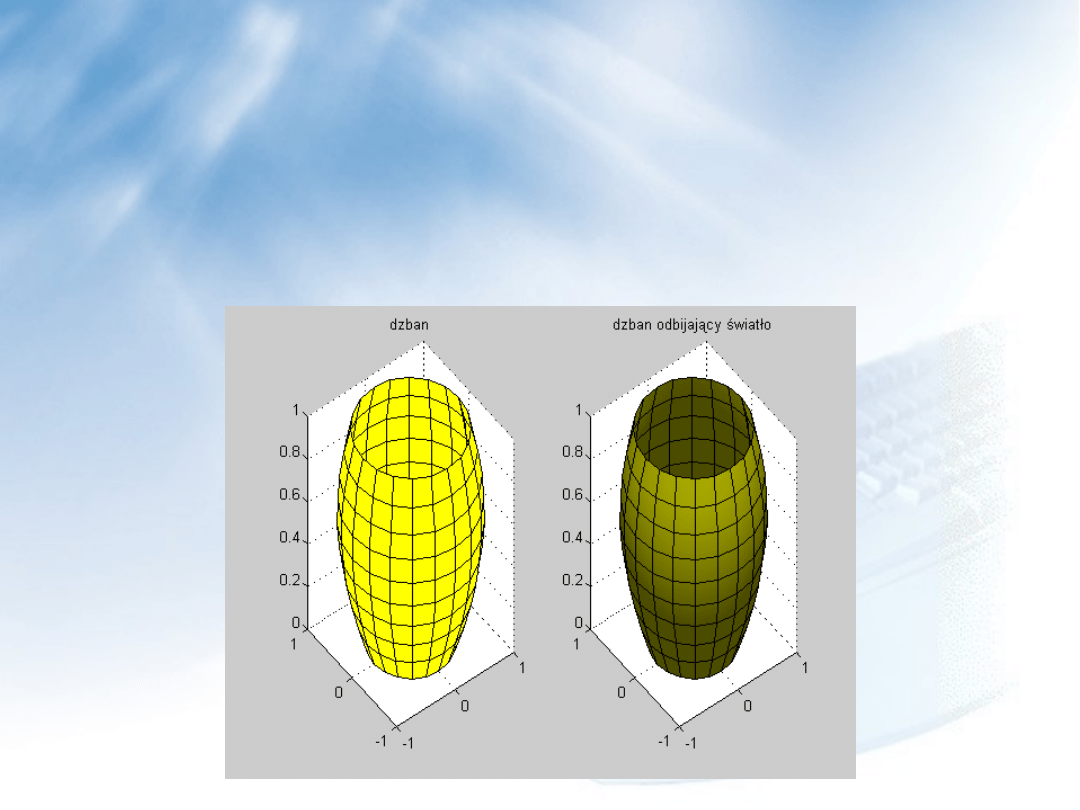
Funkcje dotyczące odbicia i źródła światła:

źródło światła, współrzędne kamery:

camlight

Ćwiczenie 1:

t=2/3:1/6:.7*pi;

y=sin(t)

[a,b,c]=cylinder(y);

%dane do narysowania bryły

subplot(1,2,1),

h1=surf(a,b,c),

title(‘dzban’)

set(h1,’facecolor’,’y’)

%nadanie bryle koloru żółtego

subplot(1,2,2),

h2=surf(a,b,c)

%druga bryła (prawa)

set(h2, ‘facelighting’,’phong’,’backfacelight’,’lit’)

%odblaski

Cechy obiektów graficznych – źródła

światła

19

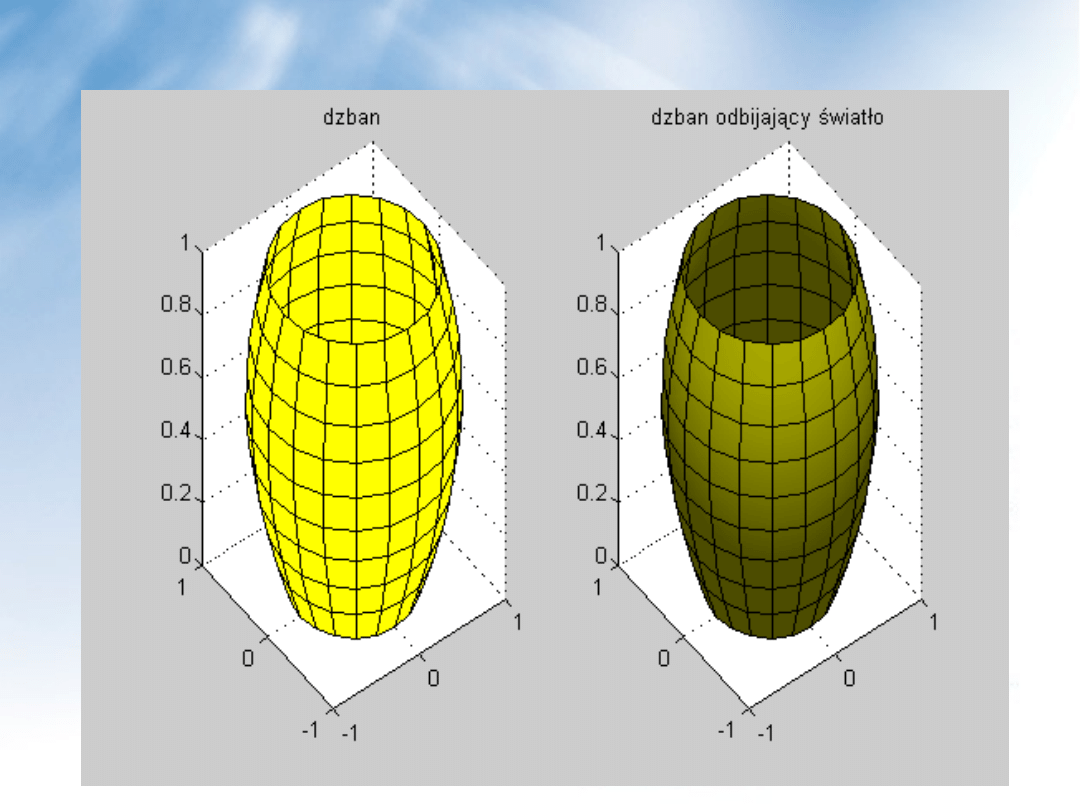
set(h2,’facecolor’,’y’) %nadanie koloru żółtego

light(‘position’,[-2,-3,6])

%utworzenie obiektu

%źródła światła

title(‘dzban odbijający światło’)

Cechy obiektów graficznych – źródła

światła

20

Cechy obiektów graficznych – źródła

światła

21

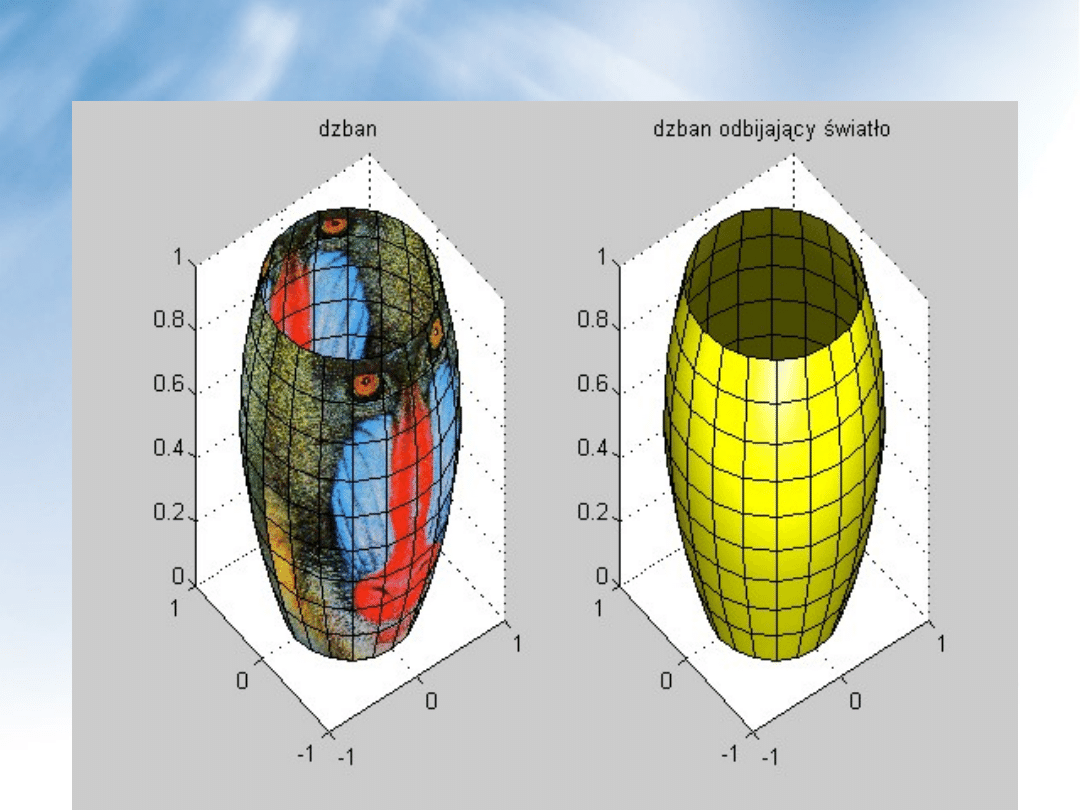
Tekstura – nakładanie płaskiego rysunku na zakrzywioną

powierzchnię trójwymiarową

%kontynuacja poprzedniego ćwiczenia

load mandrill

%wczytanie ilustracji, tablice X, map

x=[X X];

%dwukrotne powtórzenie ilustracji

x=flipud(x);

%odbicie lustrzane ilustracji:

%góra/dół

set(h1,’CData’,x,’FaceColor’,’texturemap’)

%nałożenie

%tekstury

colormap(map)

%paleta barw

set(h1,’facelighting’,’phong’,’backfacelight’,’lit’)

%odbicie światła

light(‘position’,[-2,-3,.6])

%utworzenie obiektu

%źródło światła

Cechy obiektów graficznych – tekstury

22

brighten(0.05)

%rozjaśnienie rysunku

W rysunku wykorzystano plik z grafiką:

matlab\toolbox\matlab\demos\mandrill.mat

Funkcję findobj użyto w celu znalezienia identyfikatora
powierzchni narysowanej bryły. Nałożenie tekstury na obiekt
graficzny wymaga przypisania odpowiednich wartości polom tego
obiektu:

‘texturemap’

do pola:

‘FaceColor’

x=[X,X]

do pola:

‘CData’

Cechy obiektów graficznych – tekstury

23

Cechy obiektów graficznych – tekstury

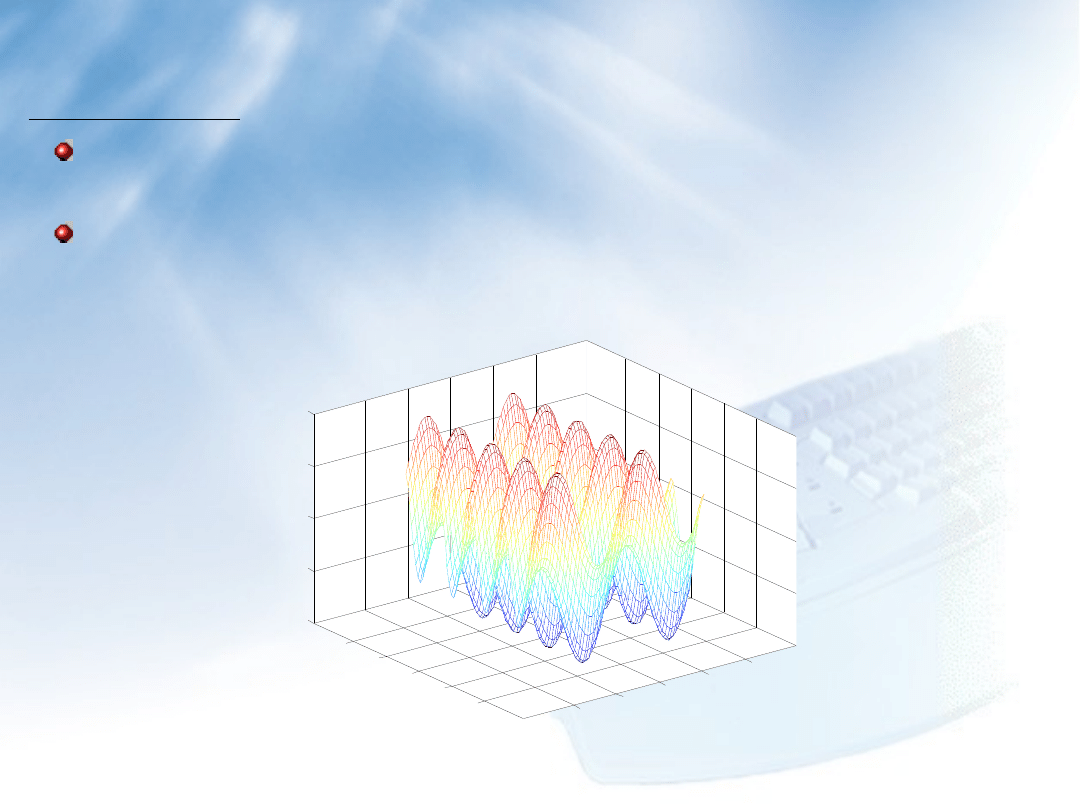
24

Ćwiczenie 2:

Narysować trójwymiarowy wykres funkcji: z(x,y)=sin(x)
+cos(2*y) w przedziale: x,y



<-2



,2



>.

Zmienić cechy obiektu axis: typ linii pomocniczych na linie
ciągłe, położenia oznaczeń na osiach x i y określone są zaś
wektorem [-2



, -



, 0,



, 2



].

Cechy obiektów graficznych

-6.2832

-3.1416

0

3.1416

6.2832

-6.2832

-3.1416

0

3.1416

6.2832

-2

-1

0

1

2

25

Ćwiczenie 2:
Polecenia skryptu osie.m:

clf

%czyszczenie aktywnego okna rysunkowego

[x,y]=meshgrid(-2*pi:0.2:2*pi);
z=sin(x)+cos(2*y);
mesh(x,y,z)
grid on;

%dodanie do rysunku siatki

axis=([-2*pi 2*pi -2*pi 2*pi])

%ustawienie zakresu osi

xt=-2*pi:pi:2*pi;
yt=-2*pi:pi:2*pi;
set(gca,'GridLineStyle','-')

%zmiana cechy obiektu

set(gca,'XTick',xt)

%określonego przez funkcję gca

set(gca,'YTick',yt)

Cechy obiektów graficznych

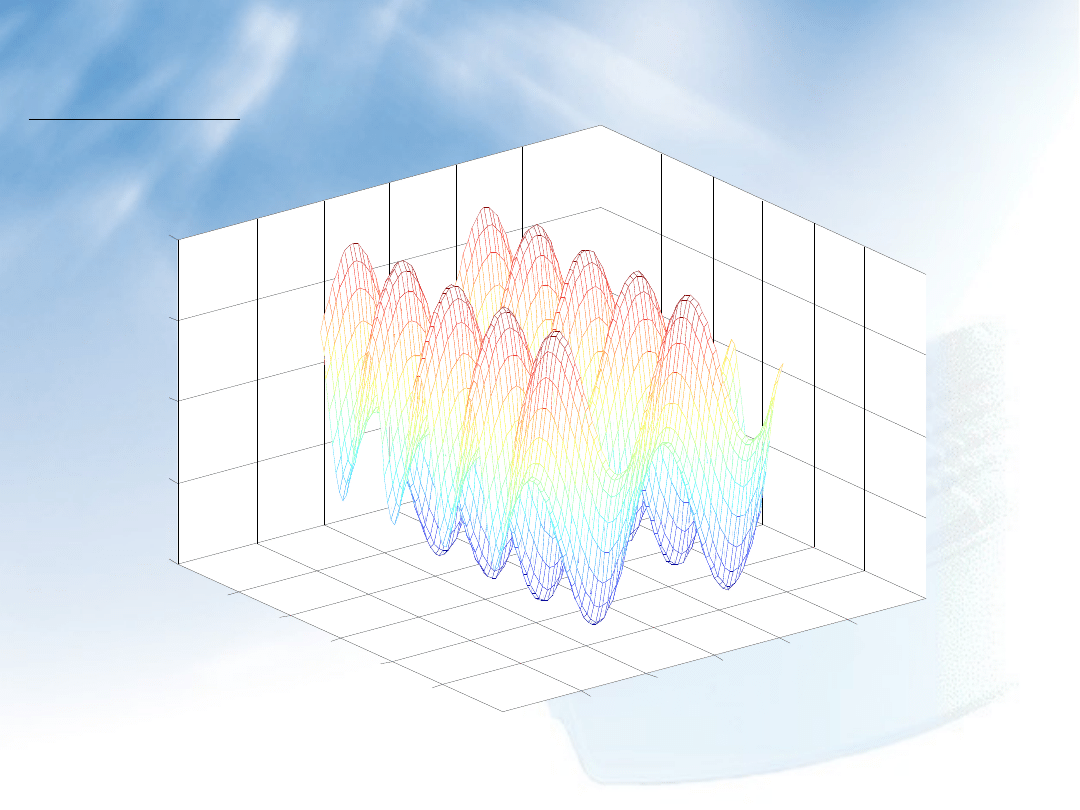
26

-6.2832

-3.1416

0

3.1416

6.2832

-6.2832

-3.1416

0

3.1416

6.2832

-2

-1

0

1

2

Ćwiczenie 2:

Cechy obiektów graficznych

27

Animacja – przykłady (3)

Wizualizacja ruchu cząsteczek powietrza
Wizualizacja ruchu cząsteczek powietrza jest pomocna przy analizie
kierunku przepływu powietrza i badaniu pola prędkości. Cząsteczki
powietrza (przedstawione za pomocą markerów) przesuwają się
wzdłuż linii prądu powietrza, Prędkość każdej cząstki jest
proporcjonalna do amplitudy (wartości bezwzględnej) pola prędkości
w każdym jego punkcie znajdującym się na linii prądu.

1. Warunki początkowe i zakres obliczeń
Analiza objętość powietrza na początku obliczeń obejmuje:

load wind

[sx sy sz] = meshgrid(100,20:2:50,5);

28

Animacja – przykłady (3)

2. Wykres linii przepływu cząsteczek powietrza
W przykładzie użyto funkcje rysujące linie przepływu stream3,
streamline wizualizujące ruch cząsteczek powietrza. Parametrami
funkcji stream3 są: x, y, u – współrzędne pola prędkości, u, v, w –
wartości pola prędkości, sx,sy, sz – początkowe położenie linii prądu.

Funkcja view definiuje punkt, z którego oglądamy wykres. Funkcja
view(2) ustala widok dwuwymiarowy. Funkcja view(3) ustala widok
trójwymiarowy izoparametryczny.

verts = stream3(x,y,z,u,v,w,sx,sy,sz);
sl = streamline(verts);
view(3)

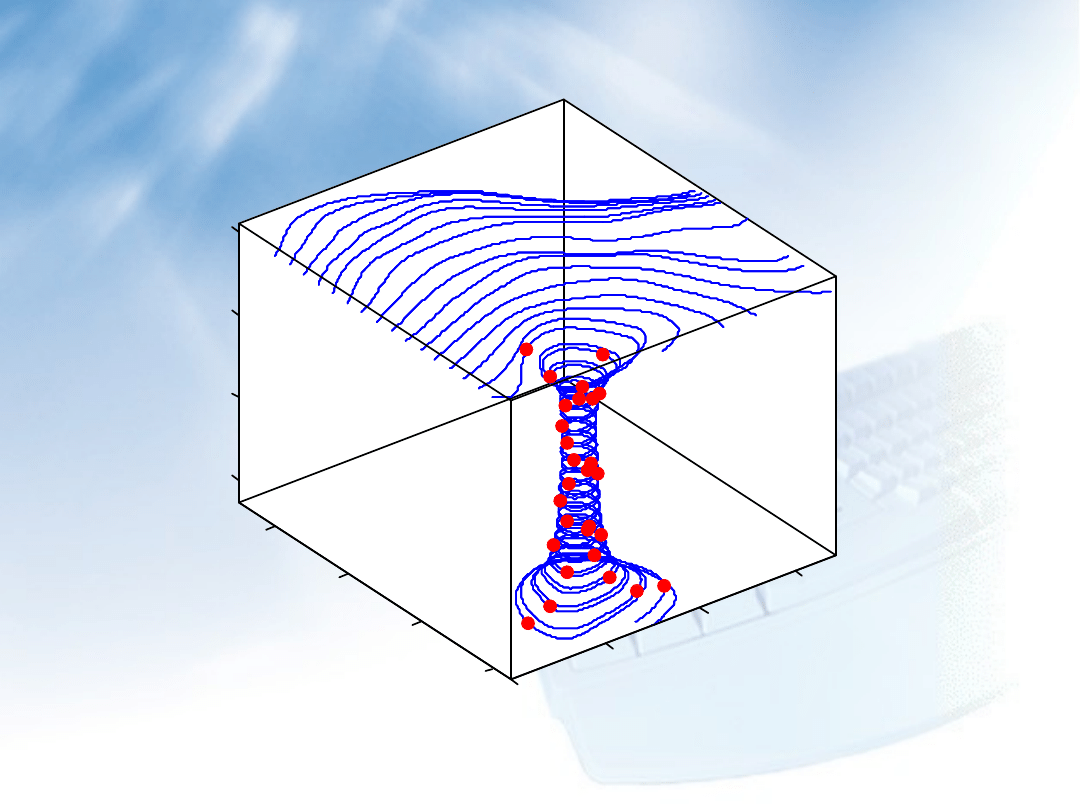
29

Animacja – przykłady (3)

100

110

120

130

20

30

40

50

3.5

4

4.5

5

30

Animacja – przykłady (3)

3. Defincja widoku
Wszystkie linie prądu rozpoczynają się z płaszczyzny z = 5, niektóre linie prądu
spadają spiralnie w dół. Kształt linii prądu określa miejsce, z którego będzie
oglądana animacja (tak by linie prądu znające się w pobliżu płaszczyzny z = 5 i
linie spiralne były widoczne) – funkcja view.

Przyjęto współczynniki perspektywy [2 2 0.125] (polecenie daspect), co
pozwala na uzyskanie największej rozdzielczości w kierunku osi z układu
współrzędnych dzięki czemu wyeksponowane są spiralne linie prądu.

Przy pomocy polecenia axis tight zamrożono osie wykresu (odpowiednik
polecenie axis manual). Wykres 3D rysowany objęty jest krawędziami
prostopadłościanu – polecenie box on.

view(-10.5,18)

daspect([2 2 0.125])
axis tight; box on

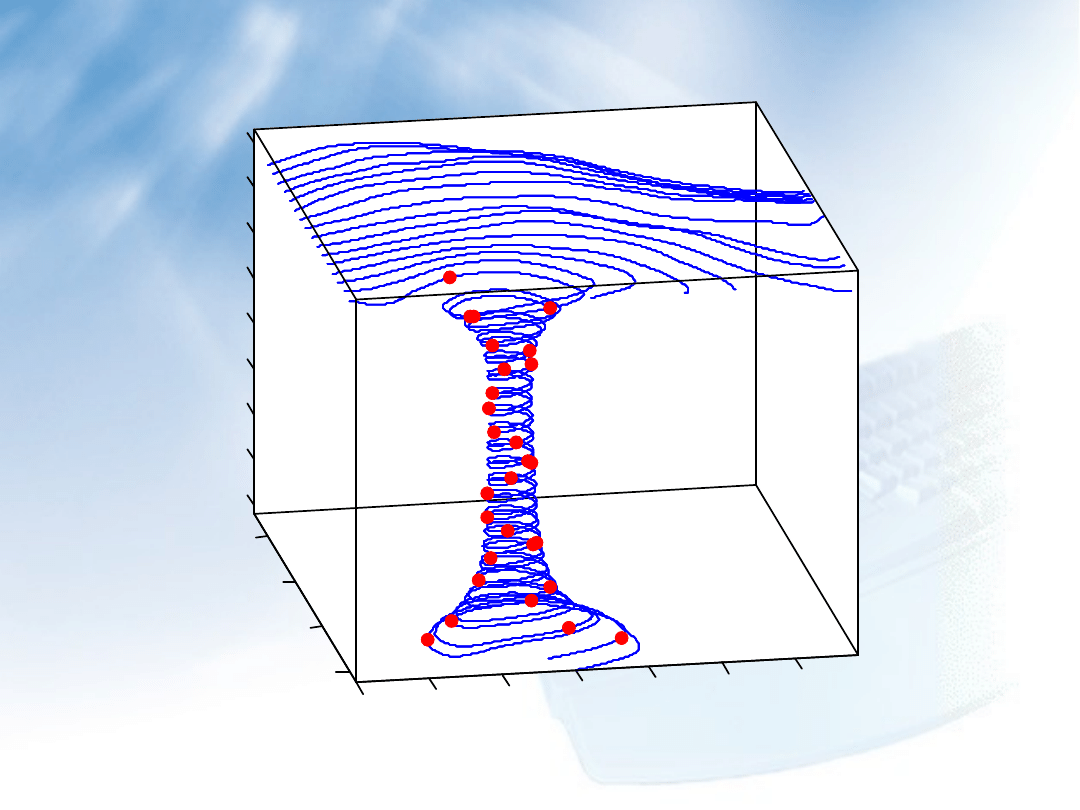
31

Animacja – przykłady (3)

100

105

110

115

120

125

130

20

30

40

50

3.4

3.6

3.8

4

4.2

4.4

4.6

4.8

5

32

Animacja – przykłady (3)

4. Wizualizacja prędkości cząsteczek powietrza
W pierwszym etapie określane są prędkości wzdłuż linii prądu w
miejscach, w których rysowane są cząsteczki powietrza (za pomocą
markerów). Funkcja interpstreamspeed oblicza powyższe parametry
w oparciu o wartości współrzędnych linii prądu oraz prędkości
cząsteczek. Przyjęto współczynnik scali 0,05 w celu zwiększenia
liczby interpolowanych wartości prędkości.

W celu zwiększenia szybkości animacji ustalono dla osi wykresu
właściwość DrawMode=fast (set(gca,'drawmode','fast').

Funkcja streamparticles pozwala na ustalenie następujących
właściwości:
1) animacja zostanie uruchomiona 10 razy (właściwość Animate),
2) ruch wszystkich cząsteczek powietrza rozpocznie się równocześnie
(właściwość ParticleAlignment),

33

Animacja – przykłady (3)

3) krawędzie markerów cząsteczek powietrza nie są rysowane
(właściwość MarkerEdgeColor), co zazwyczaj zwiększa szybkość
animacji,
4) kolor markerów ustalona na czerwony (właściwość
MarkerFaceColor),
5) markery są rysowane w postaci kółek (właściwość Marker).

iverts = interpstreamspeed(x,y,z,u,v,w,verts,0.05);
set(gca,'drawmode','fast');
streamparticles(iverts,15,...
'Animate',10,...
'ParticleAlignment','on',...
'MarkerEdgeColor','none',...
'MarkerFaceColor','red',...
'Marker','o');

34

Animacja – przykłady (4)

W przykładzie tym kamera przemieszcza się w trójwymiarowej przestrzeni rysunku wiru powietrza. W
programie MATLAB istnieje możliwość przesuwania kamery przez poszczególne regiony sceny
wykresu (ostrość kamery jest na bieżąco dostrajana na obserwowane obiekty) lub poruszania kamery
stale skierowanej na określony punkt wykresu (ostrość kamery jest ustawiona na ten punkt).

W celu osiągnięcia powyższych efektów przesuwamy krokowo kamerę wzdłuż zadanej osi x. Efekt

lotu kamery uzyskamy równocześnie przesuwając położenie kamery i zmieniając punkt, na który
skierowana jest kamera

W przykładzie tym zamodelowano ruch kamery wewnątrz izopowietrzni wiru powietrza

(powierzchni, na której cząstki powietrza mają stałą prędkość) wybranej z przestrzennego modelu pola
prędkości cząstek powietrza tornada zaobserwowanego w 1998 r. w stanie Teksas, USA.

35

Animacja – przykłady (4)

W przykładzie zastosowano:
• izopowierzchnie i wykresy, w których punkty zaznaczane są markerami w postaci stożków, w celu

ilustracji przepływu powietrza w zadanej objętości powietrza,

• źródła światła w oświetlenia izopowierzchni i stożków w zadanej objętości powietrza,
• linie prądu w celu zdefiniowania trajektorii ruchu kamery,
• równoczesną zmianę położenia kamery, punktu na który skierowana jest kamera oraz źródeł światła.

1. Wczytanie danych i ich wizualizacja

W pierwszy etapie animacji wczytano dane wykresu z pliku wind.mat i na ich postawie wykonano rysunek
przepływu powietrza przy pomocy funkcji coneplot.

load wind
wind_speed = sqrt(u.^2 + v.^2 + w.^2);

36

Animacja – przykłady (4)

W programie MATLAB funkcja patch tworzy wypełnione wielokąty zwane płatami (ang. patches).

id=patch(x,y,c)
id=patch(x,y,z,c)
id=patch(x,y,c,nazwa_cechy1, wartość1,...
nazwa_cechy2, wartość2,...)
id=patch(x,y,z,c,nazwa_cechy1, wartość1,...
nazwa_cechy2, wartość2,...)

Wektory x, y, z określają współrzędne wierzchołków wielokąta, zaś c określa jego kolor. Kolor jest określony przez

podanie indeksu koloru w powiązanej z aktualnym układem mapie kolorów. Argument c może być:
1) skalarem – płat będzie jednokolorowy,
2) jednoznakowym ciągiem – płat będzie jednokolorowy, oznaczenia
kolorów są takie same jak w przypadku funkcji plot,

37

Animacja – przykłady (4)

3) wektorem o takim samym wymiarze jak wektory x, y, z elementy
wektora określają kolory w odpowiednich wierzchołkach, kolory
poszczególnych punktów wielokąta będą miały kolory pośrednie,
płynnie zmieniające się w zależności od położenia punktu, kolor
każdego punktu będzie wynikiem interpolacji dwuliniowej kolorów
wierzchołków.

Argumenty x, y, z mogą być macierzami o identycznych wymiarach. Utworzony zostanie jeden płat dla każdej
kolumny macierzy. W tym przypadku argument c będzie wektorem wierszowym dla płatów jednokolorowych i macierzą
dla płatów o kolorach interpolowanych.

Funkcja patch zwraca kolumnowy wektor identyfikatorów obiektów typu patch. Za każdą trójką parametrów x, y, z
może wystąpić zestaw par: nazwa cechy, wartość cechy określającej dodatkowe cechy poszczególnych płatów.

38

Animacja – przykłady (4)

Funkcja isosurface:

fv = isosurface(X,Y,Z,V,isovalue)

oblicza współrzędne izopowierzchni dla danych zdefiniowanych w zadanej objętości V, dla określonej wartości
parametru isovalue (wszystkie punkty izopowierzchni mają tę wartość parametru isovalue). Macierze X, Y i Z
określają dane analizowanej objętości, w której wyznaczana jest izopowierzchnia. W rezultacie otrzymujemy zmienną
fx zawierającą parametry siatki wielokątów i współrzędne wierzchołków izopowierzchni, które mogą być bezpośrednio
użyte jako dane funkcji patch.

hpatch = patch(isosurface(x,y,z,wind_speed,35));

Funkcja isonormals:

n = isonormals(X,Y,Z,V,vertices)

39

Animacja – przykłady (4)

oblicza wektory normalne do izopowierzchni w jej wierzchołkach vertices dla gradientu danej objętości V.
Macierze X, Y i Z zawierają współrzędne objętości V. Obliczone normalne są zapamiętane w zmiennej n.

isonormals(x,y,z,wind_speed,hpatch)
set(hpatch,'FaceColor','red','EdgeColor','none');

Funkcja reducepatch:

reducepatch(p,r)

redukuje liczbę wypełnionych wielokątów zwanych płatami (ang. patches) zadanego obiektu p przy
zachowaniu ogólnego kształtu wyjściowego obiektu. Jeżeli r jest mniejsze niż 1, liczba wielokątów ulega
redukcji, np. dla r=0.2 liczba wielokątów (płatów) ulega zredukowaniu o 20%. Jeżeli r jest większe lub równe 1,
to r jest docelową liczbą wielokątów, np. dla r=400 liczba wielokąt zostaje zredukowana do 400.

40

Animacja – przykłady (4)

[f vt] = reducepatch(isosurface(x,y,z,wind_speed,45),0.05);

Funkcja daspect umożliwia określenie współczynników skali dla osi x, y i z układu współrzędnych. Przyjęcie współczynników skali
[1,1,1] przed rysowaniem markerów - stożków pozwala na właściwe przeliczenie wymiarów markerów dla końcowego widoku:

daspect([1,1,1]);

Funkcja coneplot:
coneplot(X,Y,Z,U,V,W,Cx,Cy,Cz)
wyświetla wektory prędkości w postaci stożków rysowanych w punktach pola prędkości, których osie są zgodne z kierunkami
wektorów prędkości, o długościach proporcjonalnych do długości wektorów prędkości.
X, Y, Z – współrzędne punktów pola prędkości,
U, V, W – składowe wektorów prędkości, macierze te muszą mięć te
same wymiary, monotoniczne (podobnie jak dane generowane przez
funkcję meshgrid),
Cx, Cy, Cz – położenie markerów – stożków w polu prędkości.

41

Animacja – przykłady (4)

hcone = coneplot(x,y,z,u,v,w,vt(:,1),vt(:,2),vt(:,3),2);
set(hcone,'FaceColor','blue','EdgeColor','none');

2. Parametry widoku
Kolejnym etapem animacji jest ustalenie parametrów widoku. Przyjęcie perspektywy umożliwia uzyskanie efektu głębi podczas
ruchu kamery wewnątrz izopowierzchni (funkcja camproj). Przypisanie kątowi widoku kamery stałej wartości zabezpiecza przed
automatyczną regulacją kąta tak, by wszystkie obiekty znajdowały się w obserwowanej scenie (również i powiększenie przyjmuje
zadaną wielkość – funkcja camva).

camproj perspective
camva(25)

3. Źródła światła
Ustawienie źródła światła w miejscu ustawienia kamery oraz zmiana współczynników odbicia światła izopowierzchni i stożków
poprawia realizm sceny.

42

Animacja – przykłady (4)

Ustawienie źródła światła w miejscu ustawienia kamery pozwala na podświetlanie (efekt reflektora) filmowanej
sceny podczas przesuwania kamery wewnątrz izopowierzchni (funkcja camlight). Określenie współczynników
odbicia izopowierzchni umożliwia uzyskanie efektu ciemnego pomieszczenia (własność AmbientStrength =
0.1). Dodatkowo przyjęto wysoki współczynnik odbicia materiału (własność SpecularStrength = 1 oraz
DiffuseStrength = 1). Przyjęcie w przypadku stożków cechy SpecularStrength = 1 pozwala na uzyskanie
wysokiego odbicia światła:

hlight = camlight('headlight');
set(hpatch,'AmbientStrength',.1,...
'SpecularStrength',1,...
'DiffuseStrength',1);
set(hcone,'SpecularStrength',1);
set(gcf,'Color','k')

43

Animacja – przykłady (4)

4. Cieniowanie sceny
W przykładzie ustalono źródła światła, stąd konieczne jest wykonanie cieniowania sceny.

lighting gouraud

set(gcf,'Renderer','OpenGL')

lub:

lighting phong
set(gcf,'Renderer','zbuffer')

5. Definiowanie trajektorii kamery i linii prądu
Linie prądu obrazują kierunek przepływu w polu prędkości. W przykładzie użyto współrzędne x, y i z danych pojedynczej
linii prądu do zdefiniowania trajektorii przebiegającej przez zadaną objętość. Po trajektorii tej przemieszcza się kamera.

44

Animacja – przykłady (4)

Wygenerowano linię prądu rozpoczynające się w punkcie o współrzędnych: x = 80, y = 30, z = 11. Przy
pomocy funkcji get pobrano współrzędne x, y, z linii prądu, następnie usunięto linię prądu (w programie
MATLAB istnieje również możliwość użycia funkcji stream3 do obliczeń parametrów linii prądu bez rysowania jej
w oknie rysunkowym).

hsline = streamline(x,y,z,u,v,w,80,30,11);

xd = get(hsline,'XData');
yd = get(hsline,'YData');
zd = get(hsline,'ZData');
delete(hsline)

6. Przelot kamery
W celu uzyskania przelotu kamery przez scenę zastosowano zmianę położenia kamery i punktu, na który
skierowana jest kamera wzdłuż tej samej trajektorii.

45

Animacja – przykłady (4)

W przykładzie celem kamery jest pięć elementów znajdujących się przed kamerą wzdłuż osi x lokalnego układu współrzędnych
kamery. Dodanie niewielkiej wartości do położenia kamery w kierunku x lokalnego układu współrzędnych zabezpiecza przed
przypadkiem, w którym kamera i cel kamery znajdują się w jednym punkcie (co następuje, gdy spełniony jest warunek: xd(n) =
xd(n+5)). Przelot kamery uzyskano:
1) zmieniając położenie kamery i celu kamery – obydwa obiekty poruszają
się wzdłuż zadanych współrzędnych linii prądu,
2) przesuwając źródło światła wraz z kamerą,
3) używając funkcję drawnow wyświetlającą wynik animacji

for i=1:length(xd)-50
campos([xd(i),yd(i),zd(i)])
camtarget([xd(i+5)+min(xd)/100,yd(i),zd(i)])
camlight(hlight,'headlight')
drawnow
end

46

Animacja – przykłady (4)

47

Animacja – przykłady (4)

48

Animacja – przykłady (4)

49

Dziękuję za uwagę