Schemat Hornera

Schemat Hornera

Wykorzystanie schematu

Wykorzystanie schematu

Hornera

Hornera

Jest algorytmem klasycznym służącym do:

•

szybkiego obliczania wartości wielomianu,

•

przeliczania na postać dziesiętną liczb zapisanych w innym

systemie liczbowym

•

szybkiego podnoszenia do potęgi.

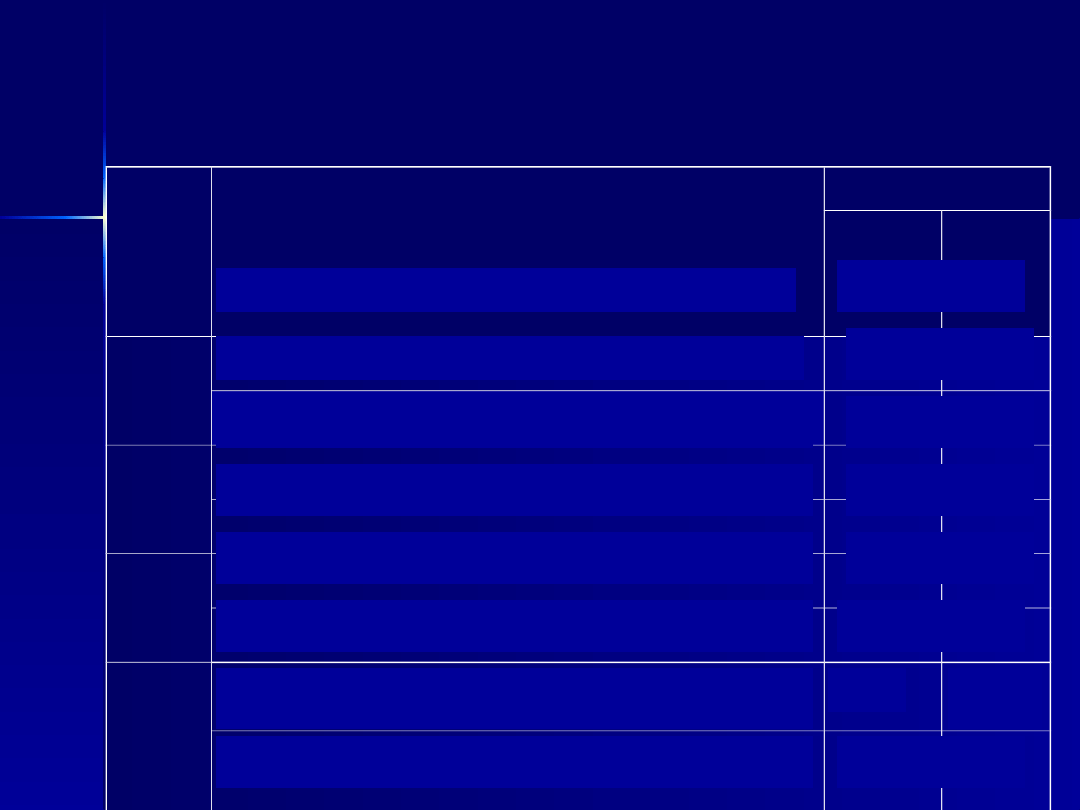
Analiza liczby działań (+, *) wykonanych

Analiza liczby działań (+, *) wykonanych

podczas obliczania wartości wielomianu

podczas obliczania wartości wielomianu

Stopie

Stopie

ń

ń

wielo

wielo

m.

m.

Postać wielomianu

Postać wielomianu

Liczba działań

Liczba działań

+

+

*

*

2

2

y=a

y=a

0

0

x

x

2

2

+a

+a

1

1

x+a

x+a

2

2

2

2

3

3

y=( a

y=( a

0

0

x + a

x + a

1

1

)x+ a

)x+ a

2

2

2

2

2

2

3

3

y=a

y=a

0

0

x

x

3

3

+a

+a

1

1

x

x

2

2

+a

+a

2

2

x+ a

x+ a

3

3

3

3

6

6

y=(( a

y=(( a

0

0

x + a

x + a

1

1

)x+ a

)x+ a

2

2

)x+ a

)x+ a

3

3

3

3

3

3

4

4

y=a

y=a

0

0

x

x

4

4

+a

+a

1

1

x

x

3

3

+a

+a

2

2

x

x

2

2

+ a

+ a

3

3

x + a

x + a

4

4

4

4

10

10

y=((( a

y=((( a

0

0

x + a

x + a

1

1

)x+ a

)x+ a

2

2

)x+ a

)x+ a

3

3

) x

) x

+ a

+ a

4

4

4

4

4

4

n

n

y=a

y=a

0

0

x

x

n

n

+a

+a

1

1

x

x

n-1

n-1

+…+a

+…+a

n-2

n-2

x

x

2

2

+ a

+ a

n-1

n-1

x + a

x + a

n

n

n

n

n(n+1)

n(n+1)

/2

/2

y=((…( a

y=((…( a

0

0

x + a

x + a

1

1

)x+…+ a

)x+…+ a

n-2

n-2

)x+ a

)x+ a

n-1

n-1

) x

) x

+

+

a

a

n

n

n

n

n

n

Zasada postępowania podczas obliczania

Zasada postępowania podczas obliczania

wartości wielomianu z zastosowaniem

wartości wielomianu z zastosowaniem

schematu Hornera

schematu Hornera

W celu obliczenia jego wartości, za początkową wartość wielomianu

należy przyjąć wartość współczynnika

a

0

, przy najwyższej potędze

zmiennej. Za każdym razem należy aktualną wartość wielomianu
pomnożyć przez

x

i dodać kolejny współczynnik.

Algorytm ten, zwany

schematem Hornera

, można zapisać

następująco:

y:= a

0

wartość początkowa wielomianu

y:= y*x+a

i

dla

i

=1,2,3,4,...,

n

– czynnik powtarzający się

(iteracja)

Schemat Hornera -lista kroków

Schemat Hornera -lista kroków

Specyfikacja

Dane

:

n

- nieujemna liczba całkowita (stopień wielomianu)

a

0

, a

1

, a2, ..., a

n

n+1 współczynników wielomianu

x

- wartość argumentu

Wynik

: Wartość wielomianu stopnia

n

dla wartości argumentu

x

Krok1

.

Za początkową wartość wielomianu przyjmij współczynnik
wielomianu przy zmiennej o najwyższej potędze.

y :=a

0

{y- zmienna pomocnicza}

Krok2

.

n

razy oblicz wartość dwumianu

y:=y*x+a

i

kolejnych

współczynników wielomianu, czyli dla

i

=1,2,...,n

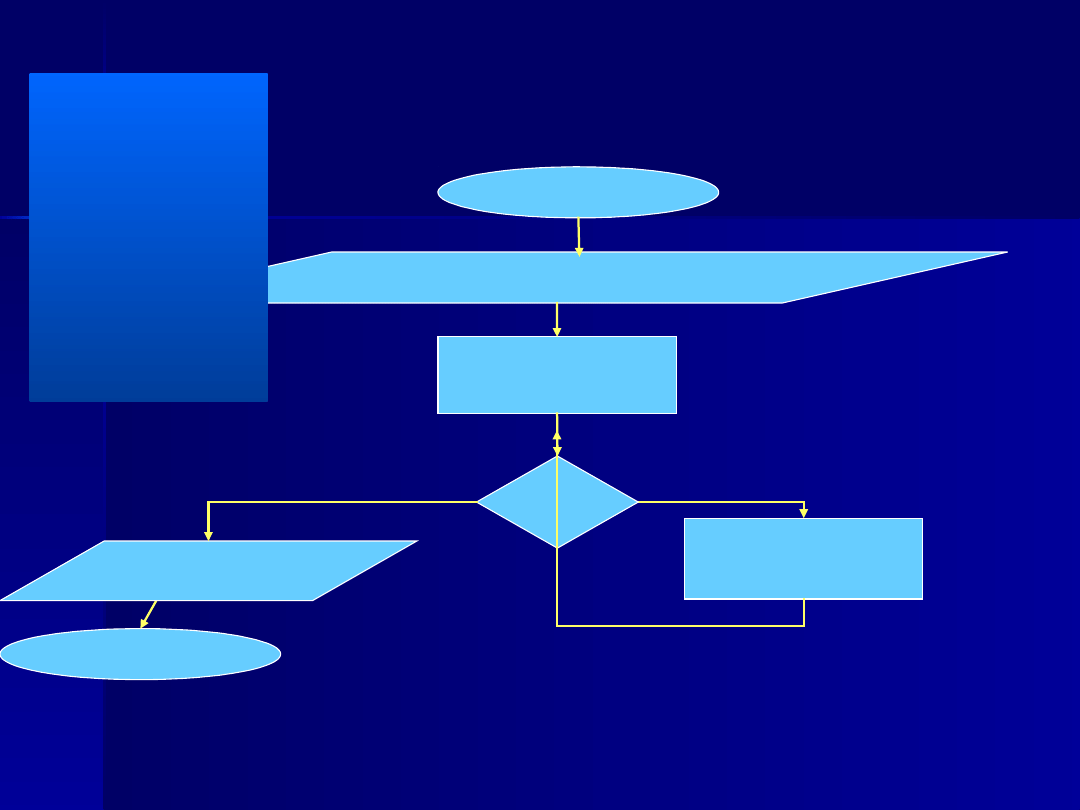
Schemat blokowy

Schemat blokowy

START

Wprowadź (n, x, a

i

, gdzie

i=0..n)

STOP

n=3, x=1, a={1,2,3,4}

y=1, i=1

KROK I

1>3

Nie

y=1*1+2; i=1+1

KROK II

2>3

Nie

Y=3*1+3; i=2+1

KROK III

3>3

Nie

y=6*1+4; i=3+1

KROK IV

4>3

Tak

Wypr

10

y :=y*x+a

i

i:=i+1

NIE

y := a

0

i:=1

i>n

TA
K

Wypr (y)

Zadania

Zadania

Zadanie1

Rozpisz wielomian 5 stopnia tak, aby można było obliczyć jego wartość
z zastosowaniem schematu Hornera.

Zadanie2

Oblicz, ile należy wykonać działań mnożenia i dodawania dla obliczenia

wartości wielomianu W(x) metodą klasyczną i za pomocą schematu
Hornera:

• 5 stopnia

• n-tego stopnia

Zadanie3

Wykonaj program obliczający wartość wielomianu stopnia

n

-tego za pomocą

schematu Hornera.

Współczynniki wielomianu:

a) wprowadź z klawiatury

b) generuj losowo

c) ustaw jako wartości stałe