Liczby Fibonacciego

Liczby Fibonacciego

 

 

 

 

 

 

Zarys historyczny problemu

Zarys historyczny problemu

1202 rok

 - włoski matematyk 

Leonardo Pisano

Leonardo Pisano

 odkrył sekwencję liczb 

analizując rozwój populacji królików w zagrodzie. 

Matematyk chciał przewidzieć, ile królików będzie w zagrodzie 

po określonej 

liczbie miesięcy.

 

Przyjął kilka założeń: 

•

  początkowo rodzi się 

1 para królików

•

  po miesiącu osiąga dojrzałość

•

  po kolejnym miesiącu rodzi następną parę i tak dalej, 

    tzn. pierwsza para wydaje potomstwo co miesiąc

•

  każda nowa para królików po miesiącu osiąga dojrzałość 

   i po każdym  następnym wydaje na świat kolejną parę królików

•

  proces ten nie ma końca

•

  zakładamy, że króliki żyją wiecznie. 

 

 

 

 

problem

problem

Pytanie:

Pytanie:

Ile królików będzie po 

n 

- miesiącach? 

Liczba królików w danym miesiącu 

(za wyjątkiem pierwszego i 

drugiego)

 zależy od dwóch wartości z poprzedniego miesiąca:

1.

 liczby par królików dorosłych

2.

 liczby par królików młodych. 

Młodych jest tyle, ile było dorosłych dwa miesiące wcześniej. 
Jeśli 

Fn

Fn

 to liczba królików w 

n

n

-tym miesiącu to:

 



















3

 

dla

         

2

,

1

 

dla

        

          

          

1

2

1

n

n

F

F

F

n

n

n

Liczby  Fibonacciego

Liczby  Fibonacciego 

–

 

ciąg  liczb  naturalnych,  o  własności:  każdy 

nastęny  wyraz  ciągu  (z  wyjątkiem  pierwszego  i  drugiego)  jest  sumą 

dwóch poprzednich, (tj. 1, 1, 2, 3, 5, 8,…).

 

 

 

 

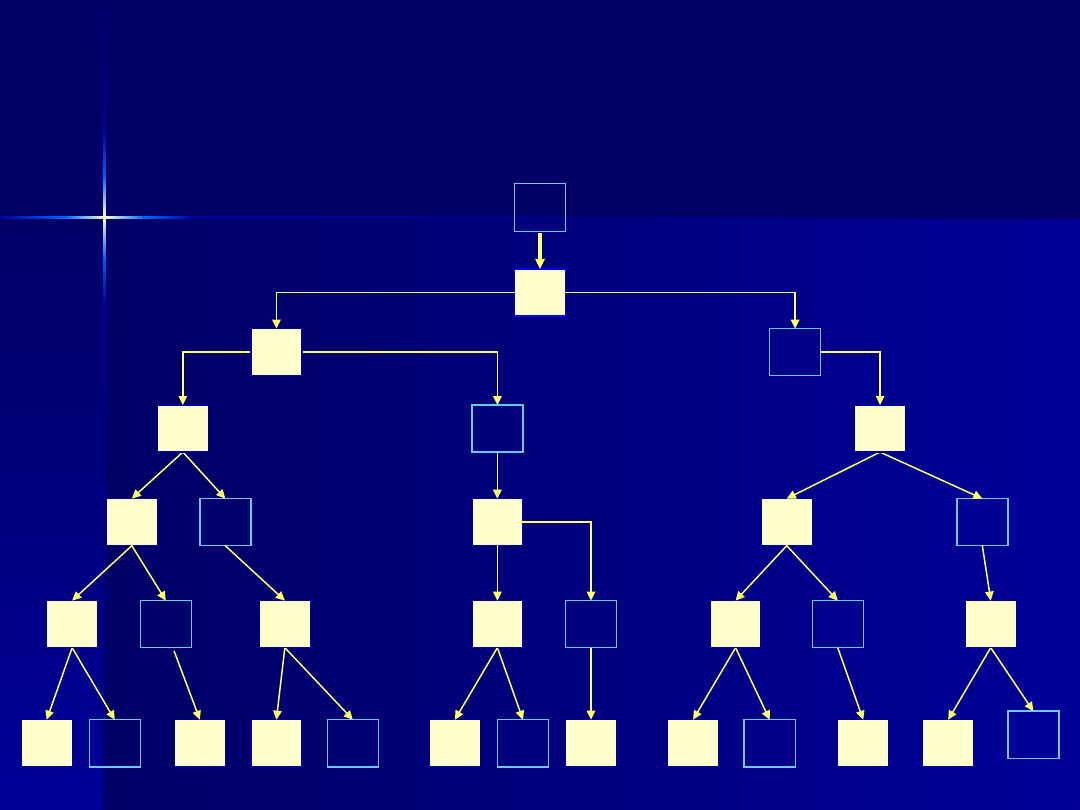
Graficzna prezentacja

Graficzna prezentacja

M

M

D

D

D

D

M

M

D

D

D

D

M

M

D

D

M

M

D

D

D

D

M

M

D

D

M

M

D

D

D

D

M

M

D

D

D

D

M

M

D

D

D

D

M

M

D

D

M

M

D

D

D

D

M

M

D

D

D

D

M

M

D

D

M

M

 

 

 

 

Ciekawostki

Ciekawostki

 

 

Istnieje ciekawa zależność między wyrazami ciągu Fibonacciego:

Stosunek sąsiednich wyrazów wynosi około 0,618 lub 

1,618.

 

Liczba 1,618 

nosi nazwę

 

złotej proporcji

złotej proporcji

.

.

 

W odcinku podzielonym na dwie części zgodnie z zachowaniem 
złotej proporcji większa część pozostaje takiej samej relacji do 
mniejszej, jak całość do większej.

Złote proporcje są wykorzystywane (w architekturze-Partenon w 
Atenach gotyckie katedry; dzieła Mozarta i Bethowena, wysokość 
do pępka to 0,618 wysokości ciała, konstrukcje wiolonczeli).

 

 

 

 

Algorytm obliczania  liczb 

Algorytm obliczania  liczb 

Fibonacciego

Fibonacciego

 

 

Dane: 
 

n

 – 

który wyraz ciągu Fibonacciego ma być policzony (liczba naturalna)

Wynik:
 

Fn 

- wartość 

n 

- tego wyrazu ciągu (liczba naturalna)

1.

Rozpocznij algorytm

2.

Podaj wartość 

n

3.

Jeżeli 

n 

=1 lub 

n 

=2 to 

Fn

 przypisz wartość 1 (

Fn

:=1) i przejdź do 

kroku 5

w przeciwnym razie 

f1

:=1, 

f2

:=1

, i

:=2 i przejdź do 

kroku 4

4.

Dopóki 

i

 nie jest równe 

n

 wykonuj: 

Fn

:=

f1

+

f2

, 

f1

:=

f2

, 

f2

:=

Fn

, 

i:=i+1

5.

Wyprowadź wynik 

Fn

6.

Zakończ algorytm.

Zmienne pomocnicze:
 

f1

, 

f2

 – sąsiednie wyrazu ciagu; 

 i 

- licznik pętli -kolejny wyraz

 

 

 

 

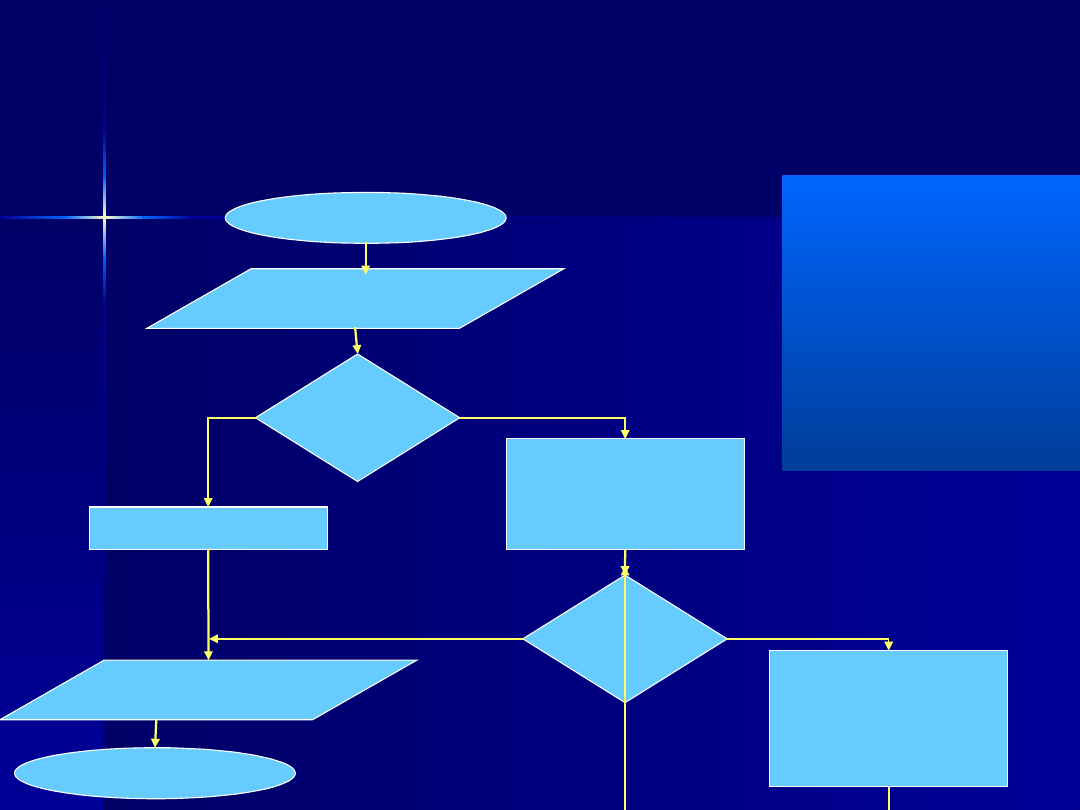
Schemat blokowy

Schemat blokowy

 

 

START

Wprowadź 
(n)

n>2

i=n

STOP

n=4

4>2 (n>2) Tak

f1=1, f2=1, i=2

KROK I

  2=4 

Nie

Fn=1+1; f1=1; f2=2; i=2+1

KROK II

 3=4 

Nie

Fn=1+2; f1=2; f2=3; i=3+1

KROK III

 4=4 

Tak

Wypr

 3

f1:=1
f2:=1

i:=2

TA
K

TA
K

Fn:=f1+f2

f1:=f2

f2:=Fn

i:=i+1

NIE

NIE

Fn:=1

Wypr (Fn)

 

 

 

 

Zadania

Zadania

 

 

Zadanie1

Napisz program wyznaczający wyraz ciągu Fibonacciego, 
którego numer wprowadzany jest z klawiatury.

Zadanie2

Zmodyfikuj program z zadania 1, tak aby sprawdzał czy 
wprowadzony numer ciągu jest mniejszy od 24, jeśli nie jest – 
ponownie prosi o jego podanie instruując przy tym, jaką 
wartość może osiągać ten numer.

Zadanie3

Zmodyfikuj program wyznaczający wyraz ciągu Fibonacciego. 
Zdefiniuj procedurę z parametrem przekazywanym przez 
wartość,
np. 

procedure fib(k:integer); 

parametr to numer elementu 

ciągu