Algorytmy na liczbach

Algorytmy na liczbach

naturalnych

naturalnych

Generowanie liczb pierwszych – sito

Generowanie liczb pierwszych – sito

Eratostenesa

Eratostenesa

Sposoby generowania liczb

Sposoby generowania liczb

pierwszych

pierwszych

Podejście naiwne

do

generowania liczb pierwszych

polega

na sprawdzeniu dla każdej liczby wszystkich jej podzielników
większych od 1, a mniejszych od niej samej. Jeżeli liczba nie
posiada takich podzielników, to jest liczbą pierwszą.
Algorytm ten jest algorytmem o złożoności obliczeniowej rzędu

O(n2).

Optymalizacja algorytmu

wynika z faktu, że jeżeli liczba nie

jest podzielna przez żadną liczbę większą od 1, a mniejszą lub
równą swojemu pierwiastkowi kwadratowemu, to na pewno nie
będzie podzielna przez liczby podzielna przez liczby większe od
tego pierwiastka.

Pozwoli to na przyspieszenie algorytmu – złożoność
obliczeniowa będzie rzędu

O(n*n^(1/2)).

generowania liczb pierwszych

generowania liczb pierwszych

–

–

podejście naiwne

podejście naiwne

Specyfikacja

Dane

:

n

- liczba naturalna, określająca górną granicę przedziału liczb

naturalnych, w którym wyszukujemy liczb pierwszych

Wynik

:

liczby pierwsze z wyznaczonego przedziału liczby

naturalnych

Krok1

.

Wczytaj liczbę

n.

Krok2

.

Każdą liczbę z przedziału

(2, n)

dzielimy przez kolejne liczby naturalne od

2

do

n-1

. Jeżeli żadna z liczb nie jest dzielnikiem danej liczby tzn. że

analizowana liczba jest liczbą pierwszą, wypisujemy ją.

Krok3

.

Zakończ algorytm.

KROK IV

5>5

Nie

P:=True;

j:=2

krok a)

p and 2< 5

Tak

;

czy 5 mod 2 = 0

Nie

;

j:=2+1;

krok b)

p and 3< 5

TAK

;

Czy 5 mod 3 = 0

Nie

;

j:=3+1;

krok c)

p and 4< 5

TAK

;

Czy 5 mod 4 = 0

Nie

;

j:=4+1;

krok d)

p and 5< 5

NIE

;

Czy P

TAK

;

wypisz 5 i:=5+1;

KROK IV

6>5

TAK

STOP

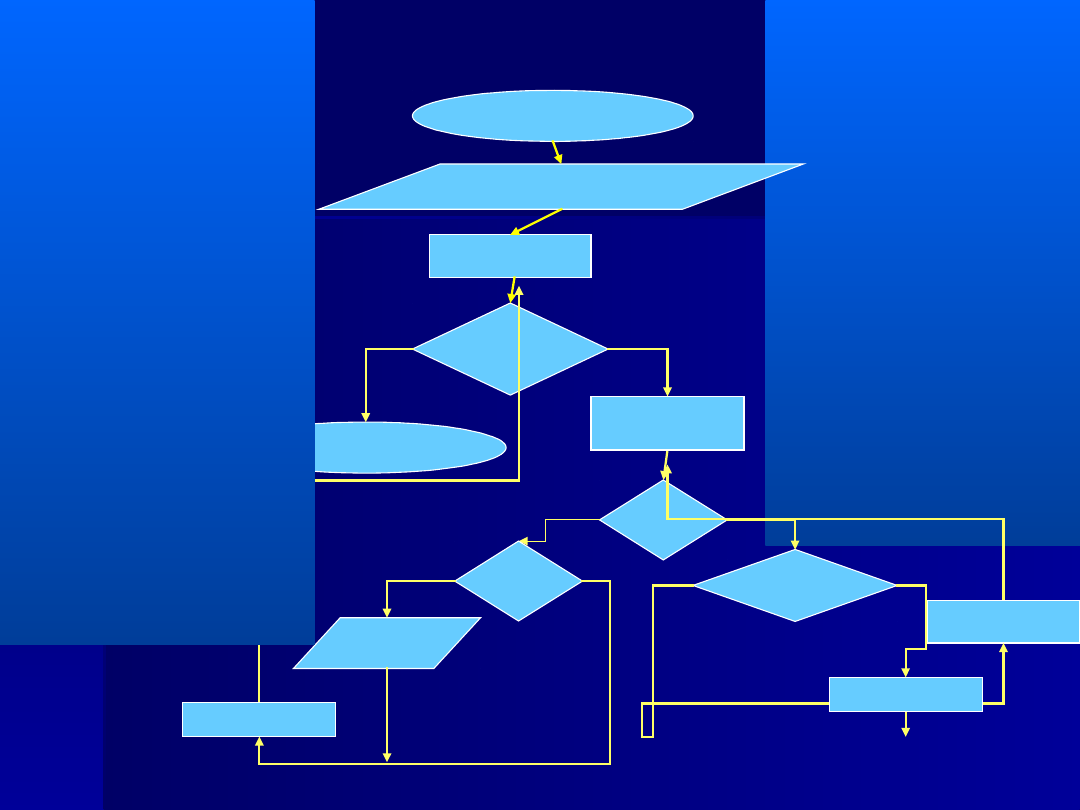
Schemat blokowy

Schemat blokowy

– podejście naiwne

– podejście naiwne

START

Wprowadź (n)

i:=2;

i>n

P and
j<i

TAK

STOP

NIE

P:=TRUE

j:=2

TAK

i mod j =0

NIE

P

Wypr (i)

TAK

j:=j+1

NIE

P:=FALSE

TAK

n=5; i:=2

KROK I

2>5

Nie

P:=True; j:=2

krok a)

p and 2< 2

Nie

;

czy P

TAK

;

wypisz

2

; i:=2+1;

KROK II

3>5

Nie

P:=True; j:=2

krok a)

p and 2< 3

TAk

;

czy 3 mod 2 = 0

Nie

;

j:=2+1;

krok b)

p and 3< 3

NIE

;

Czy P

Nie

;

wypisz

3

; i:=3+1;

KROK III

4>5

Nie

P:=True;

j:=2

krok a)

p and 2< 4

Tak

;

czy 4 mod 2 = 0

TAK

;

P := FALSE; j:=2+1;

krok b)

p and 3< 4

NIE

;

Czy P

Nie

;

i:=4+1;

NIE

i:=i+1

Zadania

Zadania

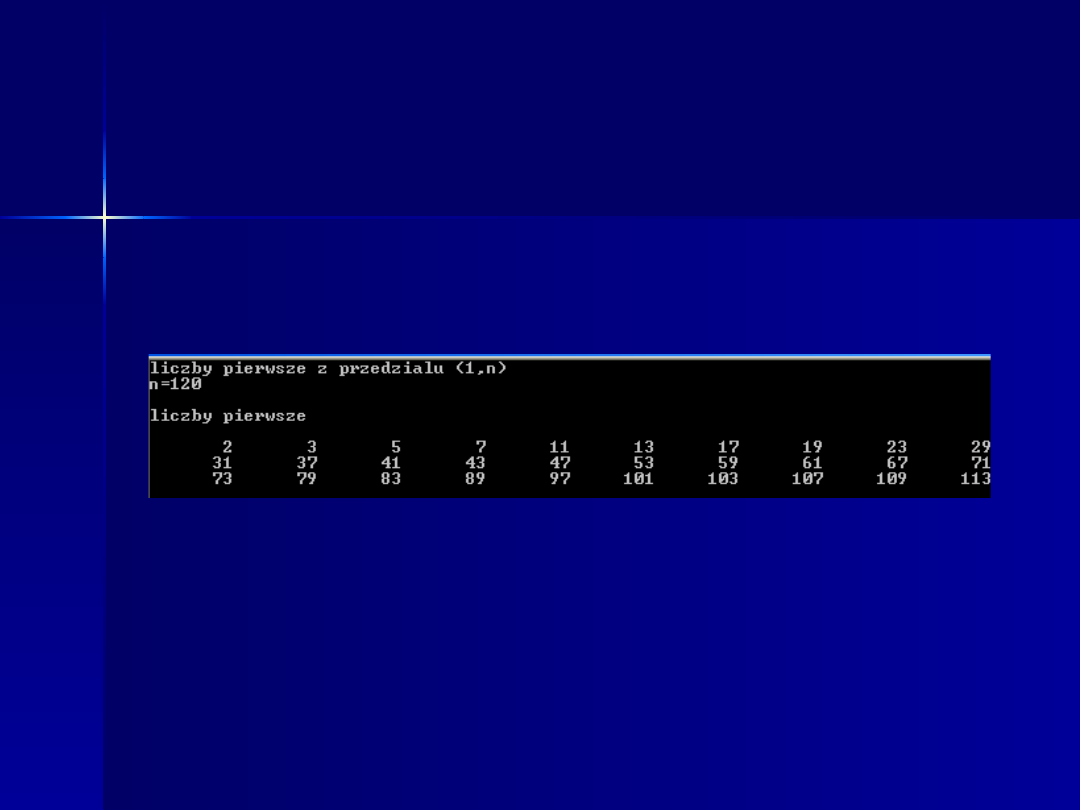
Zadanie1

Napisz program wypisujący wszystkie liczby pierwsze z przedziału liczb
naturalnych (1,

n

> korzystając z algorytmu naiwnego.

n

wprowadzamy

z klawiatury.

Zadanie2

Zmodyfikuj kod program z

zadania1

, tak aby sprawdzał tylko, czy liczba

naturalna ma dzielniki

<=

n^(1/2).

Jeżeli nie ma, to traktował taką

liczbę jako liczbę pierwszą i wypisywał ją na ekranie.

Sposoby generowania liczb

Sposoby generowania liczb

pierwszych

pierwszych

cd.

cd.

Algorytm Eratostenesa

- grecki matematyk Eratostenes z

Cyreny, żyjący na przełomie II i III wieku p.n.e. zauważył, że:

liczby niepierwsze są wielokrotnościami kolejnych liczb

pierwszych

(np. 4, 6, 8, 10…są wielokrotnościami 2; natomiast 6,9,12, …
są wielokrotnościami 3 itd.).

Wystarczy więc z tablicy wszystkich liczb naturalnych
wykreślić kolejno wielokrotności 2, z liczb które pozostaną
wykreślić wielokrotności 3, potem wielokrotności 5, potem
wielokrotności liczby 7 itd. Łatwo zauważyć, że wykreślamy
wielokrotności kolejnych już uzyskanych liczb pierwszych.
Liczby, które pozostaną w tablicy są liczbami pierwszymi.
Złożoność obliczeniowa algorytmu jest rzędu

O(n).

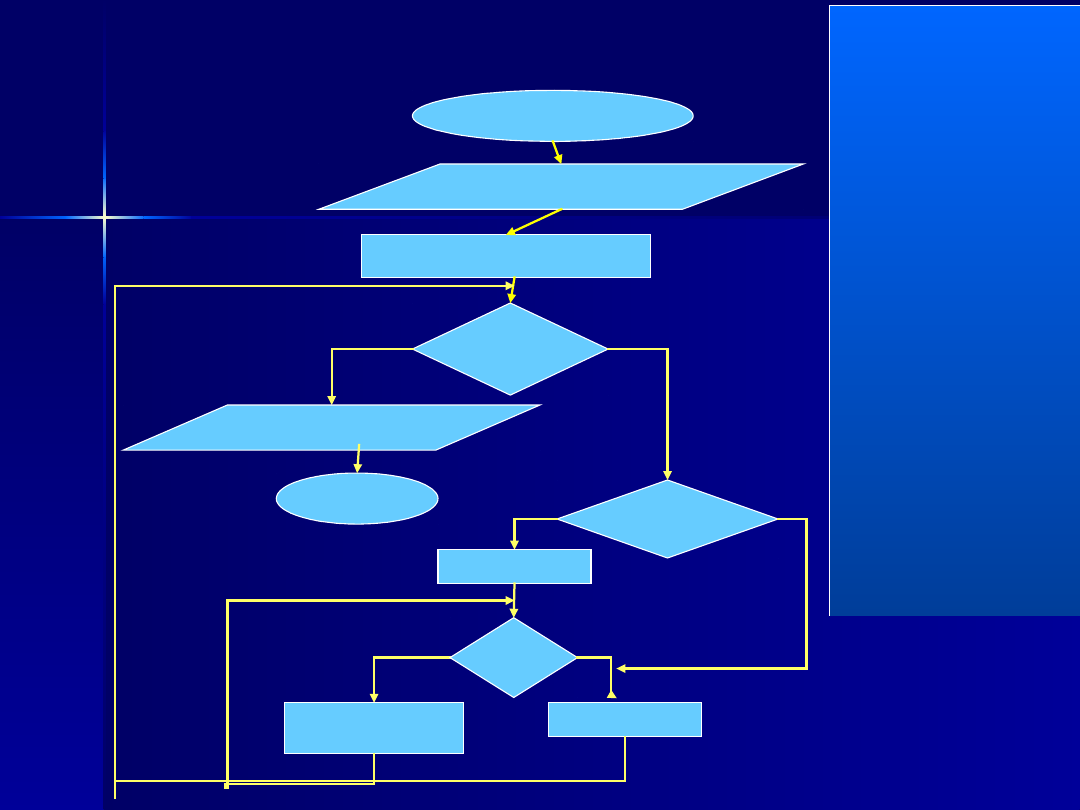
Schemat blokowy

Schemat blokowy

– sito Eratostnenesa

– sito Eratostnenesa

START

Wprowadź (n,

sito[2

..n]=true)

i:=2;

s:=round(sqrt(n))

i>s

sito[i]
=true

NIE

TAK

sito[j]:=FALSE

j:=j+i

n=7;

sito[2]=true;
sito[3]=true;

sito[4]=true;
sito[5]=true;

sito[6]=true;
sito[7]=true;

i:=2; s=7^(1/2)

KROK I

2>s

Nie

sito[2]=true

TAK

j:=2+2

krok a)

4<=7

TAK

sito[4]=false; j=4+2=6

krok b)

6<=7

TAK

sito[6]=false; j=6+2=8

krok c)

8<=7

NIE

i:=2+1=3

KROK II

3>s

TAK

Wypisz

2 3 5 7

STOP

TAK

j:=i+i

j<=n

TAK

Wypisz i, gdy sito[i]=true

STOP

NIE

NIE

i:=i+1

Zadania

Zadania

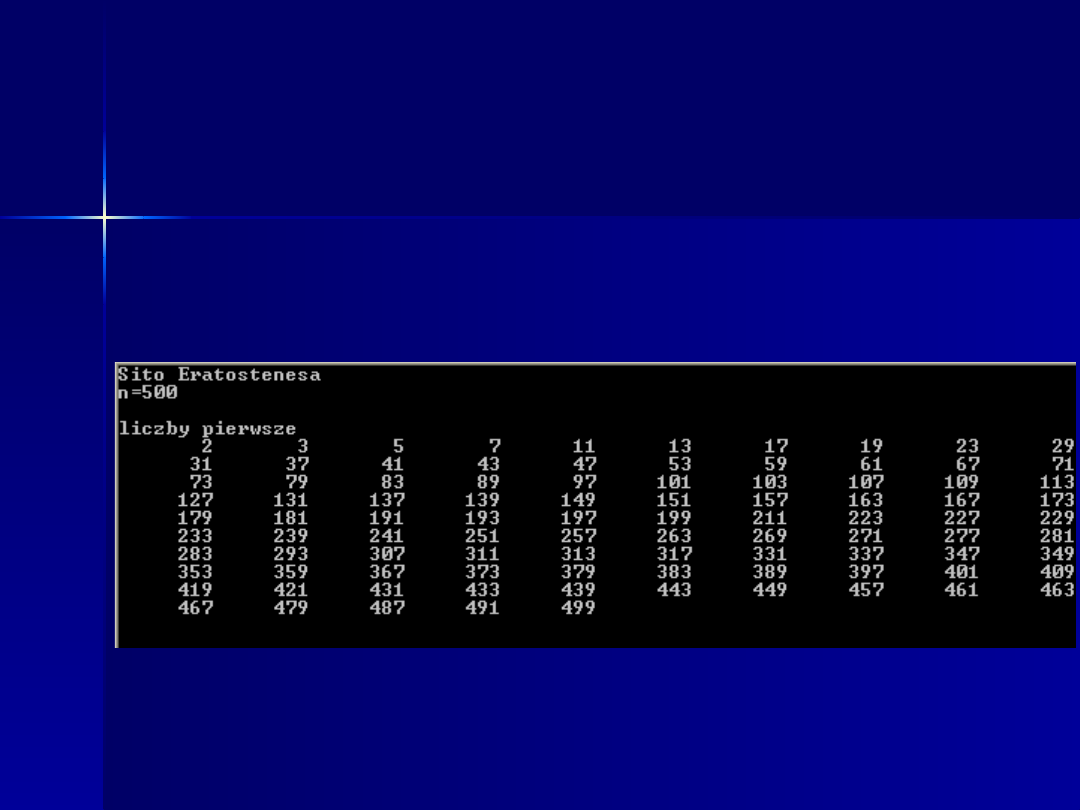
Zadanie1

Napisz program wypisujący wszystkie liczby pierwsze z przedziału liczb
naturalnych (1,

n

> wykorzystując w programie sito Eratostenesa.

n

wprowadzamy z klawiatury.