Metody numeryczne

szukanie pierwiastka metodą

stycznych

Dawid Rasała

Metoda stycznych (Newtona) opiera się na następującej zasadzie:

dla danego przybliżenia początkowego x

0

tworzy się ciąg x

1

, x

2

, …

Element x

n+1

wyznaczamy aproksymując funkcję f(x) styczną do jej

wykresu w punkcie (x

n

, f(x

n

)) i wybierając x

n+1

jako odciętą punktu

przecięcia tej stycznej z osią x. Dlatego do wyznaczenia x

n+1

służy

równanie:

f(x

n

) + (x

n+1

- x

n

)f’(x

n

) = 0

Metoda stycznych

Metody numeryczne
Dawid Rasała

Metodę Newtona określa następujący wzór iteracyjny:

x

n+1

= x

n

+ h

n

gdzie h

n

= -f(x

n

)/f’(x

n

)

Metoda stycznych

Metody numeryczne
Dawid Rasała

1. Sprawdzamy, czy w punkcie x0 funkcja spełnia warunek:

f’(x

0

) f’’(x

0

) > 0

2. Obliczamy kolejną iterację z wcześniej podanego wzoru.

3. Sprawdzamy, czy otrzymane przybliżenie jest dostatecznie

bliskie zeru.

Kroki algorytmu

Metody numeryczne
Dawid Rasała

Jeżeli dany jest przedział [a,b] występowania pierwiastka, to

możemy posłużyć się następującą zasadą wyboru punktu

początkowego, aby proces był stabilny:

1.jeżeli f’(a) f’’(a) > 0 to x

0

= a;

2.jeżeli f’(a) f’’(a) < 0 to x

0

= b.

Oczywiście na krańcach przedziału funkcja musi posiadać

przeciwne znaki, gdyż gwarantuje to istnienie pierwiastka.

Wybieranie punktu początkowego w

przypadku, gdy dany jest przedział izolacji

pierwiastka

Metody numeryczne
Dawid Rasała

1. wartość f(x

n

) leży dostatecznie blisko zera – o mniej niż zadana

dokładność

2. wartość h

n

jest mniejsza od zadanej dokładności

Warunki zakończenia algorytmu

Metody numeryczne
Dawid Rasała

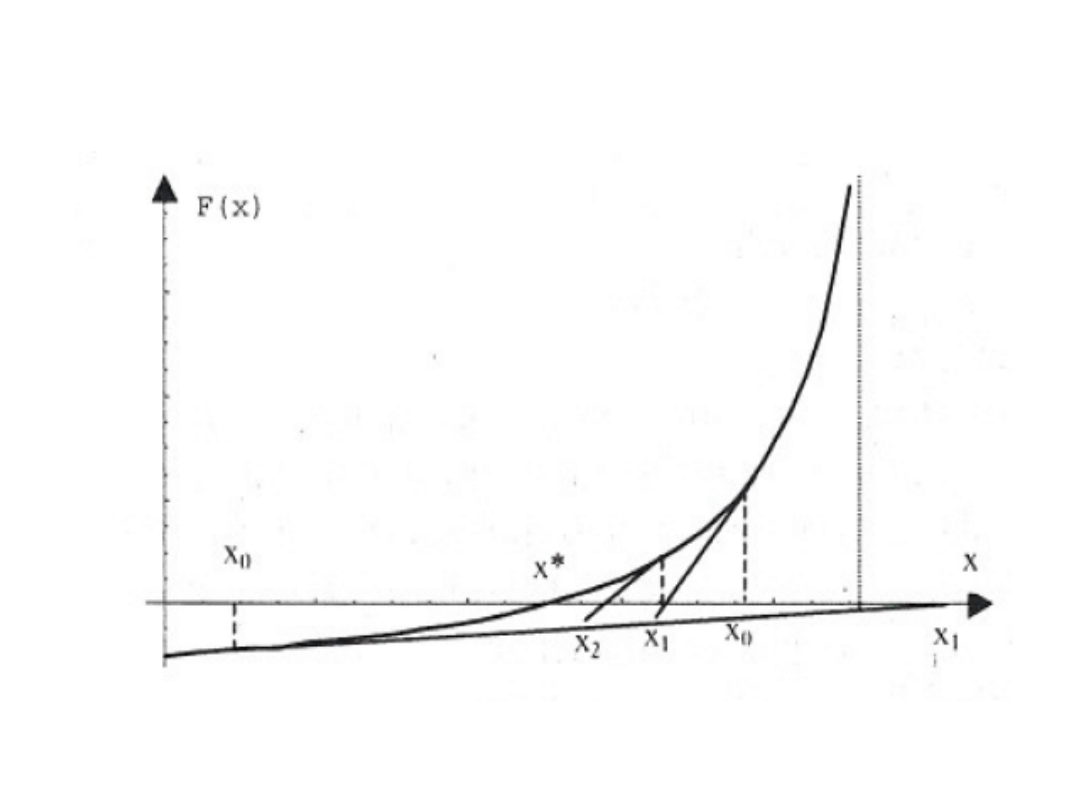
Wybór punktu początkowego przy którym

funkcja staje się nieokreślona

Metody numeryczne
Dawid Rasała

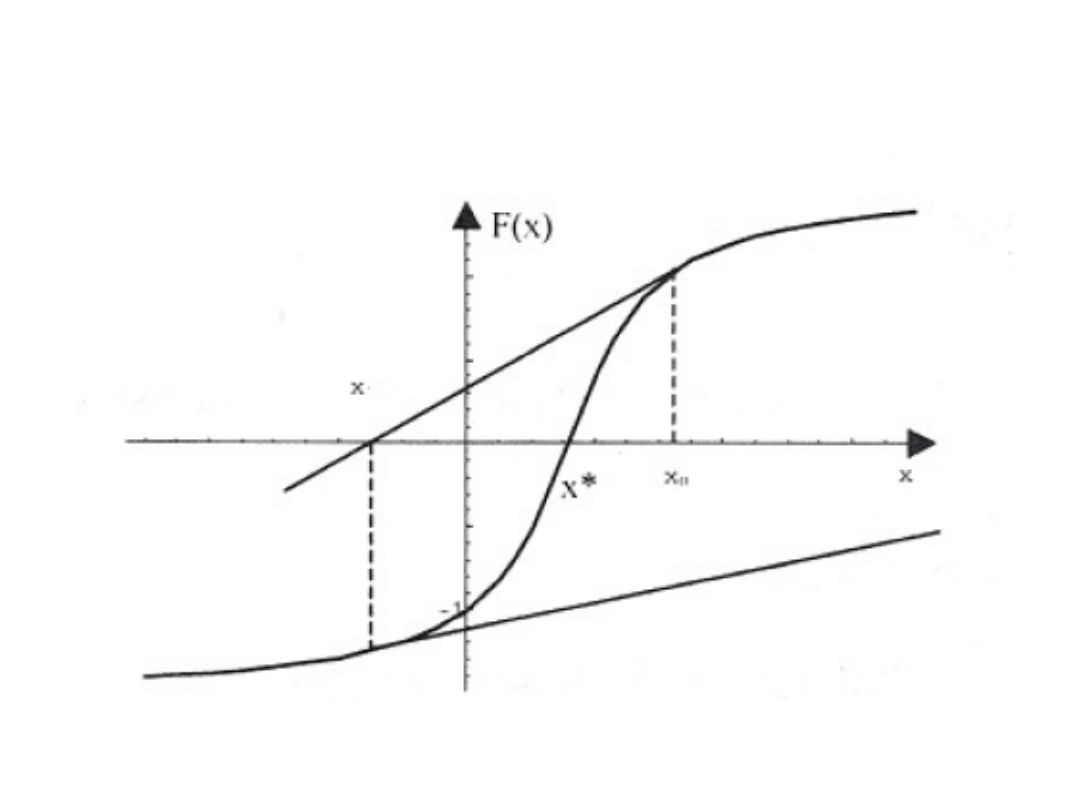
Wybór punktu początkowego przy którym

kolejne przybliżenia oddalają się od

pierwiastka

Metody numeryczne
Dawid Rasała

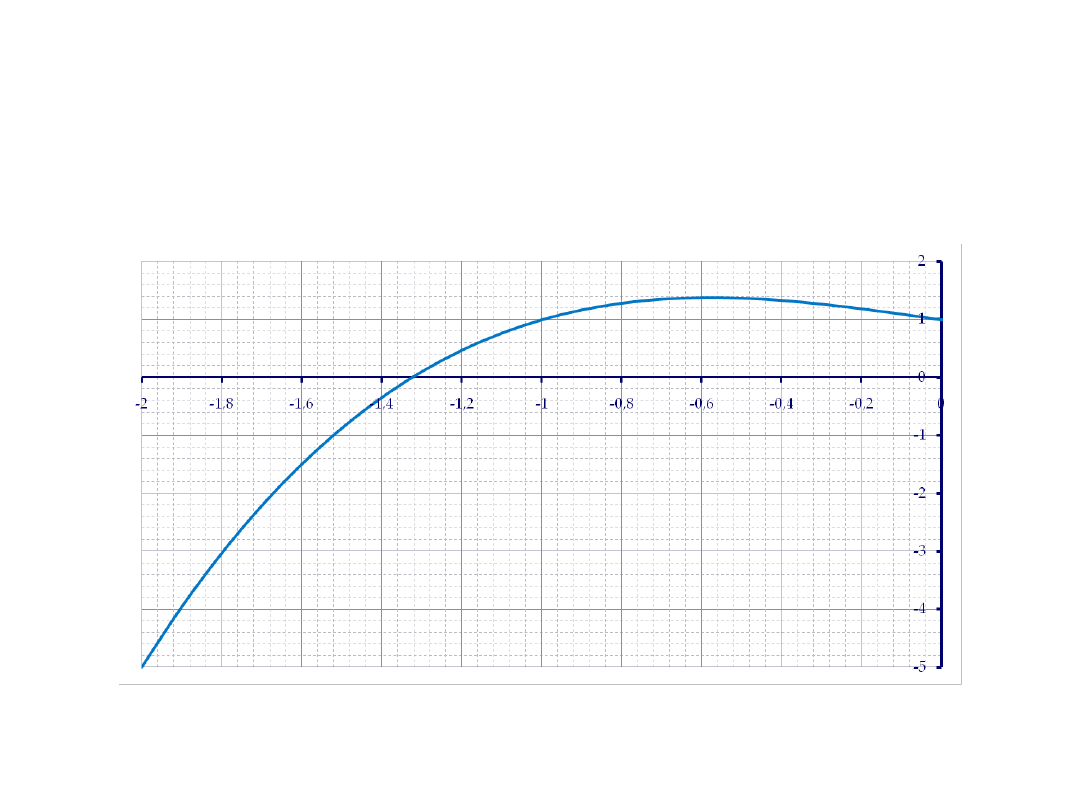
Wyznaczyć pierwiastek równania x

3

− x + 1 = 0. Przyjmijmy x

0

=

-1,8.

Przykład

Metody numeryczne
Dawid Rasała