Podstawy Sztucznej 

Inteligencji

Jan Kusiak

Sieci dynamiczne

sieci rekurencyjne, 
sieci Hopfielda,
pamięci asocjacyjne,
sieci asocjacyjne

Podstawy Sztucznej 

Inteligencji

Jan Kusiak

Dynamiczne Sieci Neuronowe

Sieć neuronowa jest statyczna gdy:

wyjście sieci w danej chwili jest 

zależne 

jedynie od wejść w tej chwili:

Sieć neuronowa jest dynamiczna gdy:

wyjście sieci w danej chwili jest 

zależne od  wejść  w danej chwili oraz w 
chwilach 

poprzednich:

€ 

y(t) =h(x(t))

Dynamika w sieciach może być uzyskana 
poprzez zastosowanie: linii opóźniających 
i/lub rekurencji.

Sieci takie dzielimy na: dynamiczne sieci 
jednokierunkowe oraz rekurencyjne.

  

€ 

y(t)=h(x(t), x(t−1),K ,x(0),y(0))

Podstawy Sztucznej 

Inteligencji

Jan Kusiak

Dynamiczne 
sieci 
jednokierunko
we

Podstawy Sztucznej 

Inteligencji

Jan Kusiak

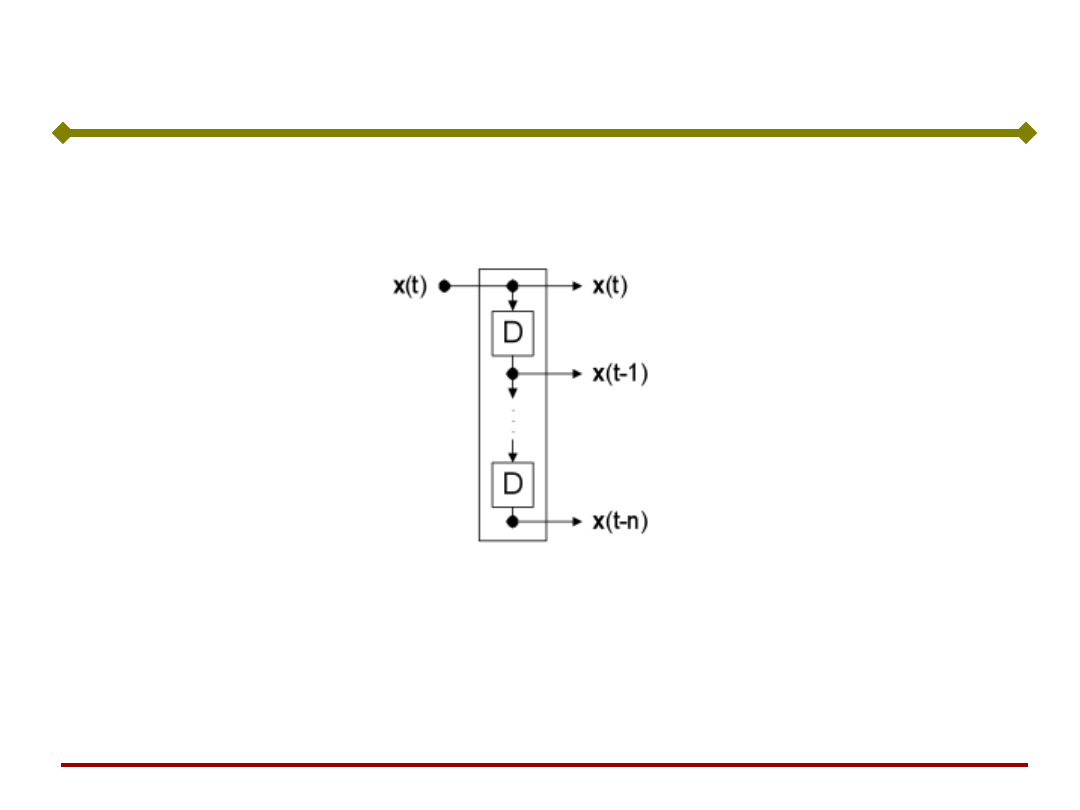
Linia opóźniająca

Podstawy Sztucznej 

Inteligencji

Jan Kusiak

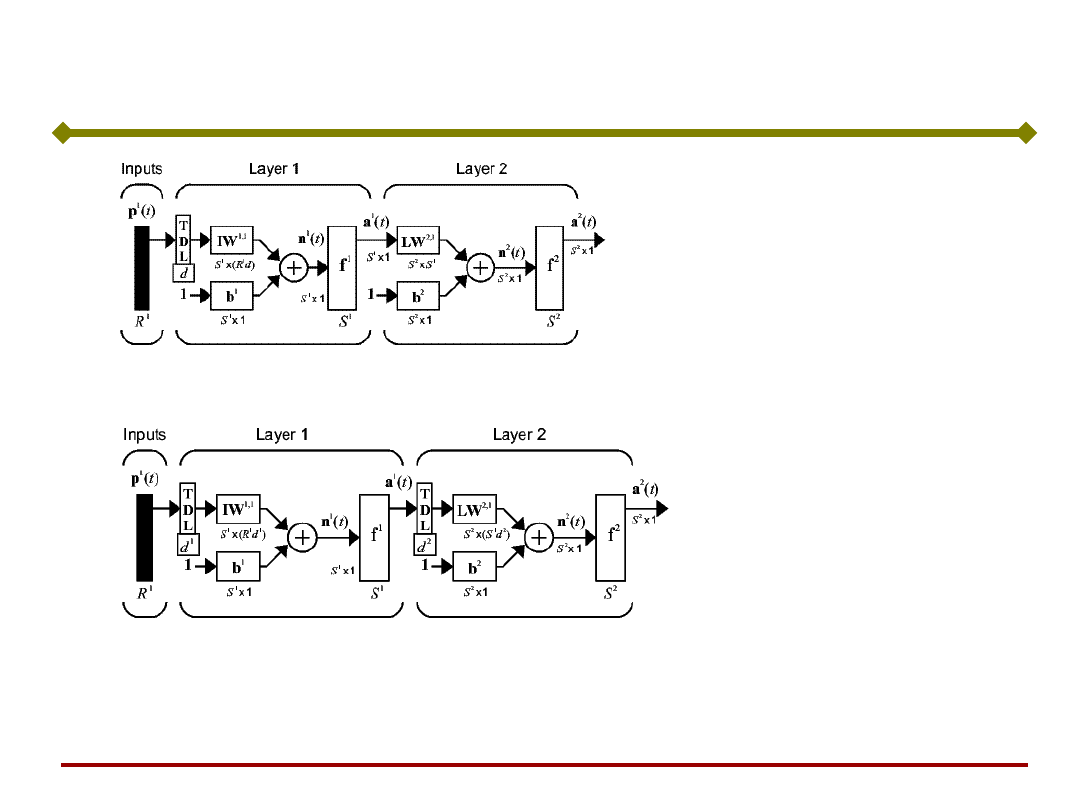
Dynamiczne Sieci Jednokierunkowe

(FTDNN)

(DTDNN)

))

(

,

),

1

(

),

(

(

)

(

d

t

u

t

u

t

u

h

t

y









))

(

,

),

1

(

),

(

(

)

(

1

d

t

u

t

u

t

u

h

t

a









))

(

,

),

1

(

),

(

(

)

(

1

1

1

d

t

a

t

a

t

a

g

t

y









Podstawy Sztucznej 

Inteligencji

Jan Kusiak

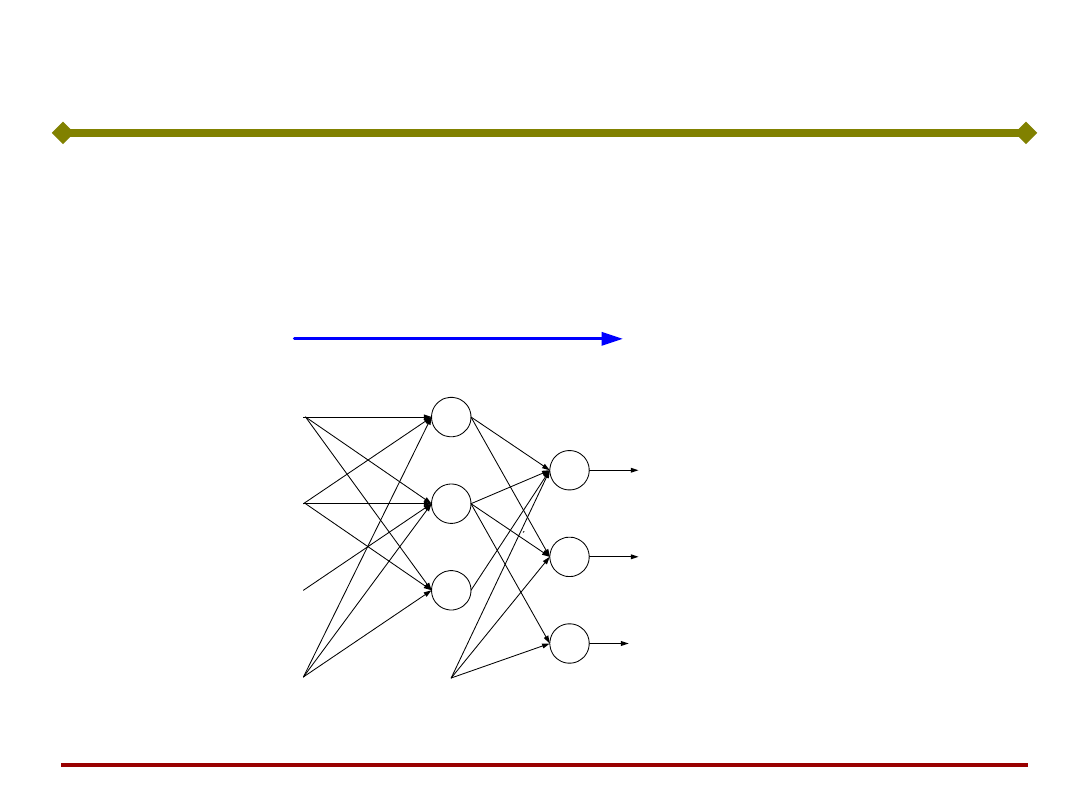
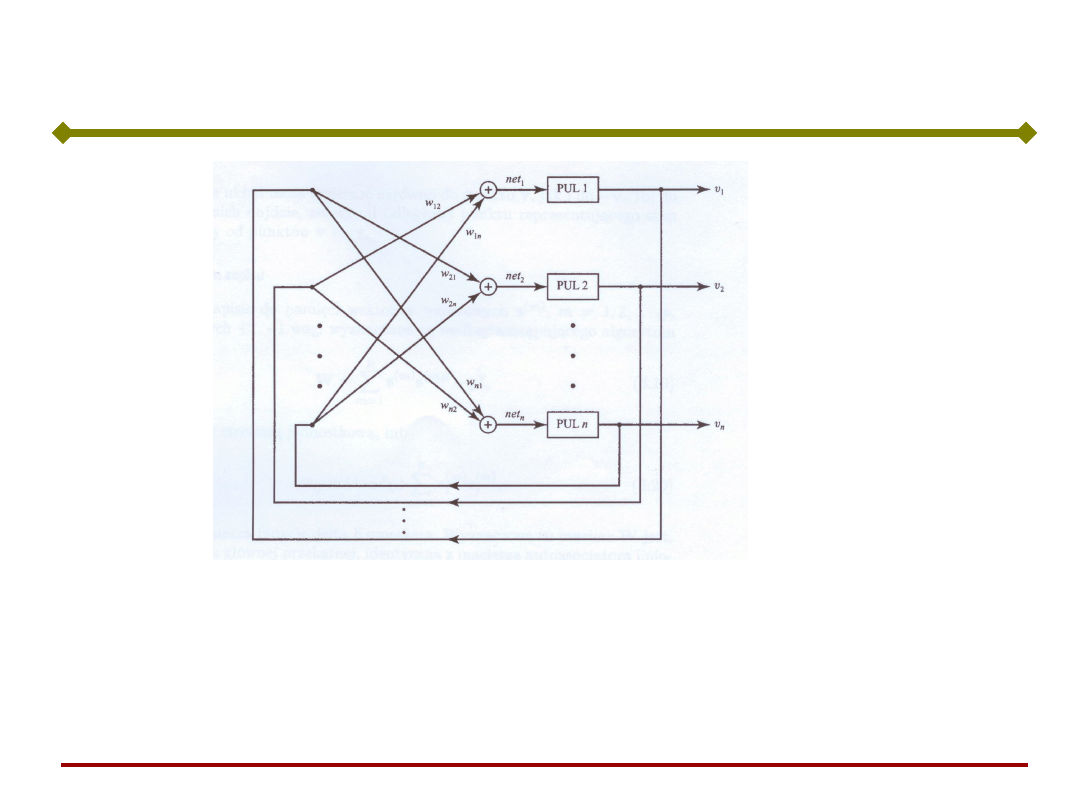
W rozważanych dotychczas sieciach sygnał był 
przekazywany w jednym kierunku – od wejścia do 
wyjścia (sieci jednokierunkowe, feedforward networks).

Sieci rekurencyjne (ze sprzężeniem zwrotnym, 
dynamiczne, pamięci asocjacyjne)

1

J -1

j

x

1

x

i

x

I-1

z

1

z

k

z

K

v

11

v

j1

v

1i

v

1i

v

1I

v

j1

v

ji

v

jI

v

J -1,I

.

.

.

.

.

.

.

.

.

.

.

.

x

J

 = -1

w

11

v

11

1

K

k

.

.

.

.

.

.

y

J

 = -1

w

k1

w

1j

w

kj

w

Kj

w

kJ

w

KJ

w

1J

warstwa wyjściowa

warstwa ukryta

WE

(x)

WY

(z)

Podstawy Sztucznej 

Inteligencji

Jan Kusiak

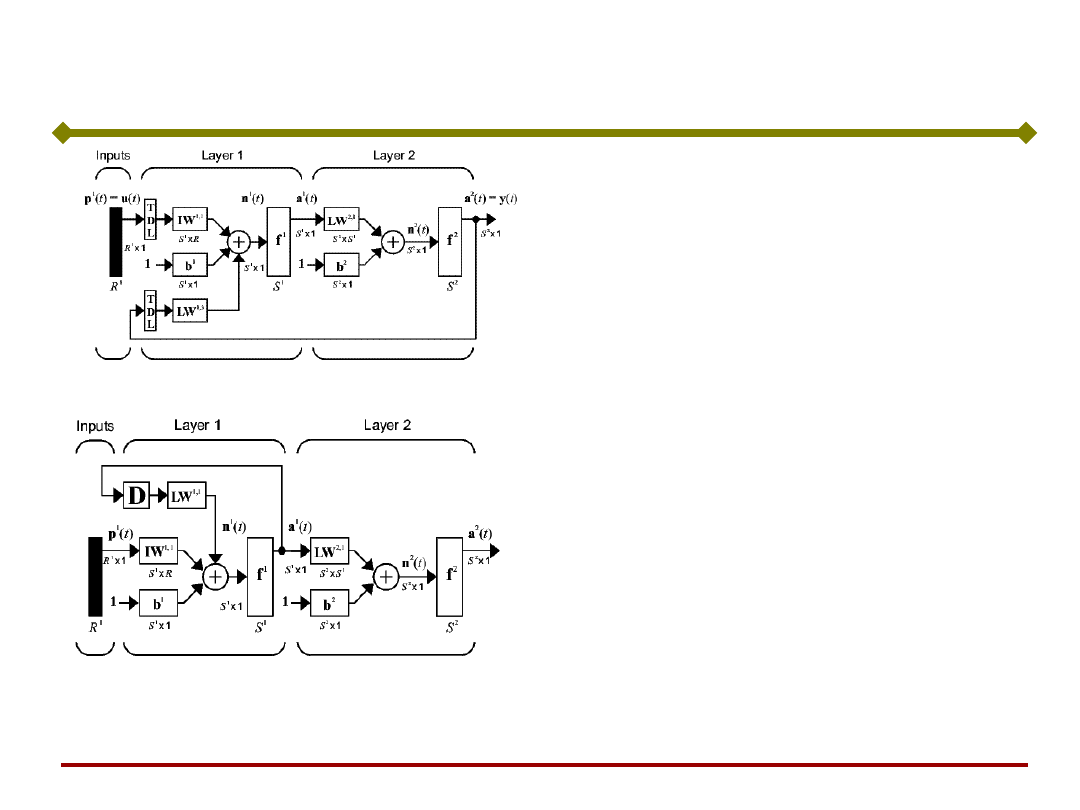
Sieci Rekurencyjne

(NARX)

(LRN)

)

),

1

(

),

(

,

),

2

(

),

1

(

(

)

(













t

u

t

u

t

y

t

y

h

t

y

))

(

),

1

(

(

)

(

1

1

t

u

t

a

h

t

a





))

(

(

)

(

1

t

a

g

t

y 

Podstawy Sztucznej 

Inteligencji

Jan Kusiak

Sieci Hopfielda 
(sieć asocjacyjna, 
pamięć 
asocjacyjna)

Podstawy Sztucznej 

Inteligencji

Jan Kusiak

Sieci asocjacyjne (sieci Hopfielda) -  klasa sieci rekurencyjnych, 
które dają możliwość rekonstrukcji i rozpoznawania wcześniej 
zapamiętanych wzorców na podstawie skojarzeń, bazując na 
dostępnym fragmencie wzorca lub wzorca podobnego do niego.

Są wykorzystywane do modelowania pamięci skojarzeniowej. 

Sieć Hopfielda (1982)

Podstawy Sztucznej 

Inteligencji

Jan Kusiak

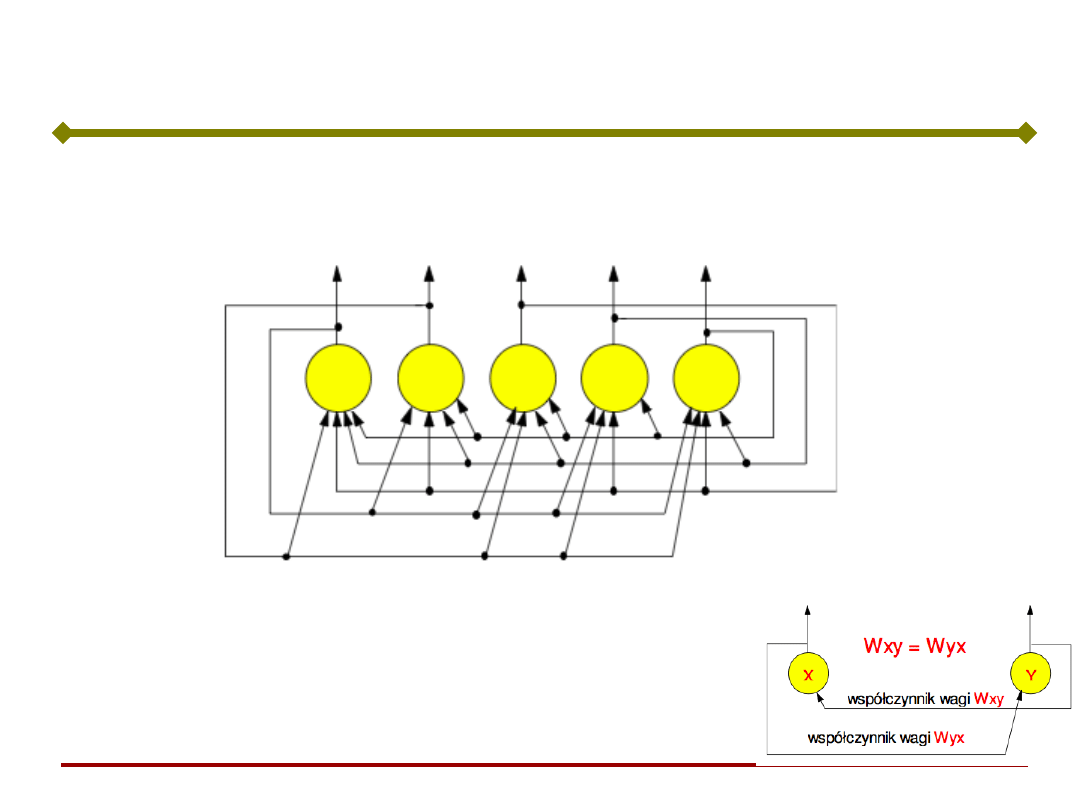
Sieć Hopfielda (1982)

Sieci Hopfielda, są to jednowarstwowe sieci ze 
sprzężeniem zwrotnym (często nazywane pamięcią 
asocjacyjną)

•Połączenie “każdy z każdym”

•Brak sprzężenia zwrotnego do siebie 
samego

•Symetryczna macierz współczynników 
wagowych

Podstawy Sztucznej 

Inteligencji

Jan Kusiak

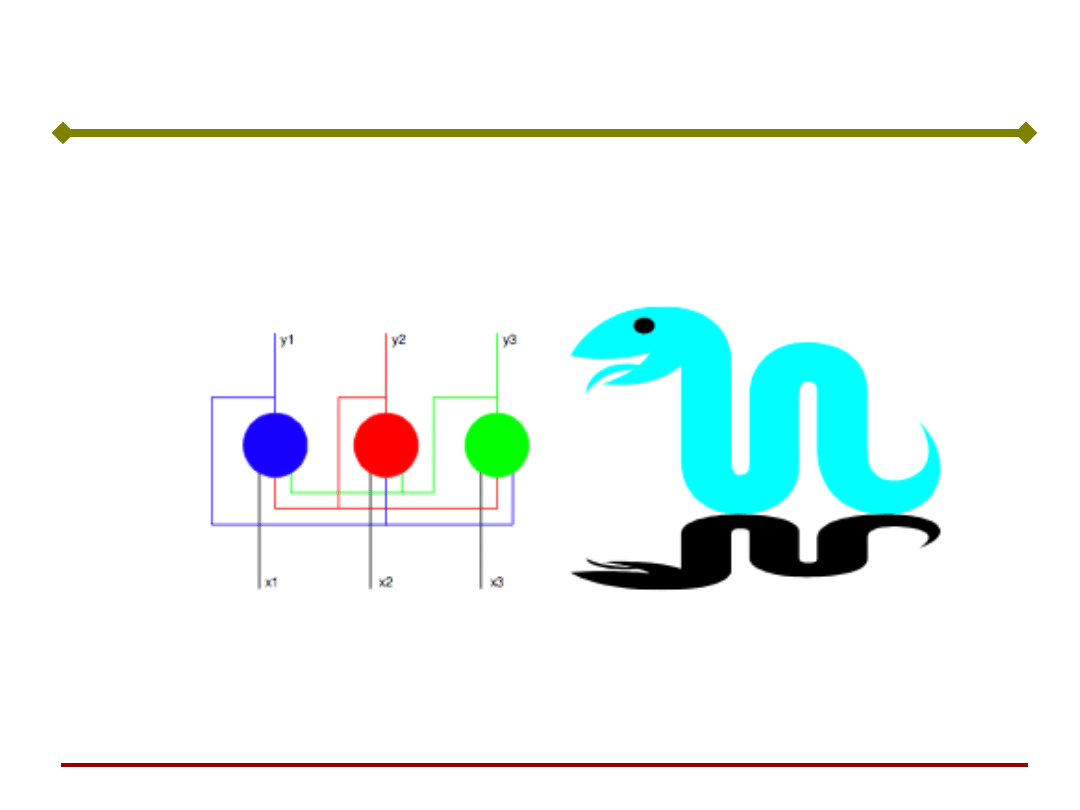
Sieć Hopfielda

[R. Tadeusiewicz]

Pytanie czy sieć Hopfielda ma sprzężenia zwrotne 
przypomina inne pytanie: czy wąż ma ogon?

Odpowiedź w obydwu przypadkach jest taka sama. 

Wyłącznie !!!

Podstawy Sztucznej 

Inteligencji

Jan Kusiak

Na skutek istnienia sprzężeń zwrotnych w sieciach 
rekurencyjnych pojawiają się dynamiczne procesy 
przejściowe, nieznane w innych rodzajach sieci.

Sieć Hopfielda

Z punktu widzenia teorii systemów sieci rekurencyjne 
są nieliniowymi układami dynamicznymi, gdyż ich 
zachowanie się w czasie jest wyznaczone nie tylko 
przez aktualnie działające wejścia, lecz zależy 
również od wejść, które występowały w przeszłości.

Podstawy Sztucznej 

Inteligencji

Jan Kusiak

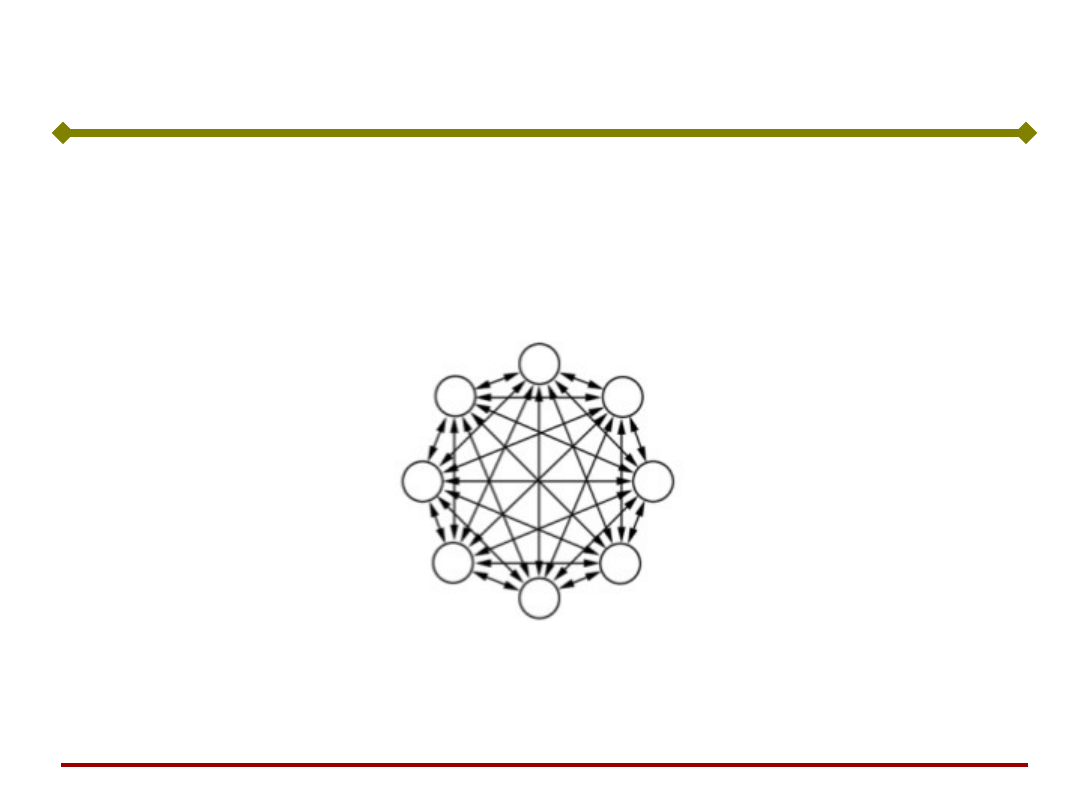
Sieć Hopfielda

Sygnały na wyjściach sieci zależą od jej stanu 
początkowego i podanych następnie pobudzeń. 

Sieć nie pobudzana zewnętrznym sygnałem 
wejściowym, której stan podlega zmianom tylko 
wskutek istniejących sprzężeń zwrotnych, nazywana 
jest siecią autonomiczną. 

Podstawy Sztucznej 

Inteligencji

Jan Kusiak

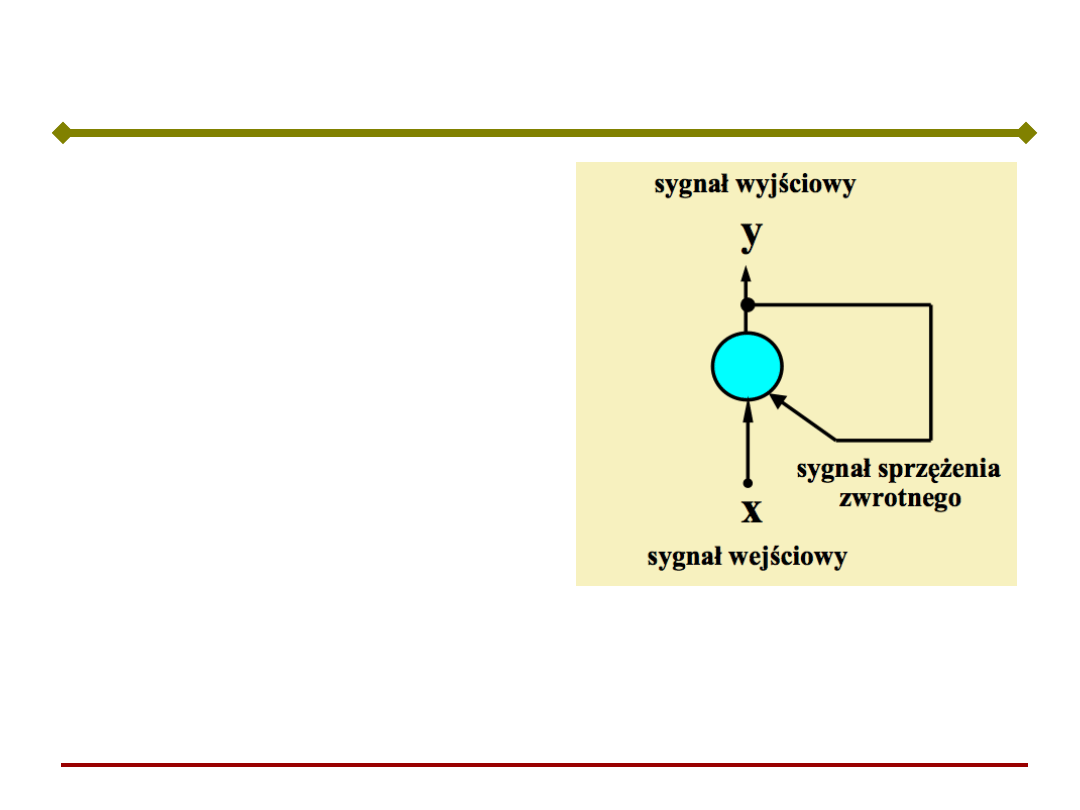
Sieć Hopfielda

Sieci Hopfielda często rysowane są w sposób bardziej 
praktyczny

Podstawy Sztucznej 

Inteligencji

Jan Kusiak

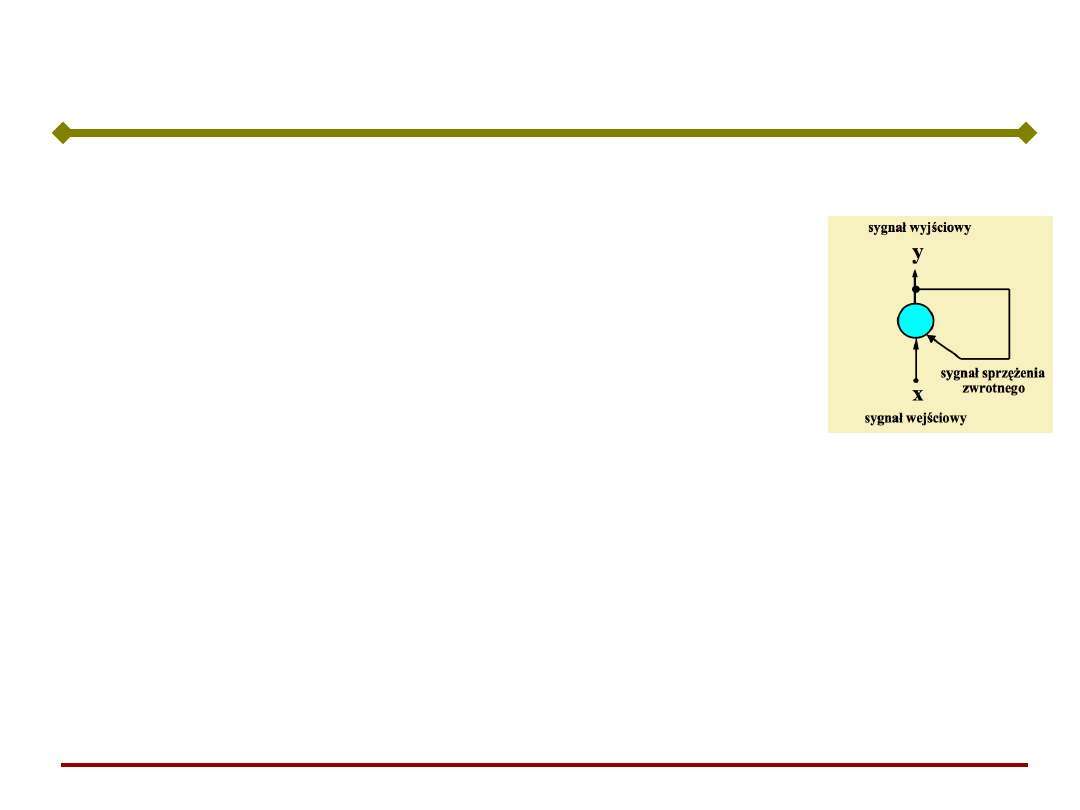
Sieci rekurencyjne 
(recurrent neural 
networks) posiadają 
sprzężenia zwrotne – 
wyjścia neuronów są 
połączone z wejściami 
neuronów.

Sieci Hopfielda

Sieci taka charakteryzuje 
się dynamiką.
Po jednorazowym podaniu 
sygnału (impulsu) na 
wejście, na wyjściu 
zachodzi długotrwały 
proces.

Sygnał wyjściowy zmienia wielokrotnie wartość zanim 
osiągnie stan równowagi - jeżeli go osiągnie  

Podstawy Sztucznej 

Inteligencji

Jan Kusiak

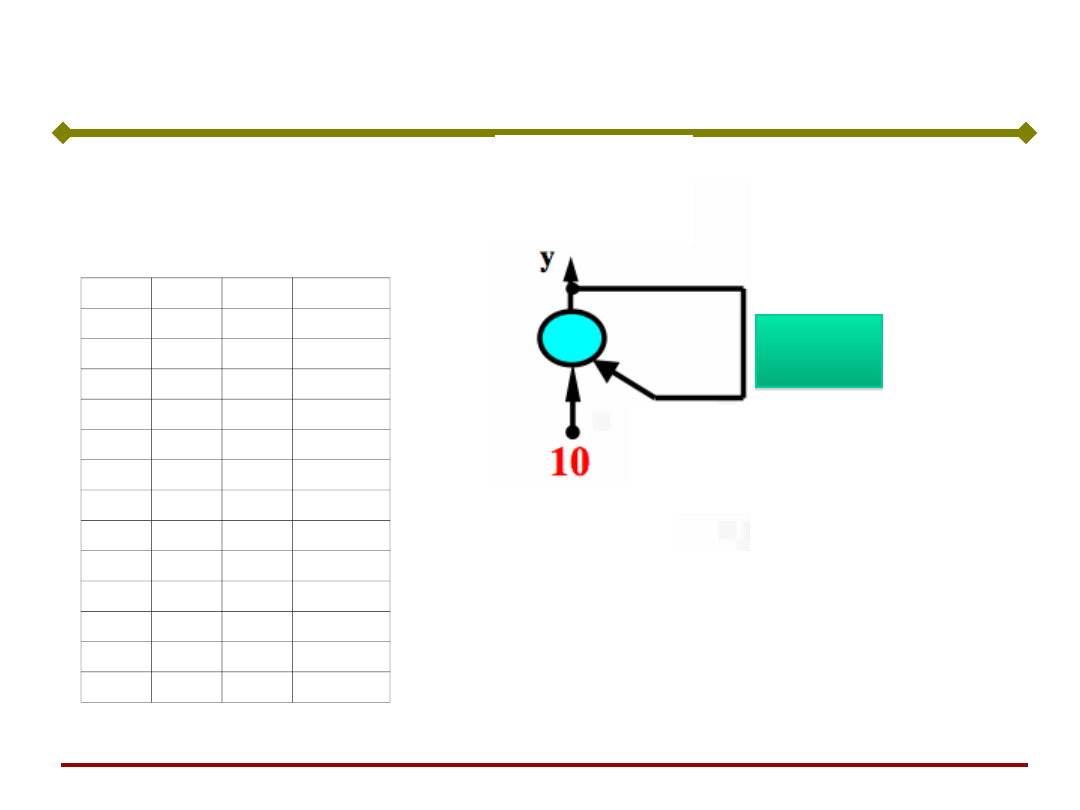
Równowaga w sieci może być 
osiągnięta (bez działającego sygnału 
wejściowego) jedynie w taki sposób, że 
sygnał wyjściowy po przemnożeniu 
przez wagę sprzężenia zwrotnego nie 
zmienia swojej wartości (pozostaje taki 
sam).

Taki sygnał nazywamy ATRAKTOREM. 

Położenie atraktora jest związane z 
parametrami sieci. 

Sieci Hopfielda

Podstawy Sztucznej 

Inteligencji

Jan Kusiak

w = 

w = 

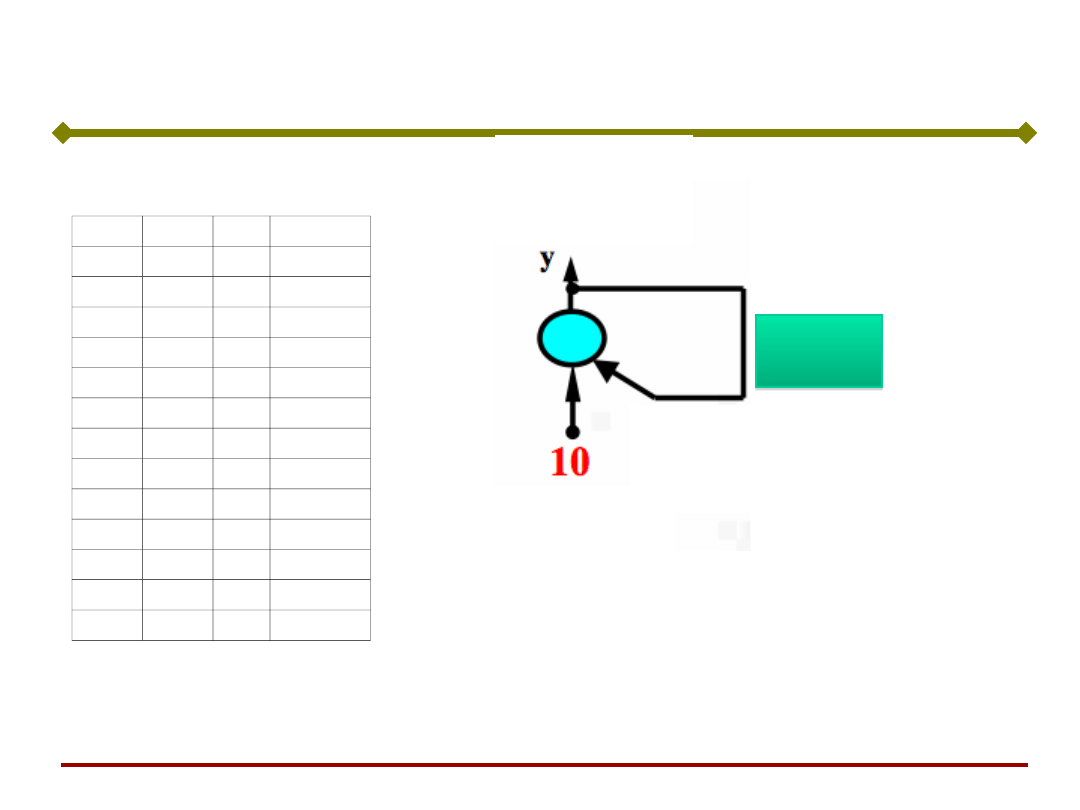
Jeżeli wartość wagi 
sprzężenia zwrotnego jest 
ujemna, wówczas sygnał 
wyjściowy ma charakter 
oscylacyjny

 

 

 

 

x0= 10

w= -1,20

 

 

 

 

 

i

 

y

 

1  

10,00

 

2  

-12,00

 

3  

14,40

 

4  

-17,28

 

5  

20,74

 

6  

-24,88

 

7  

29,86

 

8  

-35,83

 

9  

43,00

 

10  

-51,60

x

0

 = 

10 

(tylko w chwili początkowej)

; 

w = -1.20

Sieci Hopfielda

Podstawy Sztucznej 

Inteligencji

Jan Kusiak

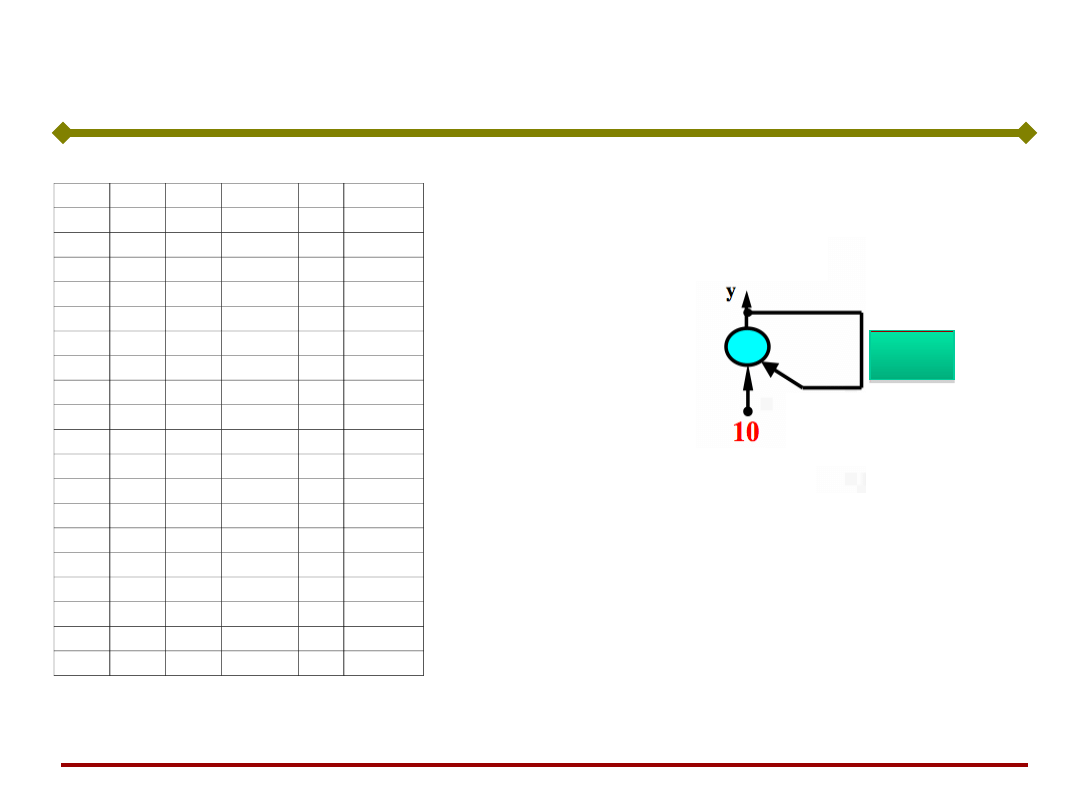
Jeżeli wartość wagi sprzężenia 
zwrotnego jest dodatnia, 
wówczas sygnał wyjściowy ma 
charakter aperiodyczny

 

 

 

 

x0= 10

w= 1,40

 

 

 

 

 

i

 

y

 

1  

10,00

 

2  

14,00

 

3  

19,60

 

4  

27,44

 

5  

38,42

 

6  

53,78

 

7  

75,30

 

8  

105,41

 

9  

147,58

 

10  

206,61

w = 

w = 

x

0

 = 10; w = 1.40

Sieci Hopfielda

Podstawy Sztucznej 

Inteligencji

Jan Kusiak

w 

= 

w 

= 

Jeżeli bezwzględna wartość wagi 
sprzężenia zwrotnego jest mniejsza 
od pewnej wartości – granicy 
stabilności – układ dąży do stanu 
równowagi.

Powyżej tej wartości układ jest 
niestabilny – odpowiedź rośnie do 
nieskończoności

x0= 10

w= 0,50

w= -0,40

 

 

 

 

 

 

 

i

 

y

 

y

 

1  

10,00  

10,00

 

2  

5,00  

-4,00

 

3  

2,50  

1,60

 

4  

1,25  

-0,64

 

5  

0,63  

0,26

 

6  

0,31  

-0,10

 

7  

0,16  

0,04

 

8  

0,08  

-0,02

 

9  

0,04  

0,01

 

10  

0,02  

0,00

 

11  

0,01  

0,00

 

12  

0,00

 

0,00

 

13  

0,00

 

0,00

 

14  

0,00

 

0,00

 

15  

0,00

 

0,00

 

16  

0,00

 

0,00

 

17  

0,00

 

0,00

1). x

0

 = 10; w = 0.50

2). x

0

 = 10; w = - 0.40

Sieci Hopfielda

Podstawy Sztucznej 

Inteligencji

Jan Kusiak

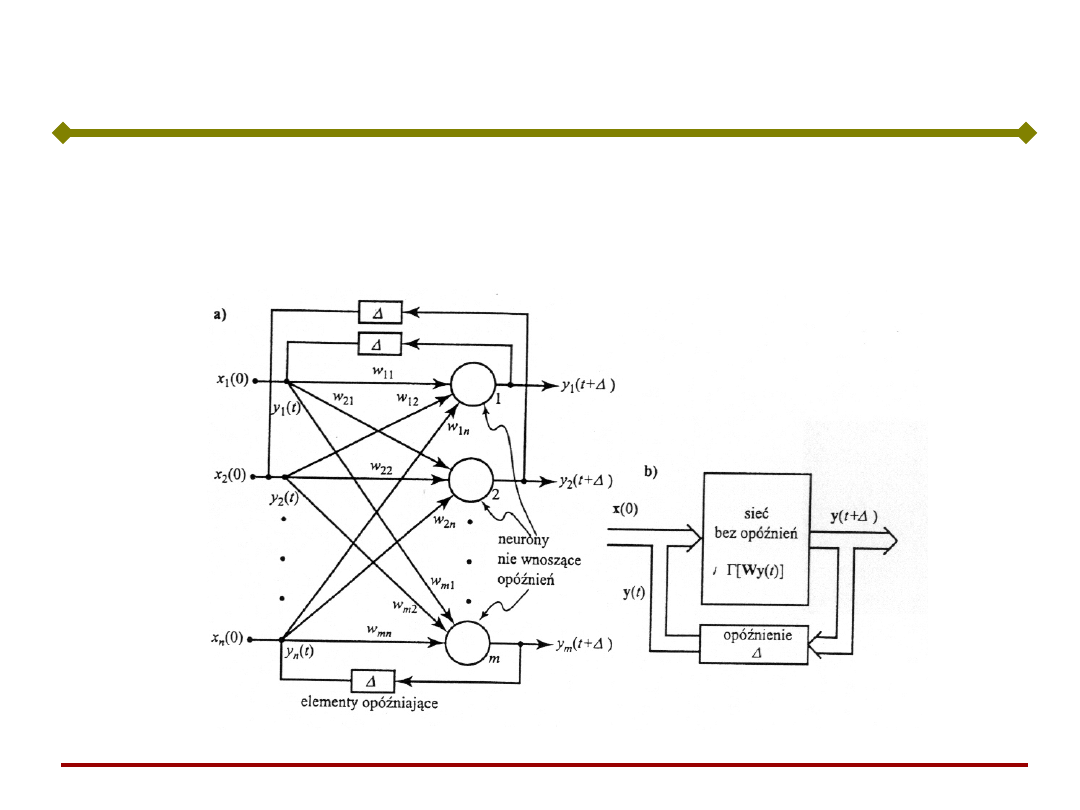
Sieci rekurencyjne (recurrent neural networks) 
posiadają sprzężenia zwrotne – wyjścia neuronów są 
połączone z wejściami neuronów.

Sieci Hopfielda

Podstawy Sztucznej 

Inteligencji

Jan Kusiak

•Sieci rekurencyjne są nieliniowymi układami 

dynamicznymi, gdyż ich zachowanie się w czasie 
jest wyznaczone nie tylko przez aktualnie działające 
wejścia, lecz zależy również od wejść, które 
występowały w przeszłości.

•Sygnały na wyjściach sieci zależą od jej stanu 

początkowego i podanych następnie pobudzeń. 

•Sieć nie pobudzana zewnętrznym sygnałem 

wejściowym, której stan podlega zmianom tylko 
wskutek istniejących sprzężeń zwrotnych, nazywana 
jest siecią autonomiczną.

Sieci Hopfielda

Podstawy Sztucznej 

Inteligencji

Jan Kusiak

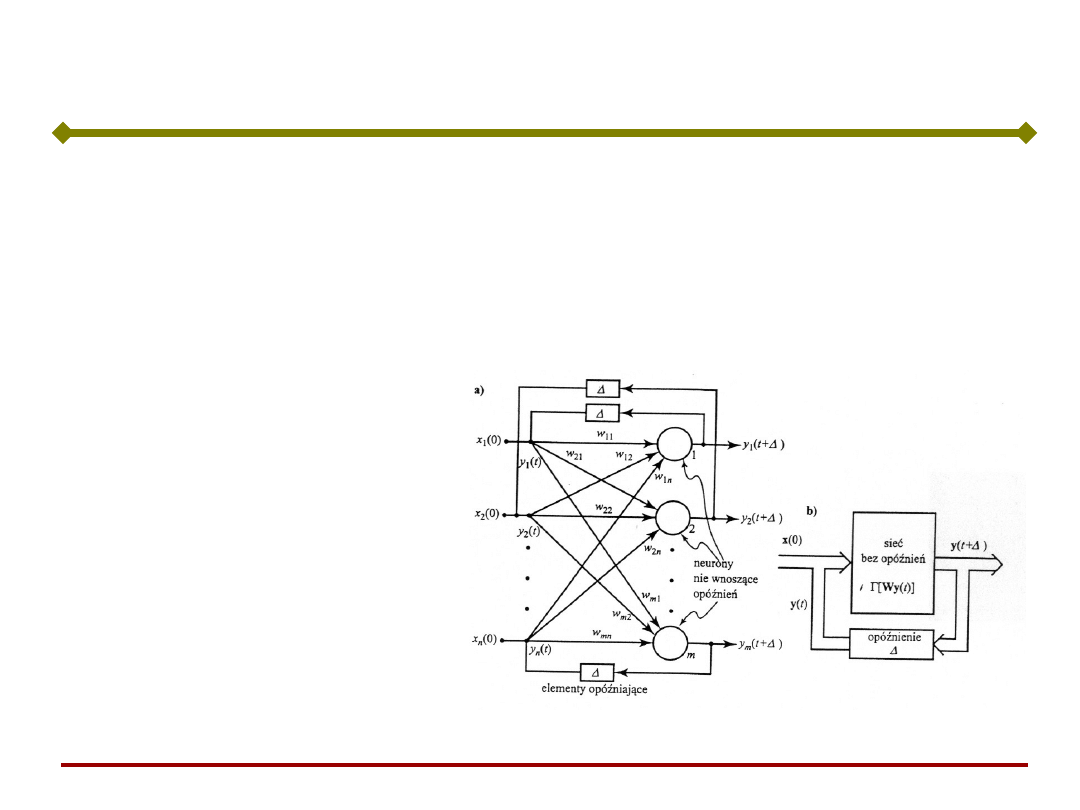
Jednorazowe pobudzenie x(0) stanowi wymuszenie 
stanu początkowego. Elementy 



 przypominają, że 

odpowiedź neuronu jest opóźniona w stosunku do 
pobudzenia. Sygnał wyjściowy:

))

(

(

)

(

t

Wy

t

y









Sieci Hopfielda

Podstawy Sztucznej 

Inteligencji

Jan Kusiak

Traktując czas jako zmienną dyskretną i obserwując 
zachowanie sieci w momentach 



, 2



, 3



,.... 

Opisujemy ją jako układ dyskretny w czasie:

,...

2

,

1

,

0

),

(

1







k

Wy

y

k

k



Sieć nazywamy rekurencyjną, gdyż jej odpowiedź w 
chwili k+1 zależy od całej historii pobudzeń, 
poczynając od chwili k=0 i odpowiedzi są ciągiem:

)...))

(

(...

(

))

(

(

)

(

0

1

0

2

0

1

Wx

W

y

Wx

W

y

Wx

y

k























Sieci Hopfielda

Podstawy Sztucznej 

Inteligencji

Jan Kusiak

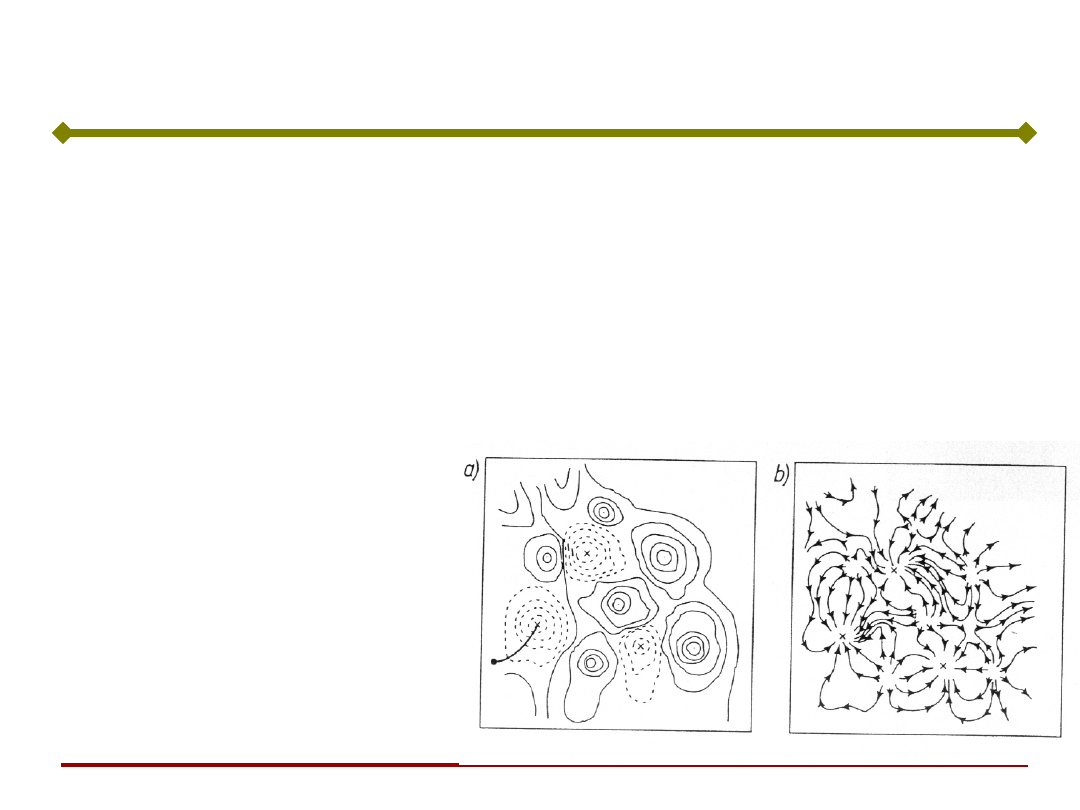
Równania powyższe opisują stan y

k

 sieci w chwilach 

k=1,2,... i dają ciąg przejść stanu. 

Przejścia stanów sieci rozpoczynają się jej 
pobudzeniem w chwili 0 sygnałem x

0

 i trwają, poprzez 

y

k

, k=1,2,..., aż do osiągnięcia przez sieć stanu 

równowagi. 

Stan równowagi 
nazywany atraktorem 
może być pojedynczym 
stanem lub ciągiem 
stanów obieganych 
cyklicznie (tzw. Cyklem 
granicznym).

Sieci Hopfielda

Podstawy Sztucznej 

Inteligencji

Jan Kusiak

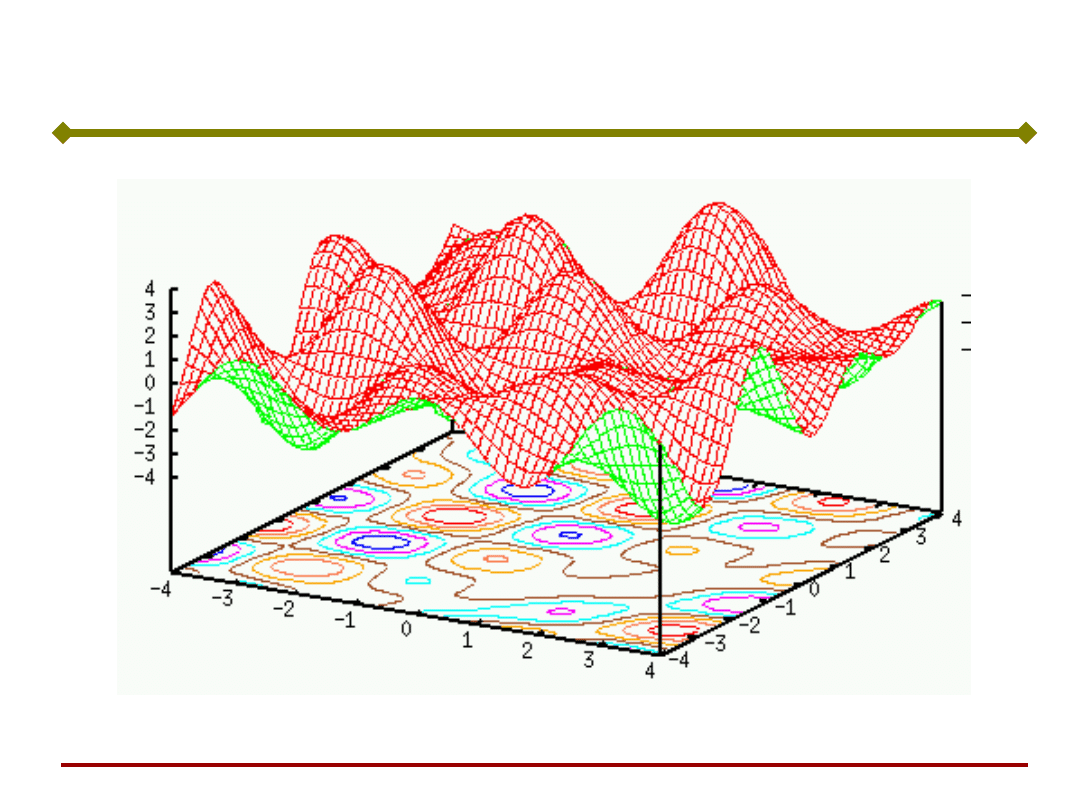
Sieci Hopfielda 

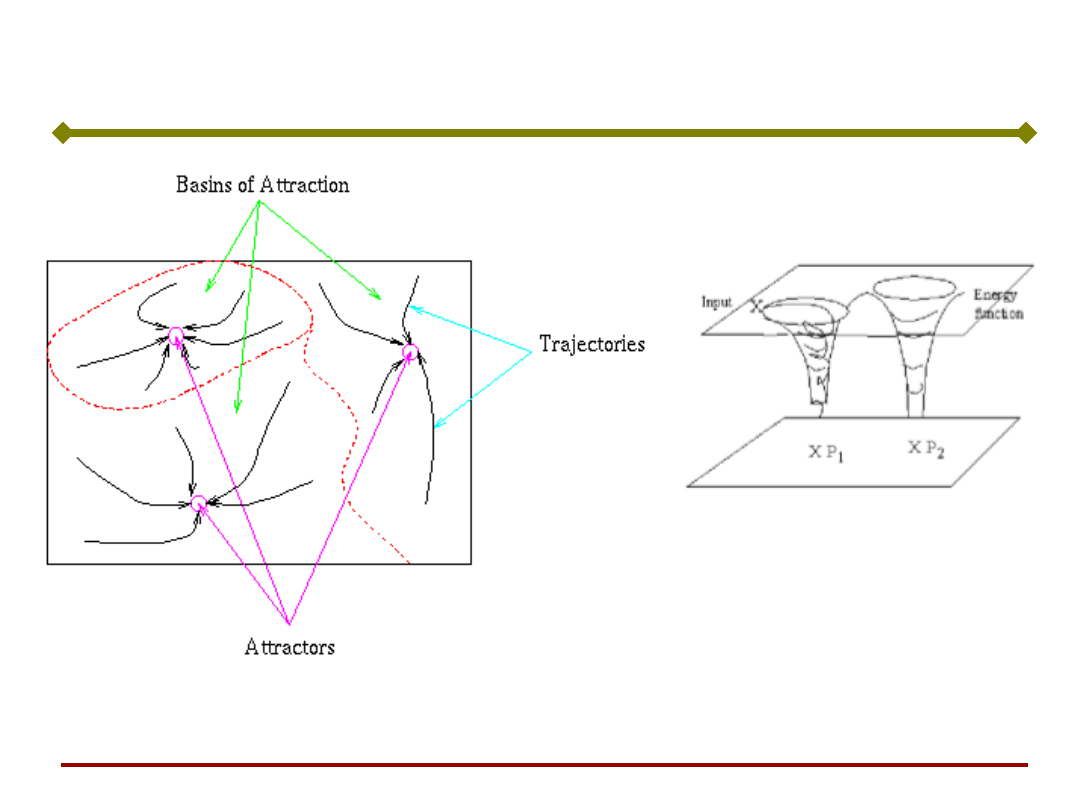
W miejscu 
występowania 
atraktora proces 
uczenia wytwarza 
„studnię” w 
powierzchni 
reprezentującej 
funkcję „energii” sieci

Podstawy Sztucznej 

Inteligencji

Jan Kusiak

Sieci Hopfielda

Podstawy Sztucznej 

Inteligencji

Jan Kusiak

Trochę teorii

Podstawy Sztucznej 

Inteligencji

Jan Kusiak

Pamięć asocjacyjna jest układem odwzorowującym 
wektory x

1

, x

2

,.., x

p

należące do R

n

 w wektory y

1

, y

2

,.., y

p

 należące do R

m

.

 

Wektory x

i

 i y

i

 nazywane są wzorcowymi lub 

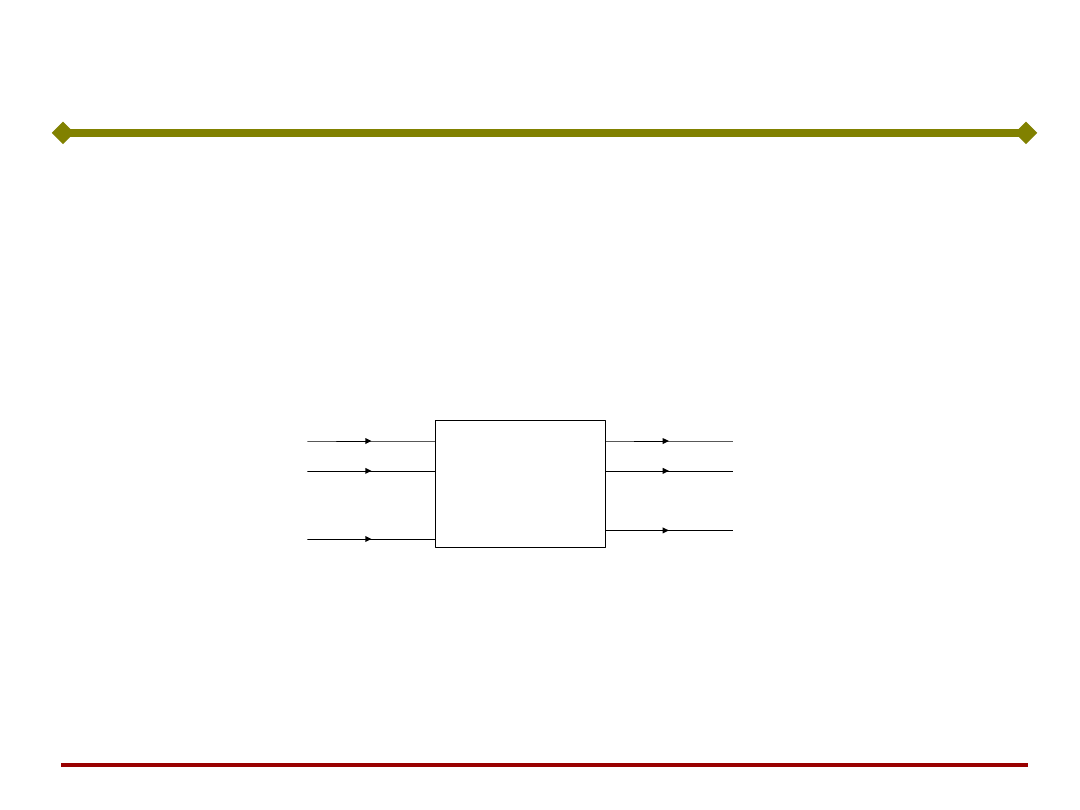
prototypowymi. Schemat blokowy pamięci asocjacyjnej:

M

x

1

x

n

x

2

y

1

y

m

y

2

Y = M(x)

M - nieliniowy operator macierzowy zależny od 
struktury sieci i wag neuronów.

Pamięć asocjacyjna

Podstawy Sztucznej 

Inteligencji

Jan Kusiak

Umieszczenie w pamięci wektorów wzorcowych 
nazywane jest „zapisem” i pociąga za sobą odpowiednie 
dobranie wag. 
Odwzorowanie Y = M(x) wykonane na wektorze 
wejściowym x (przy zamrożonych wagach) nazywane 
jest odczytem. 

Pamięć autoasocjacyjna – jeżeli asocjacje są postaci:

p

i

x

x

i

i

,

,

2

,

1

,







Pamięć asocjacyjna, c.d.

p

i

x

y

y

x

i

i

i

i

,

,

2

,

1

,

,









Pamięć heteroasocjacyjna - sieć przechowuje p 
asocjacji o postaci:

Podstawy Sztucznej 

Inteligencji

Jan Kusiak

Pamięć asocjacyjna, c.d.

Ważnym zastosowaniem odwzorowania 
autoasocjacyjnego jest odtwarzanie wzorców na 
podstawie podawanych na wejście wzorców 
zniekształconych.

Najczęściej używaną miarą odległości między 
zbiorami jest miara Hamminga.

Podstawy Sztucznej 

Inteligencji

Jan Kusiak

Dla wielkości binarnych 0 i 1 odległość Hamminga 
dwóch wektorów binarnych y = [y

1

, y

2

, ...., y

n

,]

T

 i z = 

[z

1

, z

2

, ...., z

n

,]

T

 wyniosi:



d

H

(y,z) 

1
2

y

i

 z

i

i1

n



Miara Hamminga jest równa zeru jedynie wtedy, gdy 
y = z. W przeciwnym razie jest ona równa liczbie 
bitów, o które różnią się oba wektory. 

Miara Hamminga

Podstawy Sztucznej 

Inteligencji

Jan Kusiak

Przykład: Odległość Hamminga dwóch wektorów:
y = [-1, -1, 1, 1]

T 

i z = [-1, 1, 1, 1]

T

Miara Hamminga, c.d.

Podstawy Sztucznej 

Inteligencji

Jan Kusiak

Przykład: Odległość Hamminga dwóch wektorów:
y = [-1, 

-1

, 1, 1]

T 

i z = [-1, 

1

, 1, 1]

T

 

Odległość Hamminga wynosi 1 (obydwa wektory 
różnią się jednym bitem).

Miara Hamminga, c.d.

Podstawy Sztucznej 

Inteligencji

Jan Kusiak

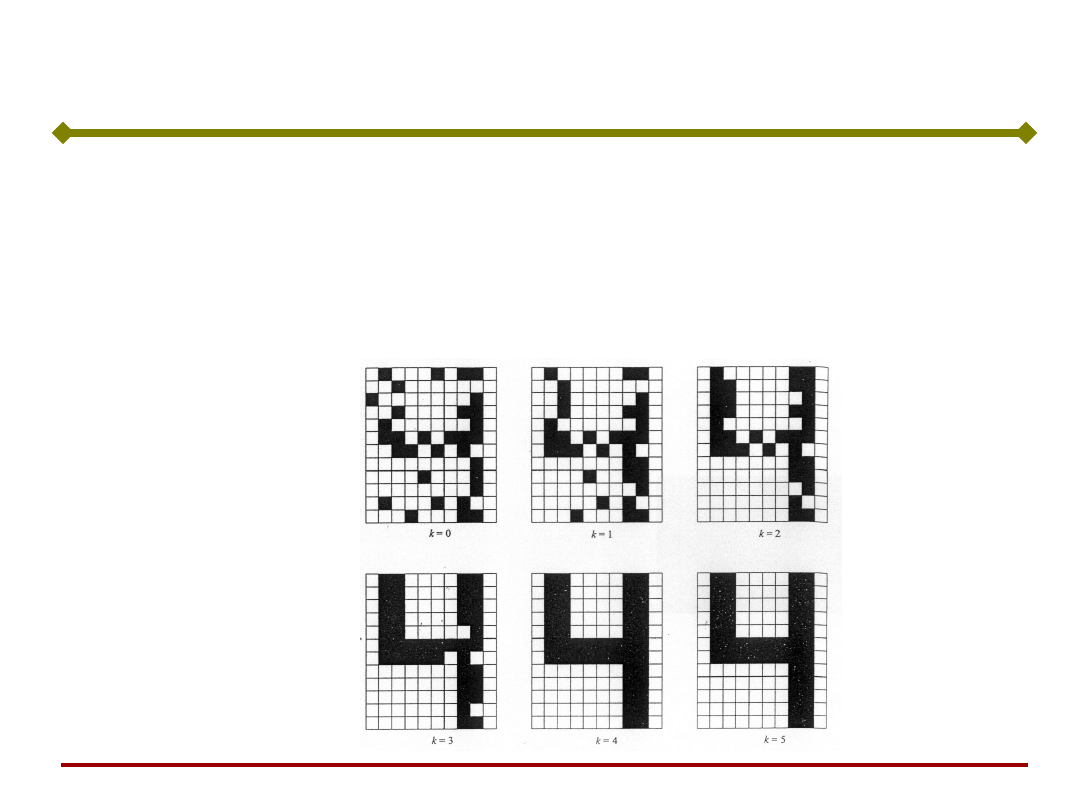
Pamięć asocjacyjna

Zadanie: Możliwość odtwarzania przez sieć przedstawionego jej 
wcześniej obrazu. 

Pamięć asocjacyjna – sieć, która odtwarza zapamiętany obraz 
nawet w przypadku jego zniekształcenia.

Podstawy Sztucznej 

Inteligencji

Jan Kusiak

Podstawowym zadaniem pamięci asocjacyjnej jest 
zapamiętanie zbioru próbek wejściowych (uczących) w 
taki sposób, aby przy prezentacji nowej próbki układ 
mógł wygenerować odpowiedź, która dotyczyć będzie 
jednej z zapamiętanych wcześniej próbek, położonej 
najbliżej próbki testującej. 

Podczas odczytu pamięć może odtworzyć oczekiwany 
wzorzec, wzorzec inny niż oczekiwany lub wektor nie 
należący do zbioru zapamiętanych wzorców. 

Pamięć 
asocjacyjna

Podstawy Sztucznej 

Inteligencji

Jan Kusiak

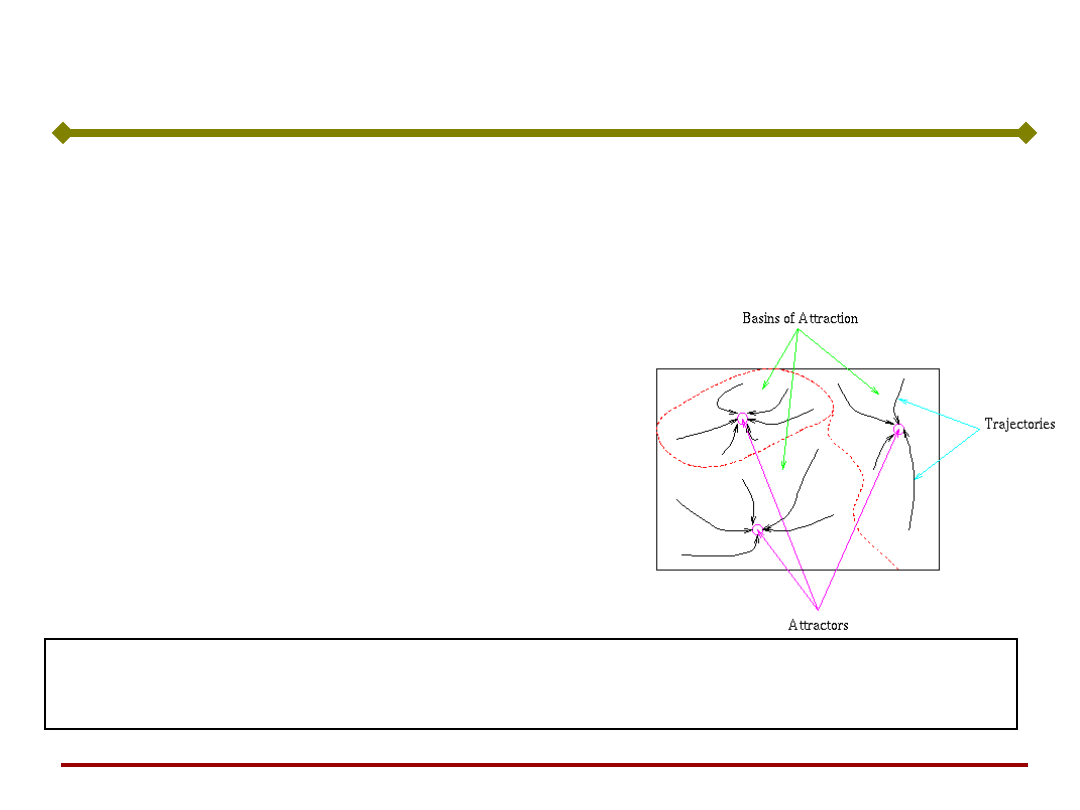
Proces uczenia sieci kształtuje obszary atrakcji 
(przyciągania) poszczególnych punktów równowagi 
odpowiadających danym uczącym. 

W przypadku pamięci 
autoasocjacyjnej występuje 
wektor uczący x lub zbiór tych 
wektorów, które w wyniku 
przeprowadzonego uczenia 
sieci ustalają położenie 
poszczególnych atraktorów.

Pamięć 
asocjacyjna

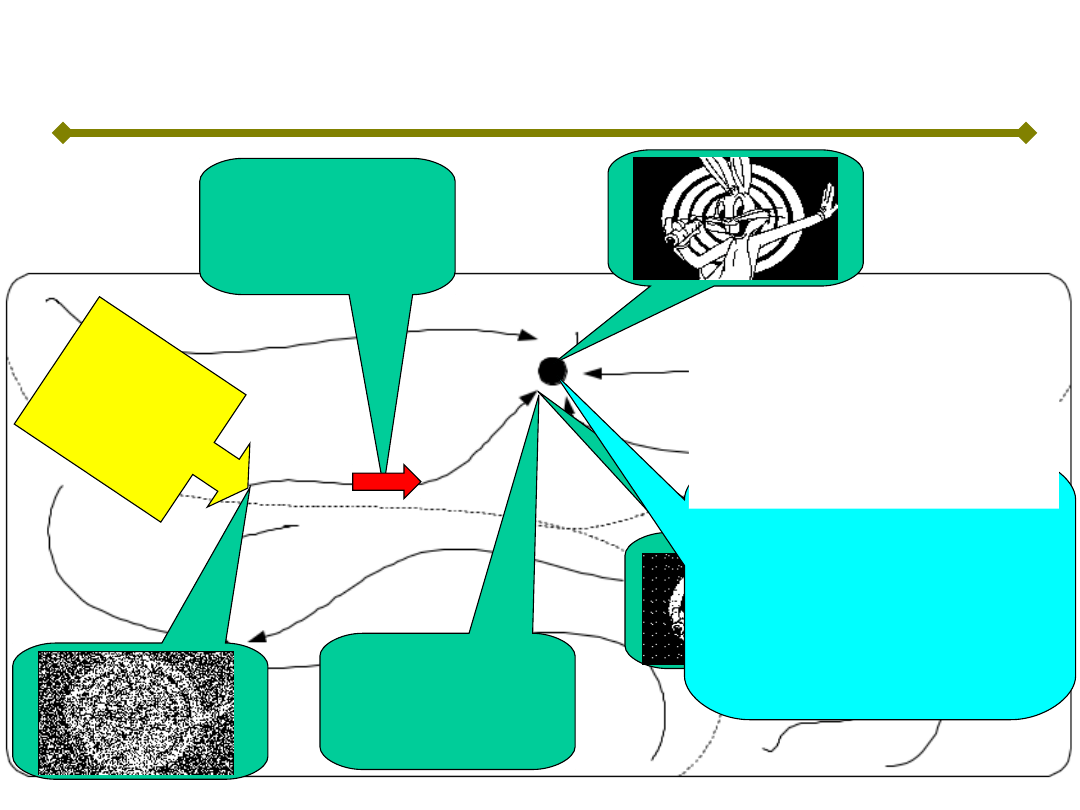
Z atraktorami w sieci Hopfielda można związać 
pewne informacje.

Podstawy Sztucznej 

Inteligencji

Jan Kusiak

Niech mapa 

stanów sieci 

Hopfielda 

wygląda jak na 

tym rysunku

Zestaw sygnałów 

wyjściowych w 

tym atraktorze 

formuje taki 

obrazek

Zestaw sygnałów 

wyjściowych w tym 

miejscu formuje 

obrazek 

zniekształcony, który 

nie jest

 atraktorem

Sieć szuka stanu 

równowagi, więc 

jej stan posuwa 

się 

w stronę 

atraktora

Zestaw sygnałów 

wyjściowych w 

tym miejscu 

formuje taki 

obrazek

Tu proces 

szukania 

równowagi się 

kończy. Sieć nie 

osiąga atraktora.

Pod

aje

my

z ze

wną

trz

dan

e, k

tóre

usta

wia

ją s

ieć

w ta

kim

 sta

nie

 

Ucząc sieć 

w tym 

miejscu 

wytworzyliś
my atraktor

Efekt: sieć odtworzyła 

prawie idealnie 

zapamiętany obraz 

(atraktor) na podstawie 

obrazu bardzo 

zakłóconego

Pamięć asocjacyjna

Wg R. Tadeusiewicza

Podstawy Sztucznej 

Inteligencji

Jan Kusiak

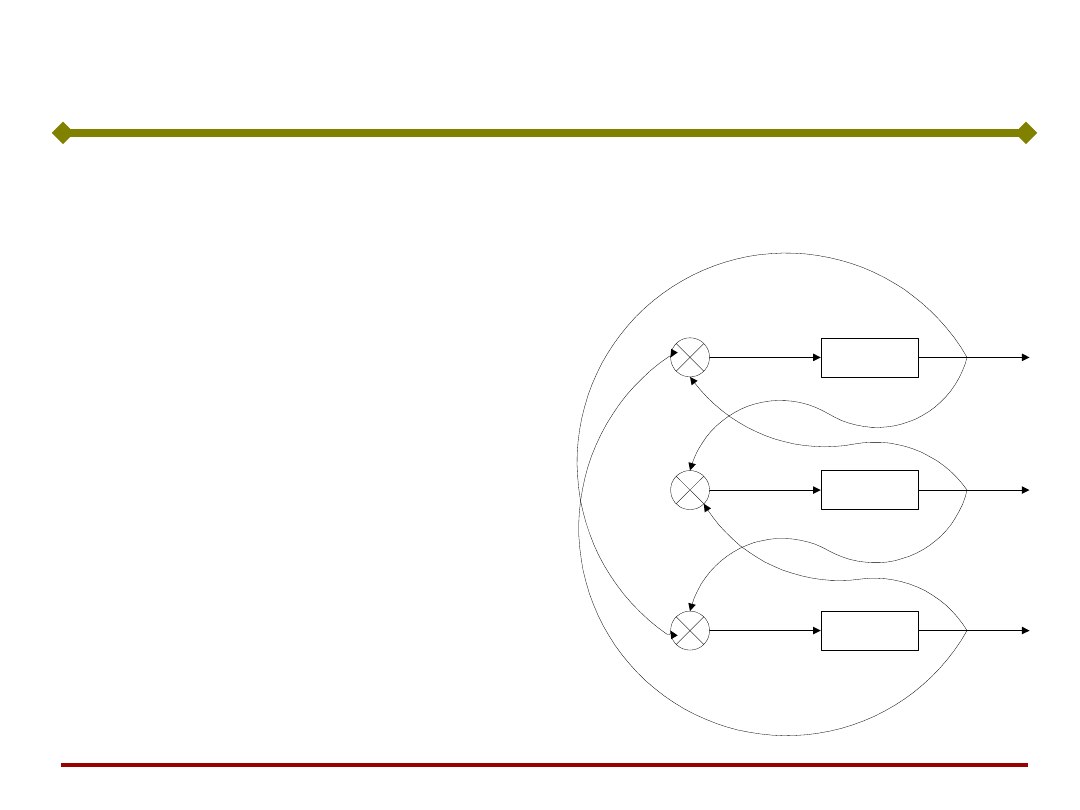
Przeanalizujemy prostą 
sieć o bipolarnej funkcji 
aktywacji. Sieć działa 
synchronicznie – w 
każdym takcie obliczane 
są sygnały wyjściowe 
neuronów. 

Gdy sygnał s

i 

 neuronu i 

wynosi 0, to jego sygnał 
wyjściowy nie zmienia 
się.

 

sgn(.)

sgn(.)

sgn(.)

-1

-1

-1

-1

1

s

1

s

2

s

3

y

1

y

2

y

3

1

Prosta pamięć asocjacyjna

Podstawy Sztucznej 

Inteligencji

Jan Kusiak

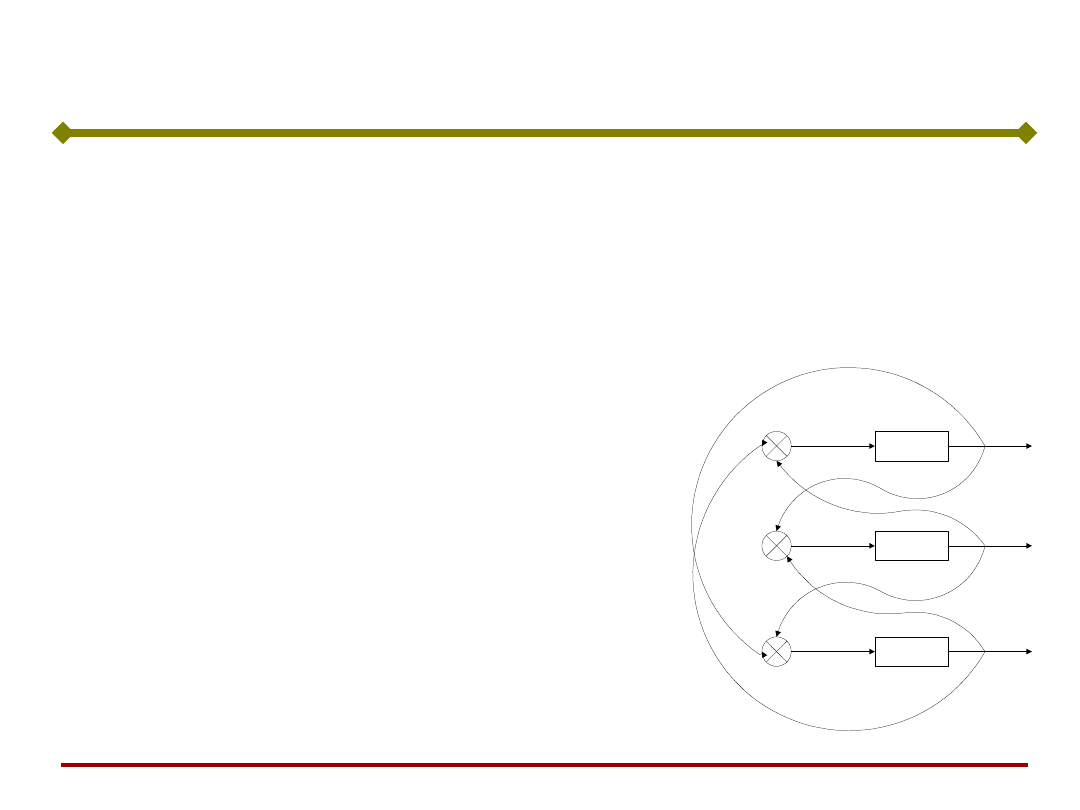
Załóżmy, że w chwili początkowej sygnały wyjściowe neuronów 
wynoszą:

1

3

2

1







y

y

y

Wtedy sygnały wejściowe 
neuronów wynoszą odpowiednio:

2

0

3

2

1









s

s

s

Ponieważ założyliśmy, że gdy sygnał s

i 

 

wynosi 0, to sygnał wyjściowy nie 
zmienia się, po pierwszym takcie nowe 
sygnały wyjściowe neuronów wynoszą:

1

1

3

2

1









y

y

y

sgn(.)

sgn(.)

sgn(.)

-1

-1

-1

-1

1

s

1

s

2

s

3

y

1

y

2

y

3

1

Prosta pamięć asocjacyjna

Podstawy Sztucznej 

Inteligencji

Jan Kusiak

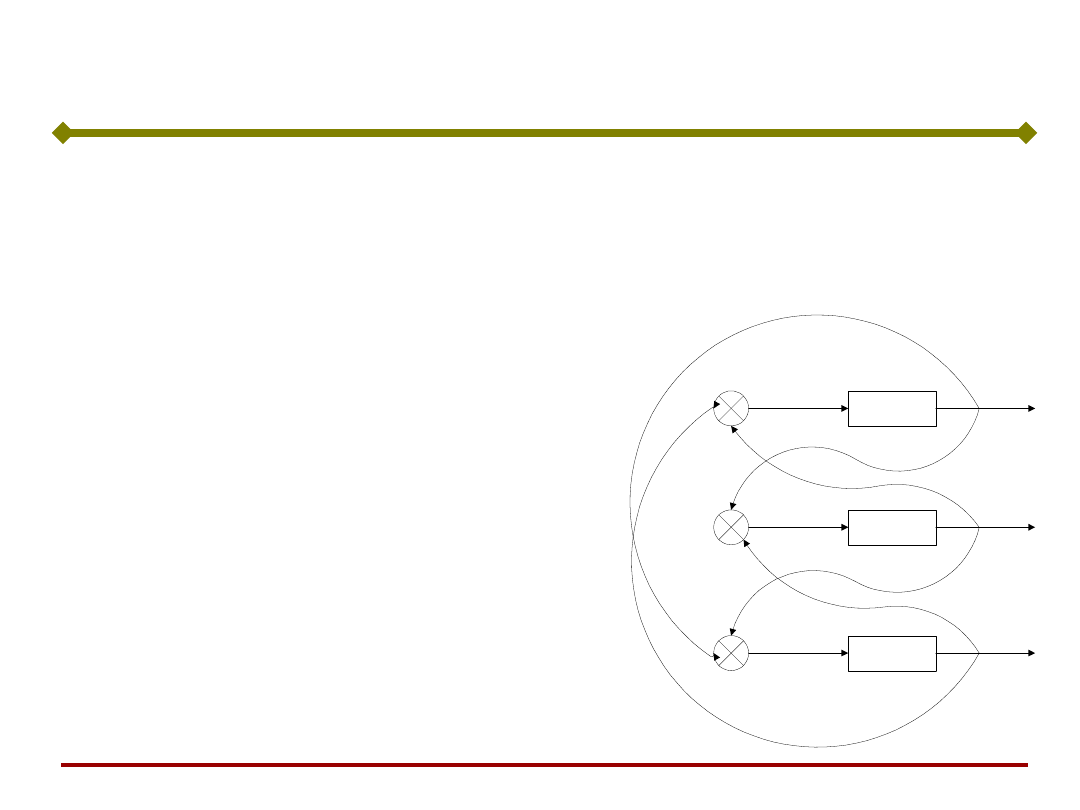
W następnym takcie i w dalszych 
sygnały wyjściowe nie ulegają już 
zmianie, ponieważ wtedy sygnały 
wejściowe wszystkich trzech 
neuronów wynoszą:

wymusza to ponownie sygnały 
wyjściowe

2

2

3

2

1









s

s

s

1

1

3

2

1









y

y

y

sgn(.)

sgn(.)

sgn(.)

-1

-1

-1

-1

1

s

1

s

2

s

3

y

1

y

2

y

3

1

Prosta pamięć asocjacyjna

Podstawy Sztucznej 

Inteligencji

Jan Kusiak

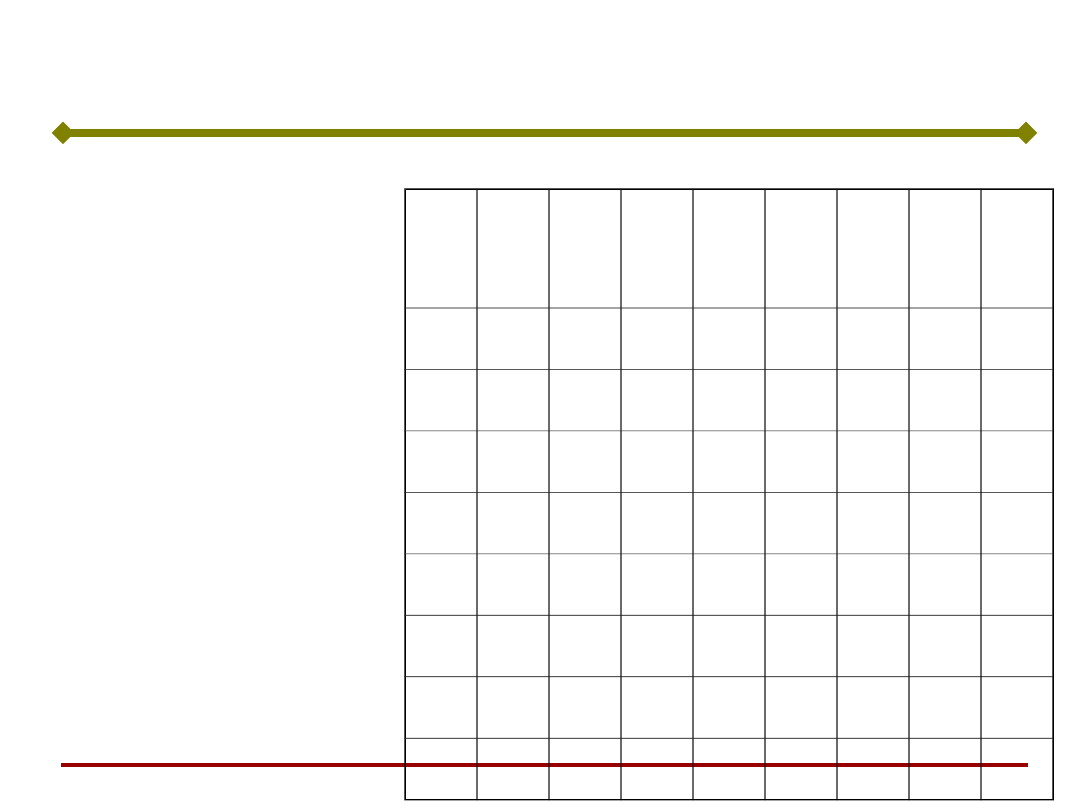
Wszystkie możliwe 
sygnały wejściowe 
sieci i odpowiadające 
im sygnały zebrano 
w tablicy:

y

1

y

2

y

3

s

1

s

2

s

3

y

1

’

y

2

’

y

3

’

-1 -1 -1 0 0 2

-1 -1 1

-1 -1 1 -2 -2 2

-1 -1 1

-1 1 -1 2 0 0

1 1 -1

-1 1 1 0 -2 0

-1 -1 1

1 -1 -1 0 2 0

1 1 -1

1 -1 1 -2 0 0

-1 -1 1

1 1 -1 2 2 -2

1 1 -1

1 1 1 0 0 -2

1 1 -1

Prosta pamięć asocjacyjna

Podstawy Sztucznej 

Inteligencji

Jan Kusiak

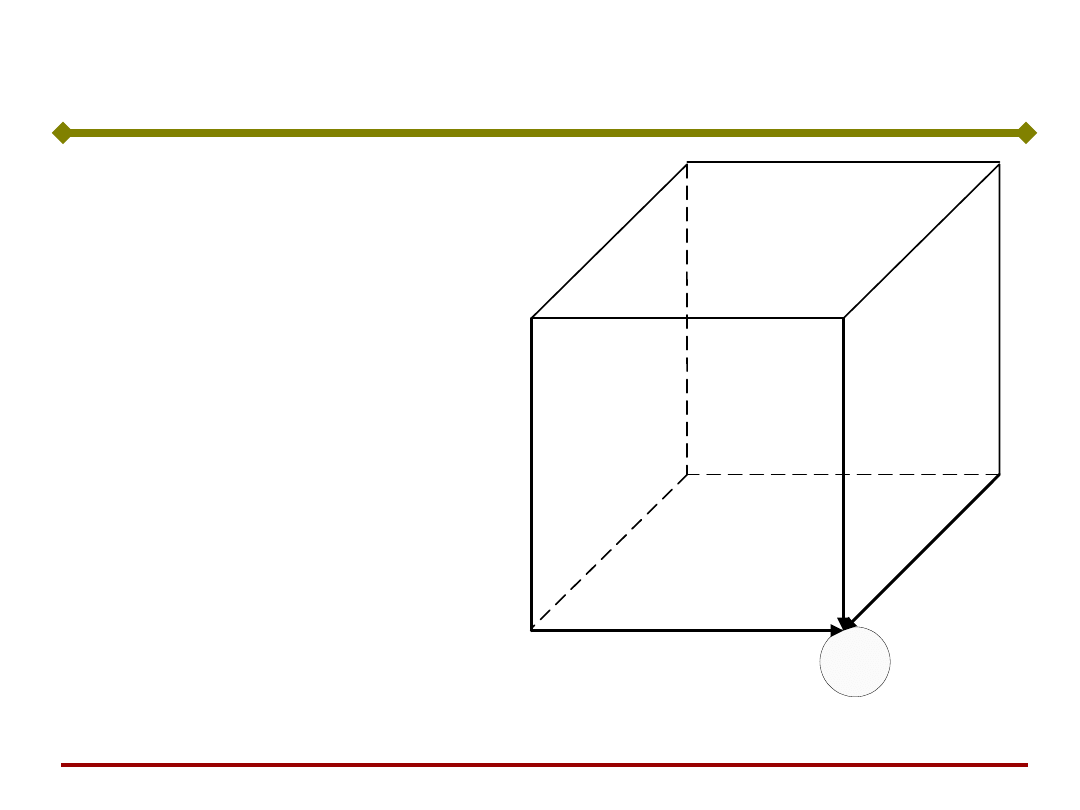
Na rysunku przedstawiono 
wynikający z tablicy fragment 
grafu przejść stanów sieci. 

P

1

P

0

P

4

P

5

P

6

P

2

P

7

P

3

(1,-1,-1)

(1,1,1)

(1,1,-1)

(-1,1,-1)

(-1,1,1)

(-1,-1,1)

(1,-1,1)

(-1,-1,-1)

Sieć ma 2 stany stabilne: 
(1,1,-1) i (-1,-1,1) do 
których dochodzi startując 
z dowolnego stanu 
początkowego. Można więc 
uznać, że sieć pamięta 2 
stany.

Prosta pamięć asocjacyjna

Podstawy Sztucznej 

Inteligencji

Jan Kusiak

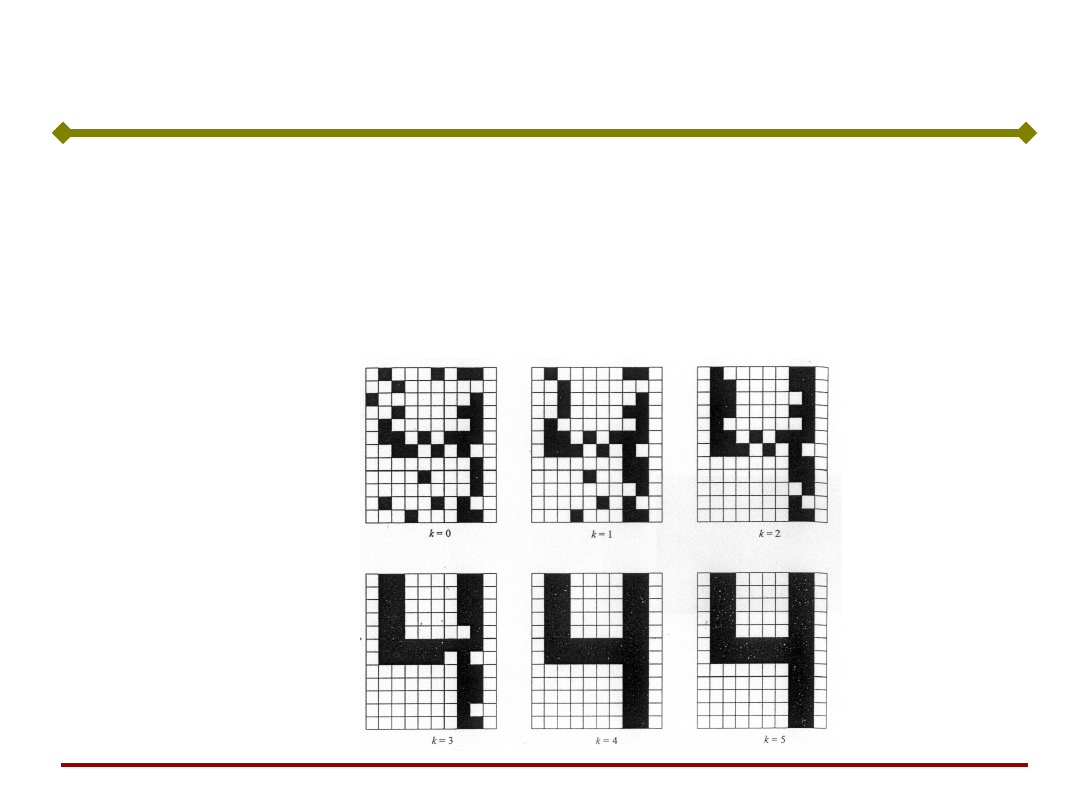
Sieć taka może rozpoznać zniekształcony obraz 

Prosta pamięć asocjacyjna

Podstawy Sztucznej 

Inteligencji

Jan Kusiak

Przedstawiona koncepcja 
pamięci łatwo można 
rozszerzyć na praktyczne 
zastosowanie. 

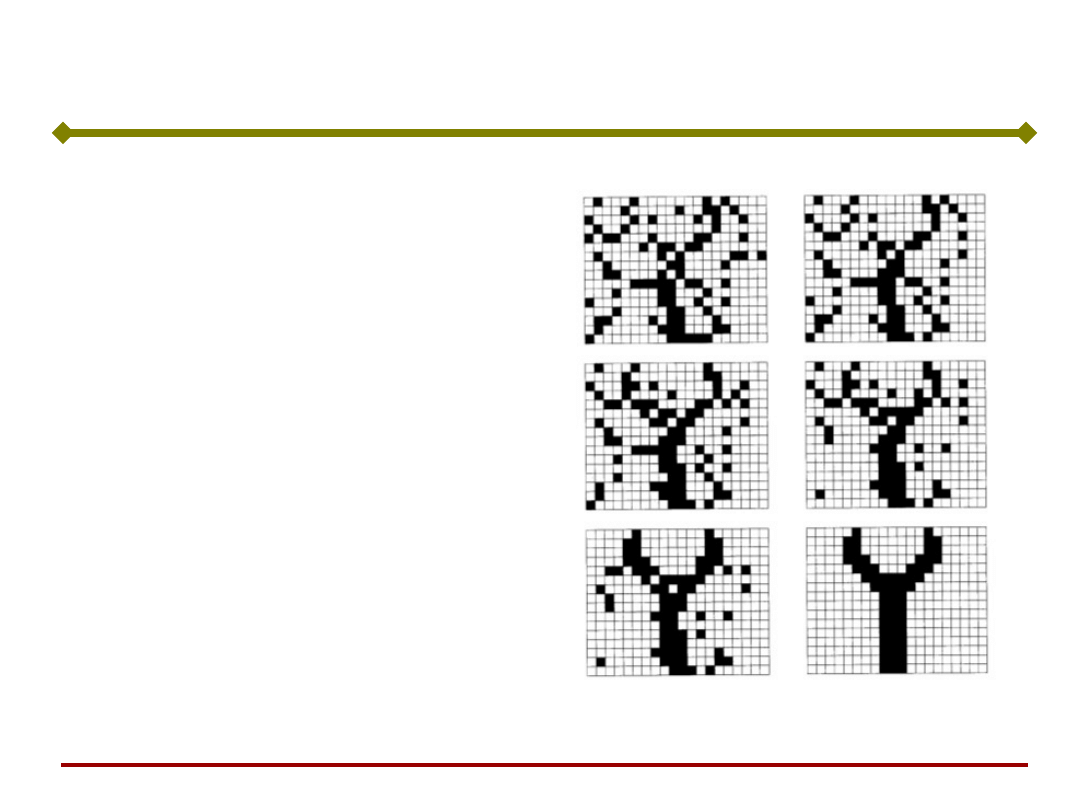
Przykład zastosowań

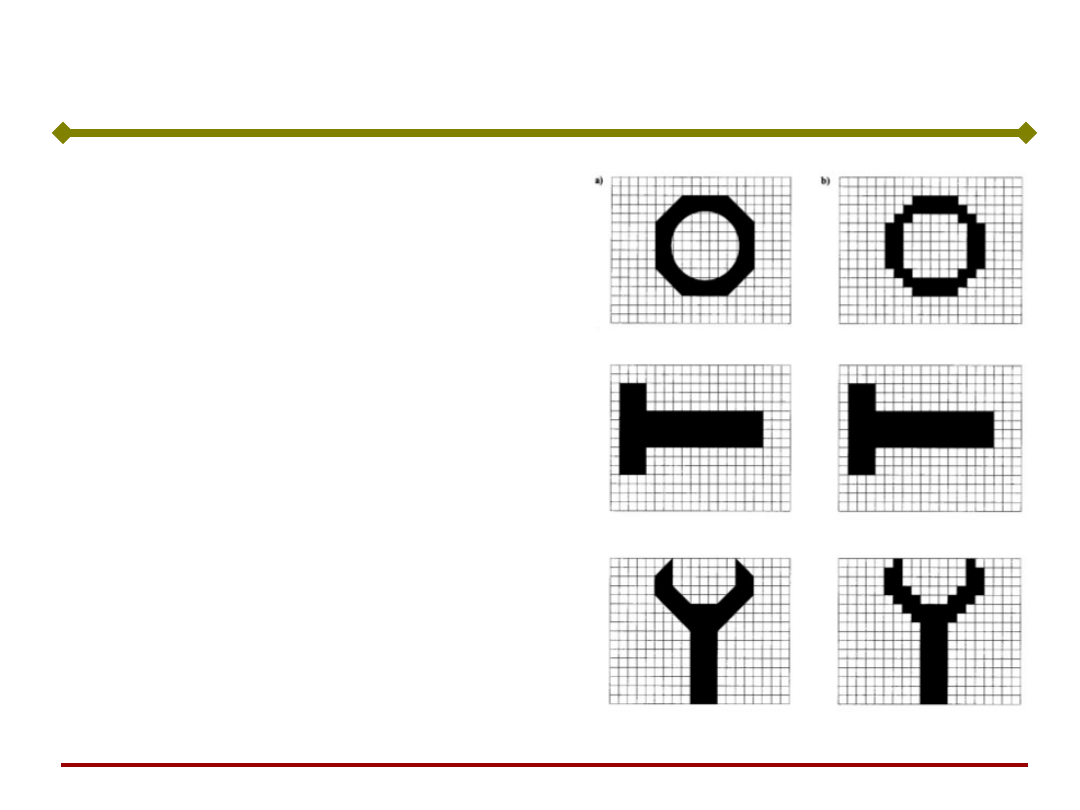
Pierwszym krokiem jest 
przedstawienie rzeczywistego 
obrazu za pomocą siatki o polach 
białych i czarnych. 

Sieć ma pamiętać 3 obrazy: 
nakrętka, nit i klucz, 
przedstawione na tle siatki o 
wymiarach m x n . 

Podstawy Sztucznej 

Inteligencji

Jan Kusiak

Przykład zastosowań, c.d.

Rozpoczynając od dowolnego 
stanu początkowego na 
wyjściu, sieć po przejściu 
pewnej liczby stanów 
pośrednich powinna 
zatrzymać się w jednym ze 
stanów stabilnych. 

Sieć może rozpoznać 
zniekształcony obraz.

Sieć ta będzie posiadać 3 stany 
stabilne odpowiadające trzem 
obrazom. 

Podstawy Sztucznej 

Inteligencji

Jan Kusiak

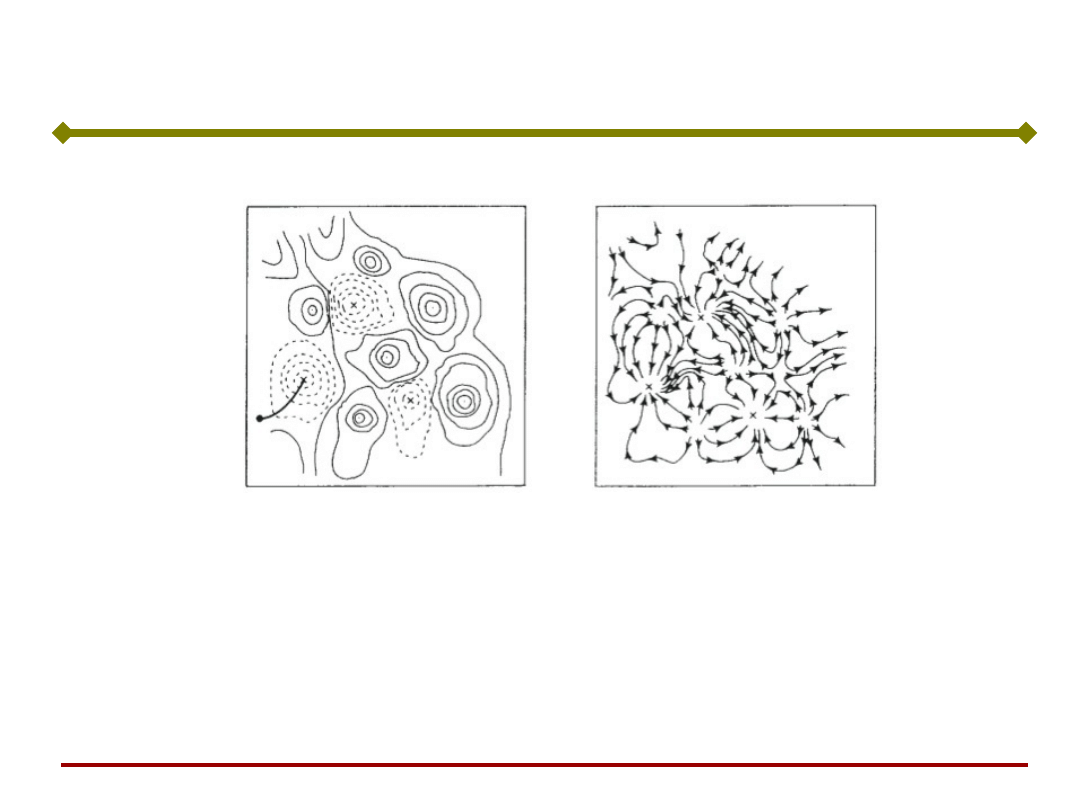
Proces uczenia sieci kształtuje obszary atrakcji 
(przyciągania) poszczególnych punktów równowagi 
odpowiadających danym uczącym. 

Uczenie sieci neuronowej realizującej pamięć 
asocjacyjną ma za zadanie taki dobór wag W

ij 

poszczególnych neuronów, aby na etapie „odczytu” 
(przy zamrożonych wagach) sieć była zdolna odnaleźć 
zbiór danych, najbliższy w sensie Hamminga, 
wektorowi testowemu. 

Uczenie pamięci asocjacyjnej

Podstawy Sztucznej 

Inteligencji

Jan Kusiak

W przypadku pamięci autoasocjacyjnej występuje 
wektor uczący x lub zbiór tych wektorów, które w 
wyniku przeprowadzonego uczenia sieci ustalają 
położenie poszczególnych atraktorów.

Uczenie pamięci asocjacyjnej, c.d.

Podstawy Sztucznej 

Inteligencji

Jan Kusiak

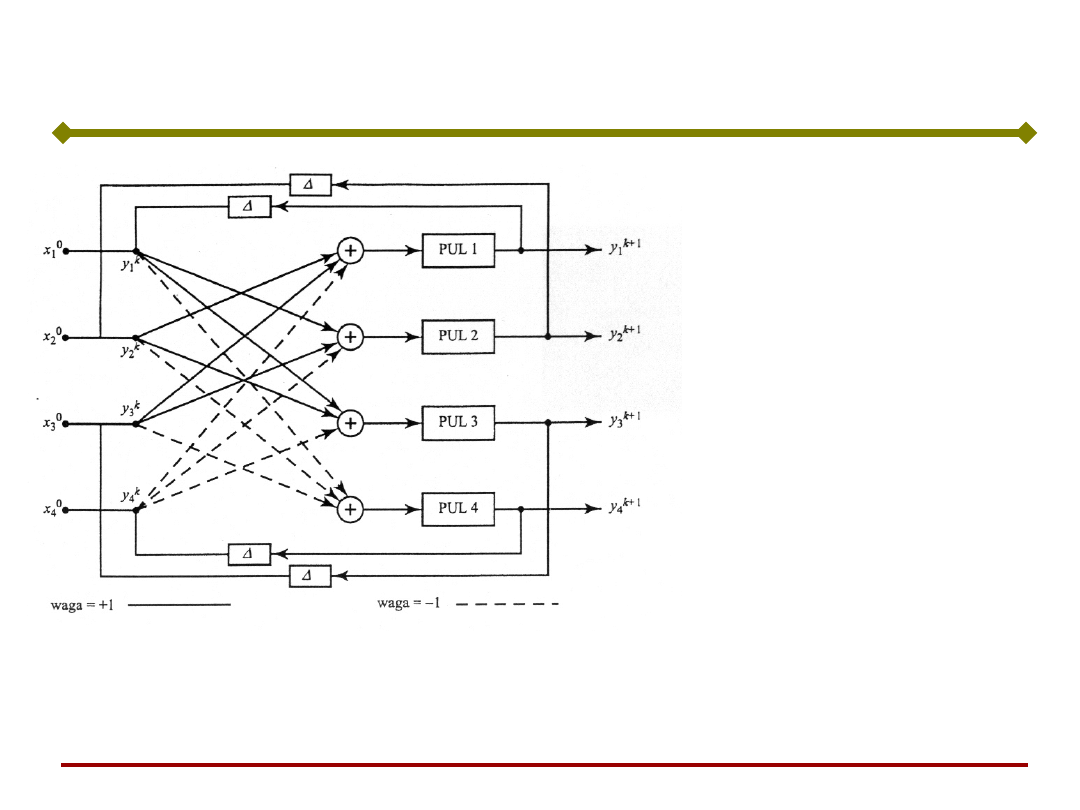
Sieć Hopfielda 
- przykład działania

Podstawy Sztucznej 

Inteligencji

Jan Kusiak

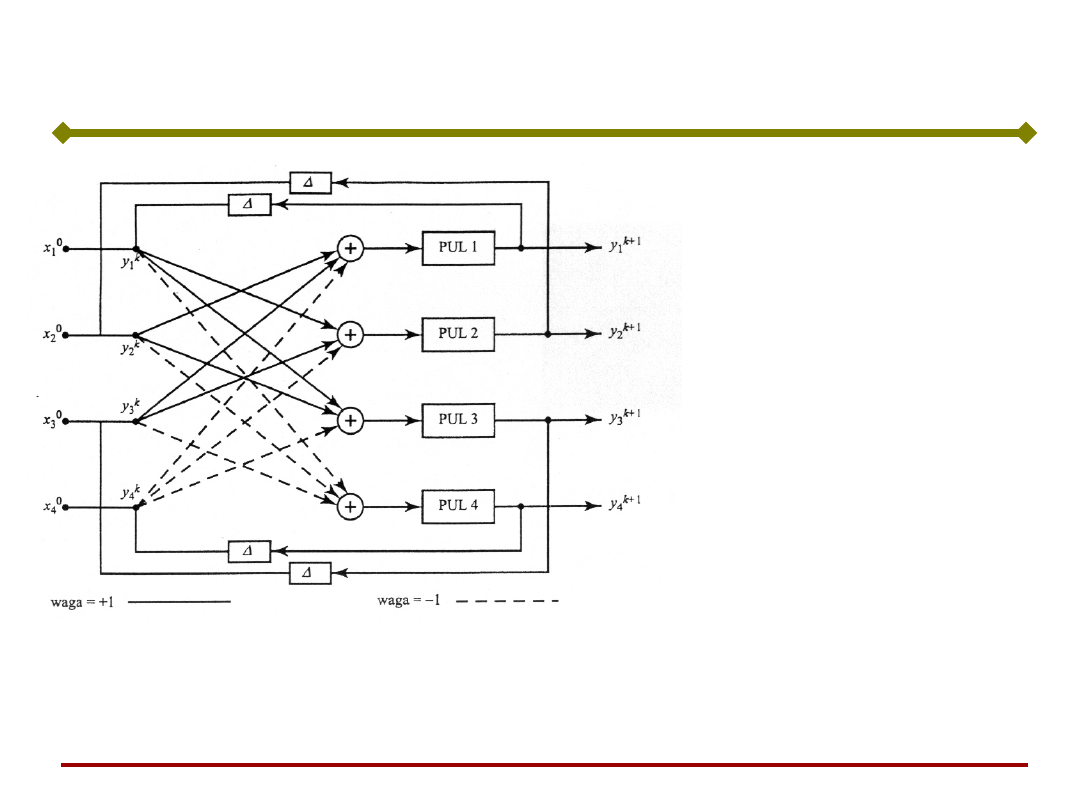
Sieć Hopfielda

Jednorazowe 
pobudzenie x

0

 ma 

sens wymuszenia 
stanu początkowego. 

Elementy  
przypominają, że 
odpowiedź neuronu 
jest opóźniona w 
stosunku do 
pobudzenia.

Sygnał wyjściowy:

))

(

(

)

(

t

Wy

t

y









Podstawy Sztucznej 

Inteligencji

Jan Kusiak

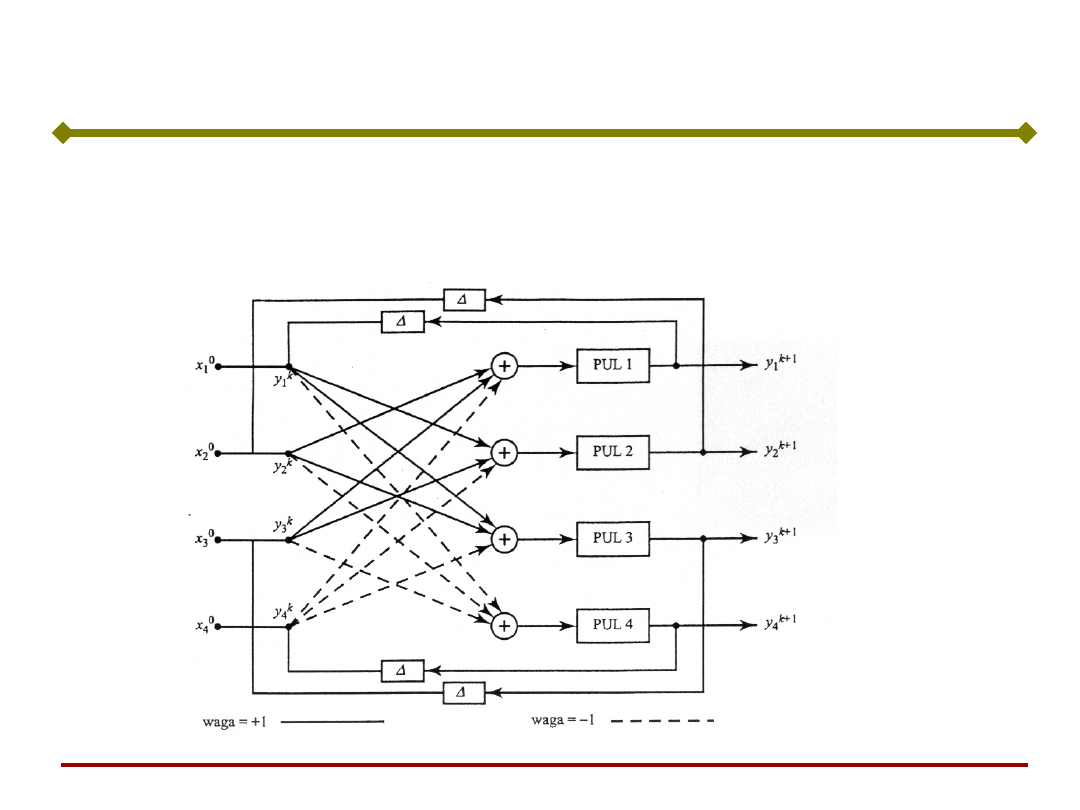
Sieć Hopfielda – prosty przykład 
działania

Przeanalizujemy sieć 
rekurencyjną 
złożoną z 4 
neuronów o 
binarnych, 
bipolarnych 
funkcjach aktywacji. 

Zilustrujemy pojęcie 
przejść stanu

Podstawy Sztucznej 

Inteligencji

Jan Kusiak

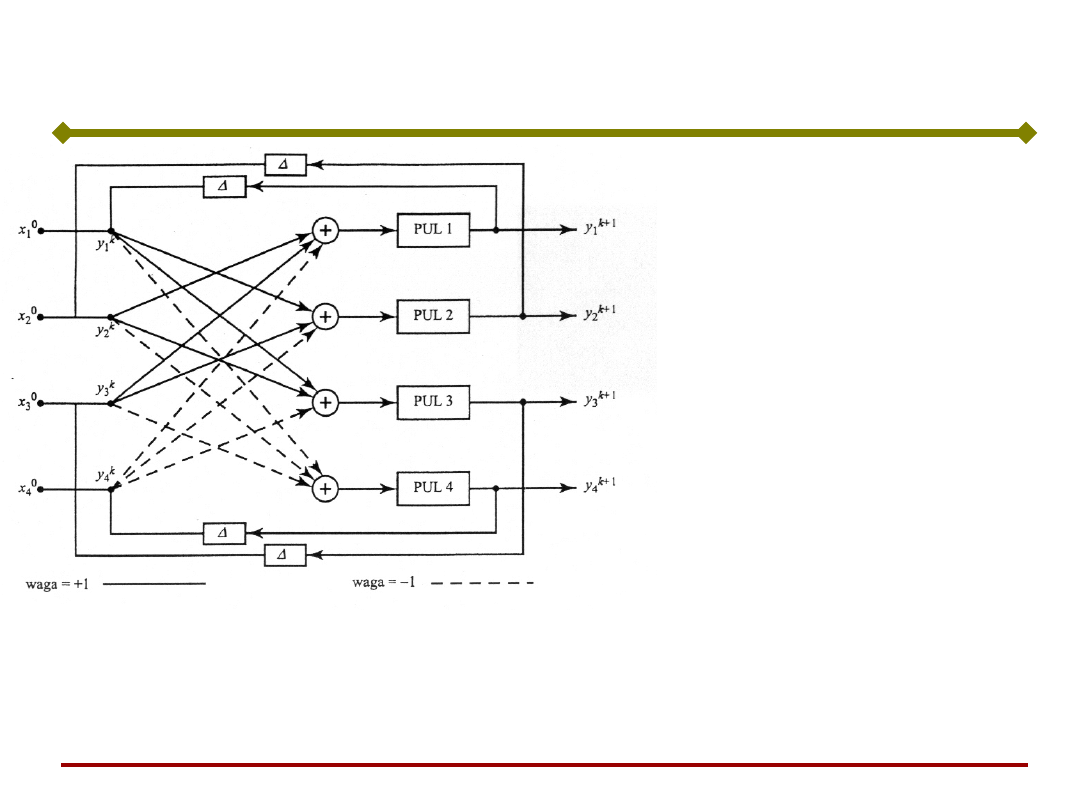
Sieć Hopfielda – prosty przykład 
działania

Macierz wag:







































0

1

1

1

1

0

1

1

1

1

0

1

1

1

1

0

W

Każdy ciąg przejść kończy się jednym z dwóch 
wektorów (punkty równowagi stabilnej – atraktory):

,

]

1

1

1

1

[

,

]

1

1

1

1

[

2

1

T

T

y

y













Podstawy Sztucznej 

Inteligencji

Jan Kusiak

Sieć Hopfielda – prosty przykład 
działania

Łatwo sprawdzić, że żaden ze stanów równowagi nie 
wywołuje dalszych przejść. Podstawiając x

0

 = y

1

 

otrzymujemy w pierwszym kroku rekurencji:

€ 

y

1

=ϕ(Wx

0

)=ϕ

0

1

1 −1

1

0

1 −1

1

1

0 −1

−1 −1 −1 0

⎡ 

⎣ 

⎢ 

⎢ 

⎢ 

⎢ 

⎤ 

⎦ 

⎥ 

⎥ 

⎥ 

⎥ 

1
1
1

−1

⎡ 

⎣ 

⎢ 

⎢ 

⎢ 

⎢ 

⎤ 

⎦ 

⎥ 

⎥ 

⎥ 

⎥ 

⎛ 

⎝ 

⎜ 

⎜ 

⎜ 

⎜ 

⎞ 

⎠ 

⎟ 

⎟ 

⎟ 

⎟ 

=

sgn(3)
sgn(3)
sgn(3)

sgn(−3)

⎡ 

⎣ 

⎢ 

⎢ 

⎢ 

⎢ 

⎤ 

⎦ 

⎥ 

⎥ 

⎥ 

⎥ 

=y

1

i ogólnie, y

k+1

 = y

k

 = y

1

. 

Podobnie, gdy stanem początkowym jest x

0

 = y

2

, 

wówczas y

1

 = ....= y

2

Podstawy Sztucznej 

Inteligencji

Jan Kusiak

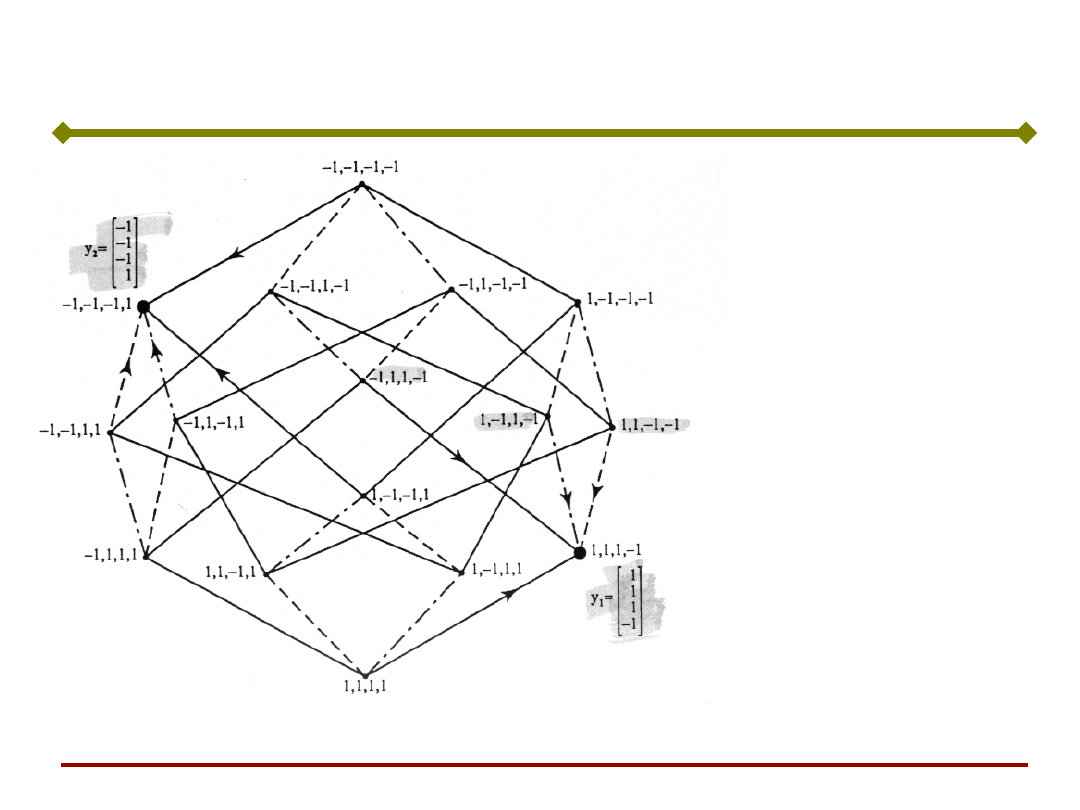
Sieć Hopfielda – prosty przykład 
działania

Wierzchołki 
czterowymiarowego 
hipersześcianu 
reprezentują 
wartości wektora 
stanu i możliwe 
przejścia stanu sieci. 

W każdym 
wierzchołku 
zbiegają się 4 
krawędzie, łączące 
go z sąsiednimi 
wierzchołkami, 
reprezentującymi 
wektory różniące się 
wartością tylko 
jedną składową.

Podstawy Sztucznej 

Inteligencji

Jan Kusiak

Sieć Hopfielda – prosty przykład 
działania

Przyjmijmy, że stanem początkowym jest stan 

sąsiadujący z y

1

. Następnym stanem będzie: 

T

x

]

1

1

1

1

[

0



T

y

)]

3

sgn(

)

1

sgn(

)

1

sgn(

)

1

[sgn(

1





czyli nastąpi przejście do najbliższego punktu 
równowagi:

T

T

]

1

1

1

1

[

]

1

1

1

1

[





Podstawy Sztucznej 

Inteligencji

Jan Kusiak

Sieć Hopfielda – prosty przykład 
działania

Można sprawdzić, że również dla każdego ze stanów 
początkowych

sieć przejdzie do stanu y

1

 = y

1

 i w nim pozostanie.

W omówionych przypadkach następuje zbieżność stanu 
początkowego do stanu równowagi odległego tylko o 
jeden (różniącego się tylko jednym bitem). 

Jeśli stan początkowy różni się dwoma bitami od obu 
stanów równowagi, czyli jest od nich jednakowo 
odległy, to zbieżność do każdego z nich jest równie 
prawdopodobna. 

T

T

T

x

x

x

]

1

1

1

1

[

,

]

1

1

1

1

[

,

]

1

1

1

1

[

0

0

0



















Podstawy Sztucznej 

Inteligencji

Jan Kusiak

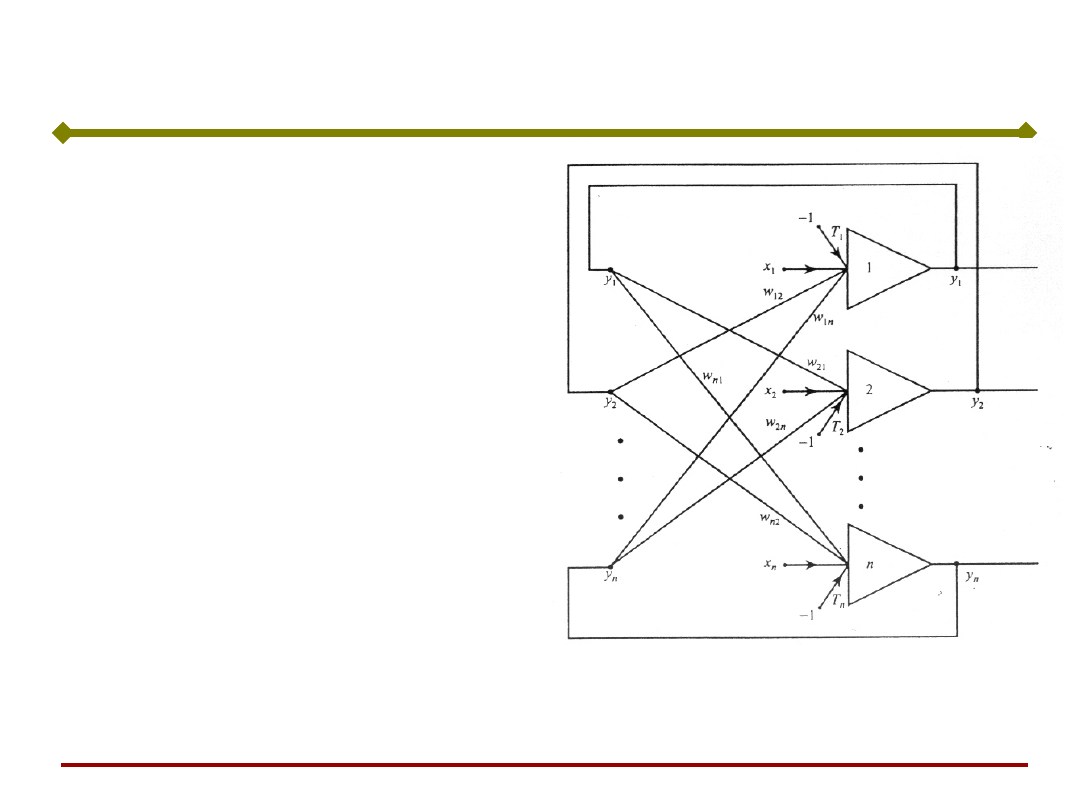
Wracamy do sieci 
Hopfielda złożonej z n 
neuronów z progami T

i

 

pobudzanych zarówno 
sygnałami z zewnątrz jak i 
sygnałami sprzężenia 
zwrotnego od innych 
neuronów, wg wzoru:

n

i

T

x

y

w

s

i

i

T

i

i

,

,

2

,

1

,











Sieć Hopfielda

Podstawy Sztucznej 

Inteligencji

Jan Kusiak

Wektory wagowy i wyjściowy dane są jako:





T

n

def

T

in

ii

i

i

def

i

y

y

y

y

w

w

w

w

w







2

1

1

2

1

,

]

0

[







Definiując wektory: pobudzeń s, wejściowy x oraz 
progowy T analogicznie jak wektor wyjściowy, 
możemy opisać liniową część sieci zależnością 
macierzową:

T

x

Wy

s







Sieć Hopfielda

























































0

0

0

2

1

2

21

1

12

2

1

















n

n

n

n

T

n

T

T

w

w

w

w

w

w

w

w

w

W

Podstawy Sztucznej 

Inteligencji

Jan Kusiak

W modelu Hopfielda zakłada się, że macierz wag jest symetryczna, 
tzn. w

ij

 = w

ji

Wyjście dowolnego neuronu połączone jest poprzez wagi z 
wejściami pozostałych neuronów, ale nie jest połączone z jego 
własnym wejściem.

Dla funkcji aktywacji typu signum, przejścia stanów zachodzą 
zgodnie z rekurencyjną zależnością:



,

2

,

1

),

sgn(

1











k

T

x

y

w

y

i

i

k

T

i

k

i

przy czym zakłada się, że ma ona charakter asynchroniczny, co 
oznacza, że w danej chwili ma miejsce aktualizacja tylko jednej 
spośród i = 1,2,....,n składowych. 

Sieć Hopfielda

Podstawy Sztucznej 

Inteligencji

Jan Kusiak

Dla oceny stabilności rozważanej sieci dynamicznej 
wprowadza się tak zwaną funkcję energetyczną 
(funkcję stanu) dodatnią i ograniczoną w przestrzeni 
wyjść. Funkcja energetyczna jest formą kwadratową:

y

T

y

x

Wy

y

E

T

T

T

def









2

1

i

n

j

i

i

n

i

i

j

i

n

i

j

j

i

ij

def

y

T

y

x

y

y

w

E























1

1

1

,

2

1

lub w postaci rozwiniętej:

Układ stabilizuje się w punkcie w którym funkcja 
energetyczna przyjmuje wartość minimum. 

Sieć Hopfielda

Podstawy Sztucznej 

Inteligencji

Jan Kusiak

Rozważmy stany przejściowe i związane z nimi 
zmiany energii w sieci jednowarstwowej z 
poprzedniego przykładu. 

Sieć Hopfielda

Podstawy Sztucznej 

Inteligencji

Jan Kusiak

Dla zerowych progów i sygnałów wejściowych oraz 
macierzy wag

Sieć Hopfielda







































0

1

1

1

1

0

1

1

1

1

0

1

1

1

1

0

W

Funkcja energetyczna ma postać:







































































4

3

2

1

4

3

2

1

0

1

1

1

1

0

1

1

1

1

0

1

1

1

1

0

2

1

)

(

y

y

y

y

y

y

y

y

y

E

Podstawy Sztucznej 

Inteligencji

Jan Kusiak

Po uporządkowaniu, funkcja energetyczna przyjmuje 
postać:

Sieć Hopfielda

4

3

4

3

2

4

3

2

1

)

(

)

(

)

(

y

y

y

y

y

y

y

y

y

y

E















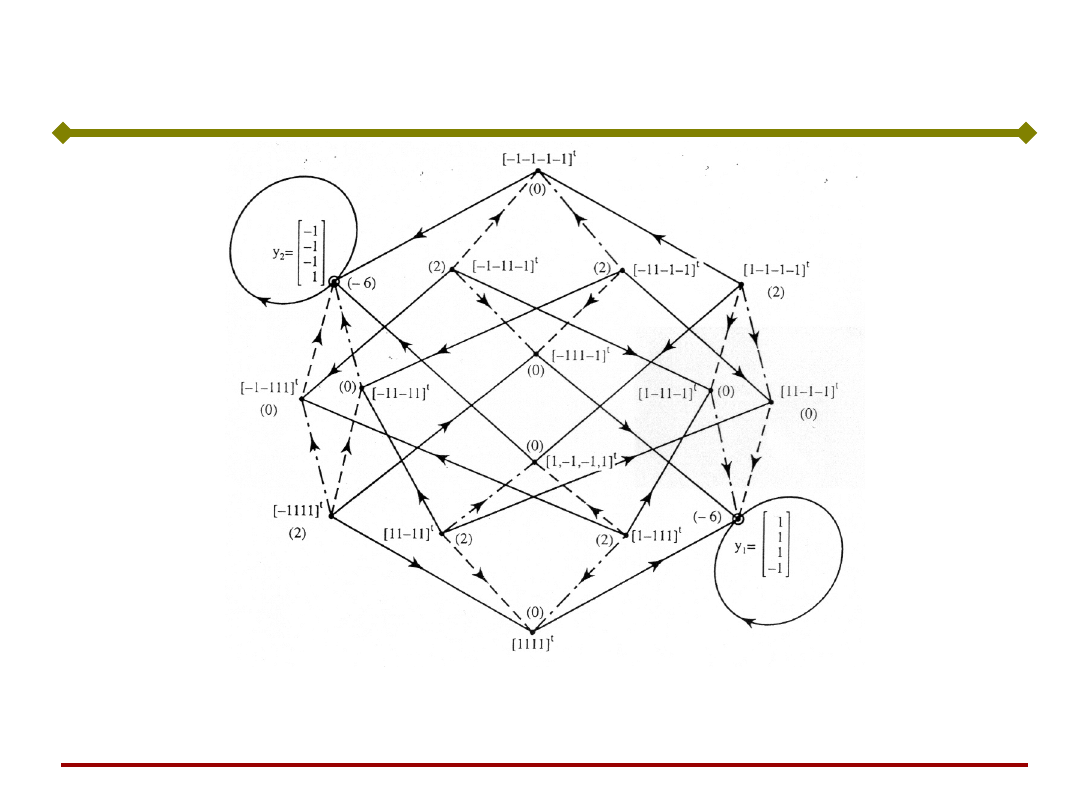
Sieć osiąga dyskretne poziomy energetyczne o 
wartościach –6, 0 i 2, co można łatwo wyliczyć jako 
energię dla każdego ze stanów począwszy od [-1 –1 –1 –
1]

T

, a kończąc na [1 1 1 1]

T

. 

Podstawy Sztucznej 

Inteligencji

Jan Kusiak

Na rysunku zaznaczono energie obliczone dla każdego z 2

4

 

wierzchołków hipersześcianu, reprezentujących stany 
analizowanej sieci. Energia przyjmuje wartość minimalną dla 
stanów równowagi y

1

 = [1 1 1 –1]

T

 lub y

2

 = [-1 –1 –1 1]

T

.

Sieć Hopfielda

Podstawy Sztucznej 

Inteligencji

Jan Kusiak

Sieci Hopfielda

•Proces odczytu (odtwarzania)

•Proces zapisu (uczenia)

Podstawy Sztucznej 

Inteligencji

Jan Kusiak

W trybie odczytu (odtwarzania), przy zamrożonych 
wartościach wag i założeniu określonego stanu 
początkowego neuronów v(0) = x następuje proces 
przejściowy, przebiegający zgodnie z zależnością:

€ 

v

i

k+1

=sgn w

ij

j=1

n

∑

v

j

k

(

)

Funkcja energii wynosi:

Uczenie sieci Hopfielda - odczyt

(1)

k – numer kroku, i – numer neuronu, którego stan 
ulega zmianie (założone zerowe sygnały progowe 
oraz wymuszenia zewn.)

€ 

E(v)=−

1

2

v

T

Wv

Podstawy Sztucznej 

Inteligencji

Jan Kusiak

W trybie zapisu (uczenia) na podstawie zadanych 
wzorców uczących dobierane są wagi w

ij

.

Uczenie sieci Hopfielda –zapis

Przy zapisie do pamięci wektorów wzorcowych s

(m)

, 

m=1,2,...,p o składowych +1, -1, wagi wyznaczane są 
wg algorytmu Hebba:

€ 

W= s

(m)

(s

(m)

)

T

−pI

m=1

p

∑

lub:

€ 

w

ij

=(1−δ

ij

) s

i

( m)

s

j

(m)

m=1

p

∑

Podstawy Sztucznej 

Inteligencji

Jan Kusiak

Uczenie sieci Hopfielda – algorytm

Danych jest p wektorów wzorcowych bipolarnych:

€ 

W← 0

Gdzie s

(m)

 ma wymiar n x 1, m = 1, 2, ..., p. 

Początkowy wektor stanu v

(0) 

ma wymiar n x 1

  

€ 

{s

(1)

,s

(2)

,K ,s

( p)

}

Zapis

Krok 1:  Podstawienie

Macierz W ma wymiar n x n

Krok 2:  Dla m = 1, ...,  p

€ 

W← s

(m)

s

( m)T

−I

Krok 3:  Zapis wektorów do pamięci zakończony. 

   W jest macierzą wag.

Podstawy Sztucznej 

Inteligencji

Jan Kusiak

Uczenie sieci Hopfielda – algorytm

Odczyt

Krok 1:  Założenie stanu początkowego v

(0)

 = x

Krok 2:  Ustawienie liczb 1, 2 ...,  n  w losowej kolejności α

1, 

α

2,

..., α

n

€ 

v'

α

i

=sgn w

α

i

j

v

j

j=1

n

∑

(

)

Krok 3:  Dla i = 1, ..., n  wykonanie: 

Krok 4:  Jeżeli 

€ 

v'

α

i

=v

α

i

dla i = 1,2, ..., n

czyli w danym cyklu nie było zmian, to 
koniec odczytu i uznanie otrzymanych 
sygnałów za sygnały wyjściowe.
W przeciwnym razie powrót do Kroku 2.

Podstawy Sztucznej 

Inteligencji

Jan Kusiak

Sieć Hopfielda – przykład

Sieć pamiętająca dwa wektory:

€ 

s

(1)

=[−1−111]

T

€ 

W=

0 0 −2 0
0 0 0 −2

−2 0 0 0

0 −2 0 0

⎡ 

⎣ 

⎢ 

⎢ 

⎢ 

⎢ 

⎤ 

⎦ 

⎥ 

⎥ 

⎥ 

⎥ 

Funkcja energii:

€ 

s

(2)

=[−111−1]

T

Obliczona zgodnie z algorytmem macierz wag:

€ 

E(v)=2(v

1

v

3

+v

2

v

4

)

Podstawy Sztucznej 

Inteligencji

Jan Kusiak

Sieć Hopfielda – przykład

Uwaga:
Asynchroniczne uaktualnianie stanu powoduje, że 
wartość funkcji energii nie rośnie i sieć osiąga 
jedno z lokalnych minimów energii.

Energia układu dla wektora komplementarnego E(-
v) = E(v).

Wartość minimum energii jest taka sama dla 
wektorów komplementarnych.

Wniosek:

Układ może zmierzać zarówno do v jak i do –v. 
Dojdzie do tego, który jest bliżej stanu początkowego. 

Podstawy Sztucznej 

Inteligencji

Jan Kusiak

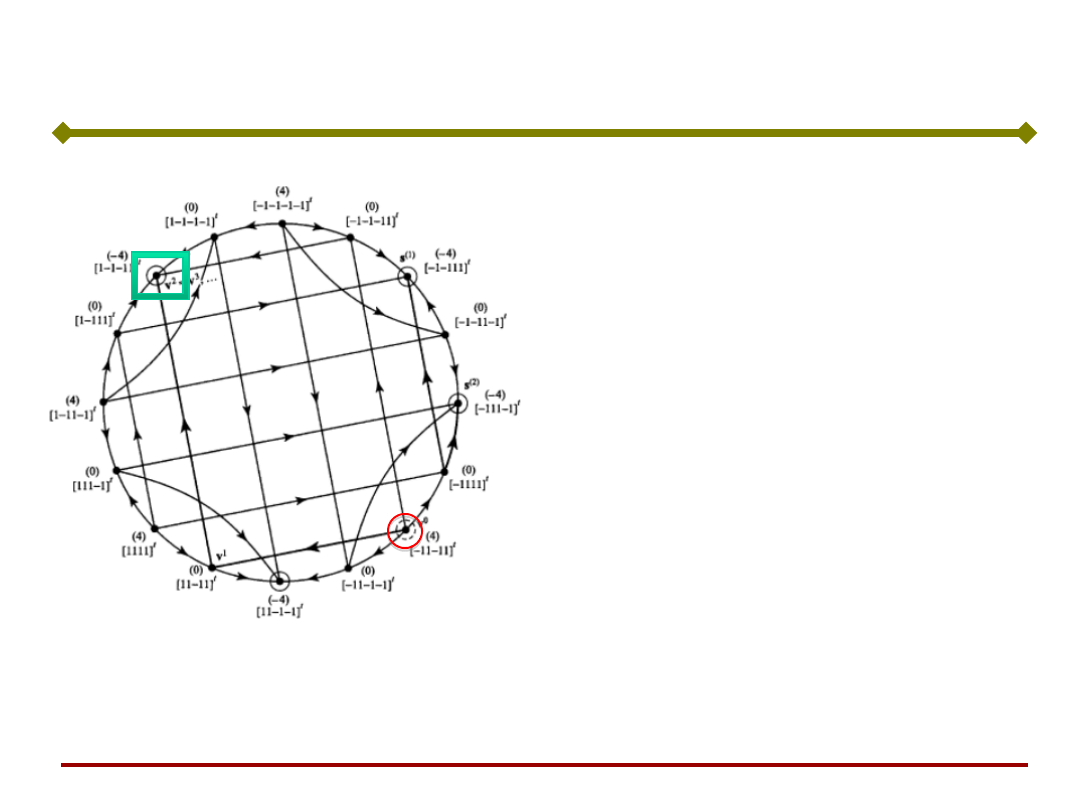
Sieć Hopfielda – przykład

Układ osiągnął stan 
stabilny, który jest 
komplementarny do 
zapamiętanego obrazu s

(2)

 

Przy innej kolejności 
aktualizowania 
neuronów, moglibyśmy 
osiągnąć wzorzec.

(bo stan początkowy nie 
był podobny do żadnego 
wzorca – odległość 
Hamminga do wzorców 
wynosiła 2, czyli 50%)

Stosunek liczby zapamiętanych obrazów do liczby neuronów 
p/n = ½ 
- pamięć była przeładowana

Podstawy Sztucznej 

Inteligencji

Jan Kusiak

Tyle na dzisiaj 

Podstawy Sztucznej 

Inteligencji

Jan Kusiak

Przy prezentacji jednego wzorca uczącego x proces 
zmian przebiega dopóty, dopóki zależność (1) nie jest 
spełniona dla wszystkich N neuronów. Warunek ten 
będzie automatycznie spełniony przy wyborze wag 
spełniających relację:

j

i

ij

x

x

N

W

1



Wówczas







N

j

i

j

j

i

x

x

x

x

N

1

)

(

1

Ponieważ wartości bipolarnych elementów wektora x, 
spełnione jest zawsze

1

)

1

(

2

2







j

x

Uczenie sieci Hopfielda

Podstawy Sztucznej 

Inteligencji

Jan Kusiak

Przy prezentacji wielu wzorców uczących x

(k)

 dla 

k=1,2,...p wagi W

ij

 są dobierane według uogólnionej 

reguły Hebba, zgodnie z którą:

)

(

1

)

(

1

k

j

p

k

k

i

ij

x

x

N

W







Przy takim trybie uczenia wagi przyjmują wartości 
uśrednione wielu próbek uczących. 

Uczenie sieci Hopfielda

Podstawy Sztucznej 

Inteligencji

Jan Kusiak

Na starcie y

0 

= x, a następnie proces iteracyjny 

powtarza się dla kolejnych wartości y

i

 aż do ustalenia 

się odpowiedzi. 

Proces iteracyjny (rekurencyjny) ustalania się 
odpowiedzi sieci trwa zwykle wiele cykli i zajmuje dużo 
czasu.

W trybie odtworzeniowym na wejście sieci podaje się 
wektor testowy x i oblicza odpowiedź sieci w postaci:

€ 

y

k+1

=sgn(Wy

k

)

Sieci Hopfielda – tryb odtworzeniowy

Podstawy Sztucznej 

Inteligencji

Jan Kusiak

Podczas odczytu pamięć może odtworzyć oczekiwany 
wzorzec, wzorzec inny niż oczekiwany lub wektor nie 
należący do zbioru zapamiętanych wzorców. 

Podstawowym zadaniem pamięci asocjacyjnej jest 
zapamiętanie zbioru próbek wejściowych (uczących) w 
taki sposób, aby przy prezentacji nowej próbki układ 
mógł wygenerować odpowiedź, która dotyczyć będzie 
jednej z zapamiętanych wcześniej próbek, położonej 
najbliżej próbki testującej. 

Najczęściej używaną miarą odległości między zbiorami 
jest miara Hamminga.

Pamięć asocjacyjna, c.d.

Podstawy Sztucznej 

Inteligencji

Jan Kusiak

Rekurencja zaczyna się od stanu y

0 

wymuszonego 

sygnałem inicjującym. W pierwszym kroku, dla k = 1, 
oblicza się y

i

1

, przy czym wskaźnik i wybierany jest 

przypadkowo. Obliczenia dla pozostałych 
składowych, również wybieranych losowo, prowadzi 
się z wykorzystaniem składowych wektora y już 
zaktualizowanych w tym kroku, uzyskując ostatecznie 
y

1. 

Dla ilustracji graficznej przedstawmy wektor 
wyjściowy w przestrzeni E

n

. Jest on tam 

reprezentowany przez jeden z wierzchołków n-
wymiarowego hipersześcianu [-1,1]

n

. Podczas 

rekurencji, przebiegającej asynchronicznie, wektor y 
przesuwa się od wierzchołka do wierzchołka, aż 
wreszcie stabilizuje się w jednym z 2

n

 możliwych 

wierzchołków. Stan końcowy y

k

, gdy k  , 

uzależniony jest od wag, progów, stanu początkowego 
i kolejności aktualizacji składowych y

i

Podstawy Sztucznej 

Inteligencji

Jan Kusiak

Inne sieci

•sieci Hamminga

•Sieci RBF

•Sieci Bayesa

•Sieci probabilistyczne PNN, 

GRNN

•Itp.