Podstawy Sztucznej

Inteligencji

Jan Kusiak

Metamodelowanie

SZTUCZNE SIECI

NEURONOWE

-

ZASTOSOWANIE

Podstawy Sztucznej

Inteligencji

Jan Kusiak

Metamodelowanie

Rozwiązywanie problemów przy pomocy

SSN

• identyfikacja problemu;
• wybór typu sieci

neuronowej (liniowa,
MLP, RBF,GRNN,
Kohonena);

• określenie struktury

sieci (liczba warstw,
liczba neuronów
w warstwach);

• uczenie sieci

(określenie wartości
parametrów neuronów).

Podstawy Sztucznej

Inteligencji

Jan Kusiak

Metamodelowanie

2007.11.0

8

Przykłady zastosowań

SSN

- Modelowanie procesów

Podstawy Sztucznej

Inteligencji

Jan Kusiak

Metamodelowanie

2007.11.0

8

Modelowanie

Podstawy Sztucznej

Inteligencji

Jan Kusiak

Metamodelowanie

Modele

Model fizyczny – opis procesów w obiekcie
(fizycznych, również ekonomicznych i społecznych).

Model matematyczny – zbiór reguł i zależności, na
podstawie których można za pomocą obliczeń
przewidzieć przebieg modelowanego procesu. Modelem
matematycznym są równania opisujące proces oraz
wszelkie relacje opisujące ograniczenia i
uproszczenia.

Model komputerowy – program komputerowy umożliwiający
otrzymanie na drodze obliczeniowej* przebiegów
czasowych zjawisk i charakterystyk modelowanego
procesu (obiektu).

*

na podstawie znajomości parametrów modelowanego obiektu i

stanu początkowego

Podstawy Sztucznej

Inteligencji

Jan Kusiak

Metamodelowanie

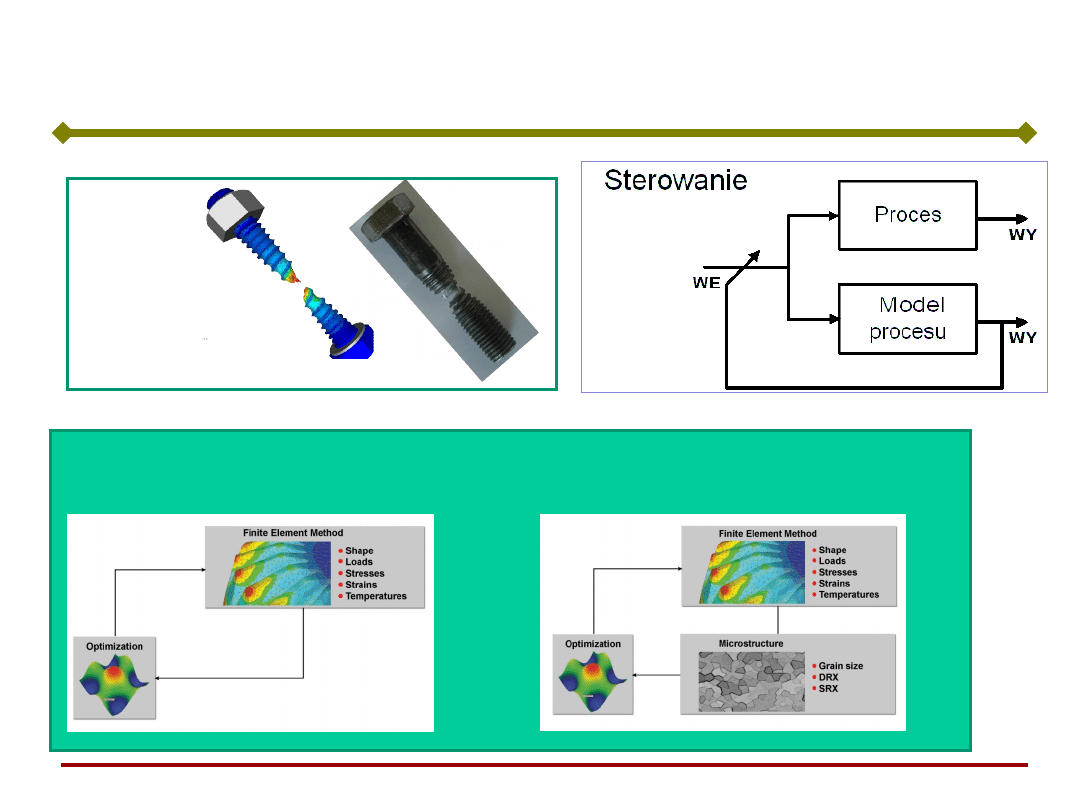
Po co modelowanie?

Projektowanie i optymalizacja

Symulacja

Podstawy Sztucznej

Inteligencji

Jan Kusiak

Metamodelowanie

Ewolucja modelowania

 Modele empiryczne
 Modele analityczne
 ......
 Modele oparte o sztuczną

inteligencję

Podstawy Sztucznej

Inteligencji

Jan Kusiak

Metamodelowanie

Modelowanie

x

y

Proces

Zmiana ciśnienia pewnej objętości gazu w zbiorniku
jest funkcją (deterministyczną) temperatury
( prawo Charlesa) oraz pewnych zakłóceń
spowodowanych, m.in. błędami pomiarowymi
(czujników pomiarowych).

Błędy te są przypadkowe i charakteryzują się
pewnym rozkładem prawdopodobieństwa od którego
zależą częstotliwość i wielkość zakłóceń.

Podstawy Sztucznej

Inteligencji

Jan Kusiak

Metamodelowanie

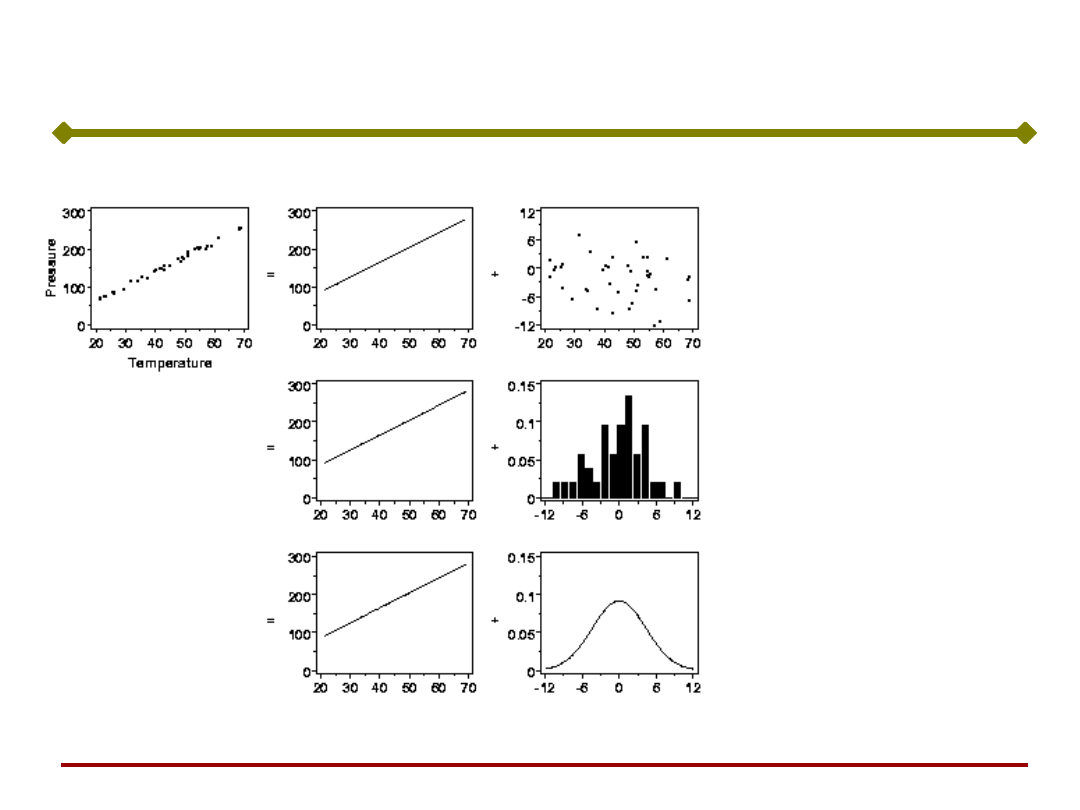
Modelowanie

Model liniowy

+

odchyłki danych od
linii prostej
(różne skale na
osiach !!!)

Model liniowy

+

histogram odchyłek
pomiarów

część
determinist
yczna

część
stochastycz
na

Model liniowy

+

znormalizowany
rozład
prawdopodobieństwa
odchyłek pomiarów

Podstawy Sztucznej

Inteligencji

Jan Kusiak

Metamodelowanie

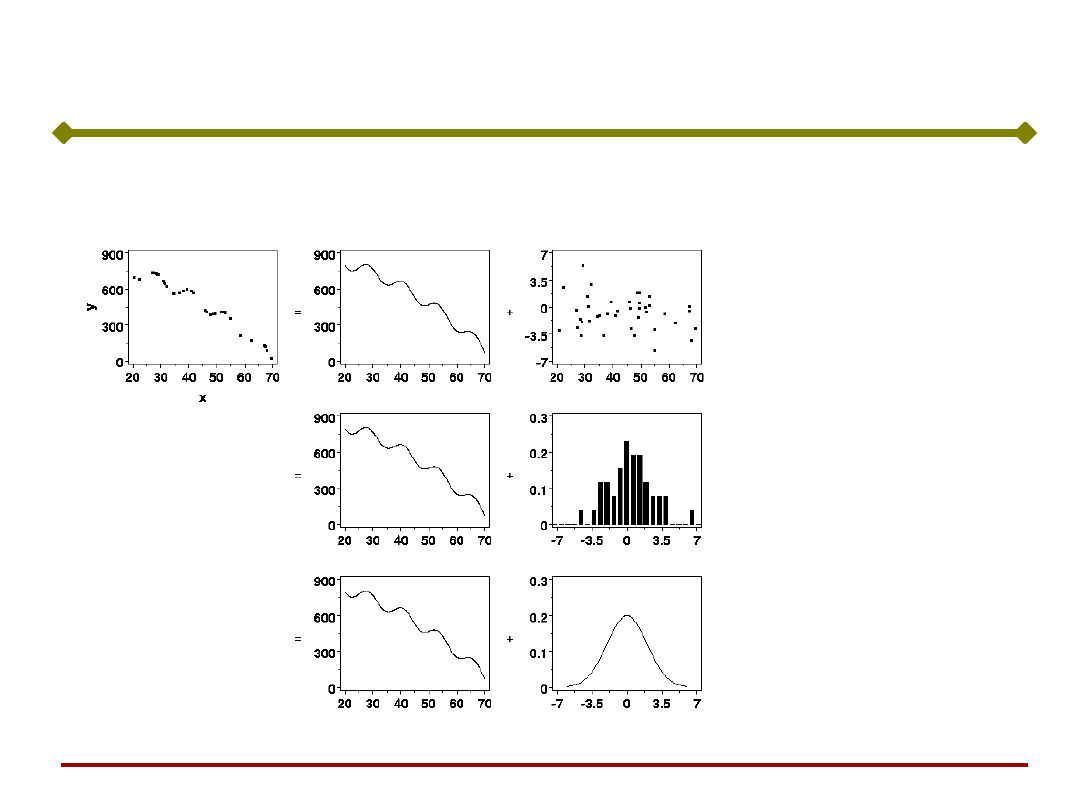
Modelowanie

część
determinist
yczna

część
stochastycz
na

Model nieliniowy

+

odchyłki danych od
linii prostej
(różne skale na
osiach !!!)

Model nieliniowy

+

histogram odchyłek
pomiarów

Model nieliniowy

+

znormalizowany
rozład
prawdopodobieństwa
odchyłek pomiarów

Podstawy Sztucznej

Inteligencji

Jan Kusiak

Metamodelowanie

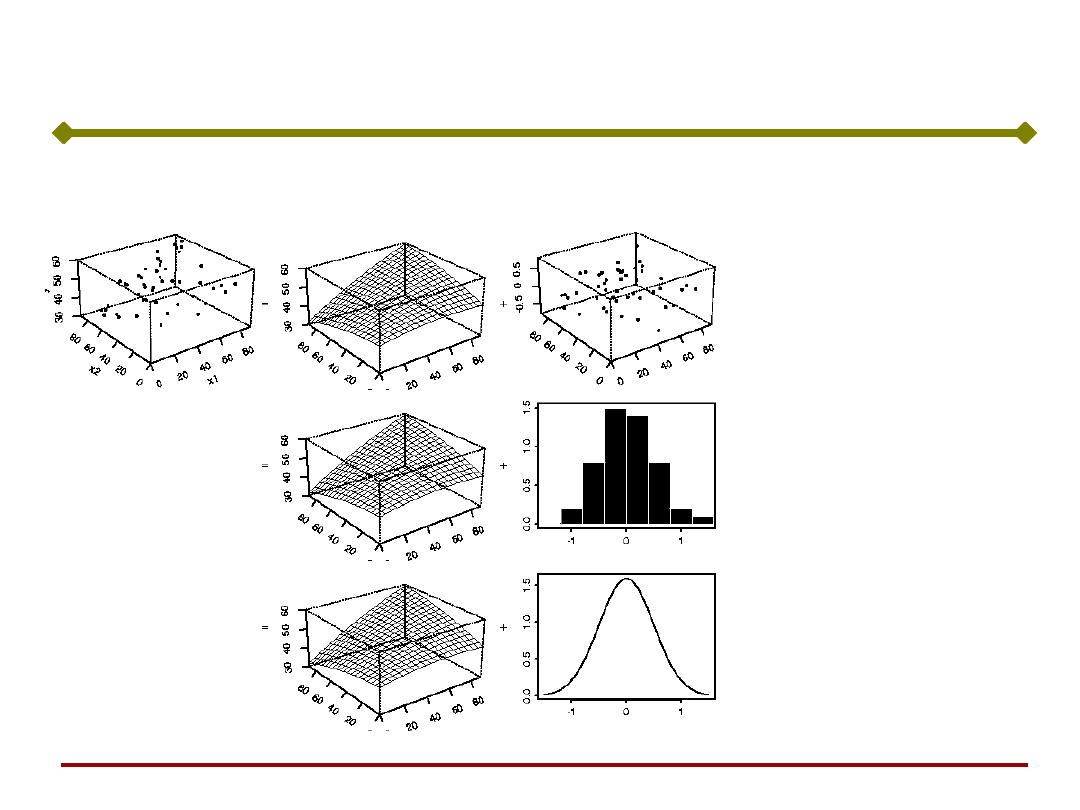
Modelowanie

część
determinist
yczna

część
stochastycz
na

Model nieliniowy

+

odchyłki danych od
linii prostej
(różne skale na
osiach !!!)

Model nieliniowy

+

histogram odchyłek
pomiarów

Model nieliniowy

+

znormalizowany
rozład
prawdopodobieństwa
odchyłek pomiarów

Podstawy Sztucznej

Inteligencji

Jan Kusiak

Metamodelowanie

Modelowanie

Modelowanie – poszukiwanie opisu zmian
wielkości sygnału wyjściowego y procesu
złożonego zazwyczaj z dwóch składowych (sygnału
wejściowego x i zakłóceń) :
1.opisu deterministycznego, stanowiącego opis
matematyczny zależności sygnału y od jednej,
lub więcej zmiennych x

y = f(x) = f(x

1

, x

2

, …, x

n

)

•składowej, będącej odpowiednikiem zakłóceń
zmieniających się w sposób przypadkowy (o
pewnym rozkładzie prawdopodobieństwa)

x

y

Proces

Podstawy Sztucznej

Inteligencji

Jan Kusiak

Metamodelowanie

Modelowanie

Podsumowanie:

Tradycyjny model procesu składa się z
następujących elementów:
1. Sygnału wyjściowego, oznaczanego
zazwyczaj jako y,
2. Matematycznego równania opisującego
zależność sygnału wyjściowego od sygnałów
wejściowych:
y = f(x, β) = f(x

1

, x

2

, …, x

n,

β

1

, β

2

, …,

β

n

)

3. Zakłóceń (błędów) ε.

Ostateczna forma modelu:

y = f(x, β) + ε

Podstawy Sztucznej

Inteligencji

Jan Kusiak

Metamodelowanie

Modelowanie

x

y

y = f(x,

β) + ε

x

y

SSN

Model tradycyjny

Model oparty o SSN

Podstawy Sztucznej

Inteligencji

Jan Kusiak

Metamodelowanie

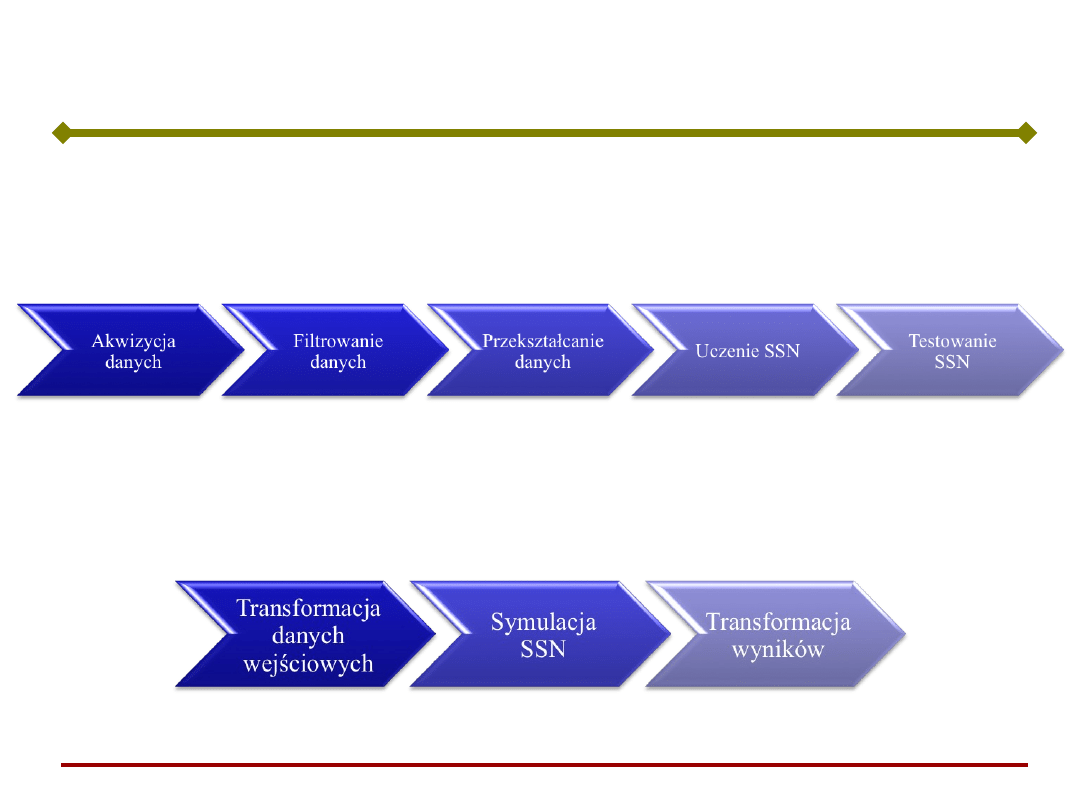
Idea budowy modelu

budowa modelu SSN

użycie modelu SSN

Podstawy Sztucznej

Inteligencji

Jan Kusiak

Metamodelowanie

SSN – przykłady

zastosowań

Podstawy Sztucznej

Inteligencji

Jan Kusiak

Metamodelowanie



Mikro:



Aproksymacja krzywych umocnienia metali odkształcanych
na zimno i na gorąco (z uwzględnieniem zmiennych
wewnętrzych)



Analiza wad w odkuwkach z materiałów kompozytowych na
bazie aluminium,



Modelowanie mikrostruktury metali

Sztuczne sieci neuronowe w metalurgii – wyniki badań



Makro:



Modelowanie ugięcia walców i wypukłości blach
grubych walcowanych na gorąco,



Przewidywanie sił i momentów walcowania,



Przewidywanie krzywizny walcowanego pasma w
asymetrycznym procesie walcowania blach,



Sterowanie procesem walcowania



Inne:



Filtrowanie danych pomiarowych



Statyczny model konwertora tlenowego



Model pieca do wytopu miedzi

Podstawy Sztucznej

Inteligencji

Jan Kusiak

Metamodelowanie

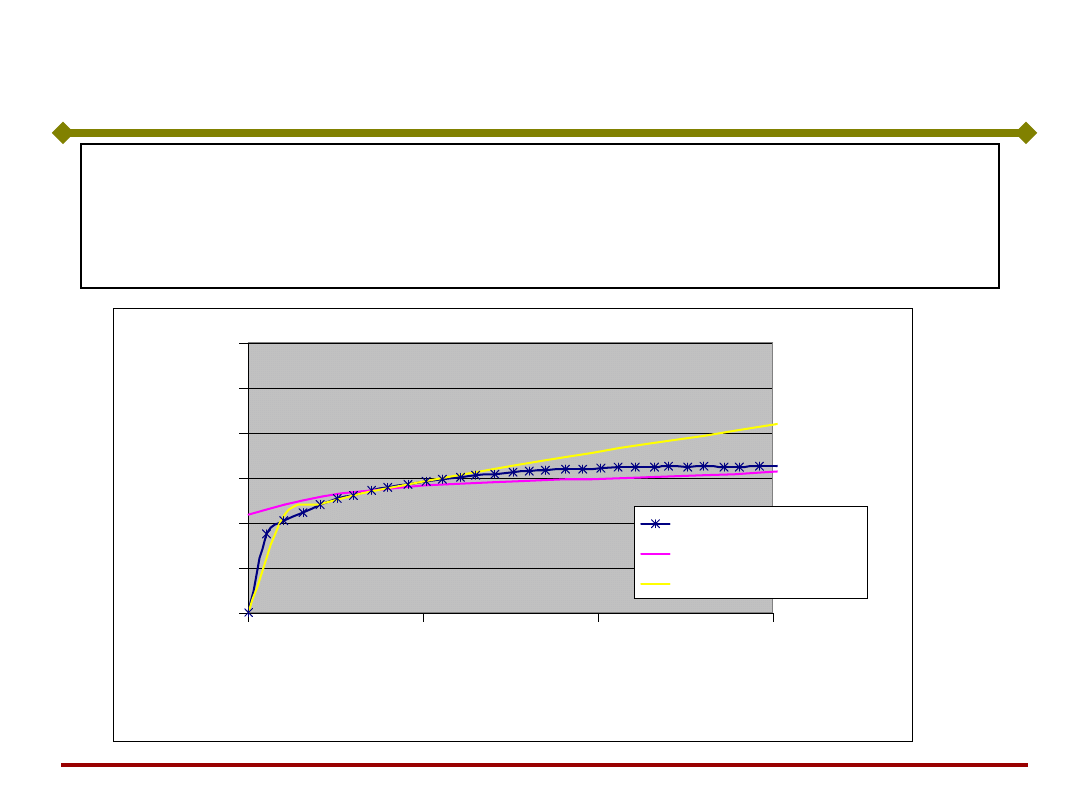
Problemy aproksymacji krzywej umocnienia



aproksymacja klasyczna



zmienne wewnętrzne



metoda inverse

0

50

100

150

200

250

300

0

0.2

0.4

0.6

odkształcenie

n

a

p

rę

ż

e

n

ie

,

M

P

a

pomiar
aproks. (zm. wewn.)
aproks. (sinh)

Podstawy Sztucznej

Inteligencji

Jan Kusiak

Metamodelowanie

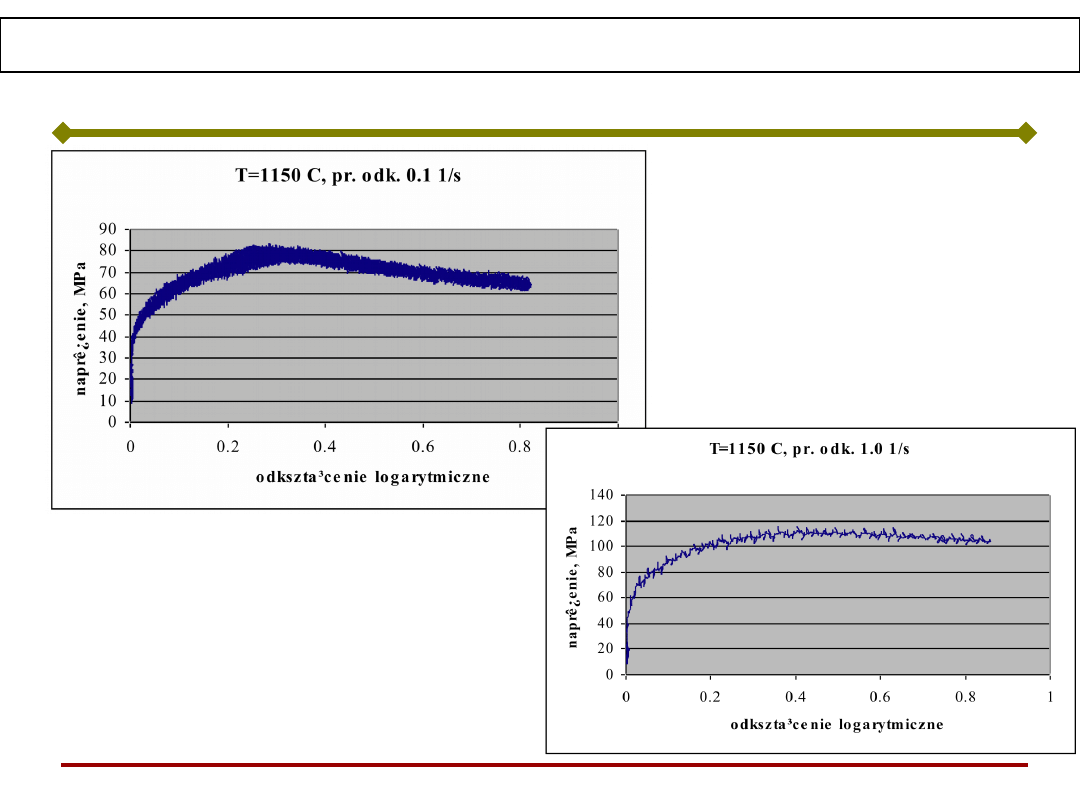
Aproksymacja sztuczną siecią neuronową

stal węglowo-manganowa, prędk. odkszt. 1.0 1/s

0

20

40

60

80

100

120

0.0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

odkształcenie

n

a

p

rę

że

n

ie

,

M

P

a

T = 950, pomiary
T = 950, SSN
T=1050, pomiary
T=1050, SSN
T=1150, pomiary
T=1150, SSN

Podstawy Sztucznej

Inteligencji

Jan Kusiak

Metamodelowanie

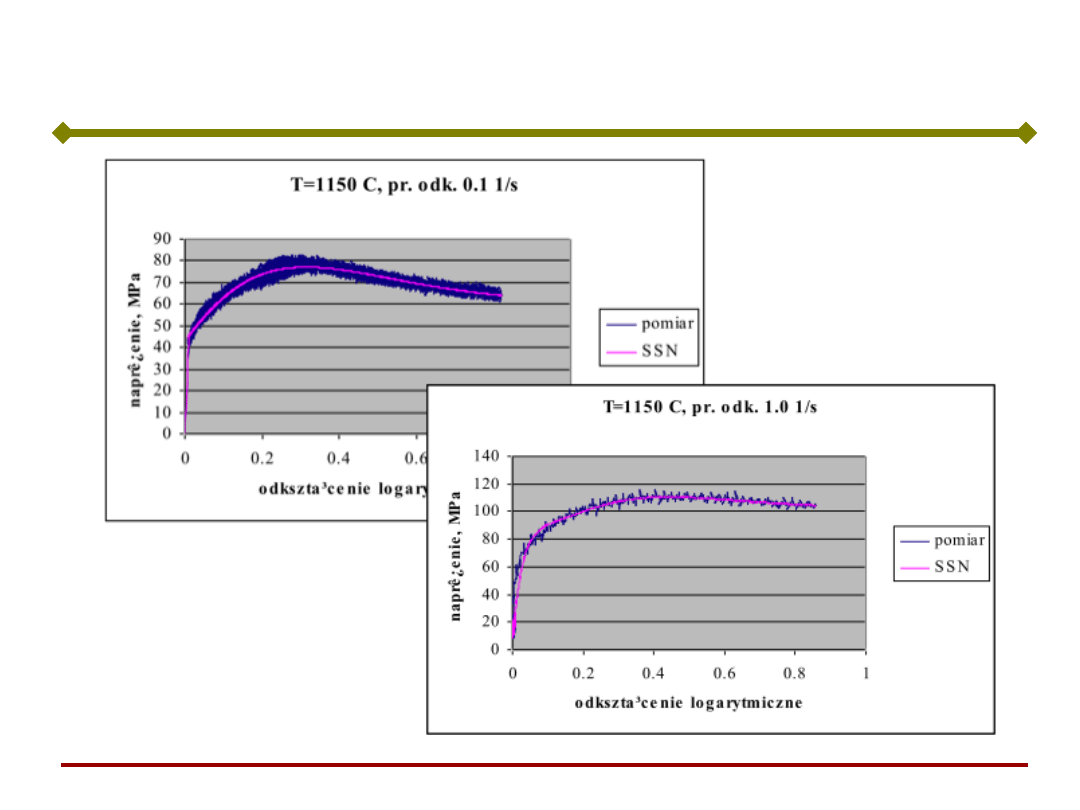
Stal austenityczna

szum „symetryczny”

szum „niesymetryczny”

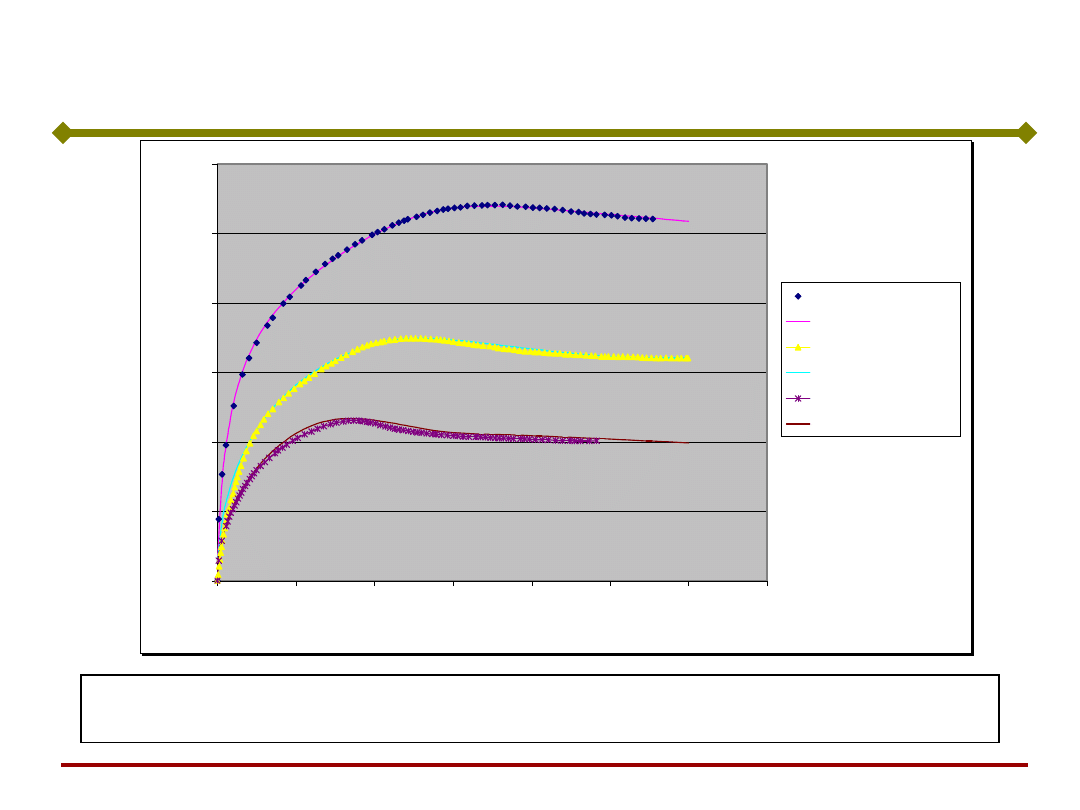
Filtrowanie szumów pomiarowych krzywej umocnienia

Podstawy Sztucznej

Inteligencji

Jan Kusiak

Metamodelowanie

Podstawy Sztucznej

Inteligencji

Jan Kusiak

Metamodelowanie

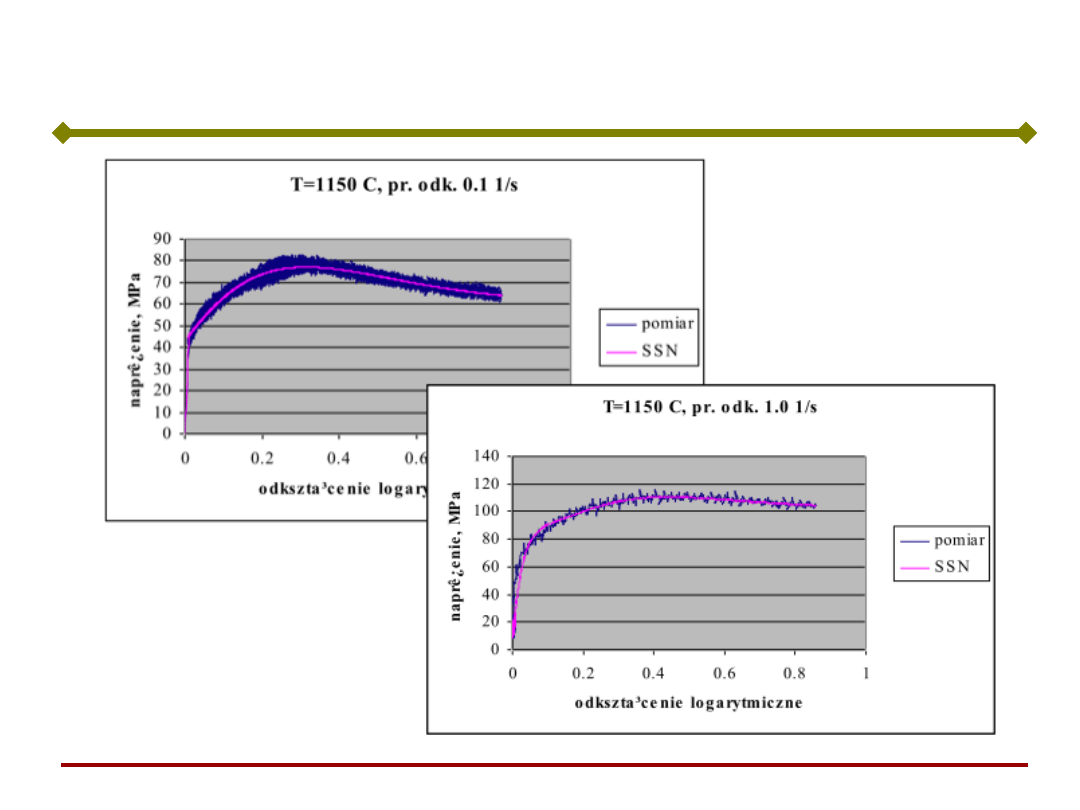
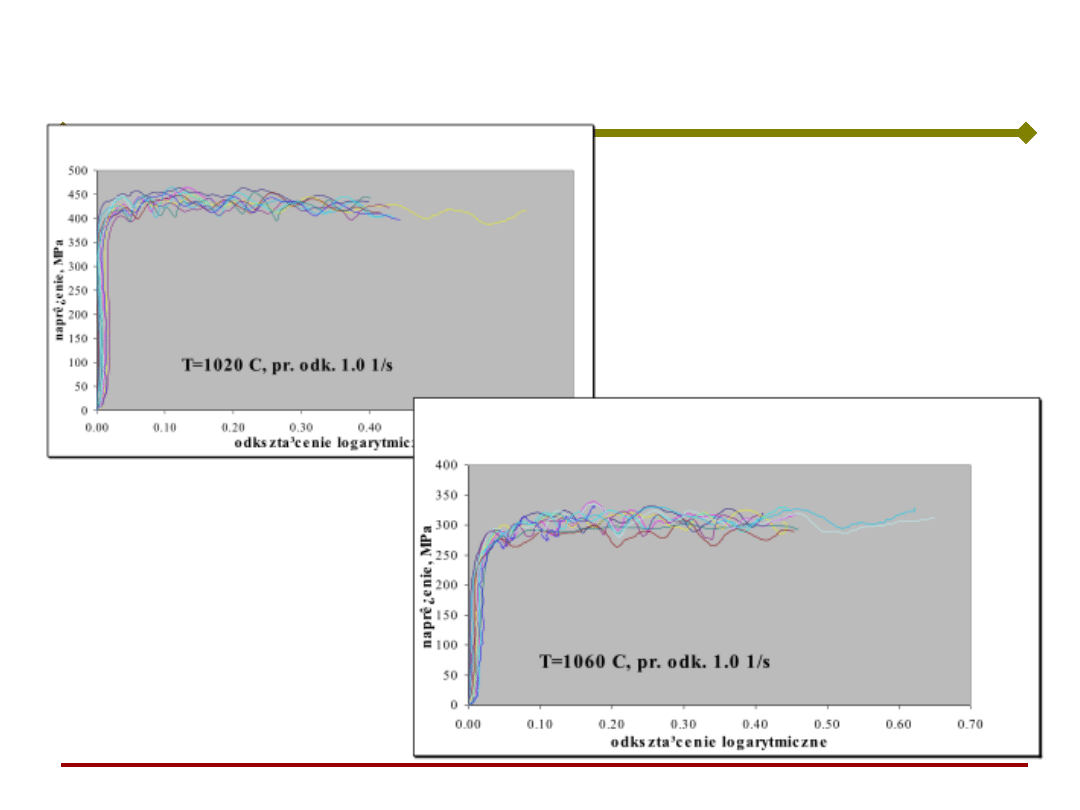
Stal austenityczna

Wynik filtrowania SSN – stal

austenityczna

Podstawy Sztucznej

Inteligencji

Jan Kusiak

Metamodelowanie

Waspaloy

Filtrowanie - krzywa umocnienia

Waspaloy

Podstawy Sztucznej

Inteligencji

Jan Kusiak

Metamodelowanie

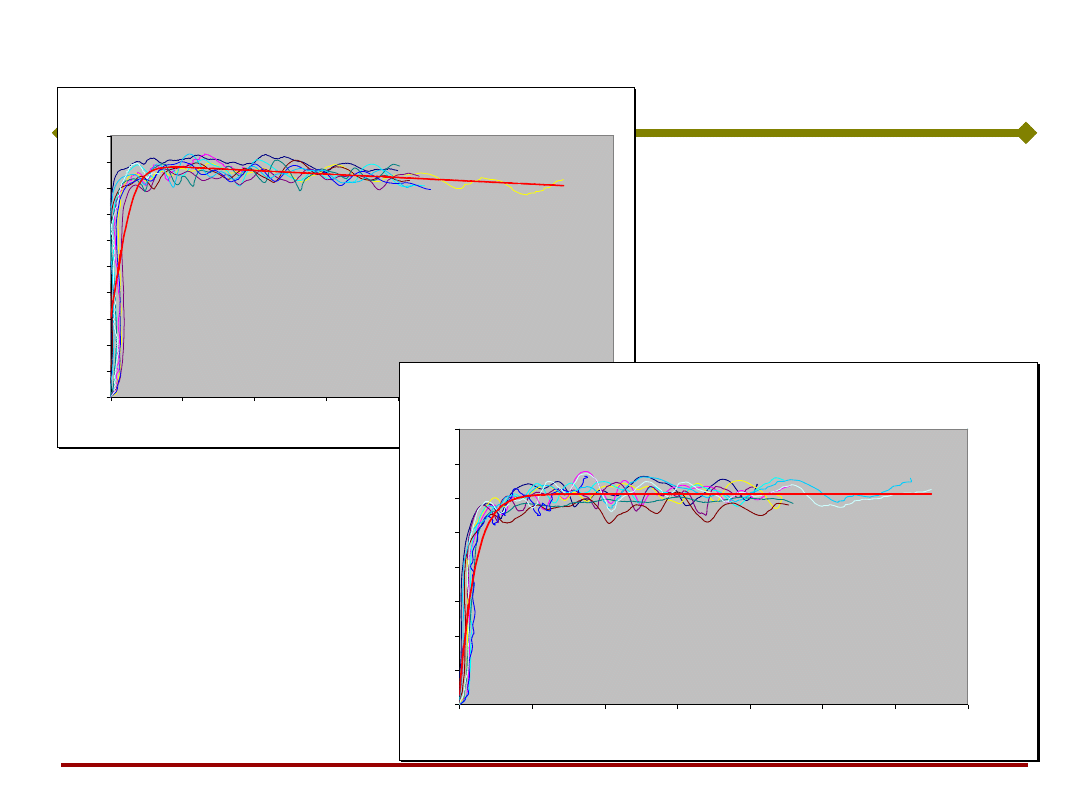
Waspaloy

Wynik filtrowania SSN – Waspaloy

T=1020 C, pr. odk. 1.0 1/s

0

50

100

150

200

250

300

350

400

450

500

0.00

0.10

0.20

0.30

0.40

0.50

0.60

0.70

odkształcenie logarytmiczne

n

a

p

rę

ż

e

n

ie

,

M

P

a

T=1060 C, pr. odk. 1.0 1/s

0

50

100

150

200

250

300

350

400

0.00

0.10

0.20

0.30

0.40

0.50

0.60

0.70

odkształcenie logarytmiczne

n

a

p

rę

że

n

ie

,

M

P

a

Podstawy Sztucznej

Inteligencji

Jan Kusiak

Metamodelowanie

Modelowanie mikrostruktury

PRZEWIDYWANIE PARAMETRÓW STRUKTURY FERRYTYCZNO-
PERLITYCZNEJ – metoda klasyczna







D

r

BC

A

D

D

)

5

.

0

(

1







•

wielkość ziarna

ferrytu

•

ułamek ferrytu

przedeutektoidalnego

•

ułamek ferrytu

Widmanstättenn’a

)]

m

γ

D

b

(

[

b

)]

n

r

C

a

(

a[

eq

F

F

1

exp

1

0

1

exp

1

















)

q

γ

D

d

(

d

)

p

r

C

c

(

c

eq

F

w

F

1

exp

0

1

exp

0











Podstawy Sztucznej

Inteligencji

Jan Kusiak

Metamodelowanie

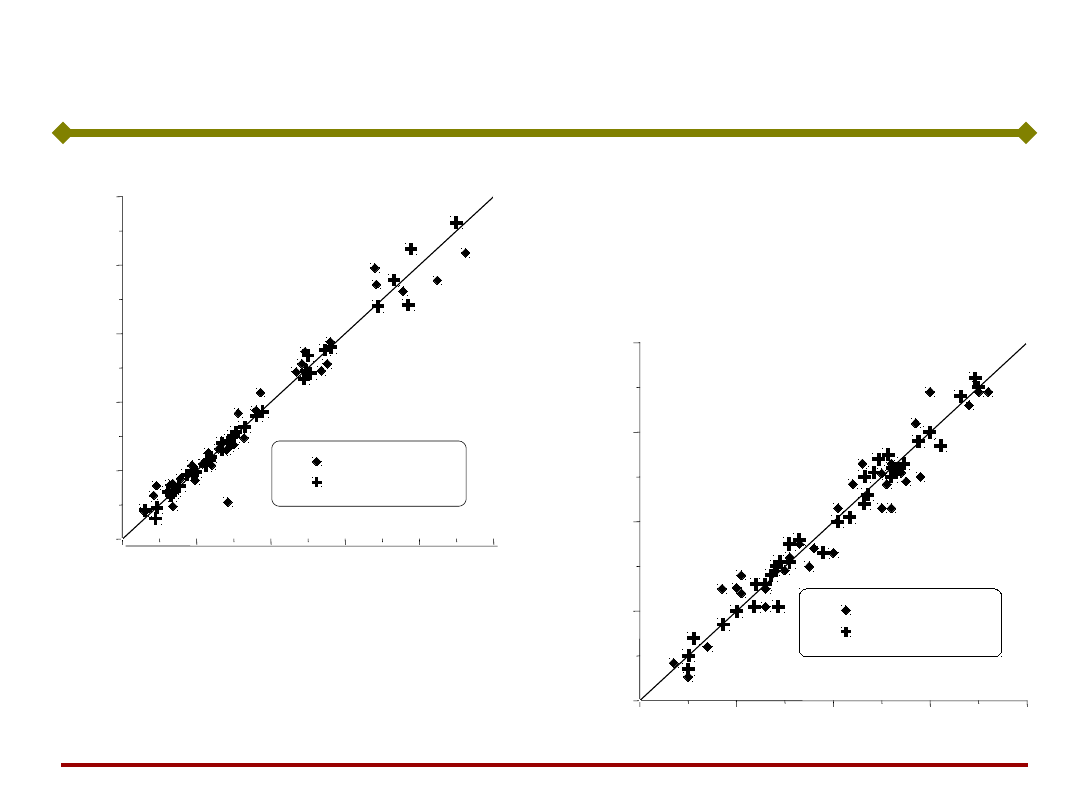
Modelowanie mikrostruktury

5

10

15

20

25

30

Zmierzona wielkość ziarna ferrytu,



m

5

10

15

20

25

30

Pr

ze

wi

dy

w

an

a

wi

el

ko

ść

z

ia

rn

a

fe

rr

yt

u,



m

Równanie (2)

SSN

0.0

0.2

0.4

0.6

0.8

Zmierzony ułamek ferrytu

0.0

0.2

0.4

0.6

0.8

Pr

ze

wi

dy

w

an

y

uł

a

m

ek

f

er

ry

tu

Równanie (3)

SSN

Badania laboratoryjne

Podstawy Sztucznej

Inteligencji

Jan Kusiak

Metamodelowanie

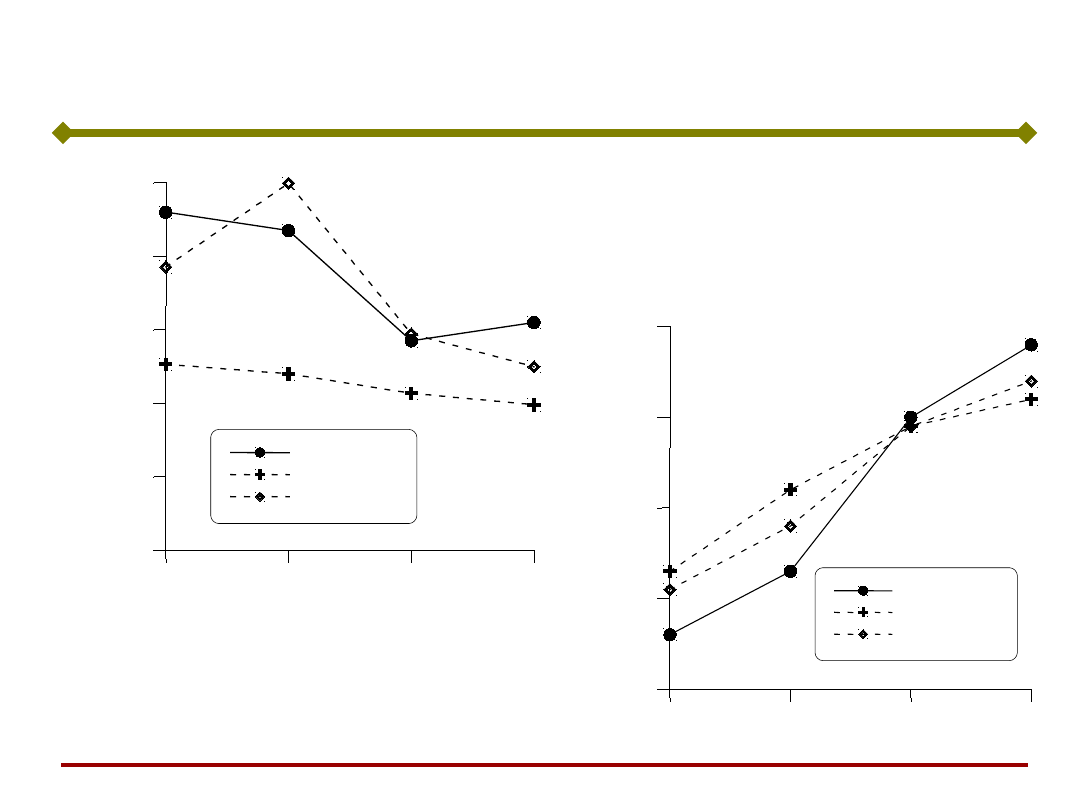
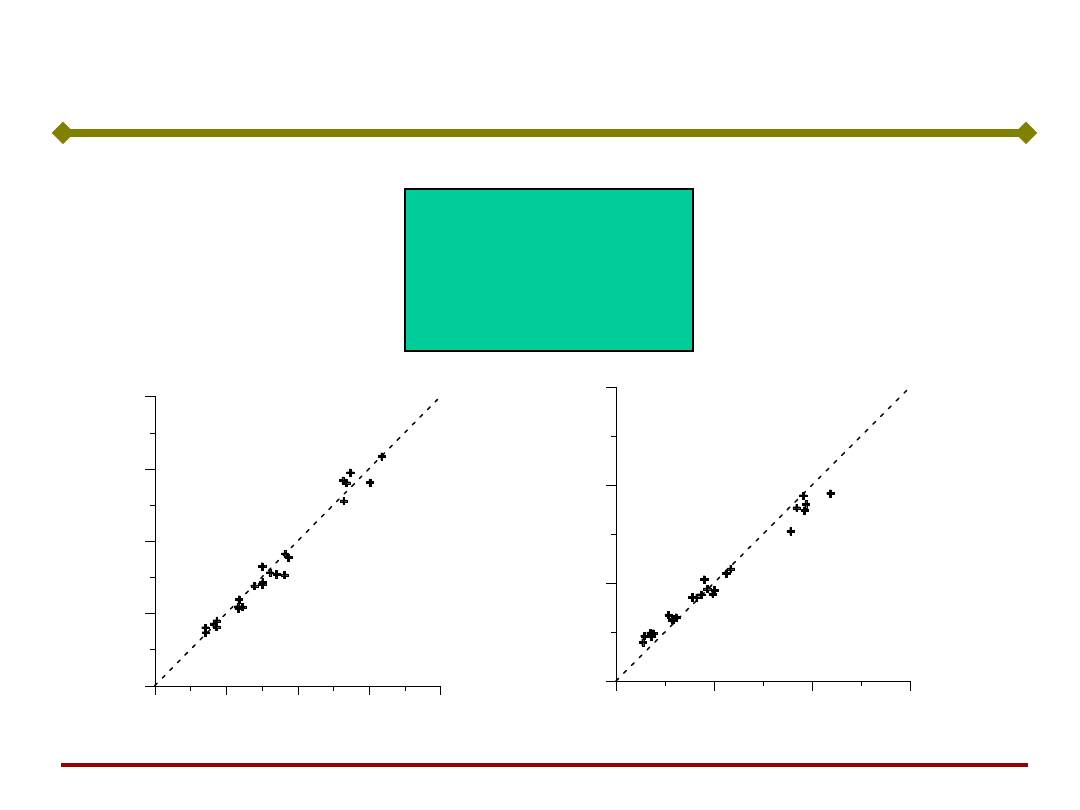
Modelowanie mikrostruktury, c.d

.

1

2

3

4

Nr próbki

4.00

6.00

8.00

10.00

12.00

14.00

Wi

el

ko

ść

z

ia

rn

a

fe

rr

yt

u

Pomiary

Równanie (2)

SSN

1

2

3

4

Nr próbki

0.20

0.30

0.40

0.50

0.60

Uł

a

m

ek

f

er

ry

tu

p

rz

ed

eu

te

kt

oi

da

ln

eg

o

Pomiary

Równanie (3)

SSN

Próby przemysłowe

Podstawy Sztucznej

Inteligencji

Jan Kusiak

Metamodelowanie

Modelowanie sił walcowania

rodzaj dodatku

smarującego 

stężenie środka

smarującego 

prędkość walcowania 

gniot 

SSN

WE

WY

 siła walcowania

 moment walcowania

0

1 0 0 0

2 0 0 0

3 0 0 0

4 0 0 0

R o llin g f o r c e - m e a s u r e m e n ts , N / m m

0

1 0 0 0

2 0 0 0

3 0 0 0

4 0 0 0

R

o

lli

n

g

f

o

rc

e

-

A

N

N

,

N

/m

m

0

1 0

2 0

3 0

R o llin g to r q u e - m e a s u r e m e n ts , N m / m m

0

1 0

2 0

3 0

R

ol

lin

g

to

rq

ue

-

A

N

N

, N

m

/m

m

Podstawy Sztucznej

Inteligencji

Jan Kusiak

Metamodelowanie

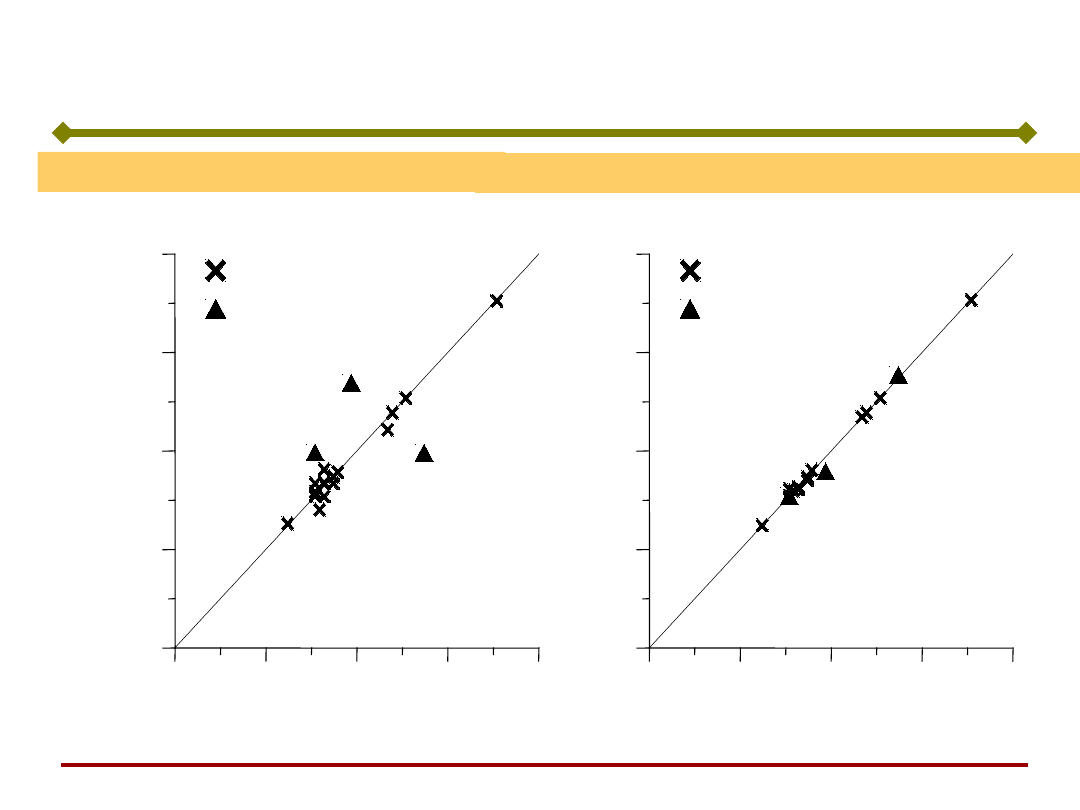
Kucie materiałów kompozytowych

Podstawy Sztucznej

Inteligencji

Jan Kusiak

Metamodelowanie

0.00

2.00

4.00

6.00

8.00

Wyniki pomiarów wad

0.00

2.00

4.00

6.00

8.00

Pr

ze

wi

dy

wa

na

w

ie

lk

oś

ć

wa

dy

Wyniki uczenia

Wyniki testu

0.00

2.00

4.00

6.00

8.00

Wyniki pomiarów wad

0.00

2.00

4.00

6.00

8.00

Pr

ze

wi

dy

wa

na

w

ie

lk

oś

ć

wa

dy

Wyniki uczenia

Wyniki testu

Przewidywanie wad w odkuwkach

Sieć oparta o kryterium pękaniaSieć uwzględniająca historię odkształcenia

Podstawy Sztucznej

Inteligencji

Jan Kusiak

Metamodelowanie

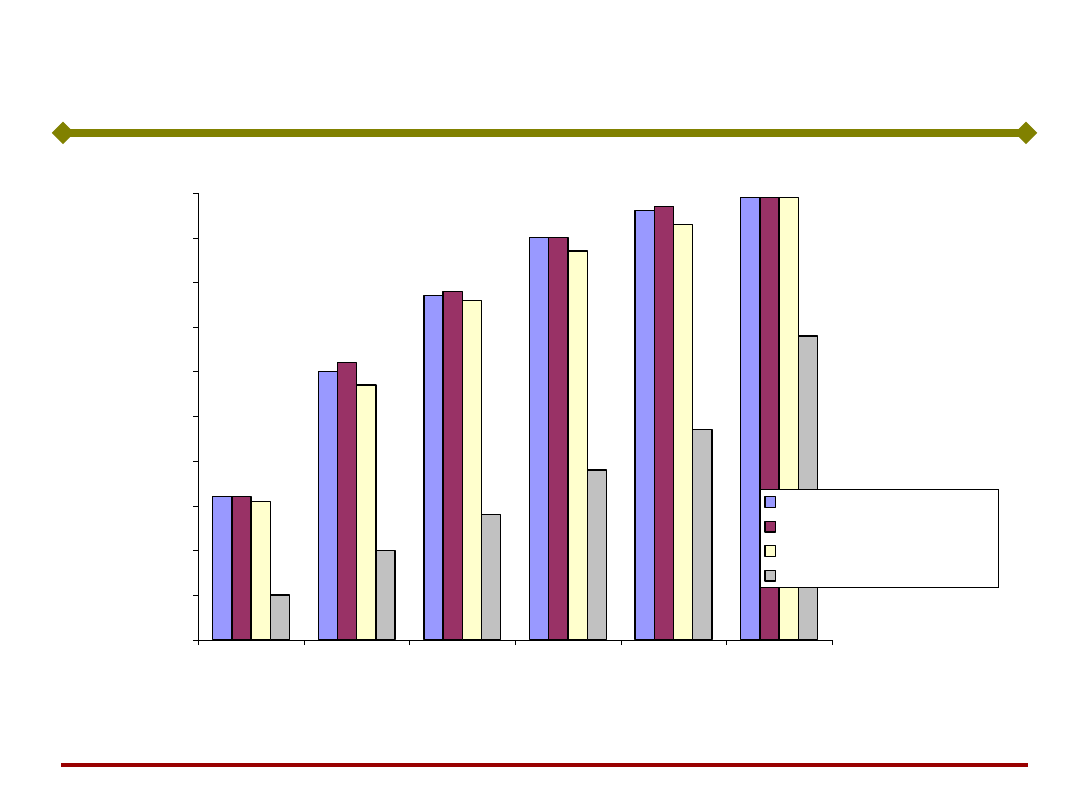
Konwertor tlenowy – model temperatury

32

60

77

90

96

99

32

62

78

90

97

99

31

57

76

87

93

99

10

20

28

38

47

68

0

10

20

30

40

50

60

70

80

90

100

< 10

< 20

< 30

< 40

< 50

< 80

Wartość błędu temperatury [

o

C]

%

w

y

to

p

ó

w

sieć neuronowa 1
sieć neuronowa 2
regresja krokowa wsteczna
bilans materiałowo-cieplny

Podstawy Sztucznej

Inteligencji

Jan Kusiak

Metamodelowanie

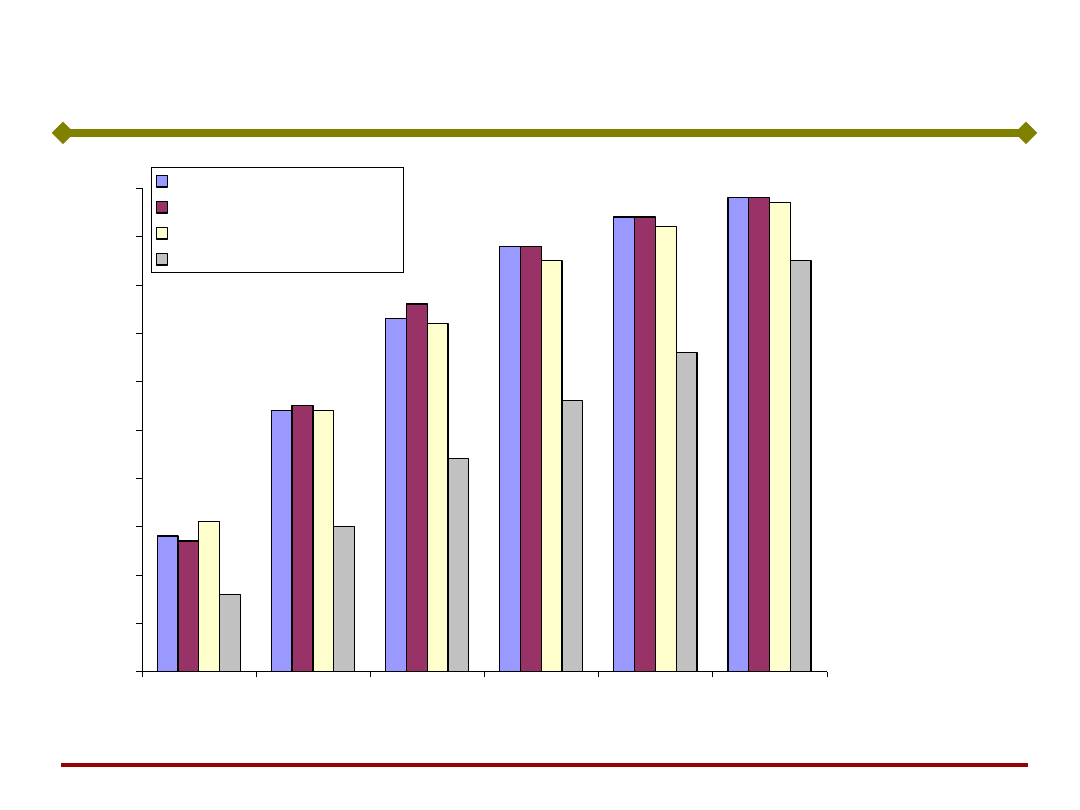
Konwertor tlenowy – model zapotrzebowania tlenu

28

54

73

88

94

98

27

55

76

88

94

98

31

54

72

85

92

97

16

30

44

56

66

85

0

10

20

30

40

50

60

70

80

90

100

< 200

< 400

< 600

< 800

< 1000

< 1500

Wartość błędu zapotrzbowania na tlen [Nm

3

]

%

w

y

to

p

ó

w

sieć neuronowa 1
sieć neuronowa 2
regresja krokowa wsteczna
bilans materiałowo-cieplny

Podstawy Sztucznej

Inteligencji

Jan Kusiak

Metamodelowanie

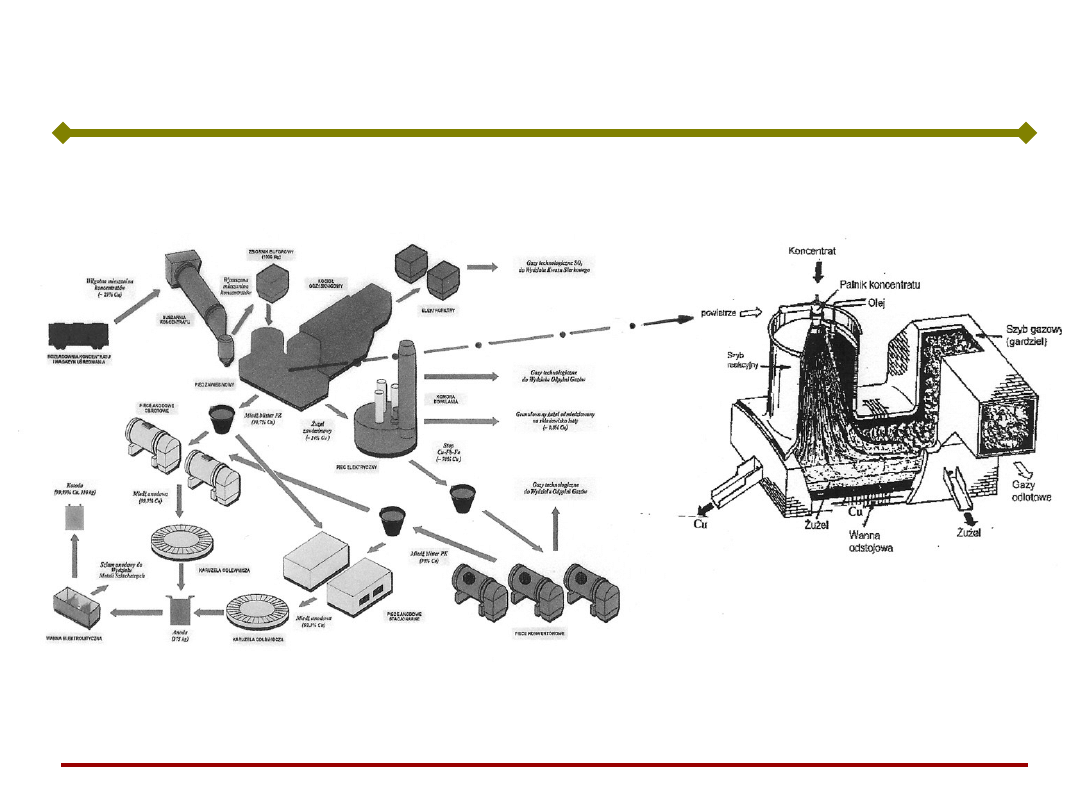
Model i system sterowania piecem
zawiesinowym do wytopu miedzi

Podstawy Sztucznej

Inteligencji

Jan Kusiak

Metamodelowanie

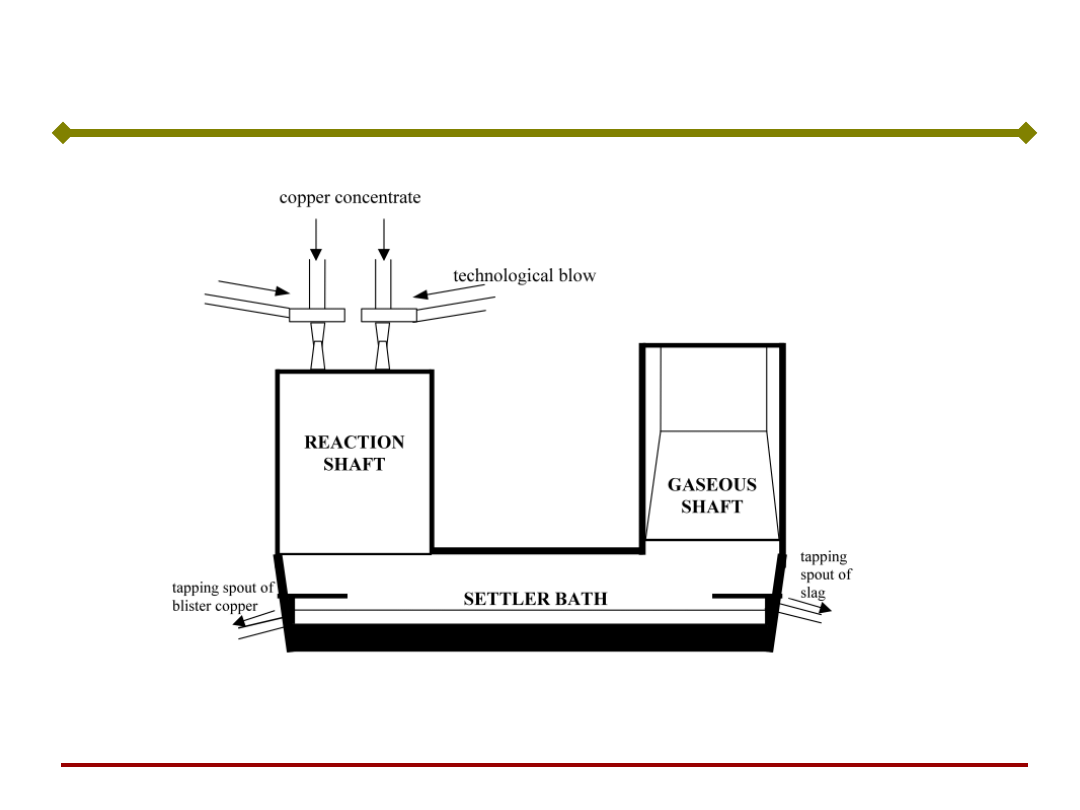
Model i system sterowania piecem
zawiesinowym do wytopu miedzi

Podstawy Sztucznej

Inteligencji

Jan Kusiak

Metamodelowanie

B a z a P Z _ IO S

S S N

W Y

S S N

W

E

W

Y

O b e c n y s y s te m

N o w e

s ta n o w is k o

W E

S T E R .

M o d u ł

n a d z o r u ją c y

p r a c a c ią g ła

W

Y

S

S

N

W

E

S

te

ru

ją

ce

A O

P

A

R

.

S

T

E

R

.

W

E

S

te

ru

ją

ce

W

Y

N

O

R

M

A

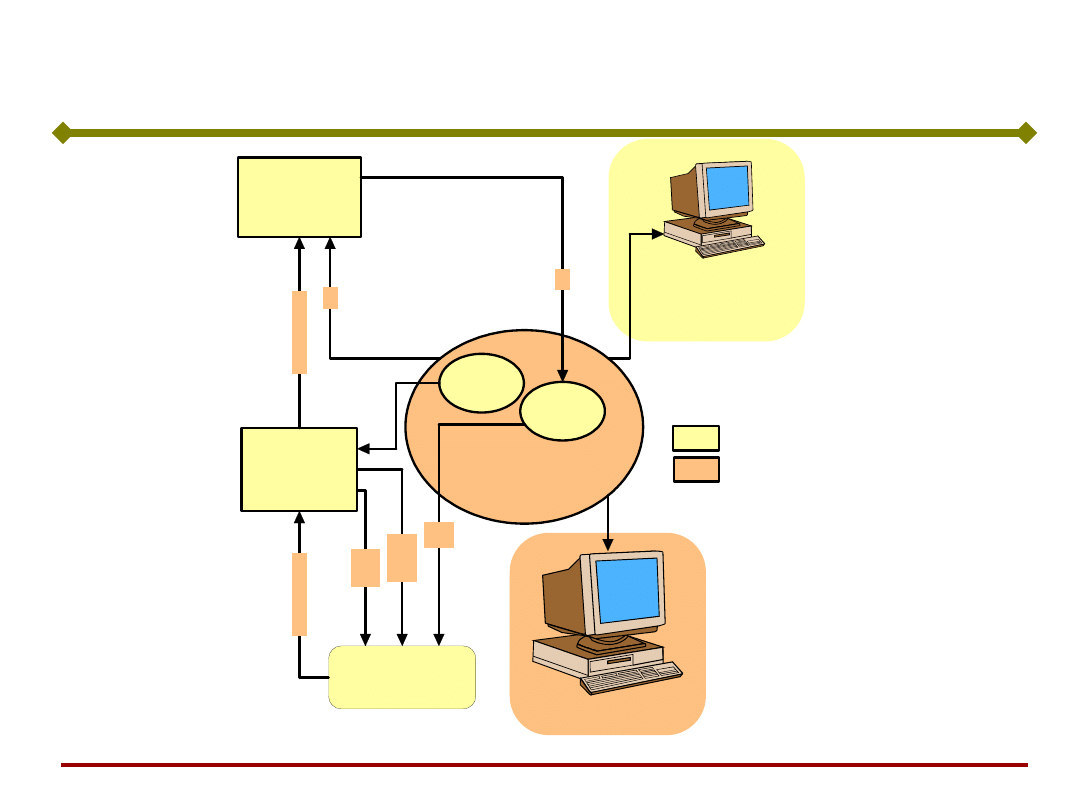
system sterowania

Podstawy Sztucznej

Inteligencji

Jan Kusiak

Metamodelowanie

0

6 0

1 2 0

1 8 0

2 4 0

3 0 0

3 6 0

4 2 0

4 8 0

5 4 0

P o m ia r y

1 2 8 0

1 2 8 5

1 2 9 0

1 2 9 5

1 3 0 0

1 3 0 5

T

em

pe

ra

tu

ra

C

u

[

o

C

]

T e m p e r a tu r a C u

z m ie r z o n a
S S N

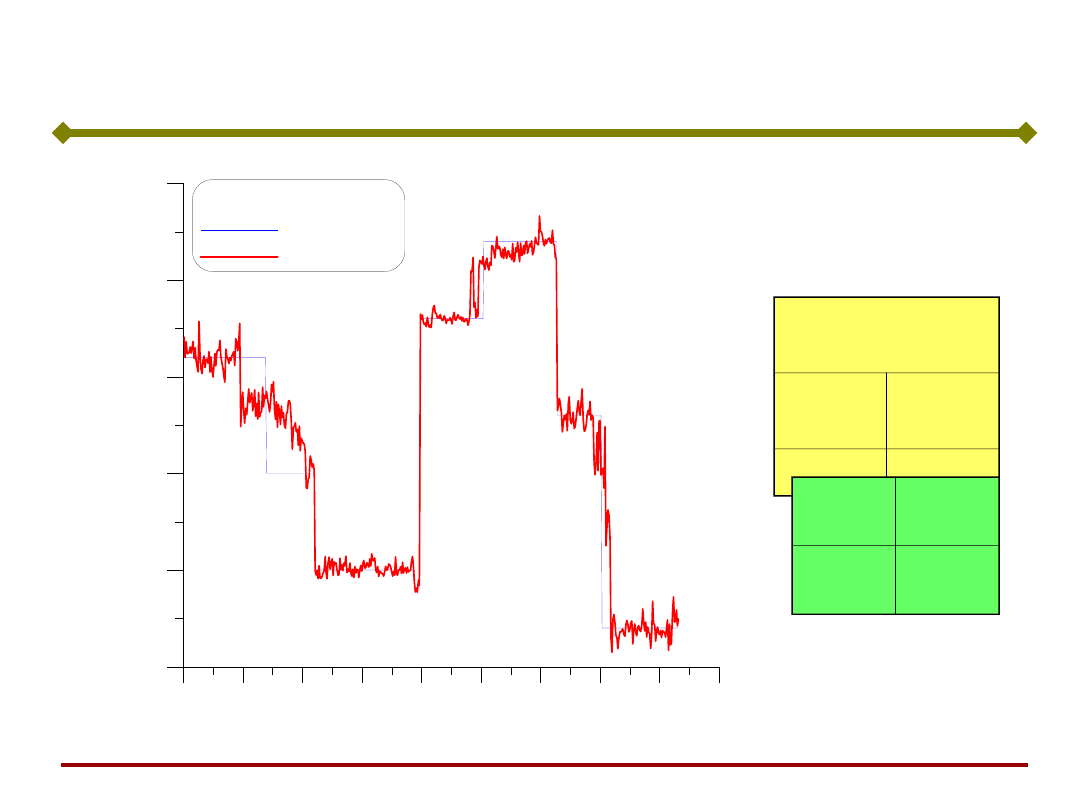
Odpowiedzi

SSN
Trafi

eń

błąd



100%

0,05

błąd
=

0,001

błąd

E=

0,856

Wyniki SSN

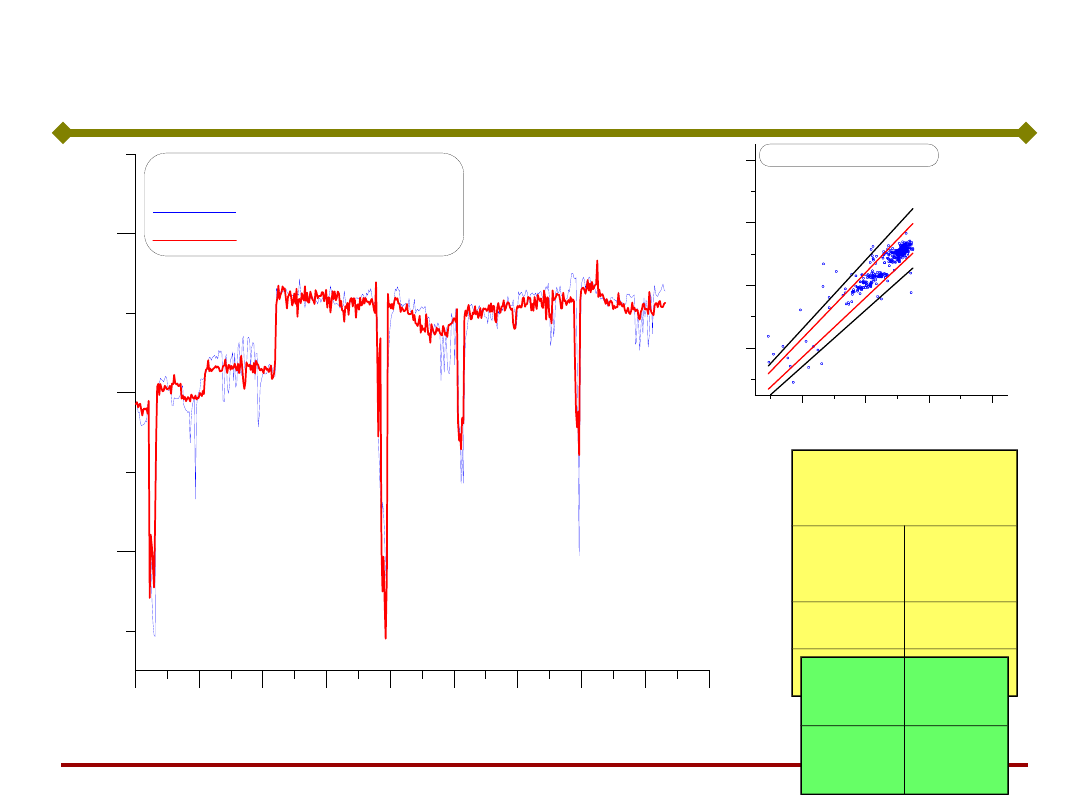
Podstawy Sztucznej

Inteligencji

Jan Kusiak

Metamodelowanie

0

6 0

1 2 0

1 8 0

2 4 0

3 0 0

3 6 0

4 2 0

4 8 0

5 4 0

P o m ia r y

1 2

1 6

2 0

S

tę

że

ni

e

S

O

2

w

g

az

ac

h

[%

]

S tę ż e n ie S O

2

w g a z a c h

z m ie r z o n e
S S N

1 2

1 6

2 0

2 4

P o m ia r y

1 2

1 6

2 0

2 4

O

bl

ic

ze

ni

a

S

S

N

- 0 . 1

- 0 . 0 5

+ 0 . 0 5

+ 0 . 1

b łą d



S tę ż e n ie S O

2

w g a z a c h [% ]

Odpowiedzi

SSN
Trafi

eń

błąd


93%

0,05

96%

0,1

błąd

=

0,039

błąd

E=

0,340

Wyniki SSN

Podstawy Sztucznej

Inteligencji

Jan Kusiak

Metamodelowanie

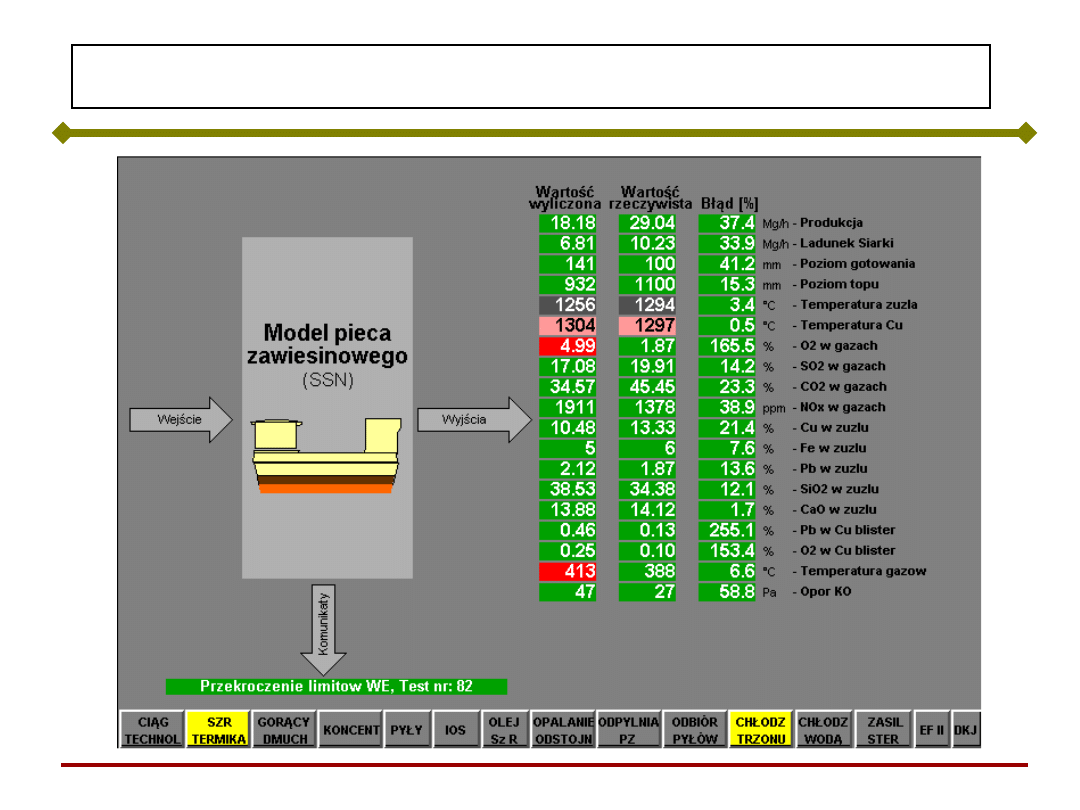
Synoptyka modelu SSN

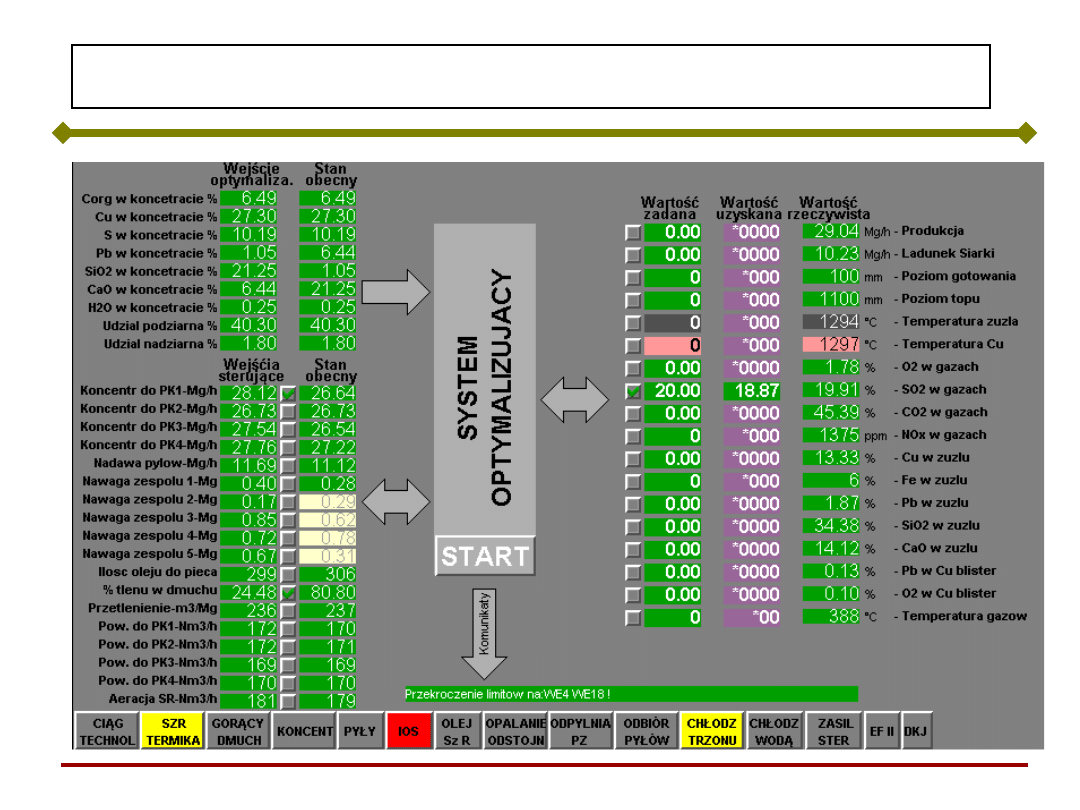
Podstawy Sztucznej

Inteligencji

Jan Kusiak

Metamodelowanie

Synoptyka optymalizatora

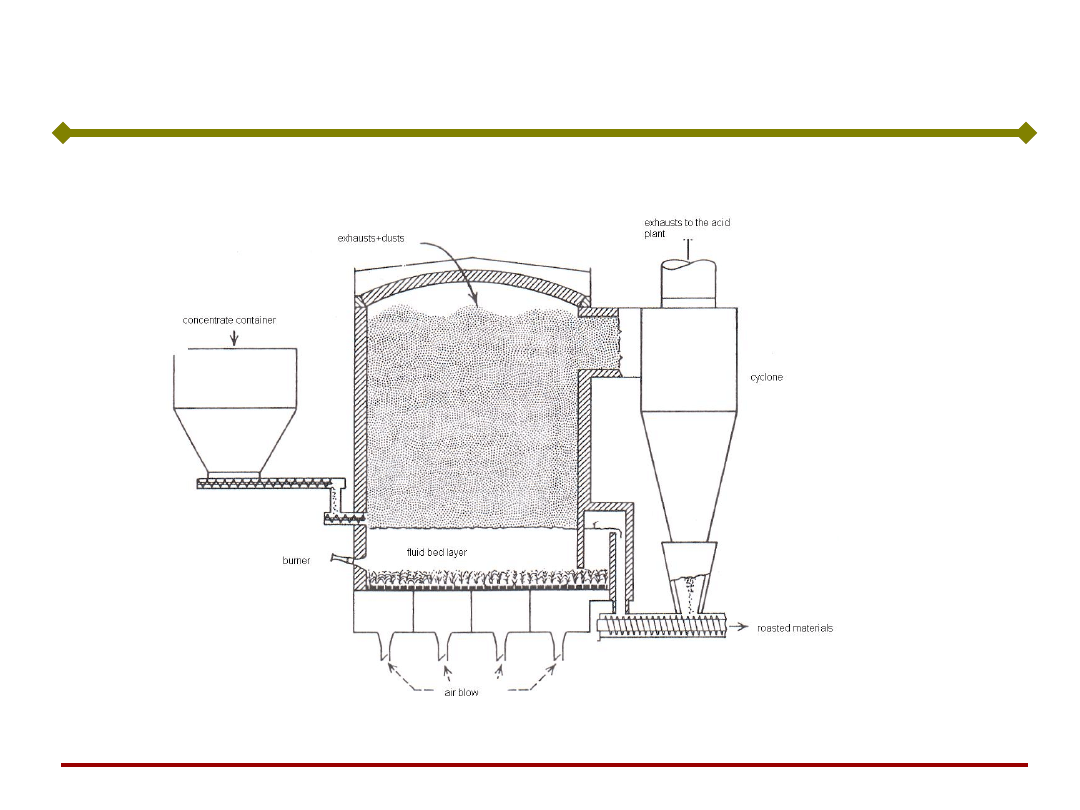
Podstawy Sztucznej

Inteligencji

Jan Kusiak

Metamodelowanie

Model pieca fluidalnego do wytopu cynku

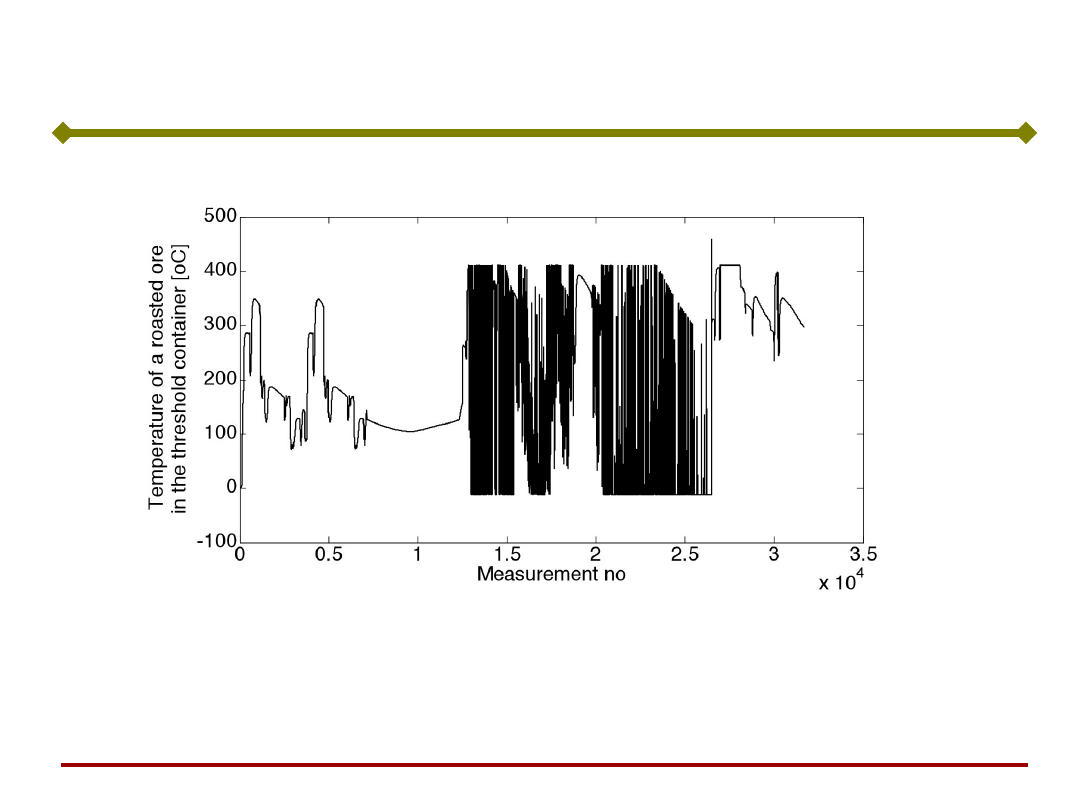
Podstawy Sztucznej

Inteligencji

Jan Kusiak

Metamodelowanie

Model pieca fluidalnego do wytopu cynku

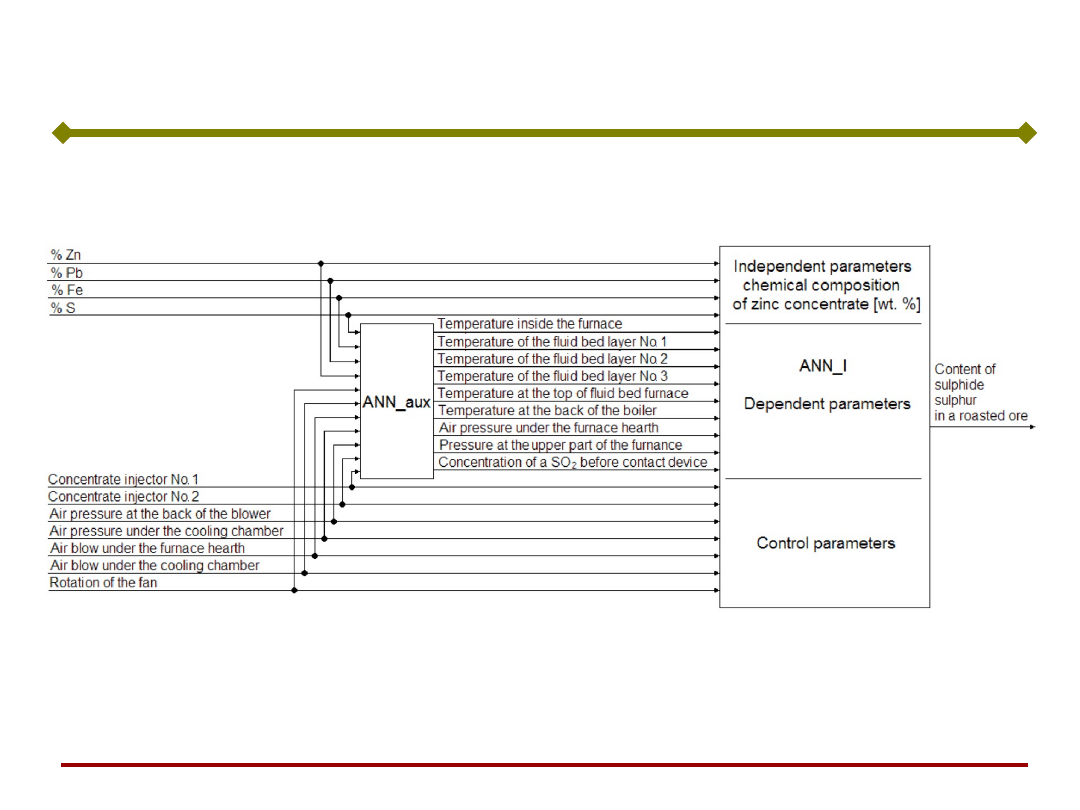
Podstawy Sztucznej

Inteligencji

Jan Kusiak

Metamodelowanie

Model pieca fluidalnego do wytopu cynku

Podstawy Sztucznej

Inteligencji

Jan Kusiak

Metamodelowanie

Model pieca fluidalnego do wytopu cynku

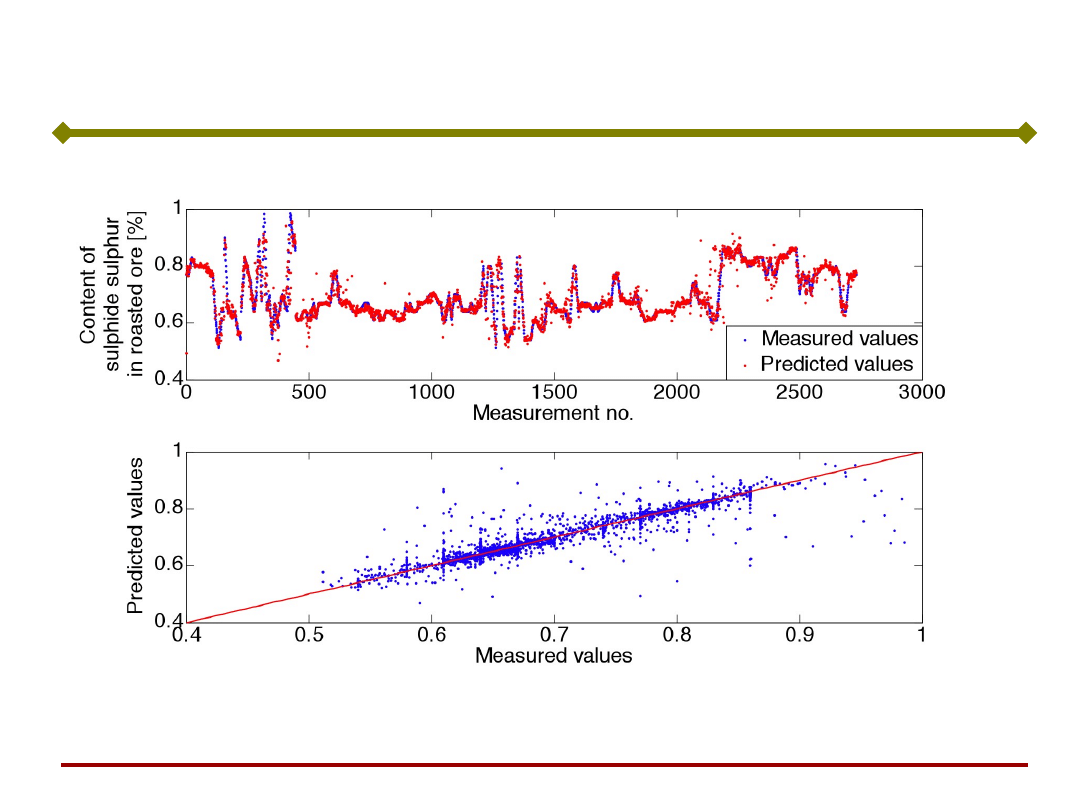
Podstawy Sztucznej

Inteligencji

Jan Kusiak

Metamodelowanie

Model pieca fluidalnego do wytopu cynku

Podstawy Sztucznej

Inteligencji

Jan Kusiak

Metamodelowanie

Zastosowanie SSN w
optymalizacji
(metamodelowanie)

Podstawy Sztucznej

Inteligencji

Jan Kusiak

Metamodelowanie

Modelowanie cyklu produkcyjnego

•Modelowanie fizyczne
•Symulacje komputerowe
•Modelowanie mikro –

makro
•Optymalizacja

Podstawy Sztucznej

Inteligencji

Jan Kusiak

Metamodelowanie

 Jak wytwarzać ?

 Z czego wytwarzać?

 Czy można robić to lepiej?

nowe technologie

nowe materiały

optymalizacja

Optymalizacja procesów

Podstawy Sztucznej

Inteligencji

Jan Kusiak

Metamodelowanie

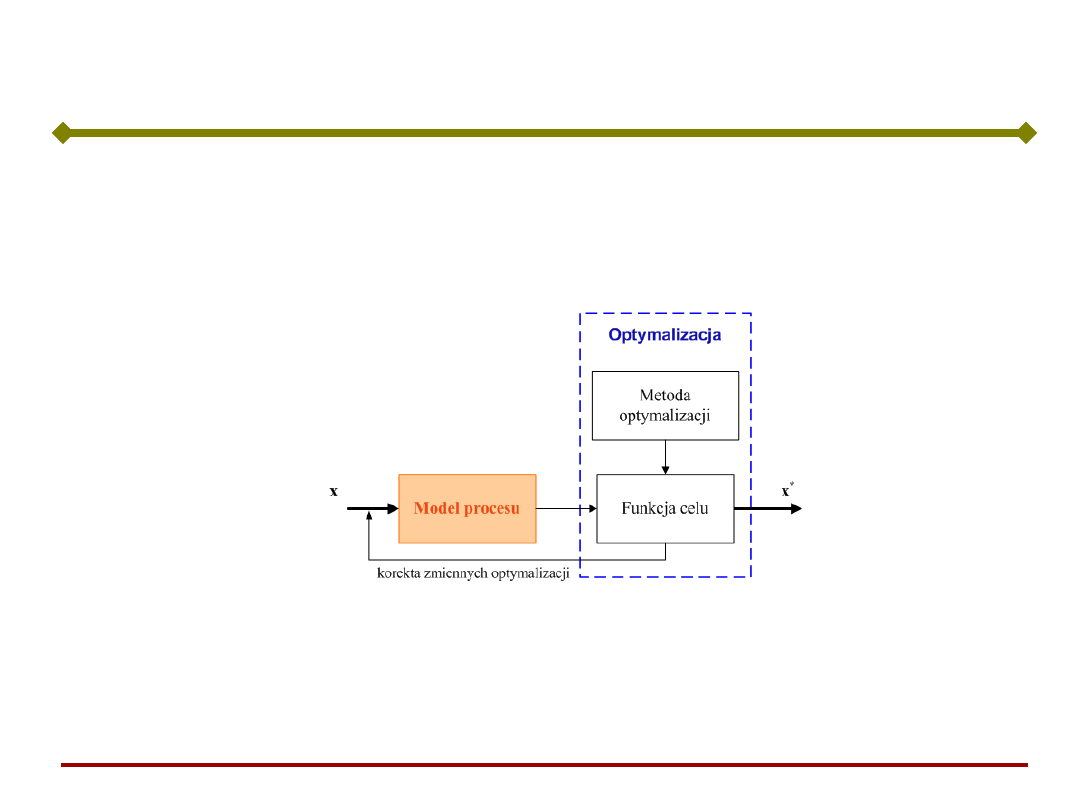
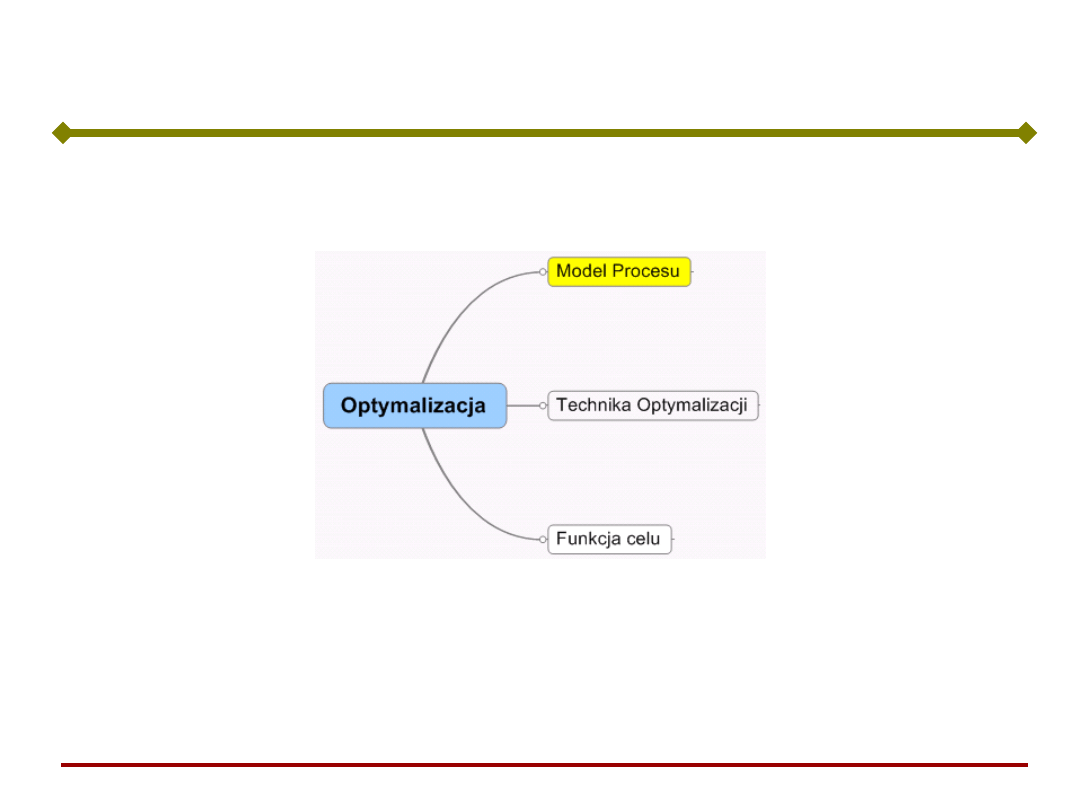
Optymalizacja procesów

klasyczne
podejście

Podstawy Sztucznej

Inteligencji

Jan Kusiak

Metamodelowanie

Optymalizacja – podejście klasyczne

Podstawy Sztucznej

Inteligencji

Jan Kusiak

Metamodelowanie

Optymalizacja – podejście klasyczne

Problemy:

- Długie czasy obliczeń symulacyjnych
- Praktycznie niemożliwe znalezienie

„najlepszego” sygnału wejściowego x metodą
prób i błędów

- itp..

Rozwiązanie:

-Metamodele

ale ....

Podstawy Sztucznej

Inteligencji

Jan Kusiak

Metamodelowanie

Metamodelowani
e

Podstawy Sztucznej

Inteligencji

Jan Kusiak

Metamodelowanie

Metamodel*

- model aproksymacyjny skonstruowany w

oparciu o wartości funkcji (analizowanego
modelu) w wybranych punktach (określanych
zazwyczaj metodami planowania
eksperymentu).

- pozwala na zastąpienie skomplikowanych i

czasochłonnych programów komputerowych
modelujących proces (np. MES) prostszymi
zależnościami.

- umożliwia skrócenie czasu obliczeń

symulacyjnych, a tym samym czasu obliczeń
optymalizacyjnych

*meta - wyżej zorganizowana, bardziej wyspecjalizowana forma
(wg W. Kopaliński ''Słownik WyrazówObcych'', Wiedza Powszechna, Warszawa, 1983)

Podstawy Sztucznej

Inteligencji

Jan Kusiak

Metamodelowanie

Narzędzia metamodelowania

Metamodel:

•Sztuczne sieci neuronowe

•RSM

•Systemy hybrydowe

Podstawy Sztucznej

Inteligencji

Jan Kusiak

Metamodelowanie

Algorytm metamodelowania

1. Wybór zbioru X R

n

zmiennych wejściowych

(DoE)

2. Przeprowadzenie niezbędnych symulacji dla

każdego wektora x  X

3. Wybór postaci metamodelu (metody

aproksymacji)

4. Dopasowanie metamodelu

Podstawy Sztucznej

Inteligencji

Jan Kusiak

Metamodelowanie

Metamodelowanie

Zał: Dany jest model komputerowy pozwalający

obliczyć wielkości wyjściowe y w funkcji
wektora zmiennych wejściowych x (zależność
y=f(x) nie jest znana explicité)

Cel: Opracowanie metamodelu dla tego modelu

komputerowego, czyli funkcji g
aproksymującej sygnał wyjściowy:

)

(

ˆ

x

g

y 

dla którego





y

y ˆ

Metody: 1. Metoda Powierzchni Odpowiedzi (RSM)

2. Metoda RBF (radialnej funkcji

bazowej)

3. Sztuczne sieci neuronowe
4. Drzewa decyzyjne
5. Metoda Kriging
6. ...

Podstawy Sztucznej

Inteligencji

Jan Kusiak

Metamodelowanie

Metamodelowanie

Zał: Dany jest model komputerowy pozwalający

obliczyć wielkości wyjściowe y w funkcji
wektora zmiennych wejściowych x (zależność
y=f(x) nie jest znana explicité)

Cel: Opracowanie metamodelu dla tego modelu

komputerowego, czyli funkcji g
aproksymującej sygnał wyjściowy:

)

(

ˆ

x

g

y 

dla którego





y

y ˆ

Metody: 1. Metoda Powierzchni Odpowiedzi (RSM)

2. Metoda RBF (radialnej funkcji

bazowej)

3. Sztuczne sieci neuronowe

4. Drzewa decyzyjne
5. Metoda Kriging
6. ...

Podstawy Sztucznej

Inteligencji

Jan Kusiak

Metamodelowanie

Metoda Powierzchni Odpowiedzi (RSM)

Funkcja g przyjmuje najczęściej postać
wielomianu niskiego stopnia, zazwyczaj funkcji
liniowej:









n

i

i

i

x

a

a

g

1

0

)

(x

lub wielomianu drugiego stopnia:



 























n

i

n

i

n

i

j

j

i

ij

i

ii

n

i

i

i

x

x

a

x

a

x

a

a

g

1

1

1

1

2

1

0

)

(x

n – liczba zmiennych wejściowych

Podstawy Sztucznej

Inteligencji

Jan Kusiak

Metamodelowanie

Metoda Powierzchni Odpowiedzi (RSM)



 





 





 































































n

i

n

i

n

i

k

m

m

m

i

ii

n

i

m

i

m

n

i

n

i

n

i

k

i

ii

n

i

i

n

i

n

i

n

i

k

i

ii

n

i

i

k

i

ik

i

k

i

ik

i

k

i

ik

i

x

x

a

x

a

x

a

a

y

x

x

a

x

a

x

a

a

y

x

x

a

x

a

x

a

a

y

1

1

1

1

)

(

)

(

2

)

(

1

)

(

0

)

(

1

1

1

1

)

2

(

)

2

(

2

)

2

(

1

)

2

(

0

)

2

(

1

1

1

1

)

1

(

)

1

(

2

)

1

(

1

)

1

(

0

)

1

(

ˆ

)

(

ˆ

ˆ

ˆ

ˆ

)

(

ˆ

ˆ

ˆ

ˆ

)

(

ˆ

ˆ

ˆ



Współczynniki wielomianów określić można
metodą najmniejszych kwadratów. Dla m par
danych (x

i

,y

i

) i=1,...,m

Problem - jakość dopasowania metamodelu
(oceniana metodami statystycznymi)

W rezultacie otrzymujemy metamodel oparty o
powierzchnię odpowiedzi (RSM).

Podstawy Sztucznej

Inteligencji

Jan Kusiak

Metamodelowanie

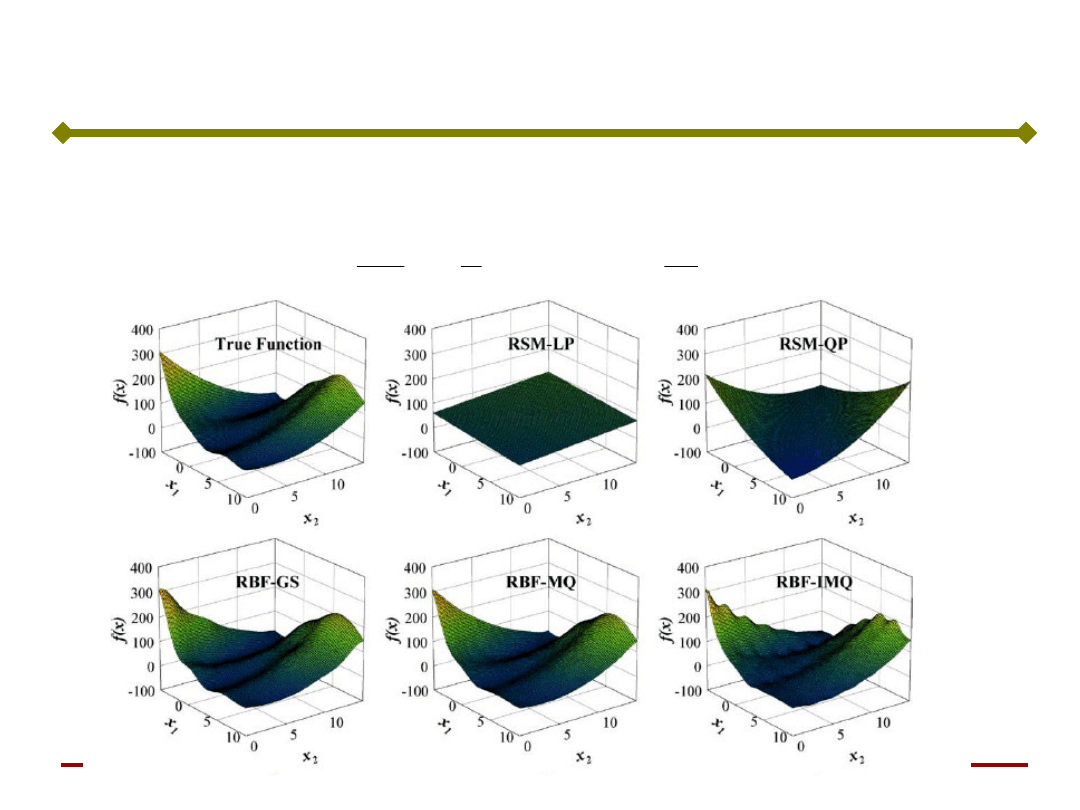
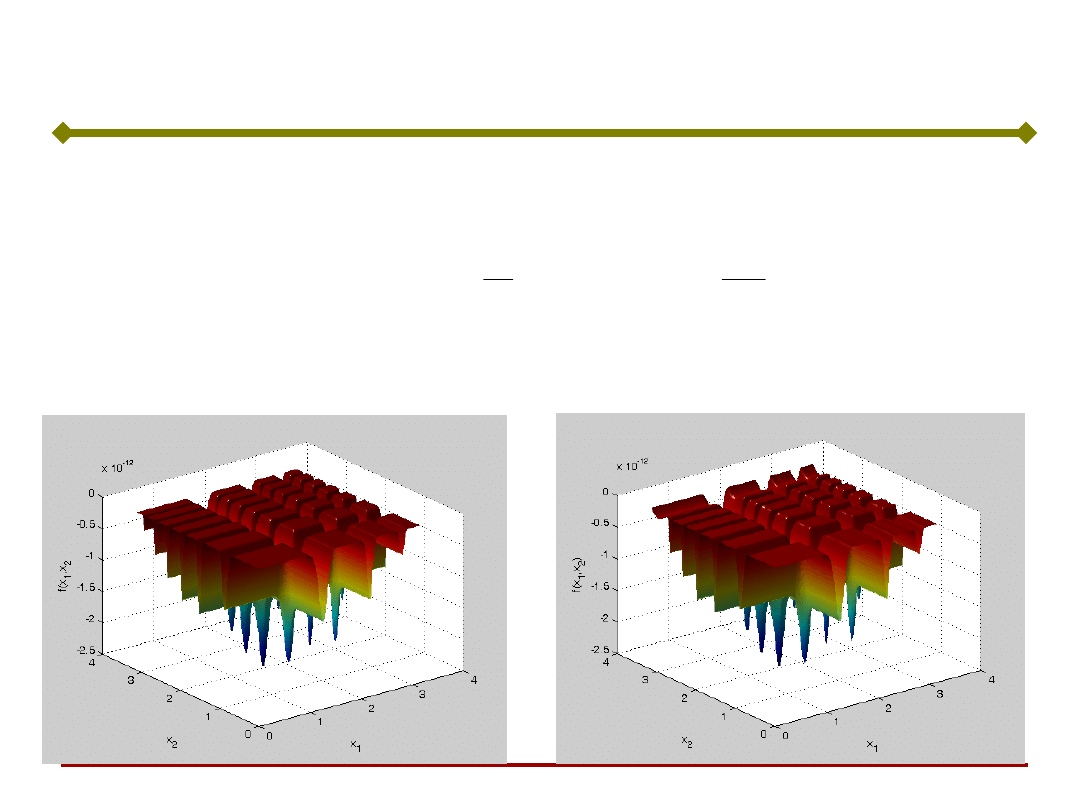
Przykład metamodelowania RSM

Funkcja testowa Branin rcos:

10

)

cos(

)

8

1

1

(

10

6

5

4

1

.

5

)

,

(

1

2

1

2

1

2

2

2

1



























x

x

x

x

x

x

f







Podstawy Sztucznej

Inteligencji

Jan Kusiak

Metamodelowanie

Przykład metamodelowania SSN

Funkcja testowa Michalewicza:

24

2

2

2

24

2

1

1

2

1

2

sin

)

sin(

sin

)

sin(

)

,

(



























































x

x

x

x

x

x

f

)

,

(

2

1

x

x

f

Metamodel SSN

Podstawy Sztucznej

Inteligencji

Jan Kusiak

Metamodelowanie

Metamodelowanie - podsumowanie

 Zalety

 Krótki czas obliczeń

 Szeroki wachlarz zastosowań - optymalizacja,

sterowanie,...

RSM

•łatwe w użyciu

•prawidłowe działanie dla liniowych lub

niewielkich nieliniowości

•skuteczne dla małej liczby zmiennych

SSN

•skuteczne dla silnie nieliniowych problemów

•duża liczba zmiennych

•wysoki koszt obliczeniowy etapu uczenia

 Wady

 Trudności w ocenie jakości metamodelu

(ocena statystyczna)

Podstawy Sztucznej

Inteligencji

Jan Kusiak

Metamodelowanie

Przykłady zastosowań
metamodeli

Podstawy Sztucznej

Inteligencji

Jan Kusiak

Metamodelowanie

Optymalizacja z metamodelowaniem

Podstawy Sztucznej

Inteligencji

Jan Kusiak

Metamodelowanie

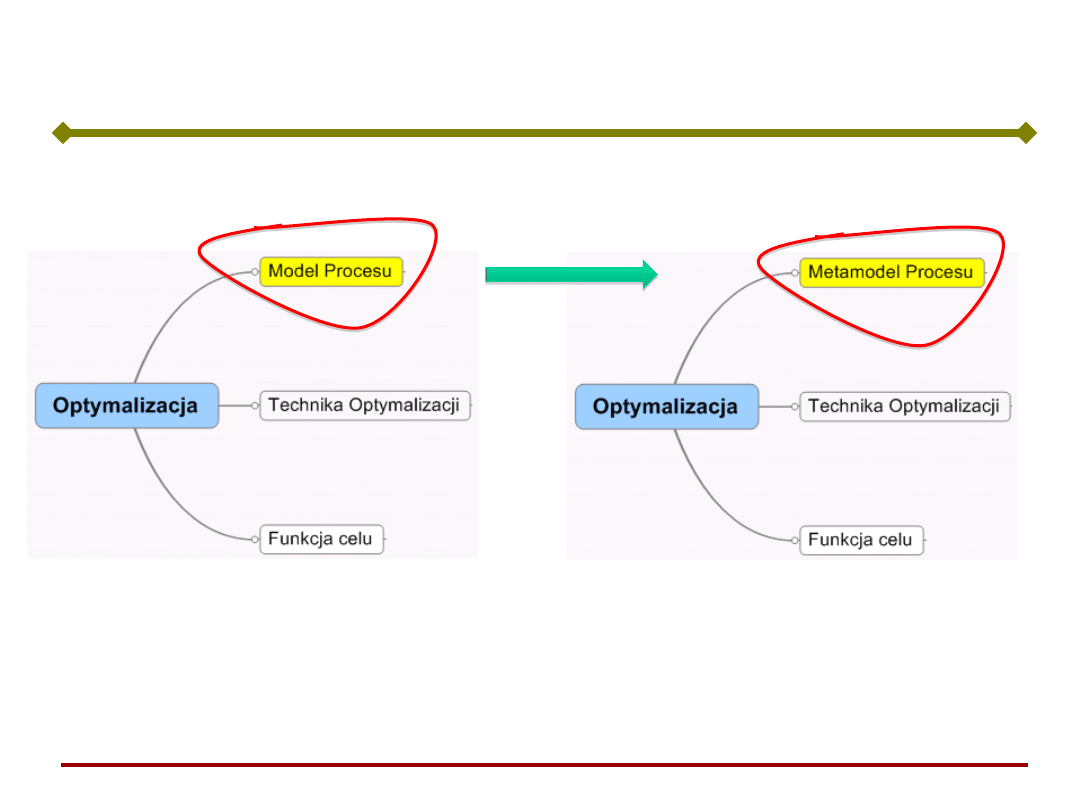
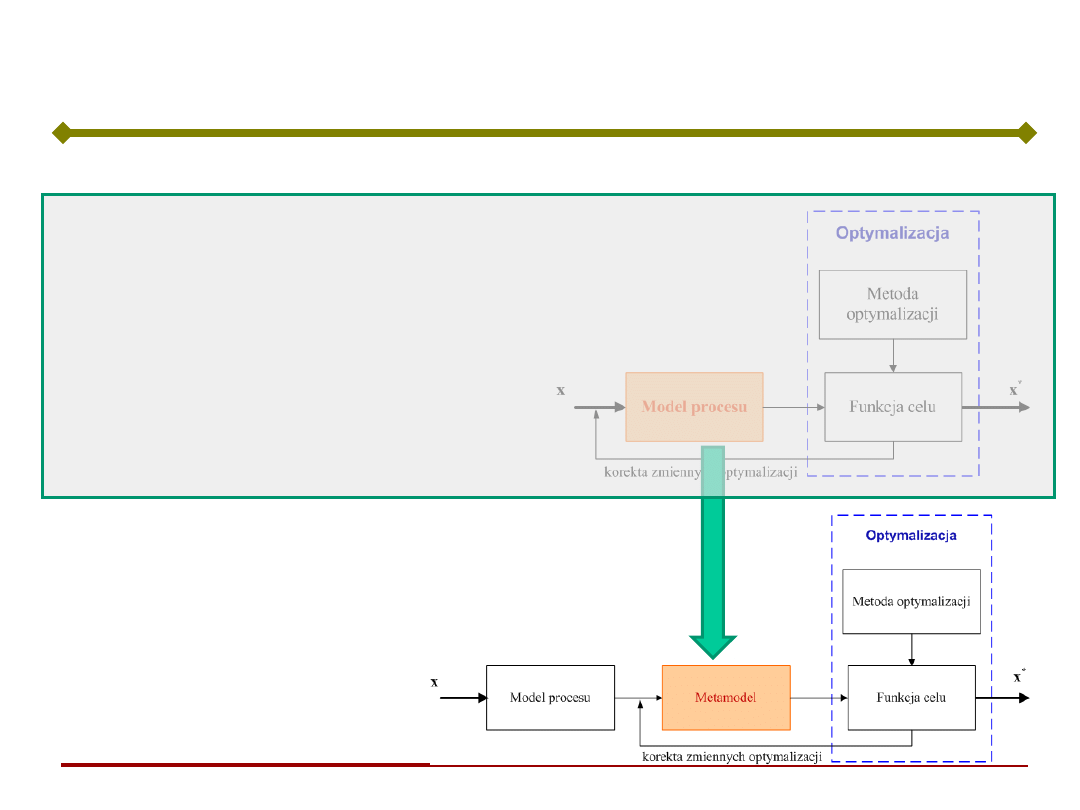
Optymalizacja z metamodelowaniem

klasyczne
podejście

metamodel

Podstawy Sztucznej

Inteligencji

Jan Kusiak

Metamodelowanie

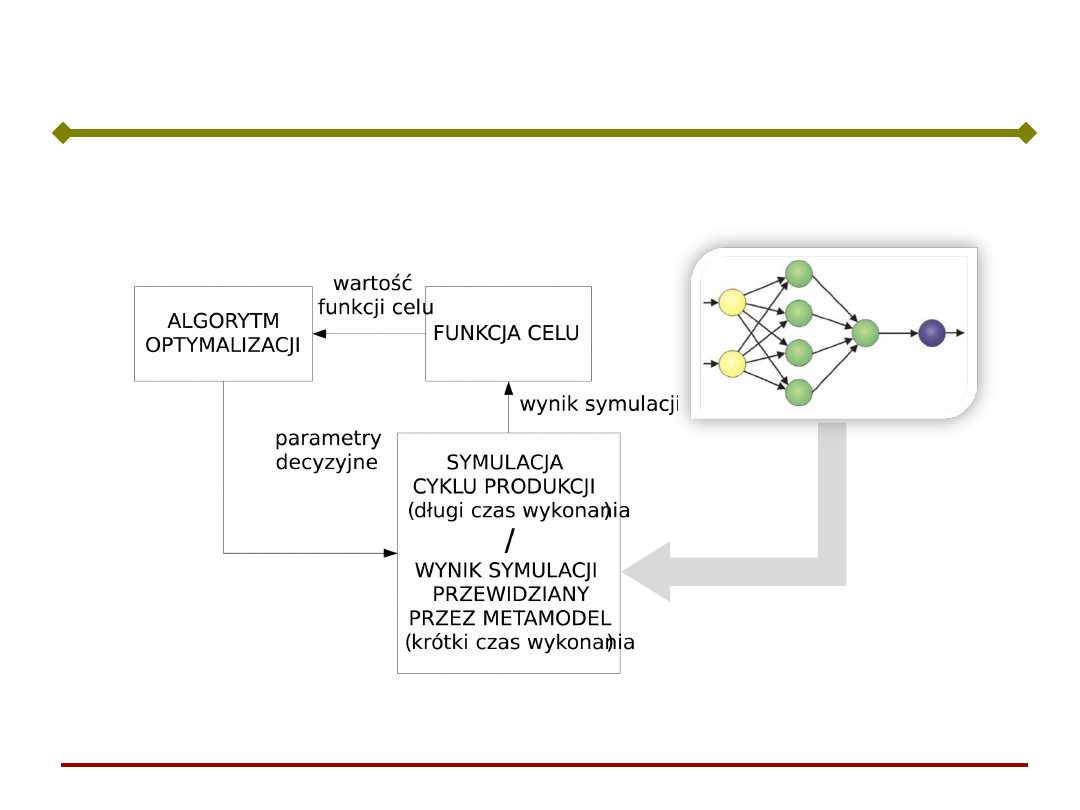
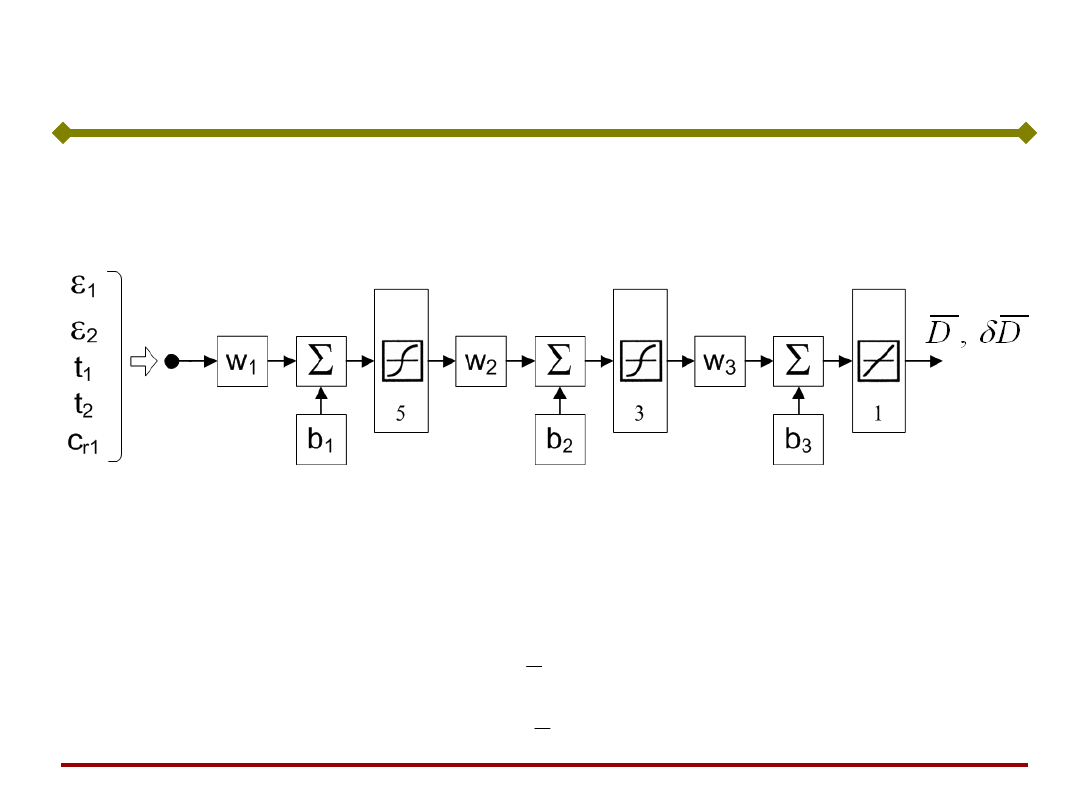
Przykłady – optymalizacja cyklu produkcji

Podstawy Sztucznej

Inteligencji

Jan Kusiak

Metamodelowanie

Opis Metamodelu

błąd średniokwadratowy obliczany na
zbiorze testowym wynosił odpowiednio:

4

4

10

3

.

3

10

6

.

1













D

D

MSE

MSE



Podstawy Sztucznej

Inteligencji

Jan Kusiak

Metamodelowanie

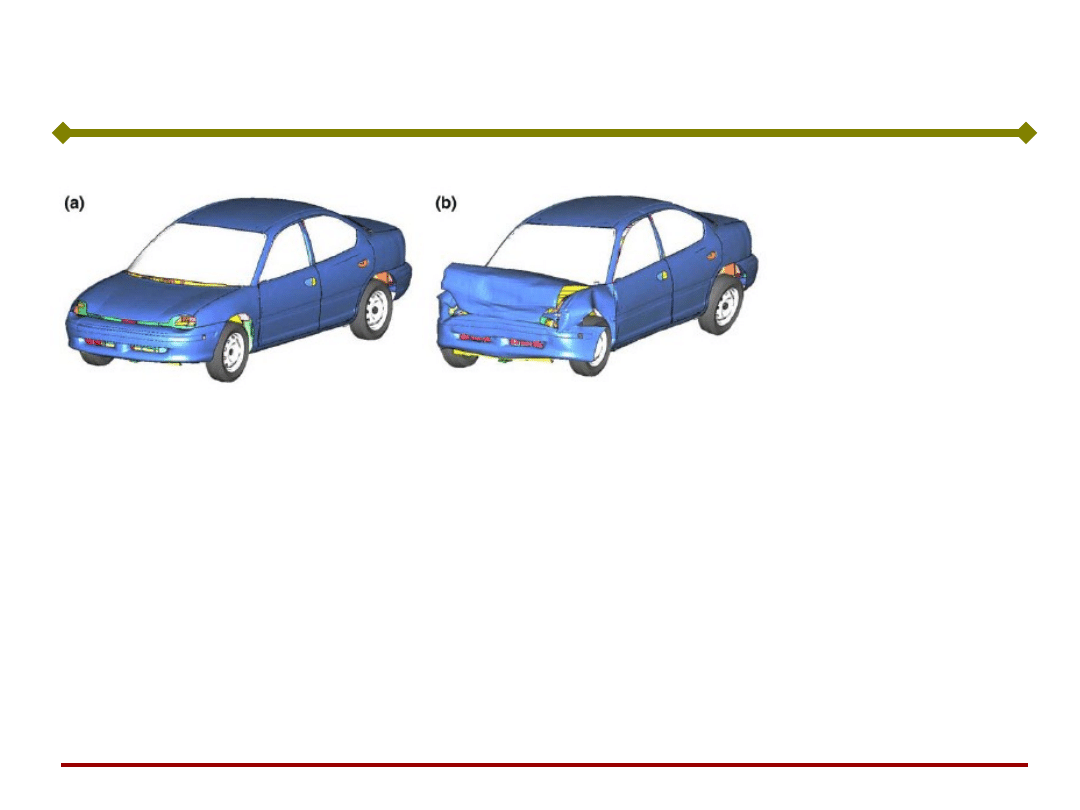
Przykłady – crash test

H. Fang,M. Rais-Rohani, Z. Liu, M.F. Horstemeyer: A comparative study of
metamodeling methods for multiobjective crashworthiness optimization.
Computers and Structures 83 (2005) 2121–2136





)

(

),

(

),

(

)

(

3

2

1

x

x

x

x

f

f

f

F







Optymalizacja wielokryterialna – minimum funkcjonału

f

1

(x), f

2

(x) – energia absorbowana po 20 ms i 40 ms

f

3

(x) – maksymalna wartość przyspieszenia

Podstawy Sztucznej

Inteligencji

Jan Kusiak

Metamodelowanie

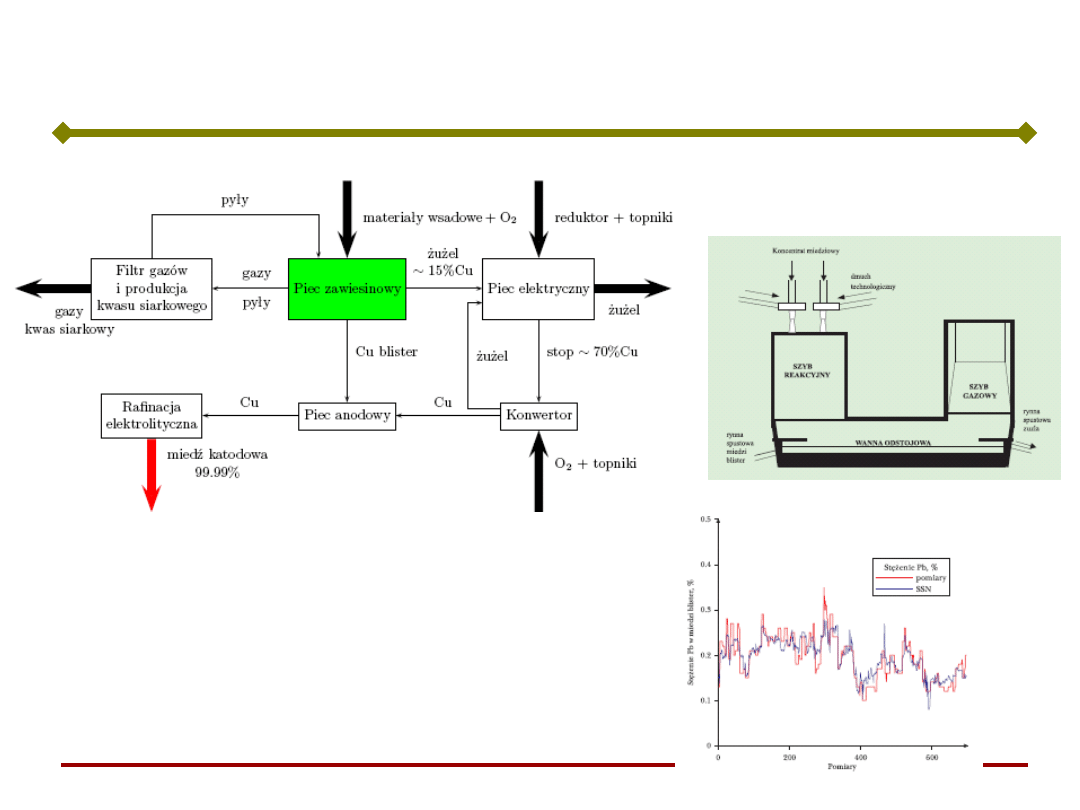
Przykłady – zawiesinowy wytop miedzi





2

)

(

)

(

)

(

p

p

p

w

SSN

Pb

Pb

J





m.in.: rozdział koncentratu na
poszczególne palniki, ilość tlenu,
itp.

10

R

p

Podstawy Sztucznej

Inteligencji

Jan Kusiak

Metamodelowanie

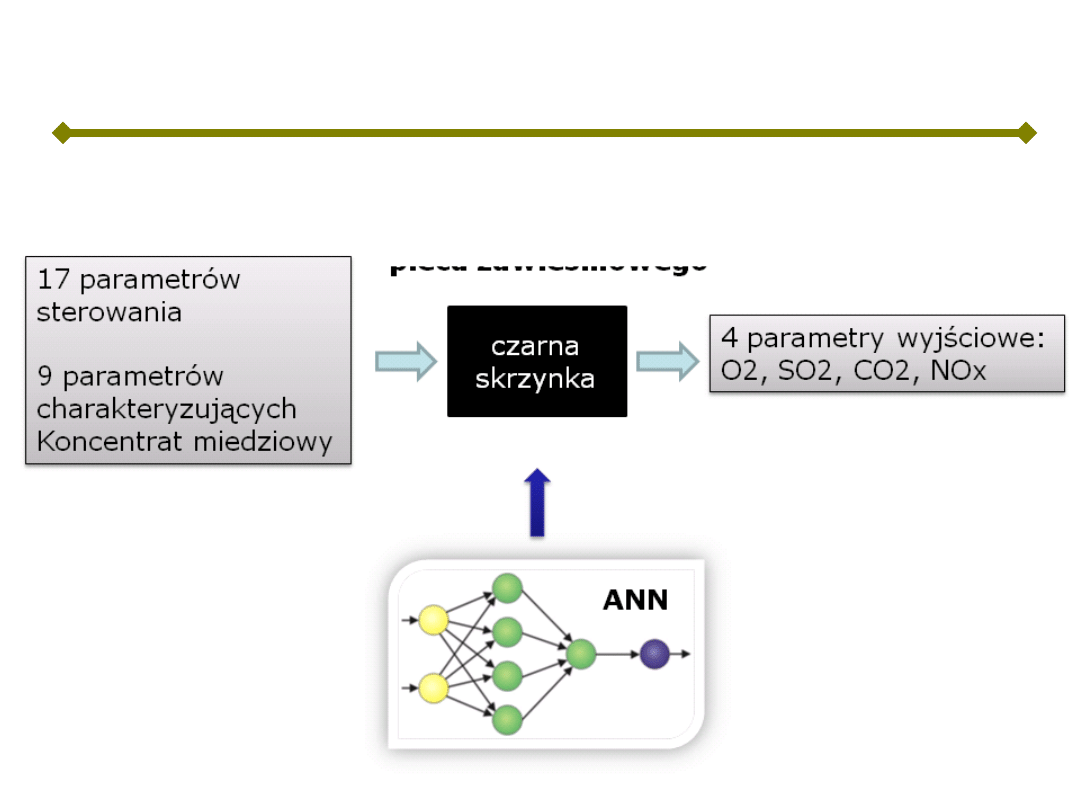
Optymalizacji procesu wytopu miedzi

Metamodel pieca
zawiesinowego

Podstawy Sztucznej

Inteligencji

Jan Kusiak

Metamodelowanie

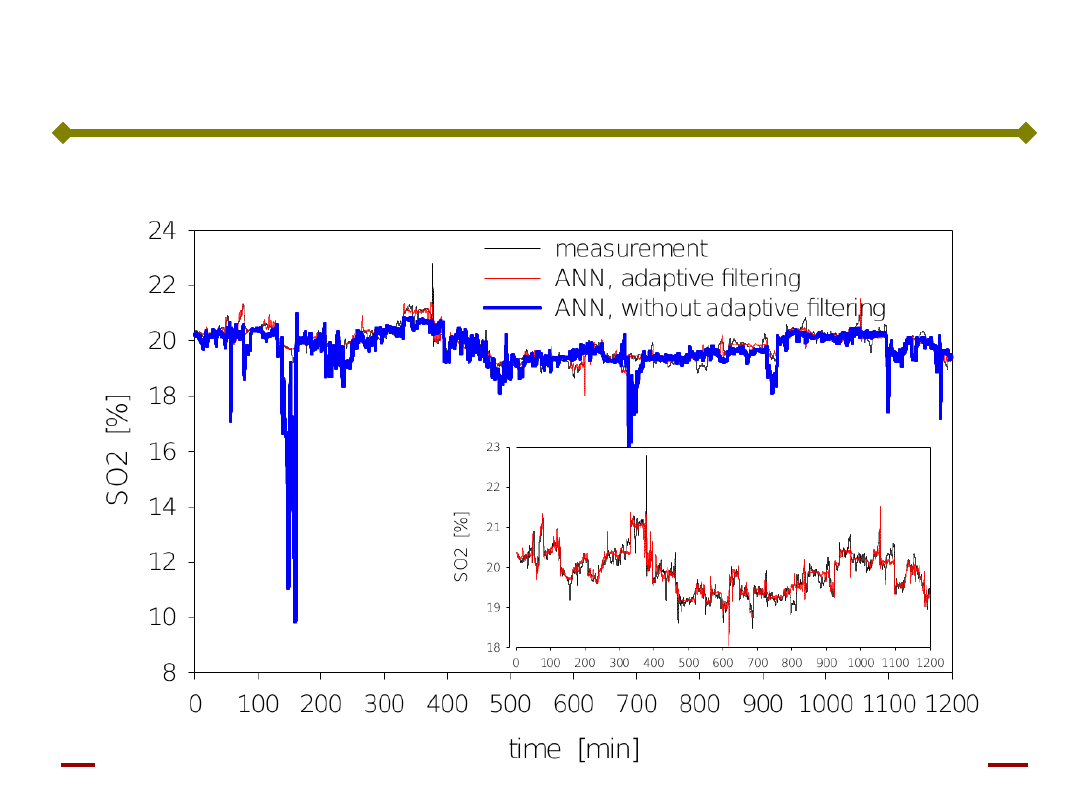
Optymalizacja stężenie SO

2

Podstawy Sztucznej

Inteligencji

Jan Kusiak

Metamodelowanie

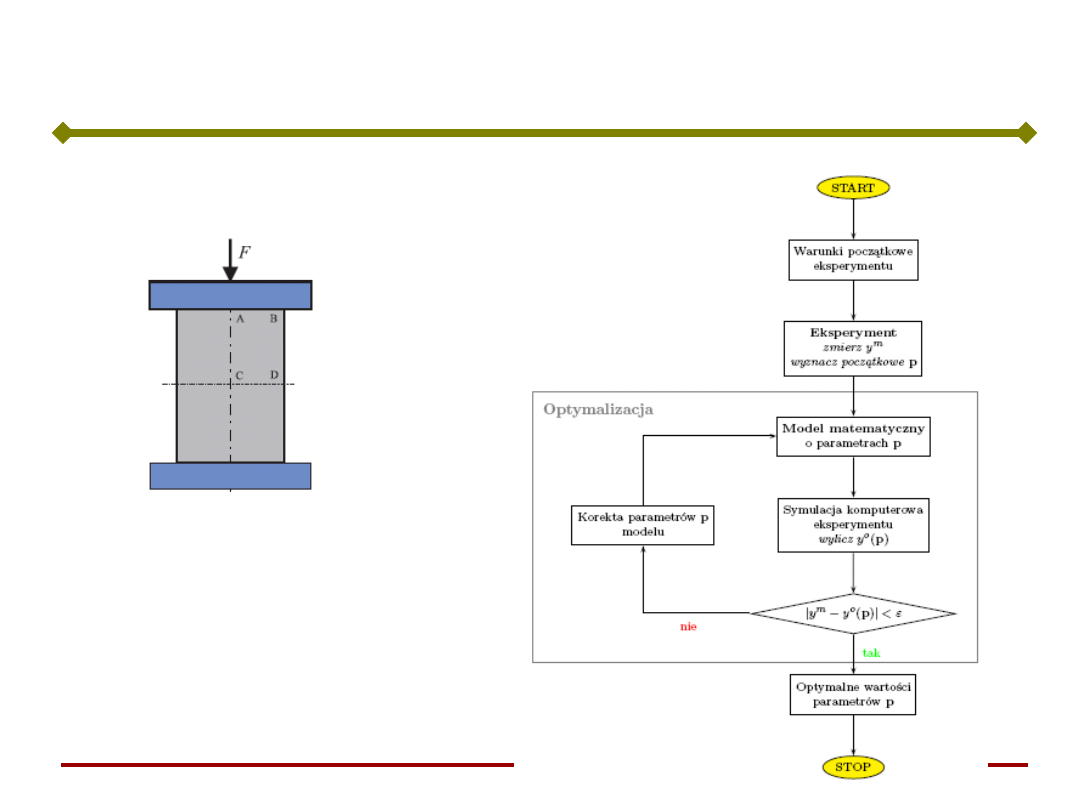
Przykłady – analiza odwrotna (inverse)





2

1

)

(

)

(









N

i

o

i

m

i

y

y

J

p

p

Funkcja celu:

Podstawy Sztucznej

Inteligencji

Jan Kusiak

Metamodelowanie

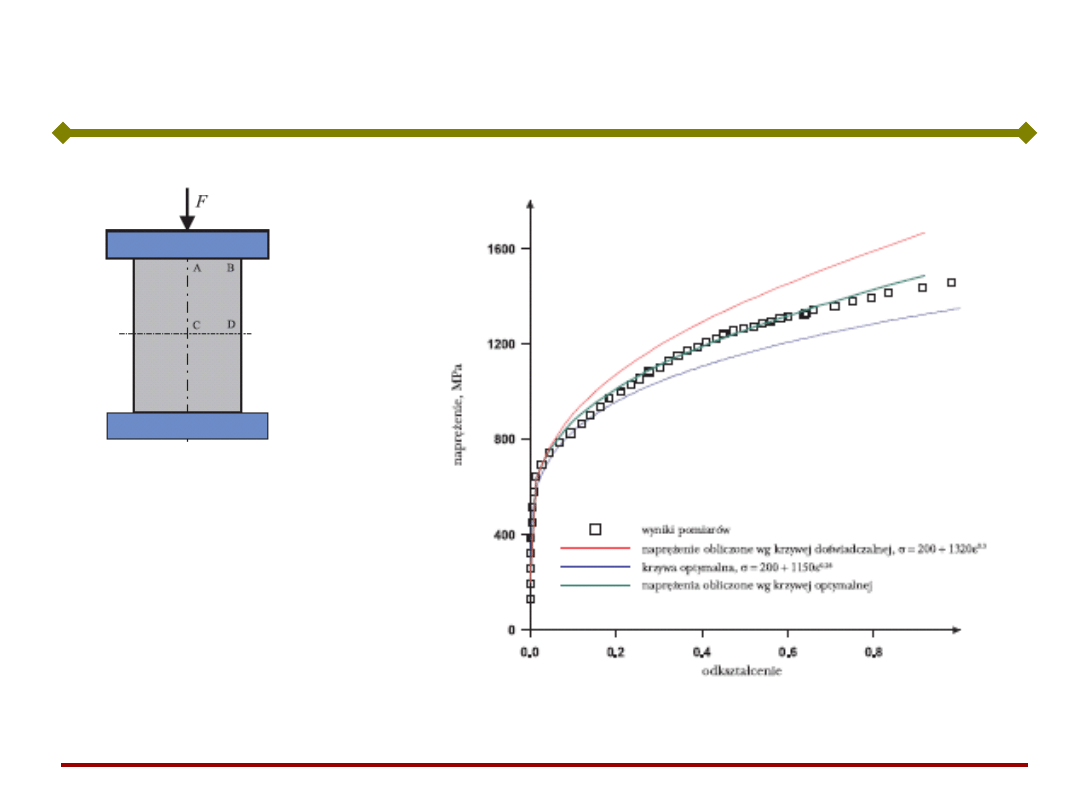
Przykłady – analiza odwrotna





2

1

)

(

)

(









N

i

o

i

m

i

y

y

J

p

p

n

a

n

a



















0

)

,

,

(

)

,

(p

Podstawy Sztucznej

Inteligencji

Jan Kusiak

Metamodelowanie

itp.,
itd.

