Podstawy Sztucznej Inteligencji

Jan Kusiak

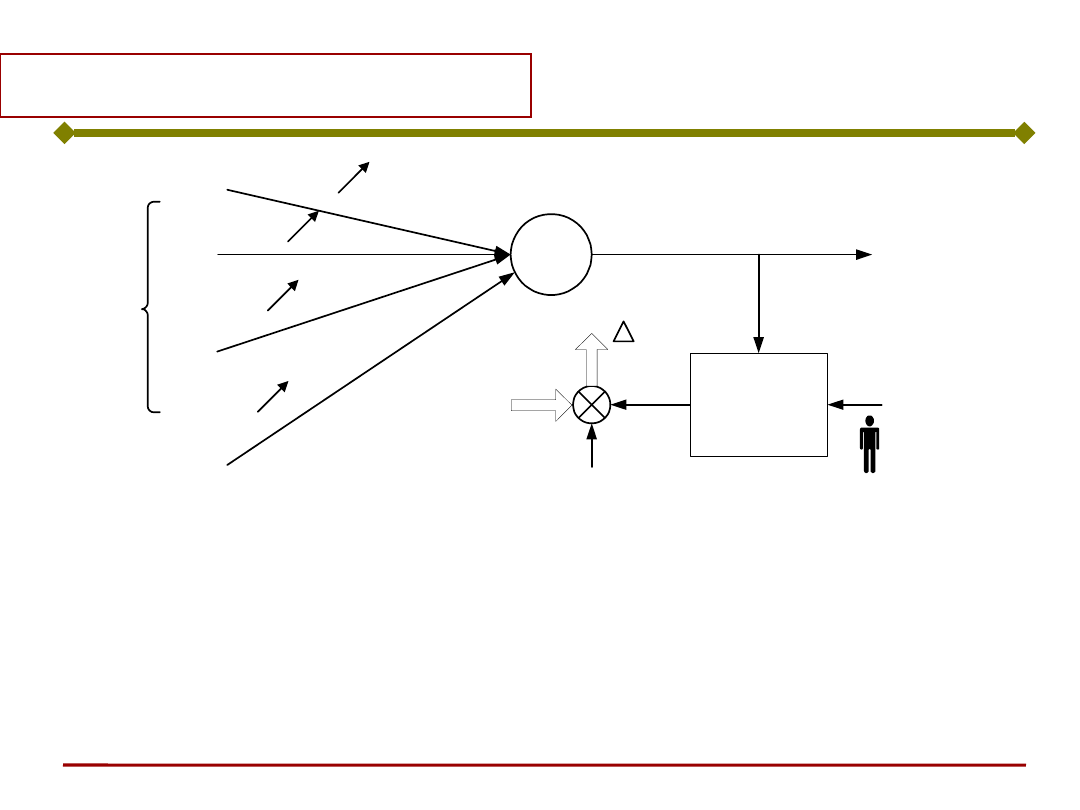
Uczenie neuronu

Podstawy Sztucznej Inteligencji

Jan Kusiak

x

1

x

2

w

i1

.

.

.
.

.

.

i-ty neuron

w

ij

w

i2

w

in

x

j

x

n

y

i

generator

sygnału

uczącego

d

i

x

w

i

x

c

r

t

i

Ogólny wzór korekty współczynników wagowych:

k

k

i

k

k

i

k

i

k

i

k

i

d

w

cr

w

w

w

w

x

x

)

,

,

(

1













Jaką postać ma sygnał uczący r ?

Uczenie neuronu

Podstawy Sztucznej Inteligencji

Jan Kusiak

Uczenie neuronu

Ogólny przepis (algorytm) uczenia neuronu
wynika z zadania minimalizacji błędu uczenia.
Zadanie to można sformułować następująco:

Dla jakich wartości współczynników wagowych,
błąd uczenia przyjmuje najmniejszą
(minimalną) wartość?

Błąd uczenia pojedynczego neuronu

gdzie:

€

y=ϕ(s) =ϕ

w

i

x

i

i=1

n

∑

⎛

⎝

⎜

⎞

⎠

⎟ =ϕ W

T

X

(

)

€

E =

1
2

(y

i

−t

i

)

2

i=1

n

∑

Podstawy Sztucznej Inteligencji

Jan Kusiak

Uczenie neuronu

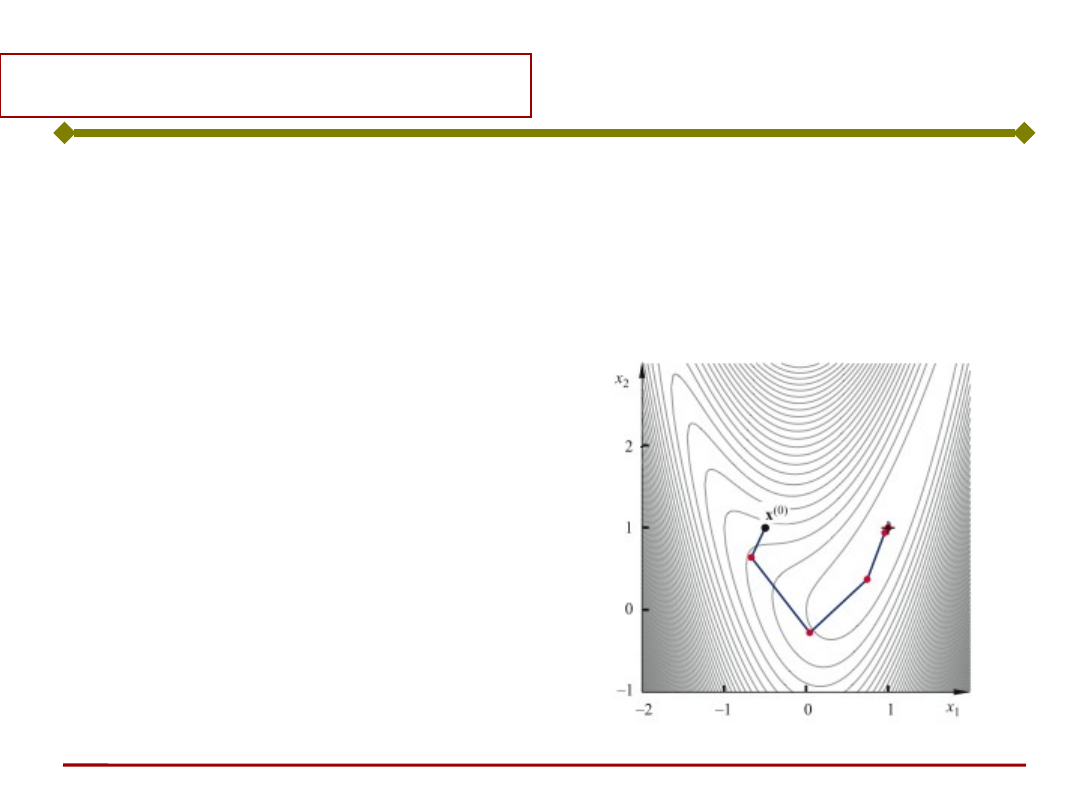
Ogólnie, zagadnienie optymalizacji sprowadza
się do poszukiwania minimum funkcji celu J
(kryterium jakości) drogą kolejnych iteracji
zgodnie z zależnością:

gdzie:

s - krok,
d - kierunek poszukiwań.

sd

x

x

k

k







)

(

)

1

(

Podstawy Sztucznej Inteligencji

Jan Kusiak

Uczenie neuronu

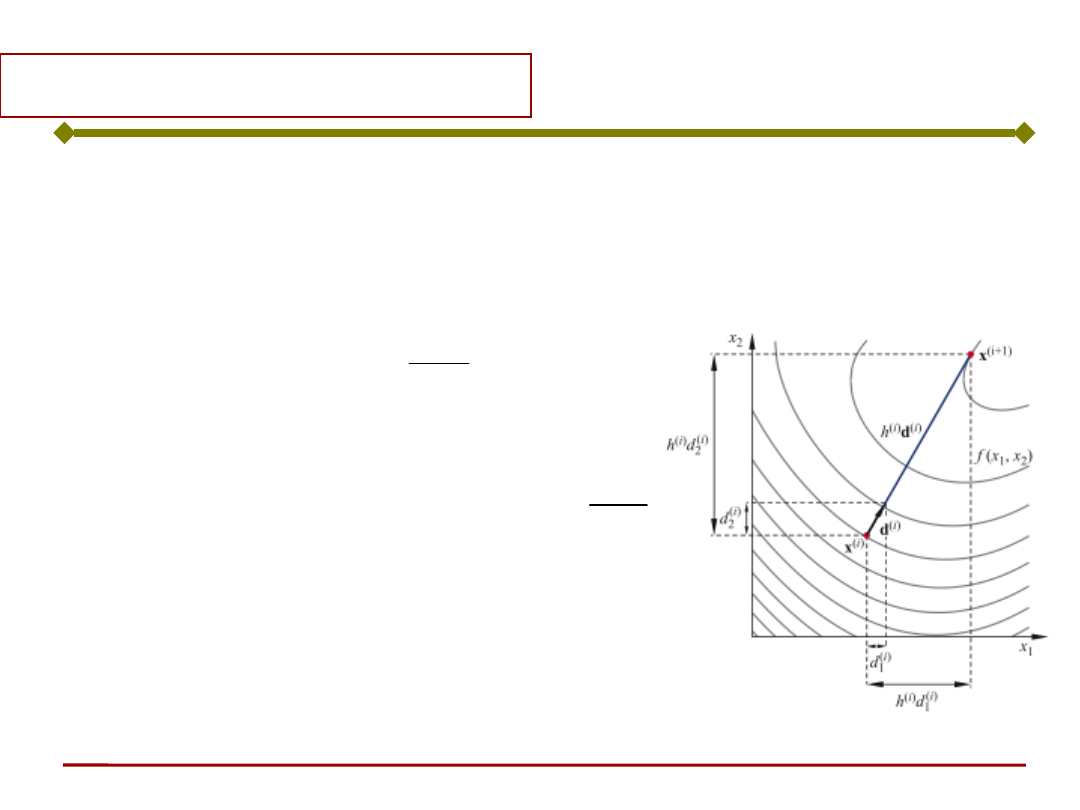
Ogólnie, do minimalizacji funkcji celu J można
wykorzystać gradientową metodę najszybszego
spadku, wg której zmiana parametrów
optymalizacji następuje zgodnie z zależnością:

czyli

Dx - przyrost zmiennej optymalizacji,
h - długość kroku.

x

J

x

x

x

x

k

k



















)

(

)

1

(

x

J

x













Podstawy Sztucznej Inteligencji

Jan Kusiak

Uczenie neuronu

W naszym przypadku kryterium jakości J=E

l

jest

funkcją współczynników wagowych E

l

= E

l

(W).

Minimalizując funkcję celu metodą gradientową,
poprawka o jaką należy zmodyfikować i-tą
składową wektora wag ma postać:

Poprawka jest proporcjonalna do i-tej
składowej gradientu funkcji E

l

(znak minus

oznacza, że poprawki dokonujemy w kierunku
najszybszego zmniejszania błędu).

i

l

i

w

E

w













Podstawy Sztucznej Inteligencji

Jan Kusiak

Uczenie neuronu

Korzystając ze wzoru na pochodną funkcji
złożonej zapisać:

€

∂E

∂w

i

=

∂E

∂y

∂y

∂w

i

Zgodnie z wzorem na
wielkość błędu:

€

∂E

∂y

=−(t−y) =−δ

€

E

l

=

1

2

(t

i

−y

i

)

2

i=1

n

∑

Podstawy Sztucznej Inteligencji

Jan Kusiak

Uczenie neuronu

€

∂E

∂w

i

=

∂E

∂y

∂y

∂w

i

€

∂y

∂w

i

=

∂ϕ(s)

∂w

i

=

∂ϕ( w

i

x

i

∑

)

∂w

i

Tak więc poprawki współczynników wagowych
zależą od przyjętej funkcji aktywacji

)

(s



Ostatecznie, wzór na zmianę współczynników
wagowych przyjmuje postać:

€

w

i

(k+1)

=w

i

(k)

+ηΔw

i

=w

i

(k)

+ηδ

∂ϕ

∂w

i

y

j

=w

i

(k)

+η(t

j

−y

j

)ϕ'y

j

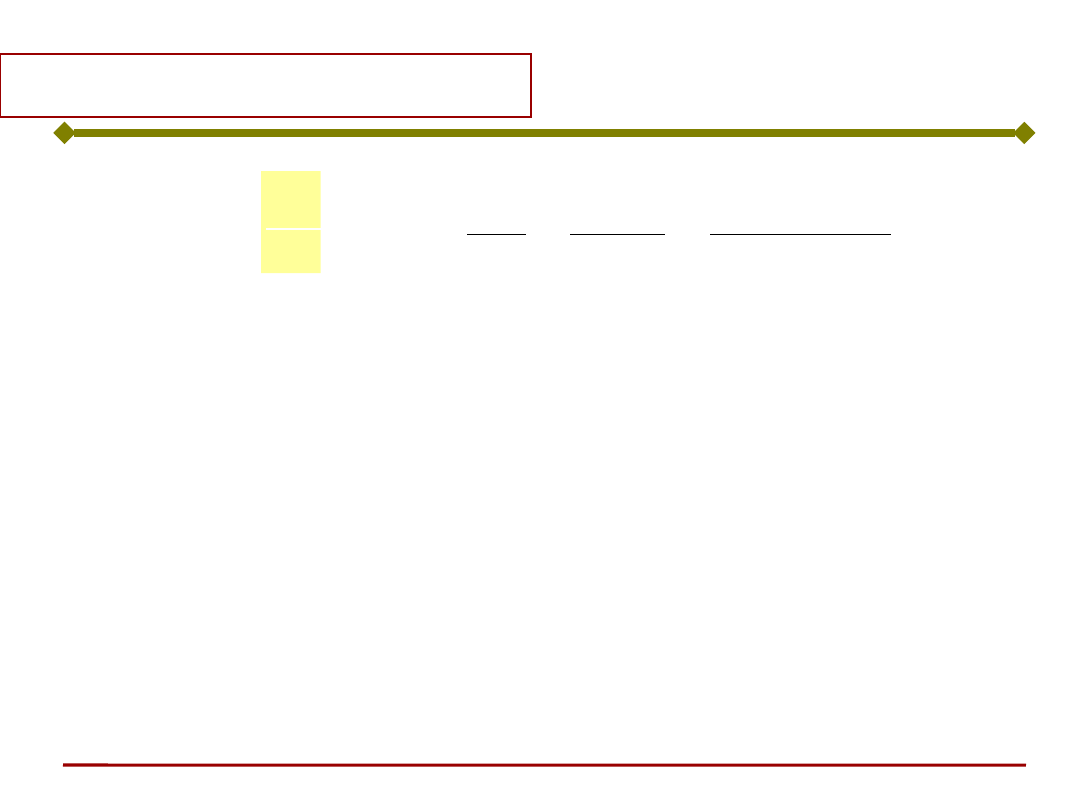
Podstawy Sztucznej Inteligencji

Jan Kusiak

+

x

1

x

2

w

i1

.

.

.
.

.

.

w

ij

w

i2

w

in

x

j

x

n

y

i

d

i

x

w

i

x

Funkcja

aktywacji

+

d

i

- y

i

+

-

c

s

i

r

gdzie j’(w

i

T

x) jest pochodną funkcji

aktywacji.

Sygnał uczący r neuronu o ciągłej funkcji
aktywacji:

€

r =δϕ'(s) =(t

i

−y

i

)ϕ'(w

i

T

x) =[t

i

−ϕ(w

i

T

x)]ϕ'(w

i

T

x)

)

(

'

i

s



)

(

i

s



t

i

t

i

- y

i

Uczenie neuronu – reguła

delta

Podstawy Sztucznej Inteligencji

Jan Kusiak

Ostatecznie, korekta współczynników wagowych
jest następująca:

• Dla

sigmoidalnej (logistycznej)

funkcji

aktywacji

:

• Dla

neuronów liniowych:

€

Δw

i

=ηδx =c(t−y)x

• Dla funkcji aktywacji

tanh:

Uczenie neuronu

€

Δw

i

=ηδy(1−y)x =η(t−y)y(1−y)x

€

Δw

i

=ηδ(1−y

2

)x =η(t−y)(1−y

2

)x

Podstawy Sztucznej Inteligencji

Jan Kusiak

Podstawy Sztucznej

Inteligencji

Jan Kusiak

Sztuczna sieć neuronowa

Podstawy Sztucznej Inteligencji

Jan Kusiak

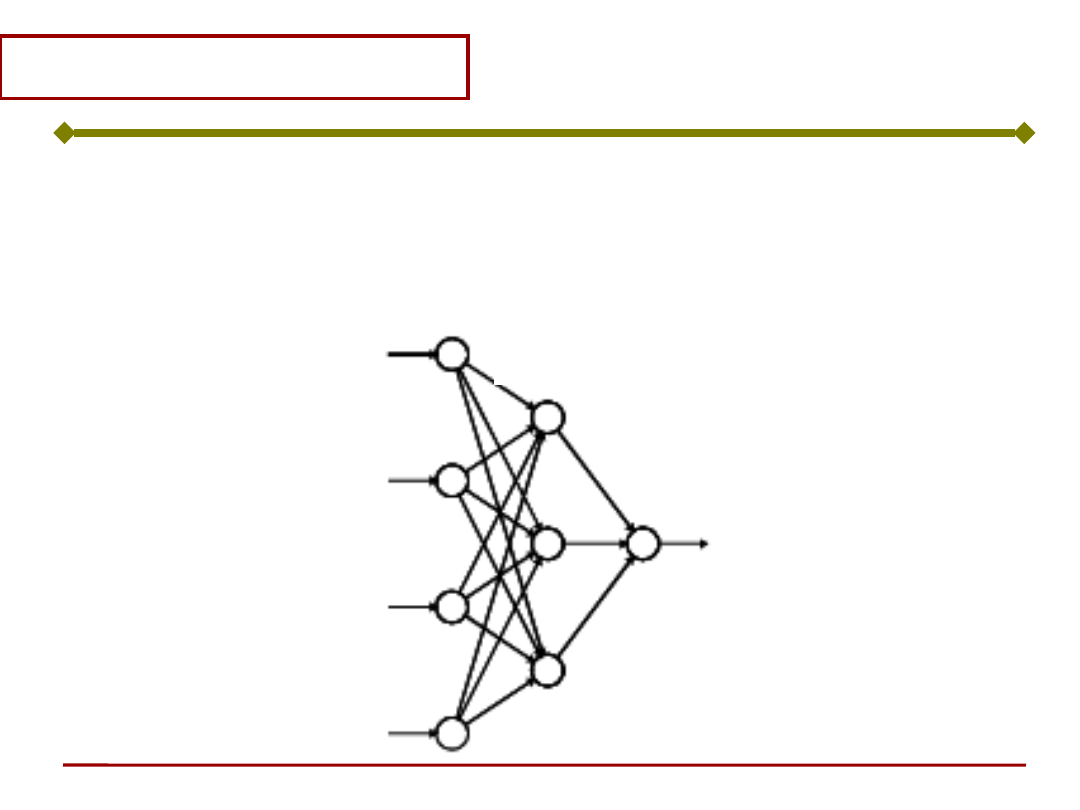
Sieć neuronowa

Sieć neuronowa jest układem neuronów
odpowiednio ze sobą połączonych w warstwy,
przy czym wyróżnia się zazwyczaj warstwę
wejściową, warstwy ukryte i warstwę wyjściową:

warstwa

wyjściowa

warstwa

ukryta

warstwa wejściowa

Podstawy Sztucznej Inteligencji

Jan Kusiak

Podstawy Sztucznej

Inteligencji

Jan Kusiak

Sztuczne Sieci Neuronowe 1

Sieć neuronowa

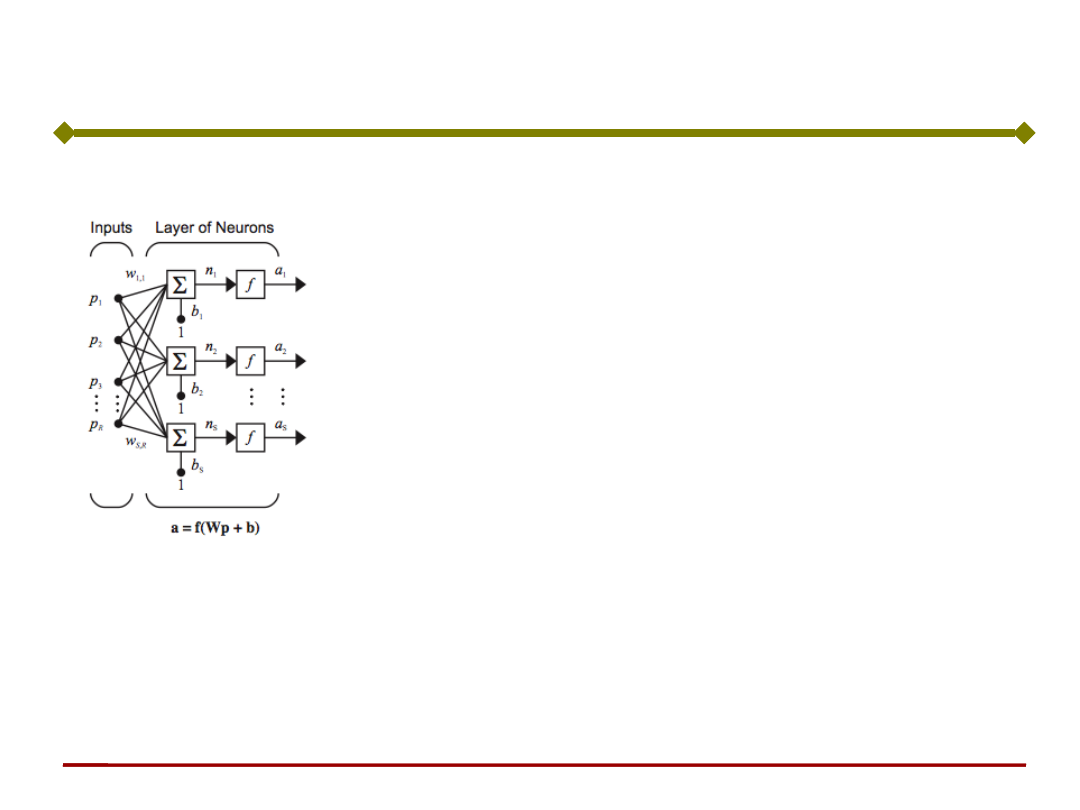
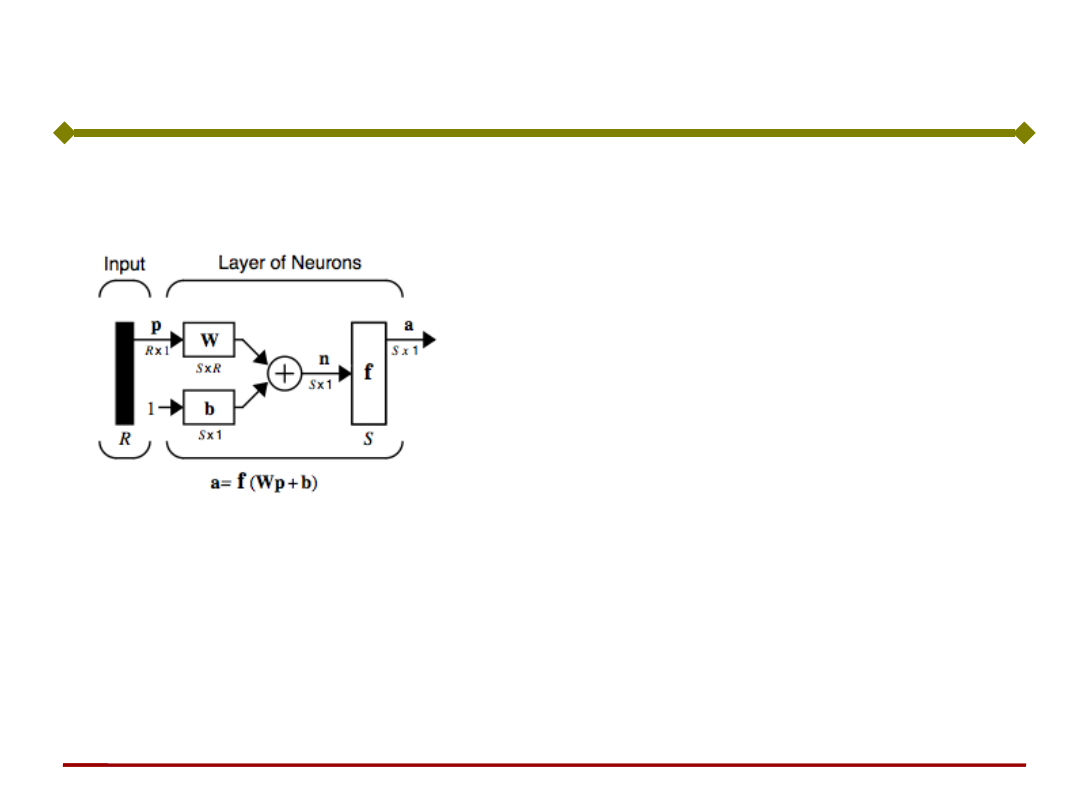
Pojedyncza warstwa (wejściowa) sieci

R – liczba elementów wektora wejściowego p
S – liczba neuronów w warstwie
Uwaga: R nie musi być równe S

• Każdy sygnał wejściowy (każdy element wektora

p) jest podawany na wejście każdego z
neuronów poprzez macierz wag W.

• Sygnałem wyjściowym jest wektor kolumnowy a.

• Macierz wag W































R

S

S

S

R

R

w

w

w

w

w

w

w

w

w

,

2

,

1

,

,

2

2

,

2

1

,

2

,

1

2

,

1

1

,

1

...

...

...

W

Uwaga: numer wiersza (pierwszy wskaźnik) to numer neuronu
docelowego, a numer kolumny (drugi wskaźnik) to numer źródła

€

n

1

=w

1,1

p

1

+w

1,2

p

2

+...+w

1,R

p

R

+b

b

Wp



n

Podstawy Sztucznej Inteligencji

Jan Kusiak

Podstawy Sztucznej

Inteligencji

Jan Kusiak

Sztuczne Sieci Neuronowe 1

Sieć neuronowa

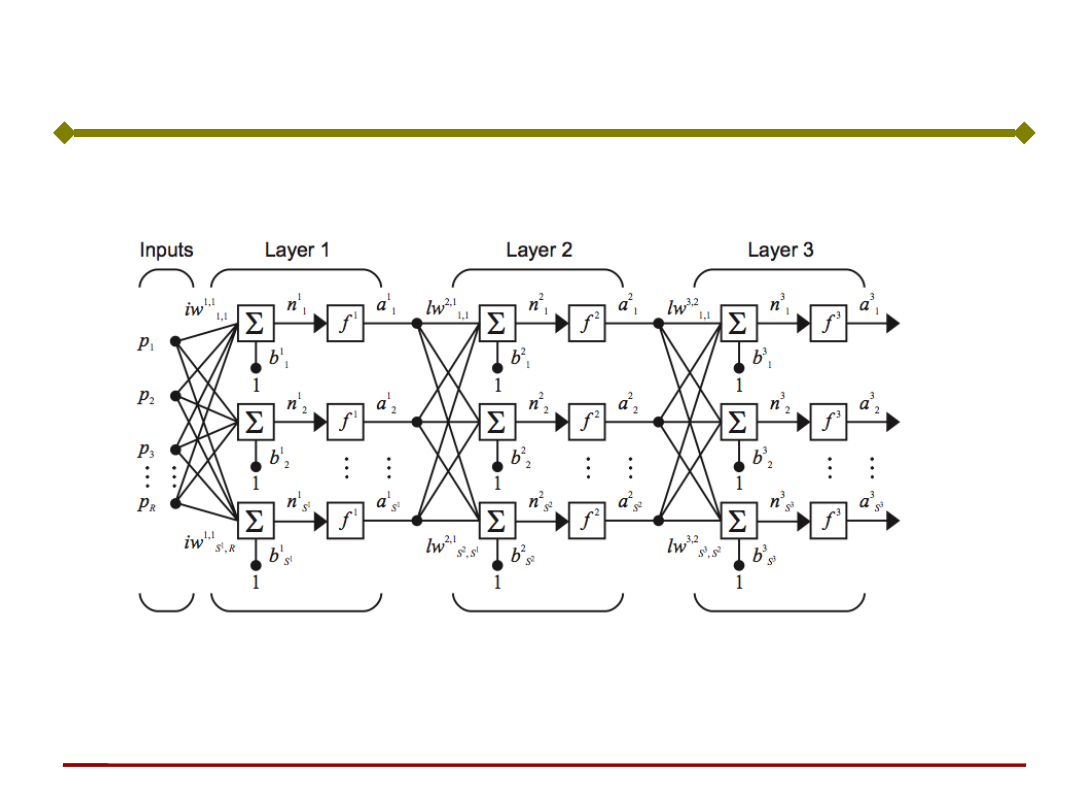
Pojedyncza warstwa (wejściowa) sieci w skróconej notacji

R – liczba elementów wektora
wejściowego p
S – liczba neuronów w warstwie
1

Podstawy Sztucznej Inteligencji

Jan Kusiak

Podstawy Sztucznej

Inteligencji

Jan Kusiak

Sztuczne Sieci Neuronowe 1

Sieć neuronowa

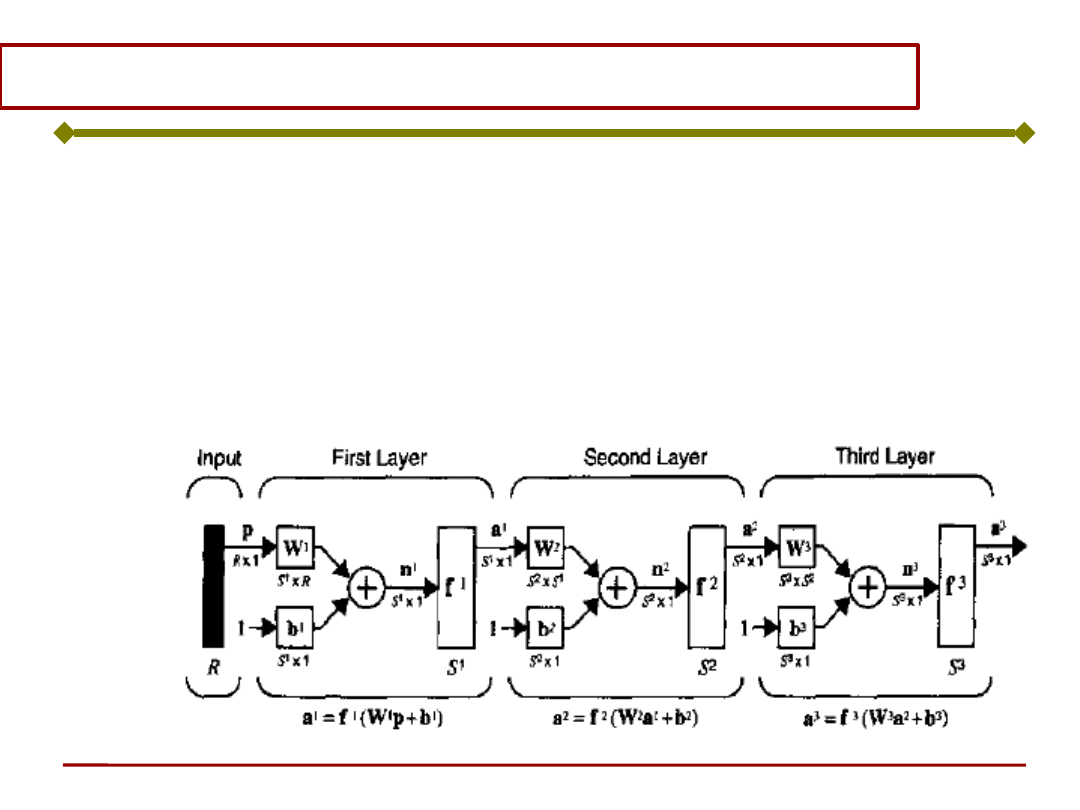
Ogólna struktura sieci neuronowej wielowarstwowej



a

2

 f

2

(LW

2,1

a

1

 b

2

)



a

3

 f

3

(LW

3,2

a

2

 b

3

)



a

1

 f

1

(IW

1,1

p b

1

)



a

3

 f

3

(LW

3,2

f

2

(LW

2,1

f

1

(IW

1,1

p b

1

) b

2

) b

3

)



LW

- Macierz wag warstwy
wewnętrznej (ukrytej)

- Macierz wag warstwy
wejściowej

IW

Sieć neuronowa

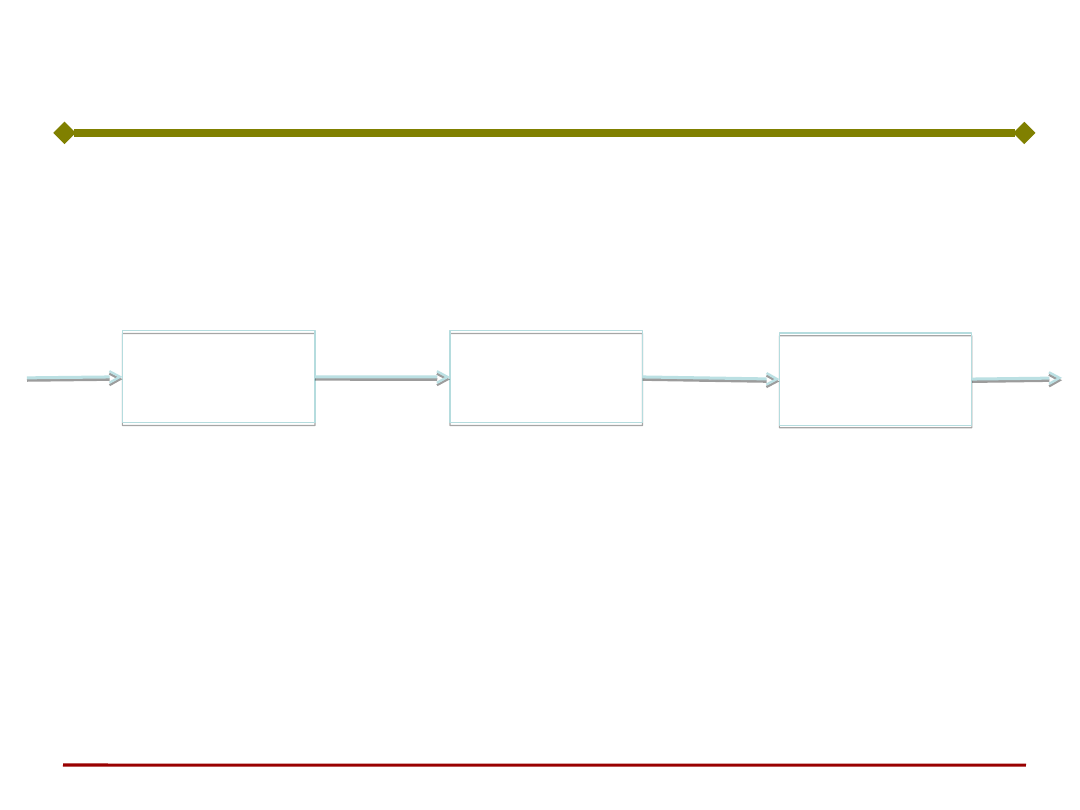
Ogólna struktura sieci neuronowej wielowarstwowej

€

a1=f1(Wx)

€

a3 =f3(V2f2(V1f1(Wx)))

Warstwa
wejściowa

x

a

1

W

V

2

a

2

V

1

...

a

3

€

a2 =f2(V1a1)

€

a3=f3(V2a2)

Warstwa
ukryta 1

Warstwa
ukryta 2

Podstawy Sztucznej Inteligencji

Jan Kusiak

Podstawy Sztucznej

Inteligencji

Jan Kusiak

Sztuczne Sieci Neuronowe 1

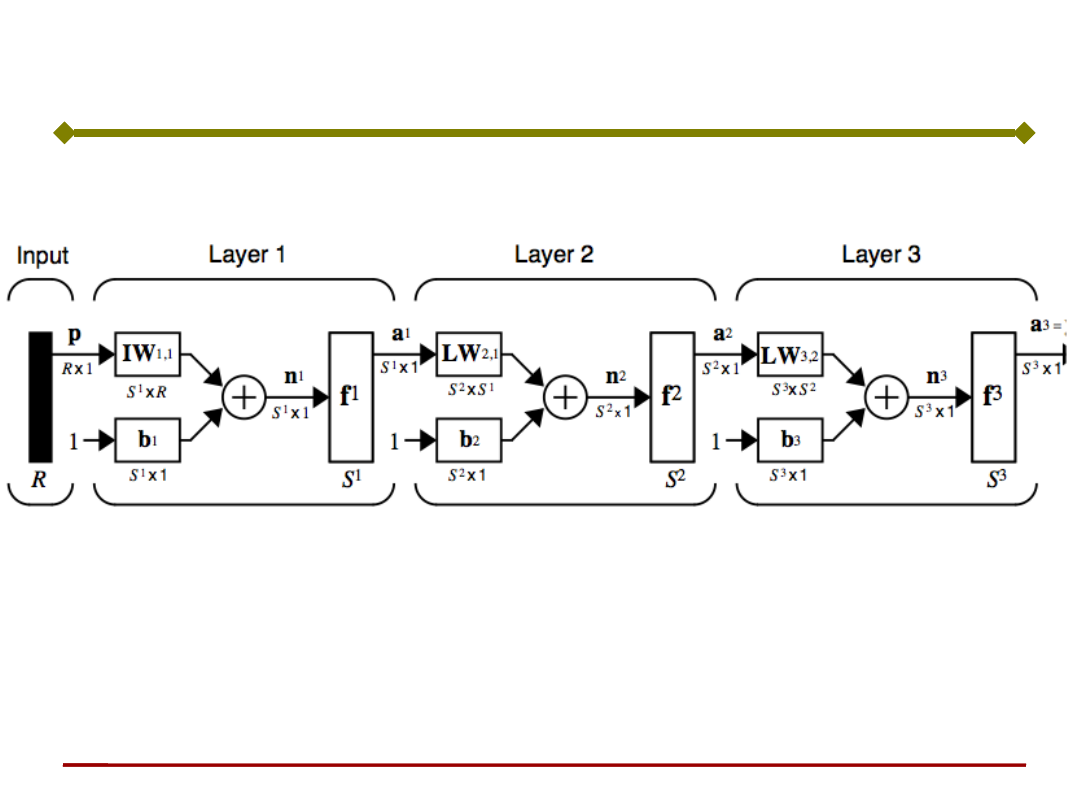
Sieć neuronowa

Sieć neuronowa wielowarstwowa w skróconej notacji



a

2

 f

2

(LW

2,1

a

1

 b

2

)



a

3

 f

3

(LW

3,2

a

2

 b

3

)



a

1

 f

1

(IW

1,1

p b

1

)



a

3

 f

3

(LW

3,2

f

2

(LW

2,1

f

1

(IW

1,1

p b

1

) b

2

) b

3

)



LW

- Macierz wag warstwy
wewnętrznej (ukrytej)

- Macierz wag warstwy
wejściowej



IW

Pierwszy indeks – warstwa docelowa
Drugi indeks – warstwa źródłowa

Podstawy Sztucznej Inteligencji

Jan Kusiak

Sygnał wyjściowy każdego z neuronów jest w
ogólnym przypadku nieliniową funkcją
pobudzenia

gdzie: w

i

= [w

i1

, w

i2

, ...,w

im

]

T

, - wektor wag

sygnałów wejściowych i-tego neuronu.

Sieć neuronowa

€

y

i

=ϕ(n

i

)=ϕ

w

ij

x

j

j=1

m

∑

⎛

⎝

⎜

⎜

⎜

⎞

⎠

⎟

⎟

⎟

=ϕ(w

i

Tx), i=1,2,K ,n

Podstawy Sztucznej Inteligencji

Jan Kusiak

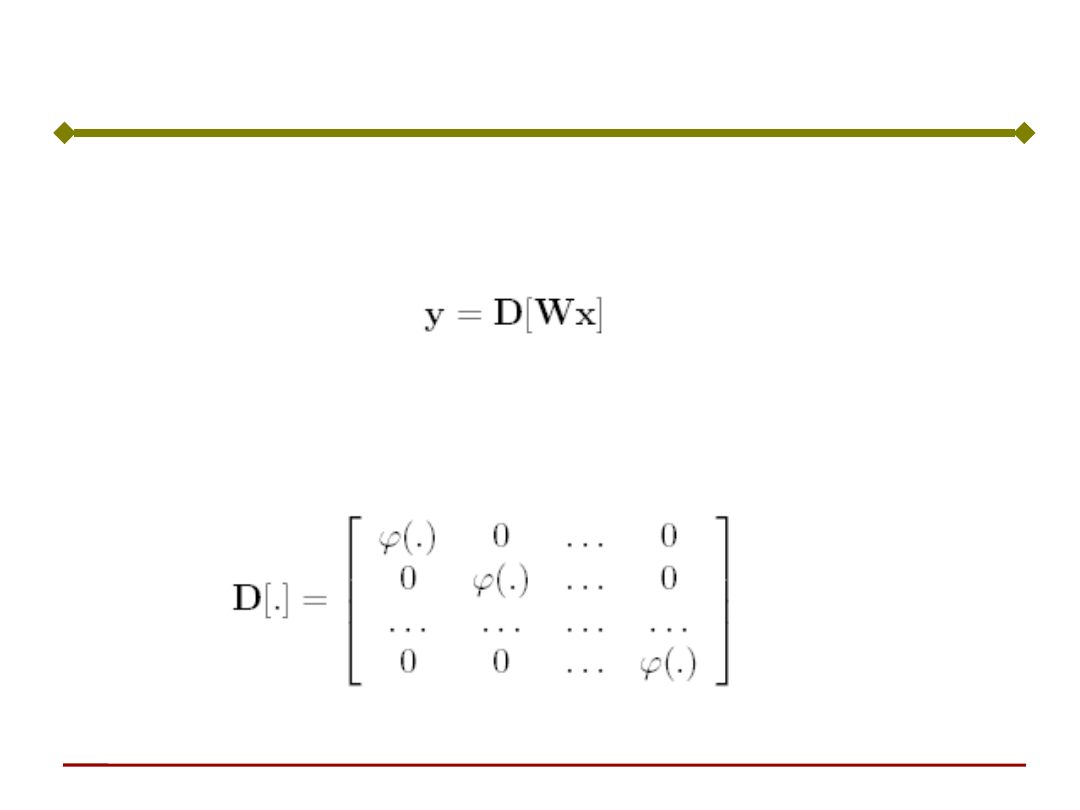
Relację wejście - wyjście można zapisać w
postaci macierzowej:

gdzie: D jest macierzowym operatorem
nieliniowym reprezentującym funkcje
aktywacji poszczególnych neuronów:

Sieć neuronowa

Podstawy Sztucznej Inteligencji

Jan Kusiak

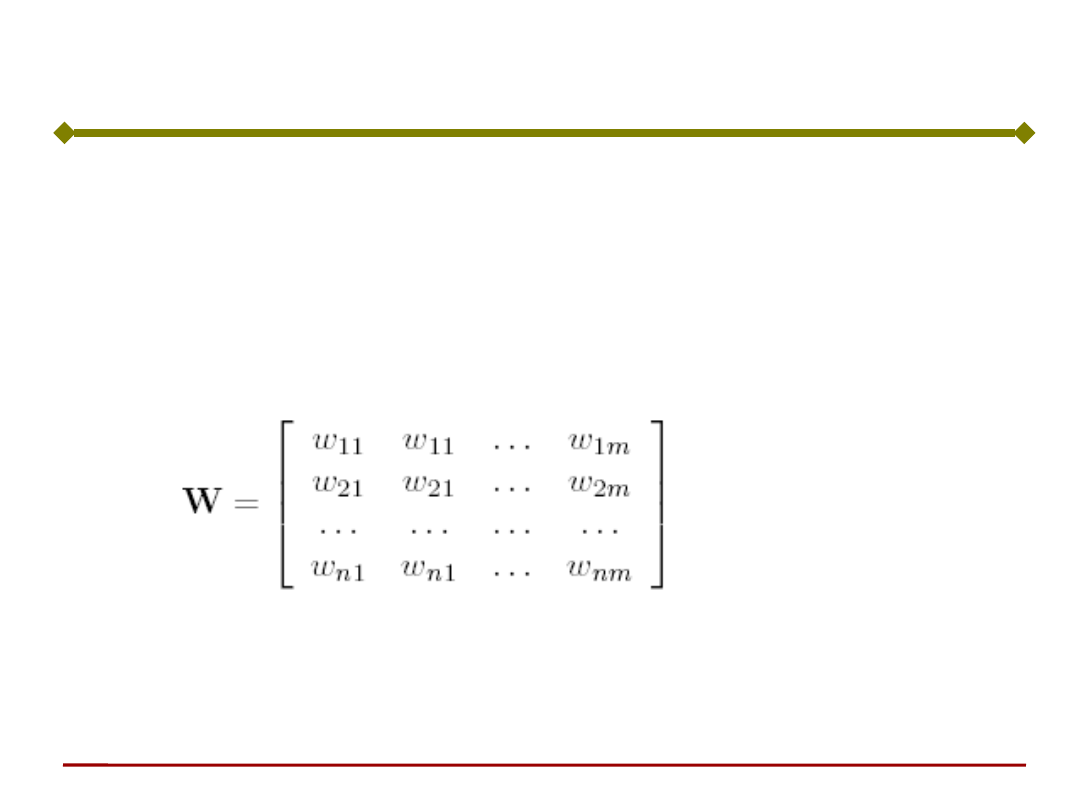
W jest macierzą wag synaptycznych,
reprezentującą tablicę połączeń poszczególnych
neuronów analizowanej warstwy z warstwą
poprzednią:

gdzie:
n - liczba warstw,
m - liczba neuronów w danej warstwie

Sieć neuronowa

Podstawy Sztucznej Inteligencji

Jan Kusiak

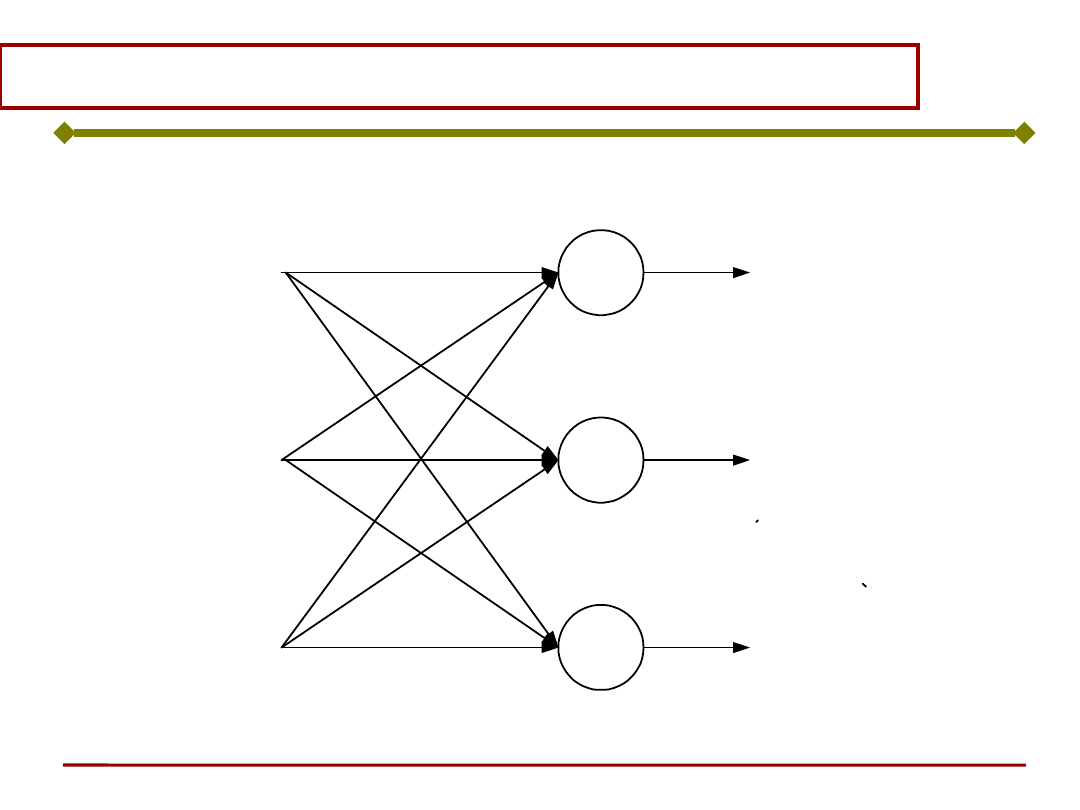
Wektor sygnałów wyjściowych z dowolnej
warstwy można wyznaczyć mnożąc wektor
sygnałów wejściowych przez macierz
współczynników wagowych

W przypadku wektorów nieliniowych, składowe
otrzymanego wektora należy przekształcić
poprzez funkcję aktywacji.

Sieć neuronowa

Podstawy Sztucznej Inteligencji

Jan Kusiak

Sygnały wejściowe przyjmują wartości z
pewnego określonego przedziału, zazwyczaj
przyjmuje się:

x Î [-1,1]

lub

x Î [0,1]

Można to osiągnąć poprzez normalizację
sygnałów wejściowych

Sieć neuronowa

Podstawy Sztucznej Inteligencji

Jan Kusiak

Budowa sieci

• Neurony tworzą warstwy

• Sygnały wyjściowe neuronów jednej warstwy

stanowią sygnały wejściowe neuronów
warstwy następnej

• Liczba wejść każdego neuronu jest

zwiększoną o 1 liczbą neuronów w warstwie
poprzedniej (sygnał progowy o stałej
wartości).

• Liczba wejść w neuronach pierwszej warstwy

jest uzależniona od liczby sygnałów
wejściowych do sieci.

• Liczba warstw (a także liczba neuronów) w

znaczący sposób decyduje o możliwościach
sieci

Podstawy Sztucznej Inteligencji

Jan Kusiak

Co ma wpływ na sygnały wyjściowe?

Sygnał wyjściowy neuronu
zależy od:

sygnałów wejściowych,
współczynników wagowych,
funkcji aktywacji,
budowy sieci

Podstawy Sztucznej Inteligencji

Jan Kusiak

Techniki uczenia

sieci neuronowych

Podstawy Sztucznej Inteligencji

Jan Kusiak

Zmieniając wartości współczynników
wagowych możemy zmieniać zależności
pomiędzy wektorami sygnałów
wejściowych i wyjściowych sieci.

Jak ustawić te współczynniki aby
uzyskać żądane zależności pomiędzy
tymi wektorami?

Sieci neuronowych się nie programuje.
Oznacza to, że wartości współczynników
wag nie ustala się bezpośrednio,
ulegają one zmianom podczas procesu
nazywanego uczeniem sieci.

Podstawy Sztucznej Inteligencji

Jan Kusiak

Dla n neuronów warstwy wyjściowej sieci, błąd

jednej epoki wynosi:

Całkowity błąd uczenia złożonego z m epok
wynosi:

€

E

e

=

1
n

(y

i

−t

i

)

2

i=1

n

∑







m

j

ej

E

m

E

1

1

Błąd uczenia sieci

Podstawy Sztucznej Inteligencji

Jan Kusiak

Uczenie sieci jednowarstwowej

1

K

k

z

1

z

k

z

K

y

1

y

j

y

J

w

11

w

k1

w

K1

w

1j

w

1J

w

k1

w

kj

w

Kj

w

kJ

w

KJ

.

.

.

.

.

.

.

.

.

.

.

.

Podstawy Sztucznej Inteligencji

Jan Kusiak

Wektor sygnałów wyjściowych sieci wynosi:

gdzie
:

a F jest operatorem
nieliniowym
zależnym od funkcji
aktywacji
poszczególnych
neuronów:



























J

y

y

y

y



2

1



























J

z

z

z

z



2

1



































KJ

K

K

kJ

k

k

J

w

w

w

w

w

w

w

w

w

W























2

1

2

1

1

12

11

Uczenie sieci jednowarstwowej

z = F[Wy]

Podstawy Sztucznej Inteligencji

Jan Kusiak

Uczenie sieci jednowarstwowej

Ogólny wzór korekty współczynników wagowych:

k

k

i

k

k

i

k

i

k

i

k

i

d

w

cr

w

w

w

w

x

x

)

,

,

(

1













Jaką postać ma sygnał uczący r ?

Podstawy Sztucznej Inteligencji

Jan Kusiak

min

)

(

2

1

1

2











K

k

lk

lk

l

z

d

E

Celem procesu uczenia jest minimalizacja
błędu E

l

prezentacji pojedynczego obrazu

wejściowego y

l

, l=1,...,p

Uczenie sieci jednowarstwowej

min



l

E

Podstawy Sztucznej Inteligencji

Jan Kusiak

Ogólnie, zagadnienie optymalizacji sprowadza
się do poszukiwania minimum funkcji celu
(kryterium jakości) drogą kolejnych iteracji
zgodnie z zależnością:

gdzie:

s - krok,
d - kierunek poszukiwań.

Uczenie sieci jednowarstwowej

sd

x

x

k

k







)

(

)

1

(

Podstawy Sztucznej Inteligencji

Jan Kusiak

Ogólnie, do minimalizacji funkcji celu można
wykorzystać gradientową metodę najszybszego
spadku, wg której zmiana parametrów
optymalizacji następuje zgodnie z zależnością:

czyli

Dx - przyrost zmiennej optymalizacji,
h - długość kroku.

x

J

x

x

x

x

k

k



















)

(

)

1

(

x

J

x













Uczenie sieci jednowarstwowej

Podstawy Sztucznej Inteligencji

Jan Kusiak

W naszym przypadku kryterium jakości J=E

l

jest

funkcją współczynników wagowych E

l

= E

l

(W).

Minimalizując funkcję celu metodą gradientową,
poprawka o jaką należy zmodyfikować i-tą
składową wektora wag ma postać:

Poprawka jest proporcjonalna do i-tej
składowej gradientu funkcji E

l

(znak minus

oznacza, że poprawki dokonujemy w kierunku
najszybszego zmniejszania błędu).

Uczenie sieci jednowarstwowej

i

l

i

w

E

w













Podstawy Sztucznej Inteligencji

Jan Kusiak

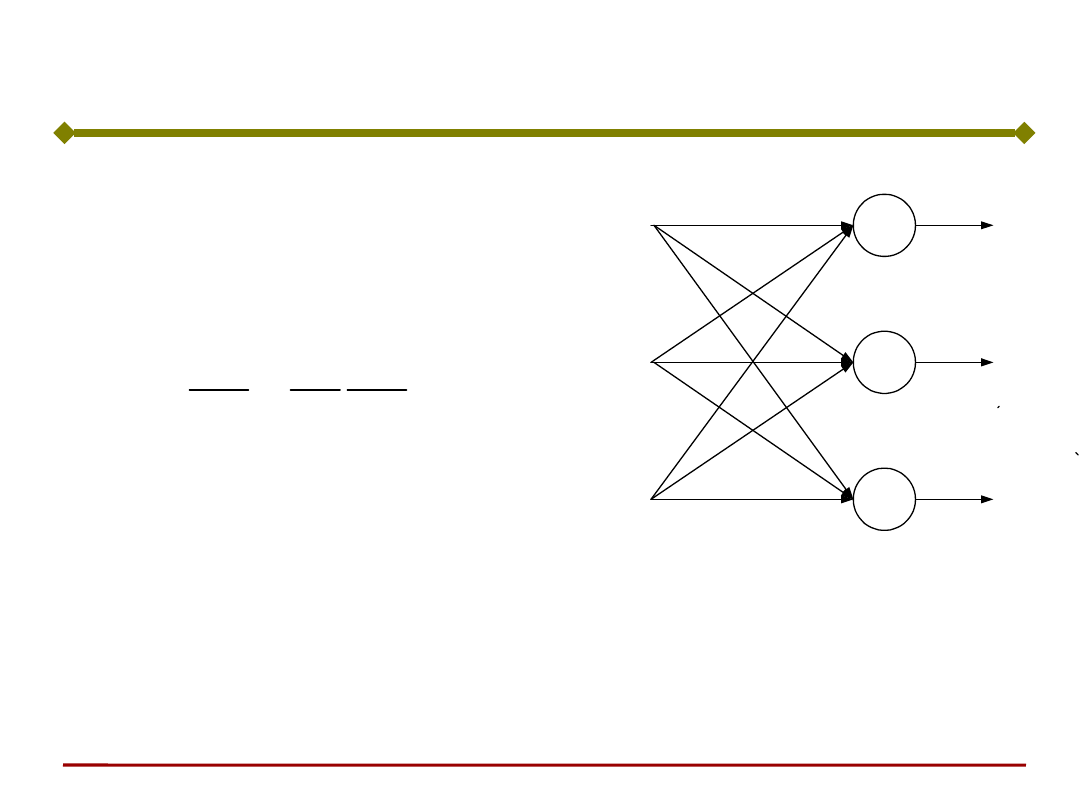
Korzystając ze wzoru
na pochodną funkcji
złożonej zapisać:

i

i

w

z

z

E

w

E















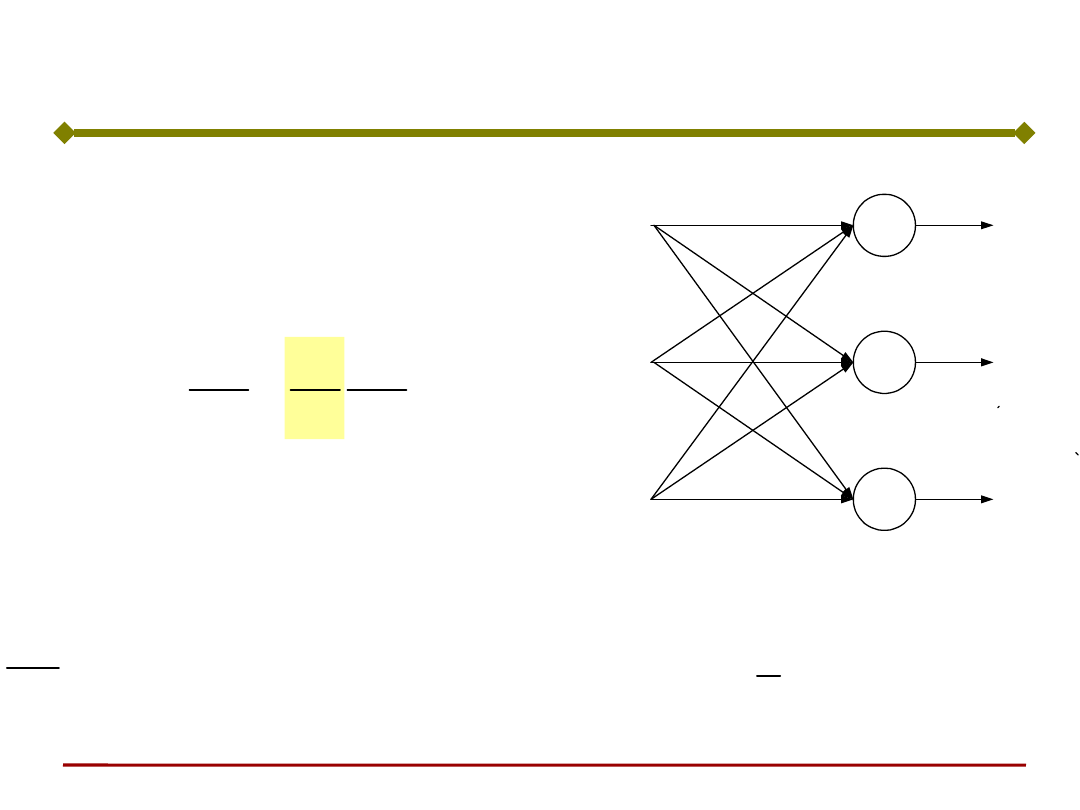
Uczenie sieci jednowarstwowej

1

K

k

z

1

z

k

z

K

y

1

y

j

y

J

w

11

w

k1

w

K1

w

1j

w

1J

w

k1

w

kj

w

Kj

w

kJ

w

KJ

.

.

.

.

.

.

.

.

.

.

.

.

Podstawy Sztucznej Inteligencji

Jan Kusiak

Korzystając ze wzoru
na pochodną funkcji
złożonej zapisać:

i

i

w

z

z

E

w

E















Uczenie sieci jednowarstwowej

1

K

k

z

1

z

k

z

K

y

1

y

j

y

J

w

11

w

k1

w

K1

w

1j

w

1J

w

k1

w

kj

w

Kj

w

kJ

w

KJ

.

.

.

.

.

.

.

.

.

.

.

.

















)

(

z

d

z

E

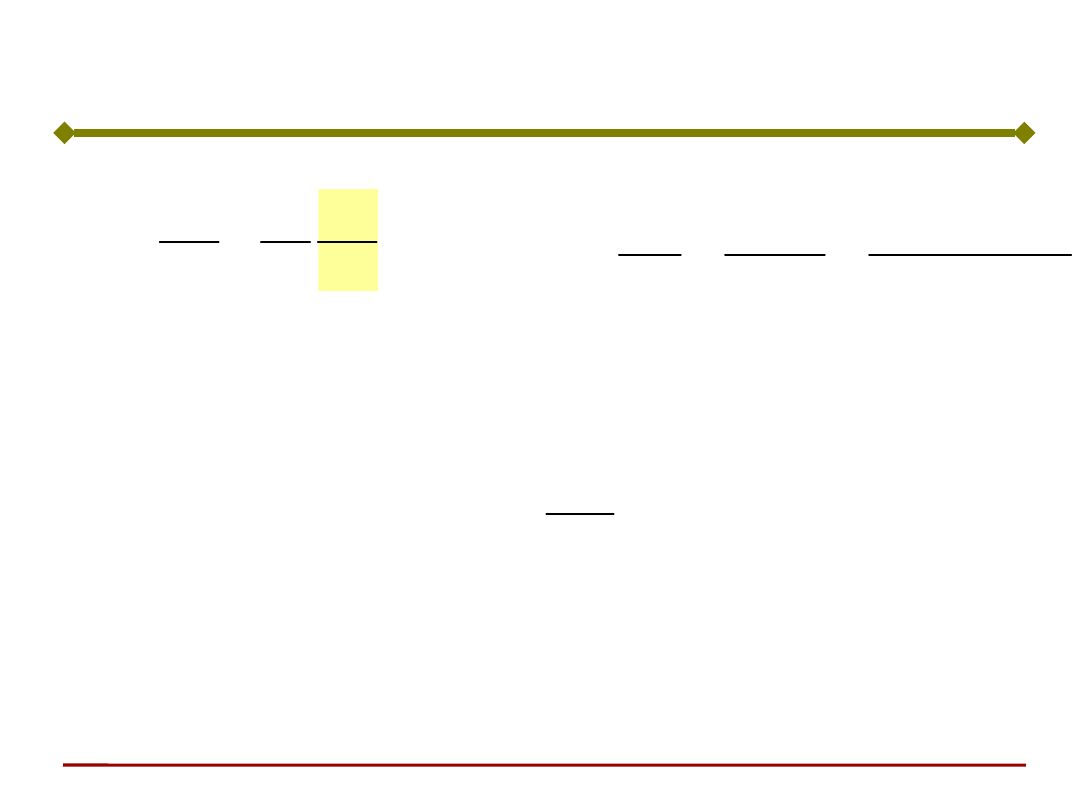
Zgodnie z wzorem na
wielkość błędu:









K

k

lk

lk

l

z

d

E

1

2

)

(

2

1

Podstawy Sztucznej Inteligencji

Jan Kusiak

i

i

w

z

z

E

w

E















Uczenie sieci jednowarstwowej

Tak więc poprawki współczynników wagowych
zależą od budowy sieci, a konkretnie, od
przyjętej funkcji aktywacji

i

i

i

i

i

w

y

w

w

s

w

z



















)

(

)

(





)

(s



Ostatecznie, wzór na zmianę współczynników
wagowych przyjmuje postać:

j

k

k

k

kj

j

j

k

kj

kj

k

kj

k

kj

y

z

d

w

y

w

w

w

w

w

'

)

(

)

(

)

(

)

(

)

1

(

































Podstawy Sztucznej Inteligencji

Jan Kusiak

Uczenie sieci jednowarstwowej

Ostatecznie, korekta współczynników wagowych
jest następująca:

• Dla

sigmoidalnej (logistycznej)

funkcji

aktywacji

:

• Dla

neuronów liniowych:

j

k

k

kj

y

w







)

(

j

k

k

k

k

kj

y

z

z

z

d

w

)

1

(

)

(











• Dla funkcji aktywacji

tanh:

j

k

k

k

kj

y

z

z

d

w

)

1

)(

(

2











J

j

,

,

1



K

k

,

,

1



Podstawy Sztucznej Inteligencji

Jan Kusiak

Algorytm uczenia ciągłej

jednowarstwowej sieci

Dane jest p par uczących:

{(y

1

,d

1

),(y

2

,d

2

),...,(y

p

,d

p

)}

gdzie y

i

ma rozmiar J ×1, d

i

ma rozmiar K ×1, a

sygnał progowy przyjmuje wartość y

iJ

= -1, i =

1, 2,..., p. Niech parametr l oznacza numer
kroku cyklu uczenia.

Krok 1: Wybór h > 0, E

max

> 0.

Krok 2: Wybór początkowych wartości elementów

macierzy wag W jako niewielkich liczb
losowych. Macierz W ma wymiar K ×J.

Krok 3: Ustawienie wartości początkowej

licznika kroków oraz wyzerowanie
wartości błędu: l = 1, E = 0.

Podstawy Sztucznej Inteligencji

Jan Kusiak

Algorytm uczenia ciągłej

jednowarstwowej sieci

Krok 4: Podanie obrazu na wejście i obliczenie

sygnału wyjściowego: y = y

l

, d=d

l

, z

k

=

j(w

k

T

y), k=1,2, ..., K gdzie w

k

T

jest k-

tym wierszem macierzy W.

Krok 5: Dla bipolarnej (tanh) funkcji

aktywacji uaktualnienie wag wg
zależności:

y

z

z

d

w

w

k

k

k

k

k

)

1

)(

(

2

1

2











K

k

,

,

2

,

1 



K

k

,

,

2

,

1 



y

z

z

z

d

w

w

k

k

k

k

k

k

)

1

(

)

(

2

1











Podstawy Sztucznej Inteligencji

Jan Kusiak

Krok 6: Obliczenie błędu łącznego:

Krok 7: Jeżeli l < p, to l=l+1 i przejście do

kroku 4.

Krok 8: Cykl uczenia został zakończony. Jeżeli

E < E

max

, to zakończenie uczenia. W

przeciwnym razie rozpoczęcie nowego
cyklu uczenia począwszy od kroku 3.

2

1

)

(

2

1











K

k

k

k

z

d

E

E

Algorytm uczenia ciągłej

jednowarstwowej sieci

Podstawy Sztucznej Inteligencji

Jan Kusiak

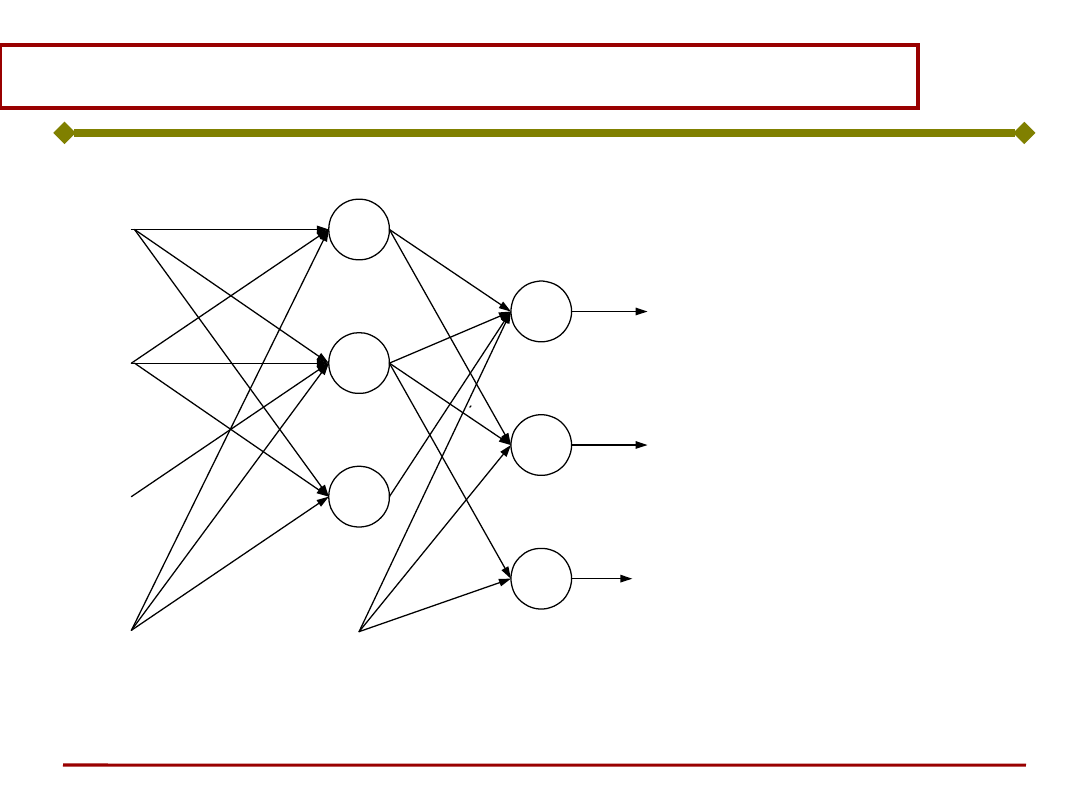
Uczenie sieci wielowarstwowej

1

J -1

j

x

1

x

i

x

I-1

z

1

z

k

z

K

v

11

v

j1

v

1i

v

1i

v

1I

v

j1

v

ji

v

jI

v

J -1,I

.

.

.

.

.

.

.

.

.

.

.

.

x

J

= -1

w

11

v

11

1

K

k

.

.

.

.

.

.

y

J

= -1

w

k1

w

1j

w

kj

w

Kj

w

kJ

w

KJ

w

1J

warstwa wyjściowa

warstwa ukryta

Czy można
stosować tę
samą regułę
uczenia co dla
sieci
jednowarstwowe
j?

Podstawy Sztucznej Inteligencji

Jan Kusiak

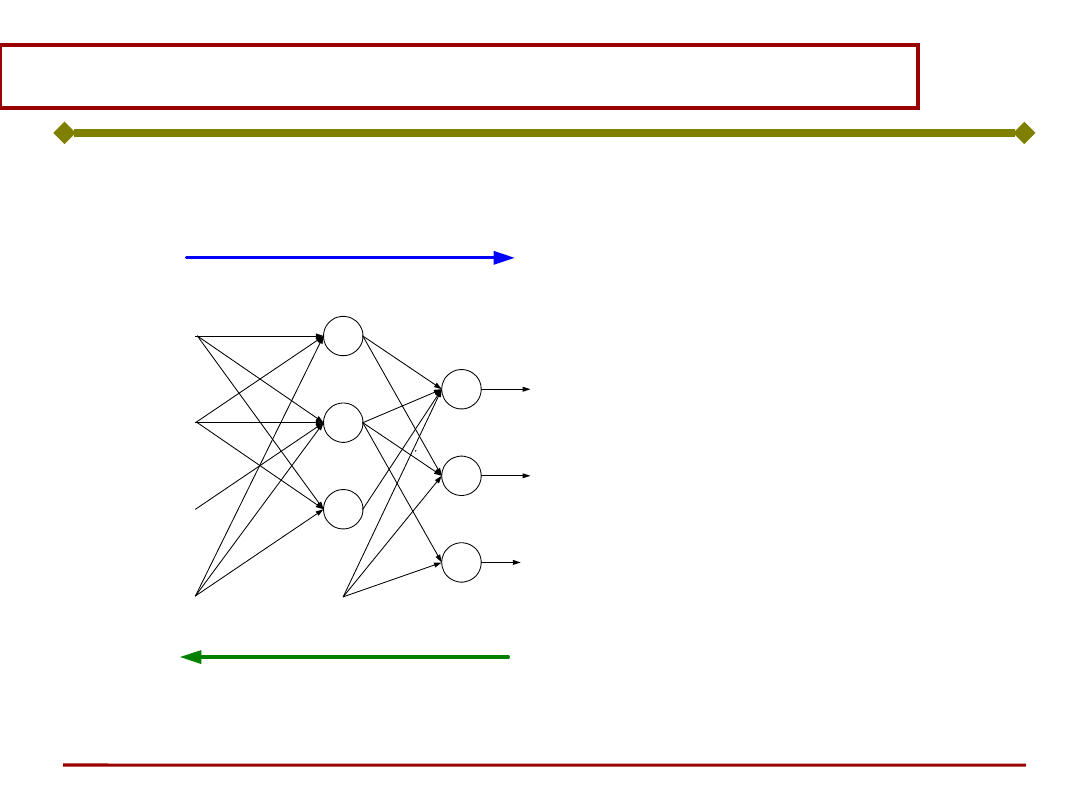
Algorytm wstecznej propagacji

błędu

Przez wiele lat nie znano metody skutecznego
uczenia sieci wielowarstwowych.

1986 - D. Rumelhart, G. Hinton i R. Williams
- Algorytm wstecznej propagacji błędu dla
jednokierunkowych sieci warstwowych. Algorytm
ten stanowi uogólnienie reguły Delta.

Mając wyznaczony błąd d

m

występujący podczas

realizacji procesu uczenia w neuronie o
numerze m, możemy "rzutować" ten błąd wstecz
do wszystkich tych neuronów, których sygnały
stanowiły wejścia dla m-tego neuronu.

Podstawy Sztucznej Inteligencji

Jan Kusiak

Algorytm wstecznej propagacji

błędu

k

k

w









1

J -1

j

x

1

x

i

x

I-1

z

1

z

k

z

K

v

11

v

j1

v

1i

v

1i

v

1I

v

j1

v

ji

v

jI

v

J -1,I

.

.

.

.

.

.

.

.

.

.

.

.

x

J

= -1

w

11

v

11

1

K

k

.

.

.

.

.

.

y

J

= -1

w

k1

w

1j

w

kj

w

Kj

w

kJ

w

KJ

w

1J

warstwa wyjściowa

warstwa ukryta

WE

(x)

WY

(z)

WE

(

k

)

WY

(

j

)

i

i

x

w

z





Podstawy Sztucznej Inteligencji

Jan Kusiak

Algorytm wstecznej propagacji

błędu

Algorytm:

gdzie: M – liczba warstw

M

m

m

m

m

m

M

m

a

a

b

a

W

f

a

p

a





















,

1

,

,

1

,

0

dla

)

(

1

1

1

1

0



1. Podanie sygnału wejściowego p i uzyskanie

na wyjściu sygnału a (kierunek sygnału od WE
do WY)

2. Rzutowanie wstecz błędu = (t – a)

(kierunek sygnału od WY do WE)

1

2

1

dla

)

)(

(

)

)(

(

2

1

1

,

,

,

M-

m

m

T

m

m

m

m

M

M

M





















s

W

n

F

s

a

t

n

F

s

Podstawy Sztucznej Inteligencji

Jan Kusiak

Algorytm wstecznej propagacji

błędu































)

(

0

0

0

)

(

0

0

0

)

(

)

(

2

1

m

s

m

m

m

m

m

m

m

m

n

f

n

f

n

f



















 n

F

Podstawy Sztucznej Inteligencji

Jan Kusiak

Algorytm wstecznej propagacji

błędu

m

m

m

T

m

m

m

m

k

k

k

k

s

b

b

a

s

W

W



















)

(

)

1

(

)

(

)

(

)

1

(

1

Korekta wag:

Problemy uczenia sieci neuronowej

Problemy uczenia

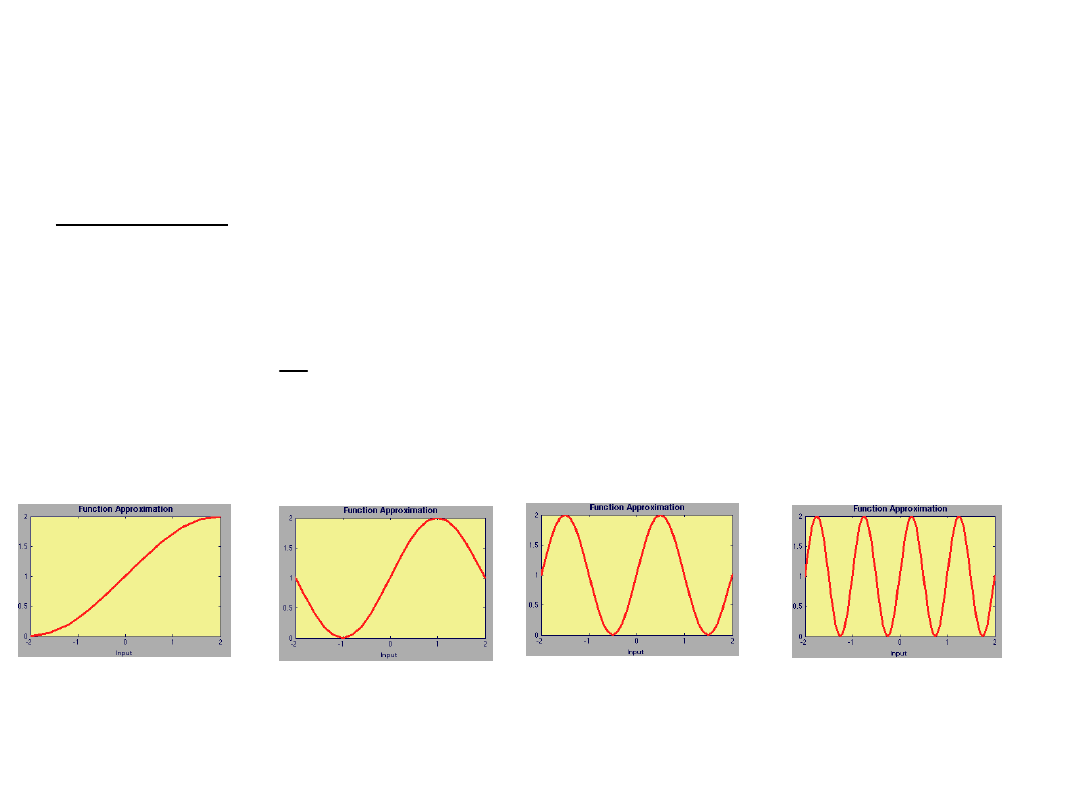
Zadanie:

Chcemy aproksymować funkcję:

nnd11fa



g(p) 1 sin(i



4

p) dla  2p2, i 1,2,4,8

i=1

i=2

i=4

i=8

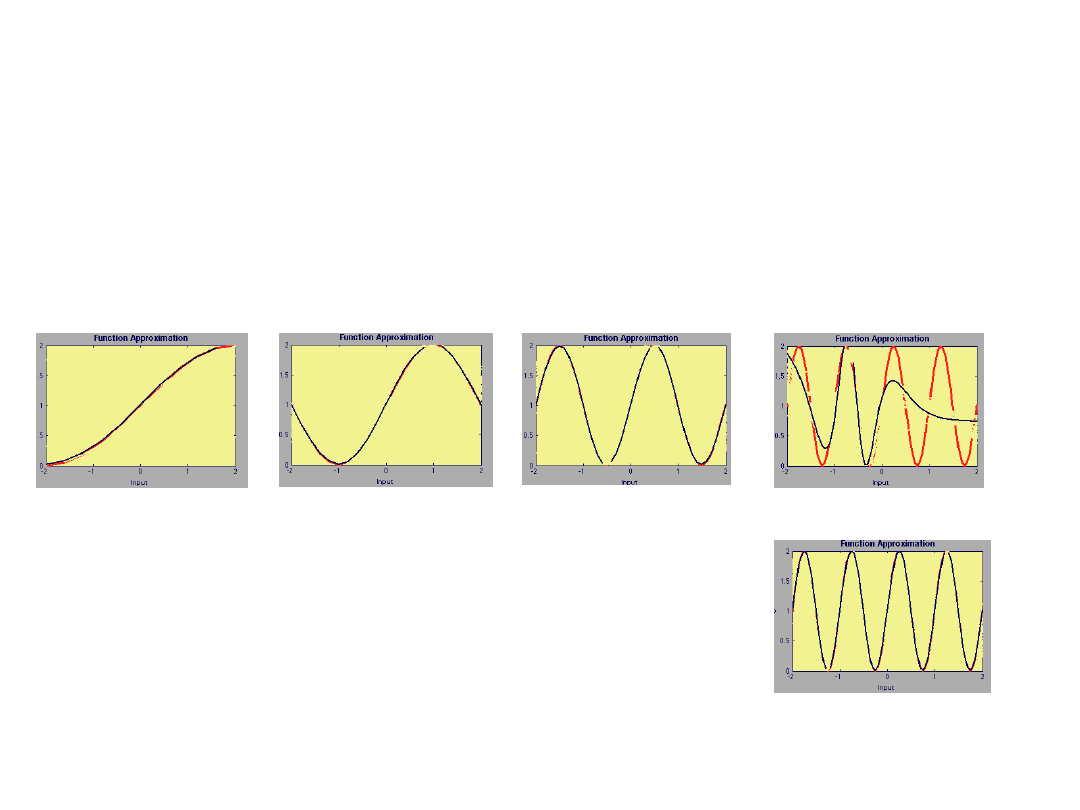
Problemy uczenia – dobór architektury

Właściwy dobór architektury
(rozmiaru) sieci

nnd11fa

i=1

i=2

i=4

i=8

Sieć 1 – 3 – 1;

logsig - linear

Sieć 1 –

6

– 1

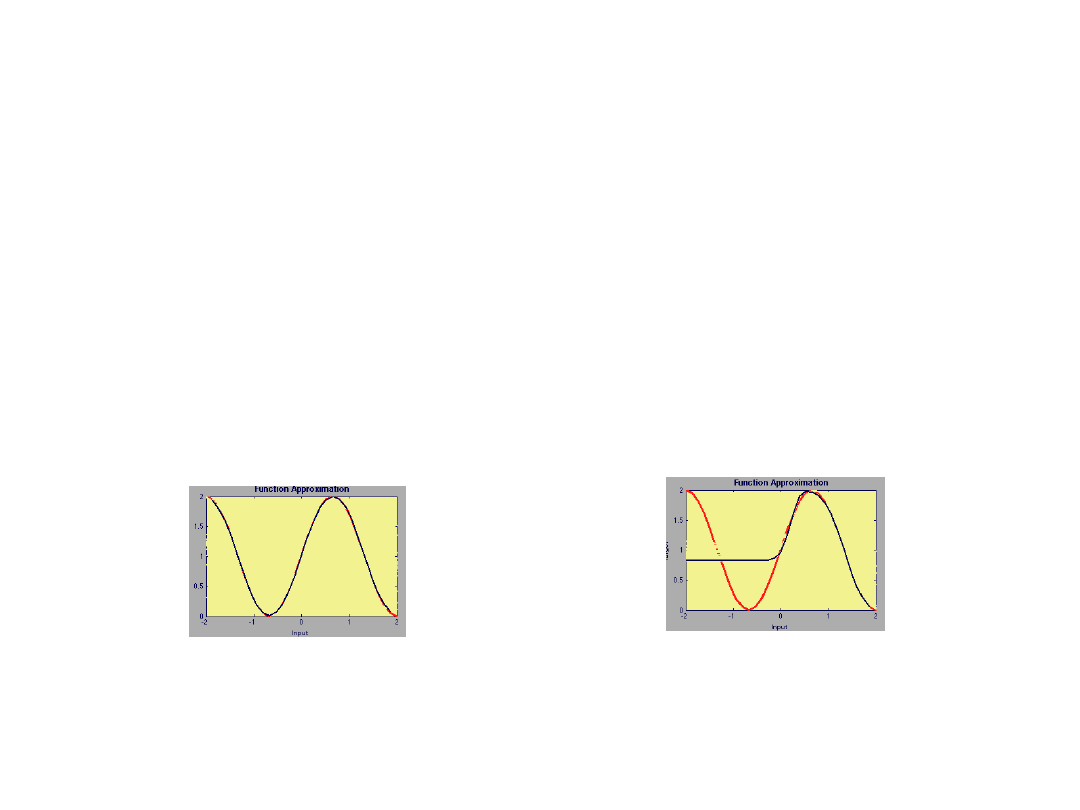
Problemy uczenia

Zbieżność

nnd11fa

Sieć: 1 – 3 – 1; logsig - linear



g(p) 1 sin(



p) dla  2p2

Funkcja aproksymowana:

a)

b)

Powód?

Minimum lokalne -punkt startowy 

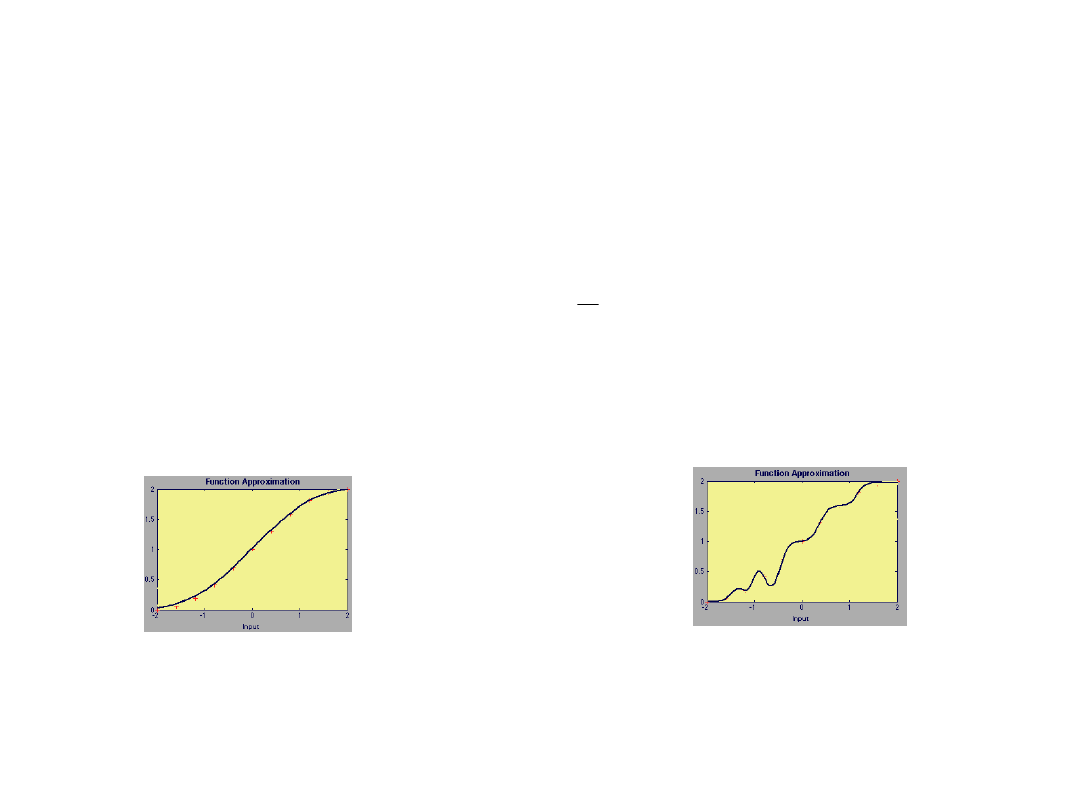
Problemy uczenia - uogólnianie

Zdolność do uogólnień

nnd11gn

Sieć: 1 – 2 – 1; logsig - linear

2

2

dla

)

4

sin(

1

)

(













p

p

p

g

Funkcja aproksymowana:

Zbiór danych uczących:

}

,

{

,

},

,

{

},

,

{

2

2

1

1

Q

Q

t

p

t

p

t

p



Zakładamy: Q=11, czyli p= -2, -1.6, -1.2, ..., 1.2, 1.6, 2

Sieć: 1 – 9 – 1; logsig - linear

Dlaczego?

7 parametrów

28 parametrów (18 wag + 10
bias)
- zbyt dużo stopni swobody
dla
11 danych uczących (za mało
danych)

Problemy uczenia

Właściwy dobór struktury (architektury)
sieci wpływa na:

• Dokładność

działania

• Czas uczenia

Skrócenie czasu uczenia:

• Rozwijanie technik heurystycznych

(optymalizacja współczynników uczenia,
zastosowanie momentum, itp.)

• Zastosowanie efektywniejszych technik

optymalizacji

Kilka uwag praktycznych

Jak konstruować sieć ?

Jaką wybrać topologię sieci?

• Ile warstw ukrytych?

• Ile neuronów w poszczególnych warstwach?

Brak jednoznacznej odpowiedzi (brak
teoretycznych podstaw)

Większość autorów opowiada się za stosowaniem

nie więcej niż dwóch warstw ukrytych (

o ile

nie ma istotnej potrzeby, zaleca się tylko
jedną warstwę ukrytą).

Ile warstw ukrytych ?

Sieci o większej liczbie warstw ukrytych uczą
się dłużej i proces uczenia jest słabiej
zbieżny.

Rozbudowanie sieci do dwóch warstw ukrytych
jest uzasadnione w zagadnieniach w których
sieć ma nauczyć się funkcji nieciągłych.

Zaleca się rozpoczynać zawsze od jednej
warstwy ukrytej.
Jeżeli pomimo zwiększenia liczby neuronów
sieć uczy się źle, wówczas należy podjąć
próbę

dodanie dodatkowej drugiej warstwy

ukrytej i

zmniejszyć jednocześnie liczbę

neuronów ukrytych.

Również i tutaj brak jednoznacznej odpowiedzi

Zbyt mała liczba neuronów w warstwie ukrytej
- mogą wystąpić trudności w uczenia sieci.

Zbyt duża liczba neuronów - wydłużenie czasu
uczenia jak również może doprowadzić do tzw.
nadmiernego dopasowania. Sieć uczy się wtedy
"na pamięć" pewnych szczegółów i zatraca
zdolność do uogólnień. Taka sieć uczy się
wprost idealnie i wiernie odwzorowuje
wartości zbioru uczącego. Jednakże wyniki
testowania sieci na danych spoza zbioru
uczącego są zazwyczaj bardzo słabe.

Ile neuronów w warstwach ukrytych ?

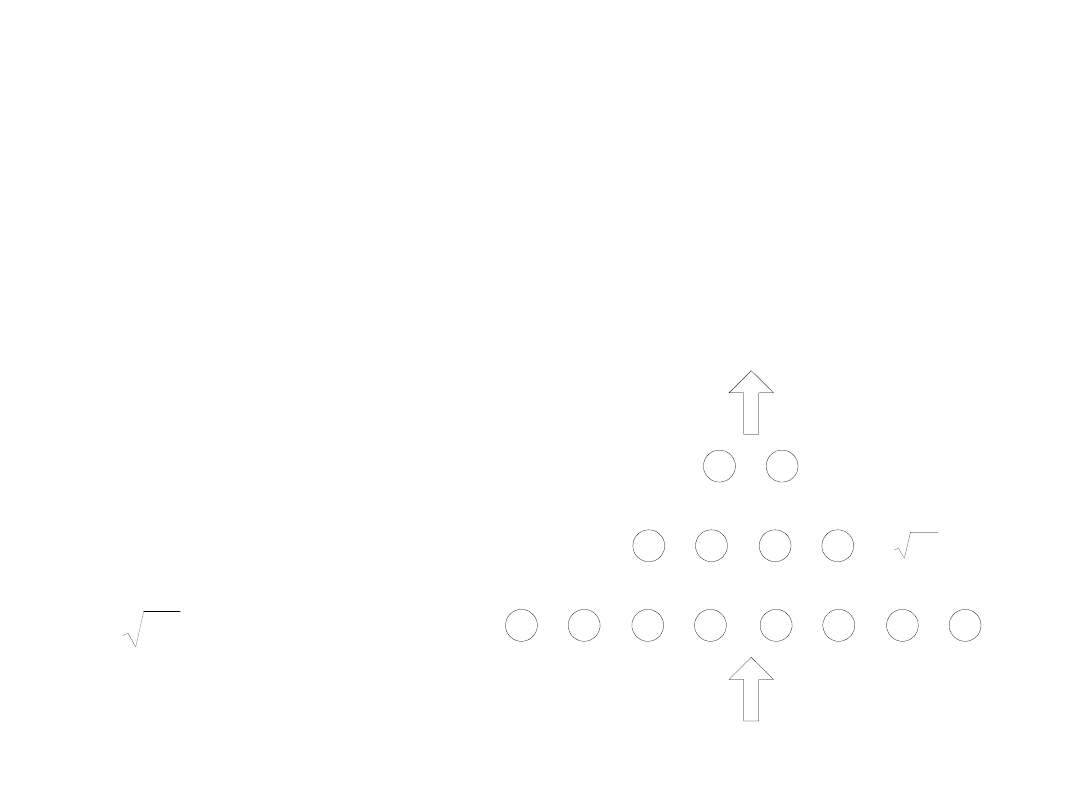
Wstępne oszacowanie liczby neuronów wg tzw.
regułę piramidy geometrycznej (liczba
neuronów maleje od wejścia do wyjścia zgodnie
z postępem geometrycznym).

kn

WE

WY

kn

n

k

Przykładowo, dla
sieci
trójwarstwowej o n
neuronach na
wejściu i k
neuronach na
wyjściu, warstwa
ukryta powinna
mieć

neuronów.

Ile neuronów w warstwach ukrytych ?

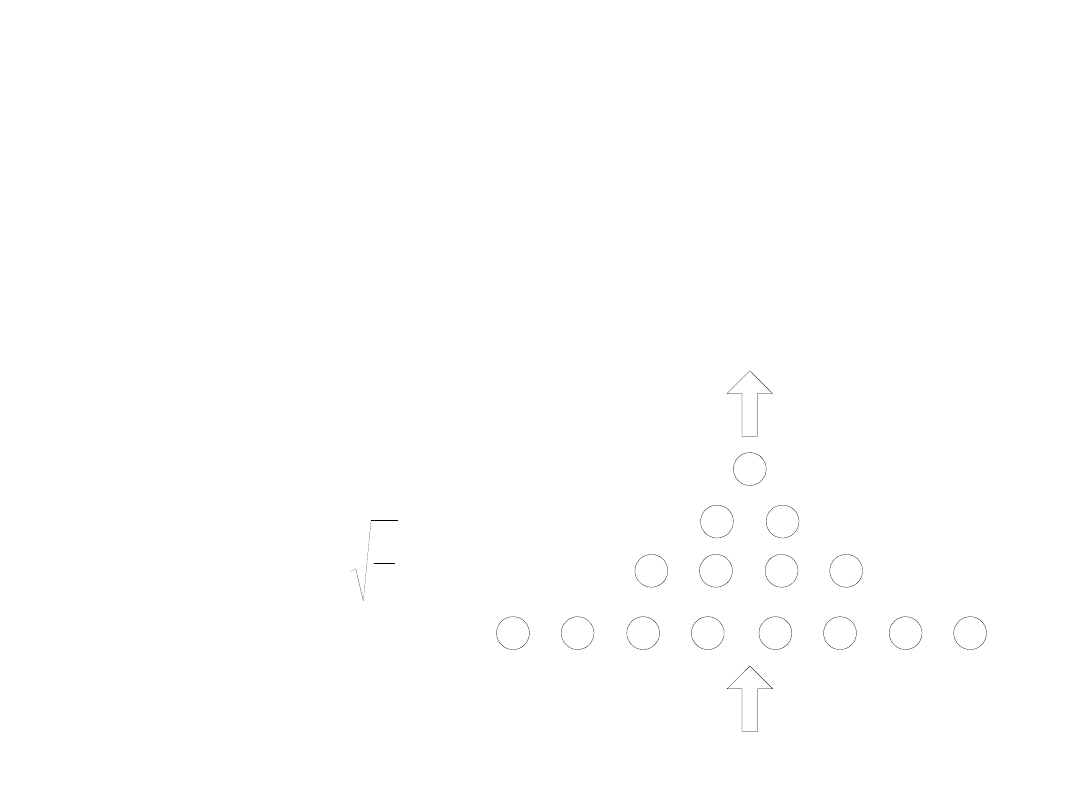
Dla sieci o czterech warstwach (dwóch
warstwach ukrytych), liczba neuronów w
poszczególnych warstwach wynosi:

WE

WY

2

kr

n

k

kr

kr

l

k

n

r

gdzie

kr

l







2

3

2

1

Ile neuronów w warstwach ukrytych ?

Wzory powyższe nie dają recepty na optymalną
topologię sieci.

Przykładowo, jeżeli sieć wykorzystywana jest do
aproksymacji złożonej funkcji jednej zmiennej,
wówczas na wejściu i wyjściu sieć ma tylko po
jednym neuronie, natomiast warstwa ukryta
zazwyczaj musi być rozbudowana.

Poszukiwanie optymalnej struktury sieci jest
zwykle czasochłonne i żmudne.

Zazwyczaj zaczynamy uczenie sieci o małej
liczbie neuronów i stopniowo ją rozbudowujemy w
miarę potrzeb. Sieć zbyt rozbudowana powoduje
utratę zdolności do uogólniania (sieć uczy się
na pamięć).

Jak konstruować sieć ?

Reasumując:

Ze względu na fakt, że brak jest
teoretycznych przesłanek do projektowania
topologii sieci, zgodnie z zaleceniami
podanymi przez Masters'a, we wstępnych
pracach nad siecią dobrze jest przestrzegać
następujących 3 zasad:

1. należy stosować tylko jedną warstwę ukrytą,
2. należy używać niewielu neuronów ukrytych,
3. należy uczyć sieć do granic możliwości.

Jak konstruować sieć ?

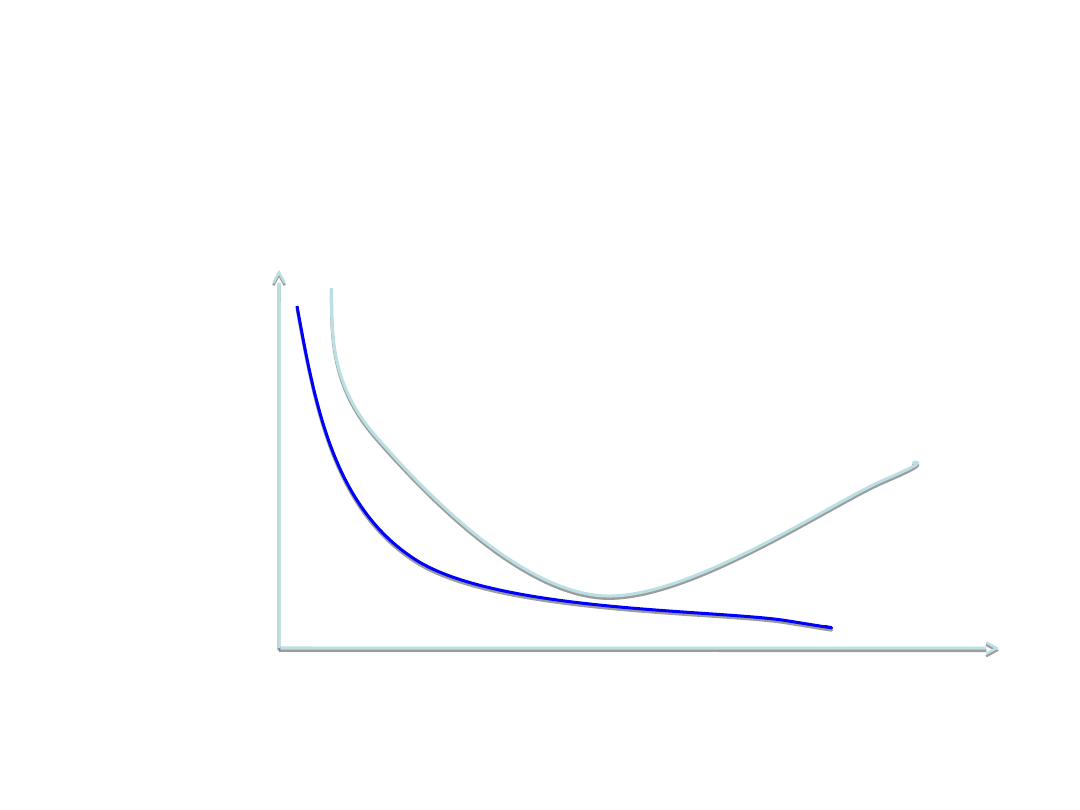
Oznaką przetrenowania jest wzrost błędu dla
danych testowych, przy malejącym błędzie
danych uczących

Jak długo uczyć sieć ?

b

ł

ą

d

l. iteracji

test

uczenie

Podstawy Sztucznej Inteligencji

Jan Kusiak

• Dla każdej próbnej liczby neuronów ukrytych

tworzymy losowe wagi początkowe i uczymy
sieć do chwili, gdy przestajemy osiągać
poprawę.

• Następnie przyjmujemy inne wartości wag

początkowych i powtarzamy proces uczenia.
Gdy nie zauważamy zmian, sieć możemy uznać
za nauczoną.

• Sprawdzamy działanie sieci przy pomocy

danych testowych. Jeżeli jakość sieci jest
wyraźnie gorsza niż na zbiorze uczącym, to:

- albo zbiór uczący jest zły (za mały

lub mało reprezentatywny)

- albo mamy za dużo neuronów ukrytych.

Sieć jest przetrenowana.

Prawidłowa procedura uczenia sieci

Podstawy Sztucznej Inteligencji

Jan Kusiak

• Ocena jakości sieci

• Zbiór danych do uczenia sieci

• Skalowanie sygnałów

• Liczebność zbioru danych uczących

• Rozkład danych w zbiorze uczącym

• Trendy danych uczących

• Sieć nie ma zdolności do ekstrapolacji

Prawidłowa procedura uczenia sieci