Podstawy Sztucznej Inteligencji

Jan Kusiak

Podstawy Sztucznej

Inteligencji

Jan Kusiak

Jak to wszystko działa?

Podstawy Sztucznej Inteligencji

Jan Kusiak

Podstawy Sztucznej

Inteligencji

Jan Kusiak

Zacznijmy od początku,

…czyli od perceptronu

Podstawy Sztucznej Inteligencji

Jan Kusiak

Podstawy Sztucznej

Inteligencji

Jan Kusiak

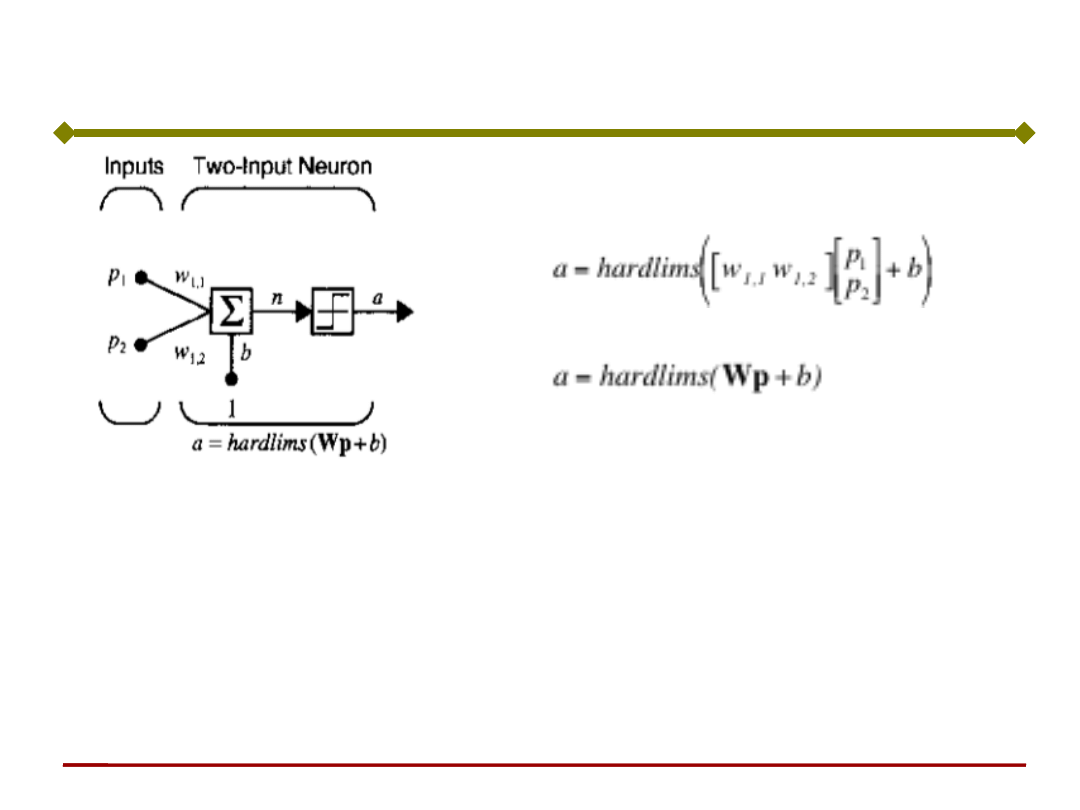
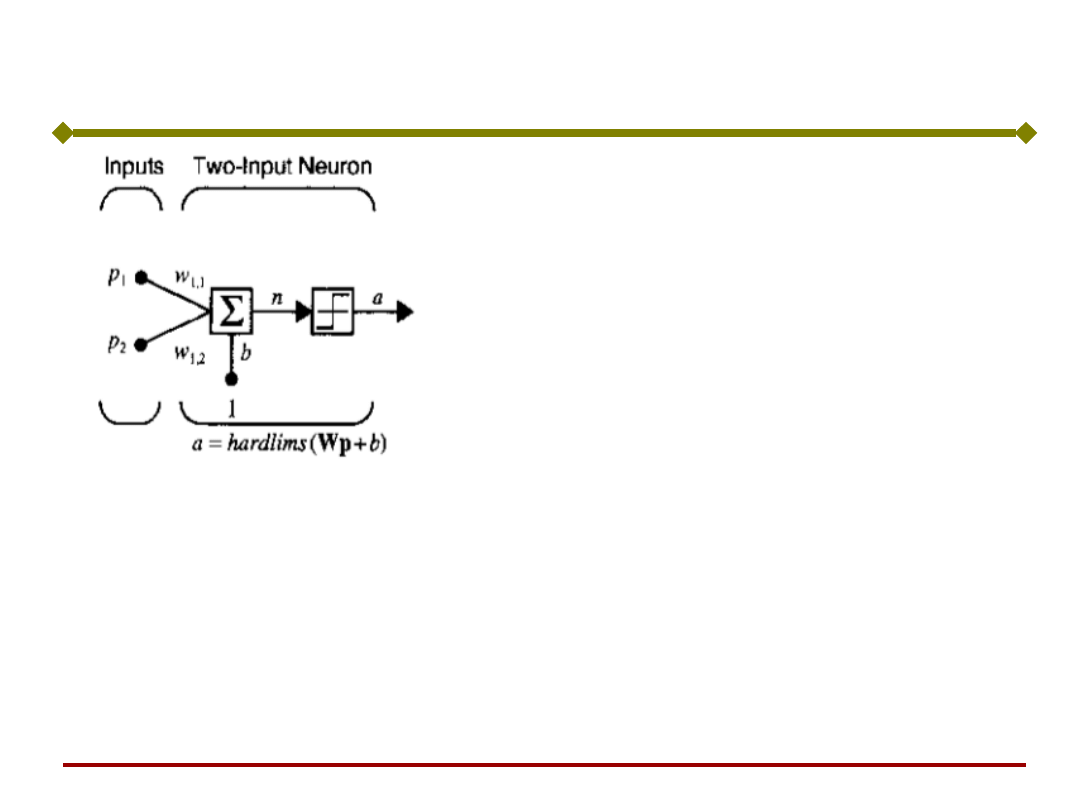
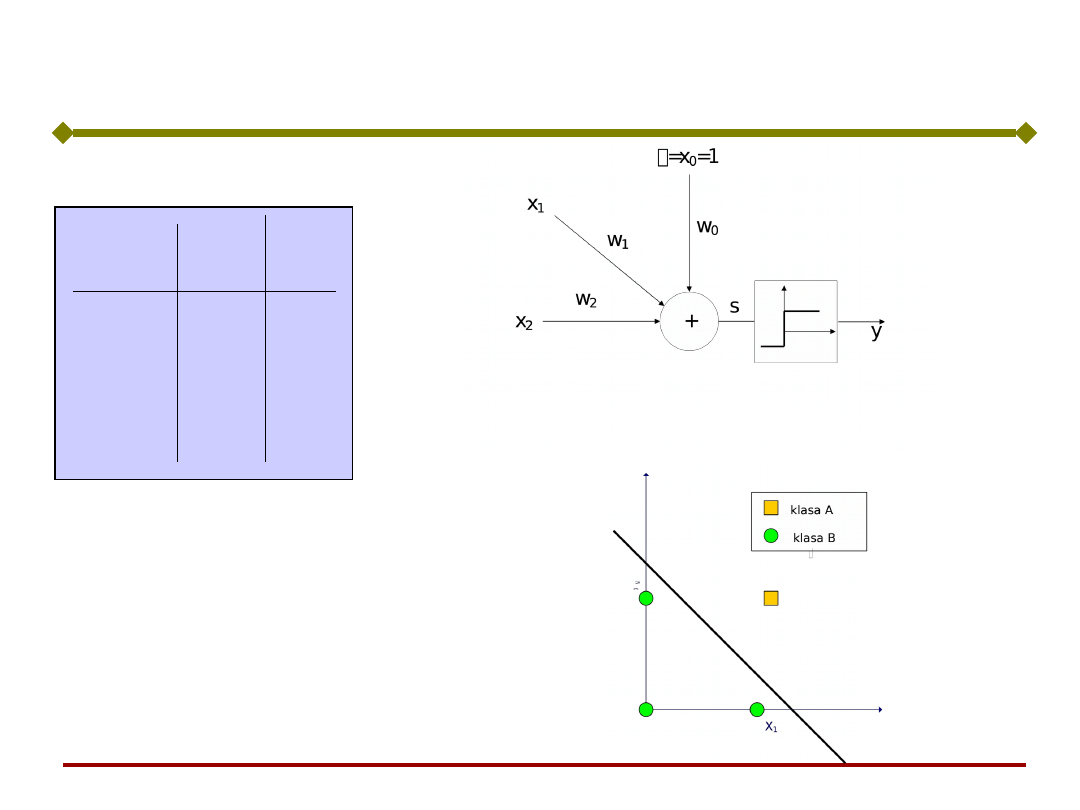
Perceptron o dwóch wejściach

Uwaga:
Binarna funkcja aktywacji nadaje
perceptronowi własności klasyfikatora
sygnałów wejściowych.

czyli:
Dzieli przestrzeń wektora wejściowego na
dwa obszary.

Podstawy Sztucznej

Inteligencji

Jan Kusiak

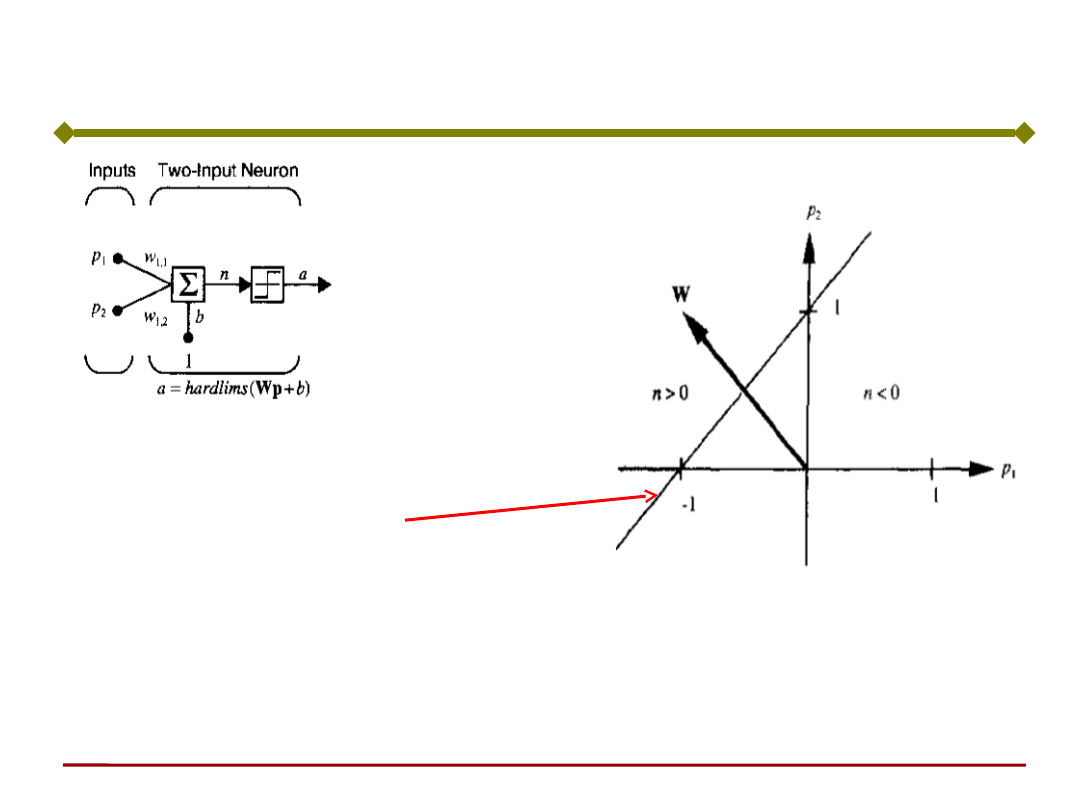
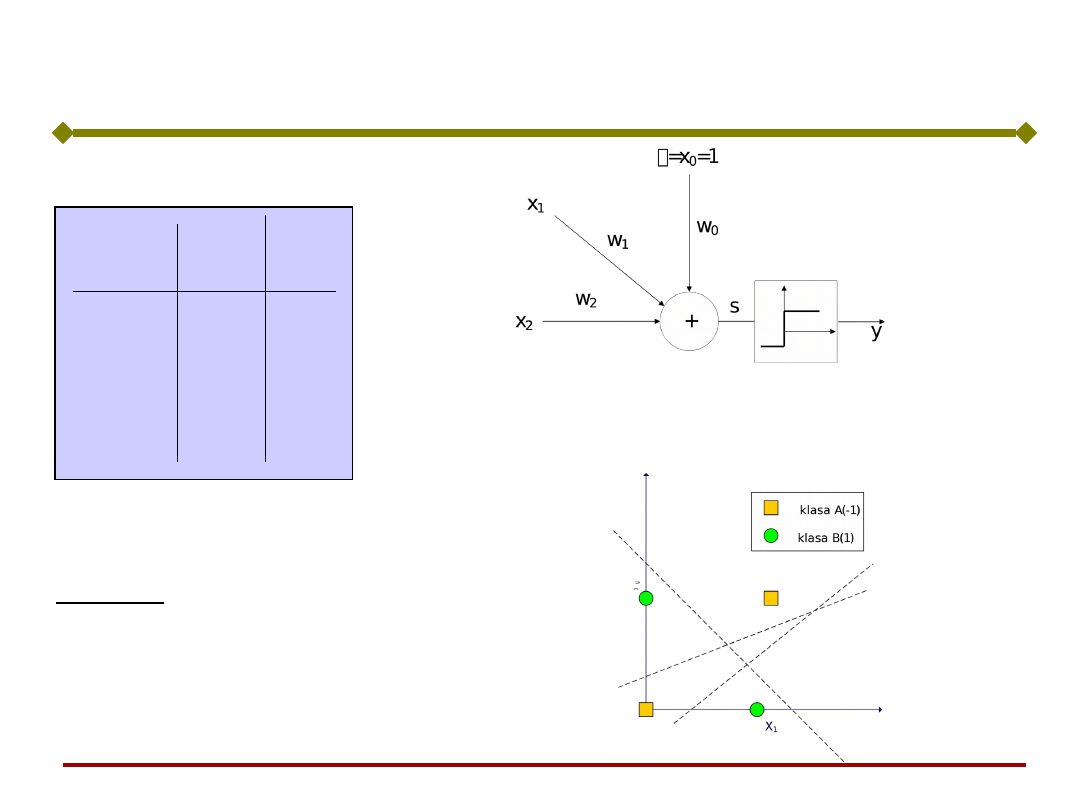
Perceptron o dwóch wejściach

b = -1

w

1,1

= -1; w

1,2

= +1

Niech

:

n = w

T

p=[-1 1]p - 1 =

0

Granica decyzyjna jest
wyznaczona przez:

Granica ta jest prostopadła do wektora wag W i
przesunięta o wartość b.

Wektor W wskazuje obszar wartości dodatnich sygnału
wyjściowego.

€

a=hardlimsw

1,1

w

1,2

[

]

p

1

p

2

⎡
⎣

⎢

⎤
⎦

⎥ +b

⎛
⎝

⎜

⎞
⎠

⎟

€

n=Wp+b=0

Gdy perceptron ma R wejść, wówczas dzieli R-
wymiarową przestrzeń wektorów wejściowych p
na dwie półprzestrzenie.

Są rozdzielone R-1- wymiarową
hiperpłaszczyzną, nazywaną granicą decyzyjną
o równaniu:

0

1









b

p

w

i

R

i

i

Podstawy Sztucznej

Inteligencji

Jan Kusiak

Perceptron (granica decyzyjna)

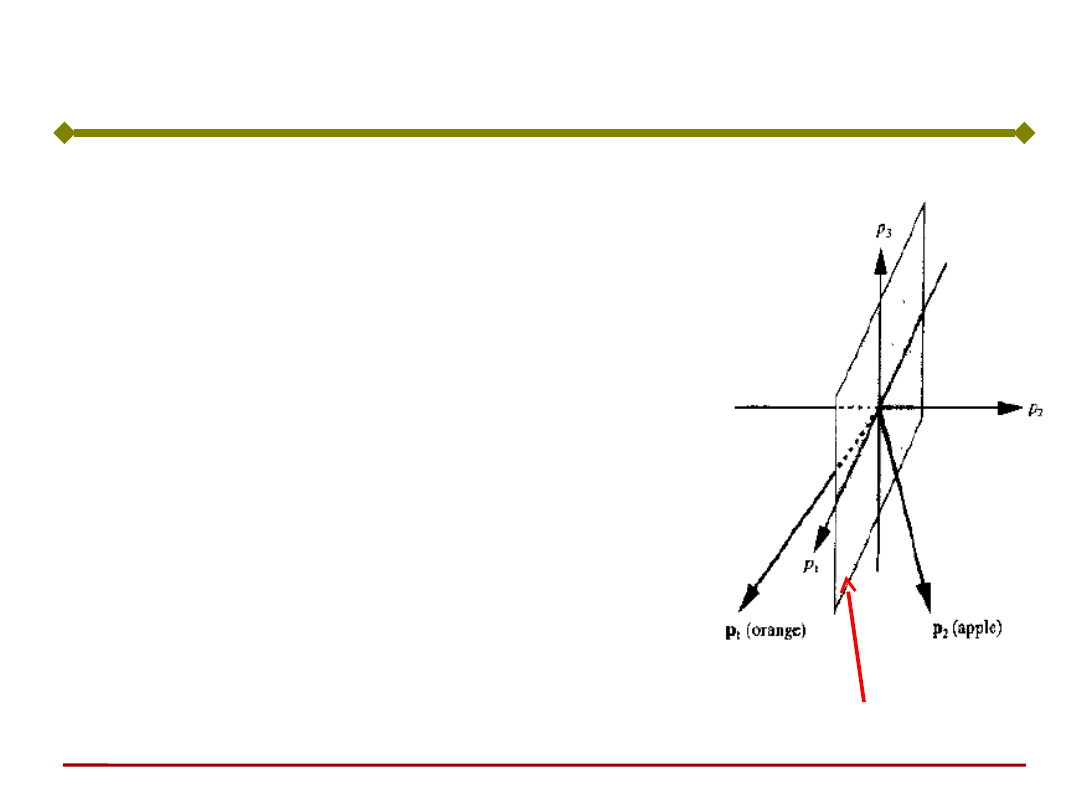
Czy perceptron można użyć do sortowania jabłek i pomarańczy?

3 sygnały wejściowe:

• p

1

- kształt,

• p

2

- tekstura skórki,

• p

3

- waga

Podstawy Sztucznej

Inteligencji

Jan Kusiak

Perceptron jako klasyfikator



p

i

 [ 1, 1]

Wzorzec pomarańczy: P

T

= [1 -1 -1]

T

Wzorzec jabłka: P

T

= [1 1 -1]

T

a = 1

a = -1

Perceptron jako prosta maszyna do sortowania
owoców.

Budowa:
1 neuron o 3 wejściach (bipolarna, binarna
funkcja aktywacji hardlims):

W = [0 1 0]
b = 0

Wzorzec pomarańczy: p

T

= [1 -1 -1]

T

;

a = hardlims(n) = harlims( [0 1 0]p + 0) =
-1

Wzorzec jabłka: p

T

= [1 1 -1]

T

a = hardlims(n) = harlims( [0 1 0]p + 0) = 1

Podstawy Sztucznej

Inteligencji

Jan Kusiak

Perceptron jako klasyfikator

Płaszczyzna decyzyjna: p

2

= 0



ahardlimsw

1,1

w

1,2

w

1,3





p

1

p

2

p

3

















 b

















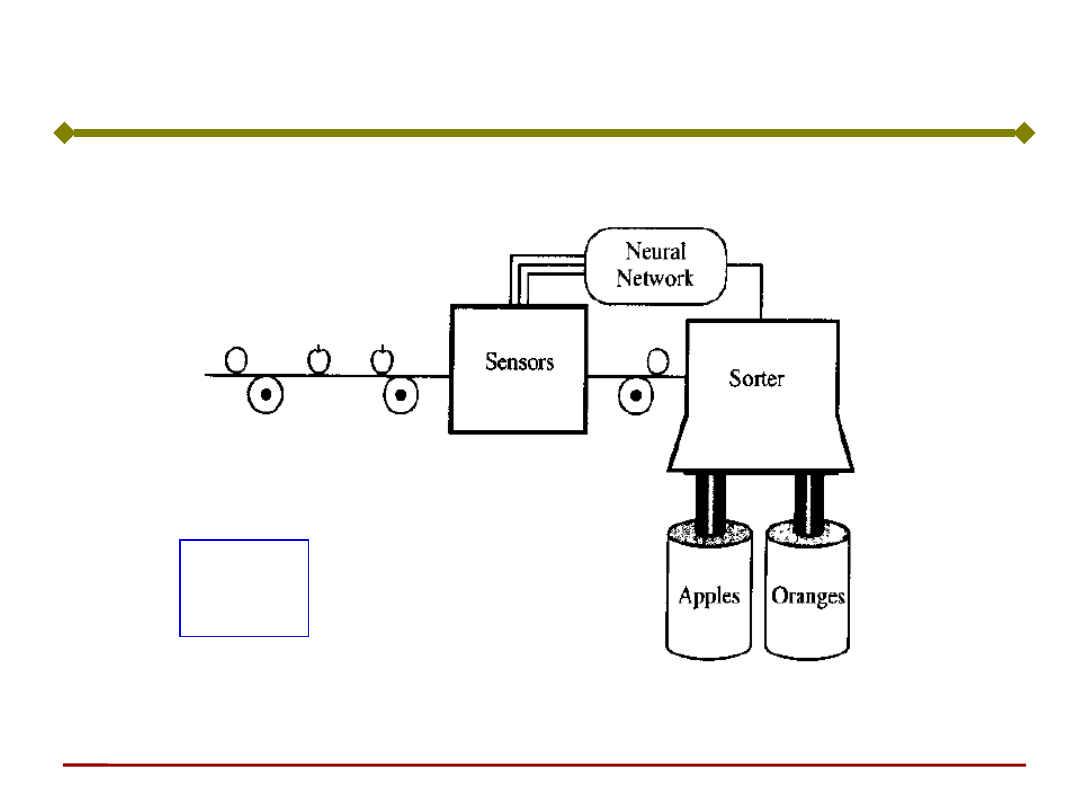
Prosta maszyna do sortowania owoców – jabłka i pomarańcze

Podstawy Sztucznej

Inteligencji

Jan Kusiak

Perceptron jako klasyfikator

nnd3
pc

Podstawy Sztucznej

Inteligencji

10

Jan Kusiak

Perceptron o dwóch wejściach - podsumowanie

Sygnał wyjściowy:

€

a =hardlims

(n) =hardlims

(Wp+b) =

=hardlims

(wT p+b)

=hardlims

(w

1,1

p

1

+w

1,2

p

2

+b) =0

Granica decyzyjna (linia na płaszczyźnie
sygnałów wejściowych) jest określona przez
wektor sygnałów wejściowych, dla których
sygnał n = 0, czyli

€

n =wT p+b=w

1,1

p

1

+w

1,2

p

2

+b=0

€

n=

Wp+b

=0

Podstawy Sztucznej

Inteligencji

13

Jan Kusiak

Perceptron o dwóch wejściach – przykład (1)

Przykład perceptronu realizującego bramkę AND
(o 2 wejściach)
Pary sygnałów WE/WY oznaczamy jako (p

i

, t

i

)

mają wartości:

















































































































1

,

1

1

,

0

,

0

1

,

0

,

1

0

,

0

,

0

0

4

4

3

3

2

2

1

1

t

t

t

t

p

p

p

p

Podstawy Sztucznej

Inteligencji

15

Jan Kusiak

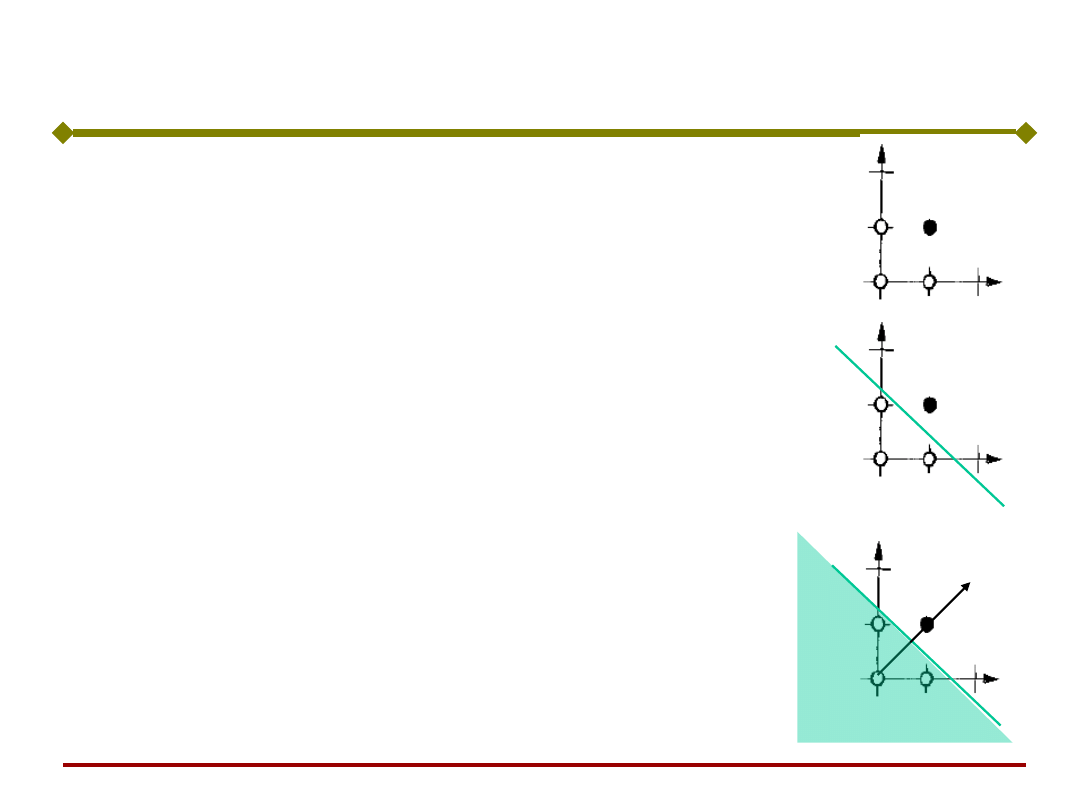
Graficznie bramkę AND przedstawia
rysunek. Czarny punkt wskazuje
sygnał wyjściowy t = 1, a puste
punkty wartość 0.

Spróbujmy wyznaczyć granicę
decyzyjną, czyli linię
oddzielającą białe punkty od
czarnych.

Następnie musimy wyznaczyć wektor
wag, który jest prostopadły do
granicy decyzyjnej. Wektor wag
może mieć dowolną długość. Niech:

€

w =

2
2

⎡
⎣

⎢

⎤
⎦

⎥

w

1

AND

Perceptron o dwóch wejściach – przykład (2)

Podstawy Sztucznej

Inteligencji

16

Jan Kusiak

Na koniec musimy wyznaczyć wartość progową b.
Określimy to wybierając dowolny punkt leżący na
linii decyzyjnej i spełniający równanie:

€

wT p+b=0

Jeżeli, przykładowo wybierzemy:





T

T

0

5

.

1



p

to:

€

wT p+b= 2 2

[

]

1.5

0

⎡
⎣

⎢

⎤
⎦

⎥

+b=3+b=0 ⇒

b=−3

Przetestujemy sieć na jednej z par sygnałów
wejściowych, np. p

2

=[0,1]

T

€

a=hardlim(

w

T

p

2

+b) =hardlim2 2

[

]

0
1

⎡
⎣

⎢

⎤
⎦

⎥ −3

⎛

⎝

⎜

⎞

⎠

⎟ =hardlim(-1)

=0

Perceptron o dwóch wejściach – przykład (3)

Podstawy Sztucznej

Inteligencji

17

Jan Kusiak

Perceptron o dwóch wejściach

Przykład granicy decyzyjnej nnd4db

Podstawy Sztucznej

Inteligencji

18

Jan Kusiak

Perceptron działa poprawnie, gdy wagi
przyjmują odpowiednią wartość,

czyli gdy

perceptron jest nauczony.

Proces uczenia wiąże się z modyfikowaniem
wag synaptycznych.

Podstawy Sztucznej

Inteligencji

Jan Kusiak

Sztuczne Sieci Neuronowe 1

Działanie perceptronu

Podstawy Sztucznej

Inteligencji

19

Jan Kusiak

Podstawy Sztucznej Inteligencji

Jan Kusiak

Jak uczyć neuron?

Podstawy Sztucznej

Inteligencji

20

Jan Kusiak

Podstawy Sztucznej Inteligencji

Jan Kusiak

Uczenie neuronu

Uczenie z nauczycielem (nadzorowane)

Na wejściu sieci pokazuje się wektor sygnałów
wejściowych, natomiast na wyjściu pokazuje się oczekiwane
wartości sygnałów wyjściowych.

Zadaniem uczenia sieci jest dokonanie takiej korekty
współczynników wagowych, aby zmniejszyć różnicę pomiędzy
oczekiwaną, a rzeczywistą odpowiedzią sieci.

Uczenie bez nauczyciela

Prezentuje się jedynie wektor sygnałów wejściowych.

Zadaniem sieci jest samodzielne utworzenie kategorii do
których będą klasyfikowane prezentowane wektory,
samodzielnie odnajdując przy tym podobieństwa pomiędzy
poszczególnymi obiektami - klasyfikacja obiektów.

Podstawy Sztucznej

Inteligencji

21

Jan Kusiak

Podstawy Sztucznej Inteligencji

Jan Kusiak

Podstawy Sztucznej

Inteligencji

Jan Kusiak

Proces uczenia polega na korygowaniu wartości
współczynników wagowych.

Uczenie neuronu

Początkowe wartości składowych wektora wag nie
mają większego znaczenia i z reguły nadaje się im
wartości losowe.

Podstawy Sztucznej

Inteligencji

22

Jan Kusiak

Podstawy Sztucznej Inteligencji

Jan Kusiak

Nadzorowane uczenie neuronu polega na tym, że
neuronowi prezentowane jest pewne zadanie z
gotowym rozwiązaniem.

Uczenie neuronu

"Nauczyciel" uczący neuron zna prawidłowe
odpowiedzi na zadane sygnały wejściowe i porównuje
je z sygnałami wyjściowymi neuronu.

Zadaniem neuronu jest rozpoznanie sygnału
wejściowego i generowanie odpowiedniego sygnału
wyjściowego. Umiejętność taką neuron zdobywa w
trakcie uczenia.

Podstawy Sztucznej

Inteligencji

23

Jan Kusiak

Podstawy Sztucznej Inteligencji

Jan Kusiak

Podstawy Sztucznej

Inteligencji

Jan Kusiak

W procesie uczenia, "nauczyciel" dysponuje określonym
ciągiem uczącym złożonym z par sygnałów wejście -
wyjście:

gdzie:
(p

i

, t

i

) - i-ta para danych uczących

p

i

- wektor sygnałów wejściowych i-tego elementu zbioru uczącego,

t

i

- oczekiwana (zadana) wartość odpowiedzi neuronu na i-ty wektor

wejścia uczącego,
Q - liczba elementów ciągu uczącego U.

Uczenie neuronu



U{(p

1

,t

1

),(p

2

,t

2

),...,(p

Q

,t

Q

)}

Korekta wag ma na celu zmniejszenie różnicy
pomiędzy oczekiwaną wartością odpowiedzi t, a
rzeczywistą odpowiedzią neuronu a.

Podstawy Sztucznej

Inteligencji

24

Jan Kusiak

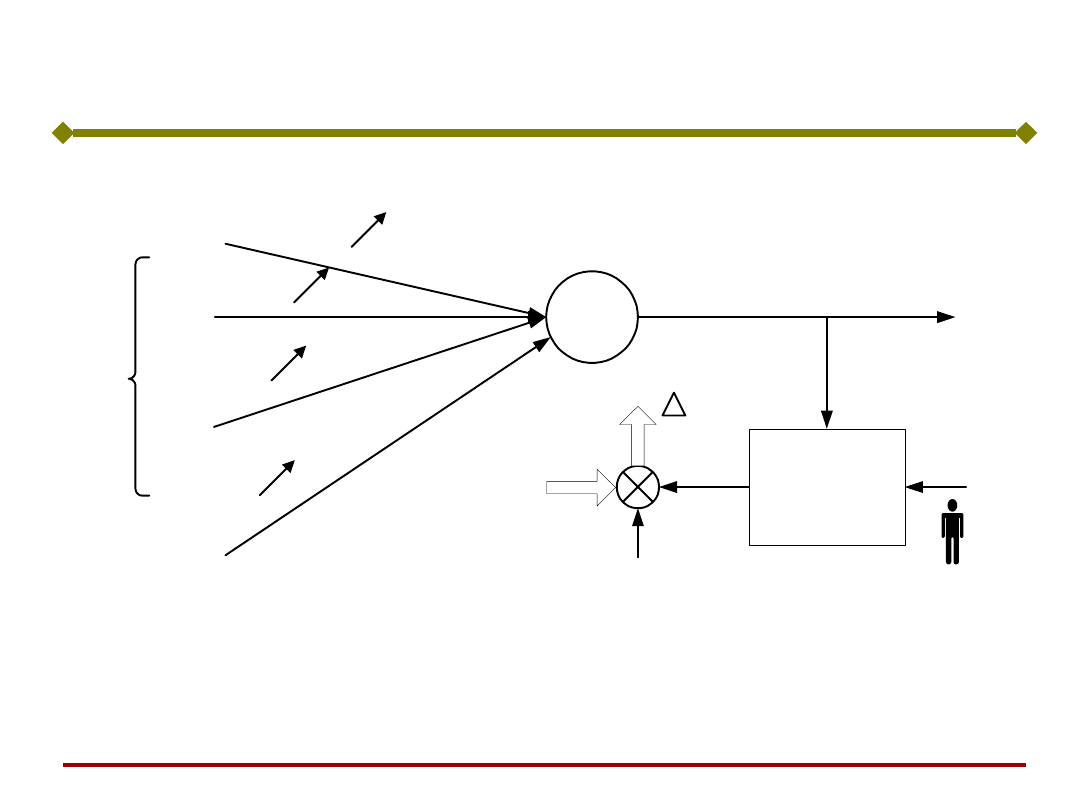
Ogólna zasada uczenia neuronu:

Wektor wag w

i

= [w

i1

, w

i2

,...,w

in

]

T

rośnie

proporcjonalnie do iloczynu sygnałów
wejściowego x i uczącego r

(Amari, Żurada).

x

1

x

2

w

i1

.

.

.
.

.

.

i-ty neuron

w

ij

w

i2

w

in

x

j

x

n

y

i

generator

sygnału

uczącego

d

i

x

w

i

x

c

r

t

i

Podstawy Sztucznej

Inteligencji

25

Jan Kusiak

c - stała uczenia c > 0, (c wpływa na szybkość
uczenia).

Wektor zmodyfikowanych wag w kolejnym kroku
czasowym k+1 wynosi więc:

€

r =r(w

i

,x,t

i

)

Sygnał uczący r jest w ogólności funkcją w

i

,

x oraz sygnału nauczyciela t

i

:

Zgodnie z ogólną regułą uczenia, przyrost
wektora w

i

w kolejnym kroku uczenia

zachodzącym w chwili k wynosi:

€

Δw

i

k

=cr(w

i

k

,x

k

,t

i

k

)x

k

€

w

i

k+1

=w

i

k

+cr(w

i

k

,x

k

,t

i

k

)x

k

Ogólna zasada uczenia neuronu:

Podstawy Sztucznej

Inteligencji

26

Jan Kusiak

Początkowa wartość składowych wektora wag nie ma
większego znaczenia. Z reguły nadaje się im wartości
losowe (nie mogą być zbyt duże, gdyż może to
spowodować ich rozbieganie się).

Ogólna zasada uczenia neuronu:

Podstawy Sztucznej

Inteligencji

27

Jan Kusiak

Podstawy Sztucznej Inteligencji

Jan Kusiak

Uczenie perceptronu

Podstawy Sztucznej

Inteligencji

28

Jan Kusiak

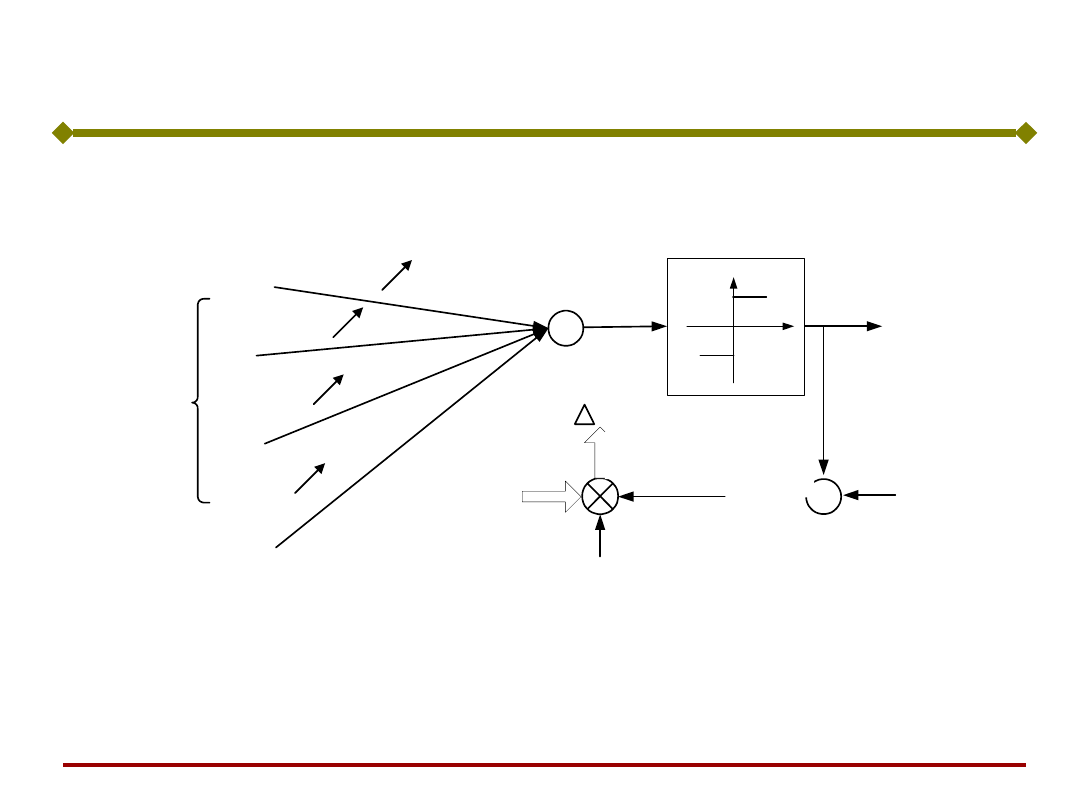
Reguła perceptronowa jest jedną z metod
uczenia nadzorowanego, stosowaną do sieci z
neuronami dyskretnymi.

Reguła uczenia perceptronowego

Sygnał uczący r jest różnicą pomiędzy
odpowiedzią pożądaną a odpowiedzią
uzyskiwaną z sieci (Rosenblatt, 1958);

€

r =t

i

−y

i

)

( x

w

sign

y

T

i



+

x

1

x

2

w

i1

.

.

.
.

.

.

w

ij

w

i2

w

in

x

j

x

n

y

i

d

i

x

w

i

x

-1

1

s

+

d

i

- y

i

+

-

c(d

i

- y

i

)x

c

s

i

t

i

c(t

i

- y

i

)x

t

i

- y

i

Podstawy Sztucznej

Inteligencji

29

Jan Kusiak

Korygowanie współczynników wag synaptycznych
(dla bipolarnej funkcji aktywacji) odbywa się
według zależności:

€

Δw=c(t−y) =c[t−sign(w

T

x)]x

Ponieważ sygnał odpowiedzi perceptronu
przyjmuje wartość albo 1, albo -1, algorytm
"doregulowania" wag redukuje się do postaci:

przy czym znak plus dotyczy przypadku, gdy
t

i

= 1 zaś minus w przypadku przeciwnym.

cx

w

i

2







Reguła uczenia perceptronowego

Dostrojenie wag następuje tylko wtedy,
kiedy występuje błąd odwzorowania przez
neuron.

Podstawy Sztucznej

Inteligencji

30

Jan Kusiak

1. Wybieramy losowo początkowe wartości wag.
2. Podajemy na wejście neuronu wektor uczący

x=x(τ)=[x

0

(τ), x

1

(τ),..., x

n

(τ)]

T

,

τ=1,2,....

3. Obliczenie wartości wyjściowej perceptronu

y.

4. Porównanie wartości wyjściowej y(τ) z

wartością wzorcową (uczącą) t=t(x(τ)).

5. Modyfikacja wag:

w

i

(τ+1) = w

i

(τ) + (t – y)x

i

(τ)

6. Powrót do punktu 2.

Algorytm uczenia perceptronu

Algorytm powtarzany jest dopóty, dopóki błąd
na wyjściu nie będzie mniejszy od
założonego, dla wszystkich wektorów ciągu
uczącego.

(Warunek: dane uczące reprezentują klasy

liniowo separowalne

)

Podstawy Sztucznej

Inteligencji

32

Jan Kusiak

Liniowa separowalność

Definicja. Dwa zbiory
punktów A i B z n
wymiarowej przestrzeni
wejściowej s są
liniowo separowalne
jeżeli istnieje n + 1
wartości w

0

, . . . ,w

n

takich,
że dla każdego punktu
x A zachodzi:







n

i

i

i

w

x

w

1

0

a dla każdego punktu x B zachodzi:







n

i

i

i

w

x

w

1

0

B

A

x

2

X

1

Podstawy Sztucznej

Inteligencji

33

Jan Kusiak

Liniowa separowalność - przykład

Funkcja logiczna AND:

€

y = f (s) =sgnw

0

+w

1

x

1

+w

2

x

2

(

)

x

1

x

2

Y

0 0 -1
0 1 -1
1 0 -1
1 1 1

Podstawy Sztucznej

Inteligencji

34

Jan Kusiak

Liniowo nieseparowalna funkcja - przykład

Funkcja logiczna XOR:

x

1

x

2

Y

0 0 -1
0 1 1
1 0 1
1 1 -1

Uwaga: Perceptron nie
może się
nauczyć funkcji liniowo
nieseparowalnej (ale
może to zrobić sieć)

€

y = f (s) =sgnw

0

+w

1

x

1

+w

2

x

2

(

)

Podstawy Sztucznej

Inteligencji

35

Jan Kusiak

Przykład uczenia perceptronu:

Początkowe wartości wag: w

1

= [1, -1, 0, 0.5]

T

(indeks górny oznacza numer kroku uczenia).
Stała uczenia przyjmuje wartość
c = 0.1.

Lp

.

x

1

x

2

x

3

x

4

t

1

1

-1

0

-
1

-
1

2

0

1.

5

-

0.

5

-
1

-
1

3

-
1

1

0.

5

1

1

Zbiór uczący składa się z następujących wartości:

Podstawy Sztucznej

Inteligencji

36

Jan Kusiak

Krok 1: Na wejściu
prezentacja
pierwszego sygnału
uczącego x

1

:

5

.

1

1

0

1

1

]

5

.

0

,

0

,

1

,

1

[

)

(

1

1





































x

w

s

T

Przykład uczenia perceptronu:

Ponieważ sygnał wyjściowy y

1

= sign(s

1

) =

sign(1.5) = 1 jest różny od sygnału uczącego t

1

= -1, musi nastąpić korekcja współczynników
wagowych. Nowy wektor wag obliczony zostaje
zgodnie z regułą perceptronową:































































































7

.

0

0

8

.

0

8

.

0

1

0

1

1

2

.

0

5

.

0

0

1

1

)

1

1

(

1

.

0

1

1

2

x

w

w

Podstawy Sztucznej

Inteligencji

37

Jan Kusiak

Krok 2: Na wejściu prezentacja kolejnego,
drugiego sygnału uczącego x

2

:

Ponieważ sygnał wyjściowy y

2

= sign(s

2

) =

sign(-1.1) = -1 jest zgodny z sygnałem
uczącym t

2

= -1, nie następuje korekcja wag i

w

3

= w

2

.

1

.

1

1

5

.

0

5

.

1

0

]

7

.

0

0

8

.

0

8

.

0

[

)

(

2

2

2







































x

w

s

T

Podstawy Sztucznej

Inteligencji

38

Jan Kusiak

Krok 3: Na wejściu prezentacja kolejnego,
trzeciego sygnału uczącego x

3

:

Sygnał wyjściowy y

3

= sgn(s

3

) = sgn(-2.3) = -1

jest różny od wartości sygnału uczącego d

3

= 1,

musi nastąpić korekcja wag. Skorygowany wektor
wag przyjmuje wartość:

3

.

2

1

5

.

0

1

1

]

7

.

0

0

8

.

0

8

.

0

[

)

(

3

3

3







































x

w

s

T





























































































5

.

0

1

.

0

6

.

0

6

.

0

1

5

.

0

1

1

2

.

0

7

.

0

0

8

.

0

8

.

0

)

1

1

(

1

.

0

3

3

4

x

w

w

Podstawy Sztucznej

Inteligencji

39

Jan Kusiak

Ponieważ zbiór uczący składa się z 3
prezentacji, pierwszy cykl uczenia na tym się
kończy.

Błąd uczenia perceptronu trudno jest oszacować
z uwagi na binarne wartości sygnału
wyjściowego. Dlatego jakość wytrenowania można
ocenić obserwując sygnał pobudzenia s.
Spróbujmy obliczyć wartość pobudzenia s

4

po

podaniu sygnału x

1

na wejście nauczonego w

powyższy sposób perceptronu. Sygnał pobudzenia
przyjmie wartość:

i jest znacznie bliższy wartości ujemnej
sygnału oczekiwanego, niż to miało miejsce na
początku uczenia (wtedy s

4

= 2.5).

Przeprowadzenie kolejnego cyklu uczenie
pozwoli na zmniejszenie błędu uczenia.

7

.

0

)

(

1

4

2





x

w

s

T