Podstawy Sztucznej Inteligencji

Jan Kusiak

Sztuczne Sieci Neuronowe 

Uczenie 
bez nauczyciela

Podstawy Sztucznej Inteligencji

Jan Kusiak

Sztuczne Sieci Neuronowe 

W procesie uczenia z nauczycielem, dla nowych 
wartości sygnałów wejściowych nauczyciel 
podpowiada pożądaną odpowiedź. Błąd odpowiedzi 
służy do korygowania wag sieci. 

Uczenie bez 
nauczyciela

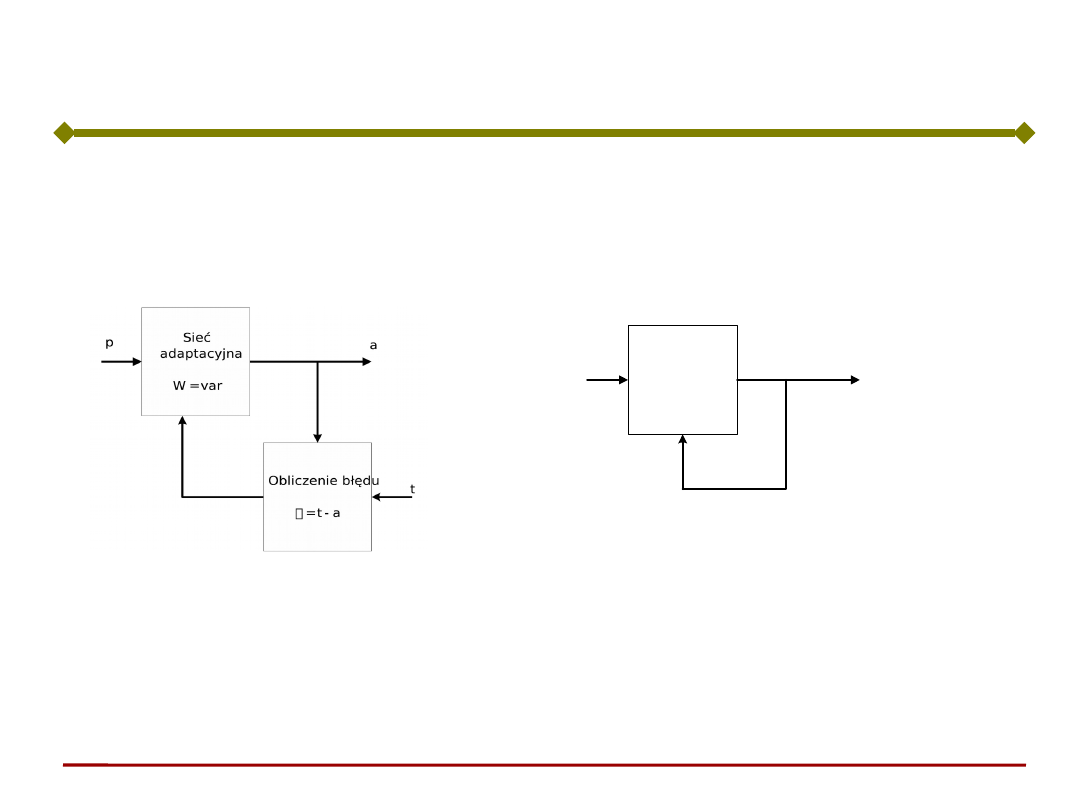
Podczas uczenia bez nauczyciela, pożądana 
odpowiedź nie jest znana. 
Sieć sama musi uczyć się poprzez analizę reakcji na 
pobudzenia 
(o których naturze wie mało albo nic).

Sieć 

adaptacyjna

W = var

p

a

Podstawy Sztucznej Inteligencji

Jan Kusiak

Sztuczne Sieci Neuronowe 

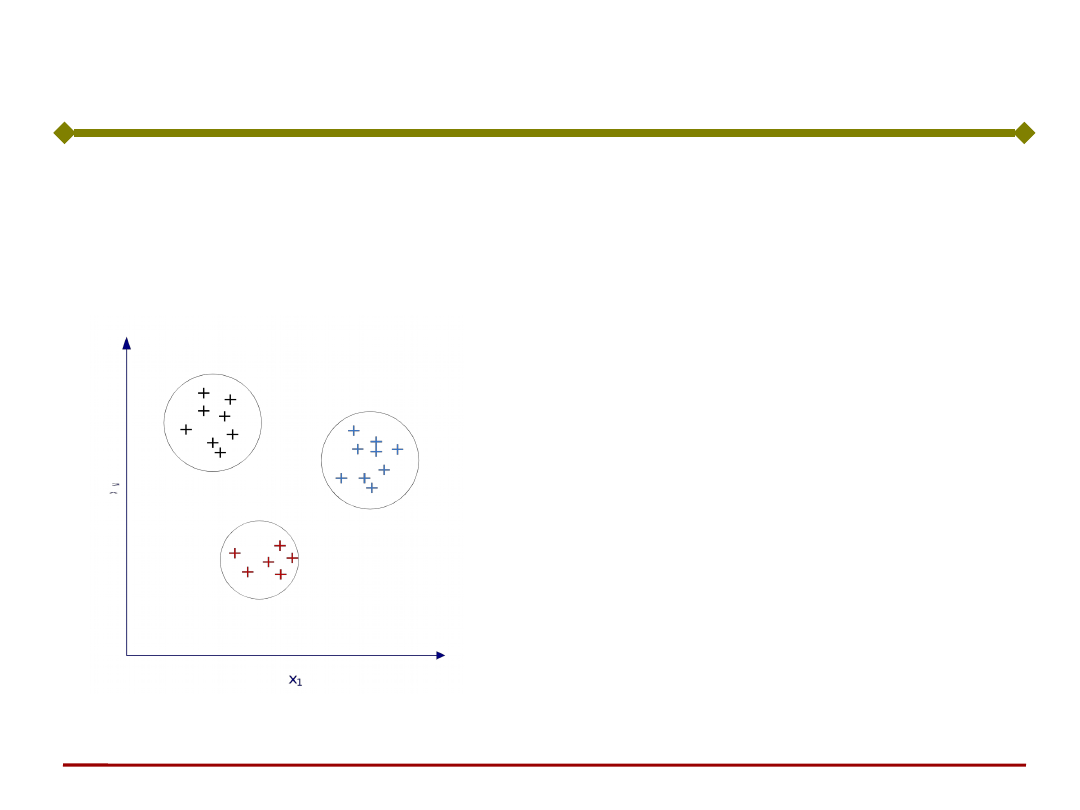
Przykładowo, samouczenie może doprowadzić do 
znalezienia granic między klasami obrazów 
wejściowych

Sieć uczy się rozpoznawać 
cechy wspólne sygnałów 
wejściowych bez 
nauczyciela. 

Zbiór danych wejściowych 
musi być wystarczająco 
liczny, by sieć mogła sama 
znaleźć klasy obiektów 
(nadmiarowość danych 
wejściowych).

Uczenie bez 
nauczyciela

Podstawy Sztucznej Inteligencji

Jan Kusiak

Sztuczne Sieci Neuronowe 

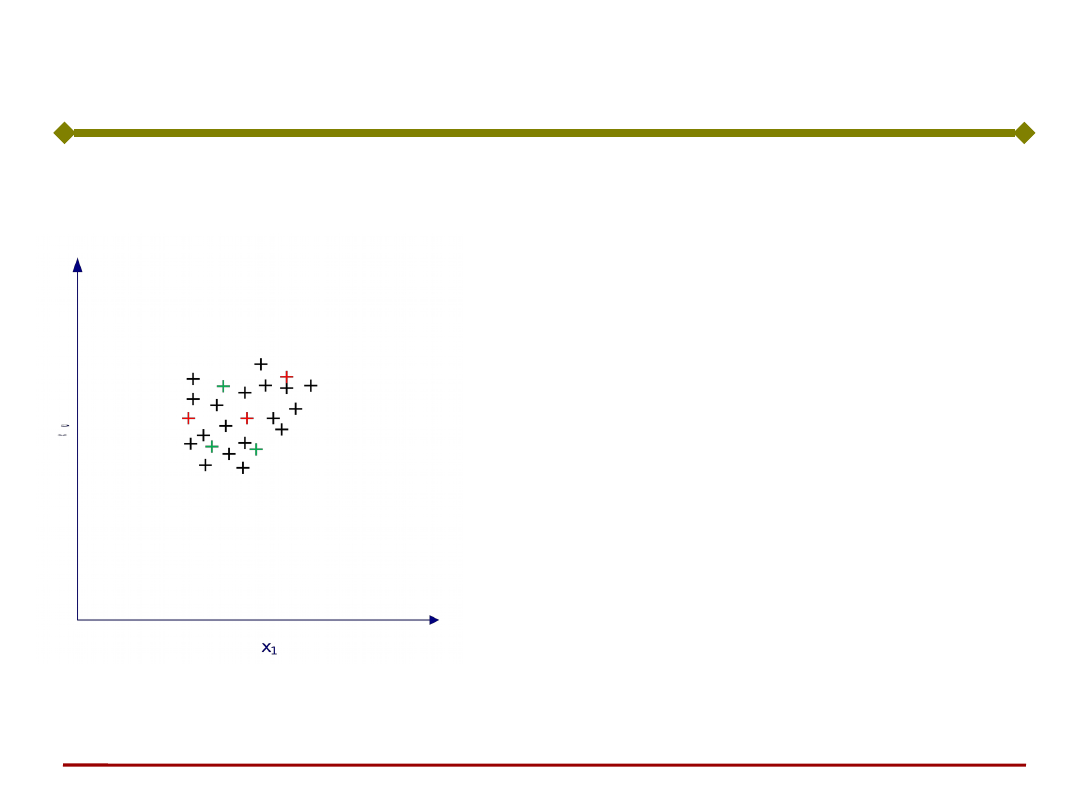
Istnieją sytuacje, gdy sieć 
nie może się sama nauczyć, 
bez nauczyciela lub bez 
dodatkowej informacji o 
analizowanym problemie. 

Uczenie bez 
nauczyciela

Podstawy Sztucznej Inteligencji

Jan Kusiak

Sztuczne Sieci Neuronowe 

Uczenie „bez nauczyciela” jest możliwe, gdy mamy 
nadmiarowość danych wejściowych.

Uczenie bez nauczyciela

Od struktury sieci zależy rodzaj rozwiązywanego 
przez nią zadania. Wyróżnić można następujące 
zadania:

Podstawy Sztucznej Inteligencji

Jan Kusiak

Sztuczne Sieci Neuronowe 

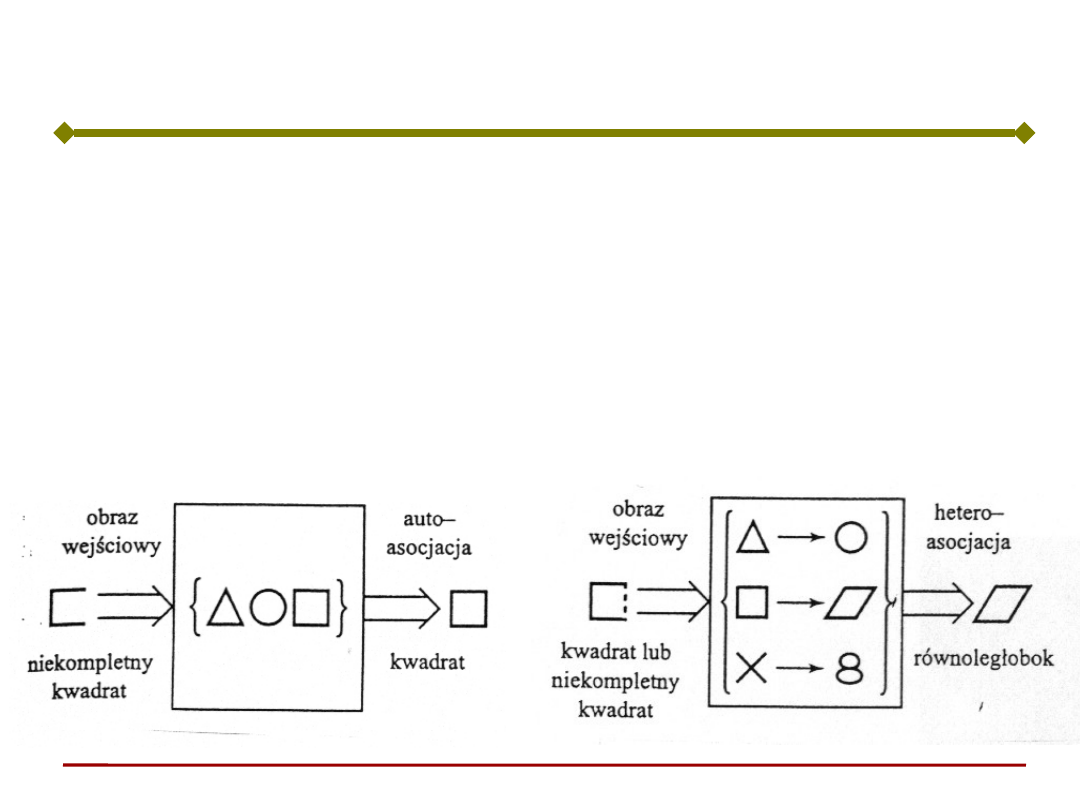
Kojarzenie (analiza podobieństwa). Pojedyncze 
wyjście sieci informuje, na ile podobny jest obraz na 
wejściu (może być niekompletny) do obrazu 
uśrednionego dotychczasowych prezentacji (obrazu 
zapamiętanego). Dwie możliwości kojarzenia:

- heteroasocjacja

– autoasocjacja

Kojarzenie 

Podstawy Sztucznej Inteligencji

Jan Kusiak

Sztuczne Sieci Neuronowe 

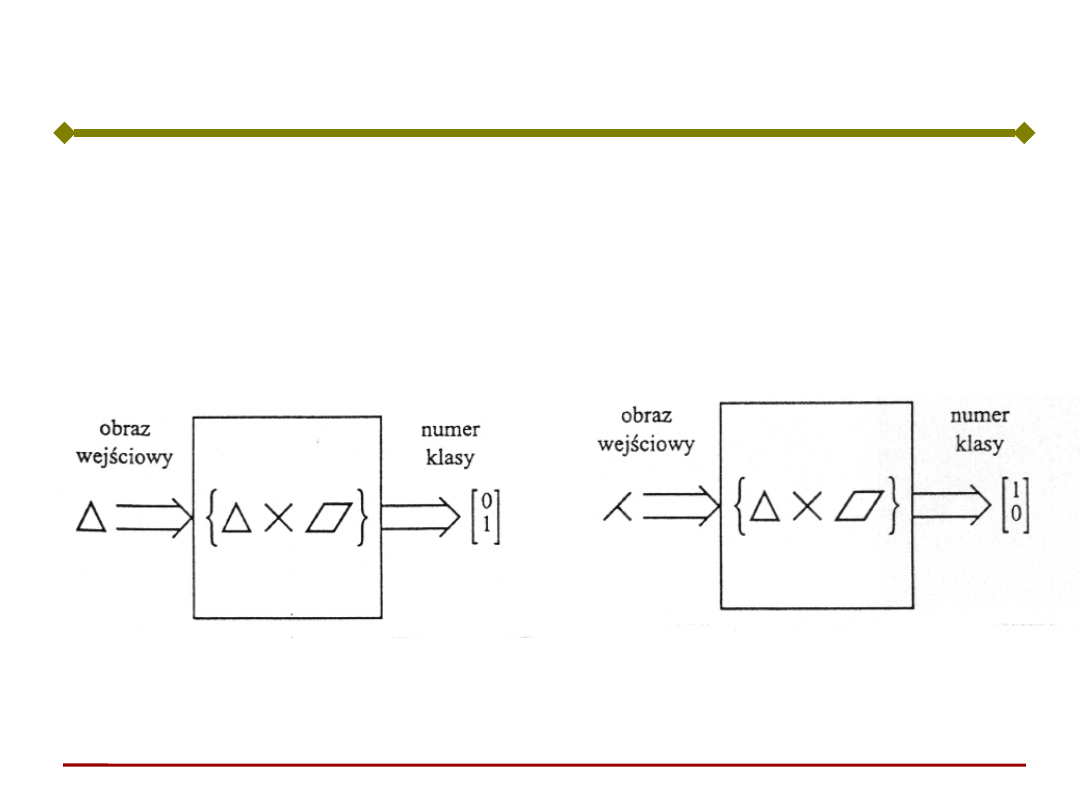
Klasyfikacja. Wyjście wieloelementowe o wartościach 
binarnych. 
Przy prezentacji obrazu uaktywnia się tylko jeden 
element wyjściowy. 
Obraz wejściowy zostaje przyporządkowany określonej 
klasie reprezentowanej przez aktywny element.

Zadaniem procesu uczenia jest podział wzorców 
uczących na klasy obrazów zbliżonych do siebie i 
przyporządkowanie każdej klasie osobnego elementu 
wyjściowego

- rozpoznawanie

- klasyfikacja

Klasyfikacja

Podstawy Sztucznej Inteligencji

Jan Kusiak

Sztuczne Sieci Neuronowe 

Tworzenie map cech. Elementy warstwy wyjściowej są 
geometrycznie uporządkowane (np. w postaci 
tablicy/kraty dwuwymiarowej). Podczas prezentacji 
obrazu wejściowego uaktywnia się tylko jedno wyjście. 
Idea jest taka, aby podobne obrazy wejściowe 
generowały aktywność bliskich geometrycznie 
elementów wyjściowych. Warstwa wyjściowa jest więc 
swego rodzaju mapą topograficzną obrazu wejściowego.

Tworzenie map cech

Podstawy Sztucznej Inteligencji

Jan Kusiak

Sztuczne Sieci Neuronowe 

Algorytmy uczenia bez 
nauczyciela

Podstawy Sztucznej Inteligencji

Jan Kusiak

Sztuczne Sieci Neuronowe 

Reguła Hebba (1949) oparta jest na doświadczeniu 
Pawłowa (odruch Pawłowa).

OB - odruch bezwarunkowy,
OW - odruch warunkowy,
BB - bodziec bezwarunkowy,
BW - bodziec warunkowy.

Reguła Hebba

pokarm (BB)

ślinienie (OB)

pokarm (BB) + dzwonek 

(BW)

ślinienie (OW)

dzwonek (BW)

ślinienie (OW)

Podstawy Sztucznej Inteligencji

Jan Kusiak

Sztuczne Sieci Neuronowe 

Jeżeli akson komórki A bierze systematycznie 
udział w pobudzaniu komórki B powodującym jej 
aktywację, to wywołuje to zmianę metaboliczną w 
jednej lub w obu komórkach, prowadzącą do 
wzrostu skuteczności pobudzania B przez A 

Zakłada wzmacnianie połączeń pomiędzy źródłami 
silnych sygnałów i osłabianie połączeń pomiędzy 
źródłami sygnałów słabych. 

A

B

y

A

y

B

Reguła (model neuronu) Hebba 

(1949)

Podstawy Sztucznej Inteligencji

Jan Kusiak

Sztuczne Sieci Neuronowe 

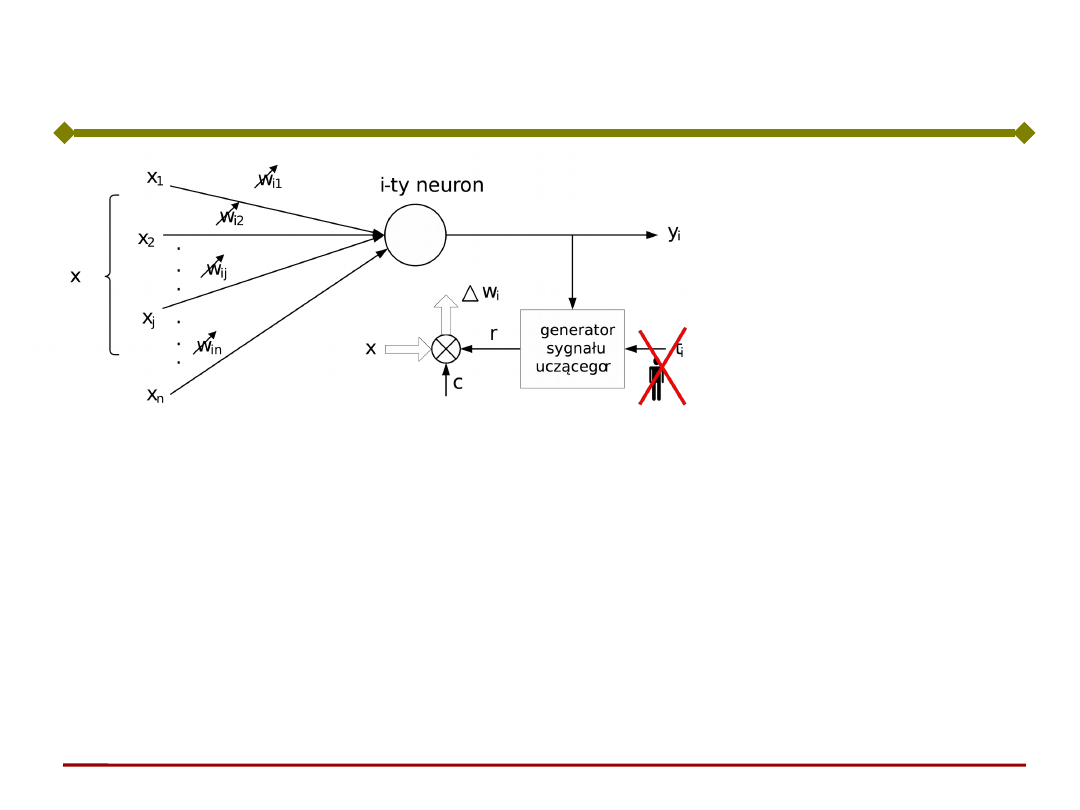
Sygnałem uczącym jest po prostu sygnał wyjściowy 
neuronu:

)

(

x

w

T

i

i

f

y

r





Korekta wektora wag:

x

x

w

x

w

)

(

T

i

i

i

cf

cy 





Reguła Hebba

x

w

w

w

w

i

i

i

i

i

cy

k

k

k













)

(

)

(

)

1

(

Reguła uczenia 
bez nauczyciela

Podstawy Sztucznej Inteligencji

Jan Kusiak

Sztuczne Sieci Neuronowe 

Z reguły tej wynika, że dodatnia wartość składnika 
korelacyjnego y

i

x

j

 powoduje wzrost wagi w

ij

, a w 

konsekwencji silniejszą reakcję neuronu przy kolejnej 
prezentacji tego samego obrazu wejściowego.

Często powtarzające się obrazy wejściowe dają więc 
silniejsza odpowiedź na wyjściu. 

Reguła Hebba

Jest praktyczną realizacją reguły neurobiologii 
(odruchu Pawłowa).  

Regułę uczenia Hebba nazywa się także niekiedy 
uczeniem korelacyjnym (“correlation learning”). 
Zmierza do takiego dopasowania wag aby uzyskać 
najlepszą  korelację pomiędzy sygnałami 
wejściowymi, a zapamiętanym w formie wartości wag 
“wzorcem sygnału”, na który określony neuron ma 
reagować. 

Podstawy Sztucznej Inteligencji

Jan Kusiak

Sztuczne Sieci Neuronowe 

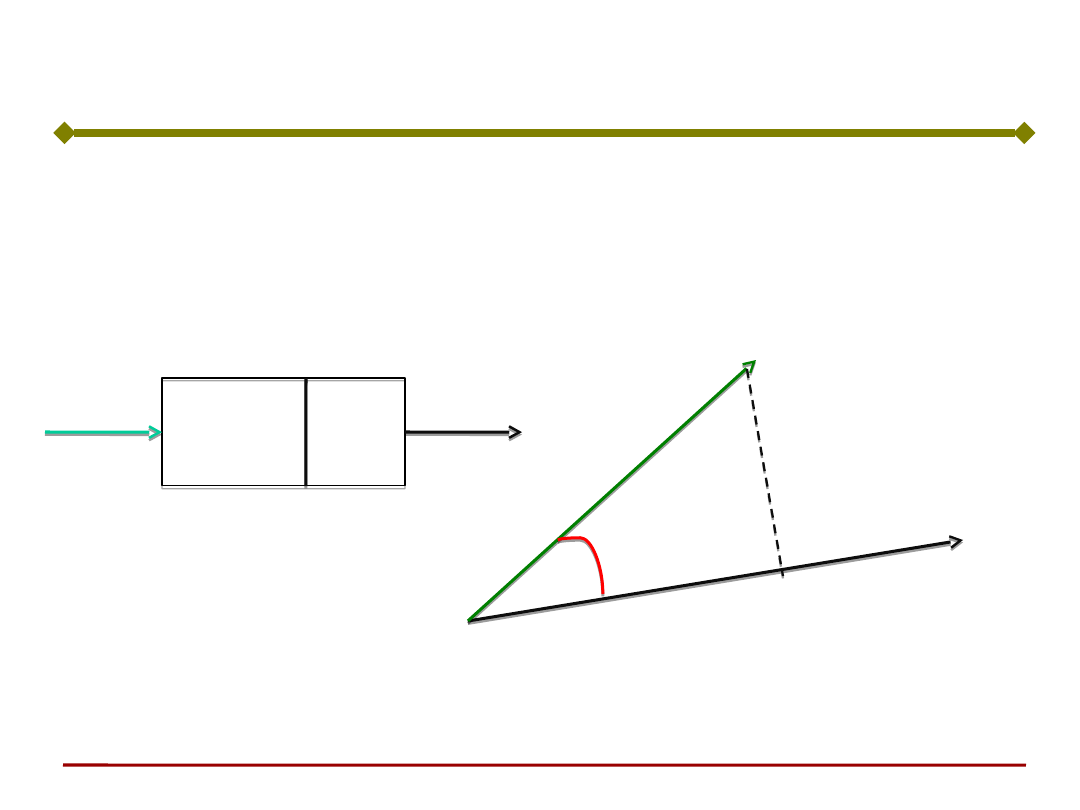
Przypomnienie:
W przypadku neuronu liniowego jego zachowanie 
daje się łatwo zinterpretować

Interpretacja geometryczne reguły Hebba

x

w

x

w

s=

w

T

x

a=s

a

φ

|w|cos(φ)

Podstawy Sztucznej Inteligencji

Jan Kusiak

Sztuczne Sieci Neuronowe 

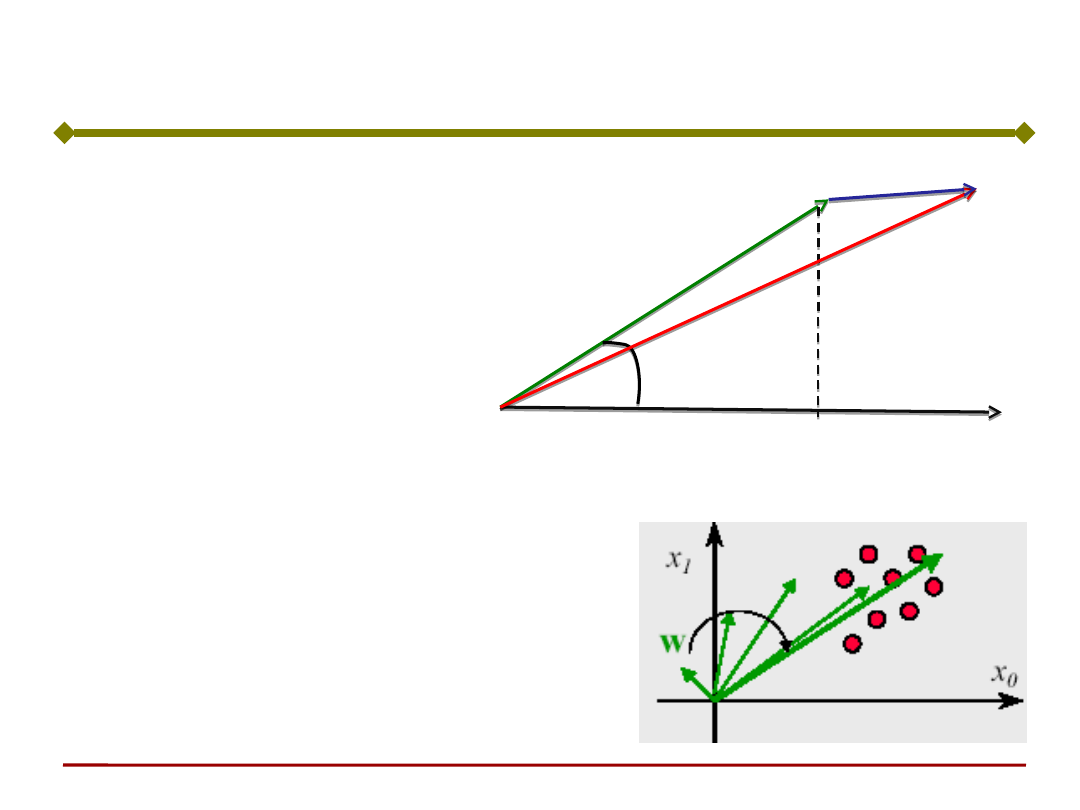
Interpretacja geometryczne reguły Hebba

x

w

φ

a=w

T

x=|x||w|cos(φ)

w(t+1)

Δw



w(t1) w(t)w

wcax

Wektor wag 
przemieszcza się w 
kierunku środka 
ciężkości wielkości 
uczących

Podstawy Sztucznej Inteligencji

Jan Kusiak

Sztuczne Sieci Neuronowe 

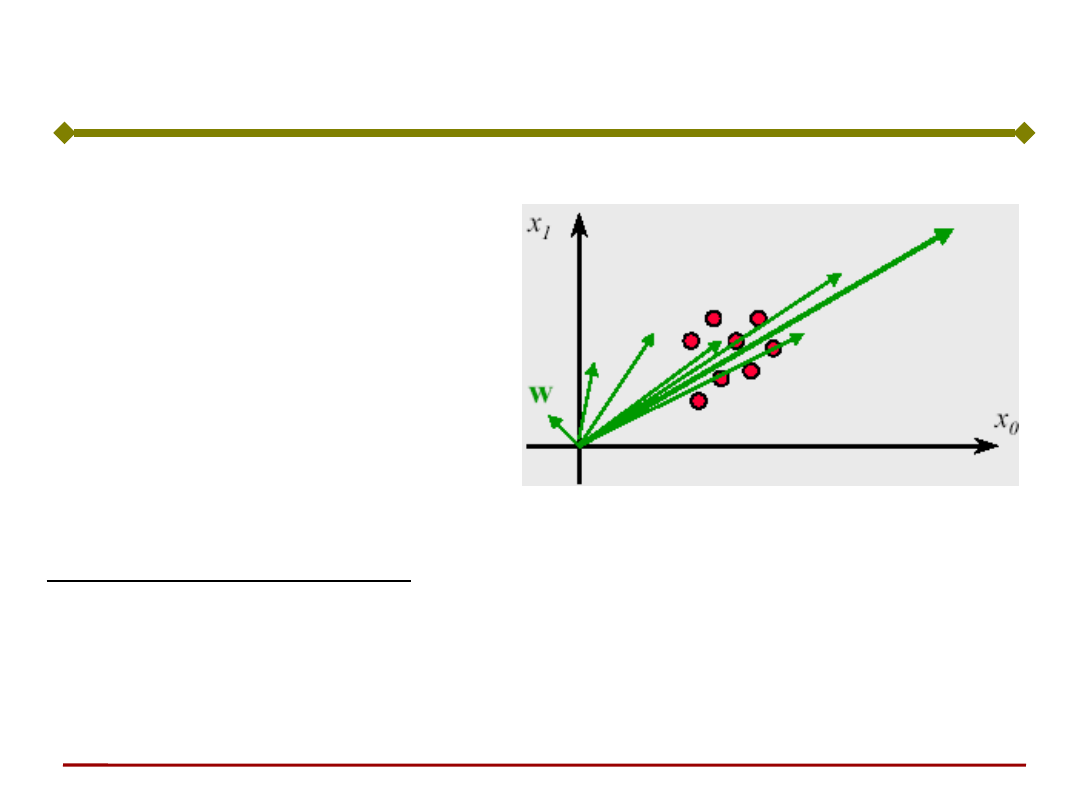
Niebezpieczeństwo:
Długość wektora wag rośnie w 
sposób nieograniczony (o ile nie 
zapewnimy stopniowego 
zmniejszania współczynnika c)

Interpretacja geometryczne reguły Hebba

Podstawy Sztucznej Inteligencji

Jan Kusiak

Sztuczne Sieci Neuronowe 

Reguła Hebba

Jedną z metod stabilizacji procesu uczenia jest 
wprowadzenie tzw. współczynnika zapominania 
0<<1 (zwykle  = 0.1).



w

ij

(t1) w

ij

(t)(1



)w

ij



w

ij

(t1) w

ij

(t)w

ij

Wagi mogą przybierać wartości dowolnie duże, gdyż 
w każdym cyklu uczącym następuje proces 
sumowania 

Podstawy Sztucznej Inteligencji

Jan Kusiak

Sztuczne Sieci Neuronowe 

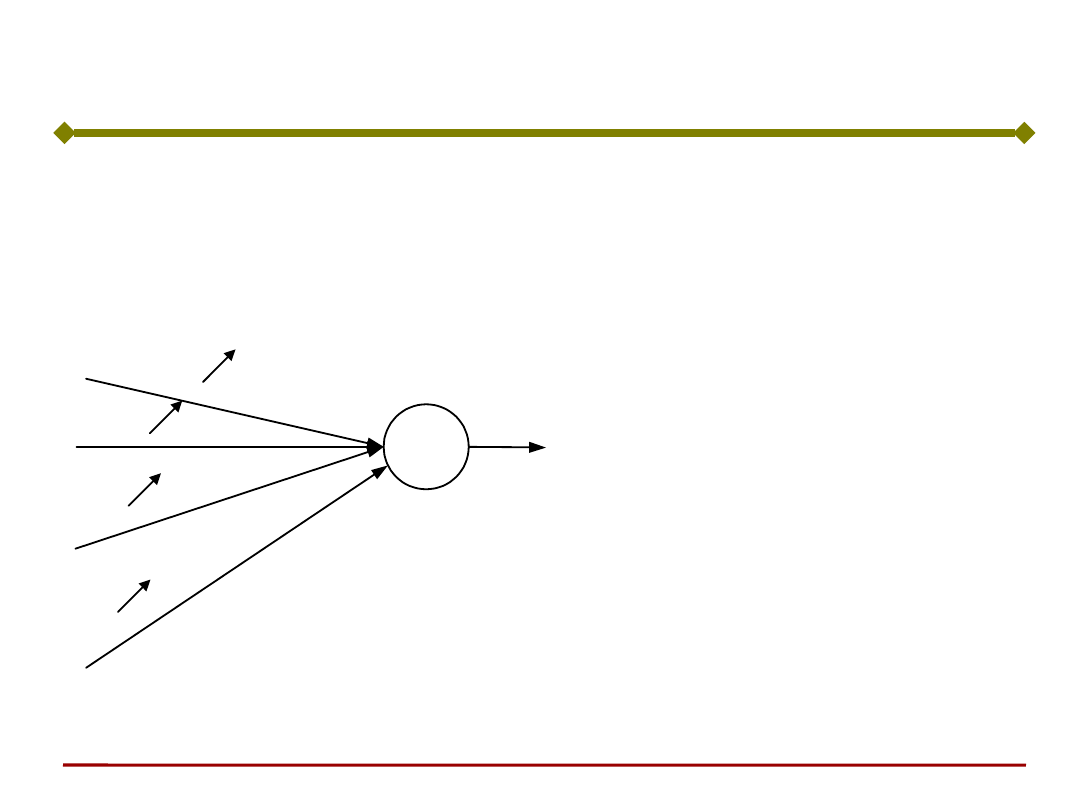
Uczenie neuronu z zastosowaniem reguły Hebba 
może być prowadzone również z nauczycielem. 

W uczeniu z nauczycielem wartość sygnału 
wyjściowego a zastępuje się wartością zadaną t. 

t

x

w

i

i







Uczenie neuronu regułą Hebba

Podstawy Sztucznej Inteligencji

Jan Kusiak

Sztuczne Sieci Neuronowe 

Przykład H1:
Uczenia prostej sieci metodą Hebba. Chcemy 
„douczyć” następującą sieć (niezerowe wartości wag 
świadczą o wcześniejszym uczeniu sieci):

p

1

p

2

w

1

w

3

w

2

w

4

p

3

p

4

a























































































5

.

1

1

1

0

5

.

1

2

5

.

0

1

0

5

.

1

2

1

3

2

1

p

p

p

Stała uczenia c = 1

Funkcja aktywacji: binarna, 
bipolarna, tzn.:  

)

sgn(

)

(

n

s 































5

.

0

0

1

1

1

w

Uczenie neuronu regułą Hebba - przykład

Podstawy Sztucznej Inteligencji

Jan Kusiak

Sztuczne Sieci Neuronowe 

Uczenie – krok 1:

Sygnał p

1

 daje sygnał pobudzenia n

1 

= 3 

[(w

1

)

T

 p

1

]

a

1

 = sgn(n

1

) = 1

Uaktualniona waga:

1

1

1

1

1

1

1

1

2

)

sgn(

x

w

p

w

p

w

w

c

n

c

ca













c = 1, więc:

























































































5

.

0

5

.

1

3

2

0

5

.

1

2

1

5

.

0

0

1

1

1

1

2

p

w

w

Przykład H1:

Podstawy Sztucznej Inteligencji

Jan Kusiak

Sztuczne Sieci Neuronowe 

Uczenie – krok 2:

Sygnał p

2

 daje sygnał pobudzenia n

2

= -0.25 

[(w

2

)

T

 

p

2

]

Uaktualniona waga:









































2

5

.

3

5

.

2

1

)

sgn(

)

(

2

2

2

2

2

2

2

2

3

x

w

p

w

p

w

w

n

c

n

cf

Przykład H1:

Podstawy Sztucznej Inteligencji

Jan Kusiak

Sztuczne Sieci Neuronowe 

Uczenie – krok 3:

Sygnał x

3

 daje sygnał pobudzenia n

3

= -3 (w

3T

 p

3

)

Uaktualniona waga:

w

4

 = w

3

 + c





































5

.

0

5

.

4

5

.

3

1

)

sgn(

)

(

3

3

3

3

3

3

3

p

w

p

w

p

n

n

f

W przedstawionym przykładzie binarnej funkcji 
aktywacji uczenie metodą Hebba sprowadza się do 
dodania lub odjęcia wektora obrazu wejściowego do 
(od) wektora wag.

Przykład H1:

Podstawy Sztucznej Inteligencji

Jan Kusiak

Sztuczne Sieci Neuronowe 

Uczenia tej samej sieci z przykładu H1 i sigmoidalnej 
funkcji aktywacji:

s

s

e

e

s

f











1

1

)

(

Uczenie – 
krok 1:

n

1 

= 0.905





























5

.

0

357

.

1

81

.

2

905

.

1

2

w

Uczenie – krok 
2:

n

2 

= -0.077





























616

.

0

512

.

1

772

.

2

828

.

1

3

w

Przykład H2:

Podstawy Sztucznej Inteligencji

Jan Kusiak

Sztuczne Sieci Neuronowe 

Uczenie – krok 
3:

n

3 

= 0.905































783

.

0

44

.

2

7

.

3

828

.

1

4

w

Z porównania obydwu przykładów wynika, że dla 
ciągłej funkcji aktywacji tylko ułamek wzorca 
wejściowego zmniejsza lub zwiększa wektor wag. 
Korekcja wag jest więc łagodniejsza, ale zasadniczo 
zachodzi w tym samym kierunku.

Przykład H2: