Parametryczny opis zbiorowości

statystycznej

– miary zmienności

Klasyfikacja miar zmienności:

1.

Klasyczne:

- wariancja i odchylenie standardowe

-

odchylenie przeciętne

-

współczynnik zmienności

2.

Pozycyjne:

-

obszar zmienności (rozstęp)

-

odchylenie ćwiartkowe

-

pozycyjny współczynnik zmienności

Zmienność

(zróżnicowanie,

dyspersja,

rozproszenie,

rozrzut)

–

określa

poziom

zróżnicowania

wartości

cechy

w

badanej

zbiorowości.

Podział miar zmienności

klasyczne

pozycyjne

absolutne:

•

wariancja

•

odchylenie standardowe

•

odchylenie przeciętne

absolutne:

• obszar zmienności

• odchylenie ćwiartkowe

względne:

•

współczynnik zmienności

względne:
współczynnik zmienności

Miary względne są niemianowane – pozwalają na
porównywanie zmienności różnych cech i zbiorowości

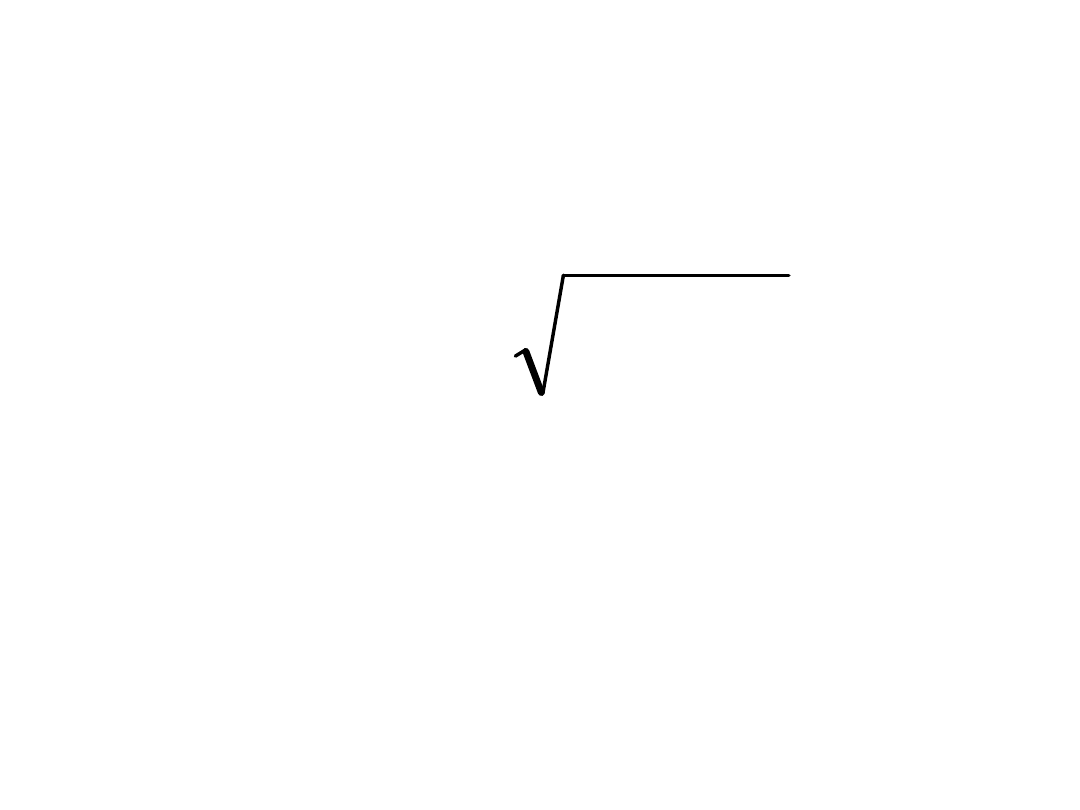
Odchylenie standardowe S(x)–

klasyczna,

absolutna miara zmienności - określa o ile
przeciętnie różnią się poszczególne wartości cechy
od ich średniej arytmetycznej. Stanowi ono
pierwiastek z wariancji:

 

Wariancja S

2

(X) -

(tj. drugi moment centralny)

jest pomocniczą (klasyczną, absolutną) miarą
zmienności; nie należy jej interpretować z uwagi na
„nienaturalne”( w stosunku do badanej cechy)
miano jakie posiada

)

(

)

(

2

X

S

X

S



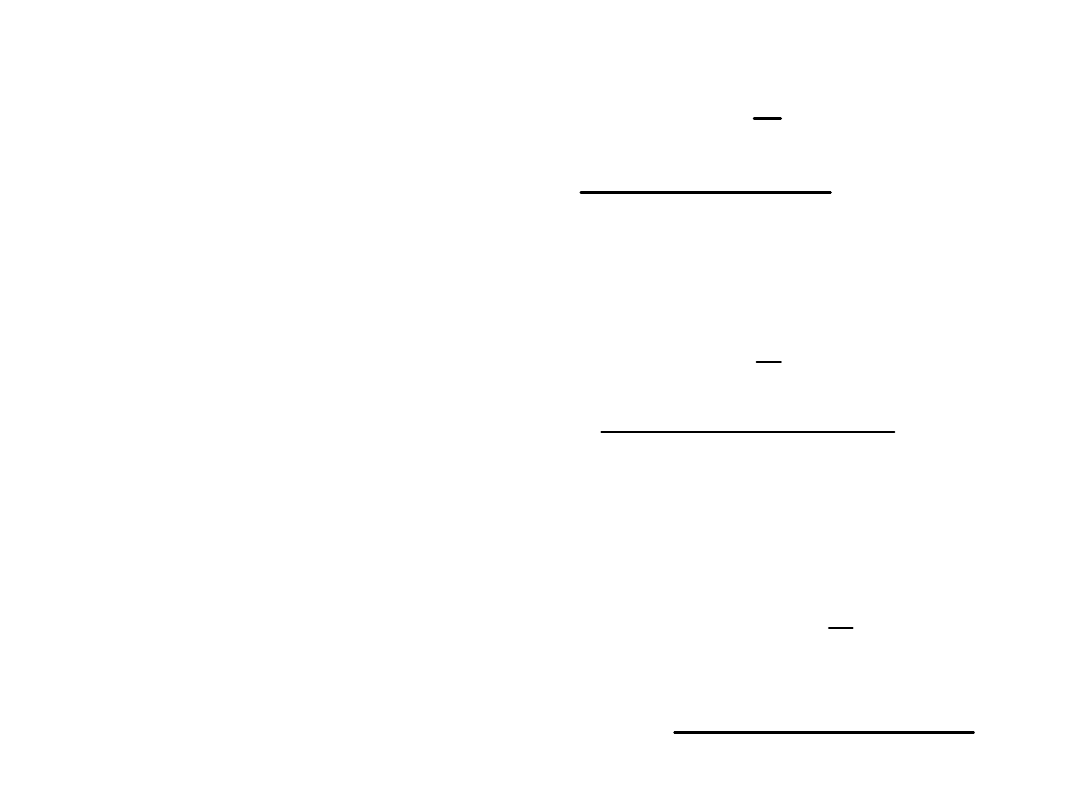
Wariancja - sposoby obliczania

 

szereg szczegółowy:





N

x

x

x

S

i

2

2

)

(







szereg rozdzielczy punktowy:





N

n

x

x

x

S

i

i









2

2

)

(

szereg rozdzielczy przedziałowy:

N

n

x

x

x

S

i

i













 





2

2

)

(



Własności wariancji

1. jako klasyczna miara zmienności liczona jest w oparciu o wszystkie wartości
cechy, a warunkiem jej wyznaczenia jest znajomość średniej arytmetycznej w
stosunku do której jest obliczana,

2. przyjmuje tylko wartości nieujemne; wartość zerową osiąga w przypadku
cechy stałej (wówczas wszystkie wartości cechy są identyczne),

3. jeśli w szeregu rozdzielczym wszystkie wagi pomnożymy bądź podzielimy
przez tę samą wielkość q, to wariancja liczona przy tak zmienionym
systemie wag będzie identyczne jak wariancja „pierwotna” (zauważmy, że
wariancja „zachowuje się” w tej sytuacji identycznie jak średnia

arytmetyczna)

4. jeśli wszystkie wartości cechy pomnożymy bądź podzielimy przez tę samą
wielkość q, to wariancja tak zmienionych wartości cechy będzie q2 razy
większa w przypadku mnożenia lub q2 razy mniejsza w przypadku dzielenia
od wariancji pierwotnych wartości cechy

Własności wariancji (c. d.)

5.

jeśli do wszystkich wartości cechy dodamy lub od wszystkich

wartości cechy odejmiemy tę samą wielkość q, to wariancja tak

zmienionych wartości cechy będzie identyczna jak wariancja

pierwotnych wartości cechy

6.

jeśli zbiorowość podzielimy na dowolną liczbę podzbiorowości

cząstkowych (grup), to wariancja ogólna badanej cechy będzie

sumą wariancji średnich grupowych i średniej wariancji

wewnątrzgrupowych, co można wyrazić wzorem:

Z powyższego wynika, że na ogólne zróżnicowanie wartości

cechy wpływa łącznie wewnątrzgrupowe zróżnicowanie tej

cechy, jak również zróżnicowanie międzygrupowe. Podana

relacja jest określana mianem równości wariancyjnej

7.

wariancja stanowi różnicę między średnią arytmetyczną

kwadratów wartości cechy a kwadratem średniej arytmetycznej

wartości tej cechy:

 

 

 

j

j

x

s

x

s

x

s

2

2

2





 

 

2

2

2

)

(

x

x

x

s





N

x

x

x

d

i







)

(

szereg rozdzielczy punktowy:

N

n

x

x

x

d

i

i









)

(

szereg rozdzielczy przedziałowy:

N

n

x

x

x

d

i

i











)

(

Sposoby obliczania odchylenia przeciętnego

szereg szczegółowy:

Obszar zmienności (rozstęp) –

różnica między

maksymalną i minimalną wartością cechy w

badanej zbiorowości

Typowy klasyczny obszar zmienności X

typ

-

wyznacza przedział najbardziej typowych wartości

i zawiera ok. 68% jednostek zbiorowości posiada

wartości cechy właśnie z tego przedziału

 

)

(

)

(

x

S

x

x

x

S

x

typ









min

max

)

(

x

x

x

R





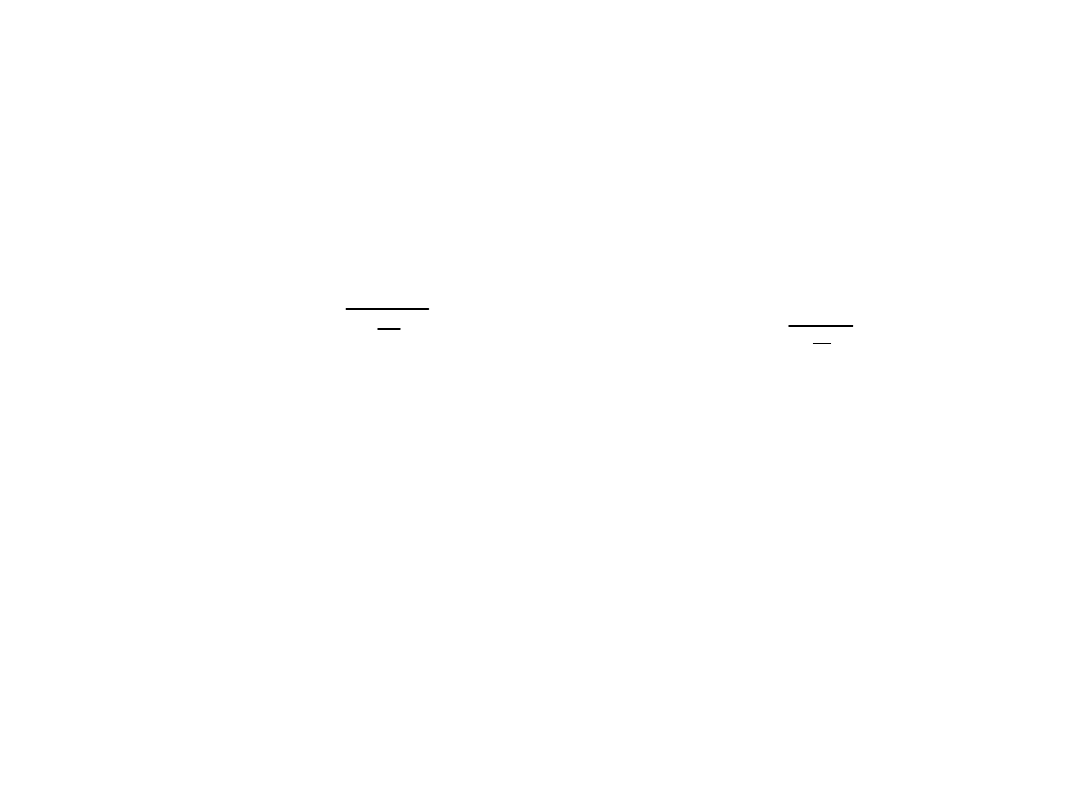
Współczynnik

zmienności

–

klasyczna,

względna miara zmienności; pozwala określić siłę
zmienności i porównywać zmienność różnych
cech i różnych zbiorowości

= 0 - brak zmienności =

0%
 
( 0 – 0,34) - zm. mała
(0 – 34%)
 
< 0,34 – 0,67) - zm. średnia
<34 – 67%)
 
< 0,67 – 1> - zm. duża
<67 – 100%>

 

 

x

x

s

x

W

z



   

100

*

x

x

s

x

W

z



)

(x

W

z

)

(x

W

z

Rozstęp

– różnica pomiędzy maksymalną a

minimalną wartością cechy

R(x) = x

max

- x

min

Odchylenie ćwiartkowe Q

– pozycyjna,

absolutna miara zmienności - średnie odchylenie
kwartyla pierwszego i trzeciego od mediany,
określa zróżnicowanie wartości cechy w dwóch
środkowych ćwiartkach zbiorowości

2

)

(

)

(

)

(

1

3

x

Q

x

Q

x

Q





Pozycyjny

współczynnik

zmienności

–

pozycyjna

miara

względna,

określa

siłę

zmienności w dwóch środkowych ćwiartkach
zbiorowości

oraz

pozwala

porównywać

zmienność różnych cech i różnych zbiorowości
(w dwóch środkowych ćwiartkach zbiorowości)

 

 

 

x

Me

x

O

x

W

c

z



 

 

 

100

*

x

Me

x

O

x

W

c

z



Typowy pozycyjny obszar zmienności

– pozwala określić przedział typowych wartości
cechy w dwóch środkowych ćwiartkach
zbiorowości

)

(

)

(

)

(

)

(

x

Q

x

Me

x

x

Q

x

Me

typ







