Prof. Stanisław Kuta
Katedra Elektroniki AGH
e-mail: [e-mail]

UKŁADY Z FAZOWĄ PĘTLĄ

SPRZĘŻENIA ZWROTNEGO

 Liniowy model pętli fazowej
 Wpływ transmitancji filtru na właściwości śledzące
pętli
 Zasada działania. Model pętli fazowej
 Procesy synchronizacji pętli PLL



Scalone pętle fazowe

 Detektor fazy
 Generatory przestrajane napięciem - VCO
 Przykłady realizacji układu scalonego PLL

Układy z fazową pętlą sprzężenia zwrotnego,

często nazywane pętlami fazowymi PLL (ang.
phase - locked - loop), znajdują bardzo szerokie
zastosowanie we współczesnej elektronice do
synchronizacji, podziału/powielania częstotliwości,
pośredniej demodulacji częstotliwości, przemiany
częstotliwości itp. Ciągle rosnący obszar licznych i
różnorodnych zastosowań pętli fazowej w
układach przetwarzania sygnałów analogowych i
cyfrowych wiąże się z tym, że parametry układów
z pętlą PLL są na ogół korzystniejsze niż
parametry układów konwencjonalnych.

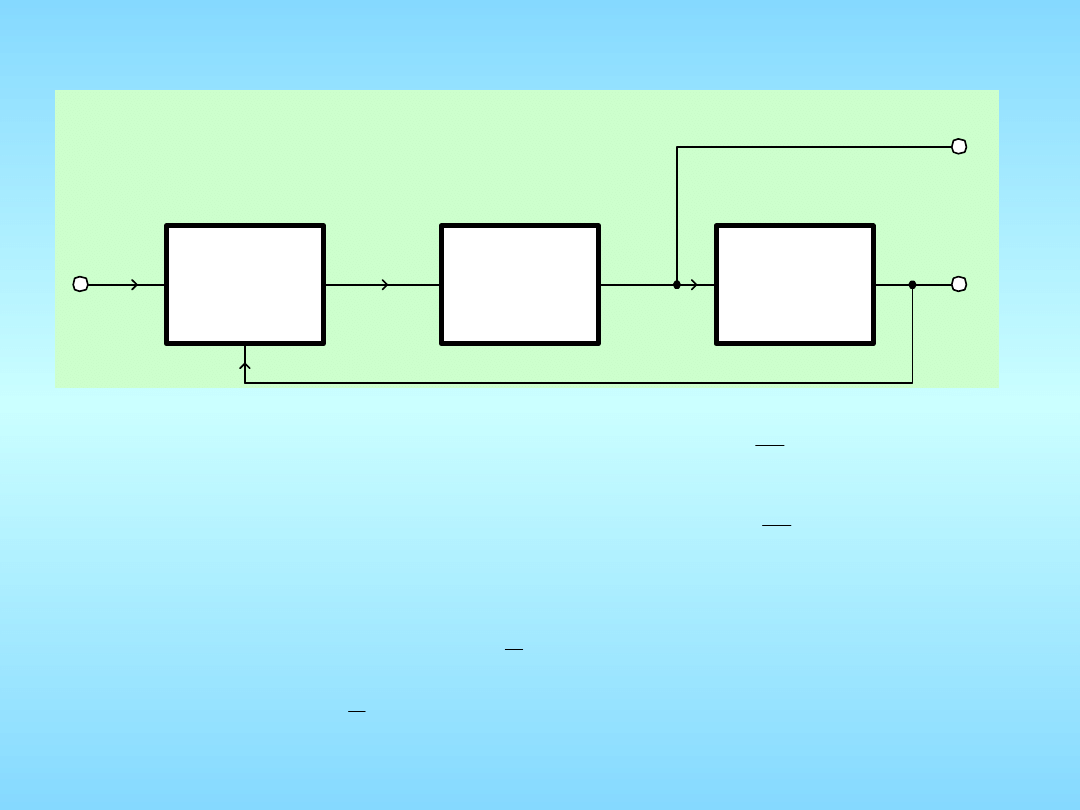
FDP

Detektor

fazy

VCO

 

u t

i

 



i

t

 

u t

D

 

u t

O

 

u t

g

 

u t

O

 



g

t

 

rad





V rad

/

 

V





V V

/

 

V





rad V

/

 

rad

Schemat blokowy układu z fazową pętlą
sprzężenia zwrotnego

 

 





 

 





cos

sin

0

0

t

t

U

t

u

t

t

U

t

u

g

g

g

i

i

i

















 

 





 

 





0

0

t

dt

d

t

t

dt

d

t

g

g

i

i





















 

   

   













t

t

U

U

k

t

u

t

u

k

t

u

g

i

g

i

m

g

i

m

D





sin

2

1

 

 





t

t

U

U

k

g

i

g

i

m













0

2

sin

2

1

k

m

- jest stała układu mnożącego

 

   





 





 





















b

D

b

b

D

g

i

g

i

m

D

U

t

k

t

t

U

U

k

t

u











sin

u

lub

sin

sin

2

1

max

D

 

   

t

t

t

g

i

b











- błąd fazy

g

i

m

D

U

U

k

k

2

1



- wzmocnienie detektora fazy

 

   

 





 

  



dt

t

h

t

k

t

h

t

k

t

h

t

u

t

u

b

t

D

b

D

D

O

sin

sin

0





















U

Dmax

u

D

 U

Dmax

arctg k

D







b



 2



 2



g



0

arctg k

G

u

G

b)

a)

a) Charakterystyka przejściowa detektora fazy, b) charakterystyka przestrajania

generatora VCO

 

 

t

u

k

t

O

G

g





0





 

 

t

u

k

dt

t

d

O

G

g





 

   





 





t

h

t

t

k

k

t

u

k

dt

t

d

g

i

D

G

O

G

g















sin

)

(

 

 

 





 





 

   















d

t

h

t

t

K

t

h

t

t

K

dt

t

d

g

i

t

g

i

g















]

[

sin

sin

0

 

 





   















d

t

h

t

K

dt

t

d

t

h

t

K

dt

t

d

dt

t

d

b

t

i

b

i

b















0

sin

)

(

)

(

sin

)

(

 

   

 

 









 

 





 

t

h

t

k

t

h

t

t

k

t

h

t

u

t

u

b

D

g

i

D

D

O





















sin

sin

D

G

k

k

K 

 

 

 

t

t

t

g

i

b











Pętla PLL opisana powyższymi równaniami jest układem

silnie nieliniowym z powodu nieliniowości charakterystyki
przejściowej detektora fazy. Nachylenie charakterystyki
przejściowej detektora fazy (w przypadku zastosowania
układu mnożącego) ulega nie tylko znacznym zmianom
co do wartości, lecz również zmienia swój znak przy
zmianie błędu fazy od (rys.a).

Przy zmianach błędu fazy w przedziałach:

nachylenie charakterystyki jest dodatnie

i w tym przypadku w pętli występuje fazowe ujemne
sprzężenie zwrotne. Dla pozostałych nachylenie
charakterystyki przejściowej detektora jest ujemne i w
pętli występuje fazowe dodatnie sprzężenie zwrotne.





b

b

 

 

do









b

n

 













2

2

2

do

dla n1 2

, , 



b

 

 

t

t

g

i







 

 

const

=

b0











t

t

g

i

 

const

:

posiada 

i

i

t

u



 

0

0

0

sin

sin

2

1

b

D

b

g

s

m

D

D

k

U

U

k

t

u

U











D

D

D

k

U

k







0

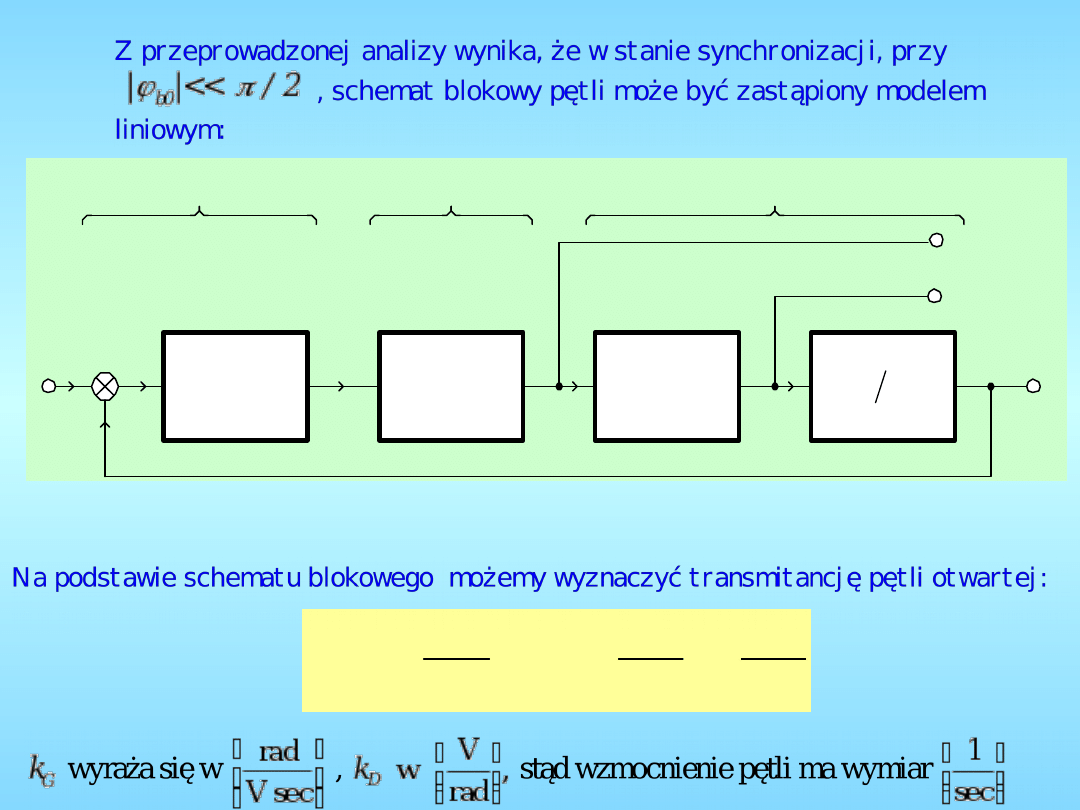
PĘTLA W STANIE SYNCHRONIZACJI

Liniowy model pętli fazowej

 

 







0

0

0

0









k k H

k k H

G

D

g

G

D

 

 

t

u

k

t

O

G

g





0





 

   

 





 

t

h

t

k

t

h

t

u

t

u

b

D

D

O











sin

 





T

G

D

k k H

K





0

 

 

 





 

 

 

 





 





















t

h

t

K

dt

t

d

dt

t

d

t

h

t

t

K

dt

t

d

b

i

b

g

i

g













 

 

 





 

 

 

   















s

H

s

K

s

s

s

s

s

H

s

s

K

s

s

b

i

b

g

i

g













 

 

 

 

 

s

H

K

s

s

H

K

s

s

s

G

i

g











 

 

 

 

 

s

H

K

s

s

s

G

s

s

s

G

i

b

b











1





 

 

s

k

s

U

s

G

O

g





 

 

 

 

 

s

s

H

K

s

s

H

k

k

s

s

s

G

G

D

O

i

g

O























 

 

t

u

k

dt

t

d

O

G

g





 

H s

k

D

k

G

 



i

s

 

U s

D

 

U s

O

 



g

s

 

U s

O





V rad

/





V V

/





rad Vs

/

 



b

s

Faza

1 s

Pulsacja

 



g

s

 



g

s





 



g

s

VCO

Filtr

Detektor fazy

Liniowy model pętli fazowej w stanie
synchronizacji

 

 

 

 

 

s

s

H

K

s

s

H

k

k

s

s

s

G

G

D

O

i

g

O























Wpływ transmitancji filtru na właściwości

śledzące pętli

W literaturze pętle fazowe klasyfikuje się jak układy

automatycznej regulacji w oparciu o transmitancje pętli
otwarte, przy czym liczba biegunów określa rząd pętli,
natomiast liczba biegunów w początku układu
współrzędnych określa typ pętli.
Najczęściej rozważa się pętle fazowe 1-go rzędu (bez
filtru) oraz pętle 2-go rzędu z typowymi pasywnymi lub
aktywnymi filtrami 1-go rzędu. Dokonując tej
klasyfikacji, niżej przedstawiono najbardziej typowe
transmitancje stosowanych filtrów i wiążące się z nimi

transmitancje pętli:

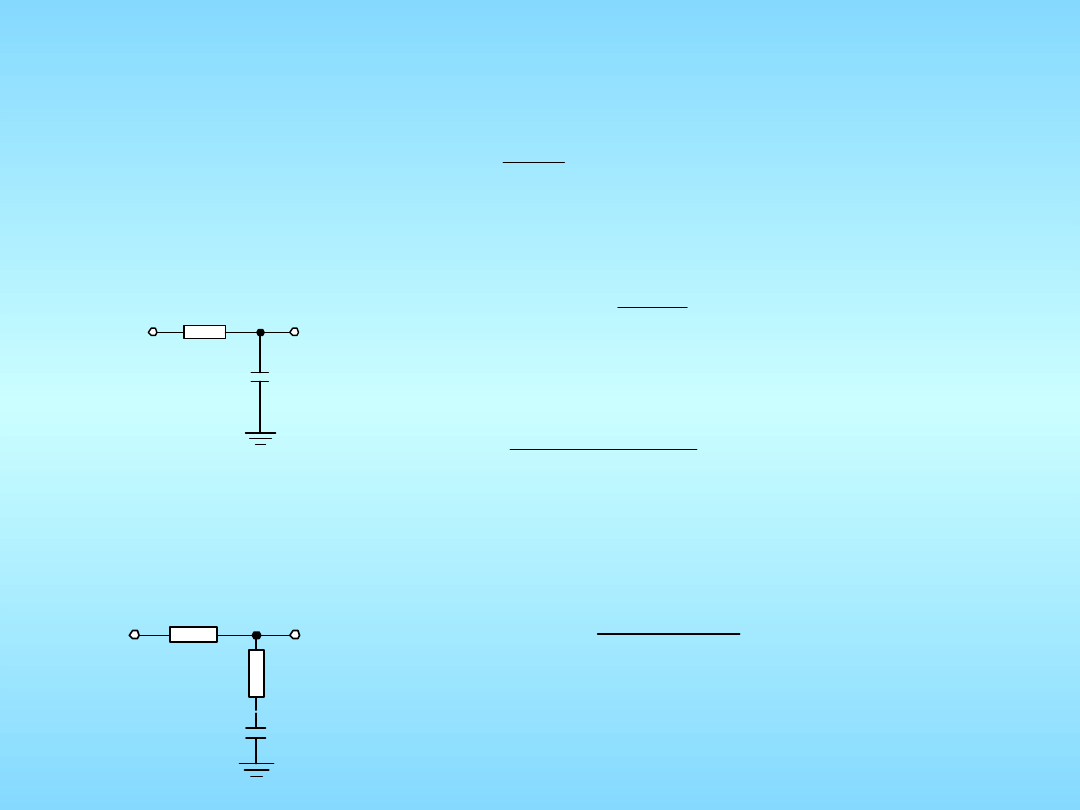
pętla pierwszego rzędu, typu pierwszego:

 

1

0



s

H

 

K

s

K

s

G





pętla drugiego rzędu, typu pierwszego z pasywnym filtrem całkującym:

R

1

C

 

 

s

s

H

s

H

1

1

1

1









C

R

1

1





 

1

1

1

1

2

1

1



















K

s

s

K

s

G

pętla drugiego rzędu, typu pierwszego z pasywnym filtrem proporcjonalno – całkującym:

R

1

R

2

C

 

 

s

s

s

H

s

H

)

(

1

1

2

1

2

2

















C

R

C

R

2

2

1

1









 

2

1

2

1

2

2

1

2

1

2

1

)

(

)

1

(



































K

s

K

s

s

K

s

G

 

2

2

2

2

2

n

n

n

n

n

s

s

s

K

s

G































 



2

/

1

2

1























K

n

- pulsacja drgań
swobodnych pętli











 

















K

K

K

2

2

/

1

2

1

1

2

1









- współczynnik
tłumienia

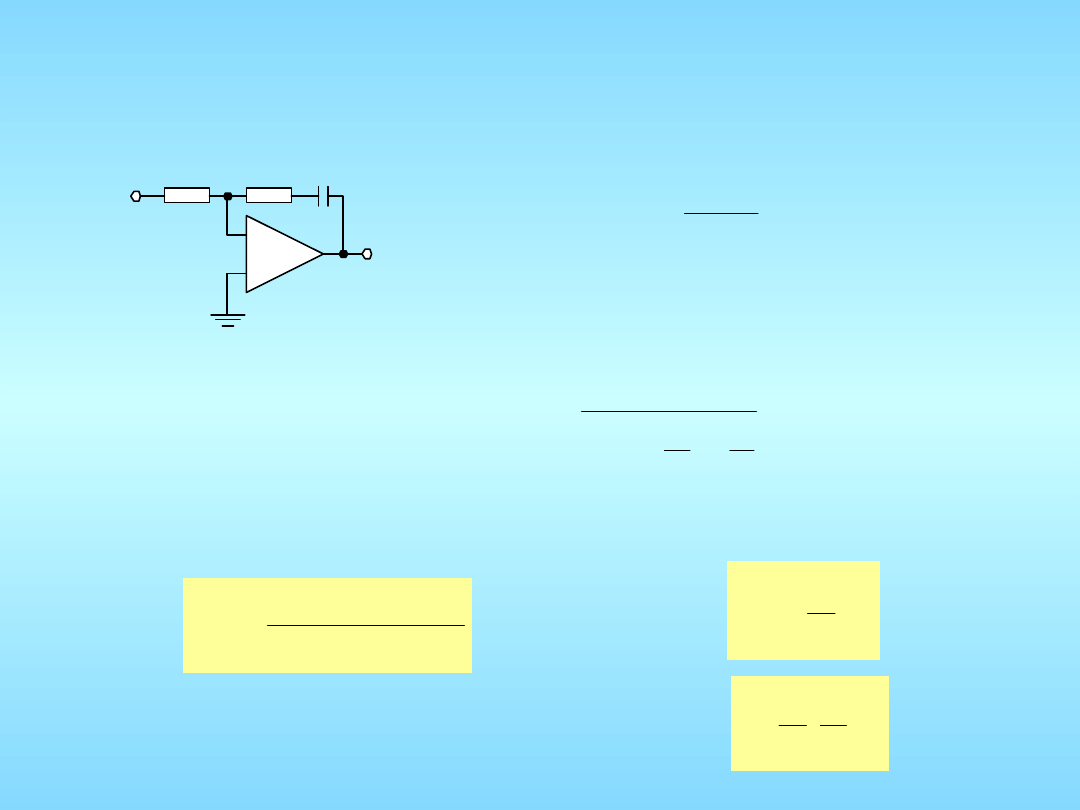
pętla drugiego rzędu, typu drugiego z aktywnym filtrem
proporcjonalno – całkującym:

R

1

R

2

C





 

 

s

s

s

H

s

H

1

2

3

1











C

R

C

R

2

2

1

1









 





1

1

2

2

1

1

2

1











K

s

K

s

s

K

s

G























Lub w postaci unormowanej:

 

2

2

2

2

2

n

n

n

n

s

s

s

s

G





















2

/

1

1



















K

n

2

/

1

1

2

2





















K

gdzie:



c

K



 

G j

O









 2

a)

 

argG j

O



1

0



c

 

G j

O





 2

b)

 

argG j

O



1

0



1

K

 20dB dek

 20dB dek

 40dB dek



1

 K





0

 

H s

0

1





1

1

1



RC



c

0



1

K

 20dB dek

 40dB dek









2

 20dB dek



 2





1

 

G j

O



 

argG j

O





2

 

H s

s

s

2

2

1

1

1

















1

1

2

1





R R C

 

H s

s

1

1

1

1









2

2

1



R C

c)

R

1

R

2

C

R

1

C

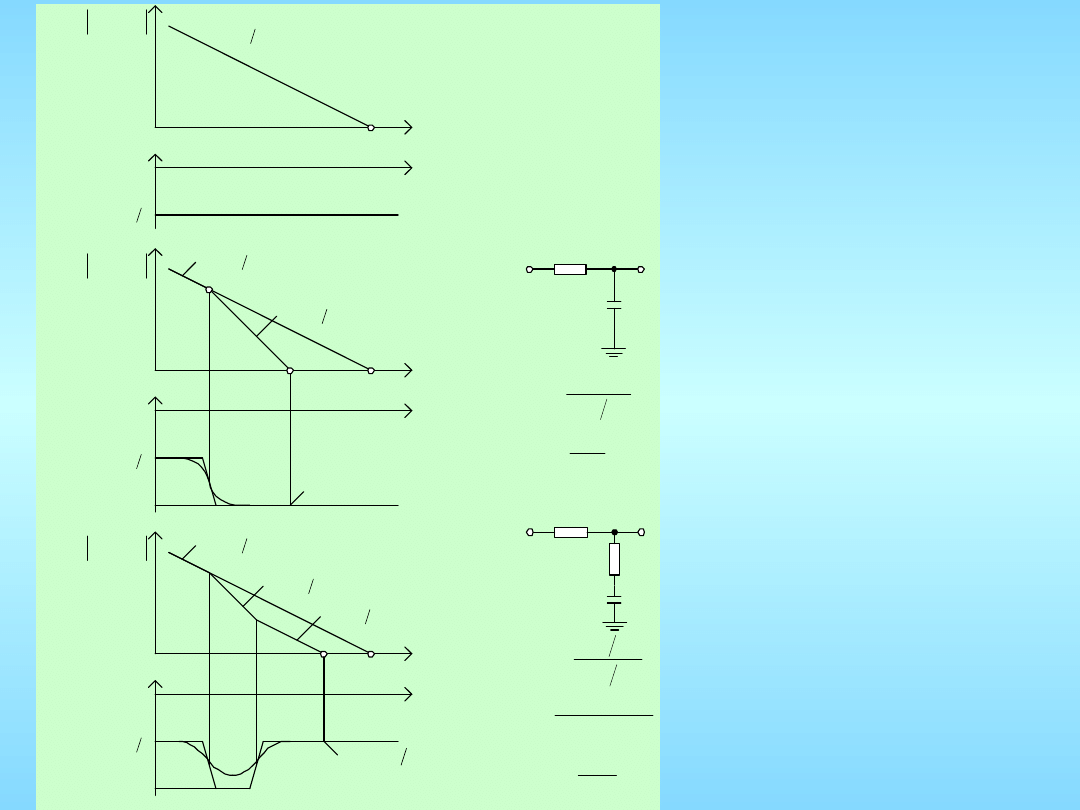
wpływ członu

całkującego VCO













Charakterystyki częstotli-
wościowe: amplitudowe i
fazowe
otwartych pętli fazowych
dla
różnych transmitancji
filtru:
a) H

0

(s), b) H

1

(s), c) H

2

(s)









i

Hz

2 250









i

kHz

2 1









i

kHz

2 1









i

Hz

2 500

u t

i

( )

u t

O

( )

05

.

 05

.

 025

.

025

.

0

t

t







1

2

k

ms

U

k

V

O

i

G

1

0

05







 

,

U

k

V

O

i

G

2

0

025







 

,

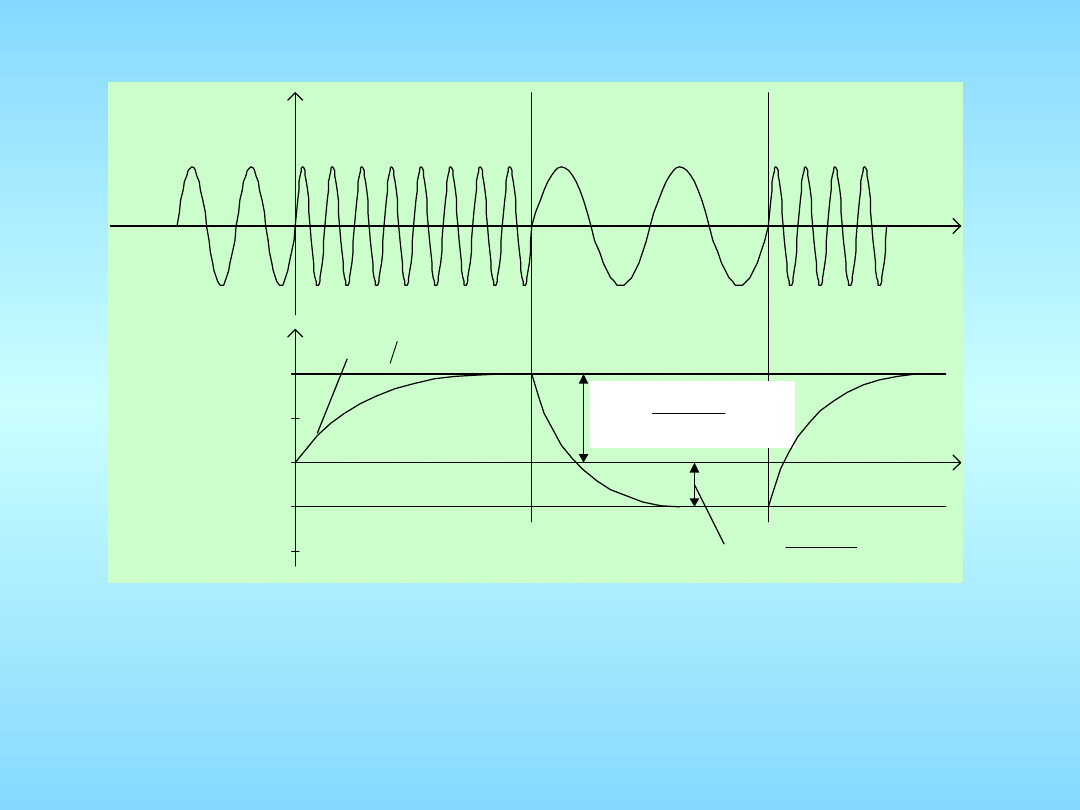
Odpowiedź pętli fazowej pierwszego rzędu na sinusoidalny

sygnał wejściowy ze

skokową zmianą częstotliwości

Zdolność śledzenia przez pętlę zmian fazy sygnału

wejściowego określa się zwykle dla standardowych
zaburzeń tego sygnału o postaci:

- skokowej zmiany fazy,
- skokowej zmiany częstotliwości,
- liniowej zmiany częstotliwości.
Przyjmując, że zaburzenie sygnału wejściowego nastąpiło w

chwili , wymienione trzy sygnały standardowe i ich
transformaty Laplace’a przedstawiono w tabeli 1.

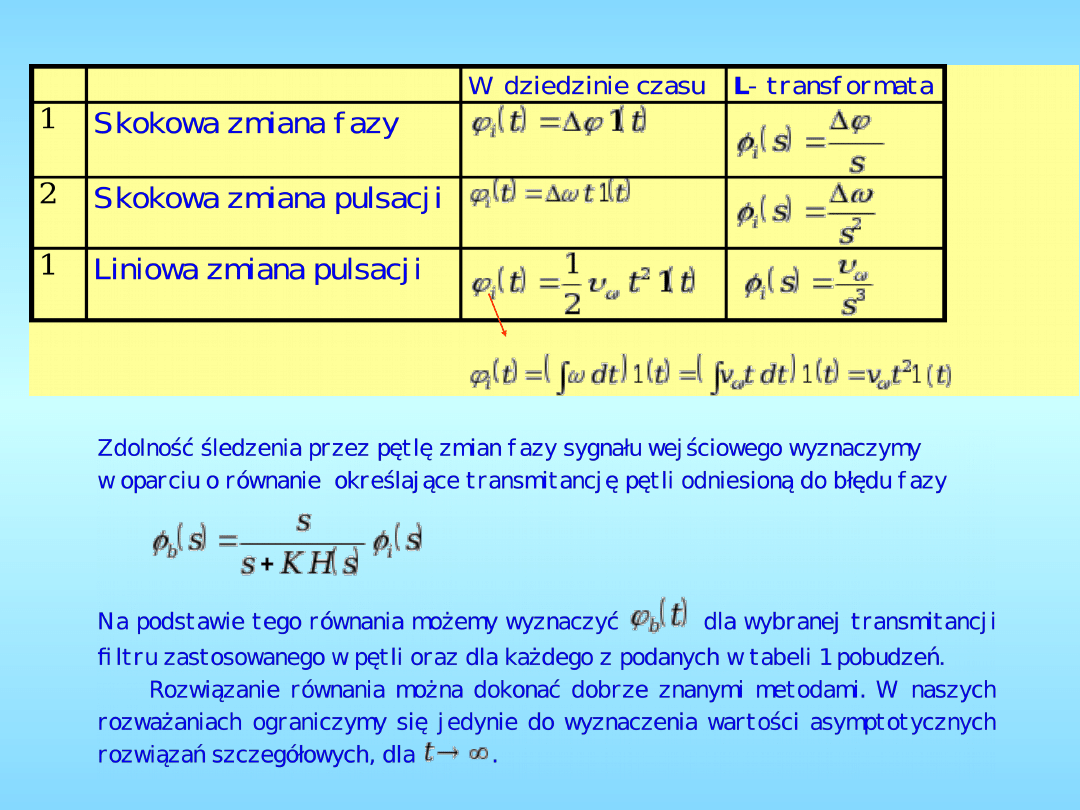
TABELA 1

 

 

   

s

s

H

K

s

s

s

s

t

i

s

b

s

b

b

t

























2

0

0

0

lim

lim

lim

skokowa zmiana
fazy:

 

 

0

lim

lim

2

0

0

















s

s

H

K

s

s

t

s

b

b

t







skokowa zmiana
pulsacji:

 

 

 

0

lim

lim

2

2

0

0

H

K

s

s

H

K

s

s

t

s

b

b

t



























 

K

t

b

b

t

















0

lim

 

1

0 

H

liniowa zmiana pulsacji:

 

 















3

2

0

lim

lim

s

s

H

K

s

s

t

s

b

t







 

 





 

K

s

s

H

K

s

s

s

s

s

s

dt

t

d

s

b

s

b

t





























3

2

0

0

lim

lim

lim

 

1

0 

H

Błąd fazy narasta nieograniczenie z szybkością:

Błąd fazy narasta w miarę upływu czasu, powodując wyjście
detektora fazy z liniowego obszaru pracy, aż przy pewnej wartości
błędu fazy następuje utrata synchronizacji.

liniowa zmiana pulsacji:

 

 

 

3

3

2

0

0

lim

lim

s

s

H

K

s

s

t

t

s

b

b

t





















2

2

2

2

0

0

2

lim

n

n

n

s

b

s

s





























Dla wystarczająco dużego współczynnika tłumienia
przebieg osiąga wartość asymptotyczną w sposób
aperiodyczny, tj. bez oscylacji o dużych amplitudach i
przy dostatecznie małym stosunku pętla pozostaje w
stanie synchronizacji.

 

 











0

2

df

j

j

B

i

g

n





Pasmo szumowe

 

 





0

sin

0

i

i

i

i

t

U

t

u









 

 





 





0

cos

cos

0

0

0

g

g

t

g

g

g

t

U

t

t

U

t

u































0

0

i

 

 





t

t

U

t

u

i

i

i









0

sin

 

 

0

i

i

t

t













PROCESY SYNCHRONIZACJI PĘTLI PLL

Dochodzenie do stanu synchronizacji - zakres

chwytania

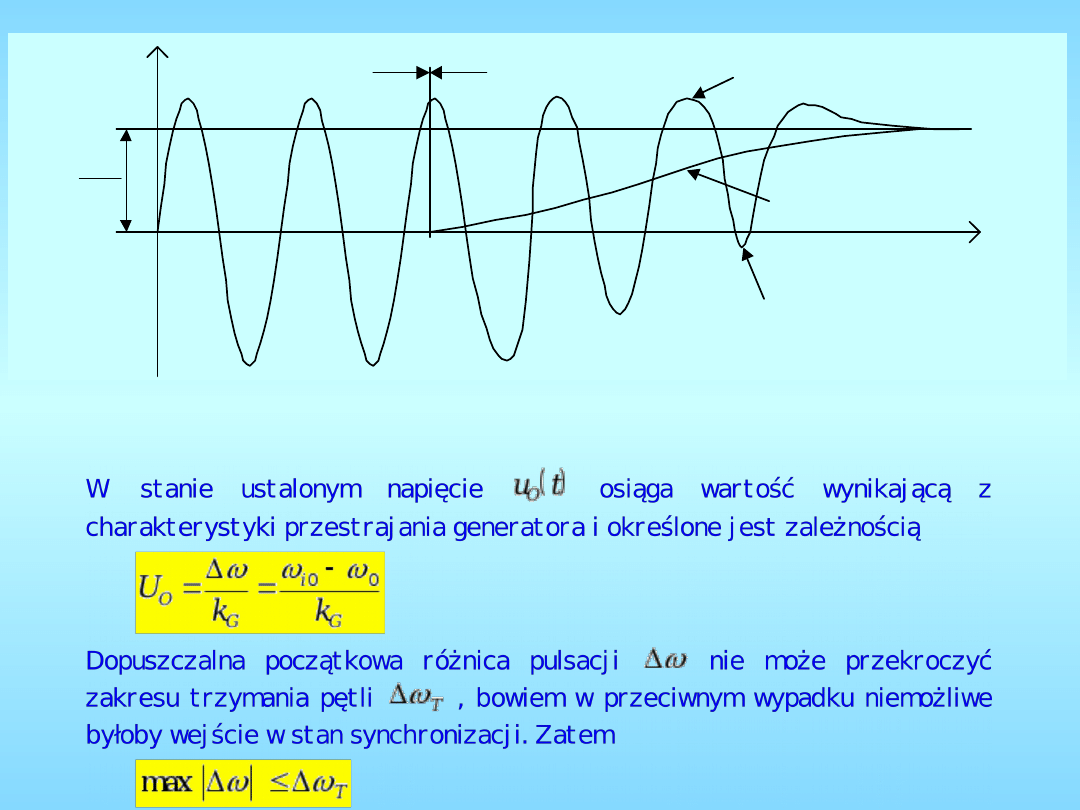
u

O

t

U

k

O

G







0

0'

pętla otwarta

proces chwytania

częstotliwości zbliżone

częstotliwości oddalone

składowa wolnozmienna

Napięcie u

o

(t) na wejściu generatora VCO pętli osiągającej

stan synchronizacji

u

O



i

1 k

G

2



C

2



T





0

 

c

G

k

P

4

P

1

P

0

P

3

P

2



0





0

 

c

G

k

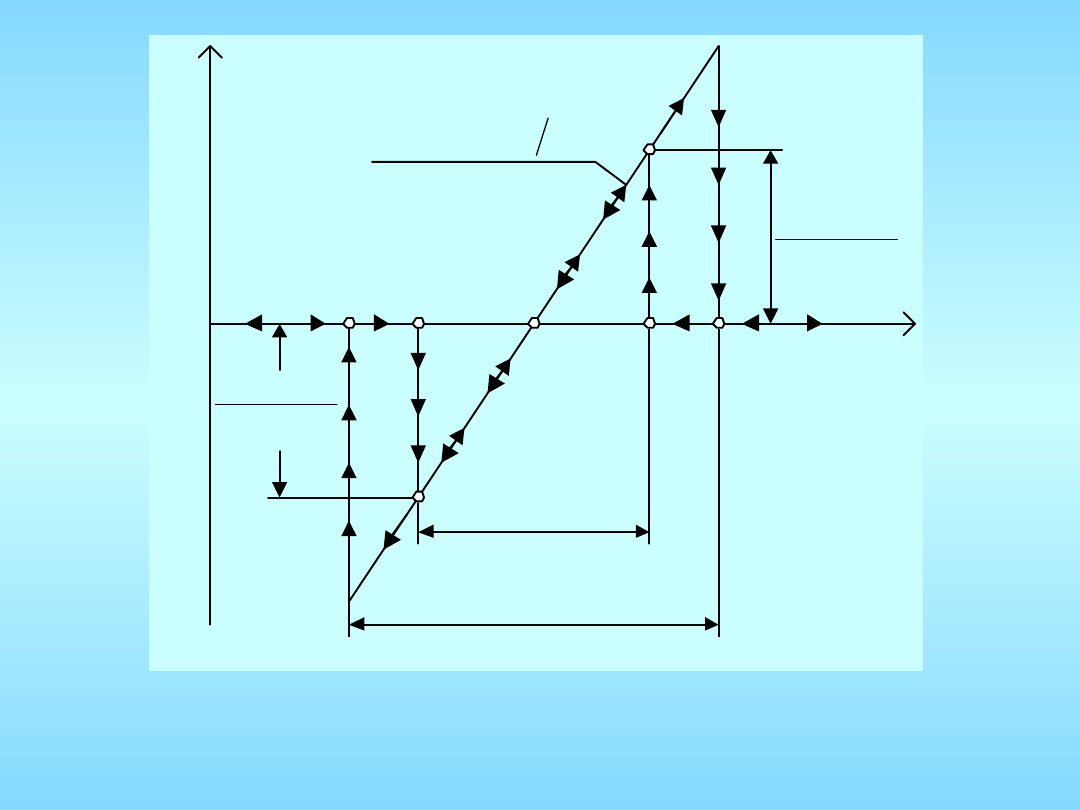
nachylenie

zakres chwytania

zakres trzymania

Zakresy chwytania i trzymania pętli
fazowej

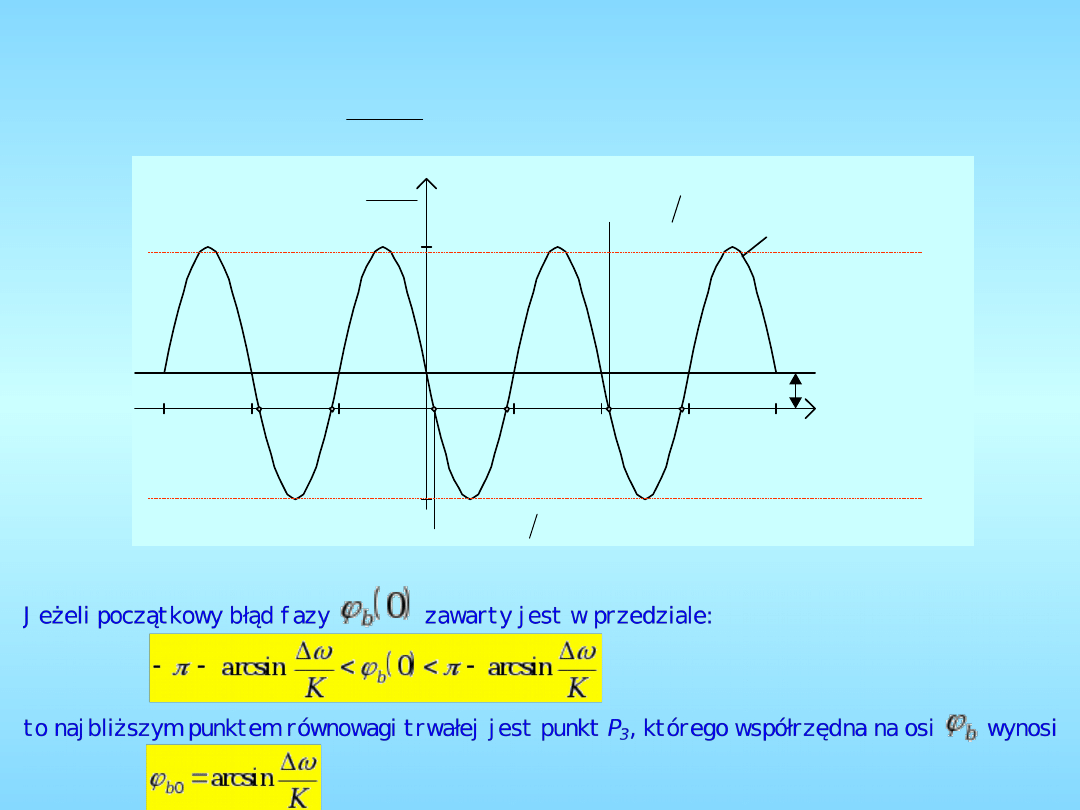
Proces synchronizacji pętli pierwszego
rzędu

 

 





t

K

dt

t

d

b

b







sin







P

2

 3





 







i0

0

 2







0

P

1



2



3



4



P

3

P

4

2





 arcsin K





 K







 K

b

sin





 K

arcsin

 K



b

d

dt

b



P

5

P

6

Odwzorowanie równania na
płaszczyźnie fazowej

 

 





t

K

dt

t

d

b

b







sin







Proces synchronizacji pętli drugiego
rzędu

 





s

s

s

H

2

1

2

2

1

1















 

 

 

 

2

1

2

1

2

1

2

2

2

sin

cos

1









































t

K

dt

t

d

t

K

dt

t

d

b

b

b

b

 

 

 

 



























K

t

dt

t

d

t

dt

t

d

n

b

n

b

b

n

b

2

2

2

2

sin

cos

2

Jeżeli:

to:

,

/

1

2

K





Bardzo często w pętli fazowej drugiego rzędu stosowany jest
dolnoprzepustowy filtr proporcjonalno - całkujący o
transmitancji

Proces synchronizacji pętli drugiego
rzędu cd.

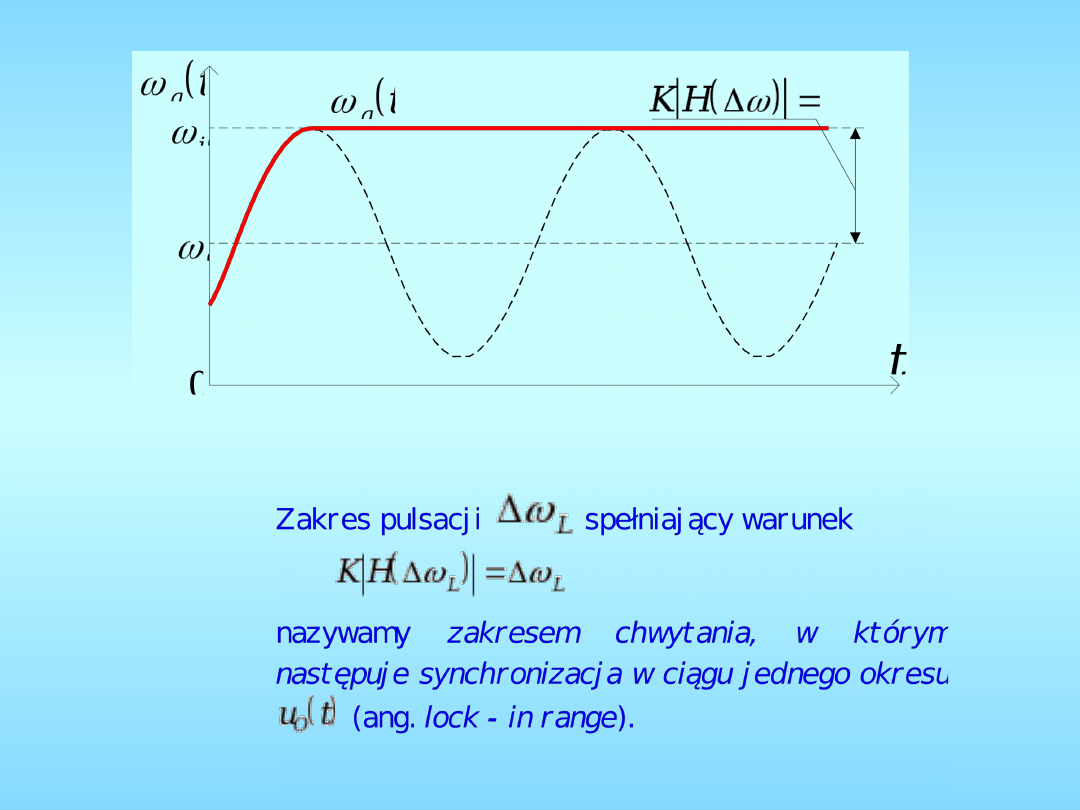
Osiąganie stanu synchronizacji w ciągu jednego
okresu





L

L

H

K











n

L









n

L







2





n

L

t



/

1



przy zastosowaniu filtru o transmitancji:

 

H s

1

w przypadku filtru o transmitancji:

 

H s

2

W obu przypadkach stan synchronizacji osiąga się po
czasie:

 

0

0

0



















i

r

 

 





 





t

t

t

H

k

t

u

r

r

D

O











sin

u

O

t

t





r





r

a)

b)





i0

0



 

 









r

i

g

t

t





0

małe (cz. zbliżone - filtr nie tłumi)

duże
(cz. oddalone - filtr tłumi)

Proces synchronizacji pętli fazowej: a) przebieg napięcia u

o

(t), b) przebieg

różnicy pulsacji

 

r

(t)=



i0

-



g

(t)

2

8

n

n

C

K

















 

2

2

2

n

C

t











Dla pętli drugiego rzędu zakres chwytania
wynosi:

Czas trwania procesu synchronizacji określony jest
zależnością:

 U

EE

T

4

T

3

T

5

T

6

T

2

T

1

 

u t

i

 

u t

g

I

EE

U

CC

R

C

R

C

 

u t

d

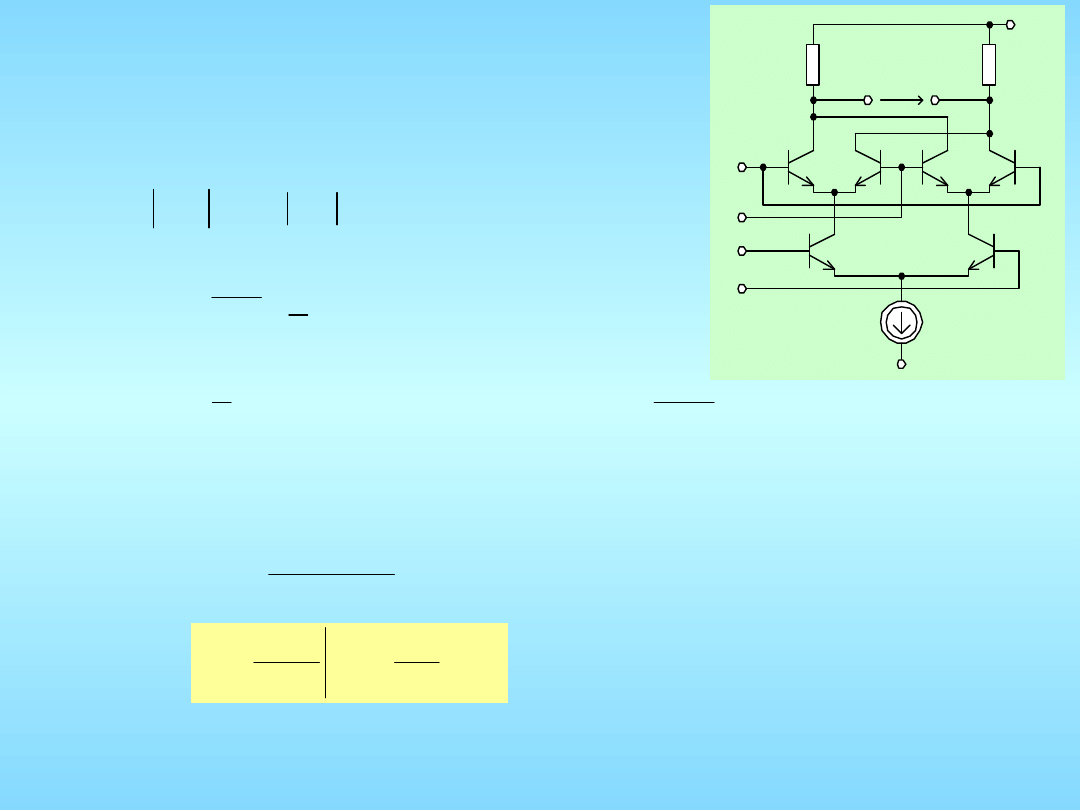
Rys. 4.11. Schemat ideowy modulatora
zrównoważonego

 

 

 

 

t

u

t

u

t

u

t

u

g

Y

i

X





,

DETEKTOR FAZY

SCALONE PĘTLE FAZOWE

 

 

T

g

T

i

t

u

t

u









;

 

 

   

t

u

t

u

R

I

R

t

i

t

u

g

i

T

C

EE

C

R

D

2

4







 





 













t

U

t

u

t

U

t

u

g

g

i

i

0

0

cos

cos







 





cos

8

2

0

i

g

T

C

EE

D

D

U

U

R

I

t

u

U





Przypade
k 1

 U

EE

T

4

T

3

T

5

T

6

T

2

T

1

 

u t

i

 

u t

g

I

EE

U

CC

R

C

R

C

 

u t

d

i

C

m

Dm

U

R

g

U







cos

2

0

i

C

m

D

U

R

g

U 

C

m

i

D

D

R

g

U

d

dU

k





2

max

0







Przypadek 2

 

 

T

i

T

g

t

u

t

u





2

;

2





 

   

 

 



























cos

2

sin

sin

1

1

0

0

0

Dm

Dm

Dm

D

D

D

U

t

d

t

U

t

d

t

U

t

d

t

u

t

u

U





































 U

EE

T

4

T

3

T

5

T

6

T

2

T

1

 

u t

i

 

u t

g

I

EE

U

CC

R

C

R

C

 

u t

d

U

D0











2

b)

 

u t

i



t

a)

 

u t

g



t

 

u t

D



t



2





U

Dm

2







U

i

U

t

i

i

sin



0 

2



3 2



2g R U

m C

i



0

0

0

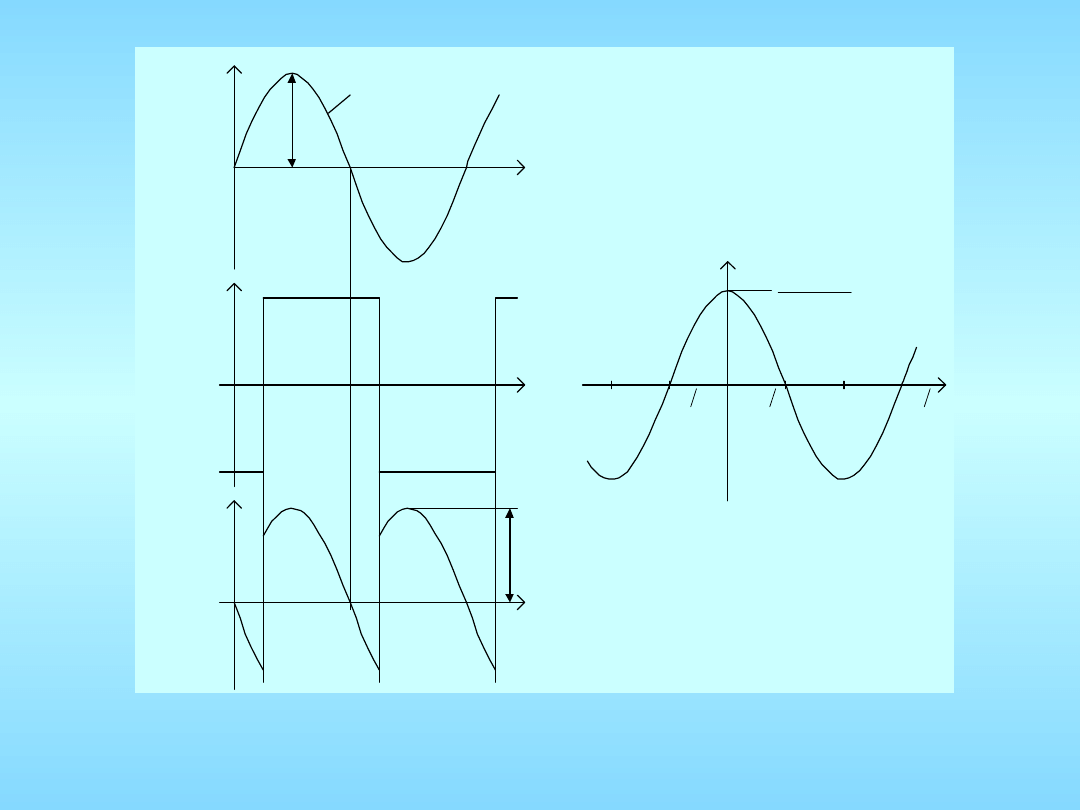
Modulator zrównoważony sterowany sygnałem sinusoidalnym i synchronizowany

przebiegiem prostokątnym: a) przebiegi czasowe, b) charakterystyki detektora

Przypadek
3

 

 

T

g

i

t

u

t

u



2

,



   











 



































2

1

1

0

0

C

EE

C

EE

C

EE

D

D

R

I

R

I

R

I

t

d

t

u

U





C

EE

D

D

R

I

d

dU

k

2

0







 U

EE

T

4

T

3

T

5

T

6

T

2

T

1

 

u t

i

 

u t

g

I

EE

U

CC

R

C

R

C

 

u t

d

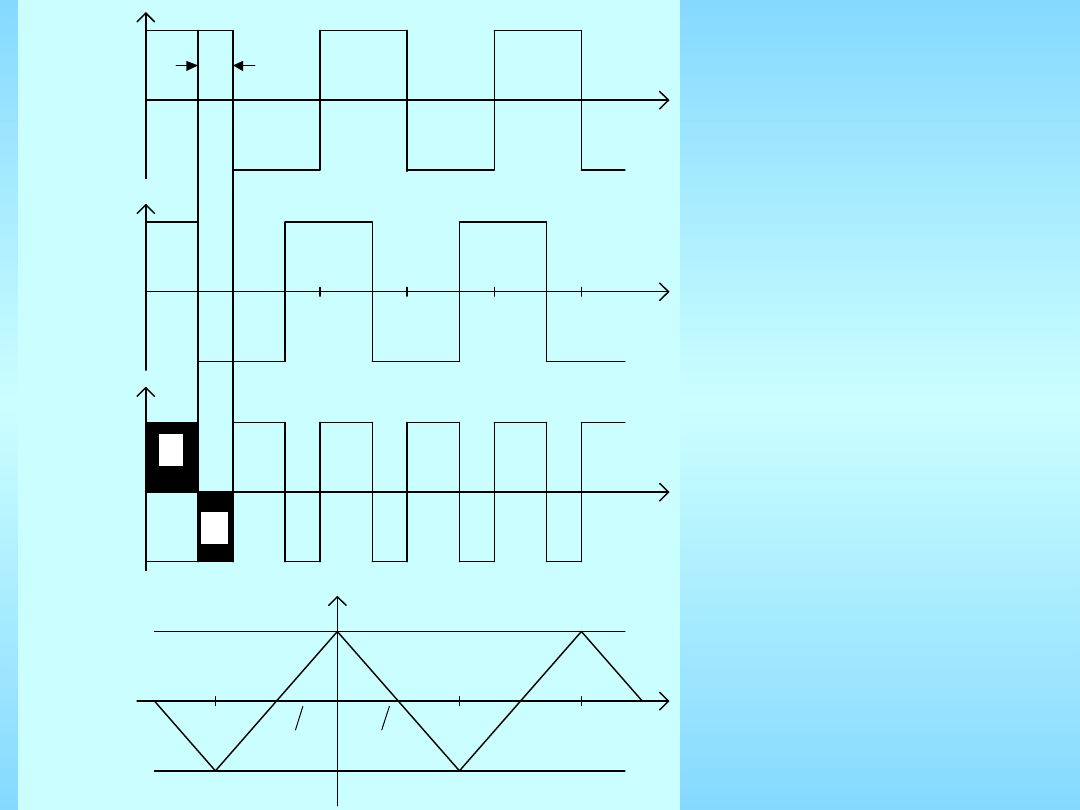
a)

 

u t

g



t

2





0

3



4



5



 

u t

i



t

2





0

3



4



5



 

u t

D



t

2





0

3



4



5



S

1

S

2

I R

EE

C

 I R

EE C



 I R

EE C

I R

EE

C

U

D0



2







2





2





b)

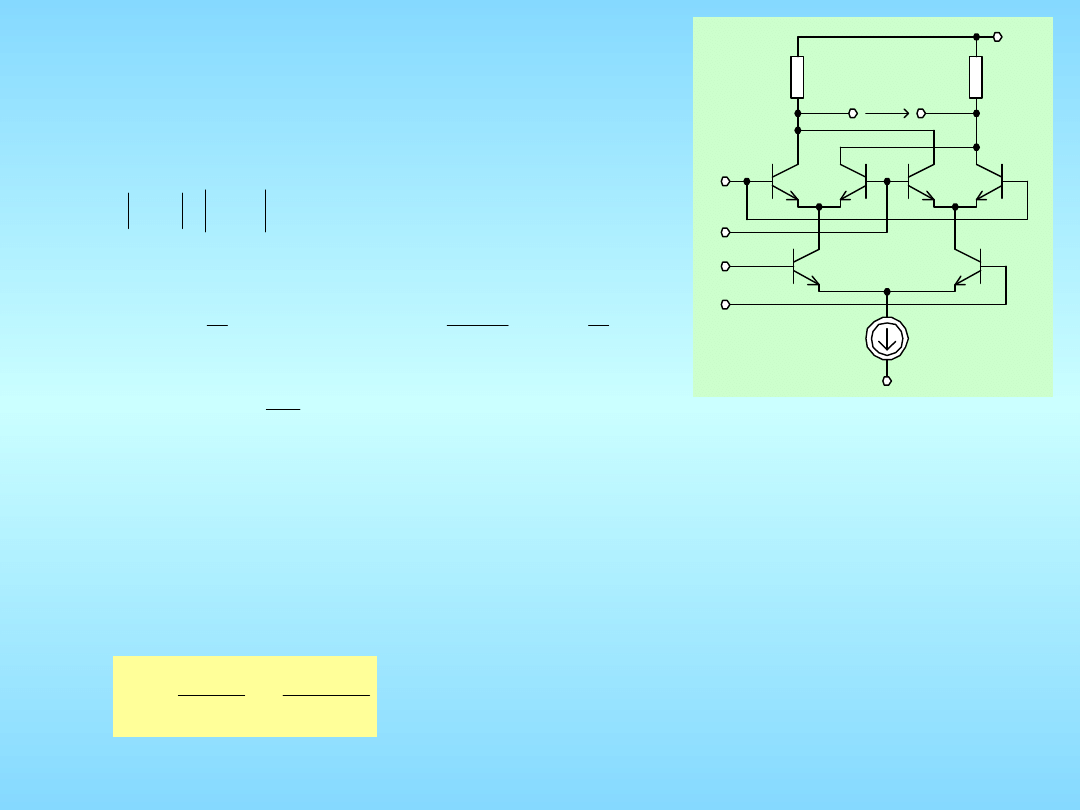
Modulator zrównowa-
żony dla dużych amplitud
sygnałów wejściowych:
a) prostokątne sygnały sterujące,
b) charakterystyka detektora

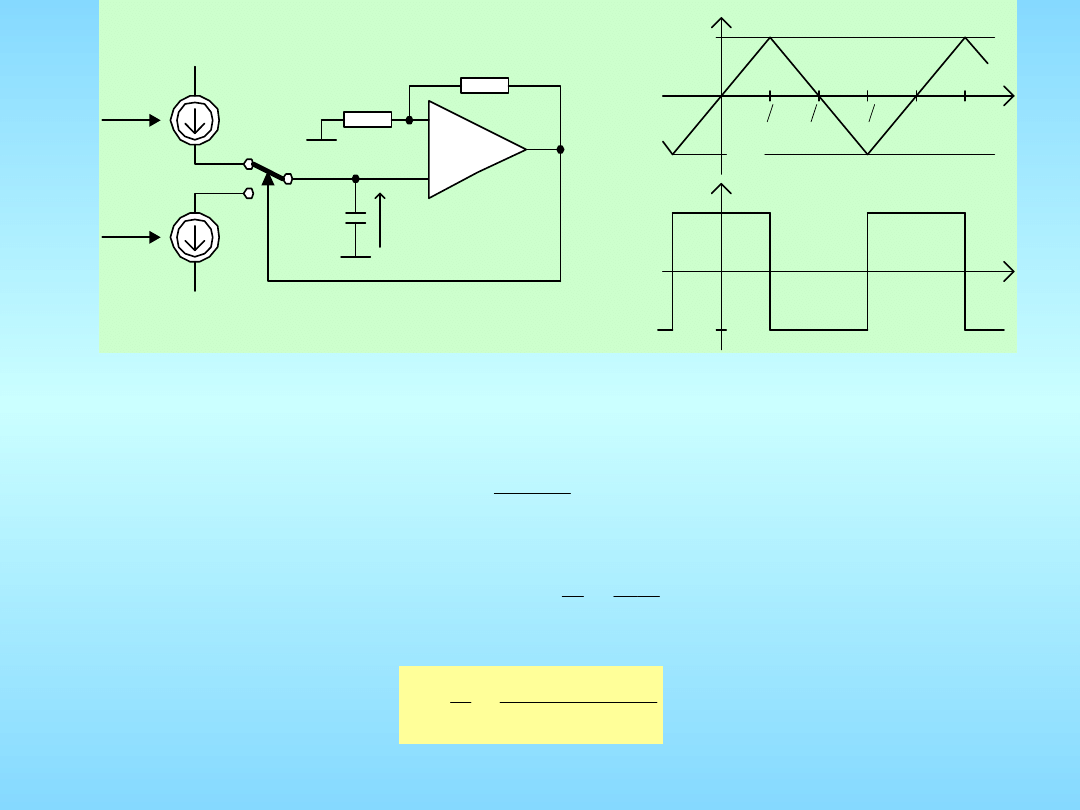
C

R

1

R

2





komp

u

1

2

u

REG

u

REG

u

C

U

P2

U

P1

u

C

U

K1

U

K2

u

T 4 T 2

3 4

T

T

t

t

VCO typu integrator - przerzutnik

2

,

1

2

1

1

2

,

1

k

p

U

R

R

R

U





2

2

tg

2

1

T

C

I

T

U

U

P

P













2

1

2

1

P

P

U

U

C

I

T

f







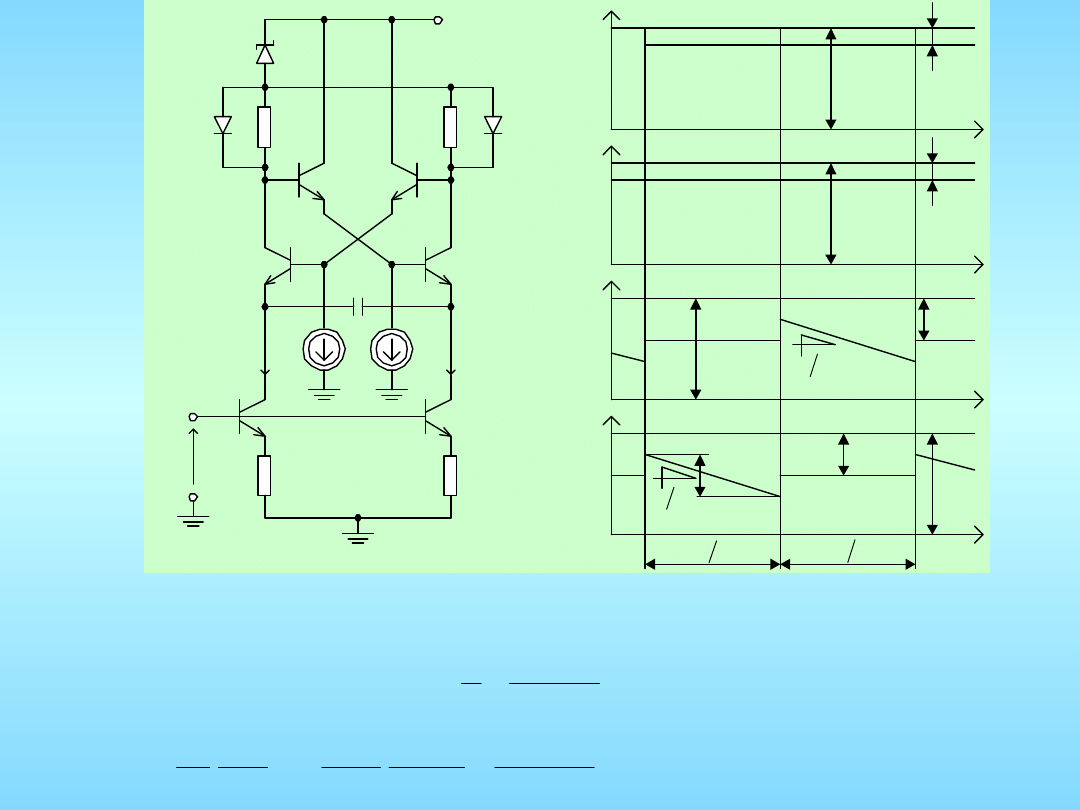
u

C1

R

E

u

REG

T

6

T

5

R

E

I

E

I

E

T

1

T

3

T

4

T

2

C

R

C

D

2

D

1

R

C

DZ

U

CC

U

CC1

u

C2

u

E2

u

E1

I

I

u

C2

u

E2

u

E1

u

C1

T 2

T 2

2U

BEP

2U

BEP

~

I C

I C

2U

BEP

U

CC1

U

CC1

t

t

t

t

U

CC1

U

CC1

U

F

U

F

a)

b)

Generator VCO w zmodyfikowanym układzie Bowesa: a) schemat ideowy,

b) idealizowane przebiegi czasowe napięć w układzie

C

U

I

T

f

BEP

4

1





C

/

ppm

3300

C

/

1

0033

,

0

mV

600

C

/

mV

2

1

1

o

o

o

0

0



















dT

dU

U

dT

d

BEP

BEP

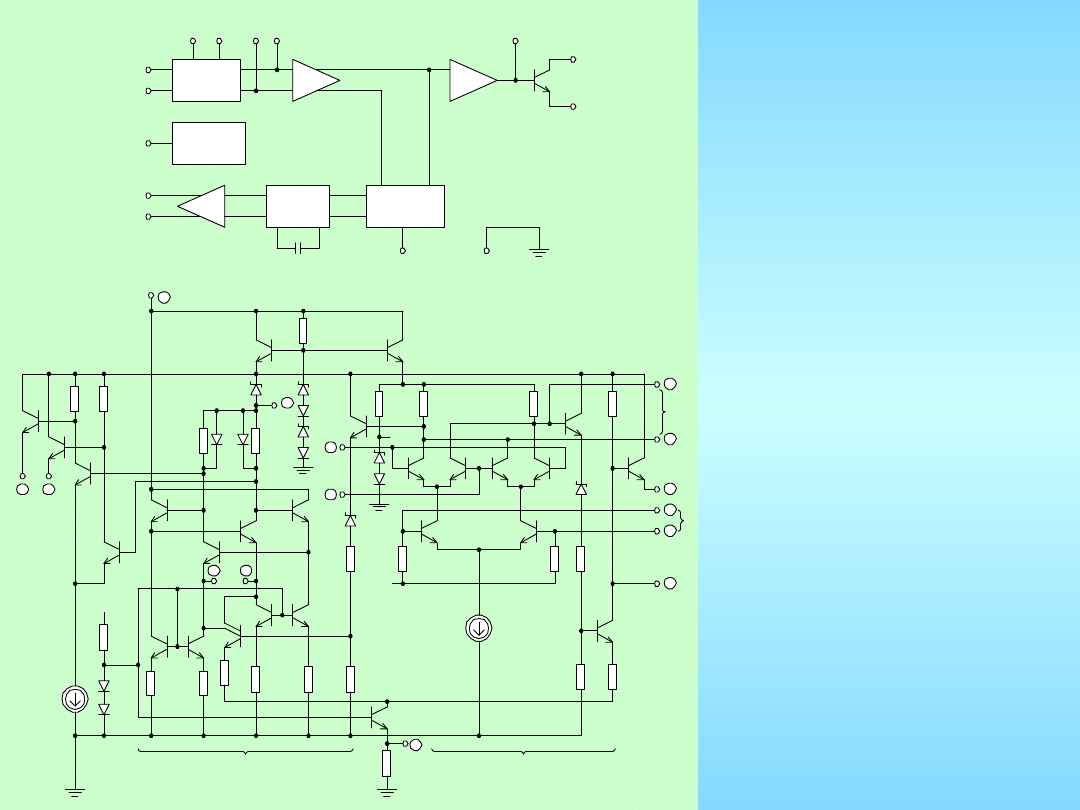
T

1

T

2

T

3

Wyjście

VCO

4

3

T

4

T

11

T

14

T

13

T

24

T

23

T

12

Pojemność

gen VCO

.

5

6

C

0

T

20

T

21

T

22B

T

22A

T

29

Bias

REF

1

1k

1k

16

U

CC

7V

25

. k

6k

6k

24

. k

12

. k

500

24

. k

12

. k

82

. k

7V

8k

8k

T

26

T

27

T

5

D

8

D

9

D

10

D

11

D

3

D

2

D

1

D

4

D

12

D

13

D

6

D

7

74

. k

T

6

T

9

T

8

T

7

2k

2k

4V

53

. k

14V

14V

We

ekt

fazy

det

.

2

15

1k

500

82

. k

82

. k

T

10

T

19

T

25

T

17

T

18

D

5

14

13

9

12

11

10

Deemfaza

Filtr

VCO

Detektor fazy

7

Zakres

przestrajania

12k

075

. mA

20

. mA

Wy

Wejście

ektora

fazy

det

VCO

Ogranicznik

A

Detektor

fazy

Układy

polaryzacji

Wzmacniacz

Filtr

FDP

 

Wejście

sygnałuu t

i

Wejście

VCO

Wyjście

VCO

Deemfaza

Wyjście

V



C

0

6

5

4

3

1

2

15

11

12

13

14

10

16

9

8

7

Zakres

przestrajania

a)

b)

1k

Pętla fazowa typu NE 562
firmy Signetics: a) schemat blokowy,
b) schemat ideowy

A

k

k

K

G

D



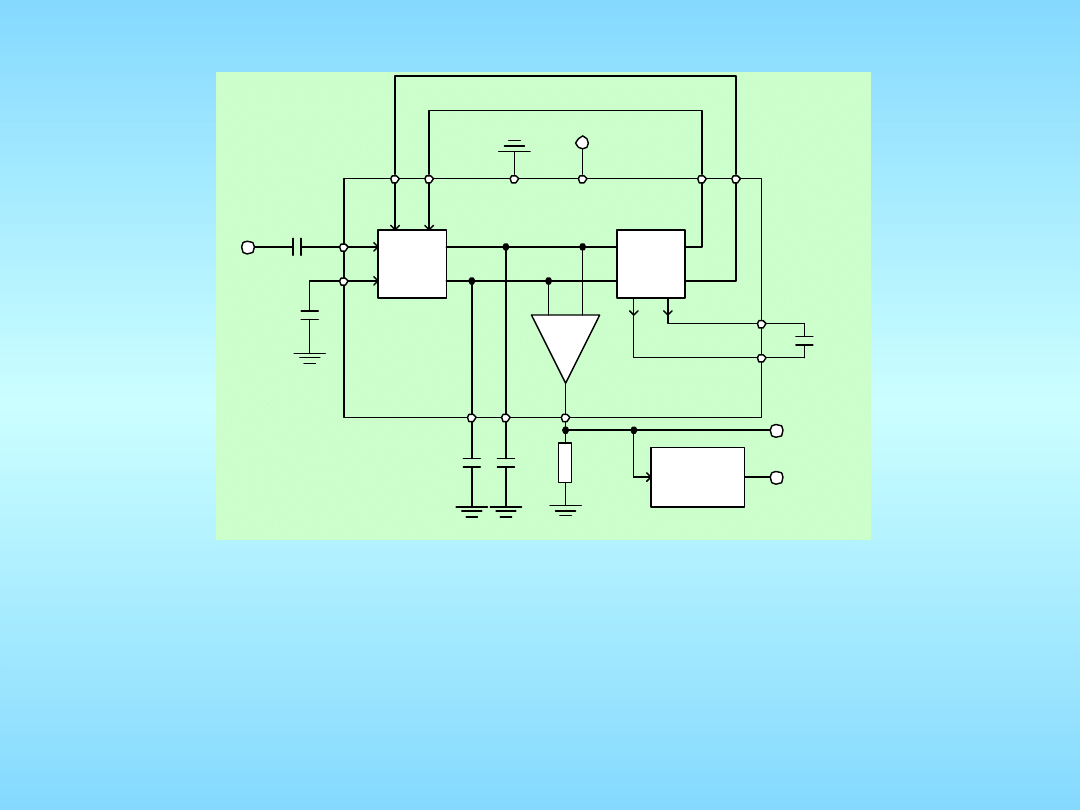
C

0

12

VCO

DF





13

15

16

8

2

4

3

U

V

CC

18

25pF

1nF

1nF

15k

Filtr

deemfazy

WY2

WY1

5

6

9

15

14

10nF

100pF

NE 562

f

i

Schemat demodulatora FM z układem NE 562 firmy Signetics