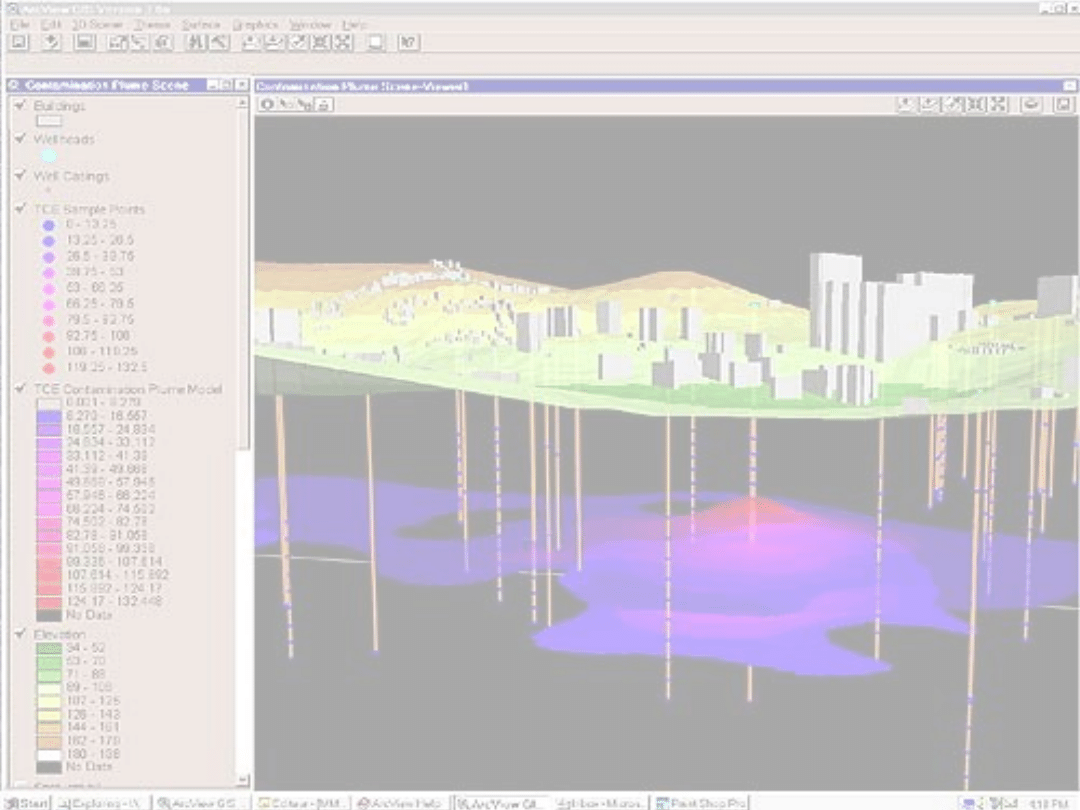
Mapa numeryczna

w zastosowaniach inżynierskich

Mapa numeryczna

– monitoring i analiza zmian

w układzie dynamicznym

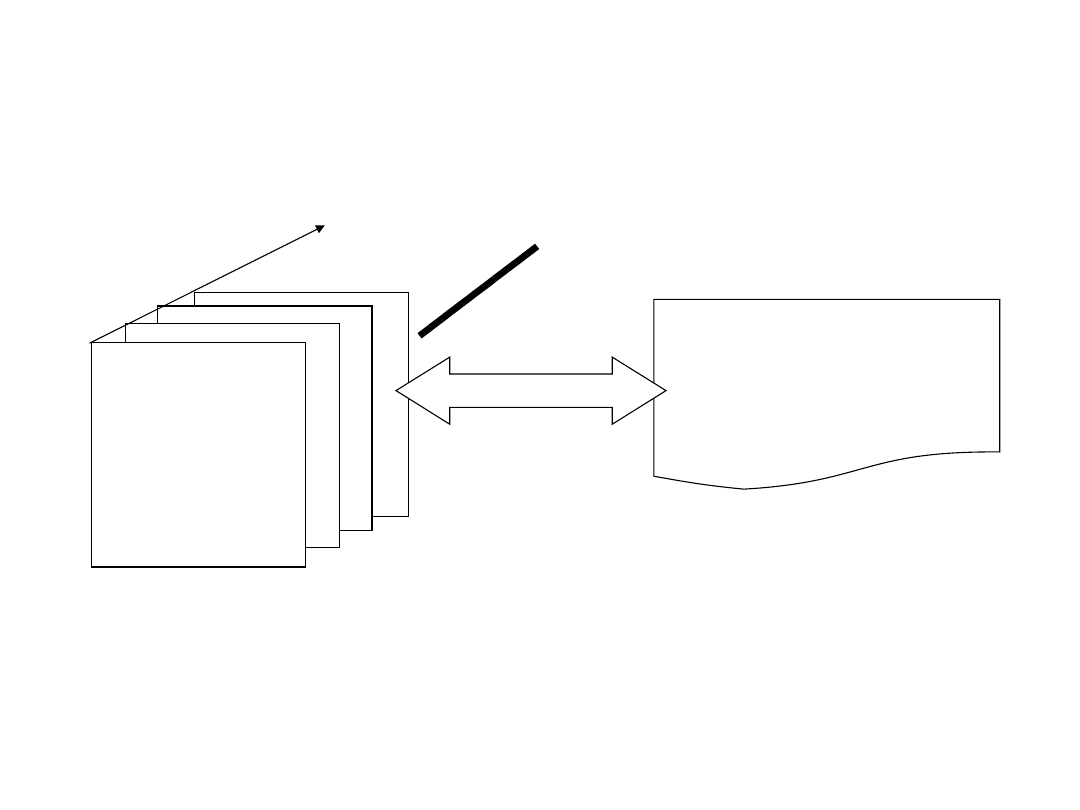
T

t

1

t

2

t

3

Zmiany rejestrowane w mapie numerycznej

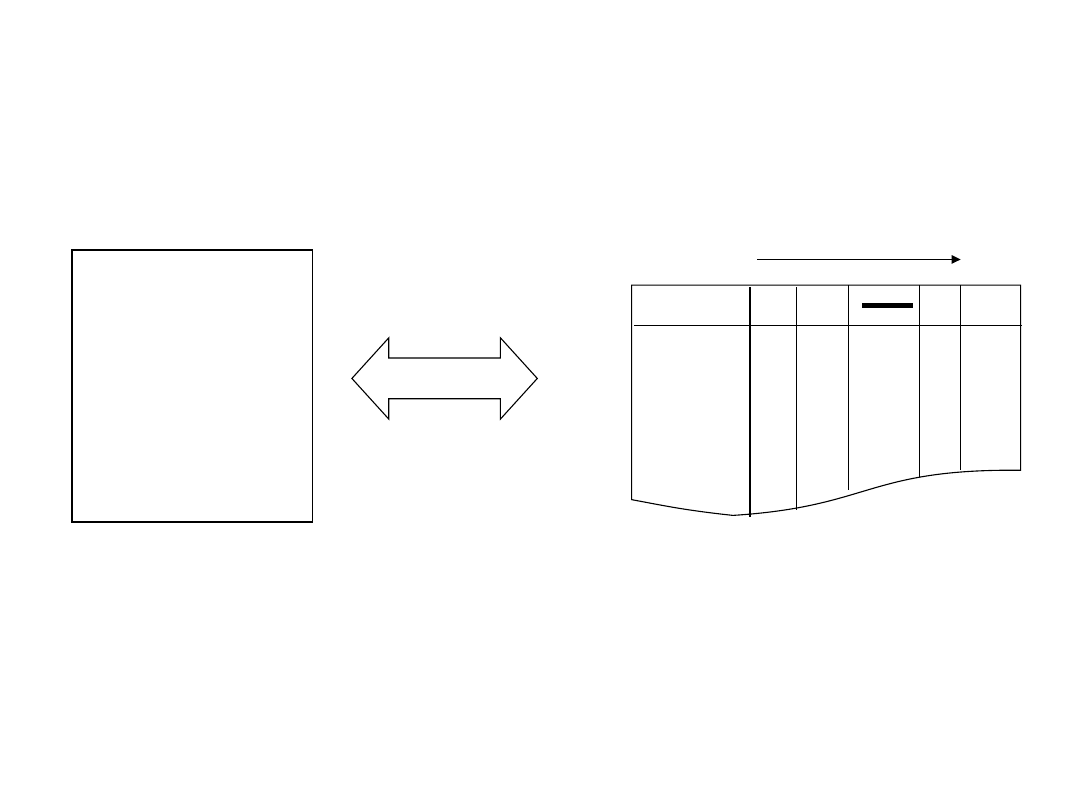
t

1

t

2

t

n

Szereg czasowy

Zmiany rejestrowane w opisowej części

bazy danych jako szeregi czasowe

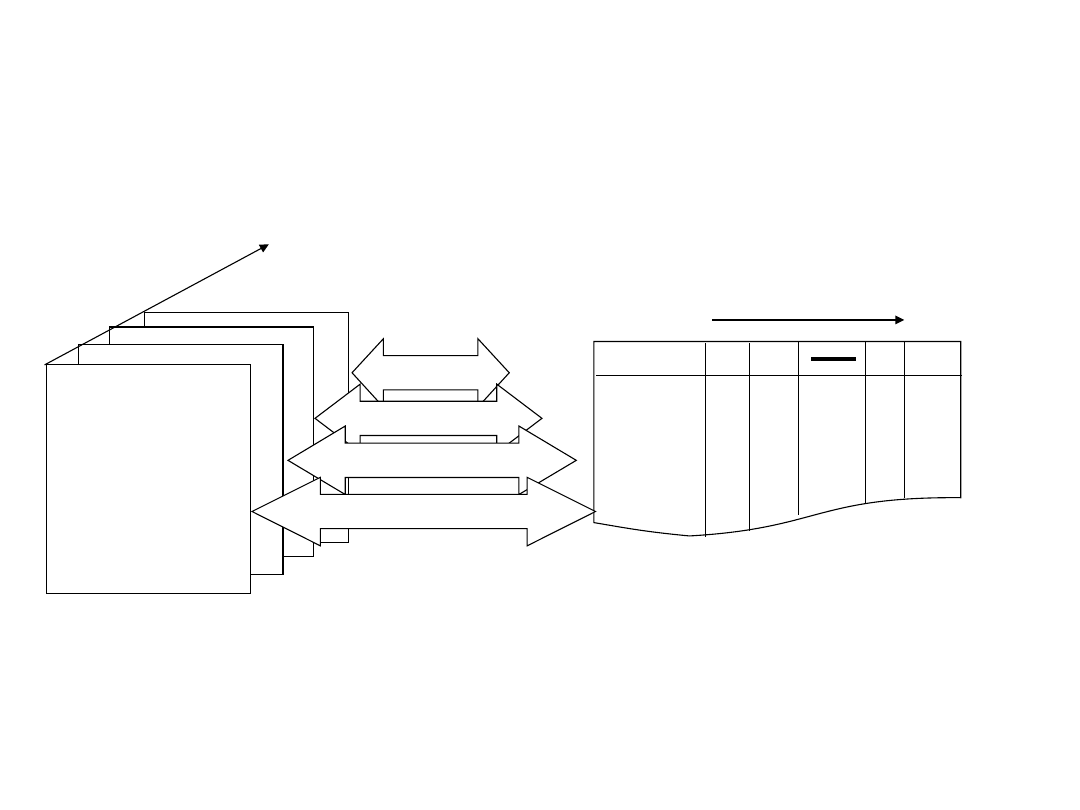
t

1

t

2

t

n

Szereg czasowy

T

t

1

t

2

t

3

Analiza zmian położenia i cech

zarejestrowanych w opisowej bazie danych

i mapie numerycznej

Etapy analizy zmienności

- przybliżone określenie charakteru zjawiska

- dobór układu (systemu) odniesienia

- stałość punktów odniesienia

- niezmienność względem analizowanych obiektów

- dobór materiałów źródłowych

- dobór metod pomiaru

- przygotowanie danych do analizy

- opracowanie algorytmów analiz statystycznych

- określenie form wizualizacji

- interpretacja wyników

Obiekty punktowe:

- przesunięcie (L)

- kierunek zmian(A lub X, Y, Z)

Obiekty liniowe:

-zmiana kształtu (zmiana położenia punktów

reprezentujących obiekt liniowy)

-zmiana długości

Obiekty powierzchniowe:

-zmiana kształtu (zmiana położenia punktów

reprezentujących granice obiektu)

-zmiana obwodu

-zmiana pola

ZMIANY

GEOMETRYCZN

E

Określenie zmian topologicznych między
obiektami punktowymi, linowymi
i powierzchniowymi typu:

-zawierania się,

-przecinania,

-sąsiedztwa,

ZMANY TOPOLOGICZNE

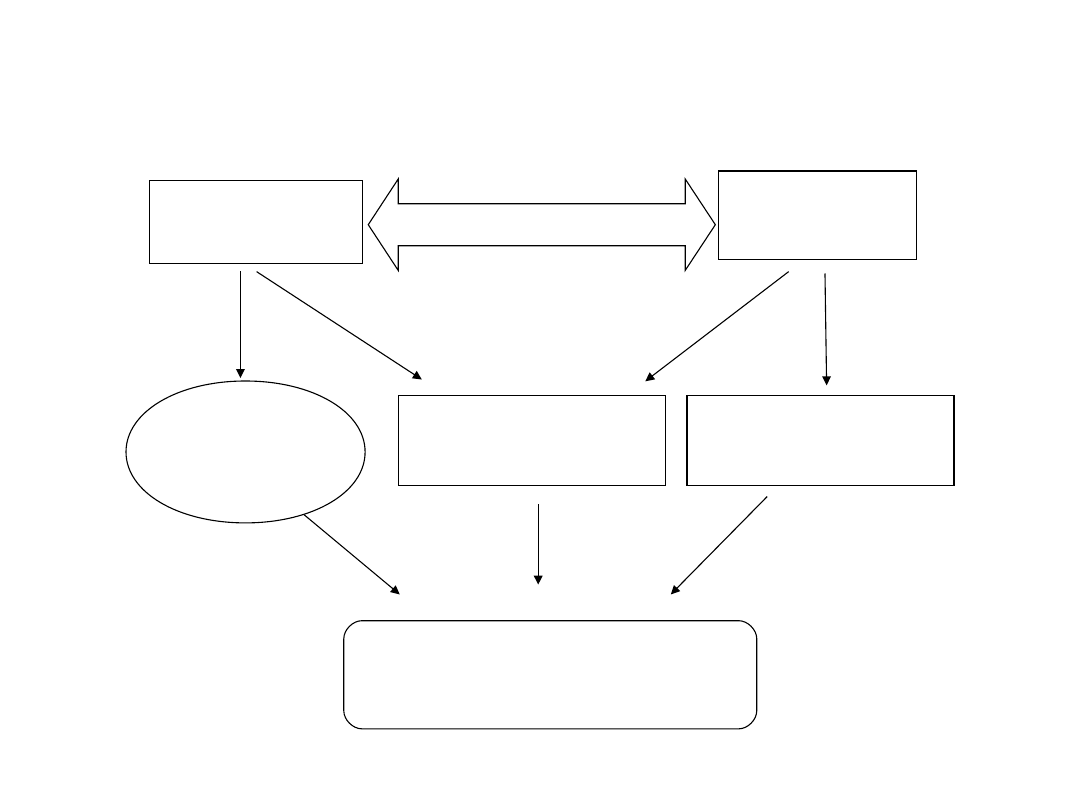
GRID

Analizy

przestrzenne

TIN

Transformacja

Zapytania

SQL

Analizy

statystyczne

Wizualizacja

ZMANY OBIEKTÓW

POWIERZCHNIOWYCH

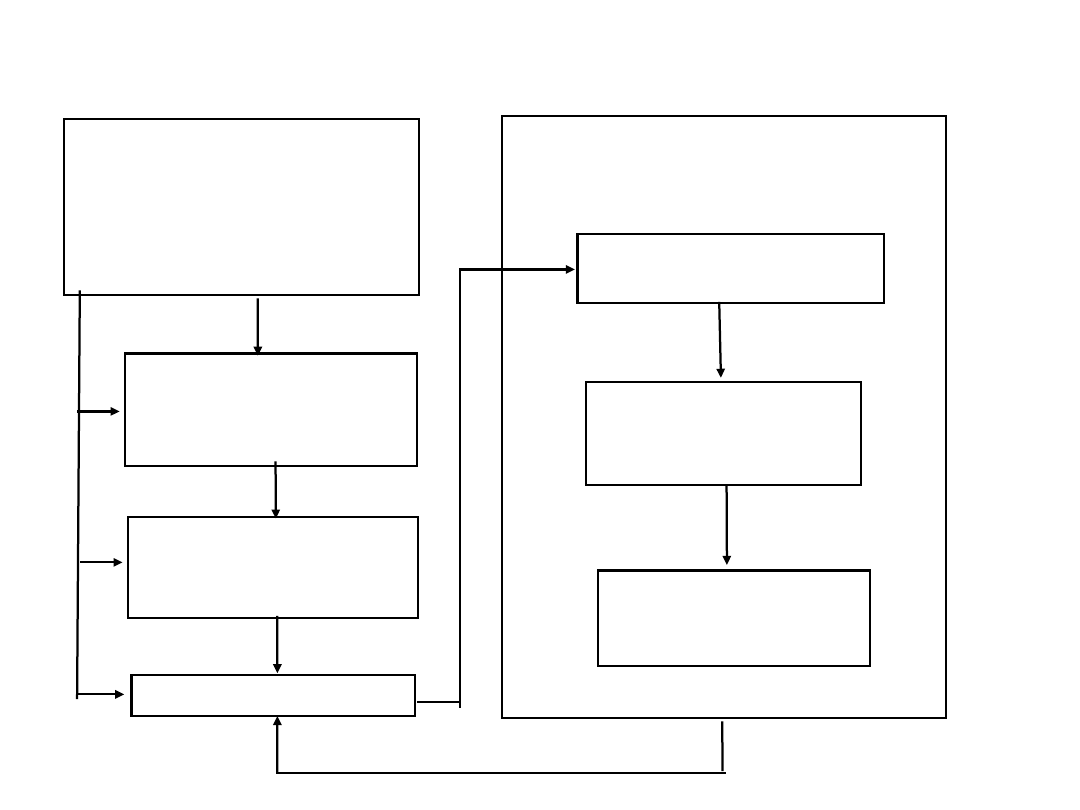
Własności obiektów

-fizyczne
-konstrukcyjne
-mechaniczne
-warunki

zewnętrzne

Zdefiniowanie

obiektu

Określenie metod

pomiaru i analiz

Pomiar

System informacji

przestrzennej

Struktura bazy

danych

Obliczenia

statystyczne i

analizy

przestrzenne

Opracowanie

wyników

Tworzenie i funkcjonowanie systemu

monitoringu

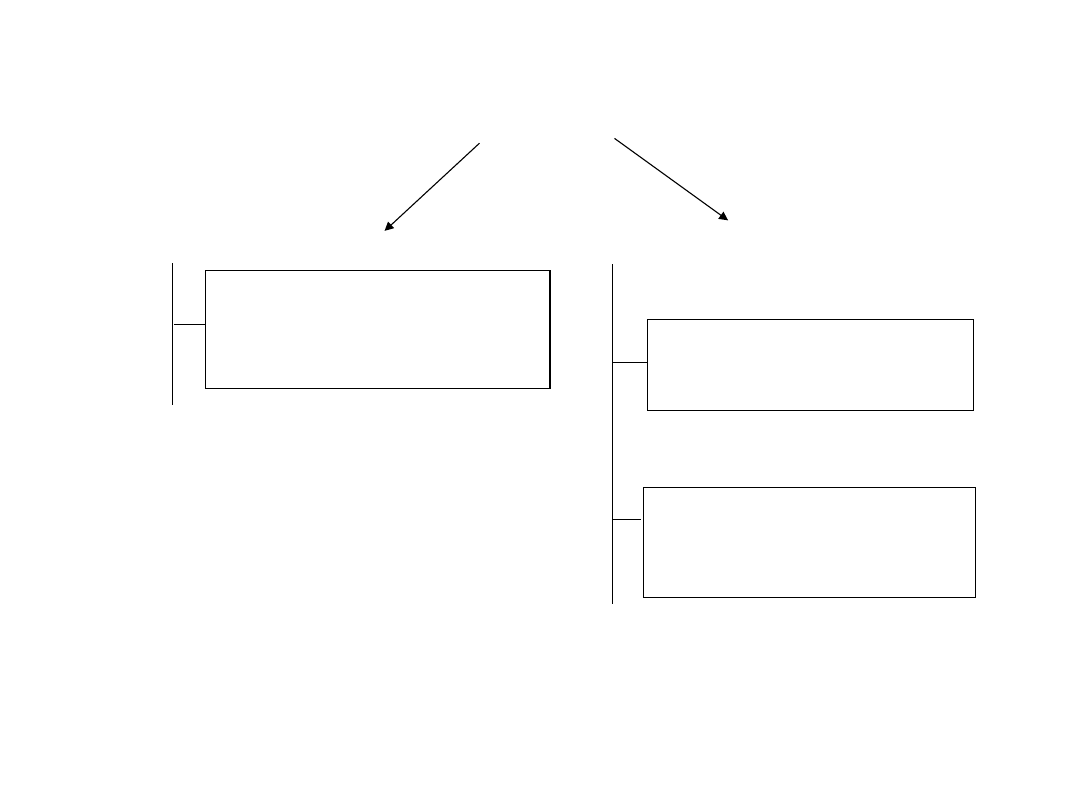
Cechy ilościowe

Cechy jakościowe

Pomiar wielkości w
ustalonych
interwałach
czasowych

Stwierdzenie
wystąpienia zmian

Ustalenie
klasyfikacji i
przyporządkowanie
cech do
odpowiednich klas

Analizy zmienności

- szereg szczegółowy
- szereg rozdzielczy punktowy
- szereg rozdzielczy z przedziałami klasowymi

Miary przeciętne

Średnia arytmetyczna

Średnią arytmetyczną - definiuje się jako sumę wartości cechy
mierzalnej podzieloną przez liczbę jednostek skończonej
zbiorowości statystycznej.

Własności
suma odchyleń poszczególnych wartości cechy od średniej równa się zero
- suma kwadratów odchyleń poszczególnych wartości cechy od średniej
jest minimalna
- średnia arytmetyczna jest wrażliwa na skrajne wartości cechy,
- średnia arytmetyczna z próby jest dobrym przybliżeniem
wartości przeciętnej.















n

1

i

i

n

2

1

x

n

1

n

x

....

x

x

x

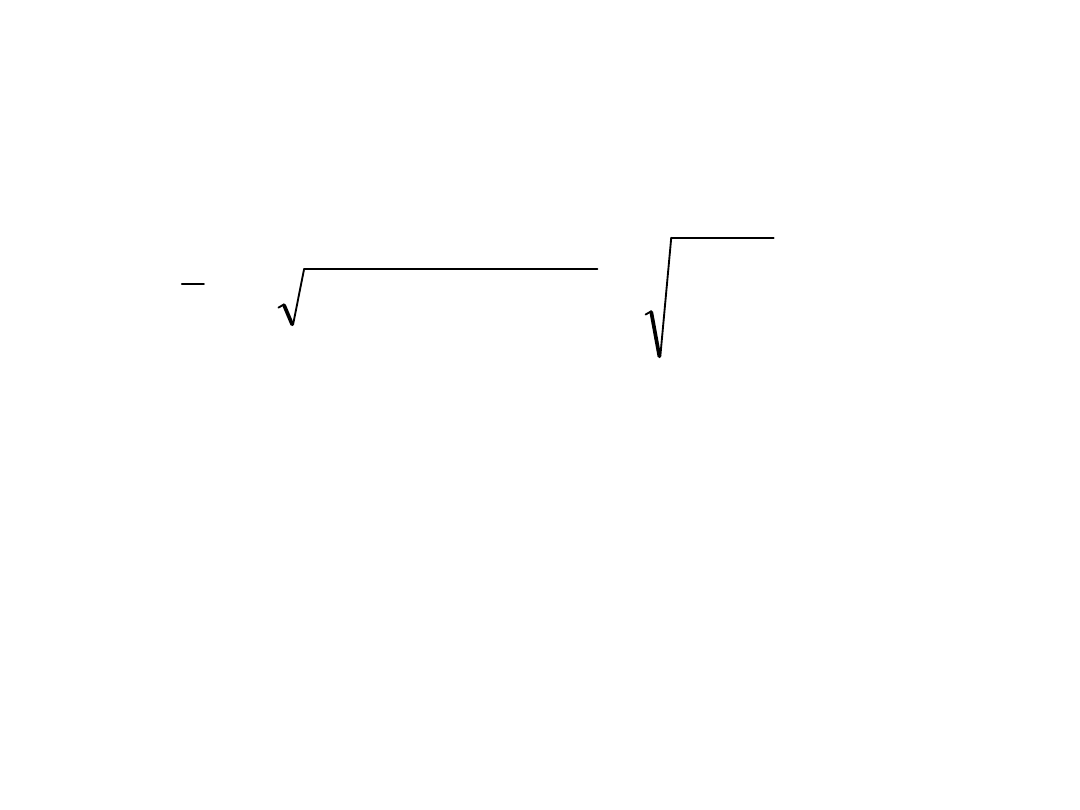
Średnią geometryczną

- stosuje się w badaniach średniego

tempa zmian zjawisk, a więc gdy zjawiska są ujmowane dynamicznie.

Modalna

Modalna Mo (dominanta D, moda, wartość najczęstsza) –
jest to wartość cechy statystycznej, która w danym rozkładzie
empirycznym występuje najczęściej.

n

x

1

i

i

n

n

2

1

G

x

x

....

x

x

x















Miary zmienności (rozproszenia, dyspersji)

Miary klasyczne

wariancja
odchylenie standardowe
odchylenie przeciętne
współczynnik zmienności

Miary pozycyjne

rozstęp
odchylenie ćwiartkowe
współczynnik zmienności

Rozstęp

- różnica pomiędzy wartością maksymalną,

a minimalną cechy - jest miarą charakteryzującą empiryczny
obszar zmienności badanej cechy, nie daje on jednak
informacji o zróżnicowaniu poszczególnych wartości cechy
w zbiorowości.

Wariancja

- jest to średnia arytmetyczna kwadratów odchyleń

poszczególnych wartości cechy od średniej arytmetycznej zbiorowości.

Odchylenie standardowe s

- jest to pierwiastek kwadratowy z wariancji.

Stanowi miarę zróżnicowania o mianie zgodnym z mianem badanej
cechy, określa przeciętne zróżnicowanie poszczególnych wartości
cechy od średniej arytmetycznej.

Odchylenie przeciętne d

- jest to średnia arytmetyczna bezwzględnych

odchyleń wartości cechy od średniej arytmetycznej. Określa o ile
jednostki danej zbiorowości różnią się średnio, ze względu na wartość
cechy, od średniej arytmetycznej.

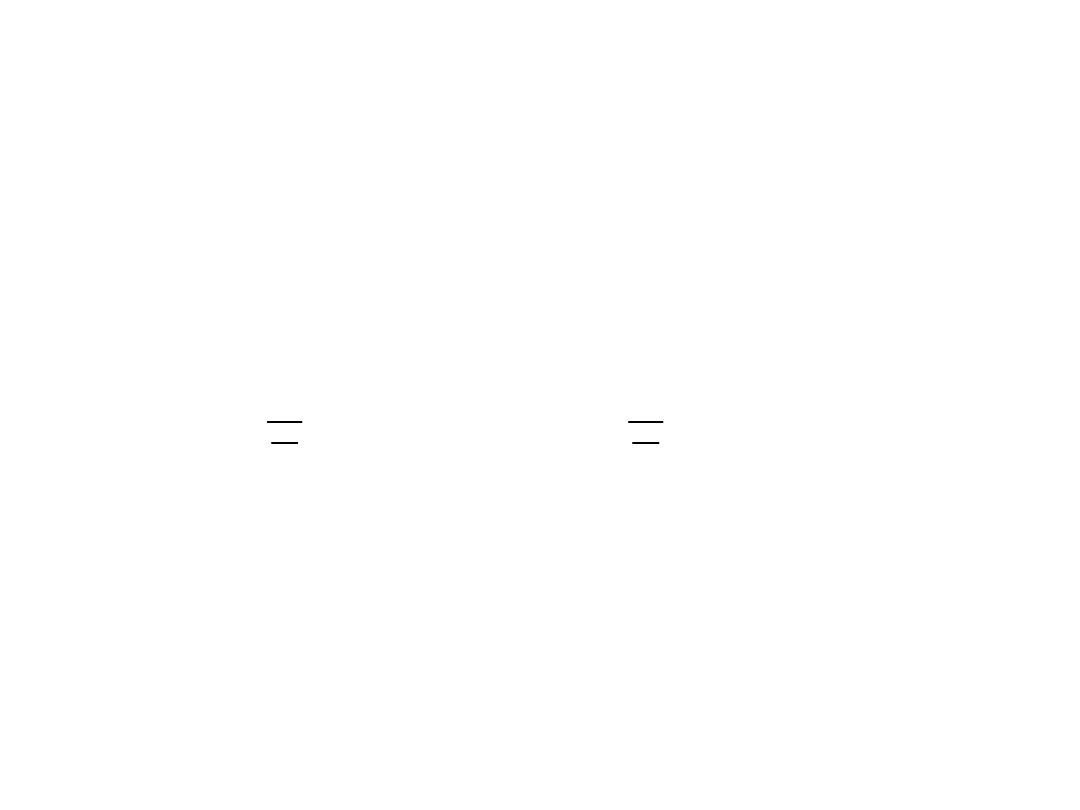
Współczynnik zmienności

jest ilorazem bezwzględnej miary

zmienności cechy i średniej wartości tej cechy,
jest wielkością niemianowaną, najczęściej podawaną w procentach.

Klasyczne współczynniki zmienności:

x

s

V

s



x

d

V

d



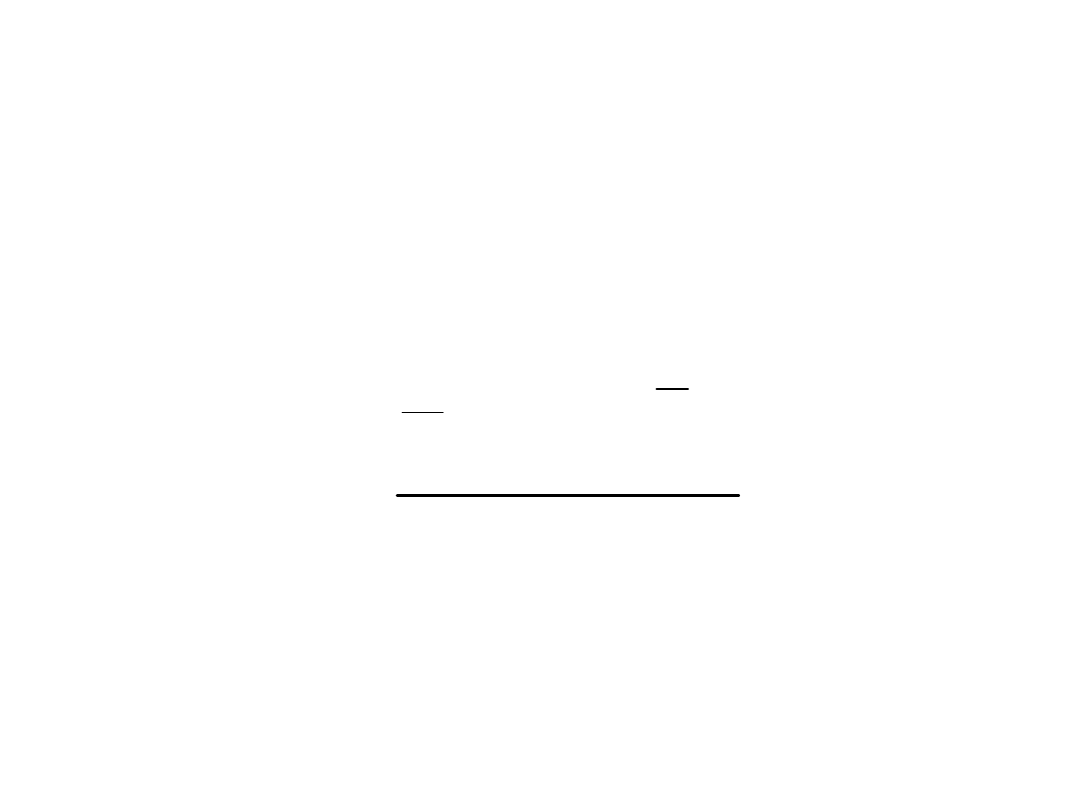
Miary koncentracji

Współczynnik skupienia (koncentracji) (kurtoza) K

- jest miarą

skupienia poszczególnych obserwacji wokół średniej.
Im wyższa wartość współczynnika tym bardziej wysmukła krzywa
liczebności, większa koncentracja wartości cech wokół średniej.





4

4

n

1

i

i

s

x

x

n

1

K









Współczynnik korelacji

jest miernikiem siły zależności między

badanymi zmiennymi. Korelacja może dotyczyć cech mierzalnych
jak i cech jakościowych. Współzależność między zmiennymi
może mieć charakter liniowy lub nieliniowy. Badania związku między
zmiennymi jest możliwe przy założeniu, że czynnik losowy występujący
w modelu regresji nie będzie brany pod uwagę, czyli nie wpływa na te
zmienne. Przyjmuje się, że zmienne porównywane są zmiennymi
losowymi.

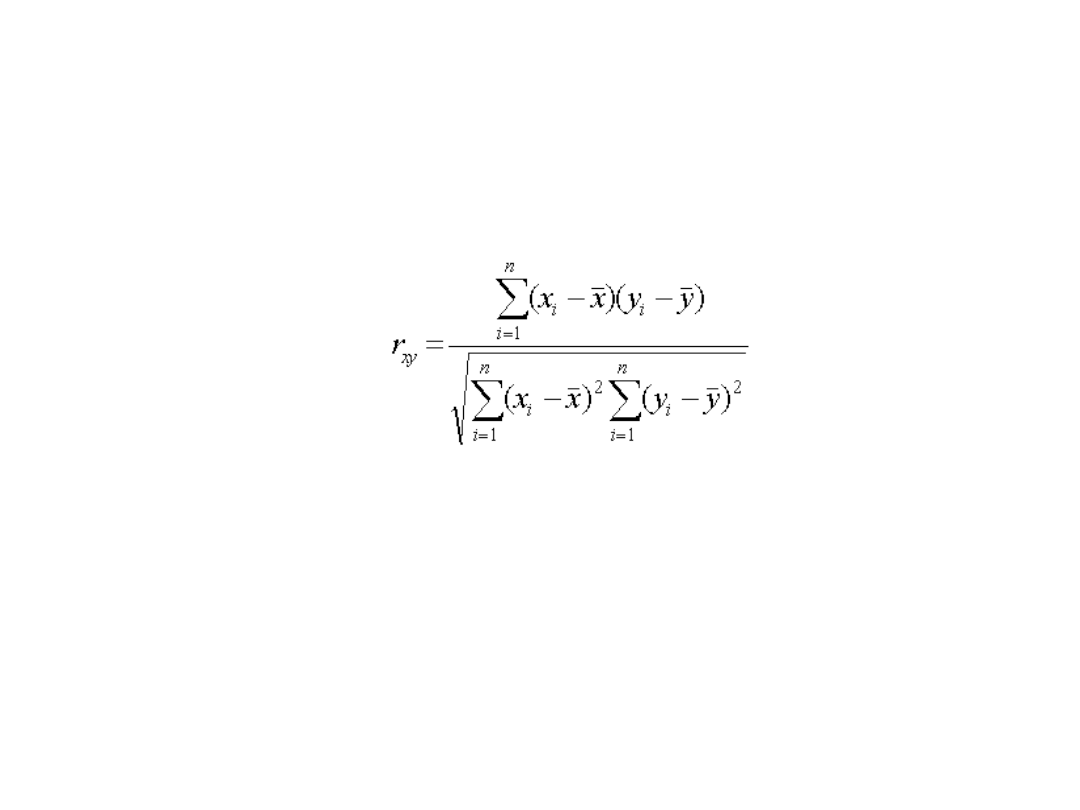
Współczynnik korelacji liniowej Pearsona

- jest opisową miarą

siły i kierunku zależności korelacyjnej dwóch cech mierzalnych
będących cechami statystycznymi x i y, gdzie:
X=(x1,x2,...,xn),
Y=(y1,y2,...,yn).
Można wówczas posłużyć się wzorem obrazującym współczynnik
korelacji liniowej Pearsona:

 

Współczynnik przybiera wartości z przedziału [-1,1].
Gdy r=1 lub -1 wówczas między zmiennymi x i y zachodzi zależność
funkcyjna - punkty empiryczne układają się na linii prostej.
Gdy r=0 wówczas brak jest zależności między zmiennymi,
nie są one wtedy skorelowane. W praktyce nie zdarza się aby r=-1,1
lub 0, zazwyczaj podaje się, że gdy |r| należy do przedziału: [0,2; 0,9] to istnieje
współzależność między zmiennymi (większa lub mniejsza w zależności od wartości r).
Natomiast gdy |r|<0,2 mówi się, że brak jest zależności między zmiennymi.

Współczynnik korelacji rang Spearmana

- miernik ten służy do

mierzenia korelacji rang dwóch zmiennych. Nie jest konieczne
dysponowanie wartościami cechy X i cechy Y, wystarczy znać ich
rangi (pozycje) co często zdarza się w analizach zjawisk społecznych
i ekonomicznych. Zaletą tej miary jest fakt, że może być ona stosowana
do mierzenia siły korelacji zmiennych mierzalnych jak i porządkowych.
Ma on zastosowanie gdy:
obie porównywane cechy są mierzalne ale zbiorowość jest mało liczna,
obie względnie jedna cecha ma charakter jakościowy i jest możliwość
ustalenia w kolejności poszczególnych obiektów analizy względem
natężenia tych cech.

Etapy wyznaczania współczynnika korelacji rang
Spearmana:

- uporządkowanie obiektów rosnąco lub malejąco (w
zależności od
rodzaju cechy) ze względu na obie cechy (tworzenie
podwójnego
rankingu),

- każdemu obiektowi zostaje przypisana ranga (kolejna
liczba) w
zależności od miejsca zajmowanego przez obiekt po
uporządkowaniu
dla obydwu cech. Ze względu na cechę x wyznacza się
rangę c

i

x (jest

to pozycja i-tego obiektu w rankingu ze względu na
cechę x).
Podobnie się postępuje dla cechy y wyznaczając rangę
c

i

y.

- wyznacza się zmienną d

i

, która powstaje w wyniku

różnicy rangi c

i

x

i c

i

y:

y

c

x

c

d

i

i

i





Mając powyższe dane można wyznaczyć współczynnik
korelacji rang Spearmana wg. wzoru:

Współczynnik korelacji rang Spearmana przyjmuje
wartość [-1,1] a interpretacja wyników jest podobna jak
dla współczynnika korelacji liniowej Pearsona.





1

n

n

d

6

1

r

2

n

1

i

2

i

s











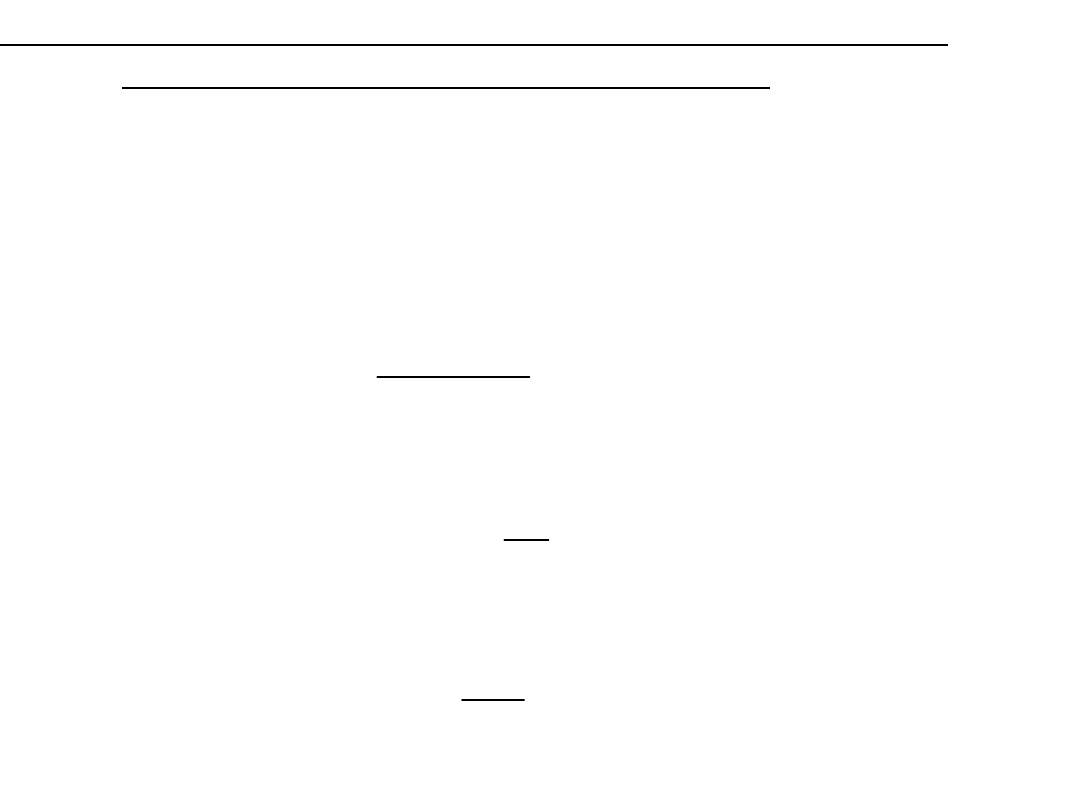
Metody statystyczne wykorzystywane w analizach

zmienności szeregów czasowych

przyrost absolutny

tempo

wskaźnik jednopodstawowy

-wskaźnik łańcuchowy

100

y

y

y

T

1

i

1

i

i











o

i

o

y

y

i 

1





i

i

o

y

y

i

1

i

i

ab

y

y

P







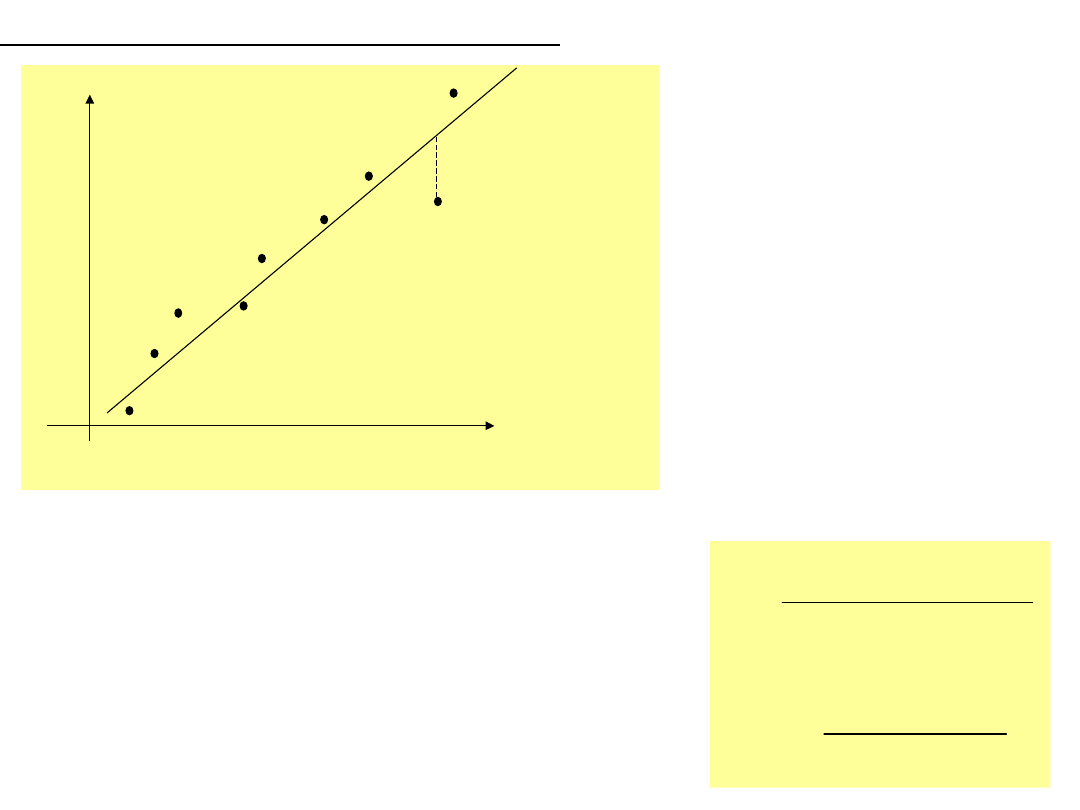
Linie regresji ( trend zjawiska)

y

i

=a+

bt

i

y

i

-y

i

’





min

y

y

2

'
i

i















min

bt

a

y

2

i































min

t

b

t

ab

2

na

ty

b

2

y

a

2

y

2

2

2

i

i

2

i

Różniczkując względem a i b



































0

t

b

2

t

a

2

ty

2

0

t

b

2

na

2

y

2

2

i

i





























0

t

b

t

a

ty

2

t

b

na

y

2

i

i

 







 







2

2

i

i

t

t

n

y

t

ty

n

b

n

t

b

y

a

i







