S

S

t

t

a

a

t

t

y

y

s

s

t

t

y

y

k

k

a

a

Ćwiczenia z SPSS

Ćwiczenia z SPSS

-1-

-1-

Podstawowe terminy

Podstawowe terminy

statystyczne

statystyczne

Cel zajęć

Cel zajęć



Celem ćwiczeń jest zdobycie przez studentów

Celem ćwiczeń jest zdobycie przez studentów

podstawowych umiejętności niezbędnych

podstawowych umiejętności niezbędnych

przy planowaniu badań empirycznych oraz

przy planowaniu badań empirycznych oraz

analizie i interpretacji ich wyników; tj:

analizie i interpretacji ich wyników; tj:



właściwego formułowania problemów badawczych

właściwego formułowania problemów badawczych

i hipotez,

i hipotez,



dobierania właściwych narzędzi statystycznych do

dobierania właściwych narzędzi statystycznych do

danego problemu badawczego,

danego problemu badawczego,



oceny jakości uzyskanych danych,

oceny jakości uzyskanych danych,



interpretowania wyników analiz statystycznych.

interpretowania wyników analiz statystycznych.

Organizacja zajęć

Organizacja zajęć



Zajęcia mają formę praktycznych ćwiczeń przy

Zajęcia mają formę praktycznych ćwiczeń przy

komputerze. Każdy z uczestniczących w nich

komputerze. Każdy z uczestniczących w nich

studentów ma szansę osobiście przećwiczyć

studentów ma szansę osobiście przećwiczyć

omawiane na wykładzie ze statystyki metody na

omawiane na wykładzie ze statystyki metody na

danych dostarczonych przez osobę prowadzącą.

danych dostarczonych przez osobę prowadzącą.



Wszystkie zagadnienia będą objaśniane na

Wszystkie zagadnienia będą objaśniane na

konkretnych przykładach zaczerpniętych z

konkretnych przykładach zaczerpniętych z

problematyki psychologicznej. Uczestnicy zajęć

problematyki psychologicznej. Uczestnicy zajęć

posiądą umiejętność obliczania statystyk

posiądą umiejętność obliczania statystyk

(porównania międzygrupowe, techniki

(porównania międzygrupowe, techniki

korelacyjne, regresja, analiza wariancji),

korelacyjne, regresja, analiza wariancji),

tworzenia raportów i wykresów.

tworzenia raportów i wykresów.



Dodatkowo, do każdych zajęć zostaną

Dodatkowo, do każdych zajęć zostaną

przygotowane stosowne materiały dydaktyczne.

przygotowane stosowne materiały dydaktyczne.

Wymagania i forma

Wymagania i forma

zaliczenia

zaliczenia



Wymagania wstępne

Wymagania wstępne



Zaliczenie wykładu ze statystyki

Zaliczenie wykładu ze statystyki



Umiejętność obsługi komputera.

Umiejętność obsługi komputera.



Kryteria i sposób zaliczania

Kryteria i sposób zaliczania



Obecność na zajęciach

Obecność na zajęciach



Zdobycie odpowiedniej ilości punktów z

Zdobycie odpowiedniej ilości punktów z

kolokwiów w trakcie trwania zajęć

kolokwiów w trakcie trwania zajęć



Uzyskanie pozytywnej oceny z

Uzyskanie pozytywnej oceny z

końcowego testu

końcowego testu

Tematy zajęć

Tematy zajęć



Zajęcia organizacyjne – przedstawienie celu zajęć (odniesienie

Zajęcia organizacyjne – przedstawienie celu zajęć (odniesienie

użycia pakietu statystycznego do szerszego kontekstu

użycia pakietu statystycznego do szerszego kontekstu

prowadzenia badań empirycznych), zakresu tematycznego,

prowadzenia badań empirycznych), zakresu tematycznego,

wymagań, kryteriów i sposobu zaliczania; Przygotowanie

wymagań, kryteriów i sposobu zaliczania; Przygotowanie

macierzy danych - organizacja macierzy, kodowanie danych,

macierzy danych - organizacja macierzy, kodowanie danych,

opis zmiennych, format zmiennych itp.

opis zmiennych, format zmiennych itp.



Ćwiczenia dotyczące organizacji macierzy danych - kodowanie

Ćwiczenia dotyczące organizacji macierzy danych - kodowanie

brakujących wartości, rekodowanie danych, wyliczanie nowych

brakujących wartości, rekodowanie danych, wyliczanie nowych

zmiennych; Organizacja pakietu SPSS - data, syntax, output i

zmiennych; Organizacja pakietu SPSS - data, syntax, output i

inne okna programu

inne okna programu



Statystyki opisowe - frekwencje, tablice wielodzielcze, miary

Statystyki opisowe - frekwencje, tablice wielodzielcze, miary

tendencji centralnej i rozproszenia – średnia, mediana,

tendencji centralnej i rozproszenia – średnia, mediana,

odchylenie standardowe – skośność, kurtoza itp; Wykresy

odchylenie standardowe – skośność, kurtoza itp; Wykresy

częstości

częstości



Test sprawdzający wiedzę z zakresu organizacji macierzy

Test sprawdzający wiedzę z zakresu organizacji macierzy

danych i statystyk opisowych; Testy istotności różnicy I - testy

danych i statystyk opisowych; Testy istotności różnicy I - testy

t (dla jednej próby, dla prób niezależnych, dla prób zależnych)

t (dla jednej próby, dla prób niezależnych, dla prób zależnych)

Tematy zajęć

Tematy zajęć



Testy istotności różnicy II – testy t, testy

Testy istotności różnicy II – testy t, testy

nieparametryczne (U-Manna-Whitneya, Z-

nieparametryczne (U-Manna-Whitneya, Z-

Kołmogorowa-Smirnowa, W-Wilcoxona, test χ2)

Kołmogorowa-Smirnowa, W-Wilcoxona, test χ2)



Test sprawdzający wiedzę z zakresu testów istotności

Test sprawdzający wiedzę z zakresu testów istotności

różnicy; Miary siły związku – r-Pearsona, τ-Kendalla i

różnicy; Miary siły związku – r-Pearsona, τ-Kendalla i

ρ-Spearmana, φ-Yulea i V-Cramera

ρ-Spearmana, φ-Yulea i V-Cramera



Test sprawdzający wiedzę z zakresu miar siły

Test sprawdzający wiedzę z zakresu miar siły

związku; Analiza regresji liniowej

związku; Analiza regresji liniowej



Analiza wariancji

Analiza wariancji



Test sprawdzający wiedzę z zakresu analizy regresji

Test sprawdzający wiedzę z zakresu analizy regresji

liniowej i analizy wariancji; Ćwiczenia powtórkowe z

liniowej i analizy wariancji; Ćwiczenia powtórkowe z

wybranych partii materiału

wybranych partii materiału



Ćwiczenia powtórkowe wybranych partii materiału;

Ćwiczenia powtórkowe wybranych partii materiału;

Test końcowy

Test końcowy

Statystyka

Statystyka



Statystyka

Statystyka

– dział metodologii

– dział metodologii

naukowej, zajmujący się zbieraniem,

naukowej, zajmujący się zbieraniem,

klasyfikowaniem, opisem i

klasyfikowaniem, opisem i

interpretacją danych. Jej celem jest

interpretacją danych. Jej celem jest

opis i wyciąganie wniosków

opis i wyciąganie wniosków

dotyczących właściwości ilościowych

dotyczących właściwości ilościowych

populacji.

populacji.

Populacja

Populacja



Populacja

Populacja

– zbiór elementów (rzeczy,

– zbiór elementów (rzeczy,

zdarzeń), podlegających badaniu

zdarzeń), podlegających badaniu

statystycznemu. Elementy populacji są do

statystycznemu. Elementy populacji są do

siebie podobne pod względem badanej cechy,

siebie podobne pod względem badanej cechy,

ale nie są identyczne.

ale nie są identyczne.



Ze względu na liczebność zbioru, populacje

Ze względu na liczebność zbioru, populacje

można podzielić na:

można podzielić na:



populacje skończone

populacje skończone

- np. liczba ludzi w Polsce,

- np. liczba ludzi w Polsce,

liczba psów w schronisku

liczba psów w schronisku



populacje nieskończone

populacje nieskończone

- np. czas, liczba

- np. czas, liczba

możliwych rzutów kostką

możliwych rzutów kostką

Parametr, a estymator:

Parametr, a estymator:



Parametr

Parametr

-właściwość opisująca

-właściwość opisująca

populację. Zazwyczaj parametry pozostają

populację. Zazwyczaj parametry pozostają

nieznane, szacujemy je na podstawie

nieznane, szacujemy je na podstawie

wartości uzyskanych z prób. (oznaczenia -

wartości uzyskanych z prób. (oznaczenia -

litery greckie)

litery greckie)



Estymator

Estymator

-właściwość próby pobranej

-właściwość próby pobranej

losowo z populacji. Wartość uzyskana przy

losowo z populacji. Wartość uzyskana przy

badaniu próby jest estymatorem

badaniu próby jest estymatorem

odpowiedniego parametru populacji.

odpowiedniego parametru populacji.

(oznaczenia - litery łacińskie)

(oznaczenia - litery łacińskie)

Zmienna, stała:

Zmienna, stała:



Zmienna

Zmienna

– właściwość, pod względem,

– właściwość, pod względem,

której elementy grupy lub zbioru różnią się

której elementy grupy lub zbioru różnią się

między sobą (np. płeć, wiek, inteligencja).

między sobą (np. płeć, wiek, inteligencja).



Stała

Stała

- właściwość, pod względem, której

- właściwość, pod względem, której

elementy grupy lub zbioru nie różnią się

elementy grupy lub zbioru nie różnią się

między sobą (w pewnym sensie to

między sobą (w pewnym sensie to

szczególny przypadek zmiennej, która nie

szczególny przypadek zmiennej, która nie

zmienia się w zależności od elementu

zmienia się w zależności od elementu

grupy lub w konkretnym zbiorze

grupy lub w konkretnym zbiorze

określonych warunków).

określonych warunków).

Klasyfikacje zmiennych 1

Klasyfikacje zmiennych 1



Zmienna niezależna

Zmienna niezależna

to zmienna

to zmienna

sprawcza; jej określona wartość

sprawcza; jej określona wartość

bezpośrednio wpływa na wartość

bezpośrednio wpływa na wartość

innych zmiennych.

innych zmiennych.



Zmienna zależna

Zmienna zależna

ulega zmianom pod

ulega zmianom pod

wpływem zmiennej niezależnej; jej

wpływem zmiennej niezależnej; jej

wartość wynika bezpośrednio z kształtu

wartość wynika bezpośrednio z kształtu

zmian wartości zmiennej niezależnej.

zmian wartości zmiennej niezależnej.

Klasyfikacje zmiennych 2

Klasyfikacje zmiennych 2



Ilościowa

Ilościowa

- wyraża określoną właściwość

- wyraża określoną właściwość

lub cechę danego obiektu, której poziom

lub cechę danego obiektu, której poziom

lub natężenie można wyrazić liczbowo

lub natężenie można wyrazić liczbowo

(wzrost, wiek, zarobki).

(wzrost, wiek, zarobki).



Jakościowa

Jakościowa

– ( zaliczamy do nich z.

– ( zaliczamy do nich z.

dychotomiczne) wyraża określoną

dychotomiczne) wyraża określoną

właściwość lub cechę danego obiektu nie

właściwość lub cechę danego obiektu nie

przy pomocy wartości liczbowych, ale przez

przy pomocy wartości liczbowych, ale przez

skategoryzowanie tych cech czy

skategoryzowanie tych cech czy

właściwości (np. kobieta – mężczyzna).

właściwości (np. kobieta – mężczyzna).

Klasyfikacje zmiennych 3

Klasyfikacje zmiennych 3



Ciągłe

Ciągłe

– mogą przyjmować dowolne

– mogą przyjmować dowolne

wartości z określonego zakresu. Między

wartości z określonego zakresu. Między

dwiema dowolnymi wartościami zmiennej

dwiema dowolnymi wartościami zmiennej

znajduje się nieskończenie wiele wartości

znajduje się nieskończenie wiele wartości

pośrednich (np. wzrost, ciężar, czas).

pośrednich (np. wzrost, ciężar, czas).



Dyskretne

Dyskretne

(nieciągłe) – może

(nieciągłe) – może

przyjmować tylko niektóre wartości (np.

przyjmować tylko niektóre wartości (np.

liczba dzieci w rodzinie, liczba rzutów

liczba dzieci w rodzinie, liczba rzutów

kostką).

kostką).

Klasyfikacje zmiennych 4

Klasyfikacje zmiennych 4



Dychotomiczna

Dychotomiczna

(dwuwartościowa) –

(dwuwartościowa) –

zmienna, która w naturalny sposób przyjmuję

zmienna, która w naturalny sposób przyjmuję

tylko wartości ze zbioru dwuelementowego;

tylko wartości ze zbioru dwuelementowego;

zmienna dwukategorialna (płeć, odp: tak, nie).

zmienna dwukategorialna (płeć, odp: tak, nie).



Zdychotomizowana

Zdychotomizowana

– faktycznie

– faktycznie

wielowartościowa, ale dla jakiś celów

wielowartościowa, ale dla jakiś celów

sprowadzona do postaci dwuwartościowej (np.

sprowadzona do postaci dwuwartościowej (np.

wzrost niski – do 160; wysoki - powyżej 170).

wzrost niski – do 160; wysoki - powyżej 170).

Klasyfikacje zmiennych 5a

Klasyfikacje zmiennych 5a



Zmienne nominalne

Zmienne nominalne

– właściwości

– właściwości

elementów należących do grupy, która

elementów należących do grupy, która

została wyznaczona przez operację

została wyznaczona przez operację

pozwalającą na formułowaniu twierdzeń o

pozwalającą na formułowaniu twierdzeń o

równości lub różności (twierdzenia typu “takie

równości lub różności (twierdzenia typu “takie

same" bądź “różne”) np. płeć, kolor oczu, tryb

same" bądź “różne”) np. płeć, kolor oczu, tryb

studiów.

studiów.



Zmienne porządkowe

Zmienne porządkowe

– właściwości

– właściwości

określone przez operacje, pozwalające na

określone przez operacje, pozwalające na

szeregowanie elementów grupy; (twierdzenia

szeregowanie elementów grupy; (twierdzenia

typu „większe niż”, „mniejsze niż”), np. gdy

typu „większe niż”, „mniejsze niż”), np. gdy

musimy uszeregować grupę w/g. stopnia

musimy uszeregować grupę w/g. stopnia

agresywności, skłonności do lenistwa.

agresywności, skłonności do lenistwa.

Klasyfikacje zmiennych 5b

Klasyfikacje zmiennych 5b



Zmienne przedziałowe

Zmienne przedziałowe

- właściwości

- właściwości

określone przez operacje, pozwalające na

określone przez operacje, pozwalające na

formułowanie twierdzeń o równości

formułowanie twierdzeń o równości

przedziałów. Zmienna przedziałowa nie ma

przedziałów. Zmienna przedziałowa nie ma

prawdziwego punktu zerowego, ale dla

prawdziwego punktu zerowego, ale dla

wygody może on zostać arbitralnie

wygody może on zostać arbitralnie

wyznaczony. Przykłady: pomiary temperatur

wyznaczony. Przykłady: pomiary temperatur

wg skali Celsjusza, czas kalendarzowy

wg skali Celsjusza, czas kalendarzowy



Zmienne stosunkowe

Zmienne stosunkowe

(ilorazowe)-

(ilorazowe)-

właściwości określone przez operacje,

właściwości określone przez operacje,

pozwalające na formułowanie również

pozwalające na formułowanie również

twierdzeń o równości stosunków (ile razy

twierdzeń o równości stosunków (ile razy

wartość jednej zmiennej jest większa/mniejsza

wartość jednej zmiennej jest większa/mniejsza

od wartości drugiej zmiennej). Przykłady:

od wartości drugiej zmiennej). Przykłady:

długość, ciężar, liczebność zbiorów.

długość, ciężar, liczebność zbiorów.

Zmienne i skale

Zmienne i skale



Metody statystyczne służą do analizowania

Metody statystyczne służą do analizowania

danych składających się ze zmiennych

danych składających się ze zmiennych

nominalnych, porządkowych,

nominalnych, porządkowych,

przedziałowych oraz stosunkowych. Z

przedziałowych oraz stosunkowych. Z

punktu widzenia praktyki opracowania

punktu widzenia praktyki opracowania

statystycznego w Psychologii nie ma

statystycznego w Psychologii nie ma

znaczenia, czy zmienna jest mierzona na

znaczenia, czy zmienna jest mierzona na

skali przedziałowej czy stosunkowej.

skali przedziałowej czy stosunkowej.



UWAGA!

UWAGA!

Każda skala silniejsza ma

Każda skala silniejsza ma

właściwości skali słabszej, tzn. że każda

właściwości skali słabszej, tzn. że każda

właściwość mierzona skalą silniejszą może

właściwość mierzona skalą silniejszą może

być też mierzona skalą słabszą.

być też mierzona skalą słabszą.

Etapy wnioskowania

Etapy wnioskowania

statystycznego

statystycznego

1.

1.

Sformułowanie hipotez (zerowej i

Sformułowanie hipotez (zerowej i

alternatywnej).

alternatywnej).

2.

2.

Określenie skali pomiarowej zmiennej

Określenie skali pomiarowej zmiennej

zależnej.

zależnej.

3.

3.

Wybór testu statystycznego.

Wybór testu statystycznego.

4.

4.

Przyjęcie poziomu istotności i określenie

Przyjęcie poziomu istotności i określenie

wielkości próby.

wielkości próby.

5.

5.

Określenie rozkładu z próby statystyki testu i

Określenie rozkładu z próby statystyki testu i

ustalenie wartości krytycznej.

ustalenie wartości krytycznej.

6.

6.

Wyliczenie statystyki testu z danych

Wyliczenie statystyki testu z danych

empirycznych.

empirycznych.

7.

7.

Porównanie wartości empirycznej z

Porównanie wartości empirycznej z

wartościami krytycznymi i podjęcie decyzji

wartościami krytycznymi i podjęcie decyzji

odnośnie hipotezy zerowej.

odnośnie hipotezy zerowej.

Hipotezy zerowe i

Hipotezy zerowe i

alternatywne

alternatywne



Hipotezy zerowa i alternatywna (robocza)

Hipotezy zerowa i alternatywna (robocza)

wzajemnie się wykluczają.

wzajemnie się wykluczają.



Hipoteza zerowa jest tak sformułowana, by

Hipoteza zerowa jest tak sformułowana, by

jej odrzucenie było równoznaczne z

jej odrzucenie było równoznaczne z

przyjęciem hipotezy alternatywnej.

przyjęciem hipotezy alternatywnej.



Hipotezy mogą być:

Hipotezy mogą być:



jednostronne (kierunkowe) lub

jednostronne (kierunkowe) lub



dwustronne (dwukierunkowe, bez określonego

dwustronne (dwukierunkowe, bez określonego

kierunku).

kierunku).

Błąd 1-go rodzaju

Błąd 1-go rodzaju



Błędem pierwszego rodzaju

Błędem pierwszego rodzaju

(zwanym

(zwanym

inaczej błędem pierwszego typu, błędem

inaczej błędem pierwszego typu, błędem

przyjęcia lub alfa-błędem) nazywamy błąd

przyjęcia lub alfa-błędem) nazywamy błąd

polegający na odrzuceniu hipotezy

polegający na odrzuceniu hipotezy

zerowej, która jest prawdziwa. Innymi

zerowej, która jest prawdziwa. Innymi

słowy jest to błąd polegający na tym, że na

słowy jest to błąd polegający na tym, że na

podstawie wyników testu statystycznego

podstawie wyników testu statystycznego

twierdzimy, że jakiś fakt jest statystycznie

twierdzimy, że jakiś fakt jest statystycznie

istotny, natomiast w rzeczywistości jest on

istotny, natomiast w rzeczywistości jest on

dziełem przypadku.

dziełem przypadku.



Prawdopodobieństwo popełnienia błędu

Prawdopodobieństwo popełnienia błędu

pierwszego rodzaju równy jest α i

pierwszego rodzaju równy jest α i

nazywamy

nazywamy

poziomem istotności testu.

poziomem istotności testu.

Błąd 2-go rodzaju

Błąd 2-go rodzaju



Błędem drugiego rodzaju

Błędem drugiego rodzaju

(zwanym inaczej

(zwanym inaczej

błędem drugiego typu, błędem przyjęcia lub

błędem drugiego typu, błędem przyjęcia lub

beta-błędem) nazywamy błąd polegający na

beta-błędem) nazywamy błąd polegający na

przyjęciu hipotezy zerowej, która jest

przyjęciu hipotezy zerowej, która jest

fałszywa. Innymi słowy jest to błąd

fałszywa. Innymi słowy jest to błąd

polegający na tym, że na podstawie wyników

polegający na tym, że na podstawie wyników

testu statystycznego twierdzimy, że jakiś fakt

testu statystycznego twierdzimy, że jakiś fakt

jest dziełem przypadku, natomiast w

jest dziełem przypadku, natomiast w

rzeczywistości jest on statystycznie istotny.

rzeczywistości jest on statystycznie istotny.



Prawdopodobieństwo popełnienia błędu

Prawdopodobieństwo popełnienia błędu

drugiego rodzaju równe jest β.

drugiego rodzaju równe jest β.



Przy utrzymaniu na stałym poziomie

Przy utrzymaniu na stałym poziomie

błędu I

błędu I

rodzaju

rodzaju

można zmniejszyć

można zmniejszyć

błąd II rodzaju

błąd II rodzaju

poprzez zwiększenie liczebności próby.

poprzez zwiększenie liczebności próby.

Błąd 3-go rodzaju

Błąd 3-go rodzaju



Błąd trzeciego rodzaju

Błąd trzeciego rodzaju

(zwany inaczej

(zwany inaczej

błędem typu trzeciego ) to pojęcie

błędem typu trzeciego ) to pojęcie

wprowadzone w 1968 roku przez statystyka

wprowadzone w 1968 roku przez statystyka

Howarda Raiffa. Zaproponował on

Howarda Raiffa. Zaproponował on

wprowadzenie błędu trzeciego rodzaju, czyli

wprowadzenie błędu trzeciego rodzaju, czyli

błędu polegającego na prawidłowym i

błędu polegającego na prawidłowym i

dokładnym rozwiązaniu niewłaściwego

dokładnym rozwiązaniu niewłaściwego

problemu (np. przy niewłaściwie

problemu (np. przy niewłaściwie

sformułowanej hipotezie zerowej).

sformułowanej hipotezie zerowej).



Czasami nazwą błąd trzeciego rodzaju

Czasami nazwą błąd trzeciego rodzaju

określa się też wszelkie inne błędy które

określa się też wszelkie inne błędy które

mogą wyniknąć przy testowaniu hipotez,

mogą wyniknąć przy testowaniu hipotez,

np. błąd wynikający z zaokrąglenia wartości

np. błąd wynikający z zaokrąglenia wartości

statystyki testowej podczas obliczeń

statystyki testowej podczas obliczeń

komputerowych.

komputerowych.

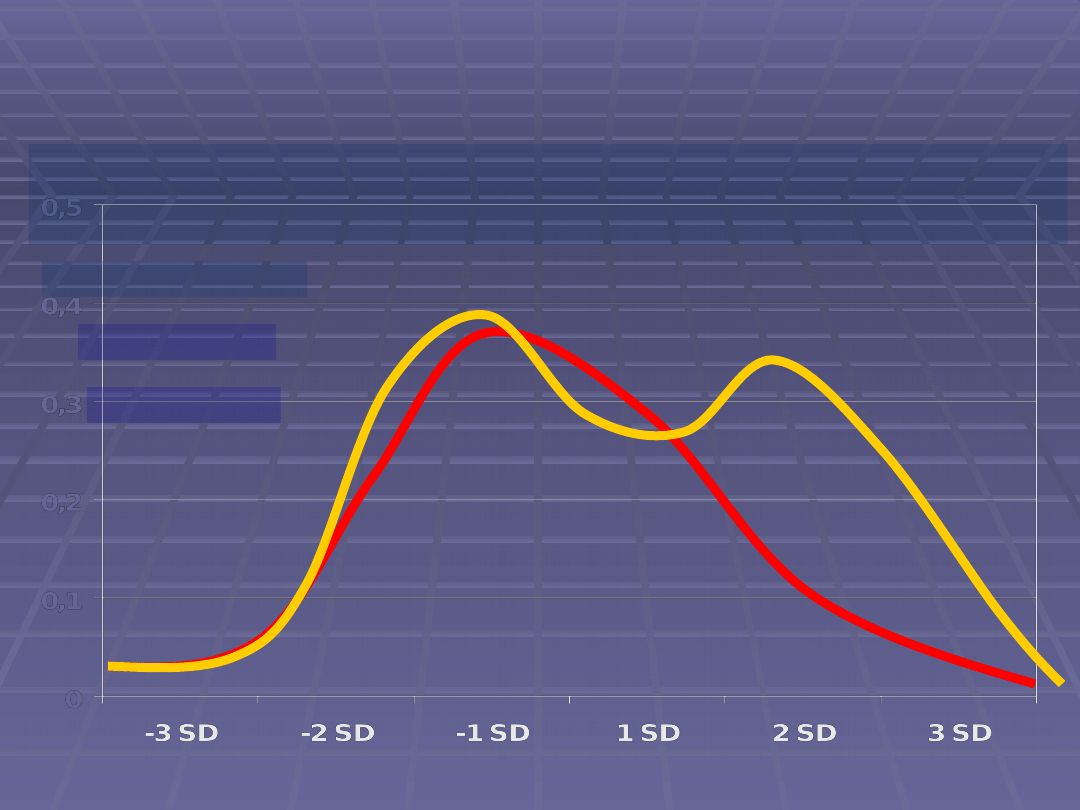
Rozkład empiryczny

Rozkład empiryczny

– przyporządkowanie kolejnym wartościom zmiennej odpowiadających im
liczebności. Odzwierciedla strukturę badanej zbiorowości z punktu widzenia
konkretnej cechy.

Rodzaje rozkładów:

jednomodalny

wielomodalny

Rozkład normalny

Rozkład normalny



Centralne twierdzenie graniczne:

Centralne twierdzenie graniczne:

– jeżeli pobieramy z populacji

– jeżeli pobieramy z populacji

nieskończenie wiele reprezentatywnych

nieskończenie wiele reprezentatywnych

prób to rozkład średnich z prób dąży do

prób to rozkład średnich z prób dąży do

rozkładu normalnego.

rozkładu normalnego.

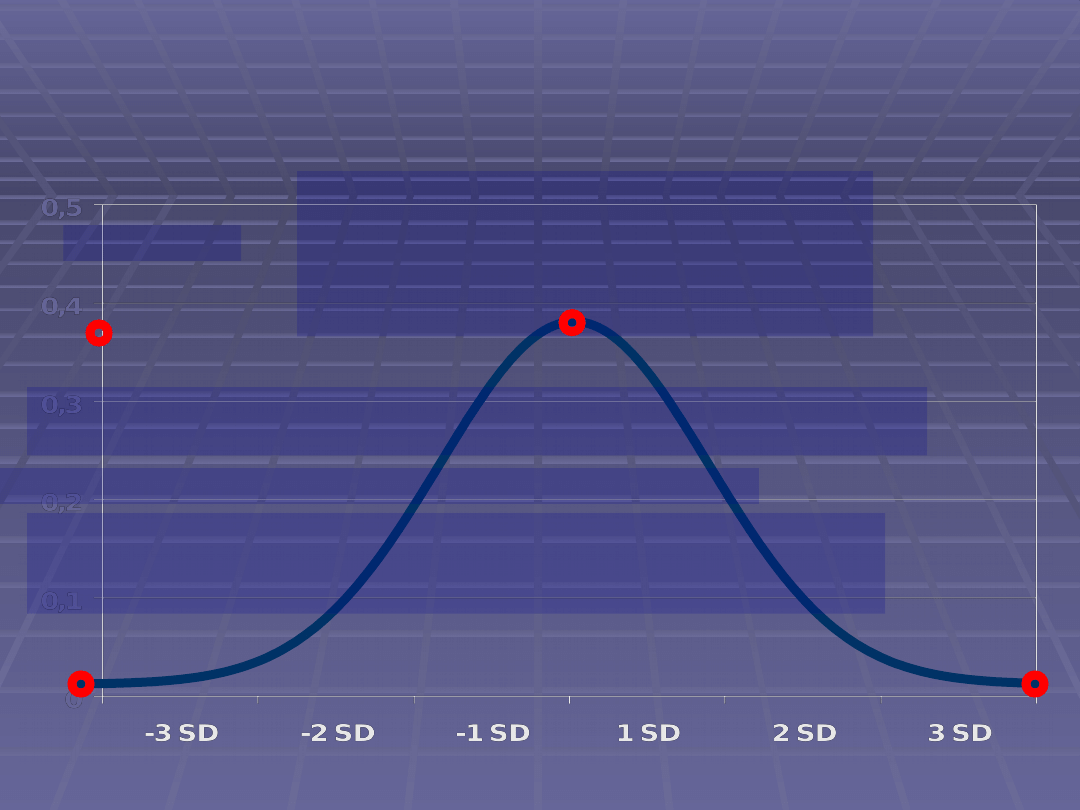
Rozkład normalny

Rozkład normalny

Rozkład normalny
(krzywa normalna, krzywa dzwonowata):
Krzywą normalną zapisuje się zwykle w
postaci właściwej dla wyników
standardowych.

Właściwości:

Krzywa jest symetryczna. Średnia, mediana i wartość modalna
zbiegają się w jednym punkcie.

Najwyższa rzędna krzywej występuje w punkcie średniej.

Krzywa jest asymptotyczna. Zbliża się ona do osi poziomej,
lecz nigdy do niej nie dochodzi i rozciąga się od minus
nieskończoności do plus nieskończoności.

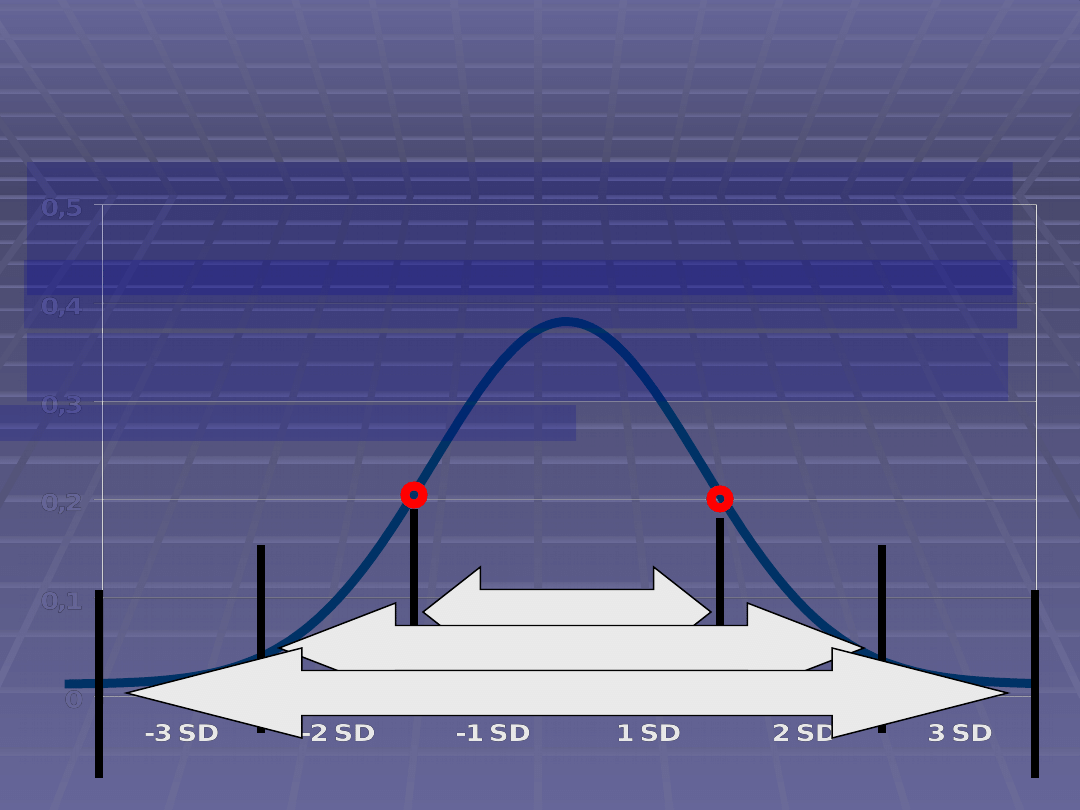
Rozkład normalny

Rozkład normalny

68%

95,5%

Punkty zagięcia krzywej znajdują się w miejscach plus lub minus jedną
jednostkę odchylenia standardowego powyżej lub poniżej średniej. W
tych miejscach krzywa zmienia się względem osi poziomej z wypukłej
we wklęsłą.

Mniej więcej 68% powierzchni pod krzywą mieści się w granicach plus
lub minus jednej jednostki odchylenia standardowego od średniej.

Około 95,5% powierzchni pod krzywą mieści się w granicach dwóch
odchyleń standardowych.

Około 99,7% w granicach trzech odchyleń.

99,7%

Przedziały, obszary,

Przedziały, obszary,

poziomy

poziomy



Poziom istotności

Poziom istotności

–

–

prawdopodobieństwo popełnienia błędu

prawdopodobieństwo popełnienia błędu

pierwszego rodzaju, polegającego na

pierwszego rodzaju, polegającego na

odrzuceniu poprawnej hipotezy zerowej

odrzuceniu poprawnej hipotezy zerowej

(α).

(α).



Poziom ufności

Poziom ufności

– prawdopodobieństwo

– prawdopodobieństwo

poprawnego wnioskowania (1-α).

poprawnego wnioskowania (1-α).



Błąd standardowy średniej

Błąd standardowy średniej

– odchylenie

– odchylenie

standardowe rozkładu średniej z próby.

standardowe rozkładu średniej z próby.



Przedział ufności

Przedział ufności

– przedział wartości

– przedział wartości

prawdopodobnych.

prawdopodobnych.



Obszar krytyczny

Obszar krytyczny

– obszar wartości

– obszar wartości

nieprawdopodobnych.

nieprawdopodobnych.

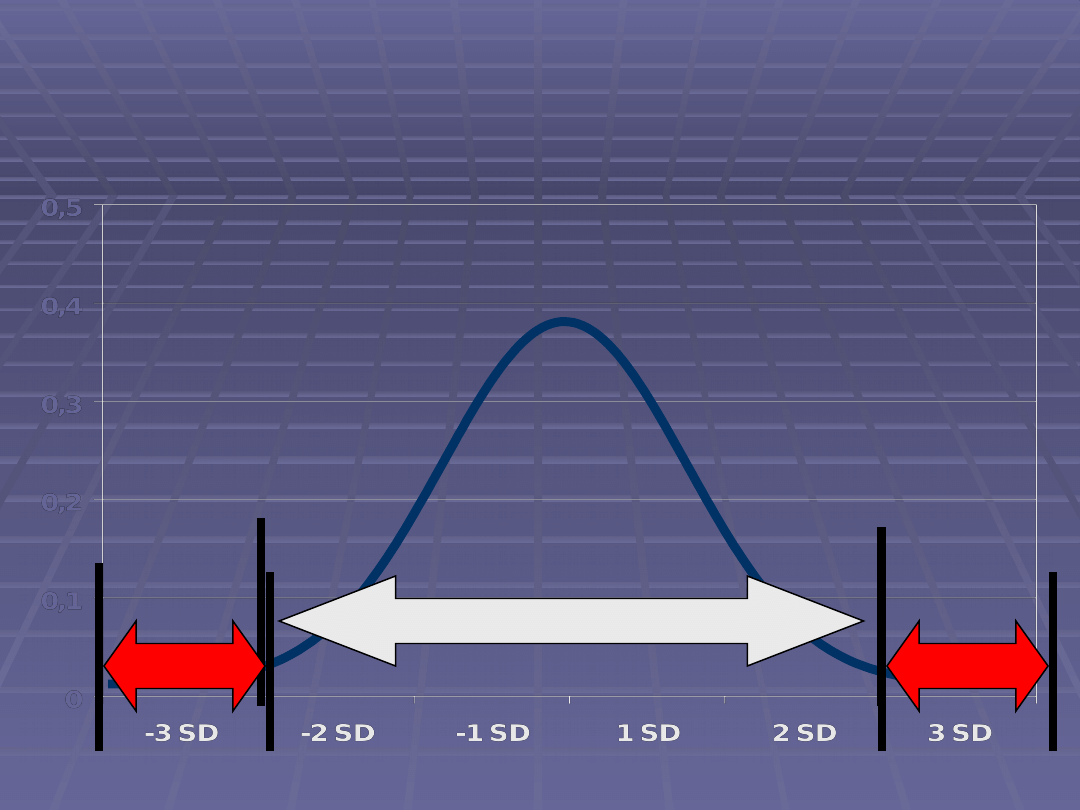
Poziom istotności a poziom

Poziom istotności a poziom

ufności

ufności

– poziom istotności

Przedział ufności



1

– poziom ufności

 

2



Obszar krytyczny

Obszar krytyczny

Miary tendencji centralnej

Miary tendencji centralnej



Są statystykami opisującymi rozkład proporcji.

Są statystykami opisującymi rozkład proporcji.



Mediana –

Mediana –

jest to 50. centyl, czyli taka wartość, przy

jest to 50. centyl, czyli taka wartość, przy

której połowa obserwacji ma wartości nie większe od

której połowa obserwacji ma wartości nie większe od

niej i równocześnie połowa obserwacji ma wartości

niej i równocześnie połowa obserwacji ma wartości

nie mniejsze. W sytuacji parzystej liczby obserwacji,

nie mniejsze. W sytuacji parzystej liczby obserwacji,

mediana jest średnią dwu środkowych obserwacji w

mediana jest średnią dwu środkowych obserwacji w

próbie posortowanej rosnąco lub malejąco.

próbie posortowanej rosnąco lub malejąco.

W przeciwieństwie do średniej, na którą wpływ może

W przeciwieństwie do średniej, na którą wpływ może

mieć nawet kilka ekstremalnie dużych lub małych

mieć nawet kilka ekstremalnie dużych lub małych

wartości, mediana jest miarą tendencji centralnej

wartości, mediana jest miarą tendencji centralnej

niewrażliwą na wartości odstające.

niewrażliwą na wartości odstające.



Modalna –

Modalna –

najczęściej spotykana wartość.

najczęściej spotykana wartość.



Średnia –

Średnia –

suma obserwacji dzielona przez ich liczbę.

suma obserwacji dzielona przez ich liczbę.

Miary rozproszenia

Miary rozproszenia



Statystyki mierzące zmienność lub rozrzut danych;

Statystyki mierzące zmienność lub rozrzut danych;

obejmują miedzy innymi:

obejmują miedzy innymi:



Odchylenie standardowe

Odchylenie standardowe

- miara rozproszenia wokół

- miara rozproszenia wokół

średniej, wyrażona w tych samych jednostkach co

średniej, wyrażona w tych samych jednostkach co

zmienna, równa pierwiastkowi kwadratowemu z

zmienna, równa pierwiastkowi kwadratowemu z

wariancji.

wariancji.



Wariancja

Wariancja

- miara rozproszenia wokół średniej, równa

- miara rozproszenia wokół średniej, równa

sumie kwadratów odchyleń od średniej podzielonej

sumie kwadratów odchyleń od średniej podzielonej

przez liczbę obserwacji minus jeden. Wariancja jest

przez liczbę obserwacji minus jeden. Wariancja jest

podawana w kwadratach jednostek, w jakich mierzona

podawana w kwadratach jednostek, w jakich mierzona

jest zmienna.

jest zmienna.



Rozstęp

Rozstęp

- różnica między największą a najmniejszą

- różnica między największą a najmniejszą

wartością zmiennej numerycznej; maksimum minus

wartością zmiennej numerycznej; maksimum minus

minimum.

minimum.



Minimum

Minimum

- najmniejsza wartość zmiennej

- najmniejsza wartość zmiennej

numerycznej.

numerycznej.



Maksimum

Maksimum

- największa wartość zmiennej

- największa wartość zmiennej

numerycznej.

numerycznej.

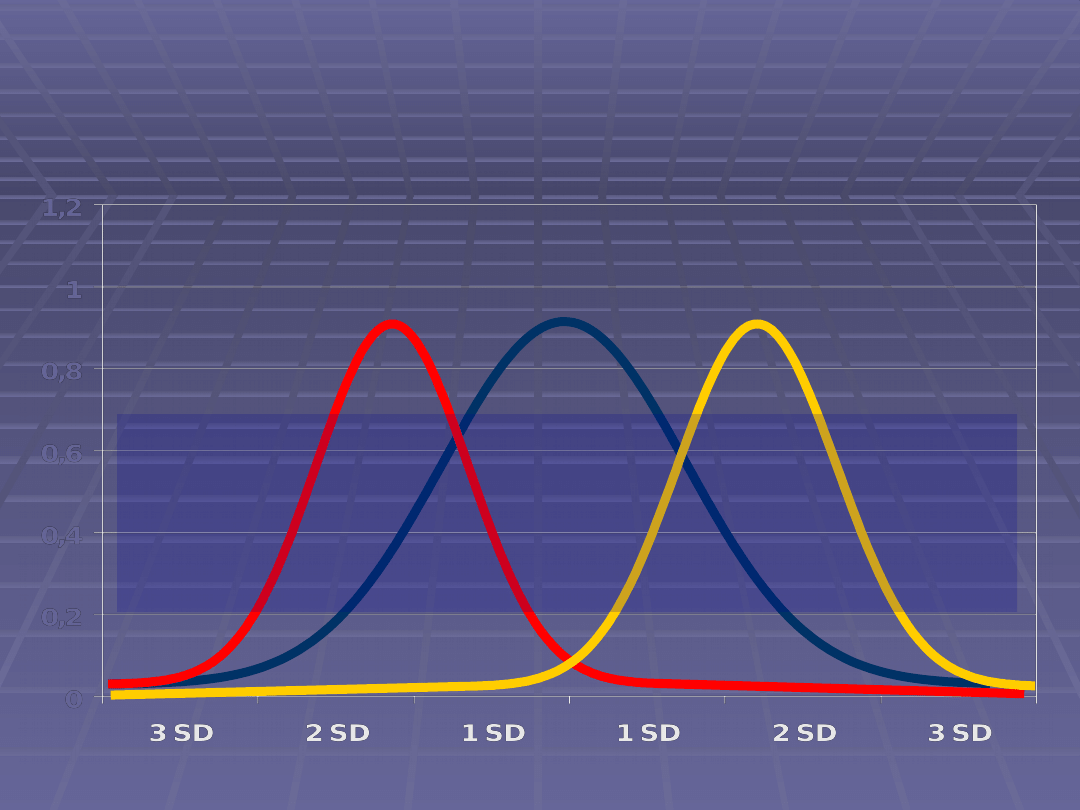
Miary asymetrii - skośność

Miary asymetrii - skośność

Skośność = 0

Skośność > 0

Skośność < 0

Rozkład normalny jest symetryczny i posiada współczynnik
skośności równy 0. Rozkład o znaczącej wartości dodatniej
współczynnika skośności ma długi ogon z prawej strony. Gdy zaś
współczynnik jest ujemny, rozkład ma długi ogon z lewej strony.
Wartość skośności większa od 1 na ogół oznacza rozkład
znacząco różniący się od rozkładu normalnego.

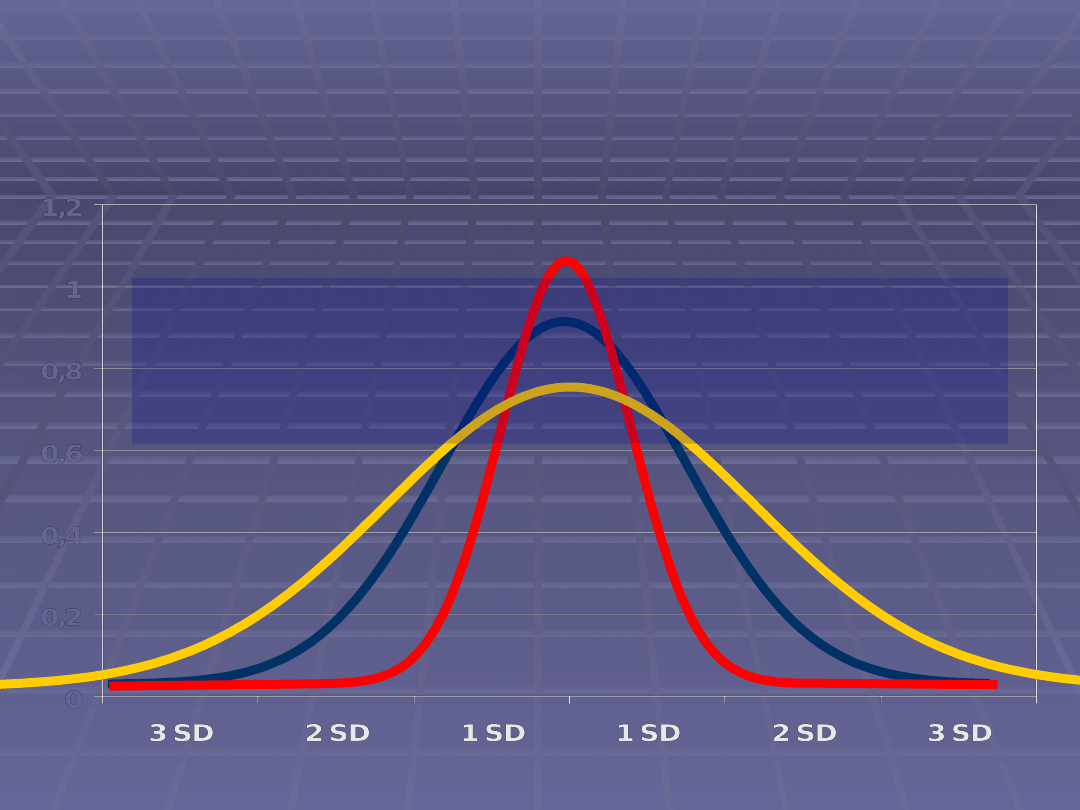
Miary koncentracji - kurtoza

Miary koncentracji - kurtoza

Kurtoza = 0

Kurtoza > 0

Kurtoza < 0

W przypadku rozkładu normalnego wartość kurtozy wynosi 0.
Dodatnia kurtoza wskazuje, że obserwacje są silniej
skoncentrowane i mają dłuższe ogony niż w przypadku rozkładu
normalnego. Ujemna kurtoza wskazuje na mniejszą
koncentrację obserwacji i krótsze ogony.