ZAWIESZENIA

ZAWIESZENIA

Drgania

2010

Andrzej Reński

Drgania

Tematyka:

- Modele fizyczne i matematyczne
pojazdu

- Charakterystyki

- Generowanie drgań
- Oddziaływanie drgań na człowieka.

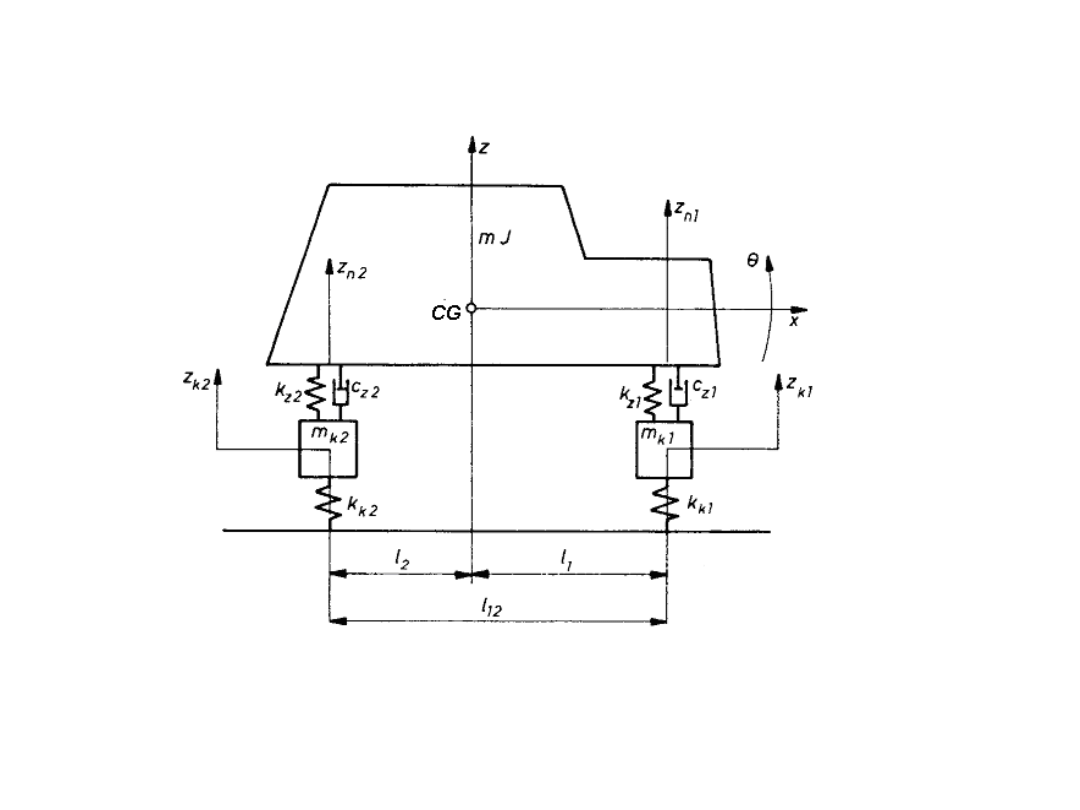
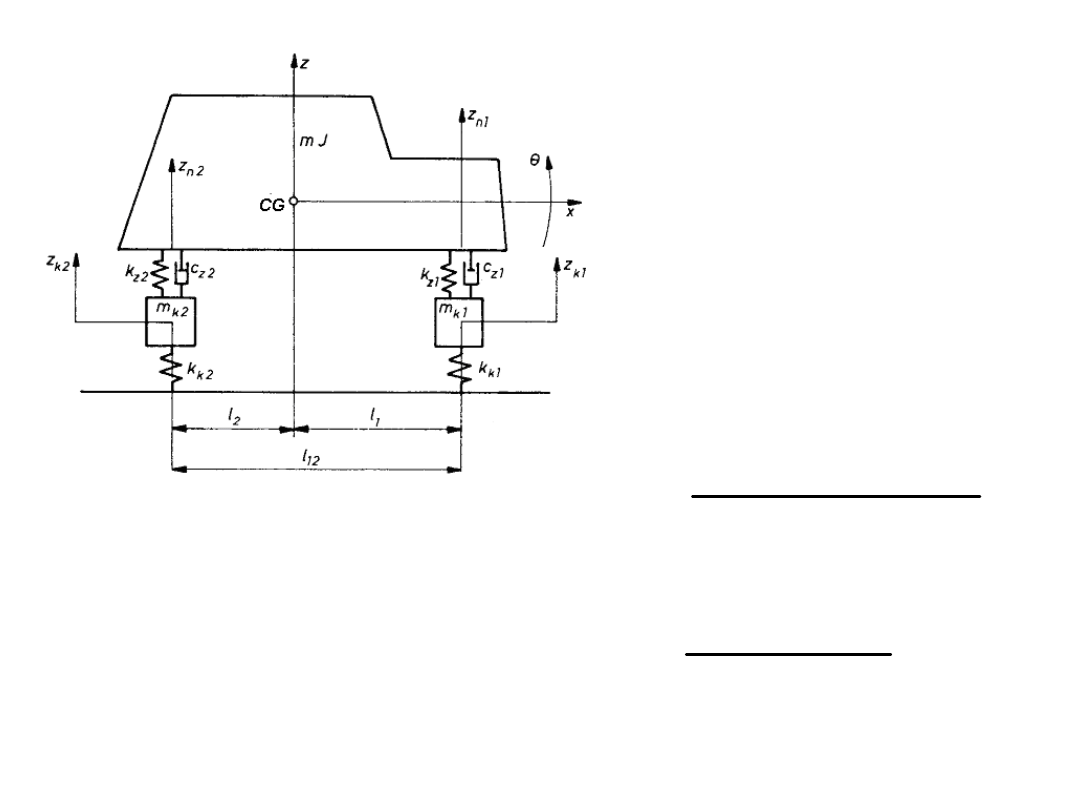
Model fizyczny pojazdu

Model płaski o 4 stopniach swobody

12

1

2

n

2

1

n

l

l

z

l

z

z





12

2

n

1

n

l

z

z 





Równanie Lagrange

i

i

i

i

Q

q

V

q

T

q

T

dt

d

































T – energia kinetyczna,

V – energia potencjalna,

q

i

– współrzędna uogólniona,

Q

i

– siła uogólniona (w przypadku drgań

swobodnych Q

i

= 0)

Energia kinetyczna układu:

2

2

k

2

k

2

1

k

1

k

2

2

z

m

2

1

z

m

2

1

J

2

1

z

m

2

1

T



















Energia potencjalna:









2

2

k

2

n

2

z

2

1

k

1

n

1

z

2

2

k

2

k

2

1

k

1

k

z

z

k

2

1

z

z

k

2

1

z

k

2

1

z

k

2

1

V













lub

2

2

k

2

k

2

1

k

1

k

2

12

2

n

1

n

2

12

1

2

n

2

1

n

z

m

2

1

z

m

2

1

l

z

z

J

2

1

l

l

z

l

z

m

2

1

T

















































0

z

k

z

k

z

l

J

l

l

m

z

l

J

l

m

1

k

1

z

1

n

1

z

2

n

2

12

2

1

1

n

2

12

2

2





















0

z

k

k

z

k

z

m

1

k

1

k

1

z

1

n

1

z

1

k

1

k











0

z

k

z

k

z

l

J

l

m

z

l

J

l

l

m

2

k

2

z

2

n

2

z

2

n

2

12

2

1

1

n

2

12

2

1





















0

z

k

k

z

k

z

m

2

k

2

k

2

z

2

n

2

z

2

k

2

k











Jesli:

to:

0

1

1

1

1

1

2

12

2
2









k

z

n

z

n

z

k

z

k

z

l

J

l

m



0

2

2

2

2

2

2

12

2

1









k

z

n

z

n

z

k

z

k

z

l

J

l

m







0

z

k

k

z

k

z

m

1

k

1

k

1

z

1

n

1

z

1

k

1

k















0

z

k

k

z

k

z

m

2

k

2

k

2

z

2

n

2

z

2

k

2

k











m l

1

l

2

 – J = 0

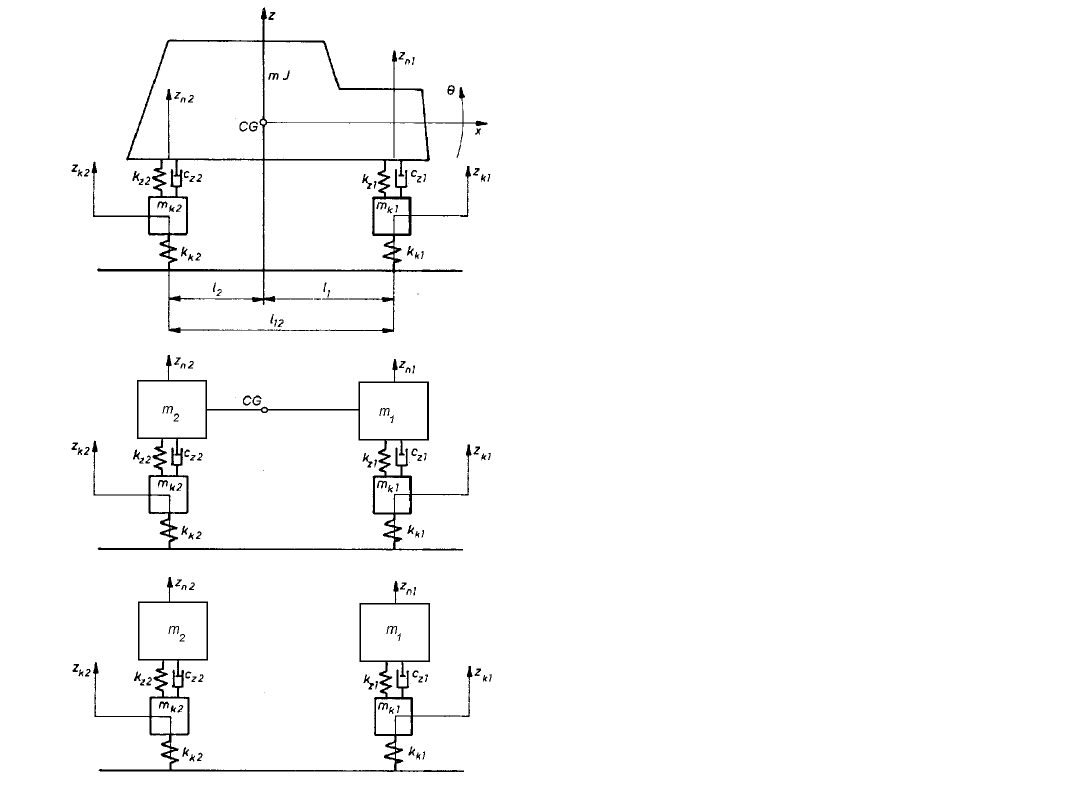
Podział modelu pojazdu o
4 stopniach swobody na 2
modele o 2 stopniach
swobody

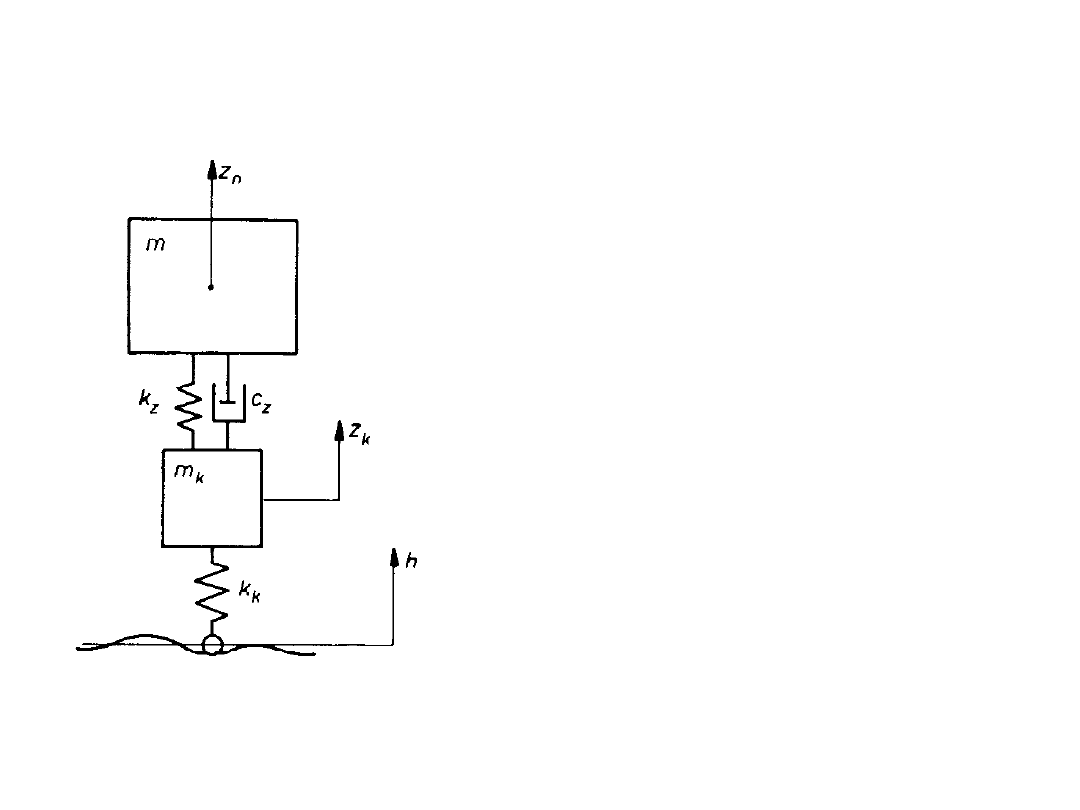
DRGANIA WYMUSZONE

Model o 2 stopniach swobody
reprezentujący przednią lub
tylną część samochodu lub
jedną stronę jego przedniej
lub tylnej części (tzw. model
ćwiartki pojazdu)

Wymuszenie kinematyczne nierównościami drogi

Równania ruchu

0

)

z

z

(

k

)

z

z

(

c

z

m

k

n

z

k

n

z

n

















)

z

h

(

k

)

z

z

(

k

)

z

z

(

c

z

m

k

k

k

n

z

k

n

z

k

k























Układ równań ruchu:

0

)

z

z

(

k

)

z

z

(

c

z

m

k

n

z

k

n

z

n

















)

z

h

(

k

)

z

z

(

k

)

z

z

(

c

z

m

k

k

k

n

z

k

n

z

k

k























Po uporządkowaniu względem niewiadomych:

0

z

k

z

c

z

k

z

c

z

m

k

z

k

z

n

z

n

z

n















h

k

z

)

k

k

(

z

c

z

m

z

k

z

c

k

k

k

z

k

z

k

k

n

z

n

z





















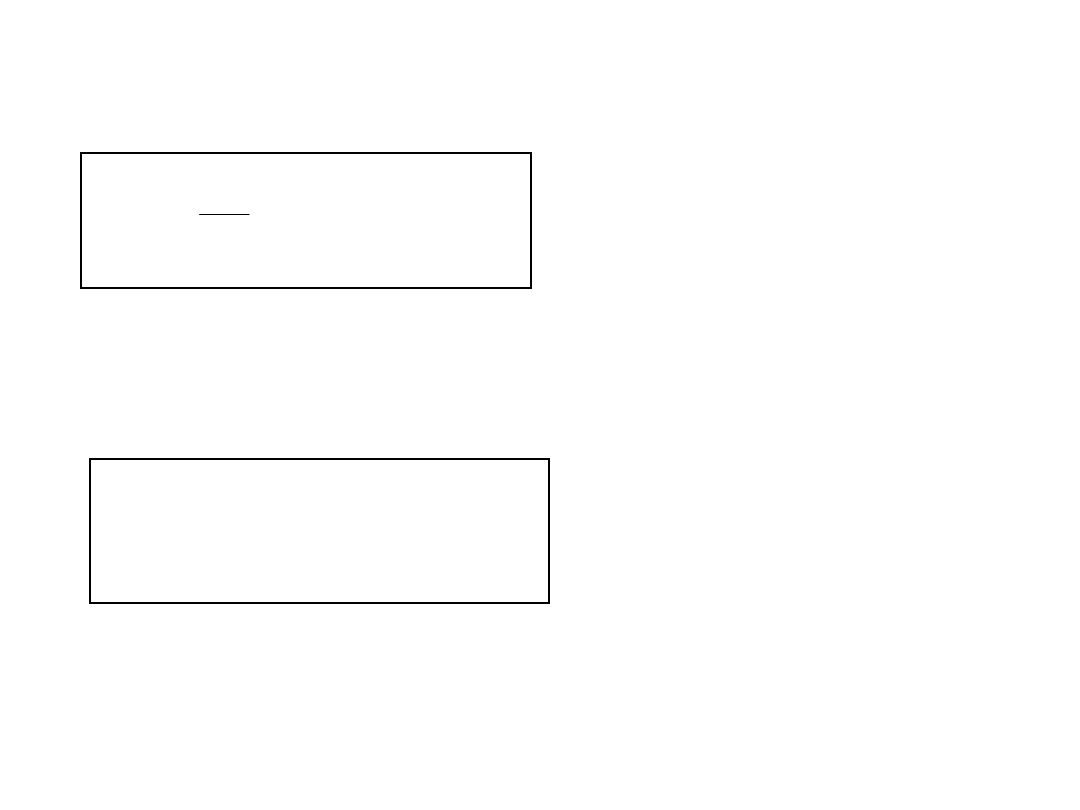
Transformacja Fouriera



















d

e

)

(

f

~

2

1

)

t

(

f

t

i

)

ω

(

f

~

















dt

e

)

t

(

f

)

(

f

~

t

i

jest transformatą Fouriera

0

z

k

z

c

z

k

z

c

z

m

k

z

k

z

n

z

n

z

n















h

k

z

)

k

k

(

z

c

z

m

z

k

z

c

k

k

k

z

k

z

k

k

n

z

n

z





















po transformacji Fouriera:

0

)

ω

c

i

k

(

z~

)

ω

c

i

k

ω

m

(

z~

z

z

k

z

z

2

n















k

z

k

z

2

k

k

z

z

n

k

h

~

)

ω

c

i

k

k

ω

m

(

z~

)

ω

c

i

k

(

z~

















Układ równań

Transmitancja

h

~

)

c

i

k

(

)

c

i

k

k

m

(

)

c

i

k

m

(

)

c

i

k

(

k

z~

2

z

z

z

k

z

2

k

z

z

2

z

z

k

n









































h

~

z~

)

ω

i

(

H

n

zn



Transmitancja dla bryły nadwozia względem
nierówności drogi

Transmitancja

h

~

)

c

i

k

(

)

c

i

k

k

m

(

)

c

i

k

m

(

)

c

i

k

(

k

z~

2

z

z

z

k

z

2

k

z

z

2

z

z

k

n









































h

~

z~

)

ω

i

(

H

n

zn



Transmitancja dla bryły nadwozia względem
nierówności drogi

2

z

z

z

k

z

2

k

z

z

2

z

z

k

zn

)

ω

c

i

k

(

)

ω

c

i

k

k

ω

m

(

)

ω

c

i

k

ω

m

(

)

ω

c

i

k

(

k

)

ω

i

(

H





























2

z

z

z

k

z

2

k

z

z

2

z

z

k

zn

)

ω

c

i

k

(

)

ω

c

i

k

k

ω

m

(

)

ω

c

i

k

ω

m

(

)

ω

c

i

k

(

k

)

ω

i

(

H





























Transmitancja:

 

ω

i

H

h

z

z

0

0

n



Współczynnik wzmocnienia – stosunek amplitud
odpowiedzi i wymuszenia jako funkcja
częstotliwości wymuszenia  lub f

0

100

200

300

400

500

600

0

20

40

60

80

100

120

Angular velocity [rad/s]

B

od

y

ac

ce

le

ra

tio

n

ga

in

[

s

-2

]

1

2

3

0,0

0,5

1,0

1,5

2,0

2,5

3,0

0

20

40

60

80

100

120

Angular velocity [rad/s]

Ti

re

d

ef

ec

tio

n

ga

in

1

2

3

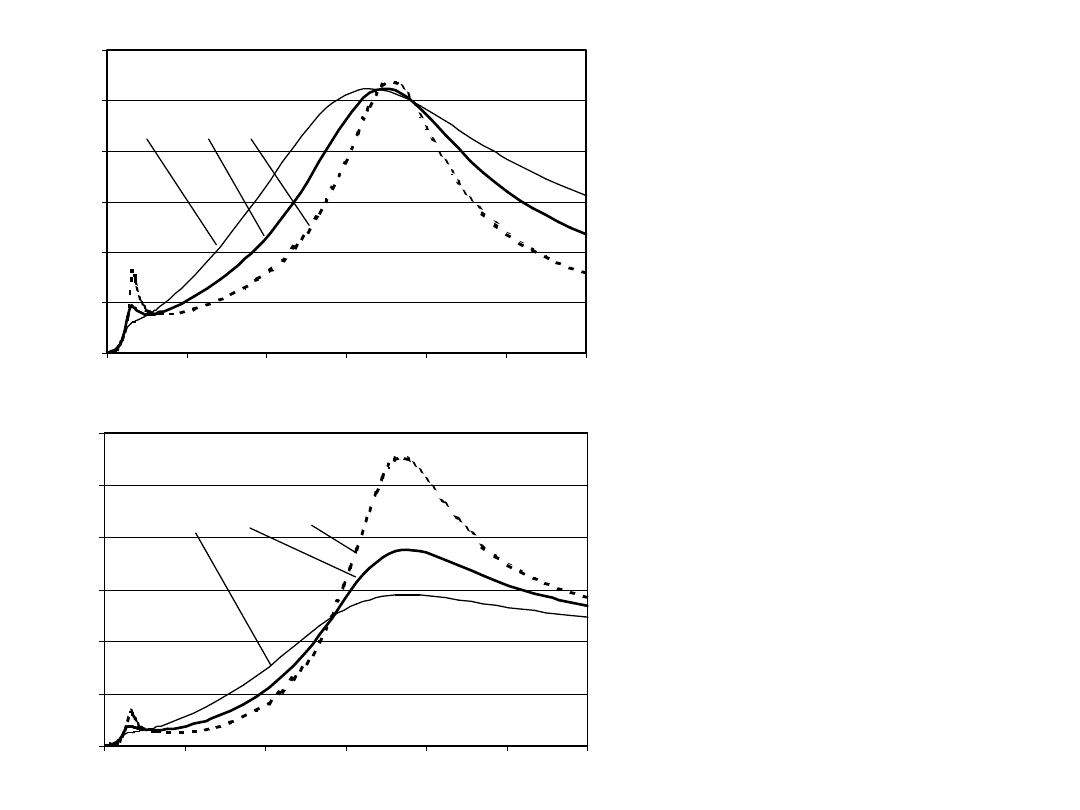
Wykresy
współczynnika
wzmocnienia dla
przyśpieszeń
nadwozia i ugięć
opony dla trzech
różnych wartości
bezwymiarowego
współczynnika
tłumienia: 1 > 2 >

3

)

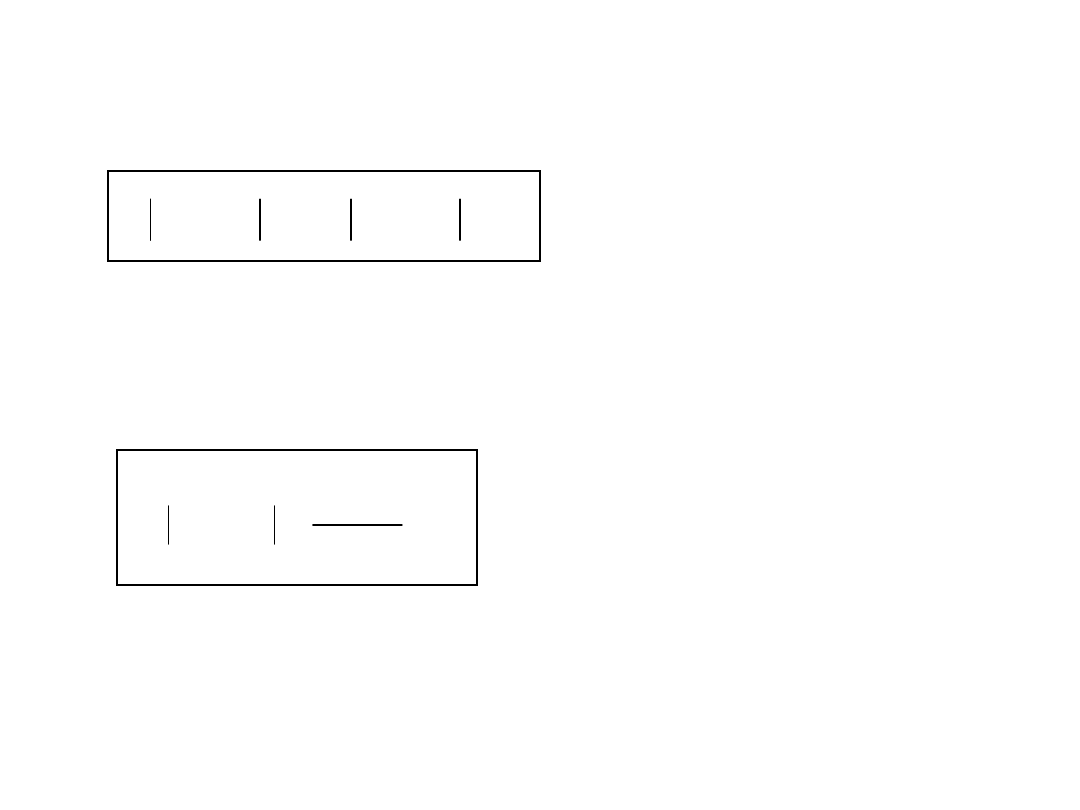
i

(

H

)

i

(

H

zn

2

n

z











0

0

dyn

k

zk

h

z

)

ω

i

(

H



Współczynnik wzmocnienia przyśpieszeń
pionowych:

Współczynnik wzmocnienia ugięć opony:

0

0

dyn

k

zk

h

z

)

ω

i

(

H



F

k dyn

= k

k

z

k

dyn

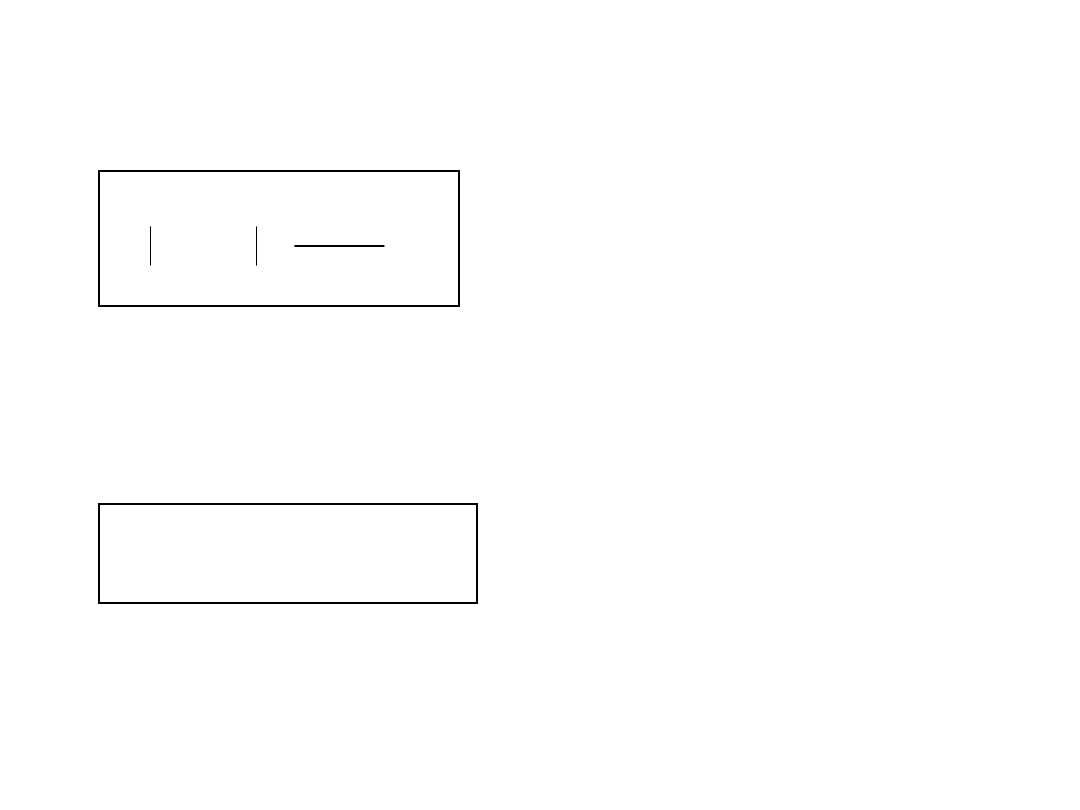
Współczynnik wzmocnienia ugięć opony:

Jest istotny przy obliczaniu siły pionowej
pomiędzy oponą i nawierzchnią F

k

dyn :





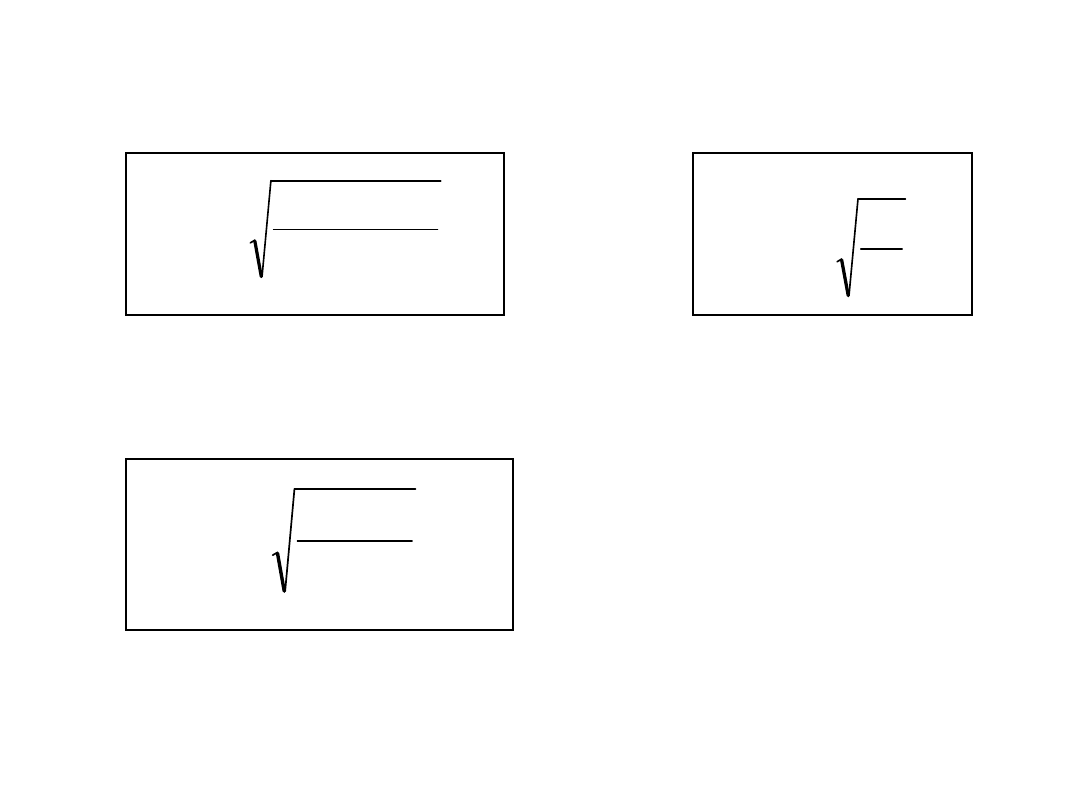
m

k

k

k

k

ω

k

z

k

z

n

0





k

z

k

k

0

m

k

k

ω





m

k

ω

z

n

0



lub

Częstotliwość drgań własnych nietłumionych
nadwozia

Częstotliwość drgań własnych nietłumionych
koła:

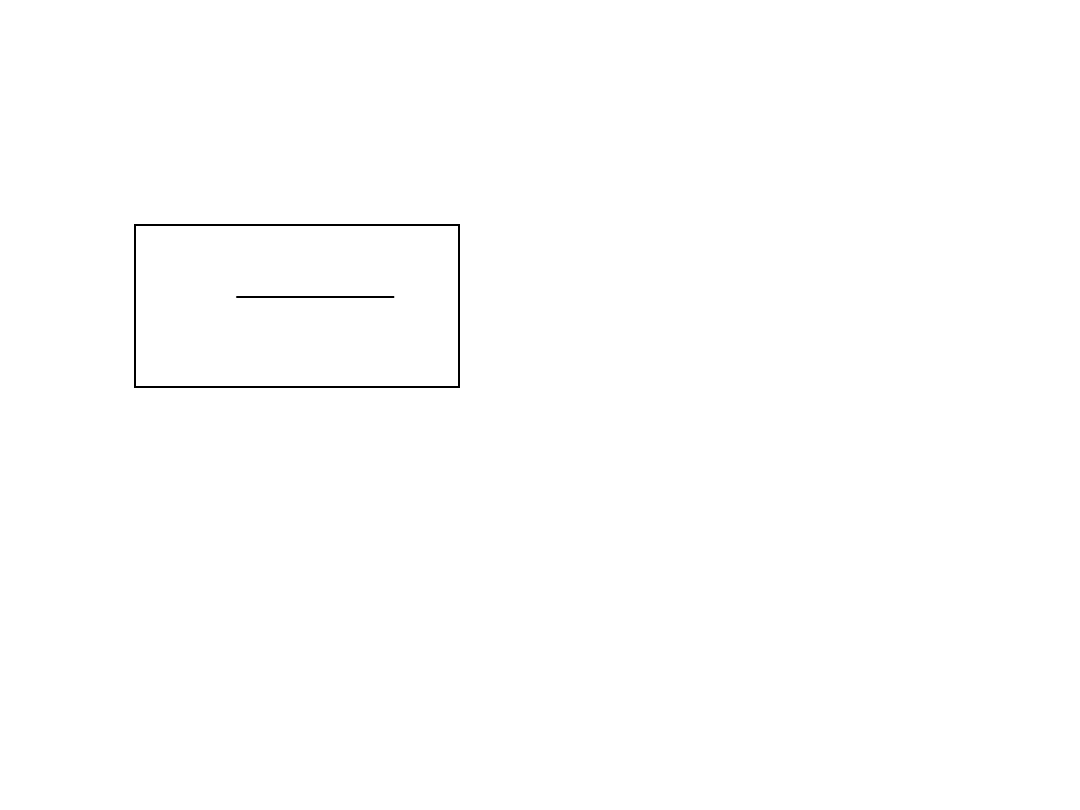
n

0

z

m

2

c







Bezwymiarowy współczynnik tłumienia:

















)

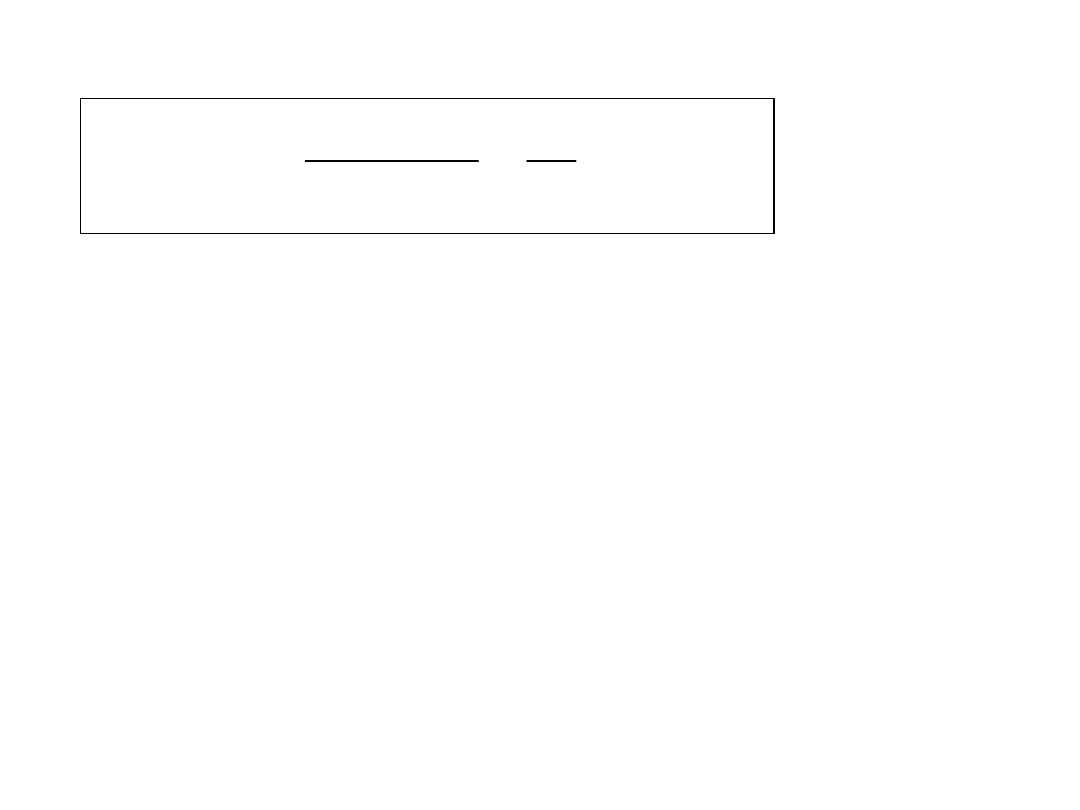
x

(

h

Ω

d

d

ΔΩ

)

x

(

h

Δ

lim

)

Ω

(

G

2

2

L

h

Gęstość widmowa nierówności drogi:

gdzie:

L – długość odcinka pomiarowego

Ω

0

= 2π/L – podstawowa częstotliwość kołowa

nierówności drogi [rad/m]

L

n

– długośc fali nierówności n-tej składowej

harmonicznej

Ω = 2π/L

n

- częstotliwość kołowa n-tej składowej

harmonicznej nierówności drogi [rad/m]. Ω jest
wielokrotnością częstotliwości podstawowej Ω

0

<h

2

(x)> - wartość średnia kwadratowa wysokości

nierówności drogi h(x) mierzonej wzdłuż drogi x

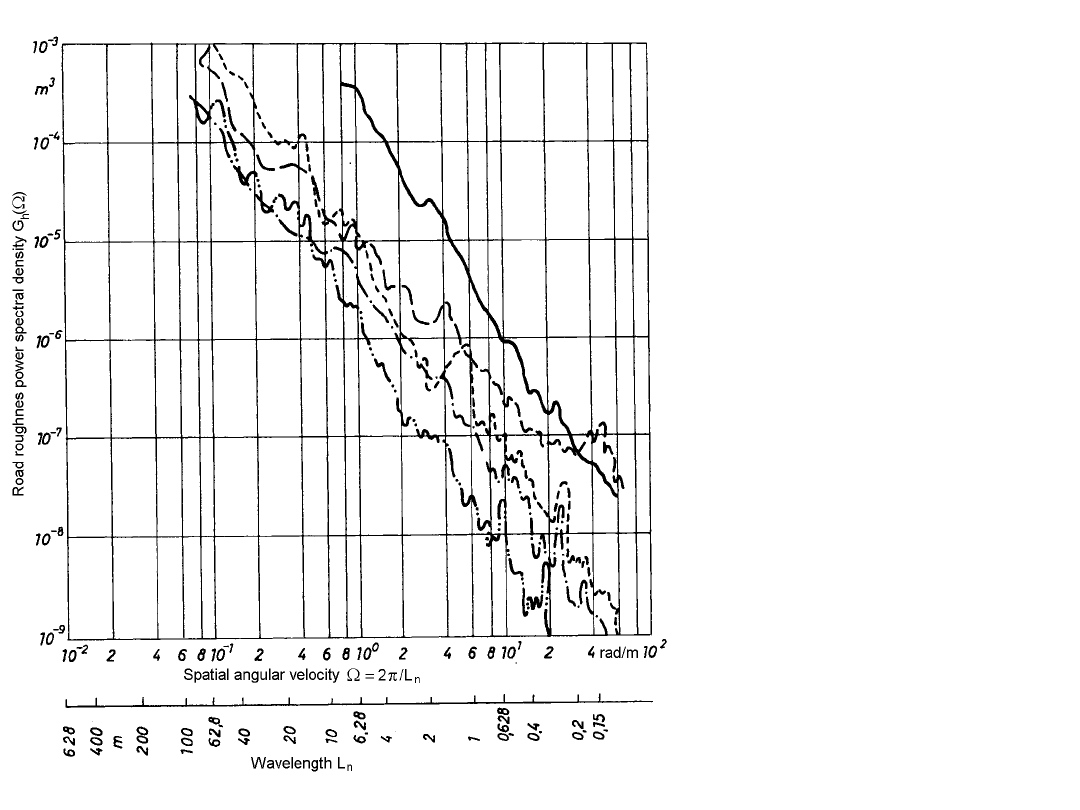
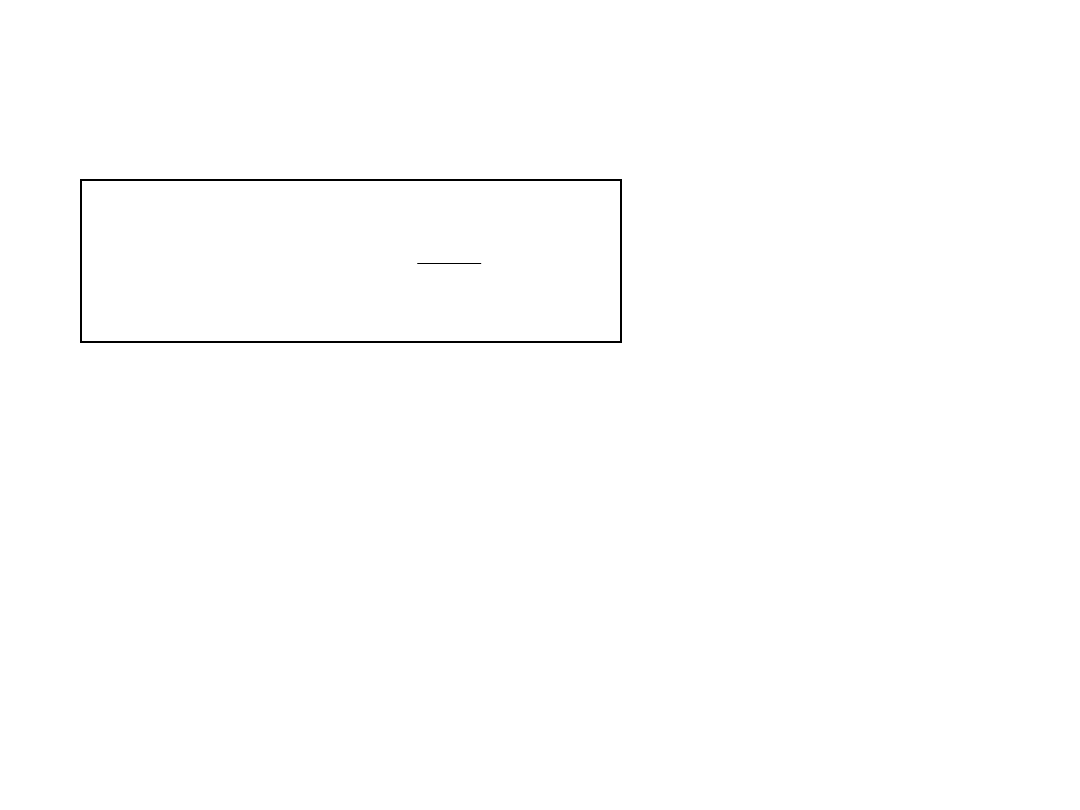
Gęstości widmowe
nierówności dróg o
różnych
nawierzchniach:

     asfalt

bardzo dobrej jakości,

     

bardzo dobry beton,

- - - - - - - - -

szuter,

   

bruk,

 droga

nieutwardzona

w

ref

ref

h

h

Ω

Ω

)

Ω

(

G

)

Ω

(

G

















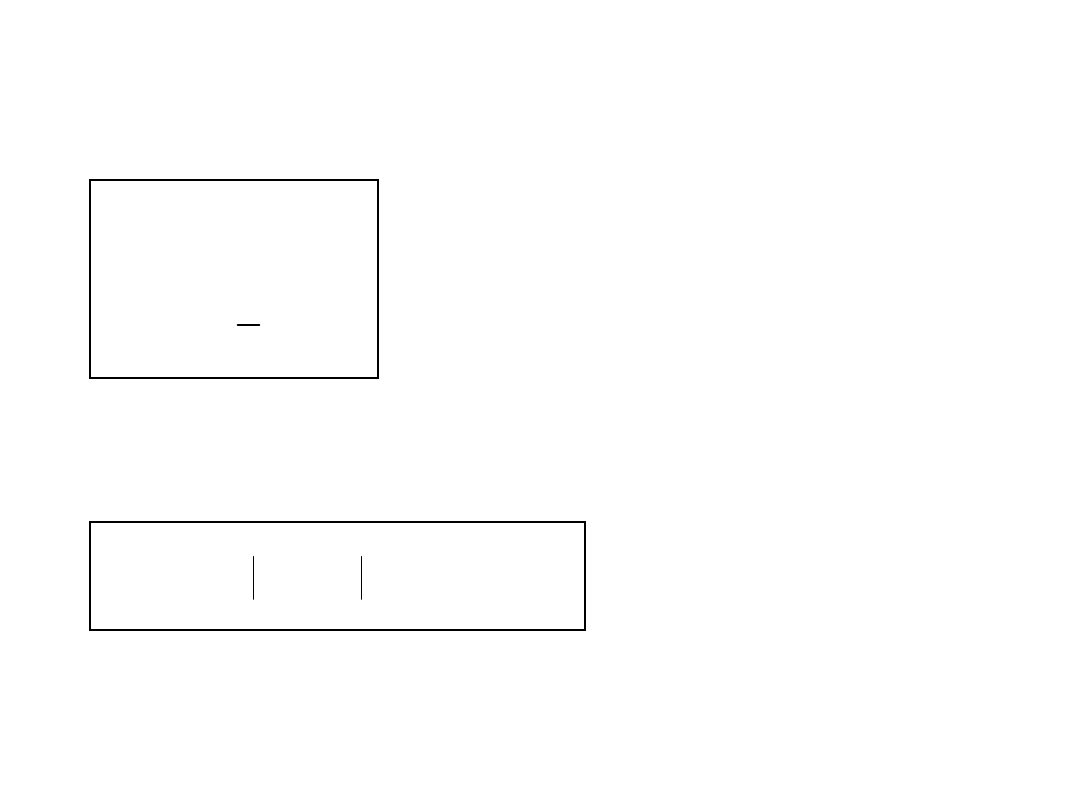
Linearyzacja wykresu gęstości widmowej
nierówności drogi

gdzie:

Ω

ref

- czestotliwość

kołowa odniesienia, zwykle Ω

ref

= 1

rad/m

G

h

(Ω

ref

) – wartość gęstości widmowej dla częstotliwości

odniesienia

Wartości G

h

(Ω

ref

) oraz w dla różnych dróg w [Mitschke]

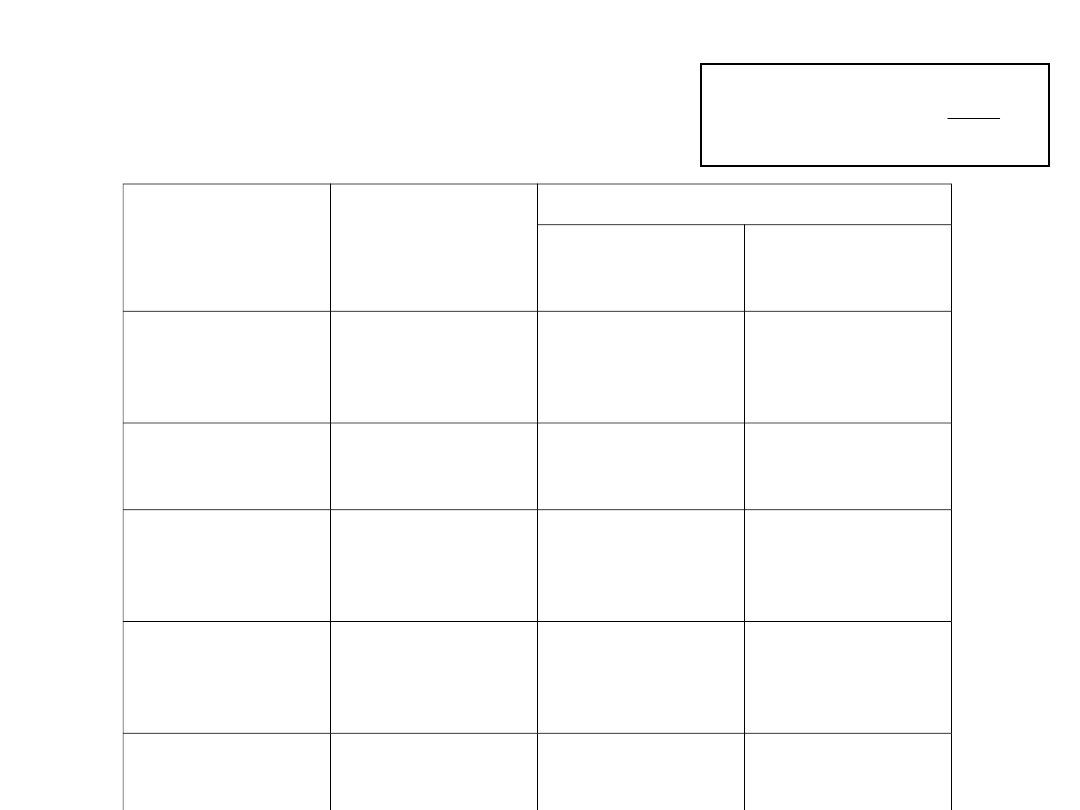
Linearyzacja wykresu gęstości widmowej
nierówności drogi

Wartości parametrów opisujących widmo
nierówności drogi; na podstawie [Mitscke
2]

Rodzaj drogi

Stan nawierzchni
ocena
subiektywna

Wartości średnie dla Ω

ref

= 1 m

-1

w

Φ

h

(Ω

ref

) [cm

3

]

Cementobeton

bardzo dobry
dobry
średni
zły

2,29
1,97
1,97
1,72

0,6
4,5
6,7

56

Asfaltobeton

bardzo dobry
dobry
średni

2,20
2,18
2,18

1,3

6

22

Szuter

dobry
średni
zły
bardzo zły

2,26
2,26
2,15
2,15

9

21
43

158

Bruk

dobry
średni
zły
bardzo zły

1,75
1,75
1,81
1,81

14
23
36

323

Droga
nieutwardzona

dobry
średni
zły
bardzo zły

2,25
2,25
2,14
2,14

32

155
602

16300

w

ref

ref

h

h

Ω

Ω

)

Ω

(

G

)

Ω

(

G

















ω = v Ω

)

Ω

(

G

v

1

)

ω

(

G

h

h



)

ω

(

G

)

ω

i

(

H

)

ω

(

G

h

2

z

z







Dla danej prędkości jazdy v

Gęstość widmowa przyśpieszeń pionowych
nadwozia wynosi

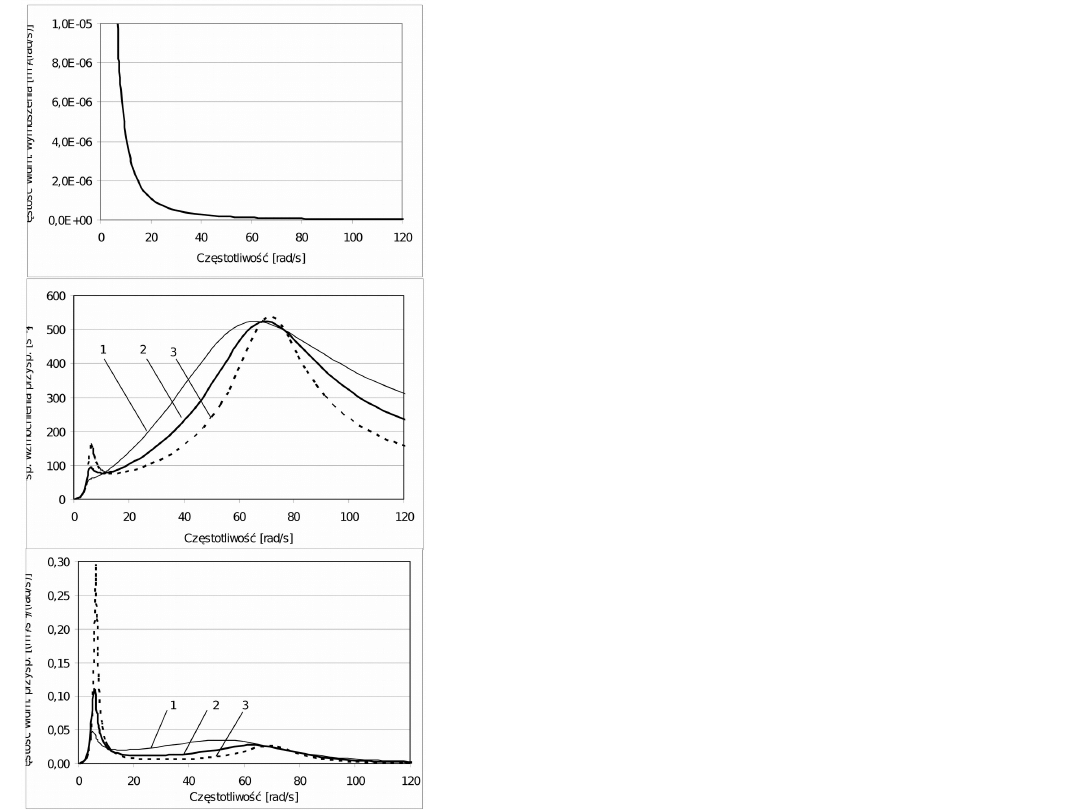
Obliczanie widma gęstości
widmowej przyśpieszeń
pionowych nadwozia z
widma gęstości widmowej
nierówności drogi i
charakterystyki
amplitudowo-
częstotliwościowej dla
przyśpieszeń nadwozia dla
różnych wartości
bezwymiarowego
współczynnika tłumienia



1

(linia 1) > 

2

(linia 2) >



3

(linia 3)

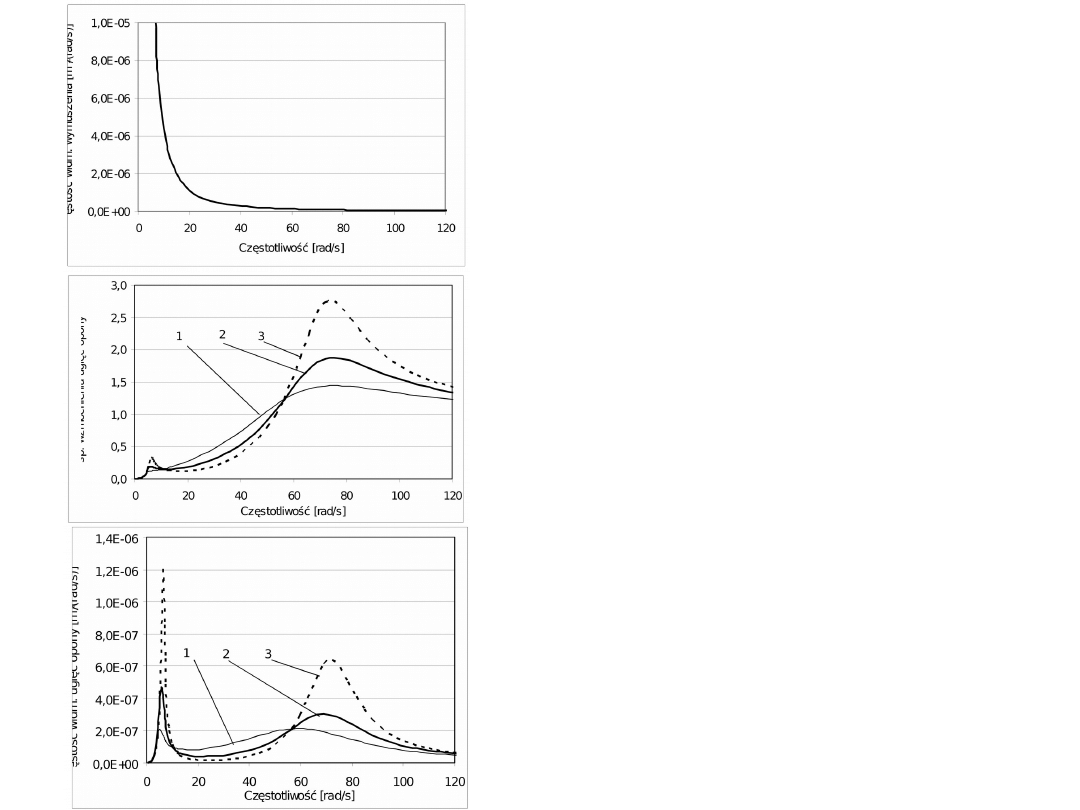
Obliczanie gęstości
widmowej ugięć
dynamicznych opon z widma
gęstości widmowej
nierówności drogi i
charakterystyki
amplitudowo-
częstotliwościowej dla ugięć
opon dla różnych wartości
bezwymiarowego
współczynnika tłumienia


1

(linia 1) > 

2

(linia 2) >



3

(linia 3)















2

1

d

)

(

G

z

2

z





2

z

z

sk

z















Wariancja pionowych przyśpieszeń
nadwozia:

Wartość średnia kwadratowa (RMS = root-mean-
square value) przyśpieszeń nadwozia jest równa
pierwiastkowi kwadratowemu z wariancji, a także
równa odchyleniu standardowemu i wartości
skutecznej (dla średniej wartości przyśpieszenia =
0)

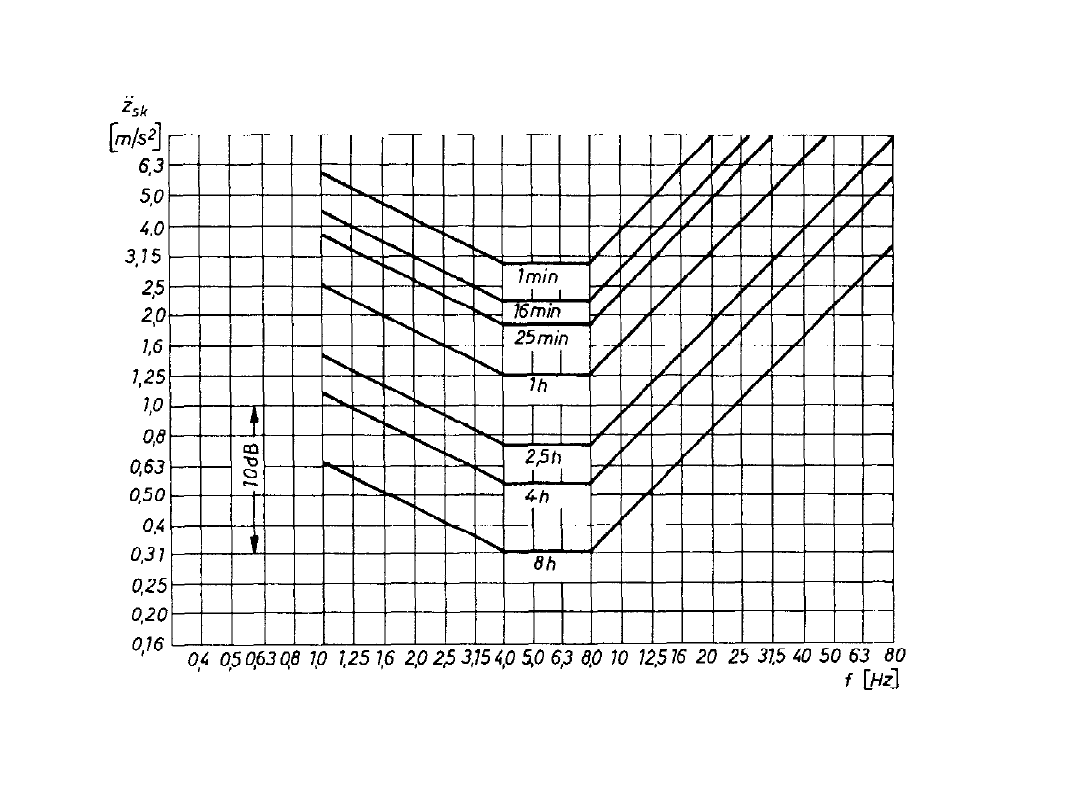
Oddziaływanie drgań na człowieka

Linie jednakowego komfortu wg normy ISO 2631. Dopuszczalne czasy
ekspozycji, kryterium średniej szkodliwości.

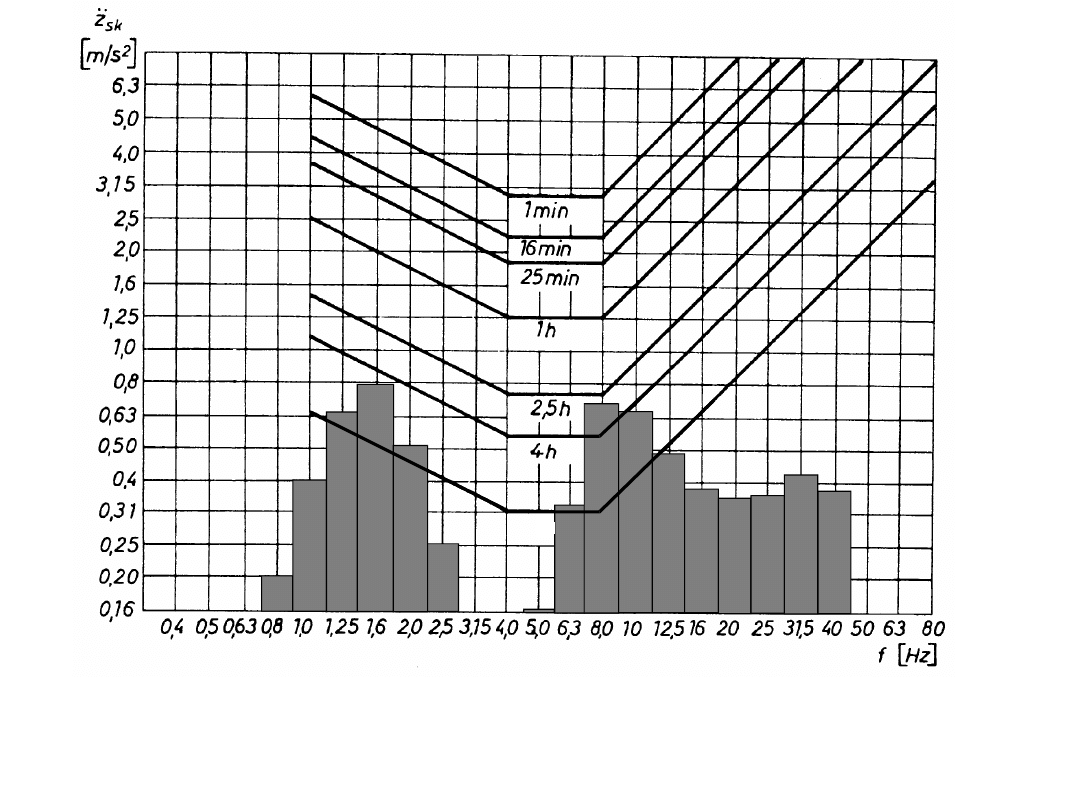
8 h

Porównanie tercjowego (szerokość pasma 1/3 oktawy) widma
przyśpieszeń pionowych nadwozia z liniami dopuszczalnych
czasów ekspozycji wg normy ISO 2631 dla średniego stopnia
szkodliwości