Geneza wykładu

Zbiory przybliżone są teorią opisaną na początku lat
osiemdziesiątych przez
prof.. Zdzisława Pawlaka.
Stosuje się je do analizy danych gromadzonych w postaci
tabelarycznej.

W szczególności można uznać, że zbiory przybliżone to przykład
na zastosowanie
relacji równoważności, pewnego specjalnego rodzaju logiki
(logiki decyzyjnej)
oraz algebry Boole`a (w szczególności funkcji Boolowskich).

Stąd na tematykę związaną z podstawowymi pojęciami zbiorów
przybliżonych (ang. Rough Sets) przeznaczymy 1.5 – 2
wykładów .

Teoria (zwłaszcza jej różne uogólnienia) doczekała się wielu
zastosowań praktycznych: medycyna, przemysł, biznes,
marketing itp.

Można śmiało powiedzieć, że jest POLSKĄ specjalnością
(prof. Pawlak, prof. Skowron, prof. Słowiński, prof.
Mrózek, ........................)

Założenia

Teoria zbiorów przybliżonych proponuje nowe spojrzenie na
wiedzę i jej reprezentację, u podstaw którego leży przekonanie,
że wiedza to zdolność do klasyfikacji. Przez klasyfikację rozumie
się zdolność do odróżniania obiektów -elementów otaczającej
rzeczywistości. Klasyfikacji dokonujemy na podstawie
znajomości cech, jakie dany obiekt lub grupa obiektów posiada.
Tak więc, do zdefiniowania wiedzy musimy mieć pewien zbiór
obiektów, które chcemy klasyfikować oraz zbiór cech, które te
obiekty opisują.

Definicja 1.1 System informacyjny
Systemem informacyjnym nazywamy parę uporządkowaną
A=(U,A), gdzie:
-  U - jest skończonym, niepustym zbiorem obiektów zwanym
uniwersum;
-  A - jest skończonym, niepustym zbiorem atrybutów
odzwierciedlających
własności (cechy) obiektów uniwersum, każdy atrybut
aA jest funkcją

a:UV

a

, gdzie V

a

jest zbiorem wartości atrybutu a,

zwanym zakresem
atrybutu a.

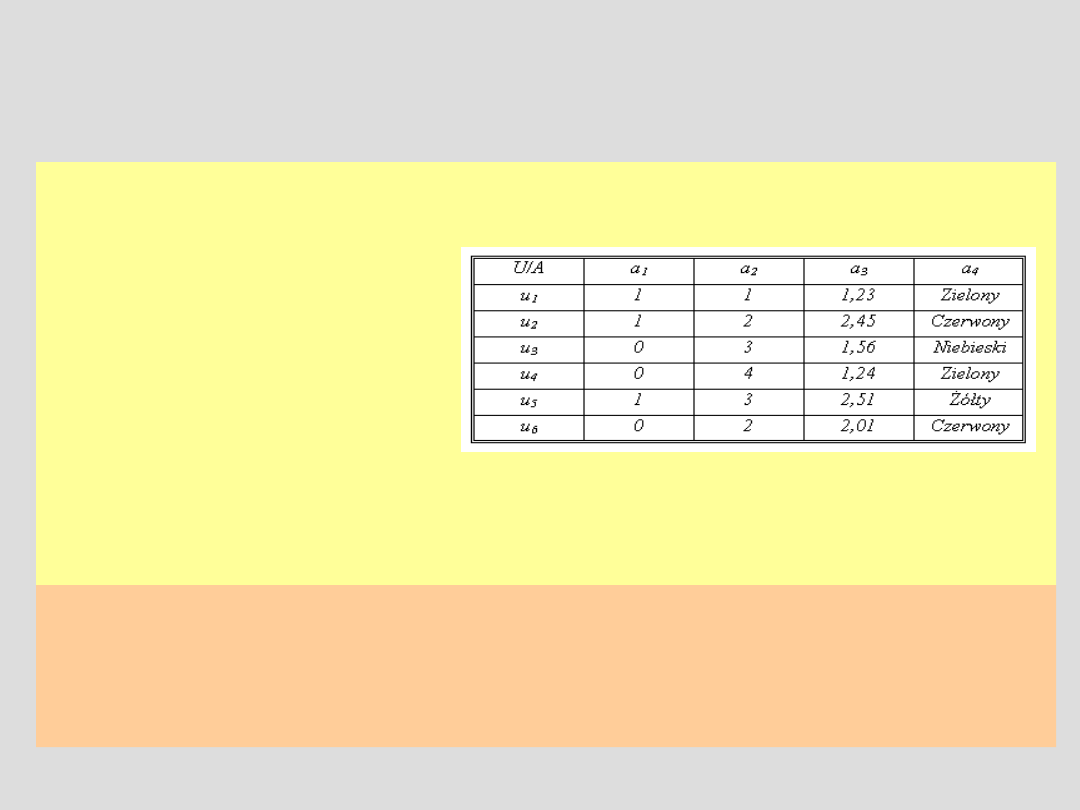
System informacyjny

Przykład:

Obiekty umieszczono w wierszach
Cechy opisujące te obiekty w kolumnach

Jak widać, cechy mogą być różnego typu w szczególności liczby, napisy, kody napisów

UWAGA: W naszych rozważaniach ograniczymy się do atrybutów typu
symbolicznego. Czyli takich atrybutów, które przyjmują wartości z ograniczonego
zbioru. Zakładamy również, że nie istnieje żaden porządek pomiędzy tymi
wartościami.

Atrybuty, pojęcie,

klasyfikacja

Zbiory przybliżone mogą operować również na atrybutach numerycznych
(dyskretyzacja – ustalenie podziału zakresu wartości atrybutu) i symbolicznych
uporządkowanych.

Każdy podzbiór X



U nazywamy pojęciem.

Jak łatwo zauważyć, każde pojęcie X ustala na zbiorze
uniwersum U podział na obiekty należące (u



X) i nie należące

(u



U\X) do pojęcia X.

Zgodnie z definicją podziału prawdziwe są własności U=X



U\X

oraz X



U\X=



.

W bardziej ogólnym przypadku zamiast dzielić U na dwa
podzbiory można podzielić go (w sensie mnogościowym) za
pomocą większej liczby pojęć.
Podział taki nazywamy klasyfikacją. Dla klasyfikacji prawdziwa
jest własność U= , gdzie X

i

są pojęciami tworzącymi

klasyfikację.



i

X

Tablica decyzyjna

Szczególnym rodzajem systemu informacyjnego jest tablica
decyzyjna. W tablicy decyzyjnej zbiór atrybutów podzielony jest
na dwa niepuste i rozłączne podzbiory, z których jeden nazywany
jest zbiorem atrybutów warunkowych, a drugi zbiorem
atrybutów decyzyjnych. W zastosowaniach praktycznych
przyjmuje się, że zbiór atrybutów decyzyjnych jest
jednoelementowy.

Definicja Tablica decyzyjna
Niech A=(U,A) będzie systemem informacyjnym oraz C,DA i C



, D



,

CD=



, A=CD. Czwórkę DT=(U,A,C,D) nazywamy tablicą

decyzyjną.
Elementy zbioru C nazywamy atrybutami warunkowymi,
elementy zbioru D
nazywamy atrybutami decyzyjnymi.
W praktyce przyjmujemy oznaczenie DT=(U,A{d}) ,

zakres wartości atrybutu a oznaczać będziemy V

a

Definicja Klasa decyzyjna
Niech DT=(U,A{d}) będzie tablicą decyzyjną oraz vV

d

;

zbiór X

v

={uU: d(u)=v} nazywamy klasą decyzyjną tablicy DT

odpowiadającą wartości v atrybutu decyzyjnego.

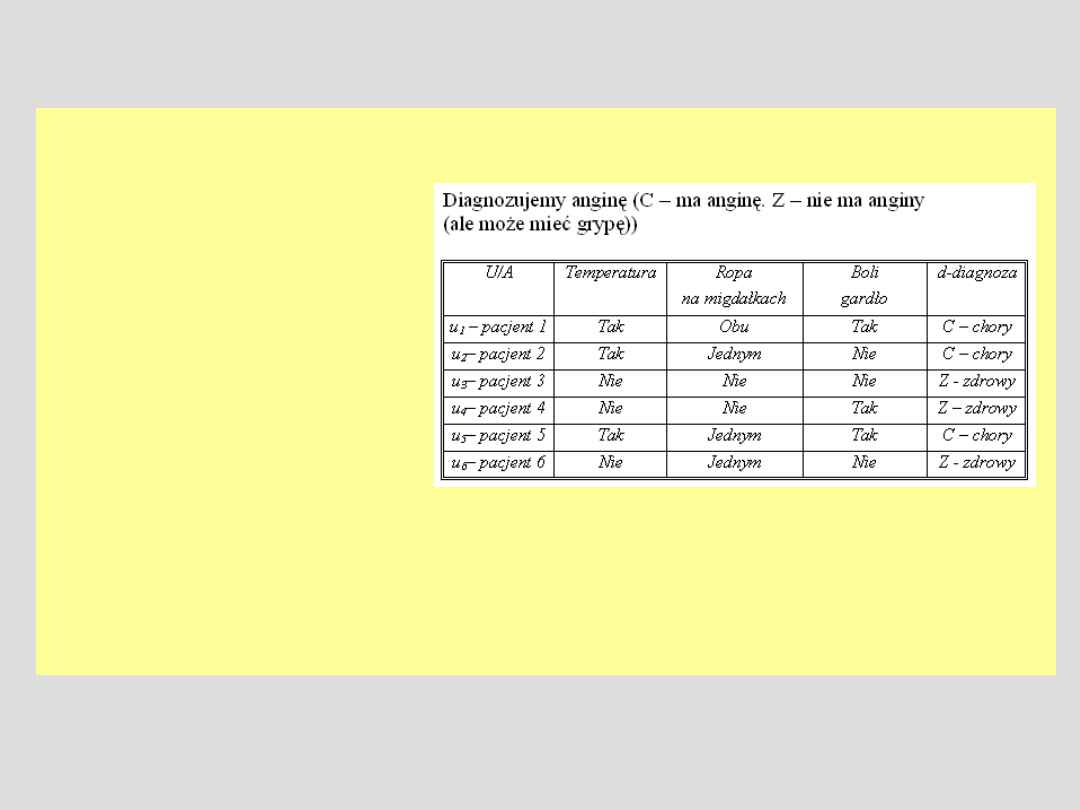
Przykład DT

Przykład:

Zbieramy informacje historyczne o
pacjentach i zapisujemy jakie mieli
objawy. Zauważmy, że są to informacje
historyczne, więc w polu diagnoza są
zweryfikowane wartości C, Z.

Otrzymujemy klasyfikację zbioru
pacjentów na tych, którzy mieli
i nie mieli anginy

Oczywiście możemy mieć więcej atrybutów warunkowych oraz mogą one być inaczej określone
np. Temperatura ={ Bardzo wysoka, Wysoka, W normie, Stan podgorączkowy}

Możemy mieć więcej obiektów (przebadanych pacjentów)

Tablica opisuje pewien interesujący nas fragment rzeczywistości

Wybrane cele analizy

DT

1. Za pomocą atrybutów warunkowych (wartości ich atrybutów) utworzyć
opisy klas decyzyjnych
INNYMI SŁOWY
Podać, w jaki sposób wartości atrybutu decyzyjnego zależą od wartości
atrybutów warunkowych

2. Językiem opisu każdej klasy są reguły decyzyjne

IF zbiór_warunków THEN decyzja

np. IF Temperatura=Tak and Boli_gardło=Tak THEN C-chory

3. Sprawdzić, czy bez utraty informacji na temat odróżniania obiektów z różnych
klas decyzyjnych, da się usunąć z tablicy decyzyjnej jakieś atrybuty warunkowe

4. Na podstawie utworzonych regułowych opisów klas decyzyjnych automatycznie
(w sposób algorytmiczny) klasyfikować obiekty do odpowiadających im klas
a) obiekty z DT b) obiekty nowe dotychczas nieznane (nie ma ich w DT)

Zbiory przybliżone

Każda cecha (atrybut warunkowy) poprzez swój zbiór wartości ustala
klasyfikację zbioru uniwersum, różne cechy mogą ustalać różne klasyfikacje.
Klasyfikację uniwersum można także otrzymać rozpatrując pewien podzbiór
cech równocześnie.
Klasyfikacja pozwala określić w zbiorze U dwuargumentową relację
równoważności zwaną relacją nierozróżnialności.

Definicja Relacja nierozróżnialności
Niech A=(U,A) będzie systemem informacyjnym oraz BA.

Relacją nierozróżnialności generowaną przez zbiór B nazywamy dwuargumentową
relację w zbiorze U zdefiniowaną w następujący sposób:

IND

B

={<x,y>UU: aB a(x)=a(y)}

Do klas abstrakcji tej relacji należą te obiekty z U, które są nierozróżnialne ze
względu na cechy, jakie reprezentuje zbiór atrybutów B.
Każdą klasę abstrakcji relacji IND

B

nazywamy zbiorem B-elementarnym.

Zbiory przybliżone

Zbiory B-elementarne relacji IND

B

pozwalają zdefiniować dowolne pojęcie.

Mówimy, że pojęcie X



U jest B-definiowalne, jeżeli X jest sumą mnogościową

pojęć B-elementarnych, w przeciwnym przypadku pojęcie X jest B-niedefiniowalne.
Kiedy pojęcie jest B-niedefiniowalne możemy jednak za pomocą zbiorów
B-elementarnych skonstruować B-przybliżony opis pojęcia X.

-

Dokładność pojęcia, DT -

sprzeczna

Obszar pozytywny DT, jakość

klasyfikacji

Analizując tablicę decyzyjną, chcemy na podstawie wiedzy o wartościach
atrybutów warunkowych wskazywać, do jakiej klasy decyzyjnej należy dowolny
obiekt z uniwersum. Interesujące jest zatem wskazanie obiektów, które możemy
zaklasyfikować jednoznacznie do klas decyzyjnych.

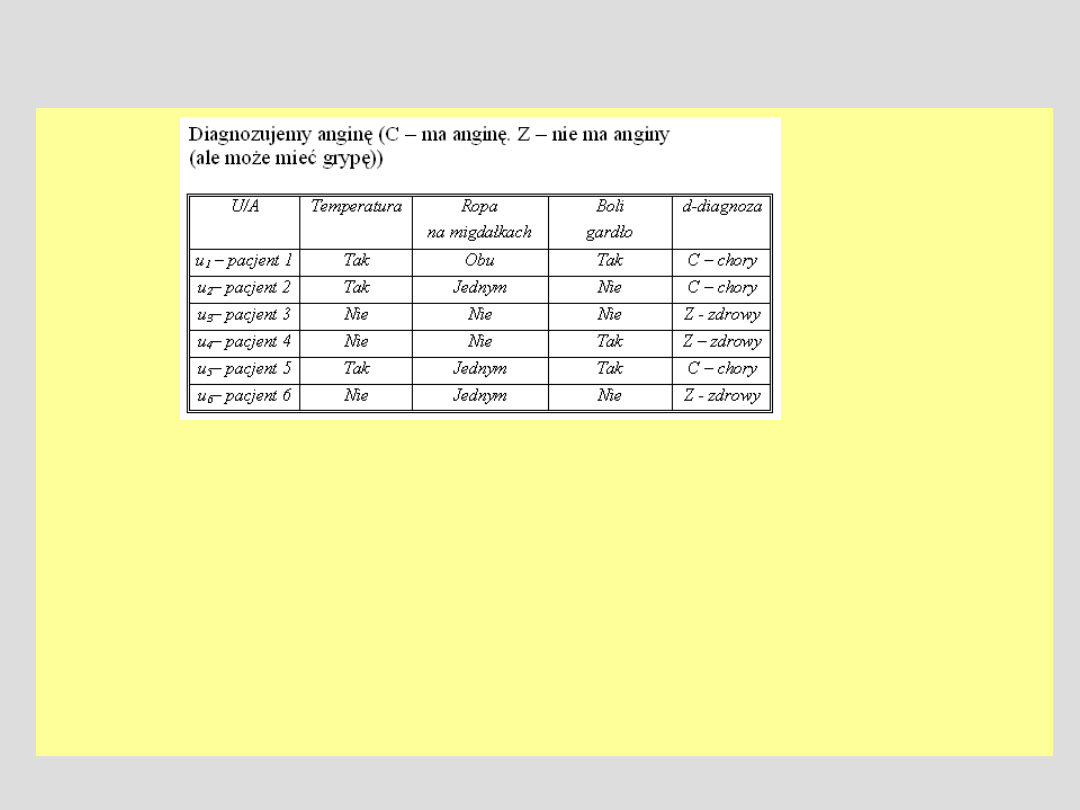
Przykłady

Przykład:

1. U\IND({Temperatura})={ {u1,u2,u5}, {u3,u4,u6} }
2. U\IND({Ropa .... })={ {u1}, {u2, u5, u6}, {u3, u4} }
3. U\IND({Temperatura, Ropa ...})={ {u1}, {u2, u5}, {u6}, {u3,u4} }
4. U\IND(A)={ {u1}, {u2}, {u3}, {u4}, {u5}, {u6} } A- wszystkie atrybuty

Pojęcie C-chory={u1,u2,u5} z pkt widzenia podziału 1. jest B-definiowalne
B={Temperatura}, ale jeśli B={Ropa na migdałkach}, to pojęcie C-chory
nie jest B-definiowalne.

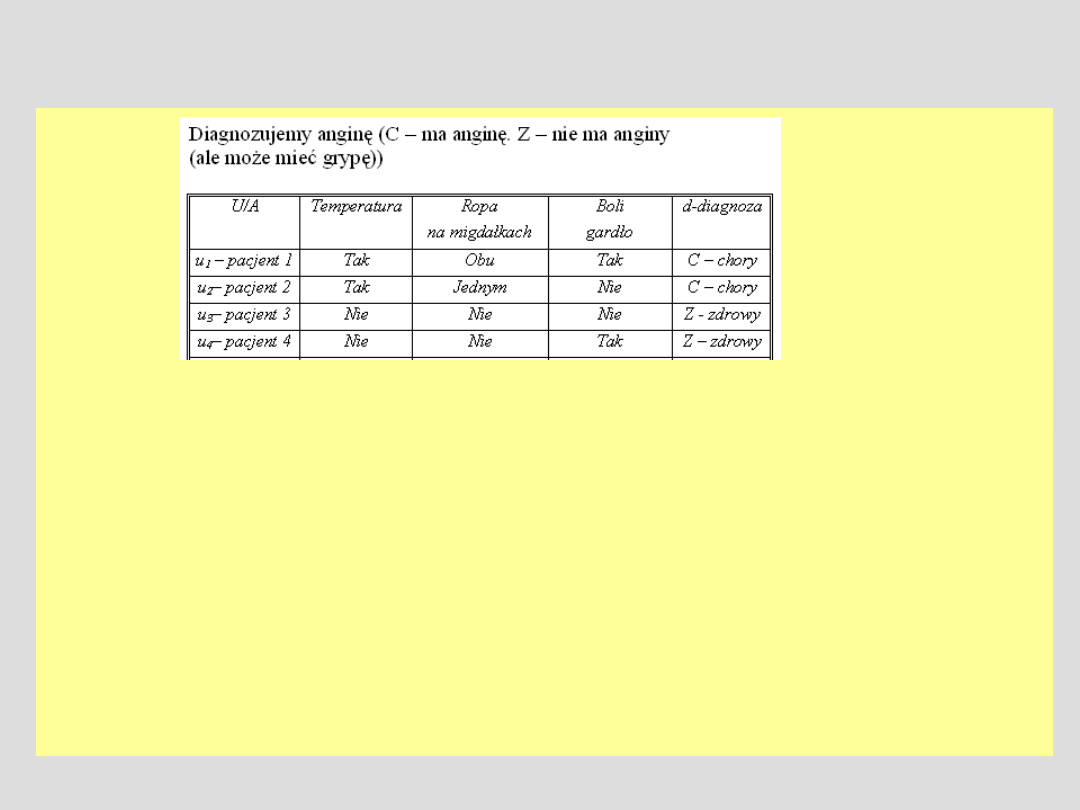
Przykład cd.

Przykład:

U\IND({Ropa .... })={ {u1}, {u2, u5, u6}, {u3, u4} }
B={Ropa na migdałkach} C-chory={u1,u2,u5} pojęcie to nie jest B-definiowalne

Można jednak podać B-górne i B-dolne przybliżenia tego pojęcia
B-dolne={u1} - u1 jest z pewnością reprezentantem pojęcia C-chory
B-górne={u1}{u2,u5,u6}

BN={u2,u5,u6} - te obiekty być może są reprezentantami pojęcia C-chory

Zatem współczynnik dokładności pojęcia C-chory, jeśli próbuje je zdefiniować
tylko za pomocą atrybutu Ropa na migdałkach, wynosi 0.25.

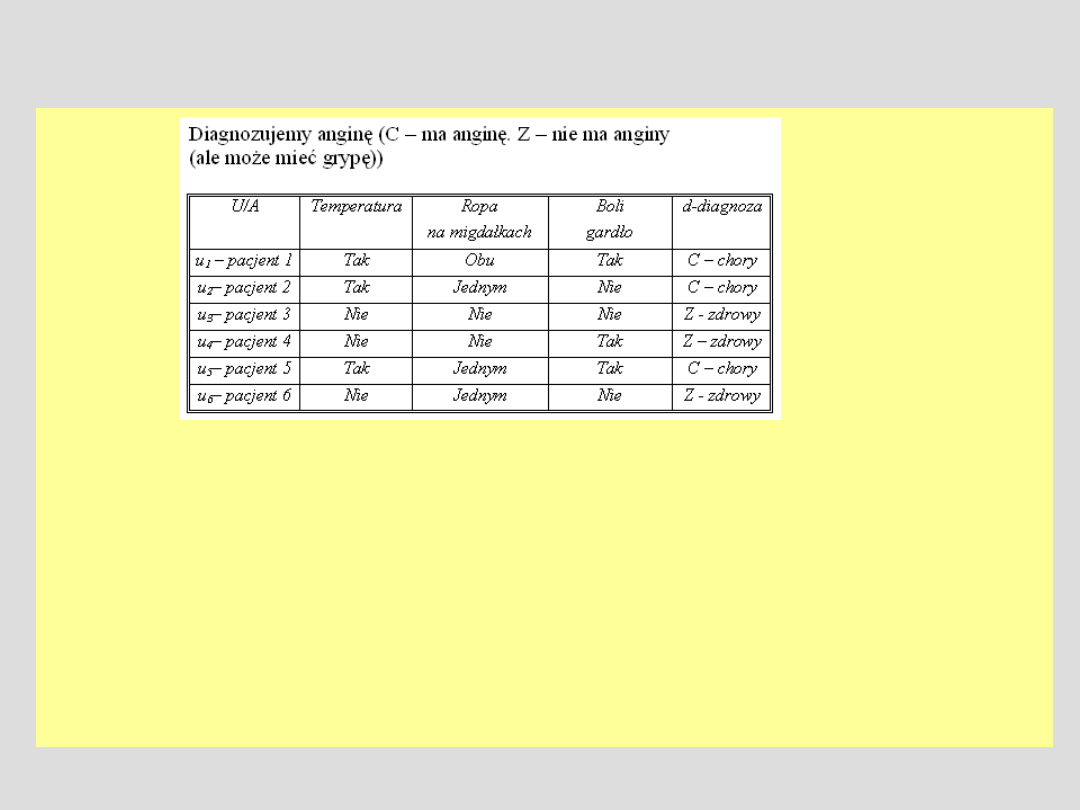
Przykład:

U\IND({Ropa .... })={ {u1}, {u2, u5, u6}, {u3, u4} }
B={Ropa na migdałkach} C-chory={u1,u2,u5} pojęcie to nie jest B-definiowalne

Z-zdrowy={u3,u4,u6} również nie jest B-definiowalne

Klasyfikacja przez atrybut decyzyjny
U\IND({d-diagnoza})={ {u1, u2, u5}, {u3, u4,u6} }
Obszar B-pozytywny POS

B

(d)={ u1, u3,u4 } - suma B-dolnych przybliżeń klas

decyzyjnych

Współczynnik jakości klasyfikacji dla naszego zbioru B i klas decyzyjnych – 0.5

Przykład cd.