1
Algorytmy i
struktury
danych
Wykład 5
2
Dziel i rządź
(c.d.)
Dzielimy problem na
mniejsze, które łatwiej
jest rozwiązać.

3
Dziel i rządź: Wyznaczanie
wartości maksymalnej
(wyszukiwanie połówkowe)
Należy znaleźć wartość maksymalną (itp. relacja
porządku) w ciągu liczb.
Rozwiązanie problemu rozpoczynamy od podziału
ciągu na 2 w miarę możliwości równe części. W
każdej z nich osobno szukamy minimum i następnie z
tych 2 minimów wybieramy mniejsze.
Jak znaleźć minimum w podtablicach? Tak samo jak w
tablicy głównej. Znów każdą podtablice dzielimy na 2
części. I tak, aż do uzyskania tablic jedno
elementowych.
Znalezienie minimum w podtablicy jedno
elementowej jest oczywiste.
Wykorzystując rekurencję i dzieląc problem na
mniejsze (strategia dziel i rządź) osiągniemy cel.
4
Dziel i rządź: „Linijka”
Kolejny problem, który łatwo rozwiązać rekurencją.
Najpierw dzielimy odcinek na pół. Potem każdą z
polówek znów dzielimy na pol., przy czym podziałka
ma już proporcjonalnie mniejszą długość. To samo
robimy z każdą ćwiartką, itd. Operacje wykonujemy
rekurencyjnie. Należy ograniczyć wywołania
rekurencyjne, aby umożliwić zakończenie podziału.
Długość odcinka dzielącego uzależniamy od kroku
(stopnia zagłębienia) rekurencji (wywołując rekurencję
przekazujemy powiększony parametr do funkcji).
5
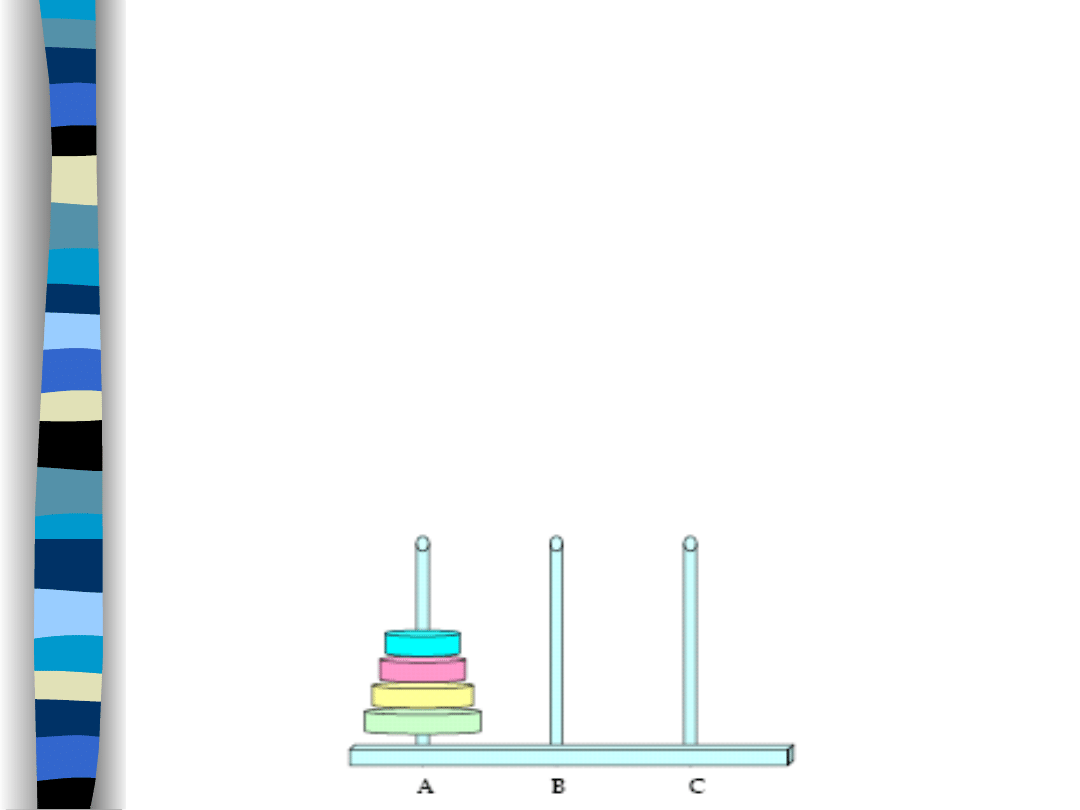
Dziel i rządź: Wieże
Hanoi
Problem polega na tym, aby przełożyć
wszystkie n krążków z słupka A na
słupek C w taki sposób, aby w trakcie
tej operacji większy krążek nigdy nie
został położony na mniejszym.Krążki
należy przekładać pojedynczo.

6
Rozwiązanie + pseudokod
Operację tę znów sprowadzamy to prostszych problemów. Przenosimy n-1 krążków
(wszystkie z wyjątkiem ostatniego - największego) na wieżę B, przekładamy
największy krążek na wieżę C. Aby przenieść pozostałe n-1 krążków z B na C znów
dzielimy problem podobnie.
Problem najbardziej naturalnie byłoby zaimplementować na 3 oddzielnych
„stosach”. Krążki mogą być reprezentowane przez liczby (proporcjonalnie do
średnicy krążka).
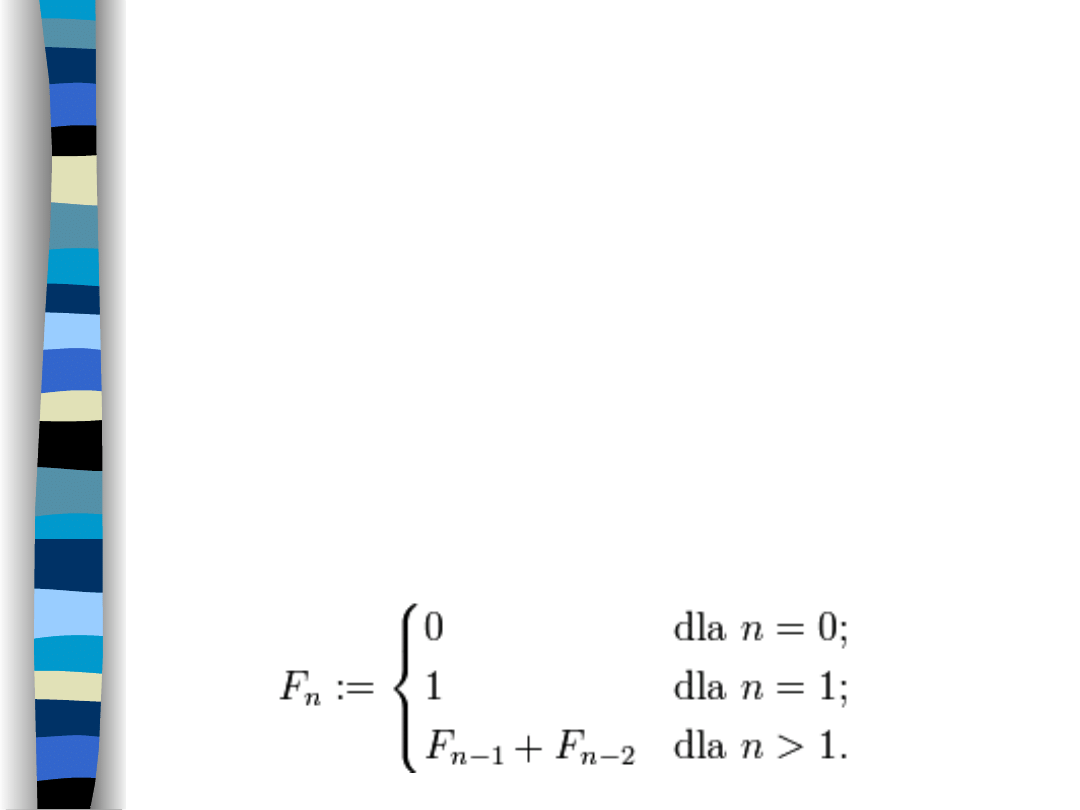
7
Ciąg liczb Fibonacciego
Problem polega na obliczeniu n kolejnych
liczb tzw. Ciągu Fibonacciego. Jest to
ciąg, w którym pierwsza liczba jest równa
0, a druga 1. Każda kolejna powstaje z
sumy dwóch poprzednich liczb.
Początkowe wyrazy ciągu: 0, 1, 1, 2, 3, 5,
8, 13, 21,…
8
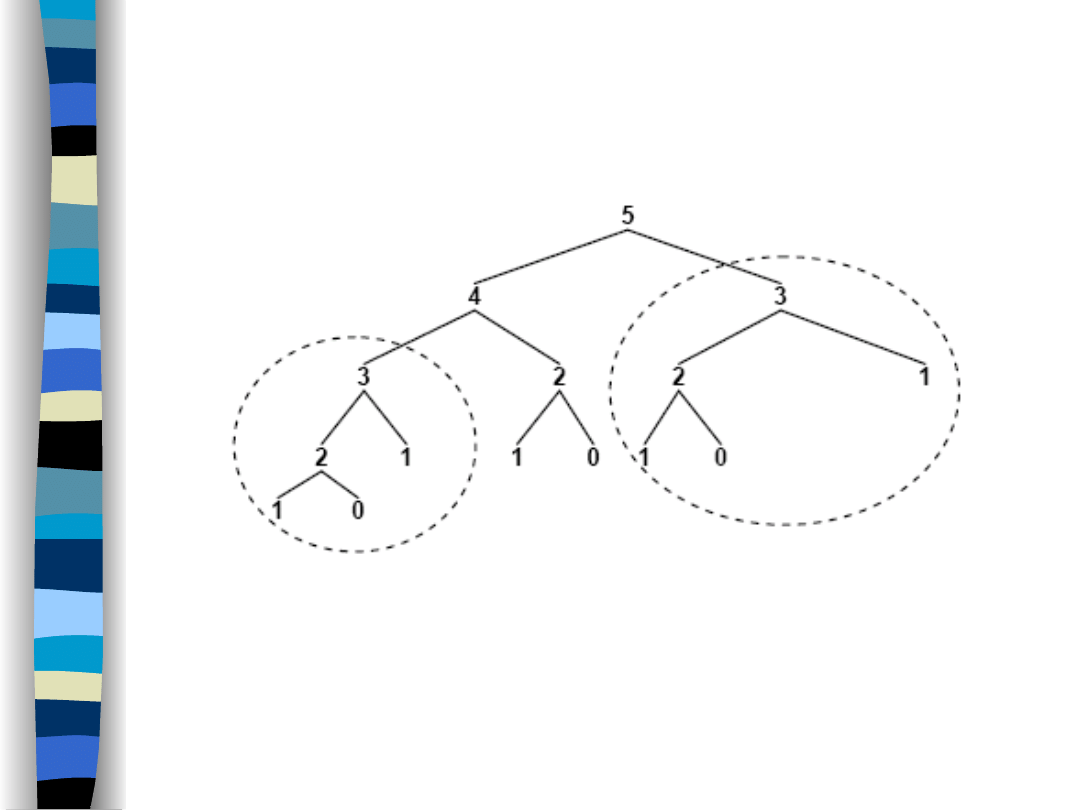
Rozwiązanie rekurencyjne
Problem ten można rozwiązać wykorzystując
rekurencję. Warto jednak zauważyć, że
obliczając kolejne liczby ciągu powtarzamy
obliczenia.
9
Programowanie
dynamiczne
Obliczając kolejne elementy
zapamiętujemy wyniki, aby w
przyszłości (gdy znów będą one
nam potrzebne) moc z nich
skorzystać.
10
Rozwiązanie Fib. z
wykorzystaniem
programowania
dynamicznego
Im dalsza liczba ciągu, tym powtarzanych
operacji obliczeniowych jest coraz więcej.
Warto by się zastanowić, czy nie da się tego
uniknąć. Rozwiązaniem jest zastosowanie
programowania dynamicznego. Obliczając
kolejne elementy ciągu zapamiętujemy
wyniki, aby w przyszłości (gdy znów będą one
nam potrzebne) moc z nich skorzystać.
Można to zaimplementować jako tablicę liczb,
gdzie indeksy to wartości n, a elementy tablicy
to wartości ciągiem Fibonacciego, czyli F(n).
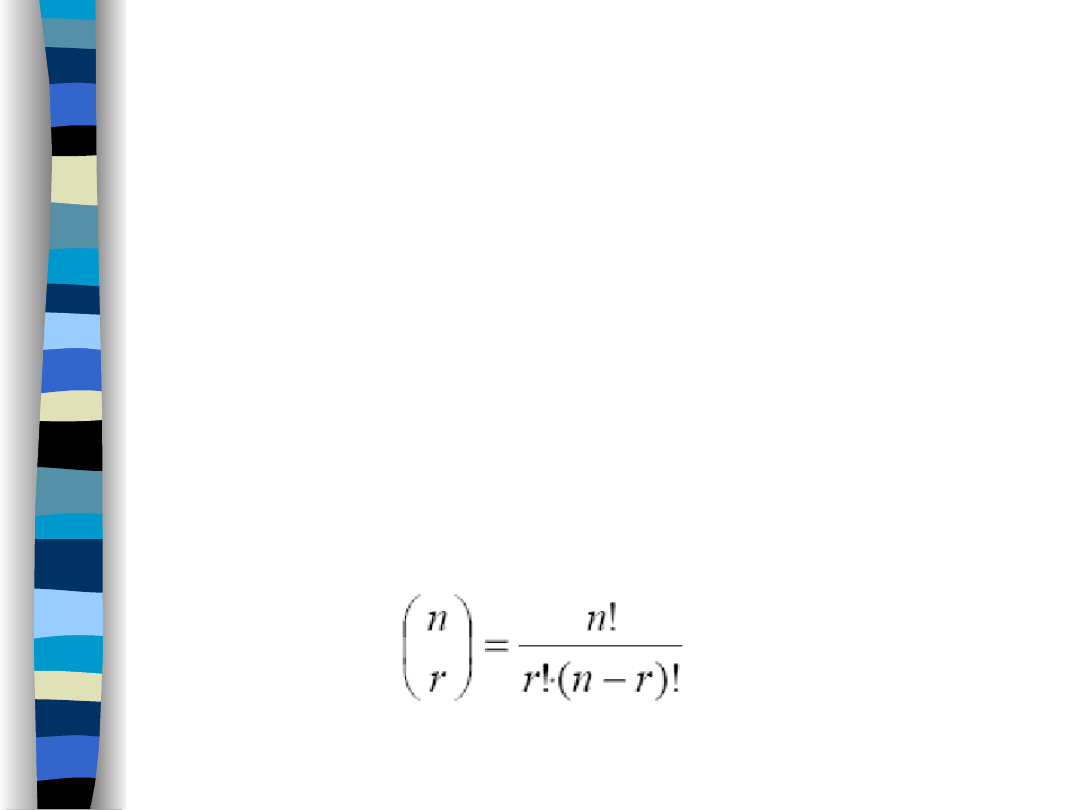
11
Liczba kombinacji –
trójkąt Pascala
Problem polega na obliczenie liczby
kombinacji, czyli ilości możliwości
wyboru r-elementowych podzbiorów z
n-elementowego zbioru.
Matematycznie obliczenia takie
można wykonać korzystając ze wzoru:
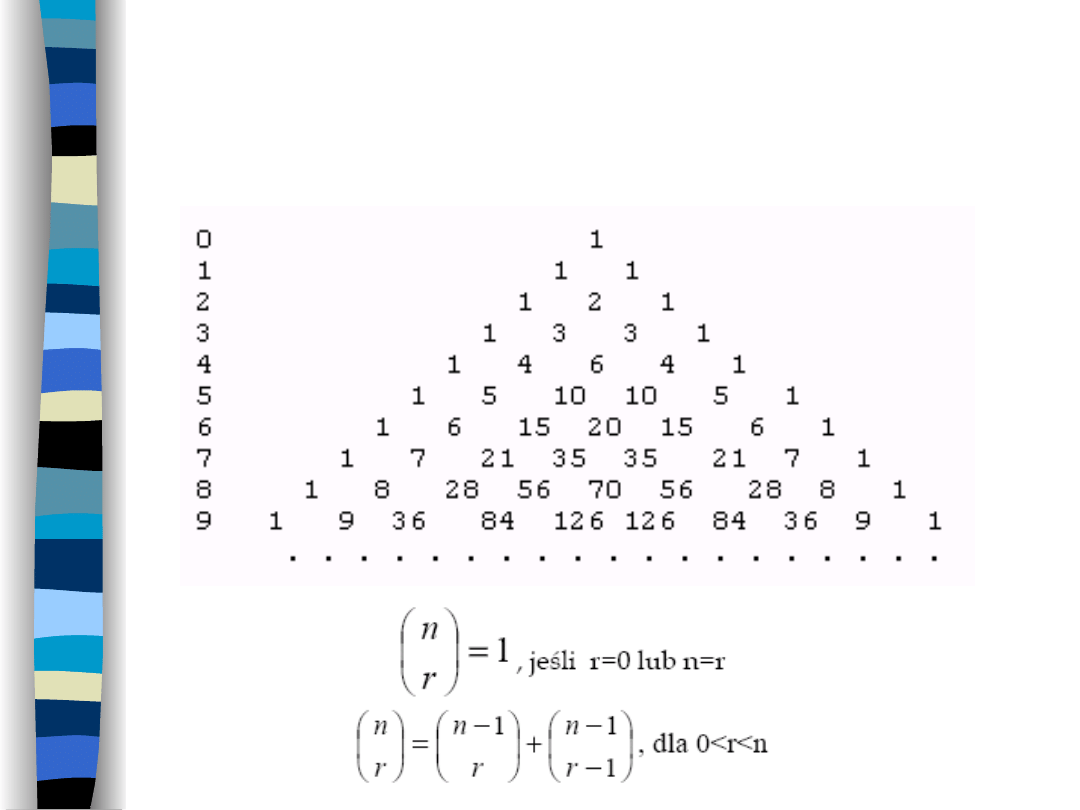
12
Trójkąt Pascala

13
Także w tym przypadku (podobnie
jak miało to miejsce przy
obliczaniu liczb Fibonacciego)
niektóre wartości się powtarzają, a
więc obliczenia będą wykonywane
kilka razy. Warto więc wykorzystać
idee programowania
dynamicznego.
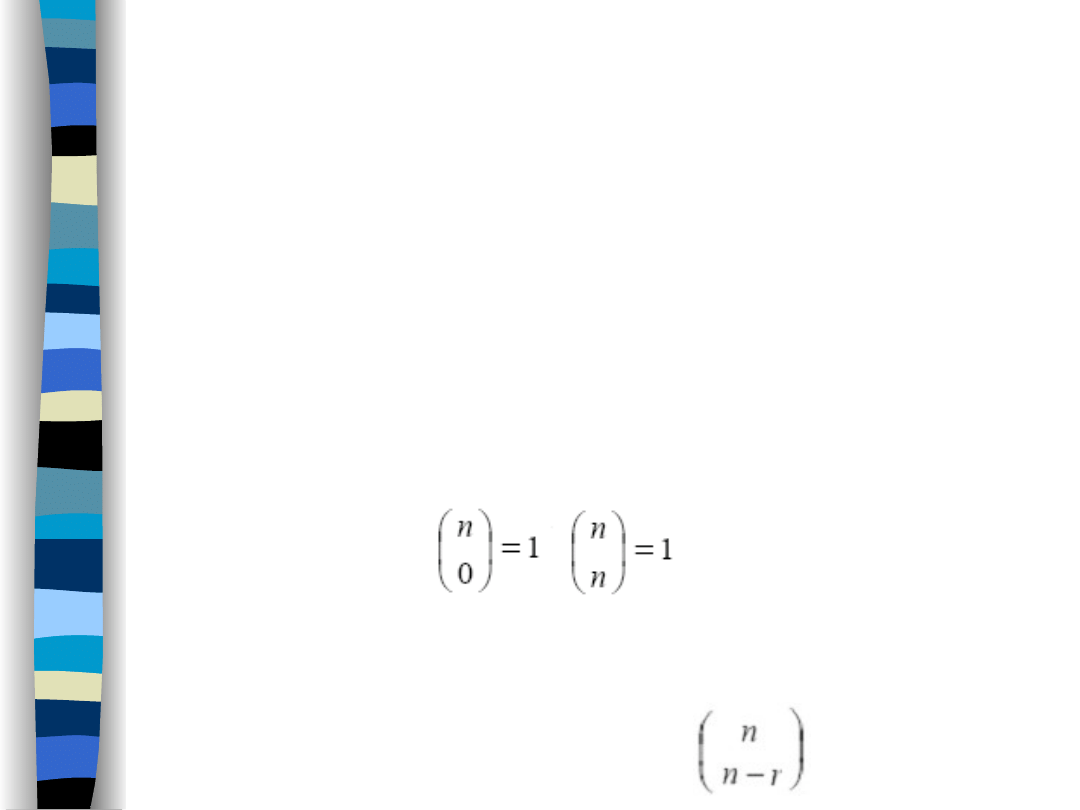
14
Rozwiązanie
wykorzystujące
programowanie
dynamiczne
Obliczone wartości n po r zapamiętujemy w
dwuwymiarowej tablicy, w której indeks
wierszy odpowiadać będzie wartościom n, a
indeks kolumn – wartościom r.
Tablice tą na starcie uzupełniamy
informacjami, które już znamy:
Pozostałe wartości będą uzupełniane w trakcie
kolejnych obliczeń. Pamiętajmy też, że trójkąt
Pascala jest symetryczny, tj.

15
Problem pakowania
plecaka (ang. knapsack
problem)
Problem polegam na tym, aby spakować
plecak x-kilogramowy rzeczami, które
mają swoją wagę i wartość w taki sposób,
aby spakowane rzeczy były najbardziej
wartościowe.
Suma wag wszystkich przedmiotów nie
może przekraczać pojemności plecaka.
Zakładamy także, że mamy nieskończenie
wiele rzeczy tego samego typu.

16
Gdybyśmy mogli dzielić pakowane rzeczy
to problem byłby banalny. Wystarczyłoby
zapakować cały plecak tym samym
rodzajem przedmiotów, których stosunek
wartości do wagi jest maksymalny.
Rozwiązanie zachłanne: pakujemy
zawsze najbardziej wartościowy przedmiot,
który się w plecaku mieści. Nie gwarantuje
nam to jednak optymalnego rozwiązania.

17
Gdy będziemy pakować zachłannie, tzn. będziemy wkładać do plecaka rzeczy o
największym stosunku c/w.
–
wkładamy rzecz p1, pozostaje nam 8 kg wolnego miejsca;
– wkładamy rzecz p2, pozostaje nam 3 kg wolnego miejsca;
– nie możemy już włożyć nic więcej;
nasz plecak ma wartość 10 zł + 4 zł = 14 zł;

18
Rozwiązanie optymalne
– wkładamy rzecz p1, pozostaje nam 8 kg wolnego
miejsca;
– wkładamy rzecz p3, pozostaje nam 4 kg wolnego
miejsca;
– wkładamy rzecz p3, pozostaje nam 0 kg wolnego
miejsca;
plecak jest pełen i ma wartość 10 zł + 3 zł + 3 zł
= 16 zł.
Jest to rozwiązanie lepsze od zachłannego (które
dało plecak 14-złotowy).

19
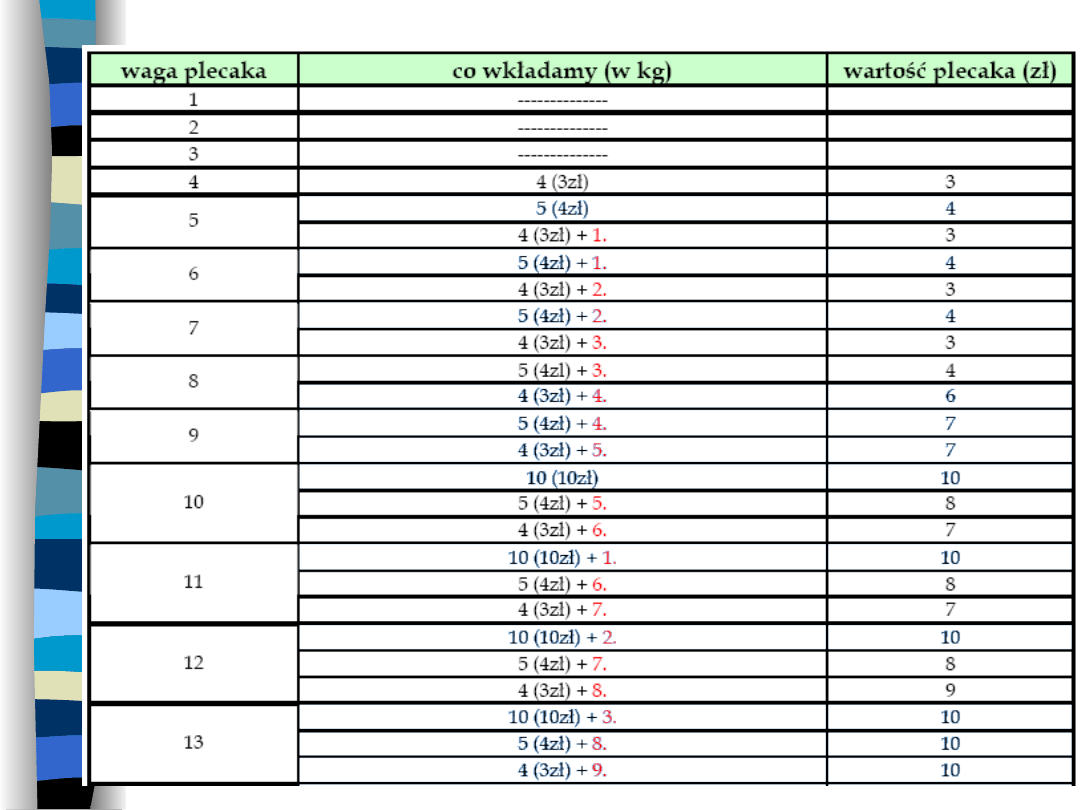
Jak algorytmicznie znaleźć
rozwiązanie optymalne?
Najlepiej w tym celu wykorzystać rekurencję oraz
programowanie dynamiczne.
Zaczynamy od plecaka 1 kg. Taki plecak jest bardzo
łatwo spakować. Następnie pakujemy plecak 2kg,
3kg i tak, aż dojdziemy do plecaka x-kilogramowego.
Przykład: aby spakować plecak, np. 8kg, możemy
wybrać rzecz:
–
5kg i to, co możemy spakować do plecaka 3
kilogramowego (8-5=3);
–
4kg i to, co możemy spakować do plecaka 4
kilogramowego (8-4=4);
Wybieramy lepszą opcję (zaznaczona na niebiesko).
20

21
Rozkład na czynniki
pierwsze liczb
naturalnych (0-1000)
Problem rozwiązujemy także korzystając z
rekurencji i programowania dynamicznego.
Rozkładając kolejne liczby naturalne
zapamiętujemy wynik tak, aby później moc
z niego korzystać. Do implementacji można
wykorzystać tablice 1001 elementową (od 0
do 1000) wskaźników do list
przechowujących czynniki pierwsze, na
które rozkładamy daną liczbę.

22
Każda lista będzie tak naprawdę
przechowywała jedną liczbę pierwszą,
która wskazywać będzie na odpowiedni
indeks innej liczby w tablicy, jako na
kolejne elementy listy.
Przykładowo, liczbę 12 rozkładamy na 2
razy to, na co rozłożyliśmy liczbę 6.
Sześć to: 2 razy to, na co rozłożyliśmy 3.
Ponieważ liczba trzy jest liczbą
pierwszą, więc to już jest koniec listy.
23
Metoda powrotów –
”prób i błędów”
(ang. backtracking)

24
Metoda powrotów
Aby rozwiązać problem w trakcie jego
rozwiązywania dokonujemy pewnych
decyzji.
Wybieramy pewną drogę, którą będziemy
dalej się poruszać. Może się zdarzyć
sytuacja, w której nasz wybór będzie zły i
doprowadzi nas to do braku rozwiązania –
nie osiągniemy celu. Wtedy należy cofnąć
ostatnią decyzję i wybrać inną drogę, która
być może doprowadzi nas do celu.

25
Aby moc dokonać wspomnianych
powrotów należy zapamiętywać
ruchy (decyzje), których dokonaliśmy
wcześniej, aby moc do nich powrócić.
Rozwiązać to można odkładając
informacje o kolejnych naszych
posunięciach na stos.
Można wykorzystać do tego rekurencję.
26
Problem skoczka
szachowego
Zadanie polega na przeskoczeniu skoczkiem
szachowym wszystkich pól szachownicy.
Zakładamy, że na każdym polu możemy
stanąć tylko raz.
Skoczek szachowy może ośmiu danego
miejsca wykonać skok w jednym z ośmiu
kierunków.

27
Zatem skacząc skoczkiem po
planszy sprawdzamy, czy już tu
byliśmy, jeśli nie to stawiamy
skoczka w tym miejscu, jeśli tak, to
należy wycofać się z poprzedniego
kroku i z ośmiu wybrać inną
możliwość. Podczas implementacji
należy wykorzystać rekurencję.
28
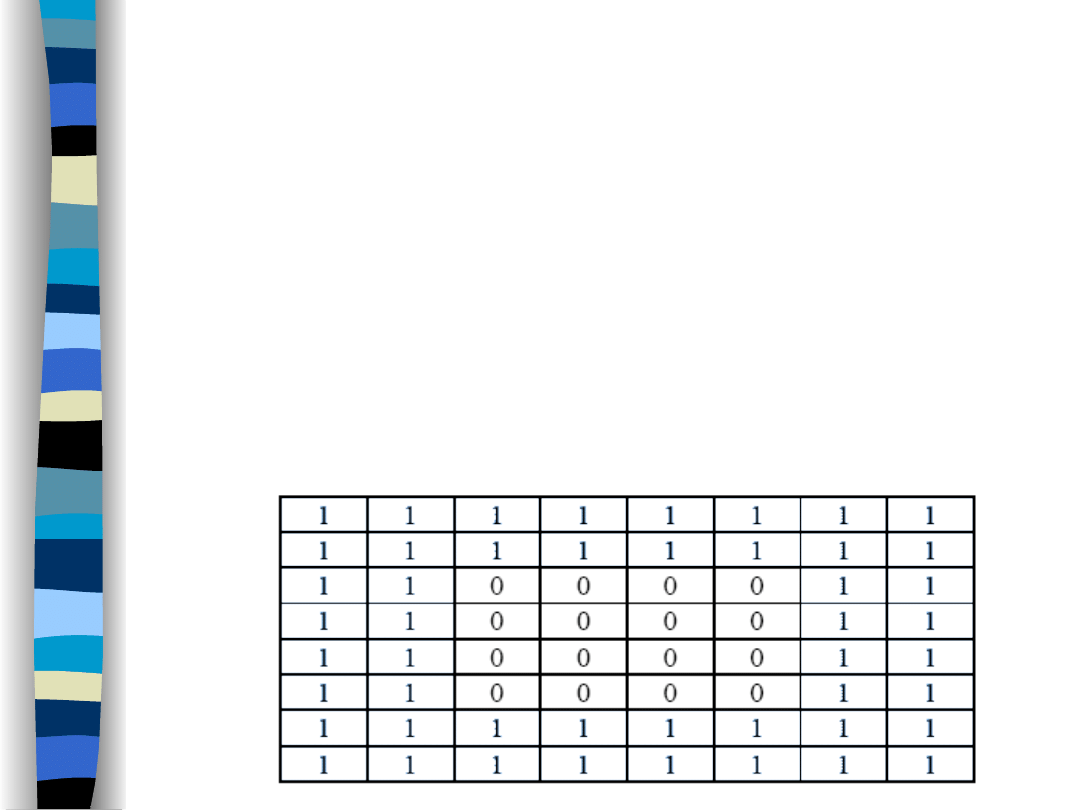
Szachownicę możemy zaimplementować jako
tabelę ośmiu wymiarach n+4 na n+4 (gdzie n to
wymiary planszy szachownicy). Każde pole
będzie przechowywać wartość 0 – gdy jeszcze na
nim nie stanęliśmy i 1- gdy już postawiliśmy tu
skoczka.

29
Dodatkowe cztery wiersze i kolumny to tzw.
„otoczka zabezpieczająca”. Poruszając się po
wierszach i kolumnach tablicy należy zadbać
o to, aby nie wyjść poza obszar pamięci
przydzielony dla tej tablicy.
–
Jednym z rozwiązań jest sprawdzanie przed
każdym skokiem, czy ma to miejsce.
–
Drugim (które stosujemy) polega na otoczeniu
naszej „szachownicy” otoczką o grubości dwóch
wierszy (kolumn). Komórki tej otoczki będą już na
starcie przechowywały wartości jeden, co
uniemożliwi skok na te pola.

30
Pseudokod rozwiązania

31
Problem ośmiu
hetmanów
Zadanie polega na rozstawieniu na
szachownicy 8 hetmanów w taki sposób,
aby żaden z nich nie znajdował się w tej
samej kolumnie, wierszu i na tej samej
przekątnej co inny hetman. Jeśli
przyjmiemy, że każdy hetman będzie
stał w innej kolumnie, to dla każdego z
nich mamy 8 możliwości ustawienia
(ponieważ mamy 8 wierszy do wyboru).

32
Rozwiązanie metodą
powrotów
Rozpoczynamy stawiając pierwszego hetmana w
pierwszym wierszu pierwszej kolumny,
Następnie przechodzimy do drugiej kolumny i
próbujemy wstawić drugiego hetmana. Nie można
tego zrobić w pierwszym ani drugim wierszu, więc
stawiamy go w trzecim.
To samo robimy z każdym kolejnym hetmanem.
Jeśli okaże się, że któregoś z nich nie da się
ustawić w żadnym wierszu, musimy wycofać się z
ostatniego ruchu – powrócić. Zdejmujemy
poprzednio postawionego hetmana i próbujemy
kolejnego możliwego wiersza.

33
Pseudokod rozwiązania

34

35

36

37

38

39
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18
- Slide 19
- Slide 20
- Slide 21
- Slide 22
- Slide 23
- Slide 24
- Slide 25
- Slide 26
- Slide 27
- Slide 28
- Slide 29
- Slide 30
- Slide 31
- Slide 32
- Slide 33
- Slide 34
- Slide 35
- Slide 36
- Slide 37
- Slide 38
- Slide 39
Wyszukiwarka
Podobne podstrony:
ASD w5
nw asd w5
ASD w5
W5 Zawiesia
W5 sII PCR i sekwencjonowanie cz 2
W5 s33 Inżynieria finanansowa
W5 Temperatura powietrza WWSTiZ
ASD od z Sawanta II Wykład17 6
W5 Rozpoznawanie 2010
IB w5 co
Architektura i organizacja komuterów W5 Pamięć wewnętrzna
W5 pieniadz i system bankowy
psychologia ogólna W5 2013
więcej podobnych podstron