Dyfrakcyjne metody
badań strukturalnych

Wykład VI

2

Metody krystalografii
dyfrakcyjnej



Rejestracja obrazu dyfrakcyjnego

–

rentgenogram oscylacyjny

–

metoda de Jonga-Boumana

–

metoda precesyjna



Interpretacja warstwic hk0 i hk1:

–

typ komórki Bravais’go

–

klasa Lauego

–

parametry komórki elementarnej

3

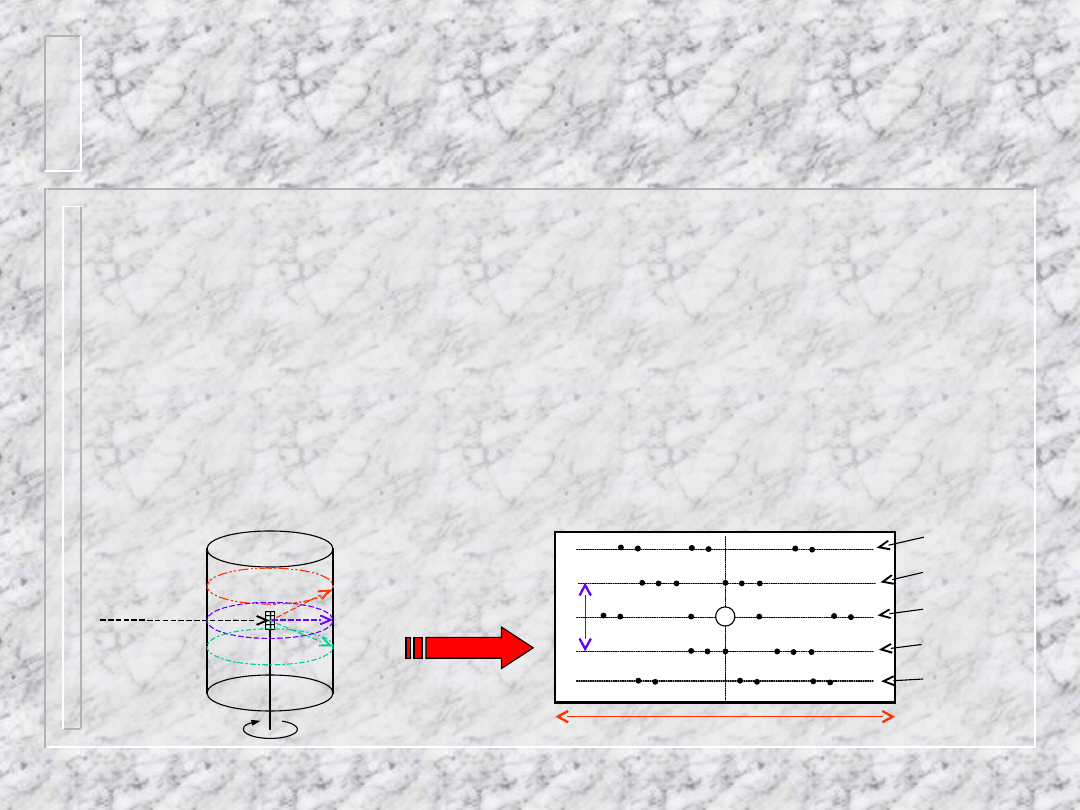
Metoda obracanego
kryształu



Kaseta cylindryczna z błoną rentgenowską



Kryształ jest obracany lub oscyluje w
zakresie kątów 2   20 wokół osi Z



Kryształ jest zorientowany osią
krystalograficzną w kierunku Z

warstwice

2

1
0

!

@

2 y

1

2  R

Rejestracja na płaskiej
błonie

5

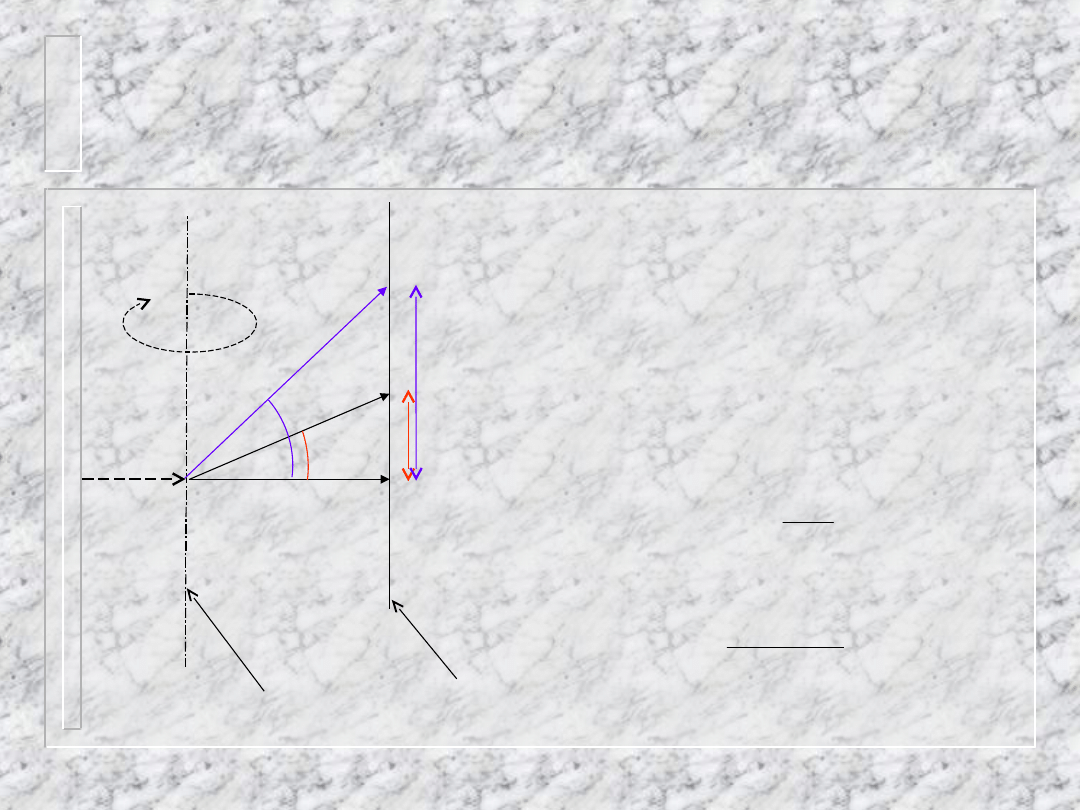
Interpretacja
rentgenogramu



Powstawanie warstwic jest analogią do
powstawania stożków przy dyfrakcji od
prostej sieciowej



warstwica zerowa zawiera refleksy hk0,
warstwica pierwsza hk1 itd.



obracanie kryształu umożliwia
ustawienie płaszczyzn w położenie
dyfrakcyjne



odległość warstwic wyznacza okres
identyczności w kierunku osi obrotu Z

6

Wyznaczanie parametru
sieci T

c

R

y

1



1

n

c

n

n

n

T

R

y







sin

tg





y

2



2

Warunek Lauego:
c(cos  - cos

0

)= n

T

c

cos(90- = n

T

c

sin  = n

błona

Oś obrotu

7

Cechy metody obracanego
kryształu



W zasadzie można by wyznaczyć
wszystkie stałe sieciowe a, b, c
odpowiednio mocując kryształ w trzech
położeniach



Informacja o dwuwymiarowej warstwicy
sieci odwrotnej jest jednowymiarowa



Zdjęcie Weissenberga - zastosowanie
przesłon i sprzężenie obrotu kryształu z
przesuwem błony umożliwia rejestrację
zdeformowanej sieci odwrotnej.

8

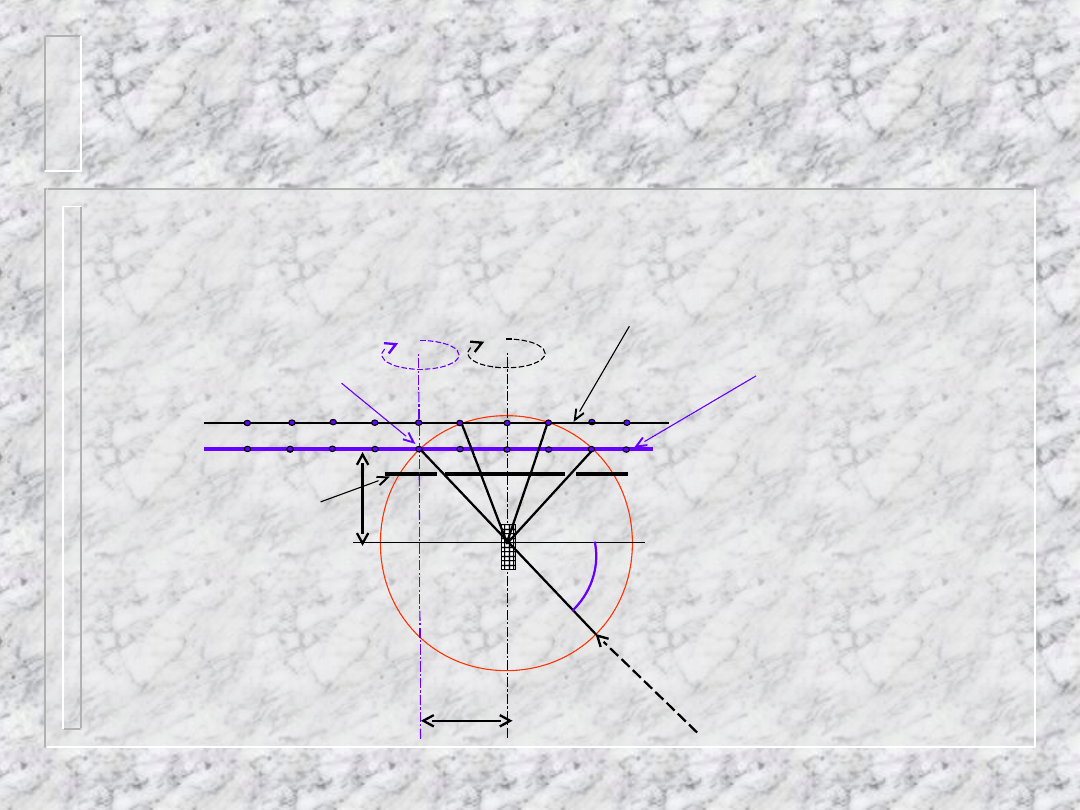
Metoda de Jonga-
Boumana



Rejestrujemy niezdeformowaną
sieć odwrotną



Przesłona pierścieniowa „wycina”
refleksy tylko jednej warstwicy



Błona, której oś obrotu jest
oddalona od osi kryształu, porusza
się synchronicznie z obrotem
kryształu

9

Metoda de Jonga-
Boumana



Aby zarejestrować warstwicę zerową wiązka
musi być nachylona do osi obrotu kryształu!

sfera Ewalda

Płaszczyzna hk0
sieci odwrotnej,
błona

Węzeł 000 sieci

Przesłona

pierścieniow

a

Wiązka promieni X

Płaszczyzna hk1



0

D



:(1/)=cos



0

=cos 



D=sin 



K= D[mm][Å]/sin 

a[Å]=K/a

*

[mm]

10

Zasada pomiaru



Obrót kryształu jest zgodny z obrotem
błony rejestrującej, oś obrotu błony jest
przesunięta od osi obrotu kryształu



Przesłona pierścieniowa wycina jedynie
stożek odpowiadający jednej warstwicy



Obrót kryształu powoduje
naprowadzanie kolejnych węzłów
warstwicy sieci odwrotnej na pierścień
będący przekrojem sfery Ewalda przez
błonę fotograficzną

11

Czynnik skali
eksperymentu



Na rentgenogramie mierzymy odstępy węzłów
lub płaszczyzn w sieci odwrotnej np. w
milimetrach



Dla przeliczenia ich na parametry sieci

rzeczywistej stosujemy czynnik skali K

–

K=  [Å] r[mm], r - promień sfery Ewalda

–

K = a a

*

skalowanie na kryształach

wzorcowych

–

|a|= K/d

*100

; |b|= K/ d

*010

; |c|= K/ d

*001

;

–

dla kątów przyjmujemy (oprócz układu
trójskośnego) =180 - 

*

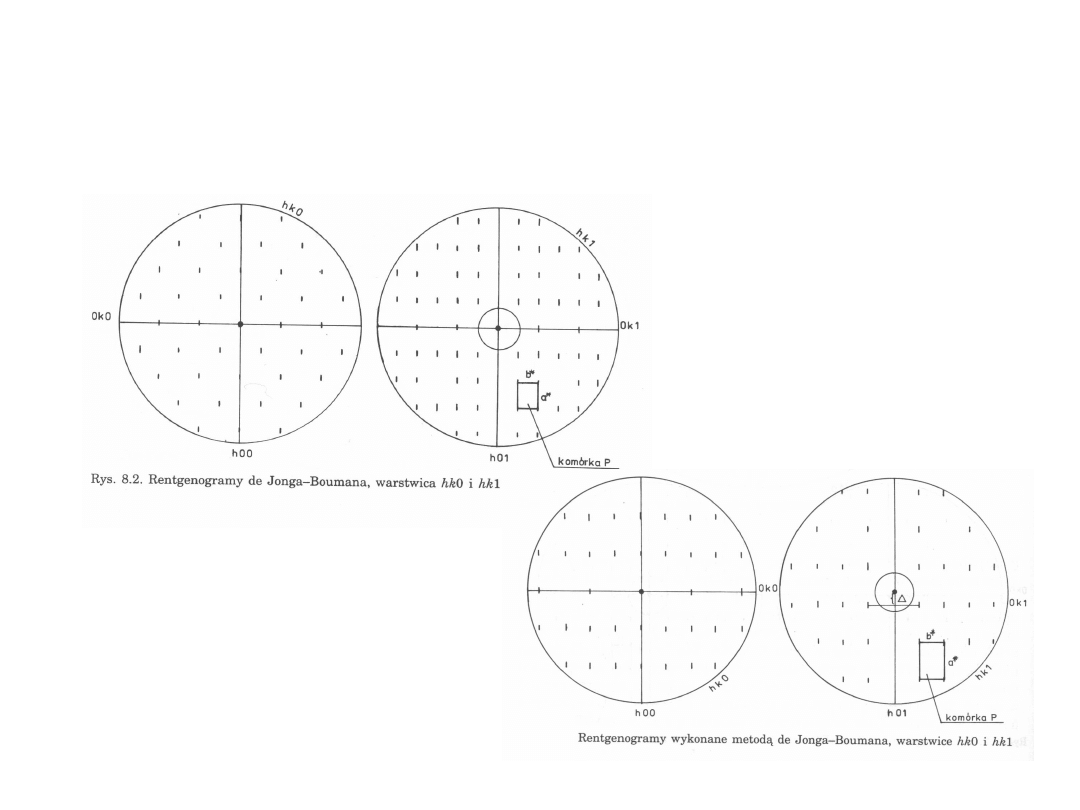
Przykłady rentgenogramów
uzyskanych metodą de Jonga-
Boumana

13

Kamera precesyjna



Inną metodą uzyskiwania zdjęć
niezdeformowanej sieci odwrotnej jest
użycie kamery precesyjnej.



W metodzie tej węzły sieci odwrotnej
nasuwane są na sferę Ewalda przez
synchroniczne wykonywanie ruchów
precesyjnych kryształu i błony.
Podobnie jak poprzednio stosuje się
przesłony wycinające określoną
warstwicę

14

Uwagi ogólne na temat
rentgenogramów



O rozkładzie przestrzennym
trójwymiarowego układu refleksów
(sieci odwrotnej) decydują
parametry komórki
elementarnej, niezależnie od
ilości atomów które ona zawiera



O natężeniu refleksów decyduje
zawartość komórki elementarnej

15

Wyznaczanie klasy Lauego



Symetria rentgenogramów w układzie
rombowym (mmm)

–

mm, mm, mm, zachowany środek



Symetria w układzie jednoskośnym
(2/m)

–

hk0 i hk1: mm i m, przesunięcie środka

–

h0k i h1k: 2, środek zachowany



Symetria w układzie trójskośnym (!)

–

warstwice zerowe: 2, pozostałe brak symetrii

16

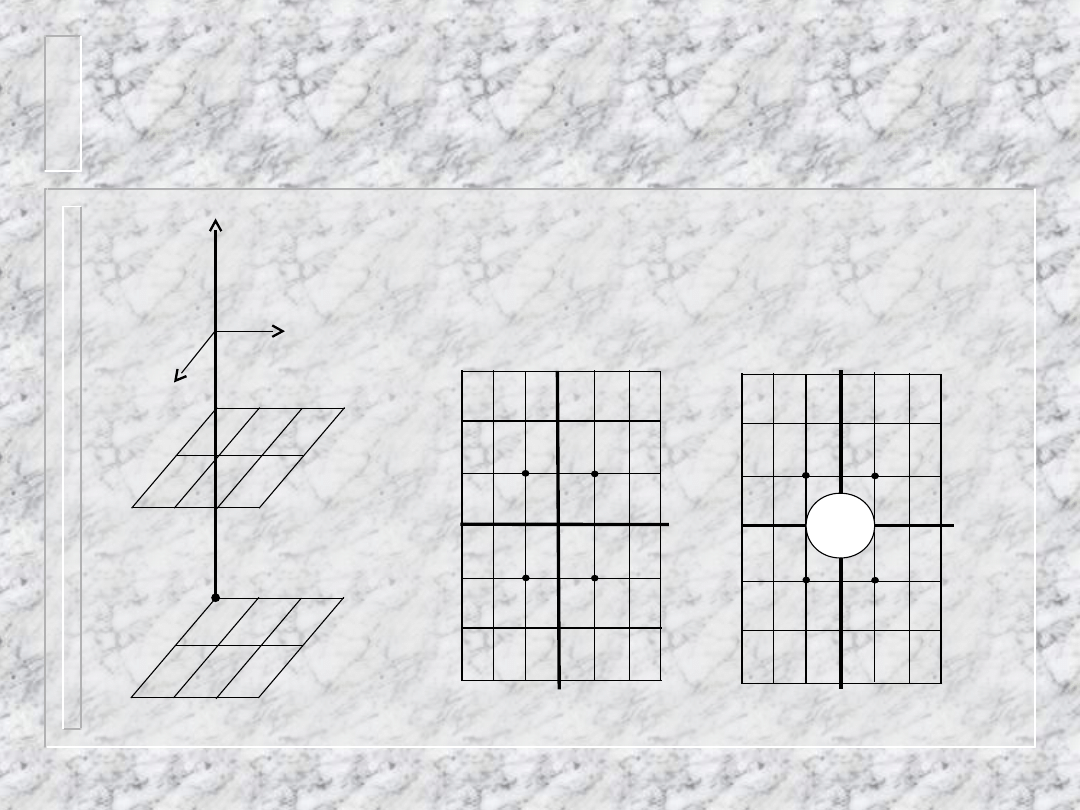
Układ rombowy

a

*

h00

0k0

hk0

hk1

h01

0k1

c

*

c

b

*

hk0

hk1

0k0

0k1

h00

h01

Oś c to oś obrotu kryształu,
oś c

*

to oś sieci odwrotnej.

Pokrywają się - ten sam kierunek

17

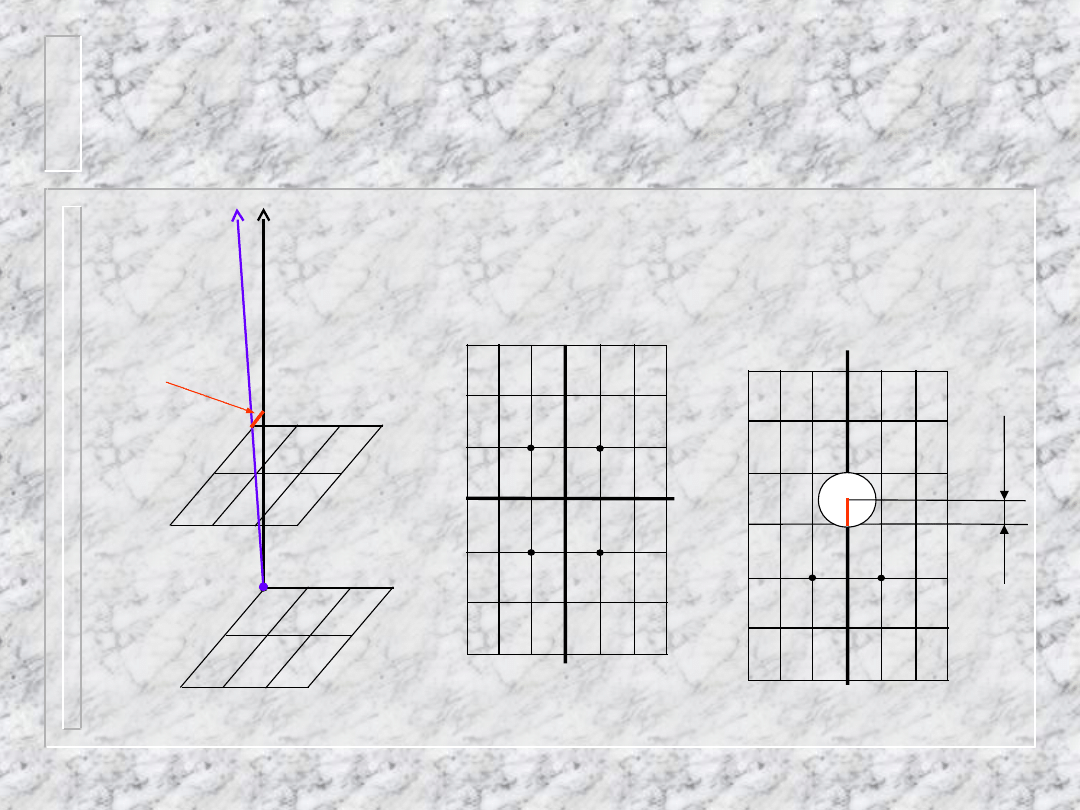
Układ jednoskośny

c

*

c



hk0

h00

0k0

hk0

hk1

h01

0k1



Oś c to oś obrotu kryształu,
oś

c

*

to oś sieci odwrotnej.

Warstwica hk1 odsunięta o 

hk1

0k0

0k1

h00

h01

18

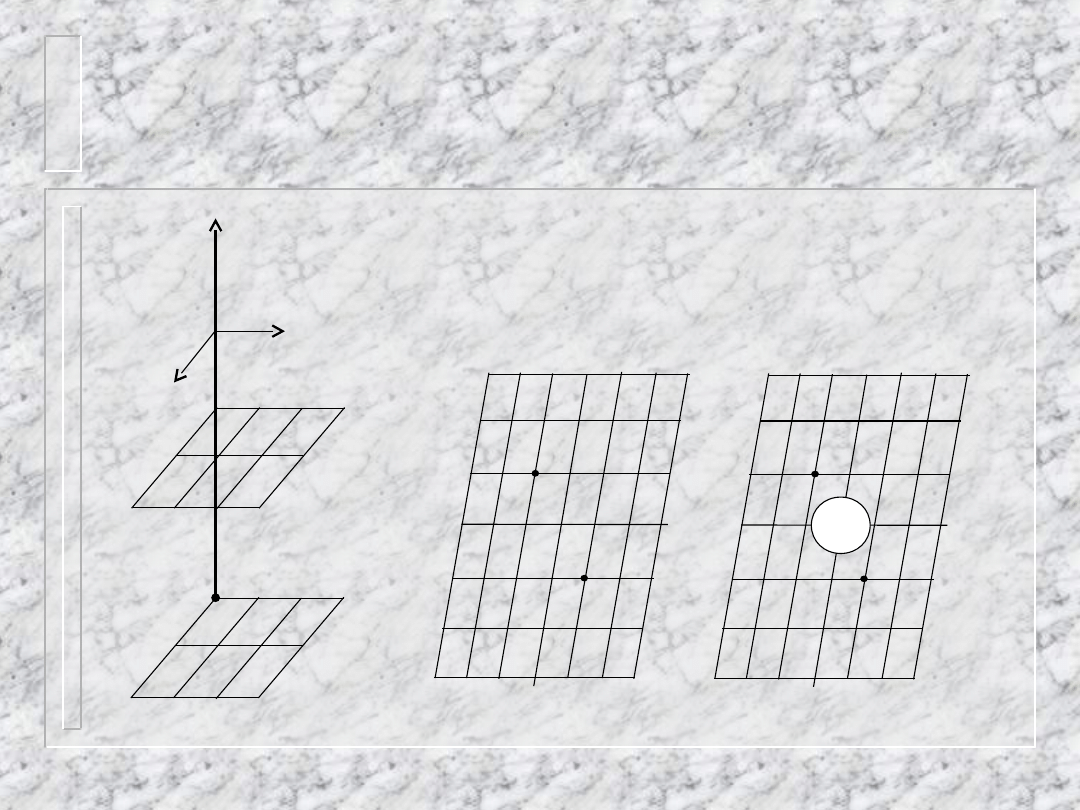
Układ jednoskośny c.d.

a

*

00l

h0l

h1l

01l

b

*

b

c

*

h0l

h1l

00l

01l

h00

h01

Oś b to oś obrotu kryształu,
oś b

*

to oś sieci odwrotnej.

Pokrywają się - ten sam kierunek

h00

h10

Ñ

Ñ

19

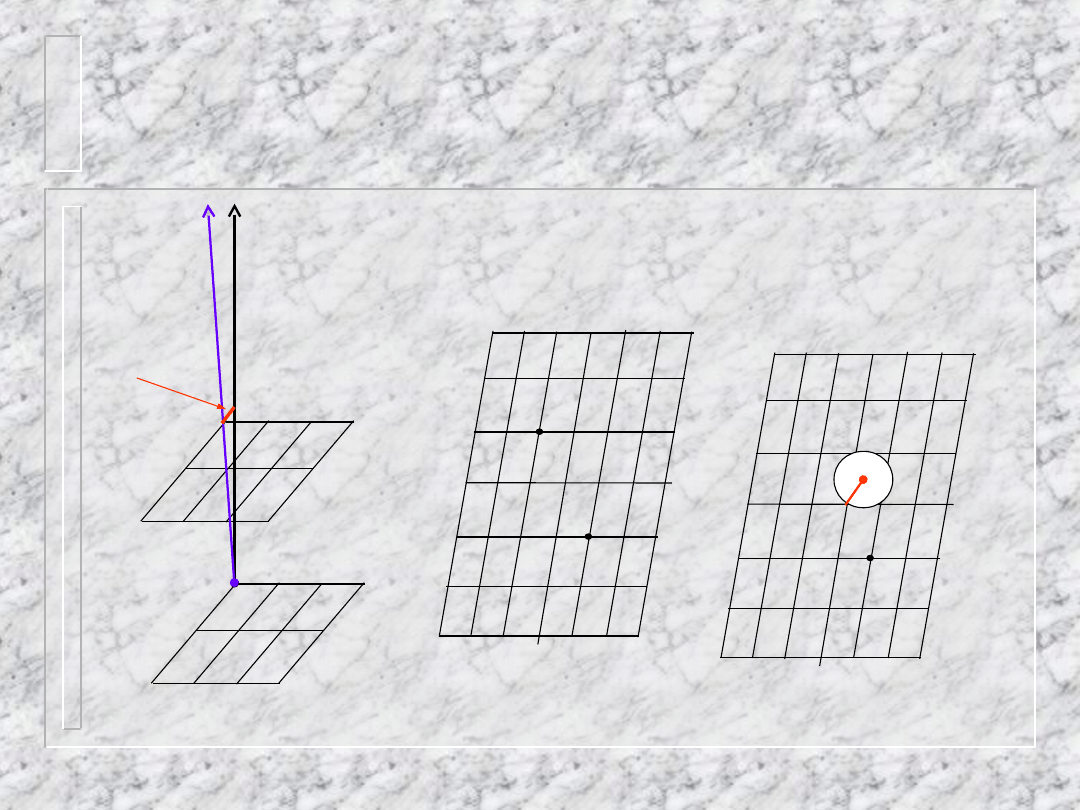
Układ trójskośny

h0l

h1l

00l

01l

h00

h01

Ñ

b

*

b



h00

00l

h0l

h1l

h10

01l

Warstwica zerowa: symetria 2 = !
Inne warstwice, symetria 1, środek przesunięty

20

Wyznaczanie typu komórki
Bravais’go



Wygaszenia systematyczne
spowodowane centrowaniem sieci

–

P brak wygaszeń systematycznych

–

C refleksy występują dla: h+k = 2n

–

I refleksy występują dla: h+k+l = 2n

–

F refleksy występują dla: h,k,l wszystkie
parzyste lub wszystkie nieparzyste, czyli
jednocześnie: h+k = 2n, k+l = 2n i h+l=
2n

21

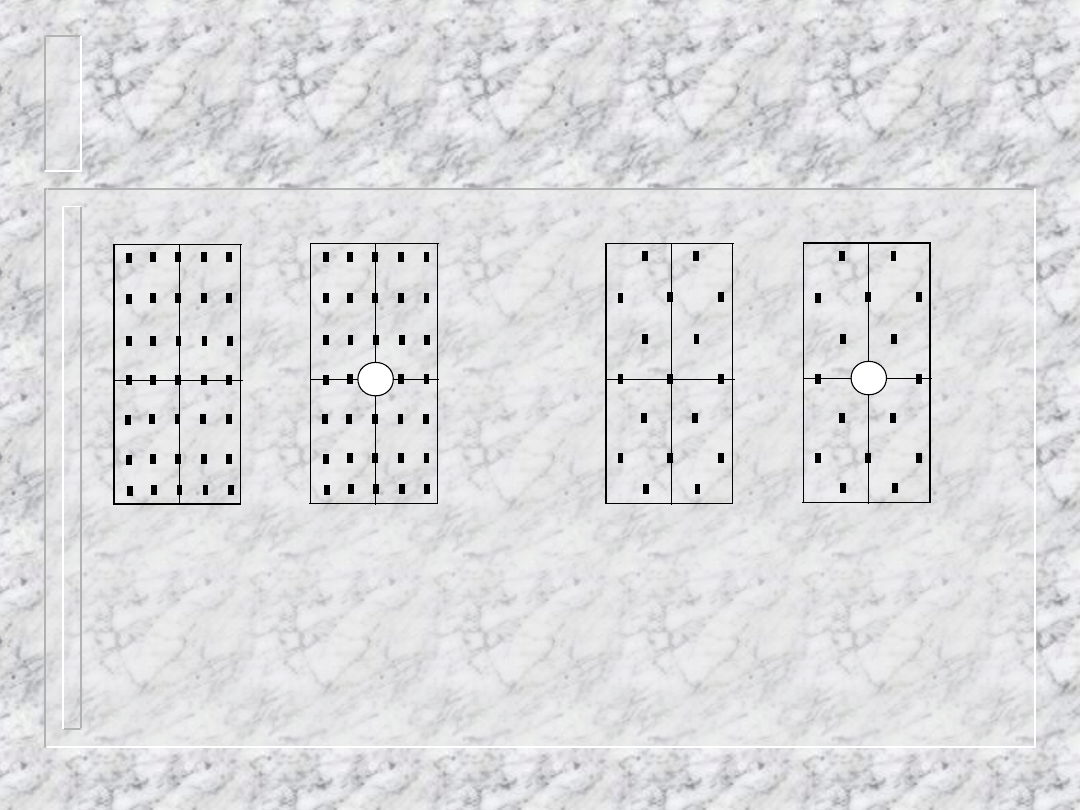
Wygląd rentgenogramów
sieci centrowanych typu P
i C

hk0

hk1

hk0

hk1

Pmmm

Cmmm
h+k=2n

22

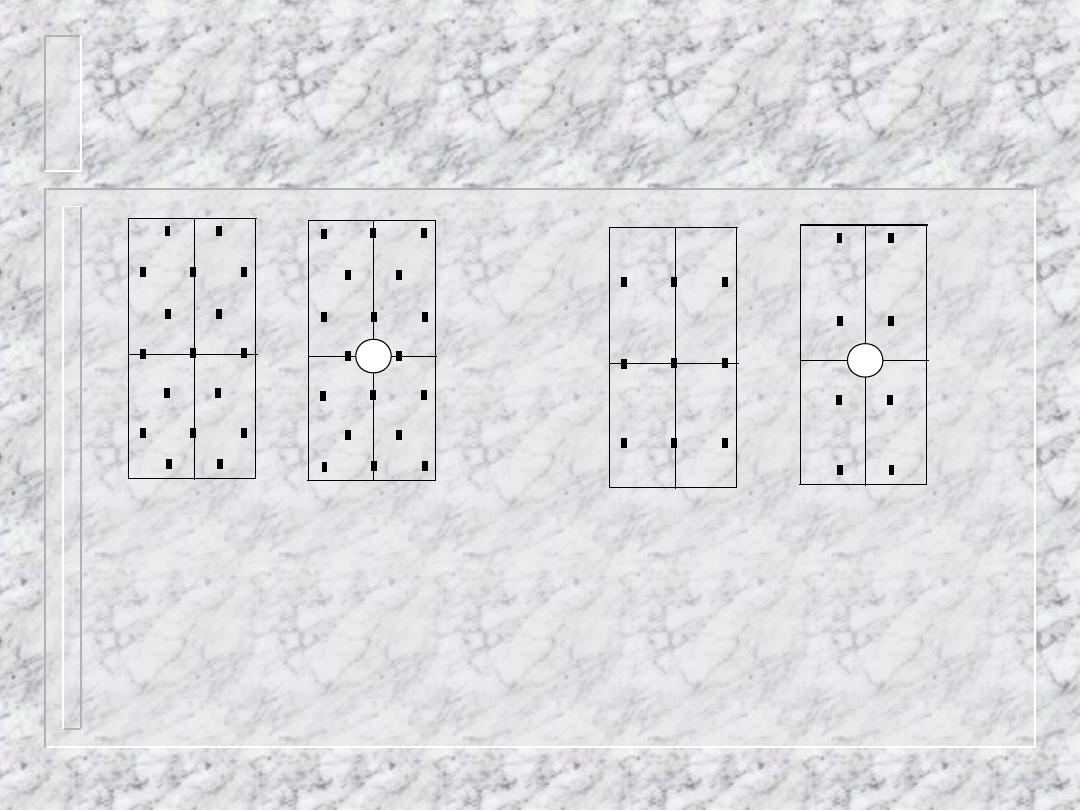
Wygląd rentgenogramów
sieci centrowanych typu I
i F

hk0

hk1

hk1

hk0

Immm

h+k+l=2n

Fmmm

h+k=2n i h+l=2n i k+l=2n

23

Wyznaczanie parametrów
sieci



W układzie rombowym
(tetragonalnym czy regularnym
też): |a|=K/a

*

itd.



W układzie jednoskośnym:
|b|=K/b

*

, a sin  = K/a

*

–

mierzymy na hk1 /c

*

= tg , =90 +



–

bezpośrednio 

*

z warstwicy h0l

24

Wyznaczanie liczby
cząsteczek w komórce
elementarnej



Znając objętość komórki V i jej zawartość
można wyznaczyć gęstość kryształu D



D=M/V; D=ZM

cz

1,66·10

-24

g/(V·10

-24

cm

3

)

–

V[Å

3

], M

cz

[u], D= 1,66 ZM

cz

/V



Z= DV/(1,66M

cz

)



W części asymetrycznej może się
znajdować jedna lub kilka cząsteczek w
położeniu ogólnym lub jej ułamek, jeśli
zajmuje położenie szczególne

25

Interpretacja
dyfraktogramów



Na podstawie zdjęć warstwic możemy:

–

wyznaczyć klasę Lauego kryształu

–

określić wartości parametrów komórki
elementarnej

–

na podstawie schematu wygaszeń
systematycznych określić typ komórki
Bravais’go



Jeżeli znamy gęstość możemy określić
liczbę cząsteczek w komórce
elementarnej Z

26

Interpretacja
dyfraktogramów c.d.



Wyznaczenie grupy przestrzennej
kryształu

–

dokładne wyznaczenie grupy nie zawsze jest
możliwe na podstawie zdjęć warstwic,
ponieważ symetria obrazu dyfrakcyjnego jest
wyższa o występowanie środka symetrii

27

Interpretacja
intensywności



Na podstawie pomiaru intensywności
poszczególnych refleksów możemy
wyznaczyć skład komórki elementarnej



I ~ F

hkl

F

*hkl

, F - czynnik struktury









j

lz

ky

hx

i

j

hkl

j

j

j

e

f

F

)

(

2



f

j

(s)= czynnik rozpraszania atomu j

funkcja s= sin / (dla s=0 jest to liczba

elektronów)
i = jednostka urojona: i=-1

28

Podsumowanie



Metoda de Jounga-Boumana lub
metoda precesyjna umożliwiają
fotografowanie niezdeformowanych
warstwic sieci odwrotnej



Na podstawie symetrii tych zdjęć
można ustalić układ krystalograficzny,
klasę Lauego oraz typ centrowania
komórki elementarnej