„Są plusy dodatnie i plusy

ujemne.”

Lech Wałęsa

Działania na liczbach

wymiernych.

Dodawanie,

odejmowanie,

mnożenie

i

dzielenie liczb to podstawowe umiejętności
bez których nie da się poznać głębiej
matematyki. Rachunki na liczbach oparte są
na kilku prostych zasadach, które poznaje się
już w szkole podstawowej. W tej lekcji
przypomnimy te zasady i pokażemy jak je
stosować

w

działaniach

na

liczbach

wymiernych – czyli wszystkich dodatnich i
ujemnych, które da się dokładnie zmierzyć i
zaznaczyć na osi liczbowej.

DEFINICJA LICZBY

WYMIERNEJ.

Liczby wymierne to takie, które można

przedstawić w postaci ilorazu liczb

całkowitych, innymi słowy są to liczby, które

można przedstawić w postaci ułamka

zwykłego:

gdzie m i n są liczbami całkowitymi i m ≠ 0.
PRZYKŁADY LICZB WYMIERNYCH:

KOLEJNOŚĆ WYKONYWANIA

DZIAŁAŃ.

Działania na liczbach wykonujemy w

następującej kolejności:

1.Działania w nawiasach (zaczynamy od
„najmniejszych” czyli (…) ).

2.Potęgowanie i pierwiastkowanie.

3.Mnożenie i dzielenie.

4.Dodawanie i odejmowanie.

W podpunkcie 3 i 4 działania wykonujemy

według kolejności występowania od lewej

do prawej.

PRZYKŁAD:
2 + 2 · 2 = 2 + 4 = 6

najpierw mnożenie,

potem dodawanie

DODAWANIE I ODEJMOWANIE

LICZB WYMIERNYCH

DODATNICH.

•Dodając lub odejmując ułamki zwykłe należy

sprowadzić je do wspólnego mianownika.

•Wspólny mianownik powinien być najmniejszą

wspólną wielokrotnością mianowników dodawanych

ułamków (najmniejszą liczbą podzielną przez

wszystkie mianowniki dodawanych ułamków).

•Dodając liczby mieszane możemy osobno

dodawać całości i osobno ułamki.

•Przy odejmowaniu liczb mieszanych, gdy

odejmowany ułamek jest większy niż ten od

którego odejmujemy, możemy „pożyczyć” 1 z

całości.

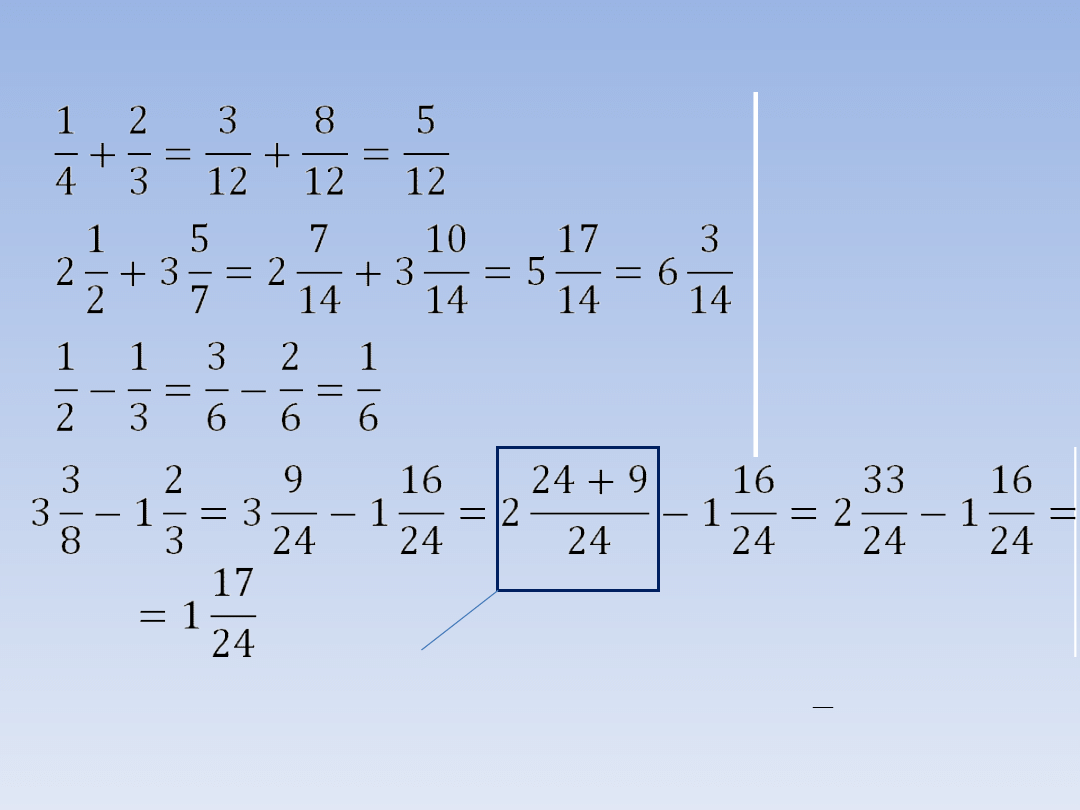
PRZYKŁADY.

Wspólny mianownik: 12. Pierwszy
ułamek rozszerzamy przez 3, a
drugi przez 4.

Wspólny mianownik:
14. Osobno
dodajemy całości i
osobno ułamki.

Wspólny mianownik: 6.

„Pożyczamy” 1 z 3 i dodajemy do ułamka. 1
zapisane w postaci ułamka o mianowniku 24
to

24

24

„EKSPRESOWY” SPOSÓB

NA WSPÓLNY MIANOWNIK.

Poniższe przykłady pokazują uniwersalny
sposób

na

znalezienie

wspólnego

mianownika.

Wystarczy „górę” i „dół” pierwszego ułamka
pomnożyć przez „dół” drugiego i na odwrót.

DODAWANIE I

ODEJMOWANIE LICZB

WYMIERNYCH DODATNICH.

•Przy dodawaniu i odejmowaniu ułamków

dziesiętnych możemy działania wykonywać
pisemnie

pamiętając

o

podpisywaniu

ułamków „przecinek pod przecinkiem”.

•Kiedy w jednym wyrażeniu występują

liczby zapisane w postaci ułamków zwykłych
i dziesiętnych przed obliczeniem zapisujemy
je w jednej postaci (ułamków zwykłych lub
dziesiętnych).

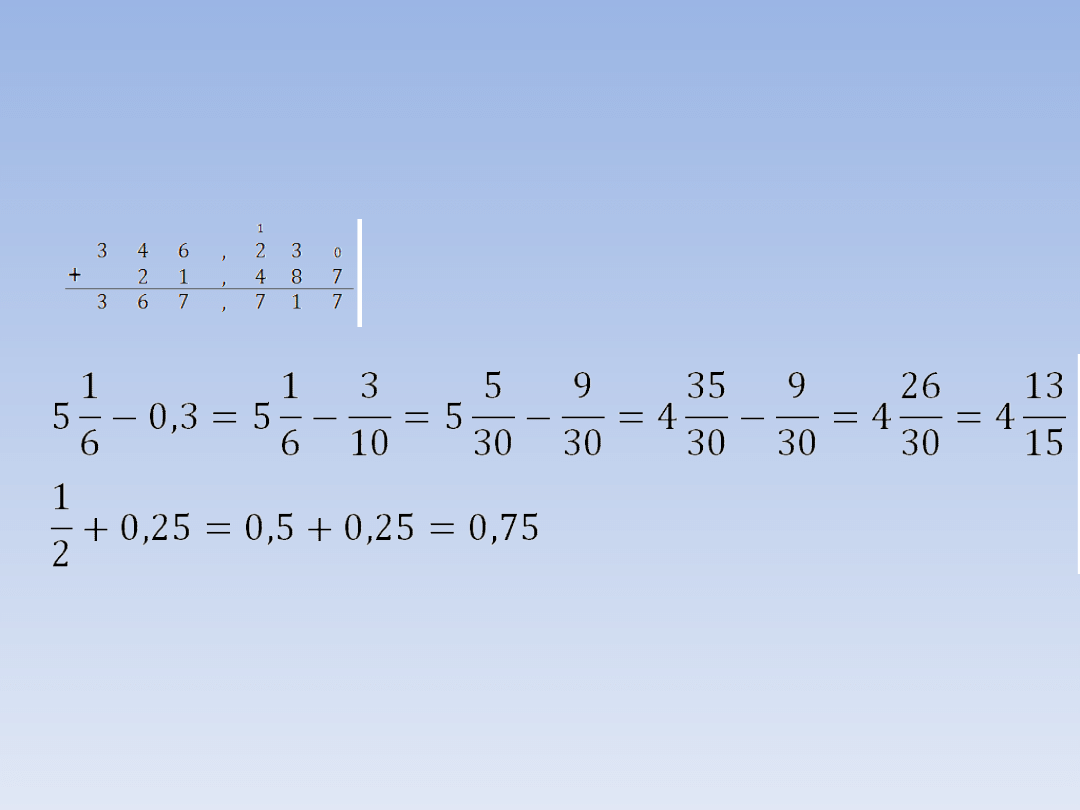
PRZYKŁADY.

346,23 + 21,487 = 357,717

Obliczenia wykonujemy pisemnie
pamiętając o zasadzie „przecinek pod
przecinkiem”.

MNOŻENIE I DZIELENIE

LICZB WYMIERNYCH

DODATNICH.

•Mnożąc ułamki zwykłe mnożymy licznik

przez licznik i mianownik przez mianownik
(„góra” razy „góra”, „dół” razy „dół”).

•Zanim pomnożymy lub podzielimy

ułamki zapisane w postaci liczb mieszanych,
należy zapisać je jako ułamki niewłaściwe.

•Skracać ułamki można tylko przy

mnożeniu.

•Dzielenie ułamków zwykłych

zamieniamy na mnożenie przez odwrotność.

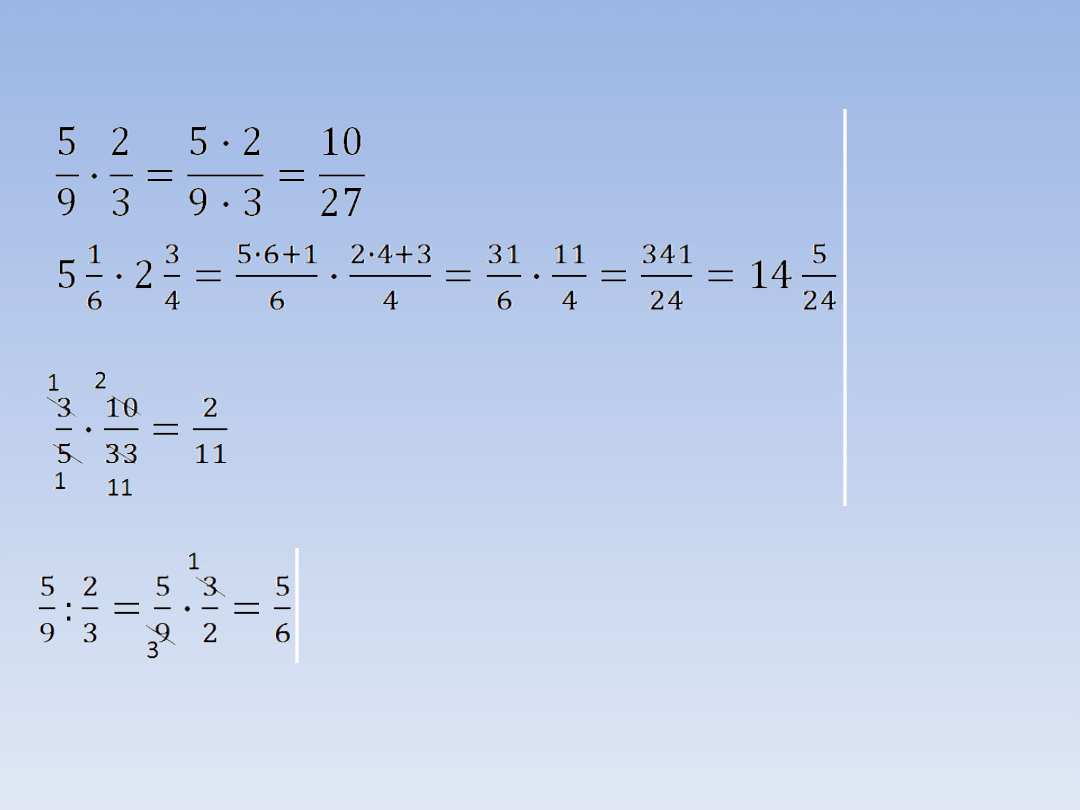
PRZYKŁADY.

Licznik razy licznik, mianownik razy
mianownik.

Liczby
mieszane
zamieniamy
na ułamki
niewłaściwe.

Przy mnożeniu możemy skracać ułamki po przekątnej.

Dzielenie zamieniamy na mnożenie przez
odwrotność.

MNOŻENIE I DZIELENIE

LICZB WYMIERNYCH

DODATNICH.

•Ułamki dziesiętne możemy mnożyć

pisemnie, pamiętając, że w wyniku należy
odciąć tyle miejsc po przecinku ile miały
wszystkie czynniki.

•Dzieląc ułamki dziesiętne pamiętajmy,

żeby doprowadzić je do takiej postaci, aby
dzielnik nie był ułamkiem.

•Gdy w wyrażeniu występują ułamki

dziesiętne i zwykłe, zapisujemy wszystkie w
jednej postaci i dopiero wykonujemy działania.

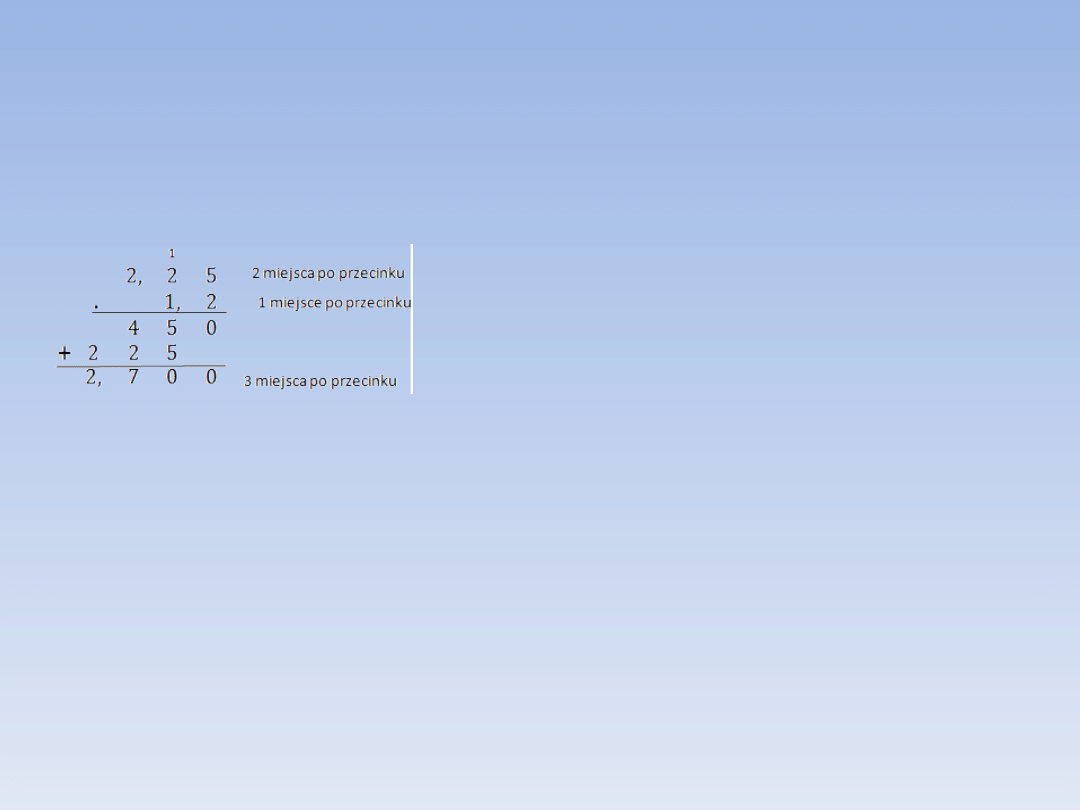
PRZYKŁADY.

2,25 ∙ 1,2 = 2,7

1,26 : 0,003 =
Aby dzielnik był liczbą całkowitą i dzielną i
dzielnik pomnóżmy przez 1000:
1260 : 3 = 420

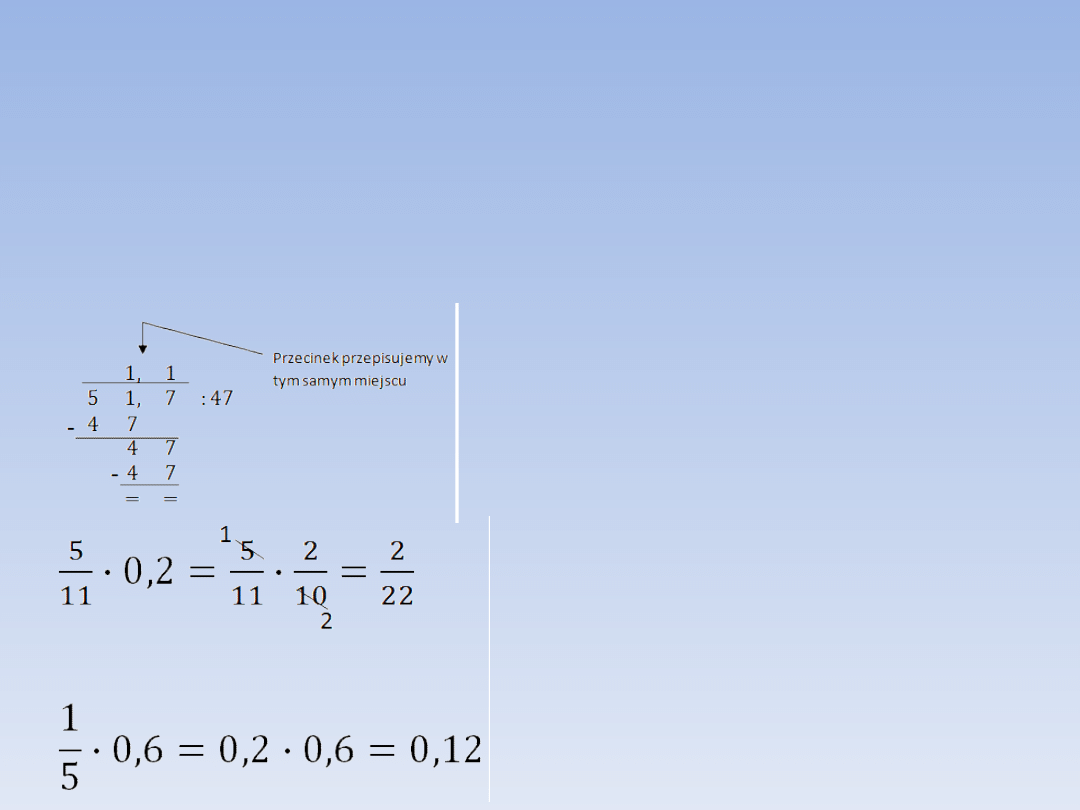
PRZYKŁADY.

5,17 : 4,7
Aby dzielnik był liczbą całkowitą i dzielną i
dzielnik pomnóżmy przez 10:
51,7 : 47

DODAWANIE I ODEJMOWANIE

LICZB WYMIERNYCH.

Dla przypomnienia kilka prostych przykładów
działań na liczbach całkowitych dodatnich i
ujemnych:
2 + (-3) = 2 – 3 = -1

-3 + 5 = 2

-4 + (-7) = -11

-5 – (-12) = -5 + 12 = 7

(-2) · 4 = -8

(-3) · (-7) = 21

(-15) : (-3) = 5

Dodając liczby o przeciwnych znakach od
większej odejmujemy mniejszą i zapisujemy
znak, który stał przy większej.

Suma liczb ujemnych jest liczbą
ujemną.

Po opuszczeniu nawiasu odejmowanie
zamienia się na dodawanie.

Mnożenie lub dzielenie liczb o przeciwnych
znakach daje liczbę ujemną.
Mnożenie lub dzielenie liczb o jednakowych
znakach daje liczbę dodatnią.

DODAWANIE I ODEJMOWANIE

LICZB WYMIERNYCH.

Dodając lub odejmując liczby wymierne
należy postępować według następujących
zasad:

Aby dodać dwie liczby o różnych znakach

należy:

zapisać znak stojący przy większej

liczbie

od większej liczby odjąć mniejszą

(działając tak, jakby obie były dodatnie)

Suma dwóch liczb ujemnych jest liczbą

ujemną.

Odejmowanie liczb ujemnych można
zamienić na dodawanie po przez

opuszczenie lub wstawienie nawiasu.

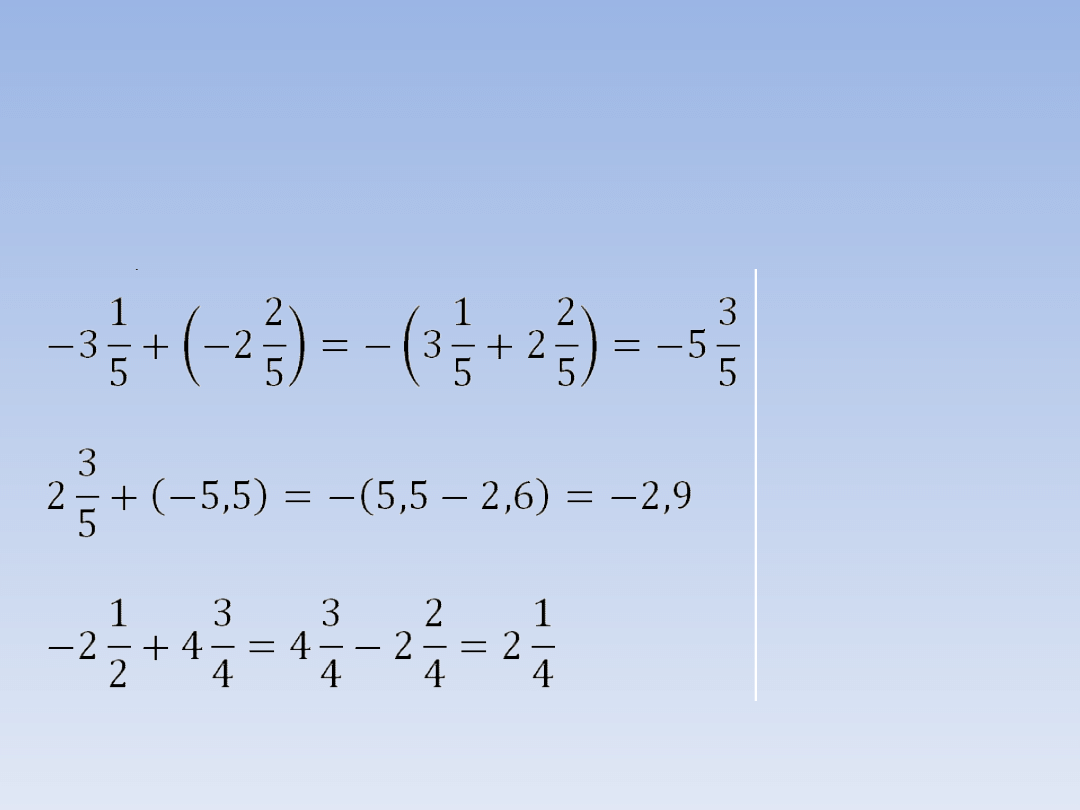
PRZYKŁADY.

Dodając lub odejmując liczby wymierne
należy postępować według następujących
zasad:

Suma liczb
ujemnych jest
liczbą ujemną.

Dodając liczby o
przeciwnych
znakach od większej
odejmujemy
mniejszą i
zapisujemy znak,
który stał przy
większej.

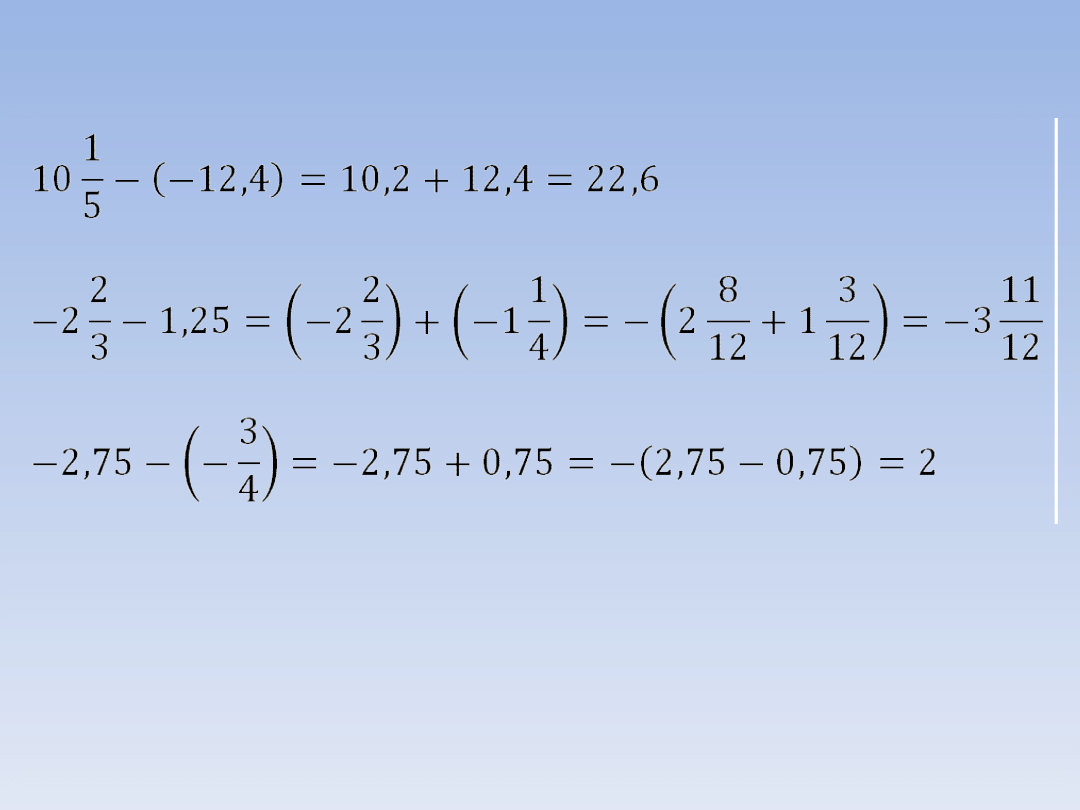
PRZYKŁADY.

Odejmowanie liczb ujemnych można zamienić na dodawanie

po przez opuszczenie lub wstawienie nawiasu.

MNOŻENIE I DZIELENIE LICZB

WYMIERNYCH.

W przypadku mnożenia i dzielenia liczb
wymiernych określanie znaku jest bardzo
proste:

Iloczyn/iloraz dwóch liczb o tych

samych znakach jest liczbą dodatnią.

„-” · „-” → „+”

„+” · „+” → „+”

„-” : „-” → „+”

„+” : „+” → „+”

Iloczyn/iloraz dwóch liczb o

przeciwnych znakach jest liczbą ujemną

„-” ·„+” →„-”

„+” · „-” →„-”

„-” : „+” →„-”

„+” : „-” →„-”

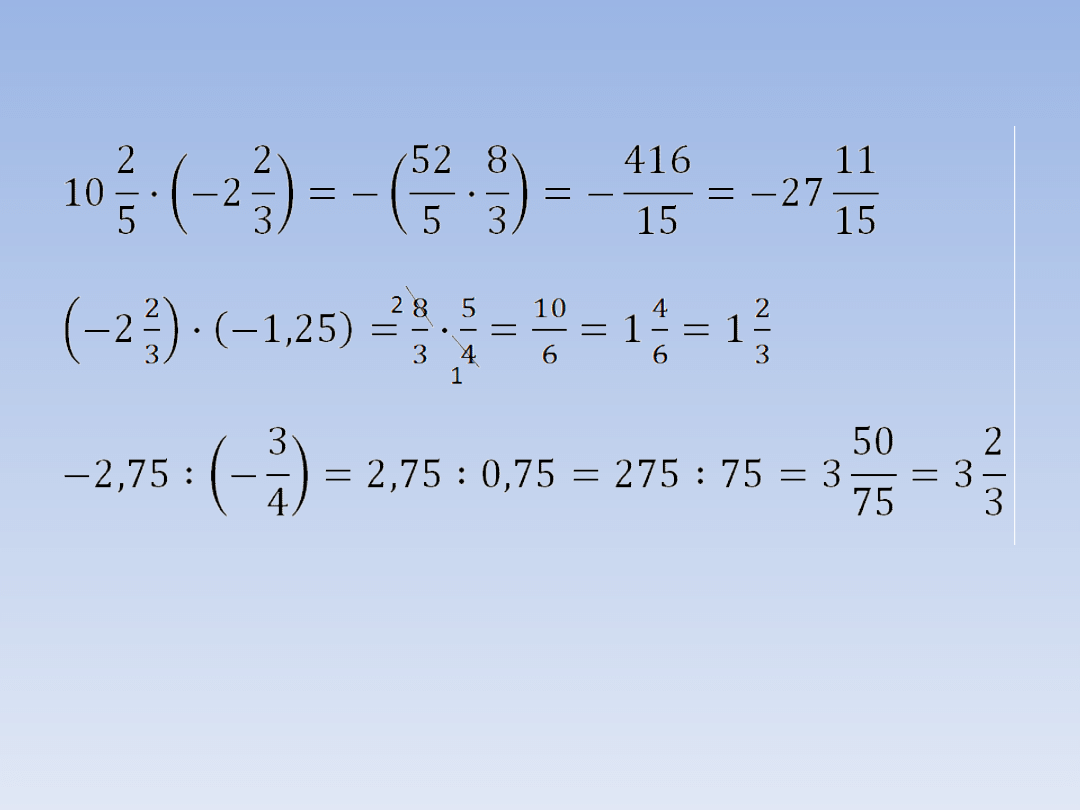
PRZYKŁADY.

„+” · „-”
→„-”

„-” · „-” → „+”

„-” : „-” → „+”

2,5 : (-0,25) = -(250 : 25) = -10

„+” : „-” →„-”