
The method of symmetrical
The method of symmetrical
components
components

2 / 48
Symmetrical system
Symmetrical system
Voltages
Currents
A
A
2
B
A
C
A
U
U
U
a U
U
aU
=
=
=
A
A
2
B
A
C
A
I
I
I
a I
I
aI
=
=
=
2
3
4
2
3
3
j
3
1
2
2
j
j
2
3
1
2
2
a e
j
a
e
e
j
p
p
- p
=
=- +
=
=
=- -
Phase notation: A, B, C lub R, S,
T
Vector diagram of voltages in three-
phase system
complex rotational
phasors:
3 / 48
Linear component
Linear component
R
S
R
’
S
’
T
T
’
N
N
’
R
I
S
I
T
I
'
R
I
'
S
I
'
T
I
T
S
R
I
I
I
T
U
S
U
R
U
'
T
U
'
S
U
'
R
U
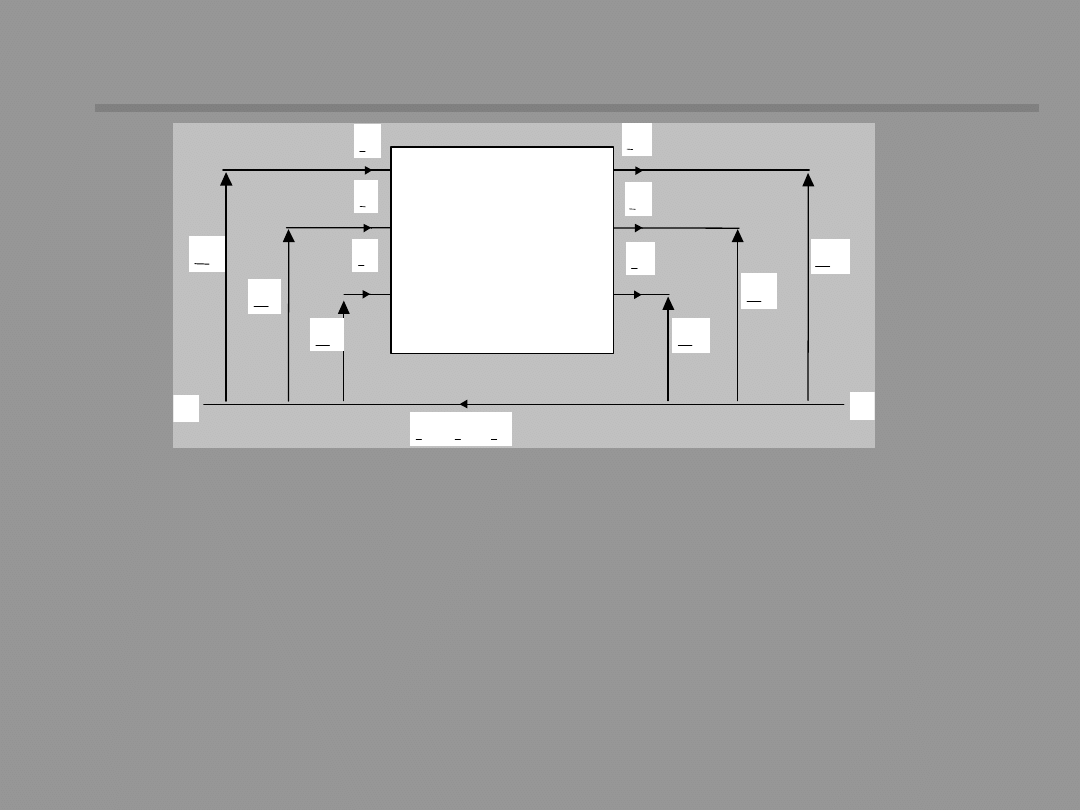
ELEMENT
TRÓJFAZOWY
OPISANY
MACIERZĄ Z
Equipment in power systems is represented by
equivalent circuits, which are designed for the
individual tasks of power system analysis. For the
calculation of short-circuits, the equivqalent
circuits iclude resistance and inductive reactance.
Shunt elements, i.e. capacitive reactance are
omitted.
The equivalent circuit has couplings in the three-
phase system which are of an inductive type.

4 / 48
The equations of linear component
The equations of linear component
D
=
-
=
+
+
'
RR R
RS S
RT T
R
R
R
U
U
U
Z I
Z I
Z I
D
= -
=
+
+
'
SR R
SS S
ST T
S
S
S
U
U
U
Z I
Z I
Z I
D = -
=
+
+
'
TR R
TS S
TT T
T
T
T
U
U
U
Z I
Z I
Z I
D =
U ZI
�
�
�
D
-
�
� �
�
�
� �
�
D = D
=
-
�
� �
�
�
� �
�
D
-
�
� �
�
R
R
R
S
S
S
T
T
T
U
U
U
U
U
U
U
U
U
U
� �
� �
=��
� �
� �
R
S
T
I
I
I
I
�
�
�
�
=�
�
�
�
�
�
RR
RS
RT
SR
SS
ST
TR
TS
TT
Z
Z
Z
Z
Z
Z
Z
Z
Z
Z
The ralationship between voltages and currents of a
three-phase system can be described by the
following equations:
In a matrix notation
where
Matrix Z is the matrix of self-impedances and mutual
(coupling) impedances of the element. Self-
impedances Zii (i = R, S, T) are located on the main
diagonal, and mutual impedances outside it. For
symmetrical elements, the self-impedances of
individual phases are equal.

5 / 48
The equations of linear component
The equations of linear component
Mutual impedances between individual phases
depend on the type of element.
Static element (line, transformer, reactor) –
impedances are reciprocal:
RS
RT
SR
ST
TR
TS
m
Z
Z
Z
Z
Z
Z
Z
=
=
=
=
=
=
Rotating element (electric motor, generator) –
impedances are circular:
Mutual impedances of a given phase in relation
to the other phases are not equal because
windings of these phases are differently
positioned in relation to the rotor.
RS
RT
ST
SR
TR
TS
Z
Z Z
Z Z
Z
�
�
�
1
2
RS
ST
TR
m
RT
TS
SR
m
Z
Z
Z
Z
Z
Z
Z
Z
=
=
=
=
=
=

6 / 48
Impedance matrix
Impedance matrix
Z
Z
�
�
�
�
=�
�
�
�
�
�
s
m
m
m
s
m
m
m
s
Z
Z
Z
Z
Z
Z
Z
Z
Z
Z
�
�
-
-
�
�
= -
-
�
�
�
�
-
-
�
�
1
2
2
1
1
2
s
m
m
m
s
m
m
m
s
Z
Z
Z
Z
Z
Z
Z
Z
Z
Z
Thus the matrices of impedances can be written
if the form:
for a static component
for a
rotating component
Sign – (minus) indicates that currents in the other
phases induce in the given phase EMFs having the
opposite sense in relation to self-induction EMFs,
which results from the mutual location of stator
phase windings.
In the equations of 3-phase circuit the voltage loss in
each phase of the component is dependent on all
phase currents, and on the self-impedance of this
phase and the mutual impedances between this
phase and the other phases.

7 / 48
The equations of linear component
The equations of linear component
(
)
D =
+
+
=
+
+
=
-
2
s R
mS
mT
s R
m R
m R
s
m R
R
U
Z I
Z I
Z I
Z I
Z a I
Z aI
Z Z I
(
)
D =
+
+
=
+
+
=
-
2
mR
s S
mT
m S
s S
m
S
s
m S
S
U
Z I
Z I
Z I
Z aI
Z I
Z a I
Z Z I
(
)
D =
+
+
=
+
+
=
-
2
mR
mS
s T
m T
m T
s T
s
m T
T
U
Z I
Z I
Z I
Z a I
Z aI
Z I
Z Z I
For balanced load the set of equations
receives the form:
Voltage drop in each
phase depends only on
the current of this
phase – the equations
are
mutually independent
and Z impedance
matrix is diagonal.
-
�
�
�
�
=
-
�
�
�
�
-
�
�
s
m
s
m
s
m
Z Z
0
0
0
Z Z
0
0
0
Z Z
Z

8 / 48
The method of symmetrical components
The method of symmetrical components
Let us consider the three-phase RL symmetrical circuit in
which currents and voltages may form unbalanced systems.
The multiplicity of couplings between phases complicates the
circuit analysis. Therefore, a mathematical transformation is
sought which transfers phase components to different
system. The following conditions should apply for the
transformation:
The transformed voltages should depend only on one
transformed current.
The transformation should be linear - the linear
relationship between current and voltage should be
retained.
The desired transformation (transformation 0, 1, 2) consists in
replacing the unbalanced systems of currents and phase
voltages by their symmetrical components, i.e. by the three
symmetrical vector systems – the zero-sequence (0), the
positive sequence (1) and the negative-sequence system (2).

9 / 48
The symmetrical component
The symmetrical component
transformation
transformation
The transformation diagonalising the matrix Z is introduced
-
D =
1
S U SZS SI
-
�
�
�
�
�
�
�
�
=
=
�
�
�
�
�
�
�
�
�
�
�
�
2
1
2
2
2
1 1 1
1 1 1
1
1 a a ;
1 a
a
3
1 a
a
1 a a
S
S
The matrix S is a third-order nonsingular
(determinant S ≠ 0) matrix, whose elements shall be
so selected that as a result of transformation S Z S
-1
the impedance matrix is diagonalised. Matrix S is
called
the
operator
matrix
of
symmetrical
components, and its element a – the complex
operator
p
p
- p
=
=- +
=
=
=- -
2
3
4
2
3
3
j
3
1
2
2
j
j
2
3
1
2
2
a e
j
a
e
e
j

10 / 48
Symmetrical components method
Symmetrical components method
where I
p
– vector of sequence
currents,
ΔU
p
– vector of sequence
voltages:
D =
p
p p
U Z I
R
R
S
T
(0)
2
2
S
R
S
T
(1)
p
2
2
T
R
S
T
(2)
1 1 1
I
I
I I
I
1
1
1 a a
I
I
a I
a I
I
3
3
1 a
a
I
I
a I
a I
I
� �
+ +
�
���
�
�
� �
�
���
�
�
= =
� =
+
+
=� �
�
���
�
�
� �
�
���
�
�
+
+
�
���
�
� � �
I SI
R
R
S
T
(0)
2
2
S
R
S
T
(1)
p
2
2
T
R
S
T
(2)
1 1 1
U
U
U
U
U
1
1
1 a a
U
U
a U a U
U
3
3
1 a
a
U
U
a U a U
U
�
�
D
D +D +D
D
�
�� �
�
�
�
�
�
�� �
�
�
D = D =
�D
=
D + D + D
= D
�
�
�
�� �
�
�
�
�
�
�� �
�
�
D
D + D + D
D
�
�� �
�
� �
�
U S U
As a result of transformation the following
equation is obtained:

11 / 48
Transformation of impedances
Transformation of impedances
s
m
m
1
2
2
m
s
m
p
2
2
m
m
s
s
m
(0)
s
m
(1)
s
m
(2)
1 1 1
Z
Z
Z
1 1 1
1
1 a a
Z
Z
Z
1 a
a
3
1 a
a
Z
Z
Z
1 a a
Z 2Z
0
0
Z
0
0
0
Z Z
0
0
Z
0
0
0
Z Z
0
0 Z
-
�
��
��
�
�
��
��
�
=
=
�
�
=
�
��
��
�
�
��
��
�
�
��
��
�
�
�
+
�
�
�
�
�
�
=
-
=�
�
�
�
�
�
�
�
-
�
� �
�
Z SZS
For a static component:

12 / 48
Transformation of impedances
Transformation of impedances
1
2
2
1
1
2
1
2
1
2
1
2
s
m
m
1
2
2
m
s
m
p
2
2
m
m
s
s
m
m
2
s
m
m
2
s
m
m
(0)
(1)
(2)
1 1 1
Z
Z
Z
1 1 1
1
1 a a
Z
Z
Z
1 a
a
3
1 a
a
Z
Z
Z
1 a a
Z Z
Z
0
0
0
Z a Z
a Z
0
0
0
Z a Z
a Z
Z
0
0
0
Z
0
0
0 Z
-
�
�
-
-
�
�
�
�
�
�
�
�
�
�
=
=
�-
-
�
=
�
�
�
�
�
�
�
�
�
�
�
�
-
-
�
�
�
�
�
�
�
�
-
-
�
�
=
-
-
=
�
�
�
�
-
-
�
�
�
�
�
�
=�
�
�
�
�
�
Z SZS
For a rotating component

13 / 48
Symmetrical component method
Symmetrical component method
Finally, the equations of 3-phase circuit may be
written in the form:
(0)
(0)
(0)
(1)
(1)
(1)
(2)
(2)
(2)
U
Z
0
0
I
U
0
Z
0
I
U
0
0 Z
I
�
� �
�� �
D
�
� �
�� �
D
=
�
�
� �
�� �
�
� �
�� �
D
�
�� �
�
�
(0)
(1)
(2)
'
(0)
(0)
(0)
'
(1)
(1)
(1)
'
(2)
(2)
(2)
U
U
Z
0
0
I
U
U
0
Z
0
I
0
0 Z
I
U
U
�
�
-
�
�� �
�
� �
�� �
�
�
-
=
�
�
�� �
�
� �
�� �
�
� �
�� �
-
�
�
The impedance matrix of symmetrical components is
diagonal.
Thus the coupled set of equations which described
the 3-phase circuit in phase variables becomes an
uncoupled set of equations in the symmetrical
components.
14 / 48
Interpretation of the symmetrical
Interpretation of the symmetrical
components system
components system
The reverse transformation of the 012-system to
the RST-system is achieved by the matrix S
-1
in
accordance with:
-
-
=
=
1
1
p
p
I S I U S U
(2)
(2)R
(2)
(2)S
2
(2)
(0)
(0)R
(0)
(0)S
(0)
(
(1)
(1)R
2
(1)
(1)S
(1)
(
(2)T
R
S
T
0
1)
T
T
)
I
I
I
I
I
a
I
I
I
I
I
I
I
a
I
I
aI
I
a I
I
I
I
I
= + + =
+
+
=
+
+ =
+
+
=
+
+ =
+
+
(2)
(2)R
(2)
(2)S
2
(2)
(0)
(0)R
(0)
(0)S
(0)
(
(1)
(1)R
2
(1)
(1)S
(1)
(
(2)T
R
S
T
0
1)
T
T
)
U
U
U
U
U
a
U
U
U
U
U
U
U
a
U
U
aU
U
a U
U
U
U
U
=
+
+
=
+
+
=
+
+
=
+
+
=
+
+
=
+
+
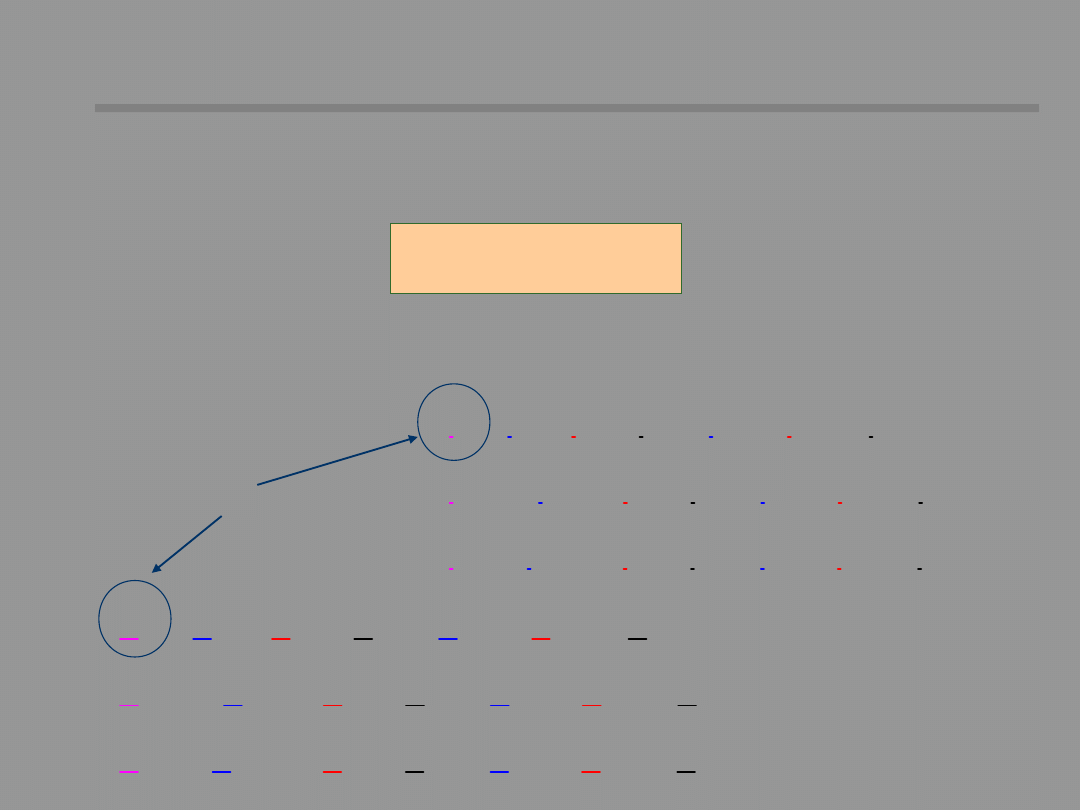
Reference
phase
The vectors of phase currents and voltages are
the linear combination of sequence
components.

15 / 48
The invariance of power in 012-system
The invariance of power in 012-system
*
=
+
+
=
*
*
*
T
R
S
T
R
S
T
S U I
U I
U I
U I
*
* *
*
=
=
=
T
T T
T
P
P
1
1
S
3
3
U I
U S S I
U I
( )
=
=
T
T
T T
P
U
SU
U S
( )
=
=
*
*
* *
P
I
SI
S I
=
T
S
S
*
-
=
1
1
3
S
S
( ) ( )
( ) ( )
( ) ( )
(
)
*
*
*
*
=
=
+
+
T
P
0
1
2
P
0
1
2
S 3
3 U I
U I
U I
U I
The transformation from RST-system to 012-
system is not invariant with respect to power.
In 012-system:
In RST-system:
because
Thus,
16 / 48
Equivalent circuits for symmetrical
Equivalent circuits for symmetrical
components
components
R
S
R
’
S
’
T
T
’
R
N
R
I
S
I
T
I
T
S
R
I
I
I
TK
U
SK
U
RK
U
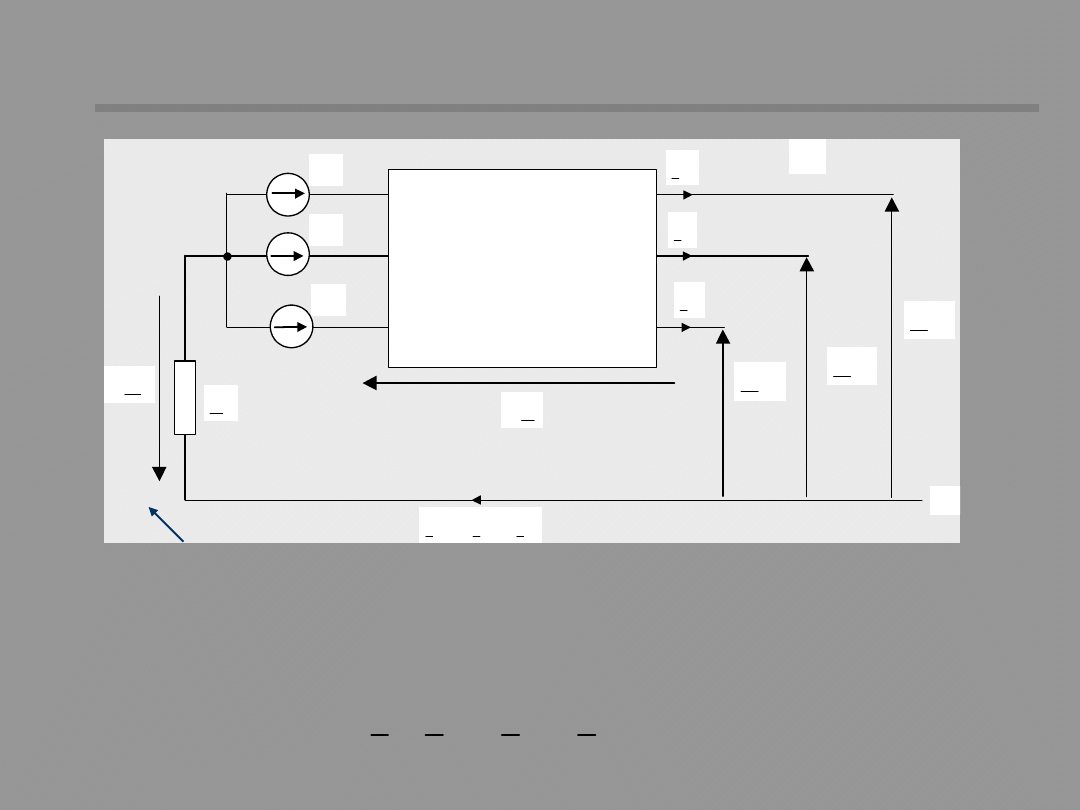
ELEM
EN
T
TRÓJFAZOW
Y
OPISAN
Y
M
ACIERZĄ
Z
E
R
E
S
E
T
U
u
Z
u
U
K
= +D +D
u
E U
U
U
Earthing impedance
The voltage equation of the
circuit:

17 / 48
Equivalent circuits for symmetrical
Equivalent circuits for symmetrical
components
components
� �
� �
=� �
� �
� �
R
S
T
I
I
I
I
(
)
D =
+ +
u R
S
T
u
U
Z I
I
I
� �
� �
=� �
� �
� �
R
S
T
E
E
E
E
� �
� �
=� �
� �
� �
R
S
T
U
U
U
U
D
� � �
�� �
� � �
�� �
D = D
=
� � �
�� �
� � �
�� �
D
� �
�
�
� �
u
u
u
R
u
u
u
u
S
u
u
u
u
u
T
u
U
Z
Z
Z
I
U
Z
Z
Z
I
U
Z
Z
Z
I
U
= + +
u
E U ZI Z I
-
-
=
+
+
1
1
u
u
SE SU SZS S I SZ S S I
= +
+
P
P P
uP P
P
E
U
Z I
Z I
012-transformation yields:
The voltage matrix equation
receive the form:

18 / 48
Equivalent circuits for symmetrical
Equivalent circuits for symmetrical
components
components
The source EMF symmetrical components:
( )
( )
( )
� �
� �
� �
=
=
� �
� �
� �
0
P
1
2
E
E
E
E
SE
( )( )
( )( )
( )( )
-
�
�
�
�
�
�
=
=
�
�
�
�
�
�
0 0
1
P
1 1
2 2
Z
0
0
0
Z
0
0
0
Z
Z
SZS
-
�
�
�
�
=
=�
�
�
�
�
�
u
1
uP
u
3Z
0 0
0
0 0
0
0 0
Z
SZ S
The transformation of impedances:
for the
element
for the
earthing

19 / 48
Equivalent circuits for symmetrical
Equivalent circuits for symmetrical
components
components
We assume that the source is
symmetrical:
2
S
R
E
a E
=
T
R
E
aE
=
=
+
+
=
+ + =
2
2
(0)
R
R
R
R
1
1
E
(E
a E
aE )
E (1 a
a) 0
3
3
=
+
+
=
=
2
2
(1)
R
R
R
R
R
1
1
E
(E
aa E
a aE )
3E
E
3
3
=
+
+
=
+ +
=
2 2
a
(2)
R
R
R
R
1
1
E
(E
a a E
aaE )
E (1 a a ) 0
3
3
In such a case the symmetrical component of EMF are the following:
( )
( )
( )
� �
� �
� �
� �
� �
=
=� �
� �
� �
� �
� �
� �
0
P
1
R
2
E
0
E
E
0
E
E
Thus:
The EMF of sources form the
positive sequence system.

20 / 48
Equivalent circuits for symmetrical
Equivalent circuits for symmetrical
components
components
( )
( )( ) ( )
(
)
( )
D
=
=
+
0 0 0
s
m 0
0
U
Z
I
Z 2Z I
( )
( )( ) ( )
(
)
( )
D
=
=
-
1 1 1
s
m 1
1
U
Z
I
Z Z I
( )
( )( ) ( )
(
)
( )
D
=
=
-
2 2 2
s
m 2
2
U
Z
I
Z Z I
( )
( )
u 0
u 0
U
3Z I
D
=
( )
u 1
U
0
D
=
( )
u 2
U
0
D
=
The equations of symmetrical components circuits:
( )
( )( ) ( )
( )
=
+
+
0 0 0
u 0
0
0 U
Z
I
3Z I
( )
( )
( )( ) ( )
=
+
1
1 1 1
1
E
U
Z
I
( )
( )( ) ( )
=
+
2 2 2
2
0 U
Z
I
( )
( )( )
(
)
( )
=-
+
0 0
u
0
0
U
Z
3Z I
( )
( )
( )( ) ( )
=
-
1
1 1 1
1
U
E
Z
I
( )
( )( ) ( )
=-
2 2 2
2
U
Z
I
or
Taking into account the Z
p
and Z
pu
matrices yield the following equations for
voltage drop ΔU and ΔU
u
in symmetrical components:
21 / 48
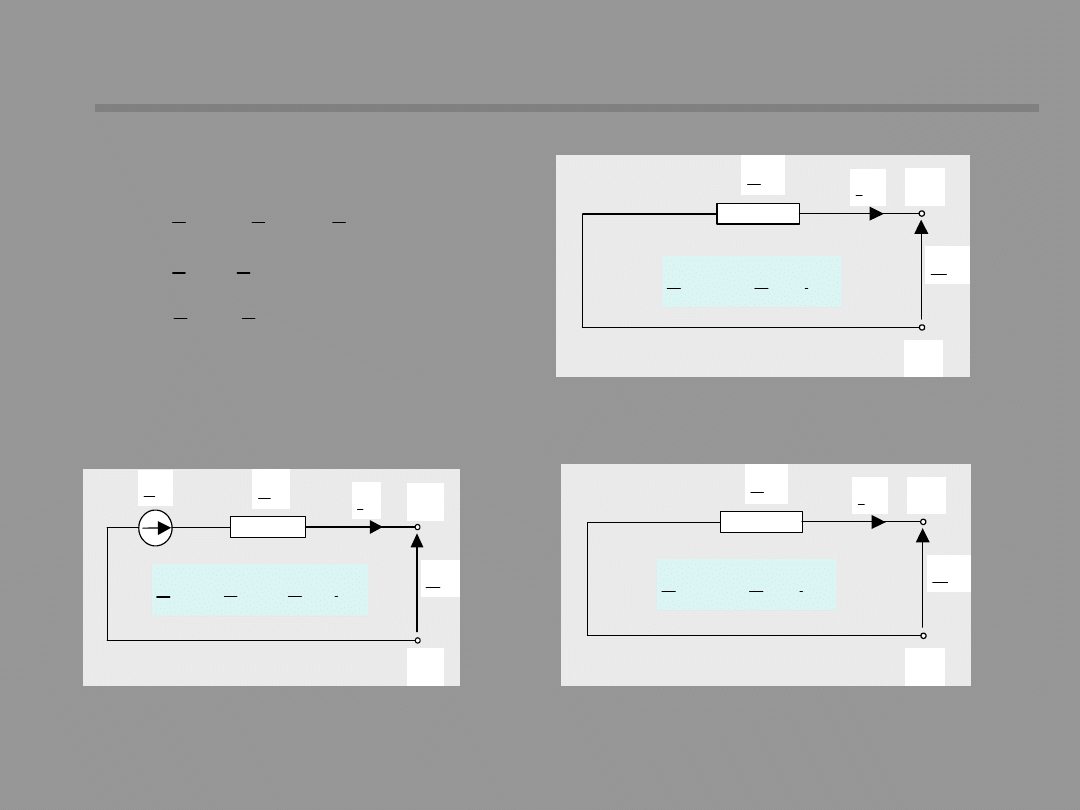
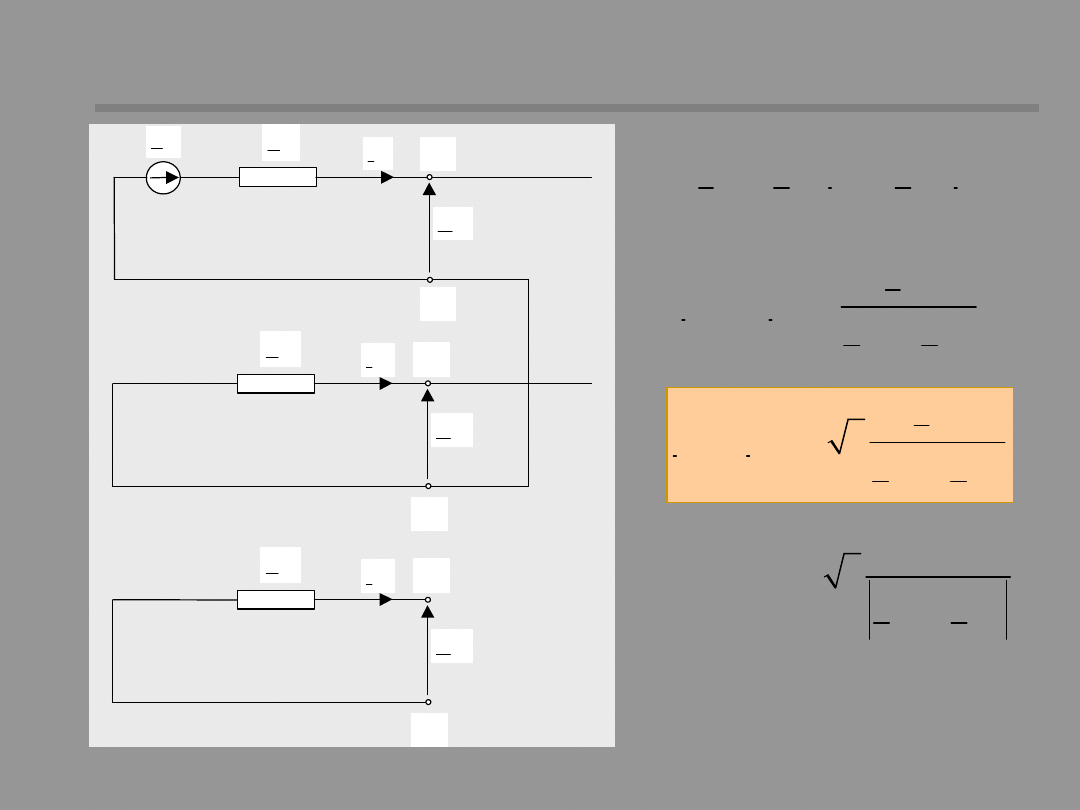
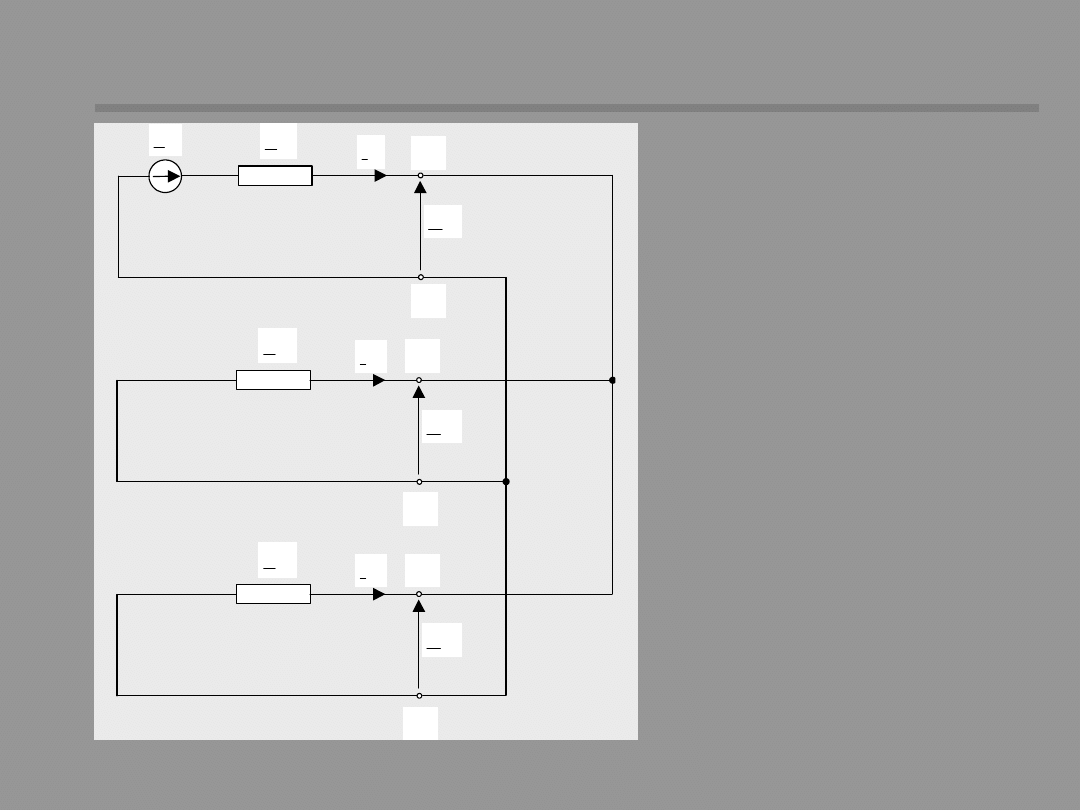
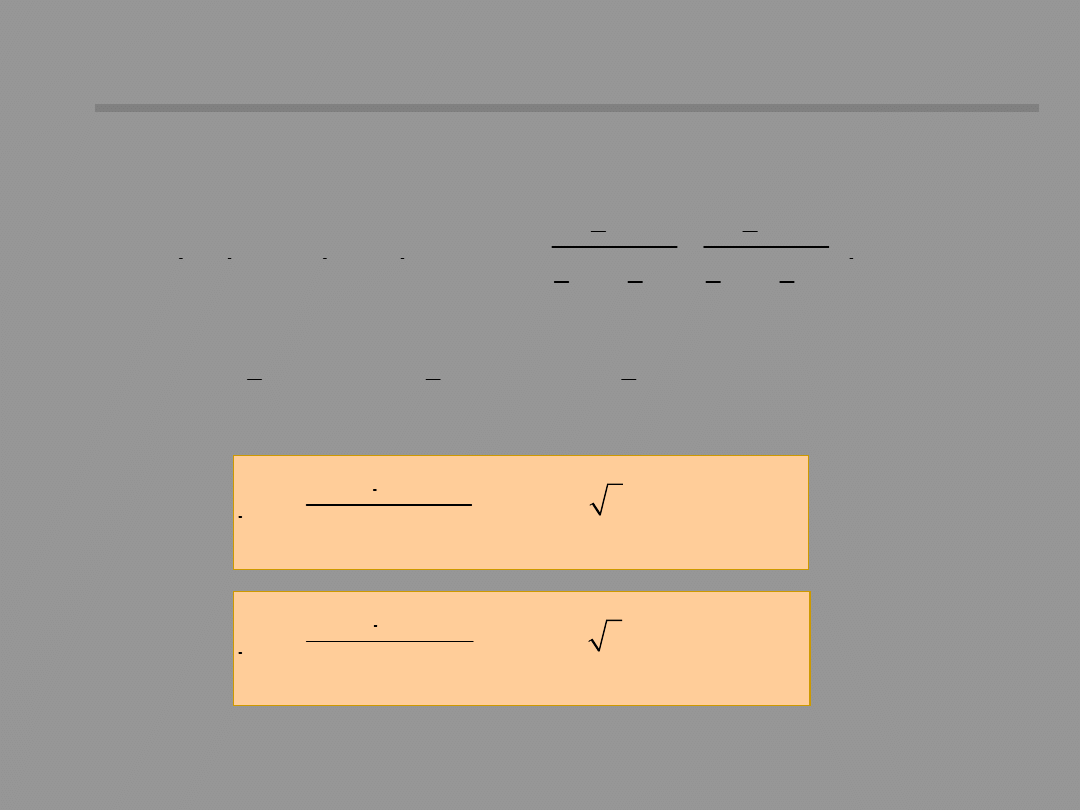
Single-phase sequence networks
Single-phase sequence networks
1
I
1
E
1
Z
1
U
P
(1)
K
(1)
2
I
2
Z
2
U
K
(2)
P
(2)
0
I
0
Z
0
U
K
(0)
P
(0)
( )
( )
(
)
=
+
0
0
u
Z
Z
3Z
( )
( )( )
1
1 1
Z
Z
=
( )
( )( )
2
2 2
Z
Z
=
( )
( ) ( )
0 0
0
U
Z I
=-
( )
( )
( ) ( )
1
1 1
1
U
E
Z I
=
-
( )
( ) ( )
2 2
2
U
Z I
=-
Z
(0)
, Z
(1)
, Z
(2)
– equivalent impedances of network for zero, positive and
negative sequence components, respectively
Using the notation:
We can describe sub-
networks for each
symmetrical
component

22 / 48
Single line-to-earth short-circuit
Single line-to-earth short-circuit
Assumptions:
•
The network is unloaded before a fault
•
Phase R is short-circuited
Boundary conditions are:
R
U
0
=
( )
( )
( )
0
1
2
U
U
U
0
+
+
=
1
)
S
T
I
I
0
= =
( )
( )
( )
0
1
2
R
1
I
I
I
I
3
=
=
=
2
)
Using the inverse of
symmetrical
component
transformation
Using the
transformation
itself
These two expressions describe the sequence
network connection.

23 / 48
Single line-to-earth short-circuit
Single line-to-earth short-circuit
( )
( )
( )
( )
( )
( )
( )
1
1
2
0
1
2
0
E
I
I
I
Z
Z
Z
=
=
=
+
+
( ) ( ) ( )
( )
( )
( )
( )
1
R
1
2
0
1
2
0
3E
I
I
I
I
Z
Z
Z
= +
+
=
+
+
( )
( )
( )
( )
1
P
R
1
2
0
3E
I
I
Z
Z
Z
= =
+
+
Using the sequence
network equations:
( )
( ) ( )
0 0
0
U
Z I
=-
( )
( )
( ) ( )
1
1 1
1
U
E
Z I
=
-
( )
( ) ( )
2 2
2
U
Z I
=-
The condition 1) gives:
( )
( ) ( )
( ) ( )
( ) ( )
1
1 1
2 2
0 0
E
Z I
Z I
Z I
0
-
-
-
=
from
here:
Phase current can be
expressed by
Initial current
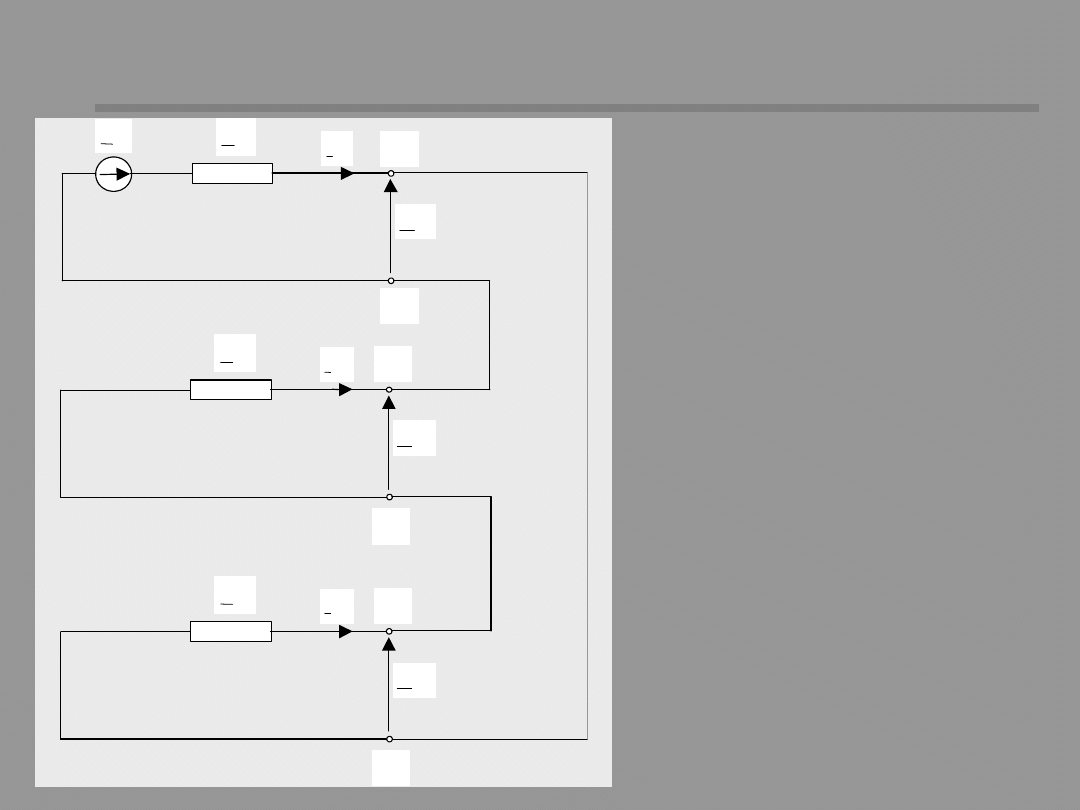
24 / 48
1
I
1
E
1
Z
1
U
2
I
2
Z
2
U
P
(1)
K
(1)
K
(2)
P
(2)
0
I
0
Z
0
U
K
(0)
P
(0)
Single line-to-earth short-circuit
Single line-to-earth short-circuit
Sequence network
connection for single
phase short-circiut has
all three sequence
networks connected in
series.

25 / 48
Single line-to-earth short-circuit
Single line-to-earth short-circuit
( )
( ) ( )
( ) ( )
( )
( )
( )
0
1
0 0
0
1
2
0
Z E
U
Z I
Z
Z
Z
=-
=-
+
+
( )
( )
( ) ( )
( )
( )
( )
( )
( )
( )
2
0
1
1 1
1
1
1
2
0
Z
Z
U
E
Z I
E
Z
Z
Z
+
=
-
=
+
+
( )
( ) ( )
( ) ( )
( )
( )
( )
2
1
2 2
2
1
2
0
Z E
U
Z I
Z
Z
Z
=-
=-
+
+
Voltage symmetrical
components:
Phase voltages:
( )
( )
( )
R
0
1
2
U
U
U
U
0
=
+
+
=
( )
( )
( )
( )
( )
( )
( )
(
)
( )
( )
( )
1
2
2
2
2
0
S
0
1
2
1
2
0
E
U
U
a U
aU
a a Z
a 1 Z
Z
Z
Z
�
�
=
+
+
=
-
+
-
�
�
�
�
+
+
( )
( )
( )
( )
( )
( )
( )
(
)
( )
(
)
( )
1
2
2
2
0
T
0
1
2
1
2
0
E
U
U
aU
a U
a a Z
a 1 Z
Z
Z
Z
�
�
=
+
+
=
-
-
+ -
�
�
�
�
+
+
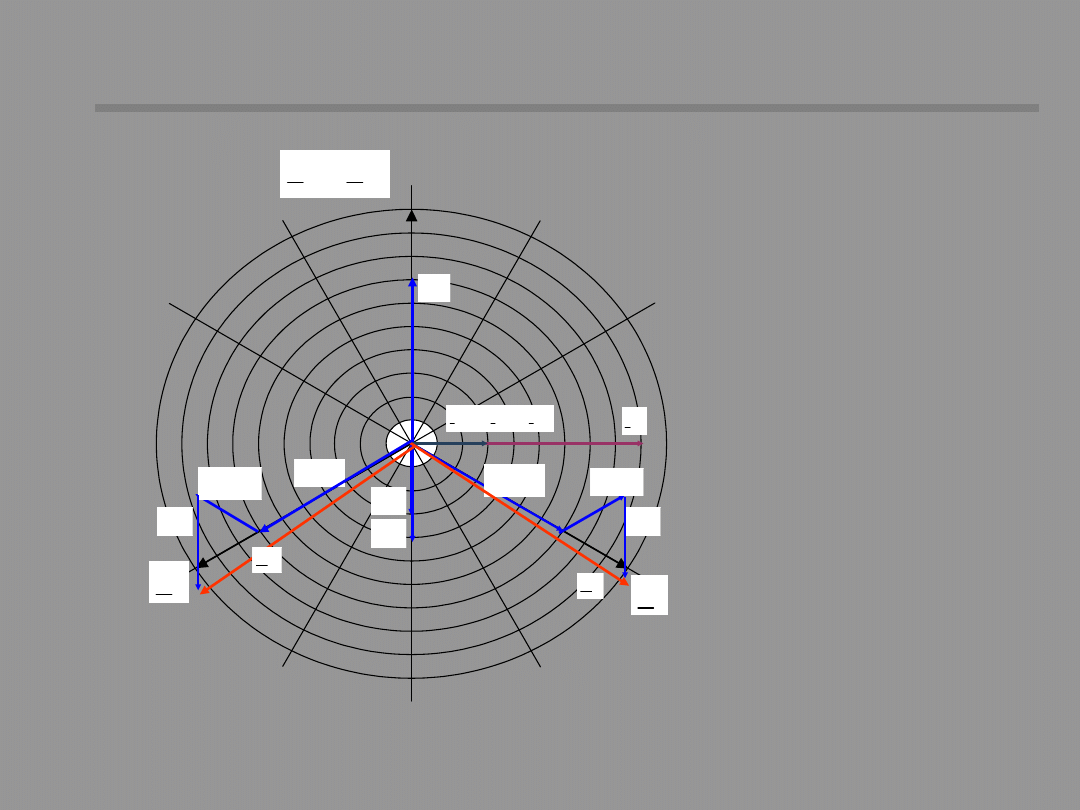
26 / 48
Single line-to-earth short-circuit
Single line-to-earth short-circuit
1
R
E
E
S
E
T
E
1
U
2
U
0
U
R
I
2
1
0
I
I
I
1
2
U
a
2
U
a
0
U
S
U
1
U
a
2
2
U
a
0
U
T
U
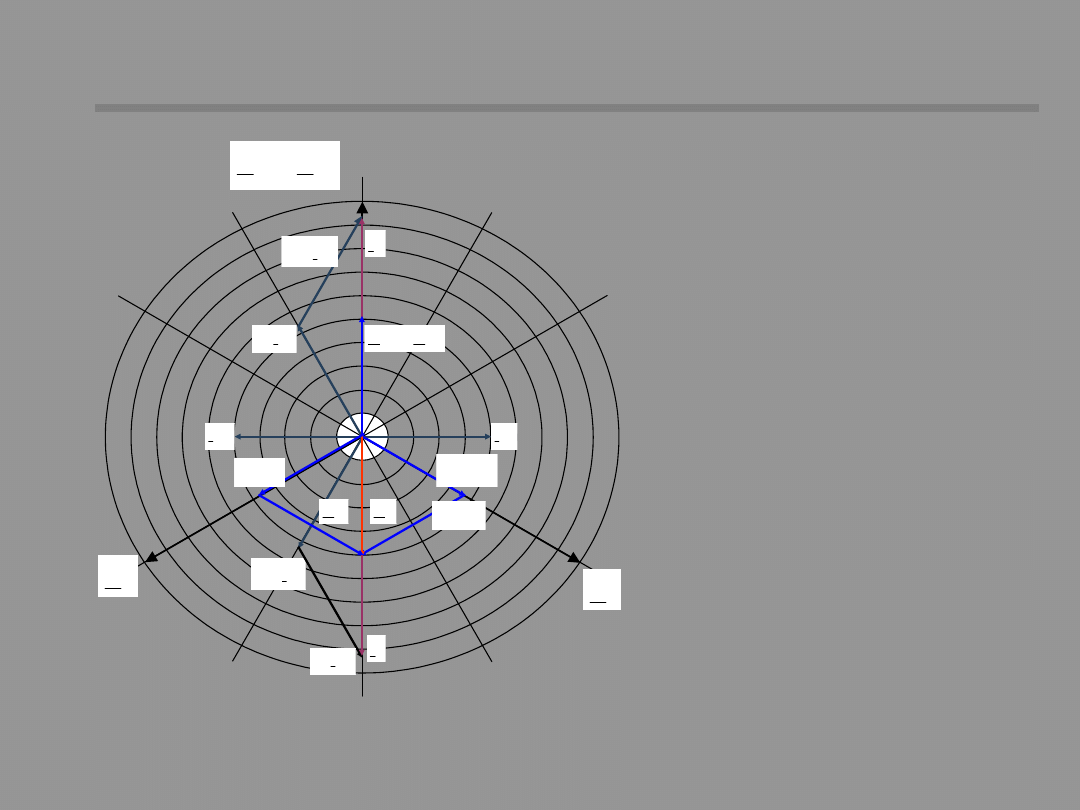
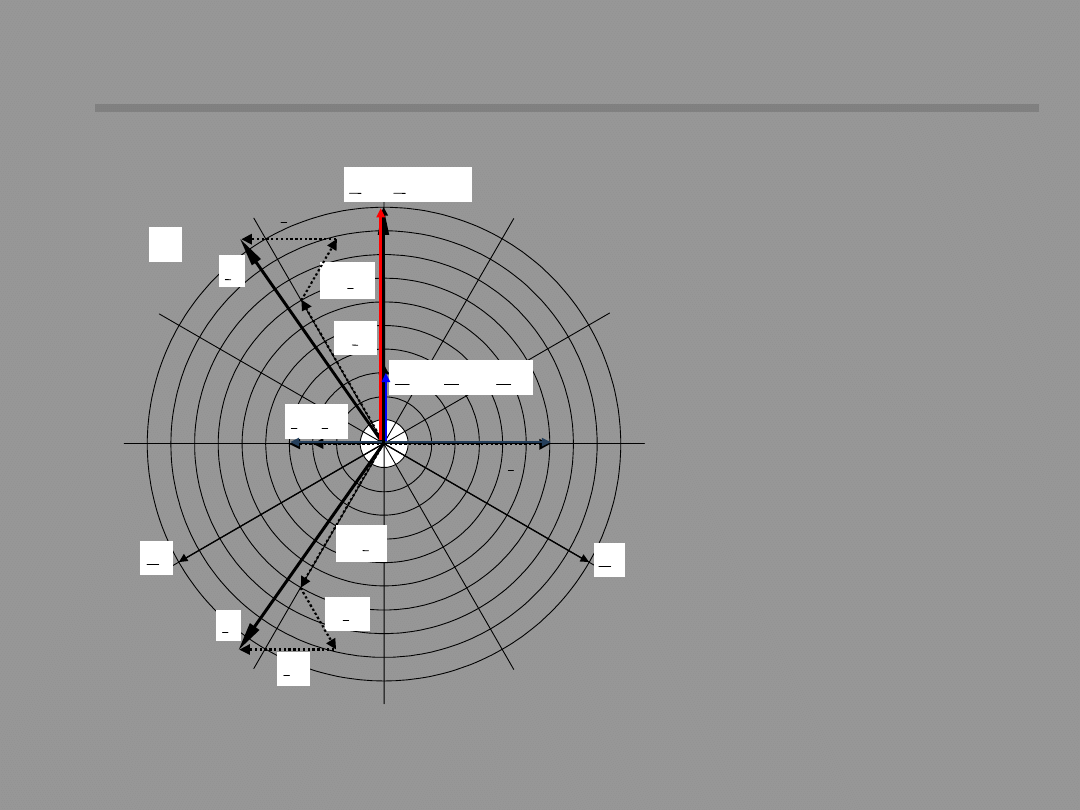
Vector diagram of currents
and voltages for single phase
short-circuit (network
resistance is omitted)
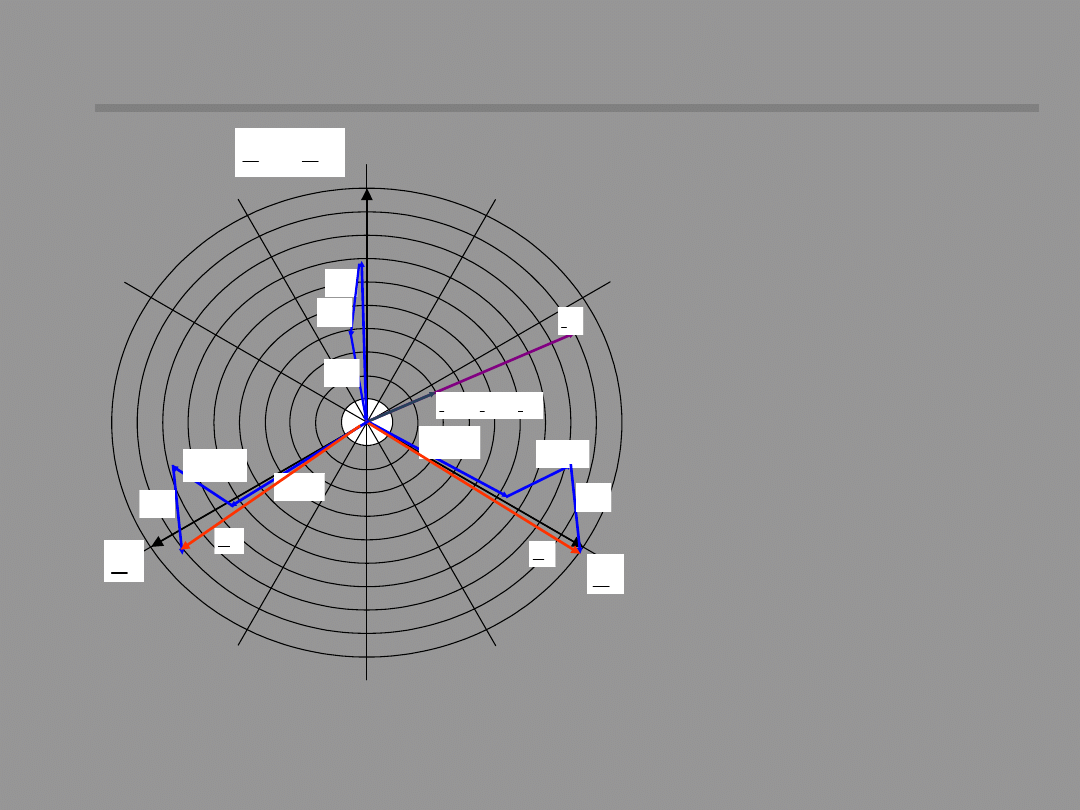
27 / 48
Single line-to-earth short-circuit
Single line-to-earth short-circuit
1
R
E
E
S
E
T
E
R
I
2
1
0
I
I
I
1
U
2
U
0
U
1
2
U
a
2
U
a
0
U
S
U
1
U
a
2
2
U
a
0
U
T
U
Vector diagram of currents
and voltages for single phase
short-circuit (network
resistance is taken into
account).

28 / 48
Single line-to-earth short-circuit
Single line-to-earth short-circuit
through
through
an impedance
an impedance
Z R
R
U
Z I
=
S
T
I
I
0
= =
( )
( )
( )
0
1
2
R
1
I
I
I
I
3
=
=
=
( )
( )
( )
( )
Z 1
0
1
2
U
U
U
3Z I
+
+
=
( )
( ) ( )
( ) ( )
( ) ( )
( )
1
1 1
2 2
0 0
Z 1
E
Z I
Z I
Z I
3Z I
0
-
-
-
-
=
( )
( )
( )
( )
( )
( )
( )
1
1
2
0
1
2
0
Z
E
I
I
I
Z
Z
Z
3Z
=
=
=
+
+
+
( ) ( ) ( )
( )
( )
( )
( )
1
R
1
2
0
1
2
0
Z
3E
I
I
I
I
Z
Z
Z
3Z
= +
+
=
+
+
+
Boundary conditions:
1
)
2
)
The condition 1) gives:
From
here:

29 / 48
Single line-to-earth short-circuit
Single line-to-earth short-circuit
through
through
an impedance
an impedance
( )
( ) ( )
( ) ( )
( )
( )
( )
0
1
0 0
0
1
2
0
Z
Z E
U
Z I
Z
Z
Z
3Z
=-
=-
+
+
+
( )
( )
( ) ( )
( )
( )
( )
( )
( )
( )
2
0
Z
1
1 1
1
1
1
2
0
Z
Z
Z
3Z
U
E
Z I
E
Z
Z
Z
3Z
+
+
=
-
=
+
+
+
( )
( ) ( )
( ) ( )
( )
( )
( )
2
1
2 2
2
1
2
0
Z
Z E
U
Z I
Z
Z
Z
3Z
=-
=-
+
+
+
Voltage symmetrical components:

30 / 48
Single line-to-earth short-circuit
Single line-to-earth short-circuit
through
through
an impedance
an impedance
( )
( )
( )
( )
( )
( )
( )
Z
1
R
0
1
2
1
2
0
Z
3Z
U
U
U
U
E
Z
Z
Z
3Z
=
+
+
=
+
+
+
( )
( )
( )
2
S
0
1
2
U
U
a U
aU
=
+
+
=
( )
( )
( )
( )
(
)
( )
( )
( )
1
2
2
2
2
0
Z
1
2
0
Z
E
a a Z
a 1 Z
3a Z
Z
Z
Z
3Z
�
�
=
-
+
-
+
�
�
�
�
+
+
+
( )
( )
( )
2
T
0
1
2
U
U
aU
a U
=
+
+
=
( )
( )
( )
( )
(
)
( )
(
)
( )
1
2
2
0
Z
1
2
0
Z
E
a a Z
a 1 Z
3aZ
Z
Z
Z
3Z
�
�
=
-
-
+ -
+
�
�
�
�
+
+
+
( )
( )
( )
( )
( )
u
u 0
1
u
1
2
0
Z
3Z
U
3Z I
E
Z
Z
Z
Z
D =
=
+
+
+
Phase voltages:
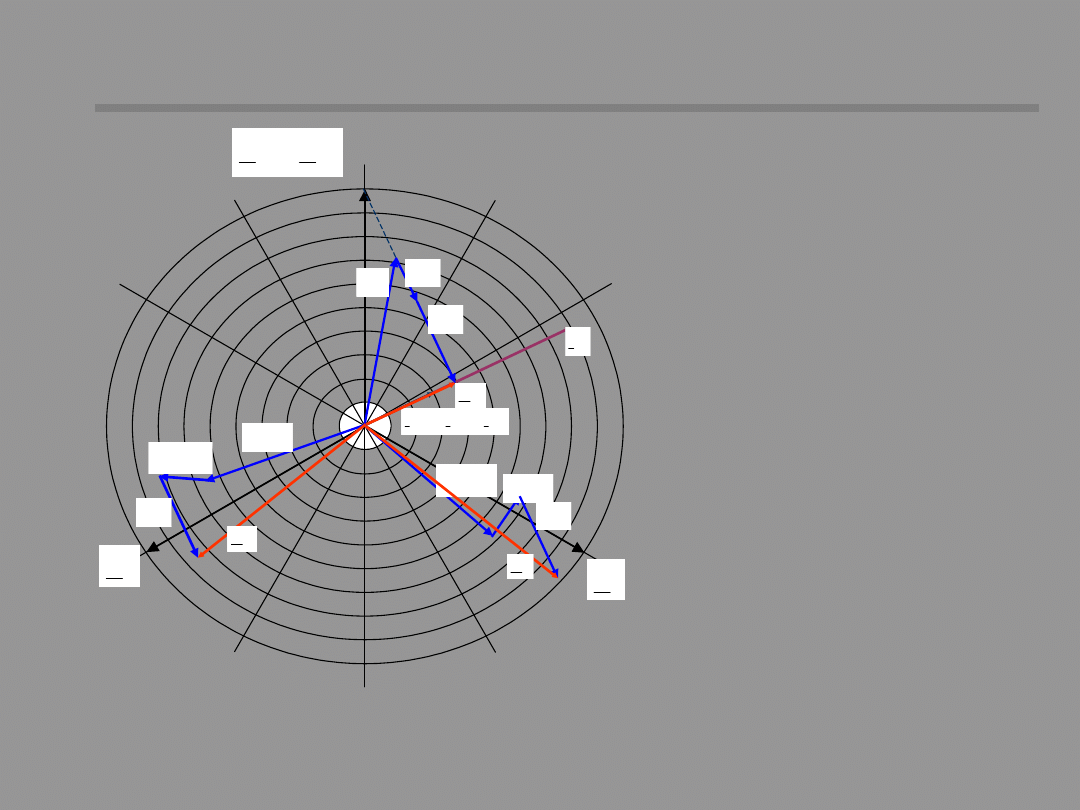
31 / 48
Single line-to-earth short-circuit
Single line-to-earth short-circuit
through
through
an impedance
an impedance
1
R
E
E
S
E
T
E
R
I
2
1
0
I
I
I
1
U
2
U
0
U
R
U
1
2
U
a
1
U
a
0
U
S
U
1
U
a
2
2
U
a
0
U
T
U
Vector diagram of currents
and voltages for single phase
short-circuit through an
impedance (network
resistance is omitted)

32 / 48
Line-to-line short-circuit
Line-to-line short-circuit
S
T
U
U
=
R
I
0
=
S
T
I
I
=-
( )
(
)
2
1
S
S
1
3
I
a a I
j
I
3
3
=
-
=
( )
(
)
2
2
S
S
1
3
I
a a I
j
I
3
3
=-
-
=-
( )
(
)
0
S
1
I
1 1 I
0
3
=
-
=
( )
( )
1
2
I
I
=-
( )
0
I
0
=
Assumptions:
•
Load currents are omitted.
•
The fault involves the phases S and T
Boundary conditions:
1
)
2
)
Expressing these relationships in terms of the
symmetrical components:

33 / 48
Line-to-line short-circuit
Line-to-line short-circuit
( )
(
)
(
)
0
R
S
T
R
S
1
1
U
U
U
U
U
2U
3
3
=
+ +
=
+
( )
(
)
(
)
2
1
R
S
T
R
S
1
1
U
U
aU
a U
U
U
3
3
=
+
+
=
-
( )
(
)
(
)
2
2
R
S
T
R
S
1
1
U
U
a U
aU
U
U
3
3
=
+
+
=
-
( )
( )
1
2
U
U
=
Voltage sequence components:
34 / 48
Line-to-line short-circuit
Line-to-line short-circuit
1
I
1
E
1
Z
1
U
2
I
2
Z
2
U
P
(1)
K
(1)
K
(2)
P
(2)
0
I
0
Z
0
U
K
(0)
P
(0)
( )
( ) ( )
( ) ( )
1
1 1
2 1
E
Z I
Z I
-
=
( )
( )
( )
( )
( )
1
1
2
1
2
E
I
I
Z
Z
=-
=
+
( )
( )
( )
1
S
T
1
2
E
I
I
j 3
Z
Z
=- =-
+
( )
( )
( )
1
S
T
P
1
2
E
I
I
I
3
Z
Z
= = =
+
Sequence network connection for
line-to-line short-circiut has two
sequence networks connected in
parallel.

35 / 48
Line-to-line short-circuit
Line-to-line short-circuit
( )
( )
( )
( ) ( )
( ) ( )
( )
( )
( )
( )
2
1
1 1
2 2
1
1
2
1
2
Z
U
U
E
Z I
Z I
E
Z
Z
=
=
-
=-
=
+
( )
( )
( )
( )
( )
( )
( )
( )
2
1
R
0
1
2
1
1
2
2Z
U
U
U
U
2U
E
Z
Z
=
+
+
=
=
+
( )
( )
( )
( )
( ) ( )
( )
( )
2
1
2
S
T
0
1
2
1
1
2
Z E
U
U
U
a U
aU
U
Z
Z
=
=
+
+
=-
=-
+
Phase voltages:
36 / 48
Line-to-line short-circuit
Line-to-line short-circuit
1
R
E
E
S
E
T
E
1
I
2
I
1
2
I
a
2
I
a
S
I
1
I
a
2
2
I
a
T
I
2
1
U
U
1
2
U
a
2
U
a
S
U
1
U
a
T
U
Vector diagram of
currents and voltages
for line-to-line short-
circuit (network
resistance is omitted)

37 / 48
Line-to-line short-circuit
Line-to-line short-circuit
through an
through an
impedance
impedance
Z S
S
T
U
U
Z I
-
=
R
I
0
=
S
T
I
I
=-
( )
( )
1
2
I
I
=-
( )
0
I
0
=
( )
( )
( )
( )
(
) (
)
( )
(
)
( )
2
2
2
2
S
T
1
2
1
2
1
2
U
U
a U
aU
aU
a U
a a U
a a U
-
=
+
-
+
=
-
-
-
=
( )
( )
(
)
( )
Z S
Z 1
1
2
j 3 U
U
Z I
j 3Z I
=-
-
=
=-
( )
( )
( )
Z 1
1
2
U
U
Z I
-
=
( )
( ) ( )
( ) ( )
( )
1
1 1
2 1
Z 1
E
Z I
Z I
Z I
-
-
=
( )
( )
( )
( )
( )
1
1
2
1
2
Z
E
I
I
Z
Z
Z
=-
=
+
+
( )
( )
( )
1
S
T
1
2
Z
E
I
I
j 3
Z
Z
Z
=- =-
+
+
Boundary conditions
1
)
2
)

38 / 48
Double line-to-ground short-circuit
Double line-to-ground short-circuit
S
T
U
U
0
=
=
R
I
0
=
( ) ( ) ( )
1
2
0
I
I
I
0
+
+
=
( )
( )
1
2
0
R
1
U
U
U
U
3
=
= =
( )
( )
( ) ( )
( ) ( )
1
1 1
2 2
1
U
E
Z I
Z I
=
-
=-
( )
( )
( ) ( )
( ) ( )
1
1 1
0 0
1
U
E
Z I
Z I
=
-
=-
( )
( )
( )
( ) ( )
( )
( )
1
1
2
0
1
2
0
E
I
Z Z
Z
Z
Z
=
+
+
( )
( )
( )
( )
( )
0
2
1
2
0
Z
I
I
Z
Z
=-
+
( )
( )
( )
( )
( )
2
0
1
2
0
Z
I
I
Z
Z
=-
+
The short-circuit involves phases S, T and ground.
Initial relationship at the point of the fault:
From solving the equations it follows that:
Using the sequence
transformation
39 / 48
Double line-to-ground short-circuit
Double line-to-ground short-circuit
1
I
1
E
1
Z
1
U
2
I
2
Z
2
U
P
(1)
K
(1)
K
(2)
P
(2)
0
I
0
Z
0
U
K
(0)
P
(0)
Sequence network connection
for double line-to-ground short-
circuit has three sequence
networks connected in parallel.
40 / 48
Double line-to-ground short-circuit
Double line-to-ground short-circuit
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
0
2
2
2
S
0
1
2
1
2
0
2
0
Z
Z
I
I
a I
aI
a a
I
Z
Z
Z
Z
�
�
�
�
=
+
+
=
-
-
�
�
+
+
�
�
( )
( )
1
1
Z
jX
=
( )
( )
2
2
Z
jX
=
( )
( )
0
0
Z
jX
=
( )
( )
( )
(
)
( )
( )
( )
(
)
1
S
2
2
0
2
0
I
I
3X
j 3 X
2X
2 X
X
�
�
=-
+
+
�
�
�
�
+
( )
( )
( )
(
)
( )
( )
( )
(
)
1
T
2
2
0
2
0
I
I
3X
j 3 X
2X
2 X
X
�
�
=-
-
+
�
�
�
�
+
Phase currents:
41 / 48
Double line-to-ground short-circuit
Double line-to-ground short-circuit
( )
( )
( )
(
)
( )
( )
( )
(
)
( )
( ) ( )
( )
( )
(
)
2
1
2
0
2
S
T
P
2
2
0
1
2
2
0
2
0
I
X X
I
I
I
9X
3 X
2X
I
3 1
2 X
X
X
X
= = =
+
+
=
-
+
+
Phase current magnitudes:
Voltages:
( )
( )
( )
( ) ( )
( )
( )
( )
( ) ( )
( )
( )
( )
2
0
2
0
1
1
2
0
2
0
1
2
0
Z Z
Z
Z
U
U
U
E
Z Z
Z
Z
Z
+
=
=
=
+
+
( )
R
1
U
3U
=
S
T
U
U
0
=
=
42 / 48
Double line-to-ground short-circuit
Double line-to-ground short-circuit
S
E
T
E
1
R
E
E
0
2
1
U
U
U
2
I
0
I
1
I
a
1
2
I
a
2
I
a
2
2
I
a
0
I
0
I
S
I
T
I
1
I
Vector diagram of
currents and voltages
for double line-to-
ground short-circuit
(network resistance is
omitted)

43 / 48
Double line-to-ground short-circuit
Double line-to-ground short-circuit
through an impedance
through an impedance
(
)
Z Z
Z S
T
S
T
U
U
Z I
Z I
I
=
=
=
+
R
I
0
=
( )
( )
( )
( )
( )
Z Z
Z 0
1
2
0
0
U
U
U
Z I
U
3Z I
=
=
-
=
-
( ) ( ) ( )
1
2
0
I
I
I
0
+
+
=
Boundary
conditions:

44 / 48
Three-phase, three-phase with ground
Three-phase, three-phase with ground
short-circuit
short-circuit
R
S
T
U
U
U
0
=
=
=
R
S
T
z
I
I
I
I
+ + =
( )
( )
( )
1
2
0
U
U
U
0
=
=
=
( )
( )
2
0
I
I
0
=
=
( )
( )
( )
1
1
R
1
E
I
I
Z
= =
( )
( )
1
P
R
1
E
I
I
Z
= =
Boundary conditions:

45 / 48
Initial current
Initial current
Positive sequence initial current for different
types of short-circuits
1
1
1
Z
E
I
2
1
1
1
Z
Z
E
I
0
2
1
1
1
Z
Z
Z
E
I
0
2
0
2
1
1
1
Z
Z
Z
Z
Z
E
I
Three-phase short-circuit
Line-to-line
short-circuit
Single phase line-to-earth short-circuit
Double line-
to-earth short-circuit

46 / 48
Initial current
Initial current
0
Z
2
Z
Z
0
2
Z
Z
Z
0
2
0
2
Z
Z
Z
Z
Z
General
formula:
Z
Z
E
I
1
1
1
where
Three-phase short-
circuit
Line-to-line short-
circuit
Single phase line-to-earth
short-circuit
Double line-to-earth short-
circuit

47 / 48
Initial current
Initial current
1
P
I
I
1
P
I
3
I
1
P
I
3
I
1
2
0
2
0
2
P
I
X
X
X
X
1
3
I
1
P
I
m
I
Three-phase short-
circuit
Line-to-line short-
circuit
Single phase line-to-earth short-
circuit
Double line-to-earth
short-circuit
General
expression:
48 / 48
Currents and voltages in relation with
Currents and voltages in relation with
X
X
0
0
/X
/X
1
1
( )
( )
( )
1
2
0
R
R
R
0
=
=
=
( )
( )
1
2
X
X
=
1f
P
1
3f
P
I
3
k
2
I
=
=
+a
2f
P
2
3f
P
I
3
k
2
I
=
=
2fz
2
P
2z
3f
P
I
3 1
k
1 2
I
+a +a
=
=
+ a
( )
( )
0
1
X
X
a =
Assumptio
n:
( )
2
1f
1f
1
T
S
3 1
U
U
E
2
+a +a
=
=
+a
( )
2f
1
R
U
E
=
( )
2fz
1
R
3
U
E
1 2
a
=
+ a
If X
(0)
>X
(1)
the 3-phase short-circuit current is the biggest one.
If X
(0)
<X
(1)
the single-phase line –to-earth current is the biggest
one.
If X
(0)
>X
(1)
voltages of unfaulted (healthy) phases for single-phase
and line-to-line short-circuits are > than EMF.
If X
(0)
<X
(1)
voltages of unfaulted (healthy) phases for single-phase
and line-to-line short-circuits are < than EMF.
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18
- Slide 19
- Slide 20
- Slide 21
- Slide 22
- Slide 23
- Slide 24
- Slide 25
- Slide 26
- Slide 27
- Slide 28
- Slide 29
- Slide 30
- Slide 31
- Slide 32
- Slide 33
- Slide 34
- Slide 35
- Slide 36
- Slide 37
- Slide 38
- Slide 39
- Slide 40
- Slide 41
- Slide 42
- Slide 43
- Slide 44
- Slide 45
- Slide 46
- Slide 47
- Slide 48
Wyszukiwarka
Podobne podstrony:
Symmetrical components method continued
Symmetrical components method continued
24 G23 H19 QUALITY ASSURANCE OF BLOOD COMPONENTS popr
Gunwitch Method
components microwave
Opponens Pollicis KT method
Sprawdzian symetria Iab
Definicja symetralnej
Fibularis (Peroneus) Longus KT method
ALAN42 MULTI component side
Flexor Hallucis Longus KT method
Popliteus KT method
Component Based Automation
Posterior Diaphragm KT method
Palmaris Longus KT method
Oblique Abdominis Externus KT method
Connexions 1 Methode de francais
Earned Value Method
więcej podobnych podstron