Podstawy Projektowania

Podstawy Projektowania

Inżynierskiego

Inżynierskiego

Przekładnie zębate cz. I

Przekładnie zębate cz. I

Prowadzący:

Prowadzący:

dr inż. Piotr

dr inż. Piotr

Chwastyk

Chwastyk

e-mail: [e-mail]

e-mail: [e-mail]

www.chwastyk.po.opole.pl

www.chwastyk.po.opole.pl

P o l i t e c h n i k a O p o l s k a

P o l i t e c h n i k a O p o l s k a

Wydział Zarządzania i Inżynierii Produkcji

Wydział Zarządzania i Inżynierii Produkcji

Instytut Inżynierii Produkcji

Instytut Inżynierii Produkcji

Przekładnie zębate cz. I – nr 2

Przekładnie zębate

Przekładnie zębate

dr inż. Piotr Chwastyk

Wiadomości wstępne

Wiadomości wstępne

Koło zębate jest to część mechanizmu lub maszyny, służąca
do przenoszenia ruchu bez poślizgu za pomocą zębów
rozmieszczonych na obwodach dwóch współpracujących kół.
Para lub większa liczba zazębiających się ze sobą kół
zębatych tworzy przekładnię zębatą.
Koło zębate składa się z wieńca zębatego oraz części
łączących wieniec z wałem lub piastą.

Przekładnie zębate cz. I – nr 3

Przekładnie zębate

Przekładnie zębate

dr inż. Piotr Chwastyk

Klasyfikacja kół zębatych

Klasyfikacja kół zębatych

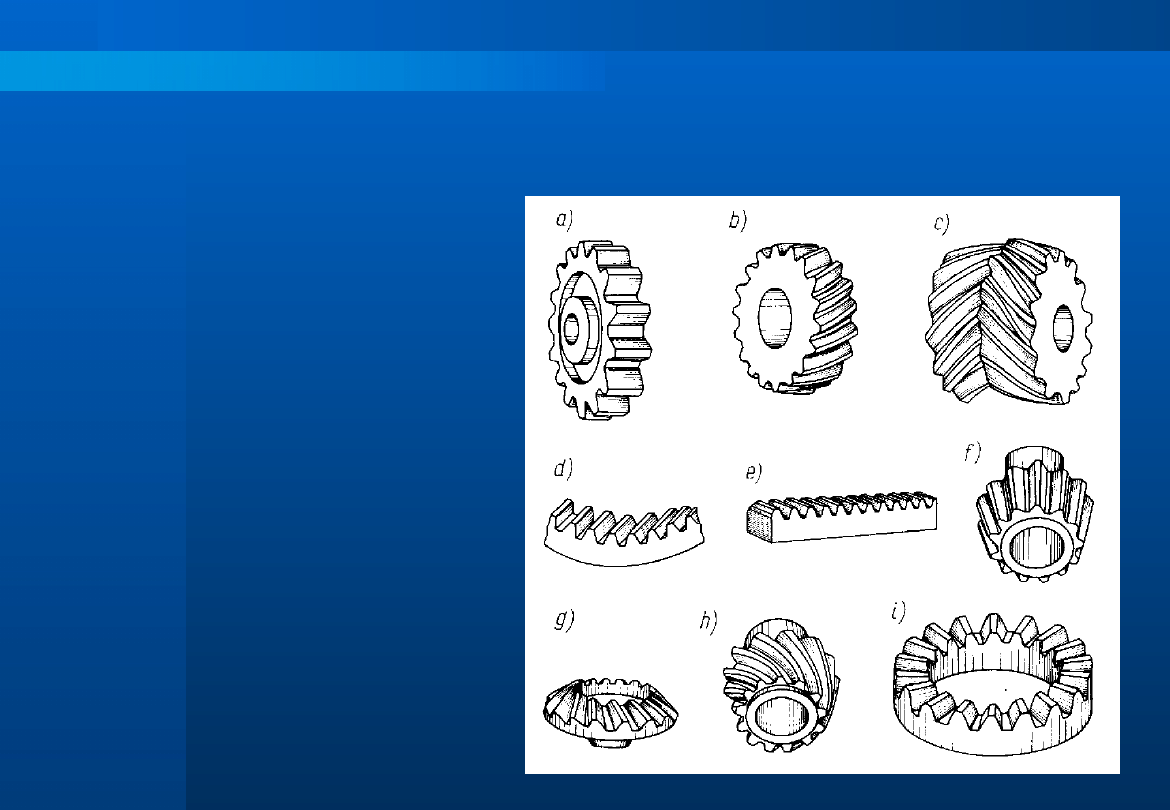
Zależnie od kształtu wieńca, koła zębate dzielimy na:
1.

Koła walcowe:

Koła walcowe:

a) o zębach prostych
b) o zębach skośnych
c) o zębach daszkowych
d) z uzębieniem wewnętrznym
e) zębatka

2.

Koła stożkowe:

Koła stożkowe:

f) o zębach prostych
g) o zębach skośnych
h) o zębach krzywoliniowych
i) płaskie

Przekładnie zębate cz. I – nr 4

Przekładnie zębate

Przekładnie zębate

dr inż. Piotr Chwastyk

Klasyfikacja kół zębatych

Klasyfikacja kół zębatych

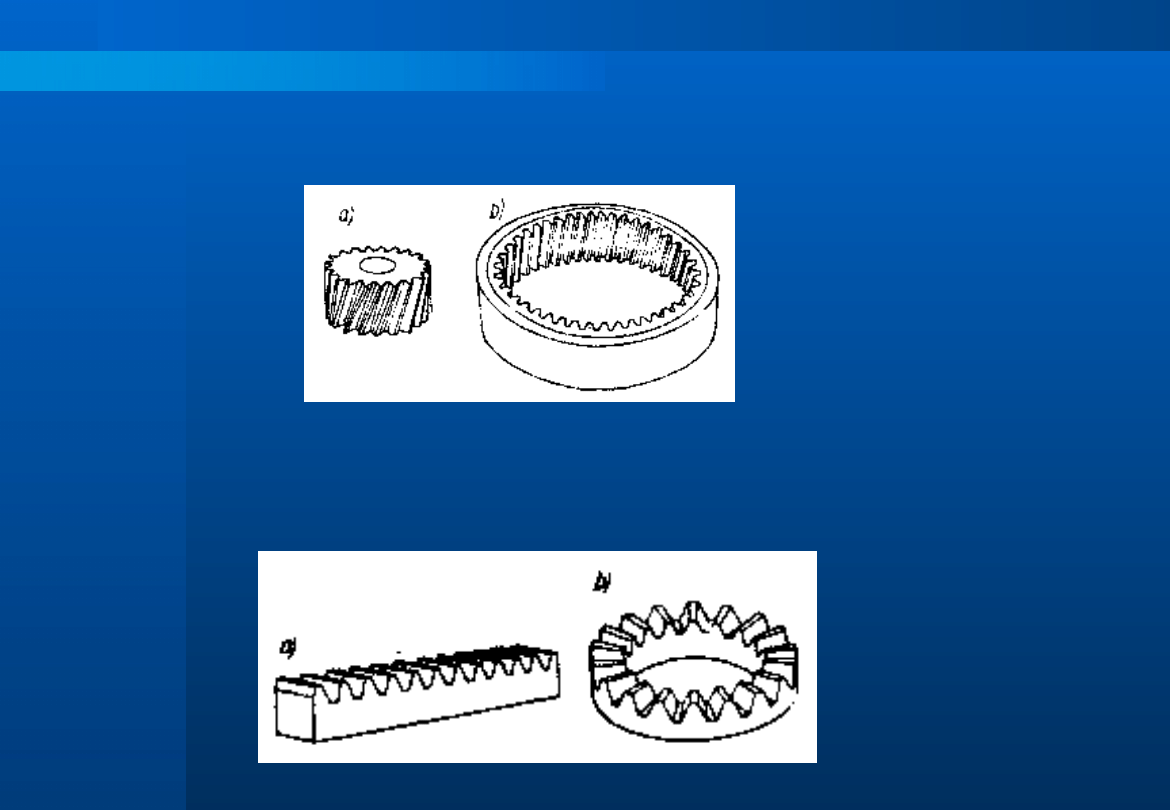
Zarówno koła walcowe jak i stożkowe mogą mieć uzębienie zewnętrzne (rys.
a) jak i wewnętrzne (rys. b).

Szczególną postać koła walcowego stanowi zębatka prosta (rys. a), którą
można uważać za koło walcowe o nieskończenie dużej średnicy.
Podobnie szczególną postacią koła zębatego stożkowego jest koło płaskie,
które nazywamy zębatką pierścieniową lub kołem koronowym (rys. b).

Przekładnie zębate cz. I – nr 5

Przekładnie zębate

Przekładnie zębate

dr inż. Piotr Chwastyk

Klasyfikacja przekładni zębatych

Klasyfikacja przekładni zębatych

Zależnie od wzajemnego położenia osi kół rozróżniamy przekładnie:

1. Równoległe

1. Równoległe

2. Kątowe

2. Kątowe

3. Wichrowate

3. Wichrowate

Ze względu na kształt kół
przekładnie o osiach równoległych
zwane są przekładniami
walcowymi, a przekładnie o osiach
przecinających się stożkowymi.

Rodzaje przekładni zębatych:

•

walcowe o zazębieniu zewnętrznym

walcowe o zazębieniu zewnętrznym
(proste (rys. a), skośne (rys. b),
daszkowe (rys. c));

•

zębatkowe

zębatkowe (rys. e);

•

o zazębieniu wewnętrznym

o zazębieniu wewnętrznym (rys. d);

•

stożkowe

stożkowe (o zębach prostych (rys.
f),

skośnych

(rys.

g),

krzywoliniowych (rys. h));

•

śrubowe

śrubowe (rys. i);

•

ślimakowe

ślimakowe (rys. j).

Przekładnie zębate cz. I – nr 6

Przekładnie zębate

Przekładnie zębate

dr inż. Piotr Chwastyk

Klasyfikacja przekładni zębatych

Klasyfikacja przekładni zębatych

Szczególną postacią przekładni zębatej wichrowatej jest przekładnia
ślimakowa, umożliwiająca przenoszenie ruchu między wałami wichrowatymi
prostopadłymi.
Przekładnie mogą tworzyć koła zębate o uzębieniu zewnętrznym i wówczas
przekładnie takie nazywamy przekładniami zewnętrznymi. Jeżeli przekładnię
tworzą koła, jedno o uzębieniu wewnętrznym, drugie - zewnętrznym, to
przekładnie takie nazywamy przekładniami wewnętrznymi.
Odmianę przekładni równoległej stanowi przekładnia z zębatką prostą, którą
nazywamy przekładnią zębatkową.

Walcowa przekładnia wewnętrzna.

Przekładnia walcowa zębatkowa.

Przekładnie zębate cz. I – nr 7

Przekładnie zębate

Przekładnie zębate

dr inż. Piotr Chwastyk

Zalety i wady przekładni zębatych

Zalety i wady przekładni zębatych

Zalety przekładni zębatych:

• zwartość konstrukcji;

• mniejsze naciski na wał i łożyska;

• niezawodność działania;

• wysoka sprawność (do 99%).

Wady przekładni zębatych:

• duży koszt wykonania;

• mniejsza odporność na przeciążenia;

• hałaśliwość;

• wymagają obfitego smarowania.

Przekładnie zębate cz. I – nr 8

Przekładnie zębate

Przekładnie zębate

dr inż. Piotr Chwastyk

Geometria kół zębatych

Geometria kół zębatych

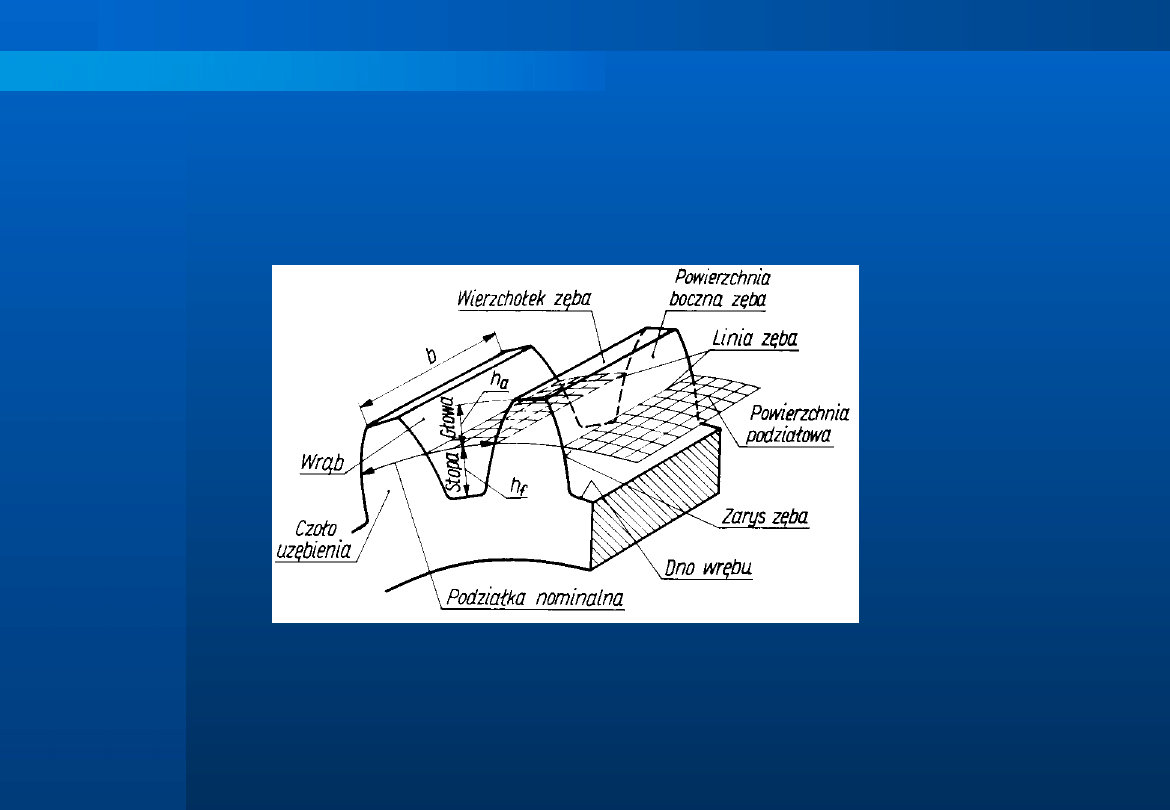
Głowę zęba oddziela od stopy walec podziałowy, a ząb od wieńca walec
podstaw.
Linia przecięcia powierzchni czołowej wieńca z powierzchnią boczną
zęba nazywa się zarysem bocznym zęba (w skrócie po prostu zarysem
zęba), a z powierzchnią podziałową - okręgiem podziałowym.

Linię przecięcia powierzchni bocznej zęba z powierzchnią podziałową
nazywa się linią zęba. Podobnie linię przecięcia powierzchni czołowej
z

powierzchnią

wierzchołkową

nazywa

się

-

okręgiem

wierzchołkowym, a linię przecięcia powierzchni czołowej z
powierzchnią podstaw - okręgiem podstaw.

Przekładnie zębate cz. I – nr 9

Przekładnie zębate

Przekładnie zębate

dr inż. Piotr Chwastyk

Geometria kół zębatych

Geometria kół zębatych

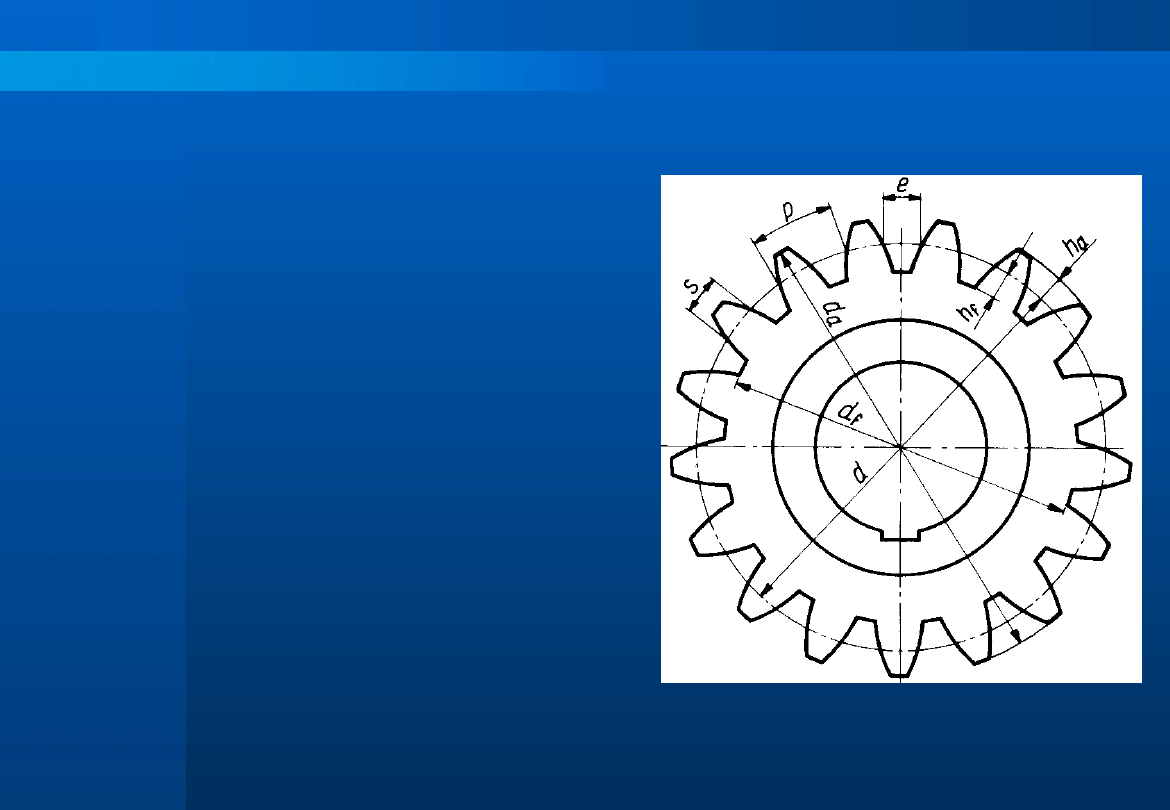
Na rysunku podane są najważniejsze
wymiary uzębienia koła walcowego o
zębach prostych. Należą do nich:
- średnica podziałowa - d
- średnica wierzchołkowa - d

a

- średnica podstaw - d

f

- podziałka - p
- grubość zęba - s
- szerokość wrębu - e
- wysokość zęba - h
- wysokość głowy zęba - h

f

Jeżeli koło zębate ma z zębów, to obwód koła podziałowego równy

π

*d

możemy podzielić na z równych części, z których każda zwana
podziałką p jest równa:

p=(

p=(

π

π

*d)/z

*d)/z

a stąd

d=(z*

d=(z*

π

π

)/p

)/p

oznaczając

p/

p/

π

π

=m

=m

otrzymuje się

d=z*m

d=z*m

Wielkość m przyjęto nazywać modułem koła zębatego. Moduł i
podziałkę wyrażamy z reguły w mm. Wartości modułów są
znormalizowane według szeregu liczb normalnych.

Przekładnie zębate cz. I – nr 10

Przekładnie zębate

Przekładnie zębate

dr inż. Piotr Chwastyk

Geometria kół zębatych

Geometria kół zębatych

p

z

d









m

z

p

z

d











Okrąg podziałowy dzielimy na tyle

odcinków ile zębów (z) przewiduję w
danym kole.

Podziałka p – długość każdego

odcinka

mierzona

po

łuku

okręgu

podziałowego.

Obwód koła podziałowego wyrażamy

wzorem:

Stąd średnica koła podziałowego

gdzie:

– moduł [mm]

Moduł jest podstawowym parametrem służącym do określenia parametrów kół
zębatych.
W budowie maszyn stosujemy moduły powyżej 1 mm. Normalne moduły m
kół zębatych wg PN-78/M-88502 z pierwszego szeregu (uprzywilejowanego) – 1;
1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8.



p

m

Podstawowe wymiary koła walcowego prostego określamy w przekroju
czołowym (płaszczyzna prostopadła do osi koła zębatego).

Przekładnie zębate cz. I – nr 11

Przekładnie zębate

Przekładnie zębate

dr inż. Piotr Chwastyk

Geometria kół zębatych

Geometria kół zębatych

Przyjmujemy

następujące wymiary
zębów normalnych:

wysokość głowy zęba
h

a

= m

wysokość stopy zęba
h

f

= 1,25m

wysokość zęba
h = h

f

+ h

a

= 2,25m

Podziałka p zawiera:
szerokość zęba – s;
szerokość wrębu – e;

Przekładnie zębate cz. I – nr 12

Przekładnie zębate

Przekładnie zębate

dr inż. Piotr Chwastyk

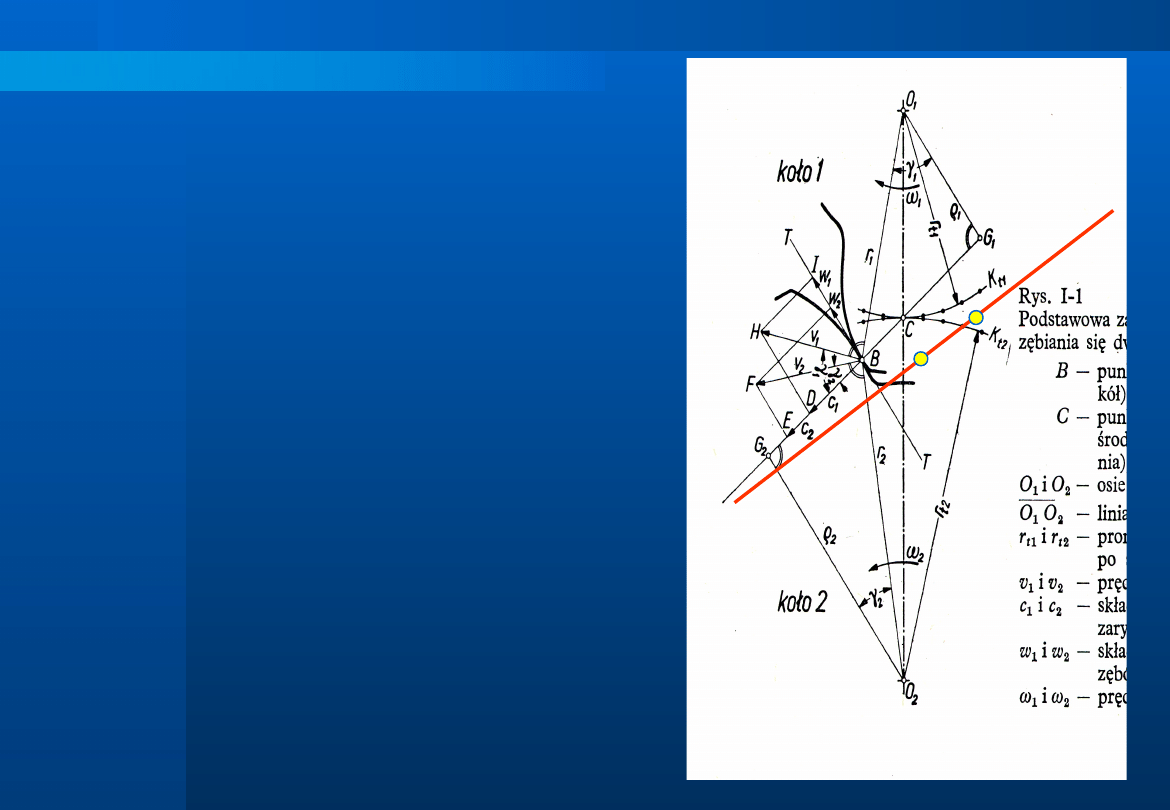
Zasada zazębienia

Zasada zazębienia

Z kinematycznego punktu
widzenia

od

zazębienia

wymaga

się

równomierności
przenoszenia

ruchu

obrotowego. Z tego zadania
wypływa główna zasada
zazębienia:

prosta prostopadła do boku

prosta prostopadła do boku

zęba w punkcie styku

zęba w punkcie styku

zębów

kół

zębów

kół

współpracujących

współpracujących

(punkt B)

(punkt B)

musi

przechodzić

przez

musi

przechodzić

przez

punkt styku kół toczących

punkt styku kół toczących

się po sobie bez poślizgu

się po sobie bez poślizgu

(punkt

C)

(punkt

C)

(tzw.

kół

(tzw.

kół

tocznych).

tocznych).

Przekładnie zębate cz. I – nr 13

Przekładnie zębate

Przekładnie zębate

dr inż. Piotr Chwastyk

Zasada zazębienia

Zasada zazębienia

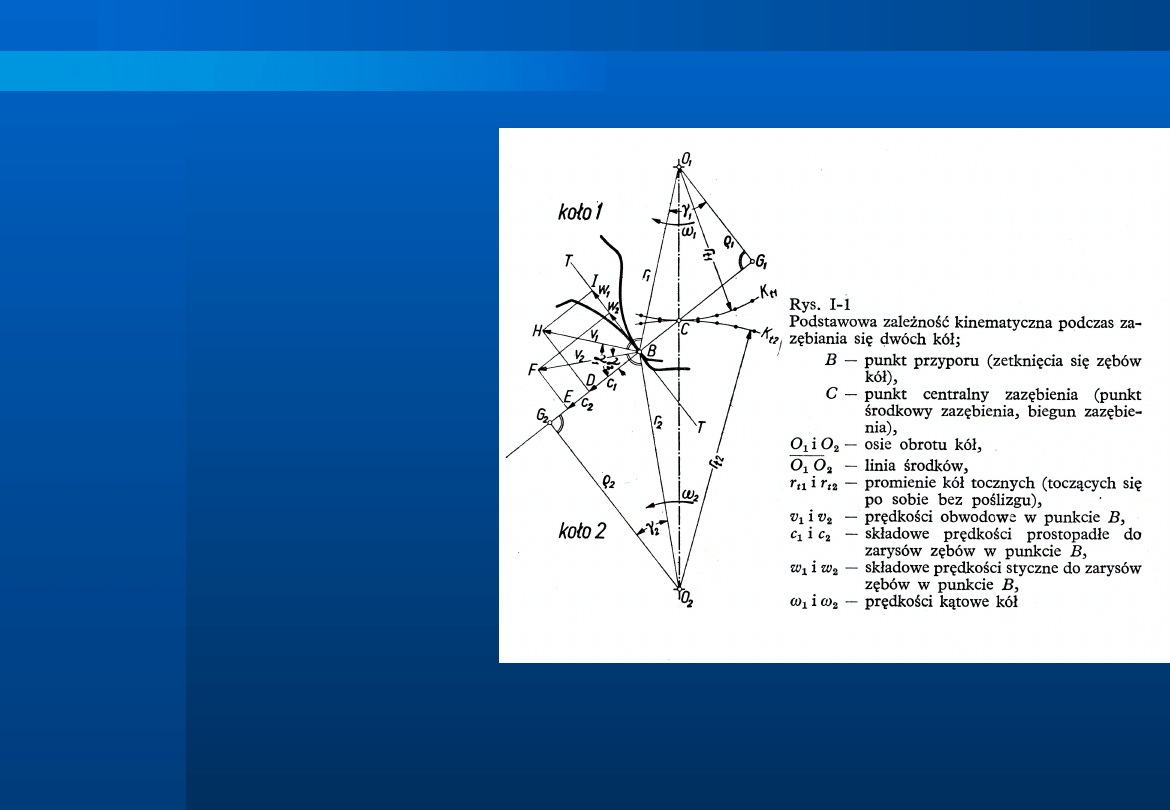
Koła 1 i 2 obracają się
dookoła swoich środków O

1

i

O

2

w ten sposób, że boki

zębów pozostają w styku.
Koło 1 obracając się z
prędkością

chwilową

ω

1

nadaje wskutek styku boków
zębów w punkcie B kołu 2
chwilową prędkość kątową
ω

2.

Równocześnie zgodnie z

zasadami

kinematyki,

otrzymujemy w punkcie B dla
koła 1 i 2 chwilowe prędkości

v

1

= ω

1

· r

1

oraz

v

2

= ω

2

· r

2

Te prędkości można rozłożyć
na składowe styczne do
boków zębów: w

1

i w

2

oraz

prostopadłe do nich c

1

i c

2

Przekładnie zębate cz. I – nr 14

Przekładnie zębate

Przekładnie zębate

dr inż. Piotr Chwastyk

Zasada zazębienia

Zasada zazębienia

)

(

;

;

2

2

2

2

1

1

1

1

2

2

2

2

1

1

1

1

a

r

v

c

r

v

c

r

v

c

r

v

c



















2

2

2

2

1

1

1

1

2

2

2

1

1

1

lub

r

r

r

r

r

v

r

v

















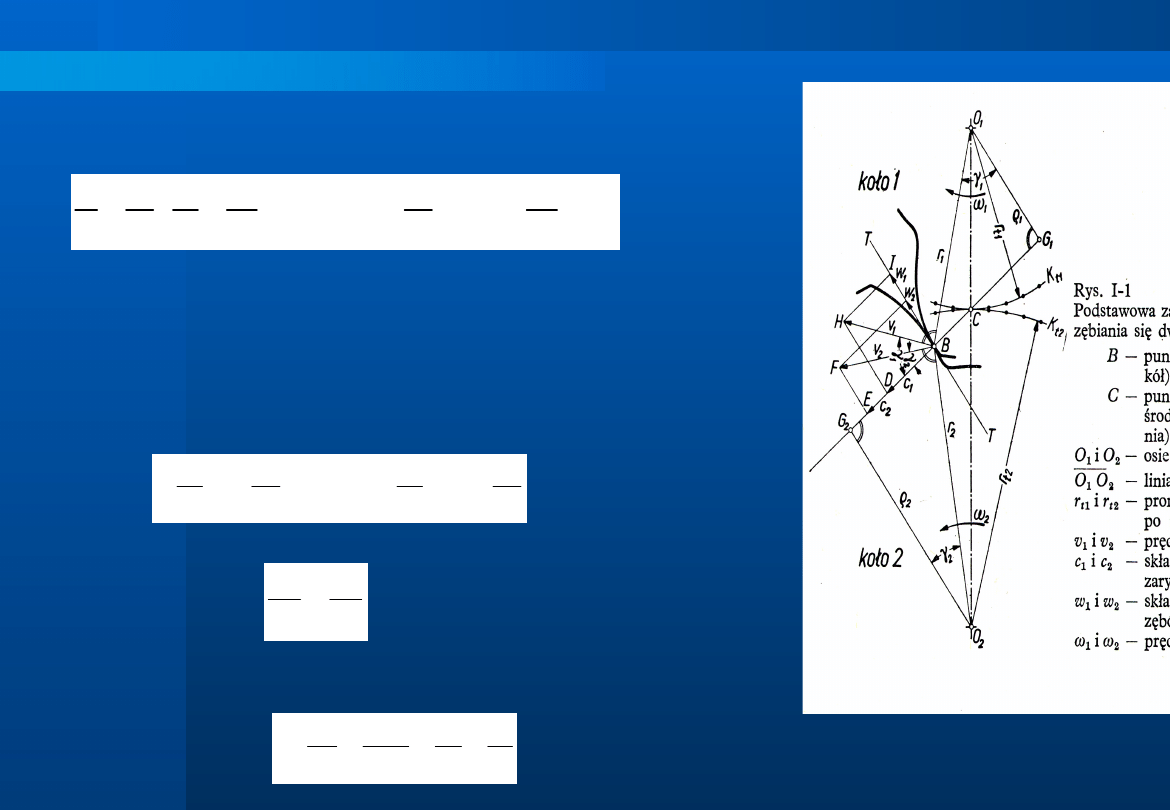
Z podobieństwa trójkątów O

1

G

1

B i BDH oraz O

2

G

2

B i

BEF otrzymamy:

Ponieważ zgodnie z założeniem, oba zęby powinny
pracować w ciągłym styku, zatem musi być spełniony
warunek:

c

1

= c

2

(b)

Gdyby c1 < c2, wówczas ząb koła 2 wyprzedzałby ząb koła 1, a to
jest absurdem.
Gdyby c1 > c2, wówczas ząb koła 1 wciskałby się w ząb koła 2, co
jest niemożliwe.

Po wstawieniu zależności a w zależność b otrzymamy

Skąd ostatecznie

A ponieważ trójkąty O

1

CG i O

2

CG są również

podobne więc otrzymujemy wzór na przełożenie
przekładni

2

1

1

2











2

1

2

1

2

1

1

2

z

z

r

r

C

O

C

O

i

t

t













Przekładnie zębate cz. I – nr 15

Przekładnie zębate

Przekładnie zębate

dr inż. Piotr Chwastyk

Warunki współpracy uzębień

Warunki współpracy uzębień

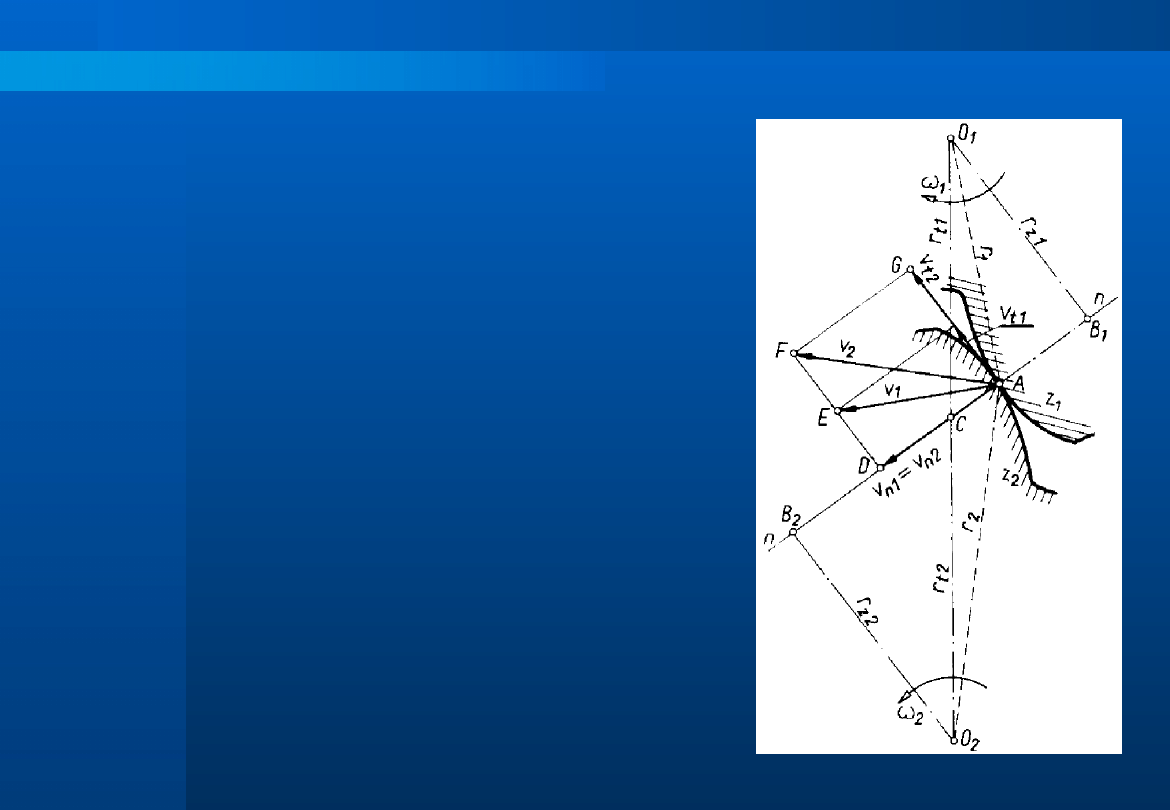
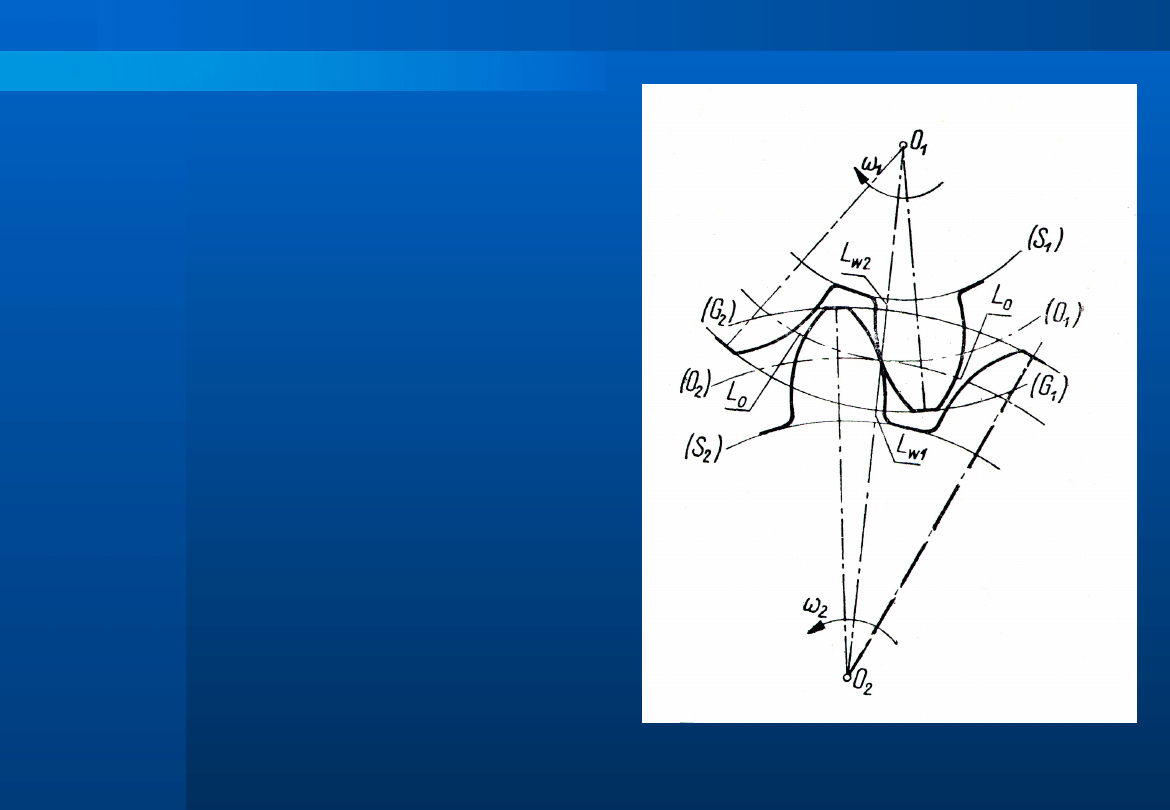
Na rysunku przedstawiono rozkład

prędkości dla współpracujących zębów.
Na podstawie analizy rysunku można
udowodnić, że warunek prawidłowej
pracy

uzębień

zostanie

dokładnie

spełniony tylko wówczas, gdy punkt C
powstały w wyniku przecięcia linii
łączącej środki kół i prostopadłej do
boku zębów wystawionej w punkcie
przyporu, zachowuje w czasie obrotu
zazębionych kół stałe położenie. Punkt
ten nazywa się centralnym punktem
przyporu (środkiem zazębienia).

W pozostałych punktach przyporu –

np. w punkcie A – prędkości v

1

i v

2

nie

są sobie równe, wskutek czego w czasie
współpracy zębów występują poślizgi
(różnice między wartościami v

1

i v

2

podane na rysunku są przesadzone dla
zwiększenia czytelności rysunku).

Przekładnie zębate cz. I – nr 16

Przekładnie zębate

Przekładnie zębate

dr inż. Piotr Chwastyk

Warunki współpracy uzębień

Warunki współpracy uzębień

Przypór

Przypór – następujący w czasie pracy chwilowy styk
zębów.

Punkt przyporu

Punkt przyporu – miejsce zetknięcia się zębów.

Linia przyporu

Linia przyporu – prosta powstała na skutek połączenia
kolejnych punktów przyporu.

Czynna linia przyporu

Czynna linia przyporu – odcinek linii przyporu, na którym
następuje stykanie się zębów.

Prawidłowa praca uzębień kół, jest zapewniona gdy:

• następuje nieprzerwany styk zębów – przypór;
• przed wyzębieniem jednej pary zębów następuje

zazębienie następnej;

• przełożenie dla każdej pary zębów jest stałe, a zatem i

stosunek prędkości kątowej jest stały.

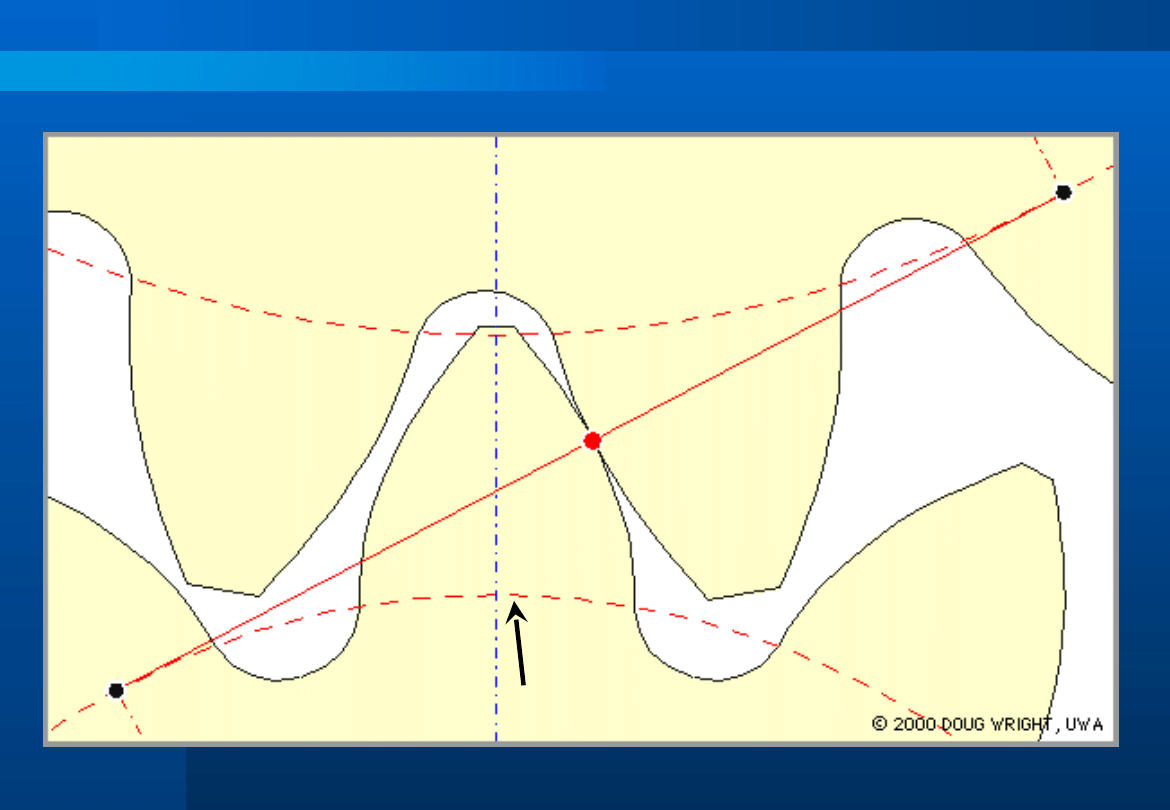
Przekładnie zębate cz. I – nr 17

Przekładnie zębate

Przekładnie zębate

dr inż. Piotr Chwastyk

Warunki współpracy uzębień

Warunki współpracy uzębień

C

C

punkt
przyporu

Przekładnie zębate cz. I – nr 18

Przekładnie zębate

Przekładnie zębate

dr inż. Piotr Chwastyk

Geometria kół zębatych

Geometria kół zębatych

We współpracy uzębień przekładni
występują następujące luzy:
Luz międzyzębny L

o

– boczny,

normalny.

L

o

= 0,04m

Luz wierzchołkowy L

w

L

w

= h

f

– h

a

= 0,25m

Szerokość zęba

s = 0,5



p – L

o

Szerokość wrębu

e = 0,5



p + L

o

Przekładnie zębate cz. I – nr 19

Przekładnie zębate

Przekładnie zębate

dr inż. Piotr Chwastyk

Geometria kół zębatych

Geometria kół zębatych

Zwykle w kołach zębach występują zęby normalne.
Wysokość tych zębów można określić:

h

a

= ym

h

f

= 1,25ym

gdzie: y – współczynnik wysokości zęba
Poza zębami normalnymi stosujemy:
Zęby niskie – współczynnik wysokości zęba y < 1 oraz h <
2,25m.
Zęby wysokie – współczynnik wysokości zęba y > 1 oraz h
> 2,25m.
Odległość osi współpracujących kół:
a = 0,5(d1 + d2) = 0,5m(z1 + z2)

Pozostałe średnice kół prostych o zębach
normalnych:
średnica wierzchołków

d

a

= d + 2h

a

= mz + 2m = m(z + 2)

średnica podstaw

d

f

= d – 2h

f

= mz + 2·1,25m = m(z –

2,5)

Przekładnie zębate cz. I – nr 20

Przekładnie zębate

Przekładnie zębate

dr inż. Piotr Chwastyk

Obliczanie geometryczne przekładni zębatej

Obliczanie geometryczne przekładni zębatej

Obliczanie to sprowadza się do określenia z i m (lub wyznaczenia go z
warunków wytrzymałościowych na zginanie), ustalenia wymiarów kół
oraz odległości pomiędzy ich osiami.
Stosujemy następujące określenia:

• koło zębate czynne;
• koło zębate bierne;
• zębnik – jedno z dwóch kół przekładni pojedynczej, które ma

mniejszą liczbę zębów;

• koło – jedno z dwóch kół przekładni zębatej, które ma większą

liczbę zębów.

W przekładniach złożonych wielorzędowych stosujemy koła zębate o
jednakowym module, ale musimy wtedy spełnić dodatkowe warunki:

a = const.

zatem

z1 + z2 = z3 + z4 = z5 + z6.

Dobranie liczby zębów w zębnikach i kołach poszczególnych par kół
zębatych, muszą odpowiadać żądanym wartościom przełożeń.

Przekładnie zębate cz. I – nr 21

Przekładnie zębate

Przekładnie zębate

dr inż. Piotr Chwastyk

Kształt zarysu boku zęba

Kształt zarysu boku zęba

Zarysy boków zębów mogą być:

- ewolwentowe

- cykloidalne

- specjalne

Najczęstsze

zastosowanie

w

przemyśle

maszynowym znalazły zarysy ewolwentowe z

powodu wielu zalet, a przede wszystkim

niewrażliwości zazębienia na zmianę odległości

osi, prostoty oraz uniwersalności metod obróbki i

pomiaru,

a

wreszcie

łatwości

montażu.

Ewolwenta w dosłownym słowa znaczeniu

oznacza „odwinięta", a w zastosowaniu do kół

zębatych oznacza, „odwinięta koła".

Przekładnie zębate cz. I – nr 22

Przekładnie zębate

Przekładnie zębate

dr inż. Piotr Chwastyk

Zarys ewolwentowy

Zarys ewolwentowy

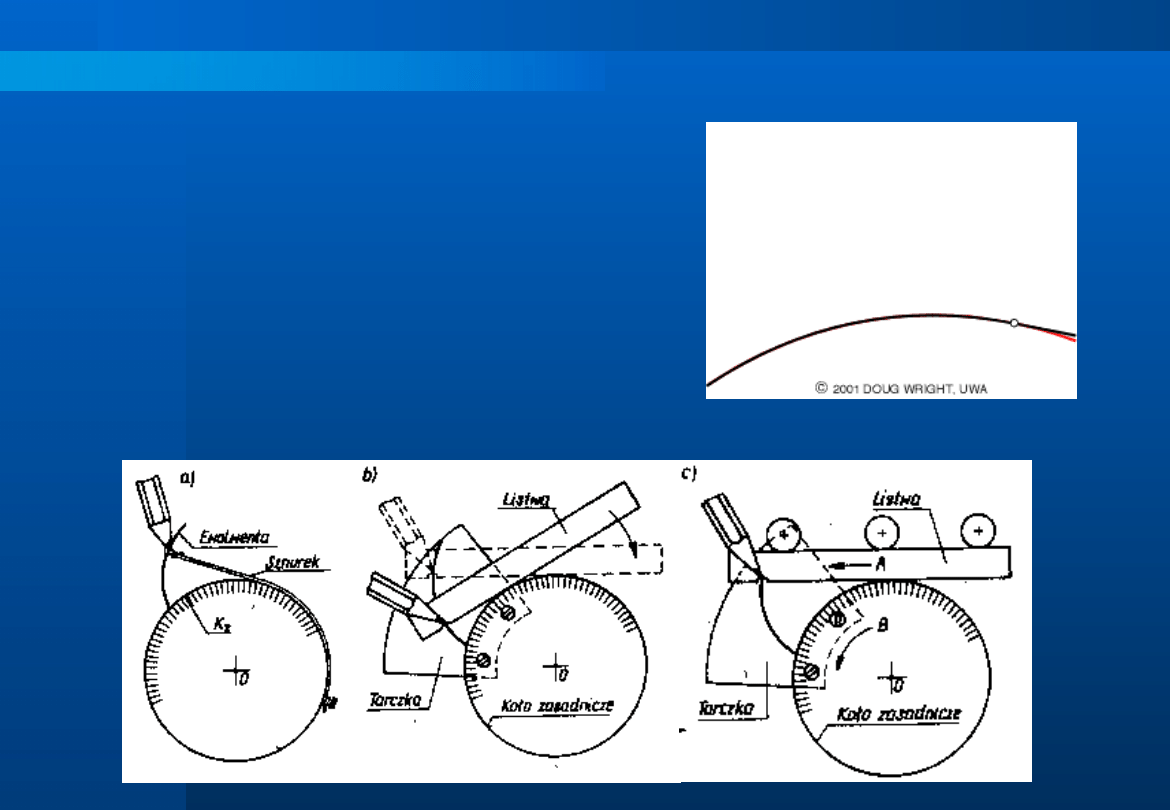
Ewolwenta – powstaje jako tor dowolnego
punktu prostej toczącej się po kole bez
poślizgu (tor punktu nierozciągliwej nici
odwijanej z koła). Sposoby tworzenia
ewolwenty:

a) przez odwijanie sznurka z koła

zasadniczego

b) przez odtaczanie listwy po kole

zasadniczym

c) przez przesuwanie listwy po kole z

jednoczesnym jego obrotem

Przekładnie zębate cz. I – nr 23

Przekładnie zębate

Przekładnie zębate

dr inż. Piotr Chwastyk

Zarys ewolwentowy

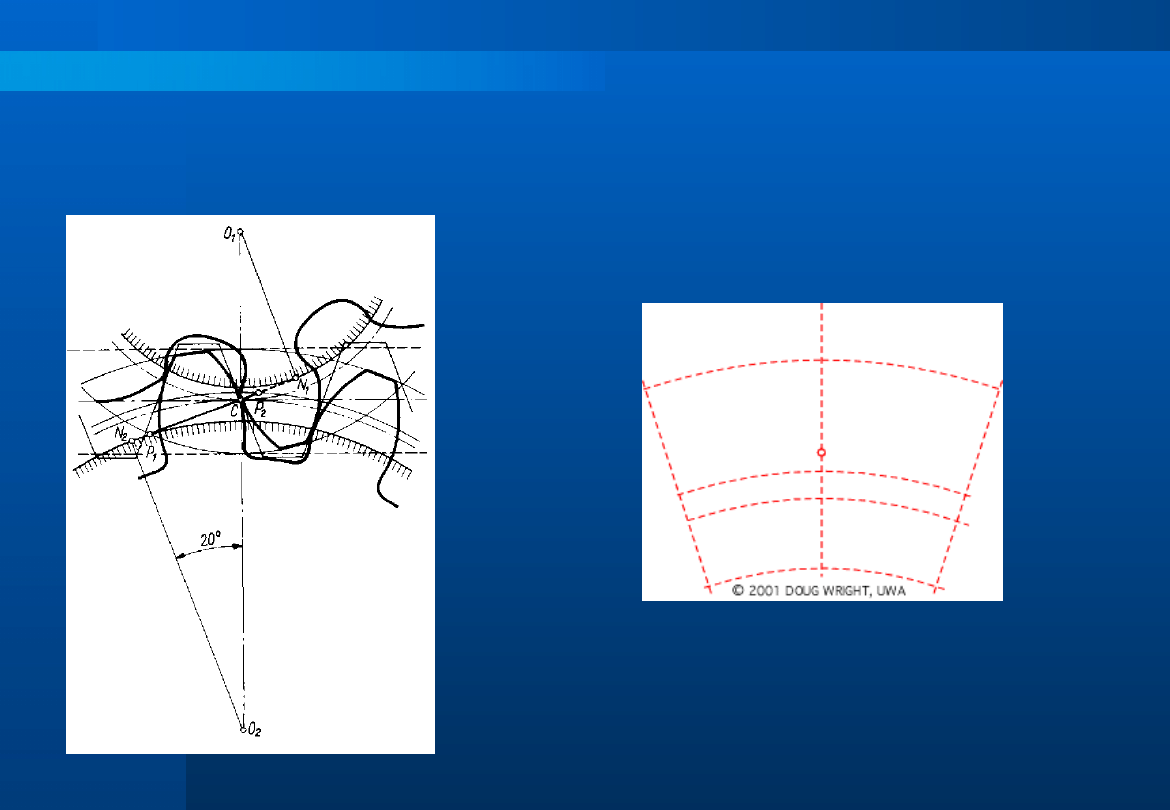
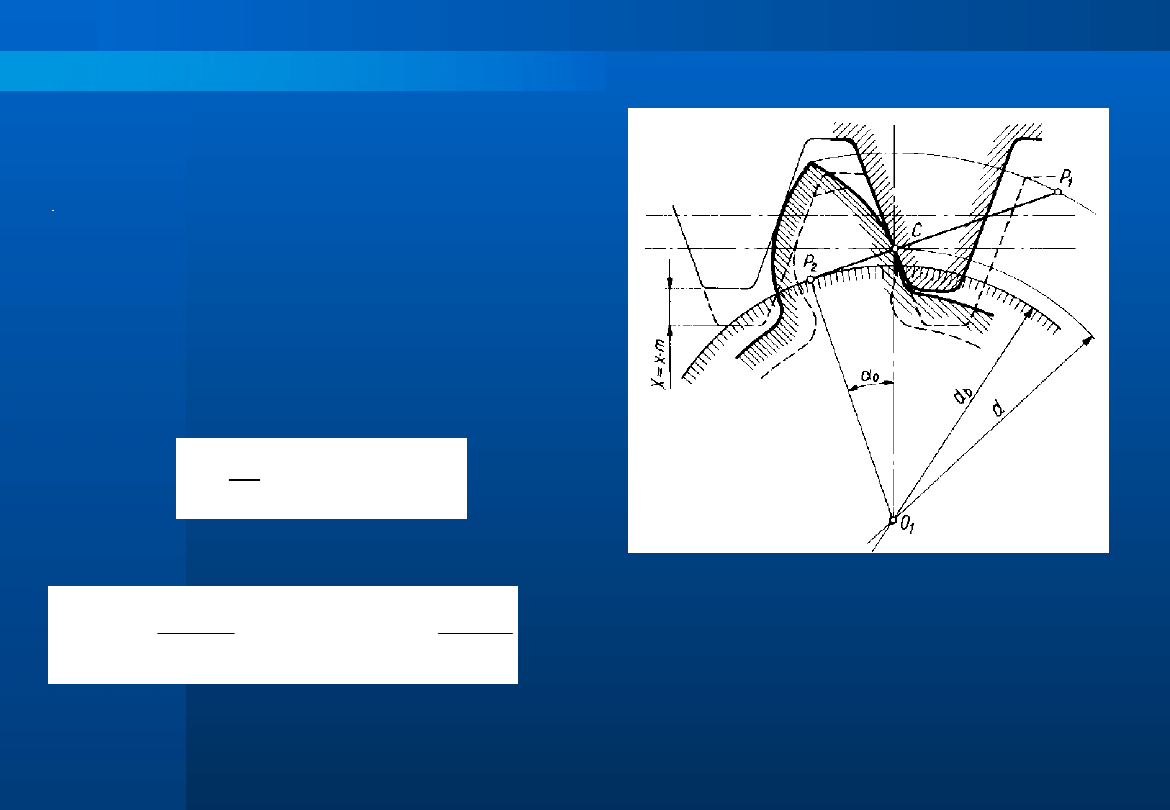
Zarys ewolwentowy

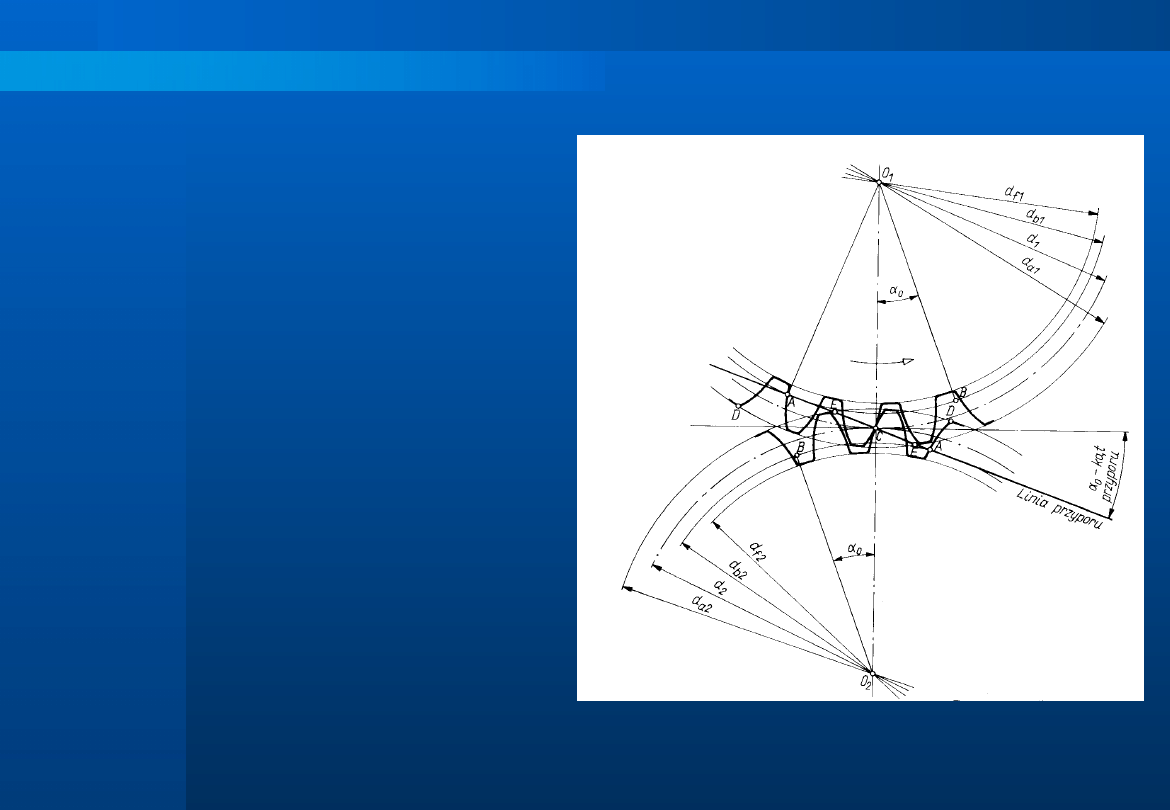
Przy współpracy zębów o

zarysie

ewolwentowym

linia

przyporu jest linią prostą –
podstawowa

cecha

tego

uzębienia.

Kąt,

który

tworzy

linia

przyporu ze styczną do kół
tocznych

(podziałowych),

prowadzoną

przez

punkt

C

nazywamy kątem przyporu



o

.

Przy

budowaniu

zarysu

ewolwentowego,

dla

współpracujących

zębów,

ewolwentę rozwija się z okręgu
zasadniczego, którego średnica
zasadnicza d

b

jest styczna do linii

przyporu.

d

b

= d



cos



o

Długość czynnej linii przyporu

wyznaczają punkty przecięcia linii
przyporu

z

okręgami

wierzchołków kół, czynnego i
biernego.

Przekładnie zębate cz. I – nr 24

Przekładnie zębate

Przekładnie zębate

dr inż. Piotr Chwastyk

Zarys ewolwentowy

Zarys ewolwentowy

Liczbą przyporu lub stopniem pokrycia



nazywamy stosunek długości łuku, do podziałki p na
kole tocznym. Liczbą przyporu łatwiej jest określić jako
stosunek długości czynnej linii przyporu e do podziałki
koła zasadniczego p

b

.



= 1,4 – oznacza to, że przez 40% czasu pracy

przekładni pracują jednocześnie dwie pary zębów, a przez
pozostałe 60% – tylko jedna para zębów.

b

p

e

p

l







Przekładnie zębate cz. I – nr 25

Przekładnie zębate

Przekładnie zębate

dr inż. Piotr Chwastyk

Zarys cykloidalny

Zarys cykloidalny

Cykloida – jest to krzywa, którą zakreśla ustalony punkt okręgu
toczącego się bez poślizgu po prostej. Dla zębów z uzębieniem
cykloidalnym linia przyporu składa się z dwóch łuków kolistych. W
porównaniu z zarysem ewolwentowym występują następujące zalety:

• mniejsze naciski powierzchniowe (p);

• możliwość wykonania kół o małej liczbie zębów (z).

Wady:

• niemożliwość zmiany rozstawu osi (a);

• niemożliwość zastosowania obróbki obwiedniowej.

Przekładnie zębate cz. I – nr 26

Przekładnie zębate

Przekładnie zębate

dr inż. Piotr Chwastyk

Metody obróbki uzębień

Metody obróbki uzębień

1. Obróbka skrawaniem.
2. Odlewanie.
3. Spiekanie z proszków.
4. Odlewanie

pod

ciśnieniem

z

termoplastycznych
tworzyw sztucznych.

5. Wykrawanie z blachy.

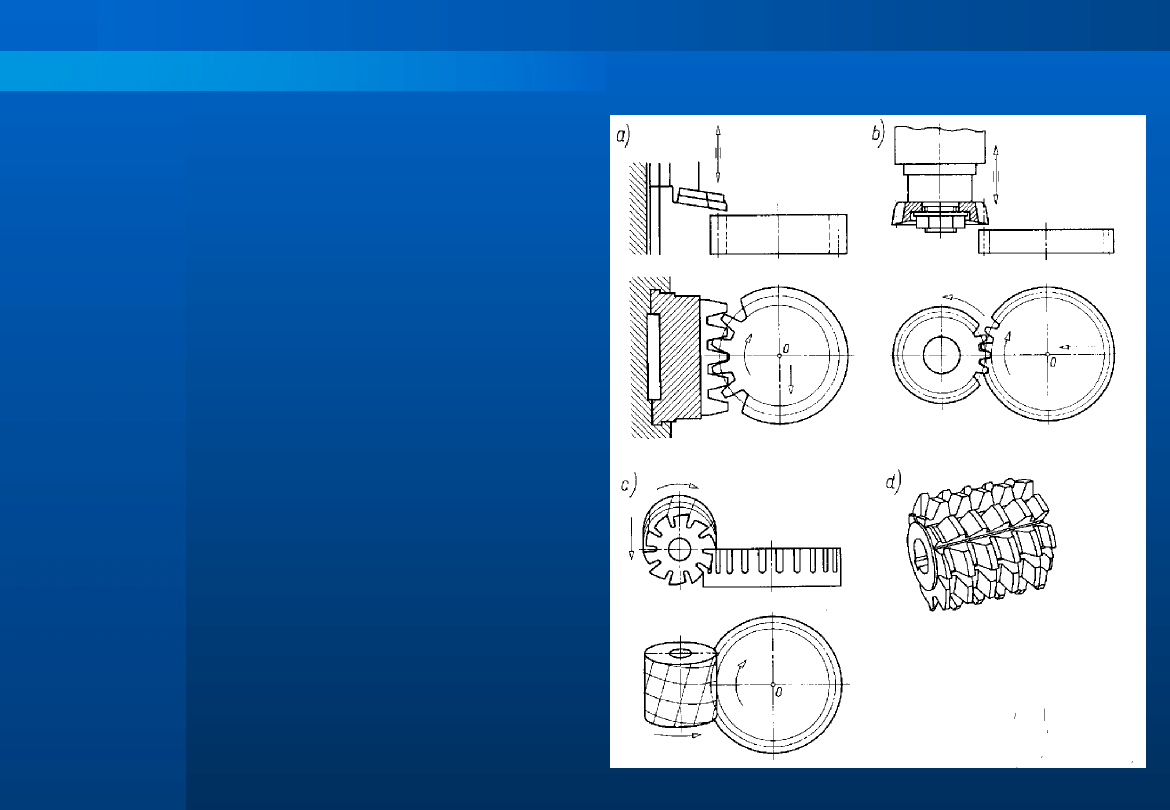
Podstawowe metody nacinania

zębów to:

Metoda kształtowa – nacinanie

zębów

za

pomocą

freza

kształtowego – modułowy frez
krążkowy komplety składające się
z: 8, 15, 26 frezów.

Metoda obwiedniowa – polega

na nacięciu zębów narzędziem w
kształcie zębatki (rys. a), koła
zębatego

(rys.

b)

lub

freza

ślimakowego (rys. c,d).

Przekładnie zębate cz. I – nr 27

Przekładnie zębate

Przekładnie zębate

dr inż. Piotr Chwastyk

Przesunięcie zarysu zęba

Przesunięcie zarysu zęba

Nacinając metodą obwiedniową uzębienie o małej liczbie zębów,
zaobserwujemy podcięcie zębów u podstawy.

Przekładnie zębate cz. I – nr 28

Przekładnie zębate

Przekładnie zębate

dr inż. Piotr Chwastyk

Przesunięcie zarysu zęba

Przesunięcie zarysu zęba

0

2

sin

2





g

z

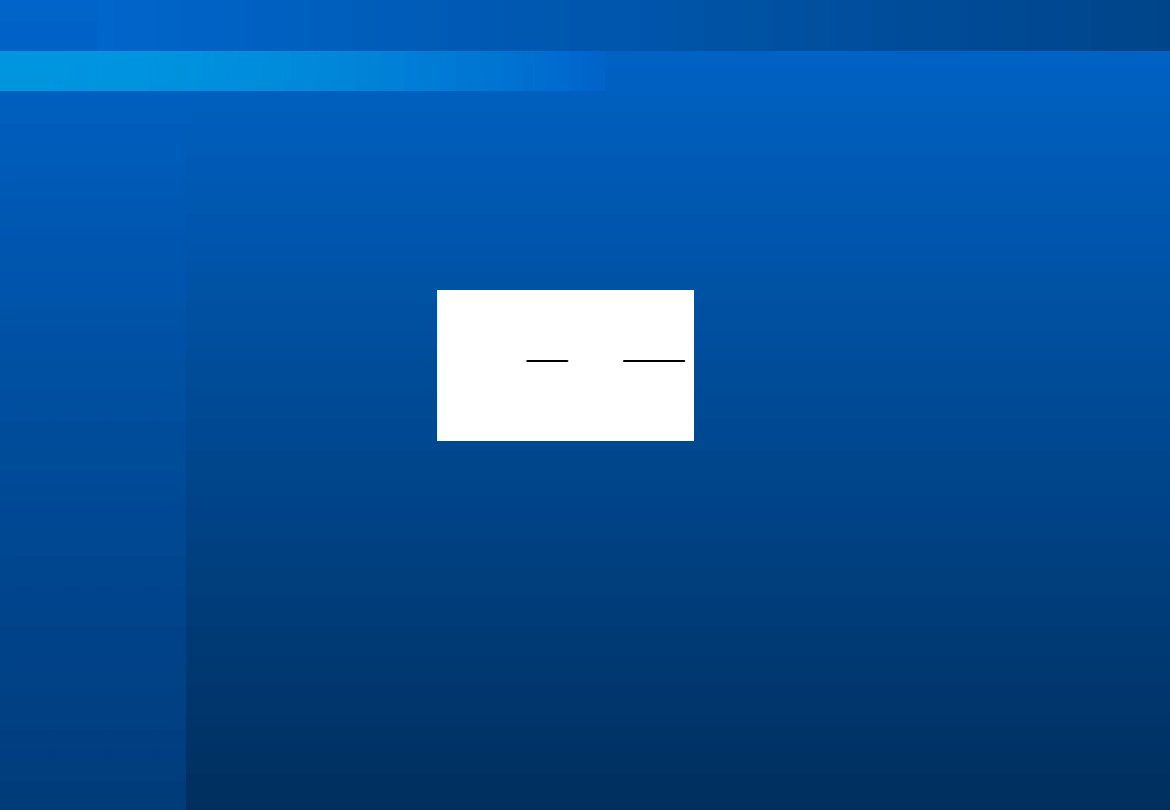
Graniczna liczba zębów

Określono najmniejszą liczbę zębów, przy której nie występuje

podcięcie (powodujące skrócenie odcinka przyporu oraz osłabienie
wytrzymałości zęba u podstawy).

Teoretyczna graniczna liczba zębów z

g

:

Praktyczna graniczna liczba zębów z`

g

:

dla 

o

= 20

o

z

g

= 17 z`

g

= 14

dla 

o

= 15

o

z

g

= 30 z`

g

= 25

g

g

z

z





6

5

'

Przekładnie zębate cz. I – nr 29

Przekładnie zębate

Przekładnie zębate

dr inż. Piotr Chwastyk

Przesunięcie zarysu zęba

Przesunięcie zarysu zęba

m

x

X

m

X

x









Aby uzyskać z < z`

g

i uniknąć

podcinania zębów, wykorzystuje się
niewrażliwość

zarysów

ewolwentowych

na

wzajemne

ustawienie

kół

i

stosuje

się

przesunięcie zarysu zęba, poprzez
odsuwanie

narzędzia

od

koła

nacinanego o wartość X.

Aby

uniezależnić

obliczanie

przesunięcia zarysu od wartości
modułu

m,

wprowadzono

współczynnik przesunięcia zarysu x.

x ustala się z zależności:

g

g

g

g

z

z

z

x

b

z

z

z

x

a

'

'

)

lub

)









Wzór a) stosuje się, gdy nie będzie

dopuszczalne nawet najmniejsze podcięcie, a
wersję b), gdy dopuszczalne będzie minimalne
podcięcie zarysu zęba.

Współczynnik x przybiera wartości w zakresie

-1 < x < 1

Oznacza to, że koła o dużej liczbie zębów mogą mieć ujemne przesunięcie zarysu
(przesunięcie narzędzia w głąb koła) przy czym średnica koła zmniejszy się o 2x.

Przekładnie zębate cz. I – nr 30

Przekładnie zębate

Przekładnie zębate

dr inż. Piotr Chwastyk

Przesunięcie zarysu zęba

Przesunięcie zarysu zęba

Przesunięcie dodatnie – zwiększa się grubość zęba, oraz wystąpi

zaostrzenie głowy zęba.

WNIOSEK – o wielkości X (odsuwania narzędzia) nie zadecyduje
podcięcie zęba, ale jego zaostrzenie.

Z powyższej tablicy odczytujemy:
Dodatnie (x > 0) – przesunięcie zarysu zęba umożliwia nacięcie koła
dla z

min

= 7.

x = (0,4



1) – o minimalnej liczbie zębów zadecyduje zaostrzenie

wierzchołków – nie podcięcie.
Ujemne (x < 0) – przesunięcie zarysu w głąb koła. Wartości z

min

rosną.

Np. w kole o z = 23 można zastosować przesunięcie ujemne x = - 0,5.

Przekładnie zębate cz. I – nr 31

Przekładnie zębate

Przekładnie zębate

dr inż. Piotr Chwastyk

Przesunięcie zarysu zęba

Przesunięcie zarysu zęba

Korekta uzębienia przy h = const. spowoduje zmianę

wymiarów:

d

a

= m(z + 2)



2X = m(z + 2



2x)

d

f

= m(z – 2,5)



2X = m(z – 2,5



2 x)

h

a

= m



X = m(1



x)

h

f

= 1,25m



X = m(1,25



x)

Podobnie jak d

a

i d

f

zmienia się średnica koła

tocznego d

w

(w kołach bez korekty uzębienia pokrywa się

ona z d).

Przekładnie zębate cz. I – nr 33

Przekładnie zębate

Przekładnie zębate

dr inż. Piotr Chwastyk

Przekładnie z przesunięciem zarysu

Przekładnie z przesunięciem zarysu

Zastosowanie jednego koła z korektą uzębienia zmusza do

wprowadzenia zmian w całej przekładni. Rozróżniamy dwa
podstawowe przypadki zastosowania kół z przesunięciem zarysu:

Bez zmiany odległości osi – oznaczenie X – X.
Ze zmianą odległości osi – oznaczenie X + X, dawniej P.
Dla X – X w kole o małej liczbie zębów z zastosujemy przesunięcie

dodatnie, a w kole z

2

przesunięcie ujemne.

X

1

= - X

2

x

1

= - x

2

Przy ujemnym przesunięciu zarysu możemy doprowadzić do

podcięcia. Aby to nie nastąpiło sprawdza się:

dla praktycznej granicznej liczby zębów:

a) z

1

+ z

2



2z`

g

dla teoretycznej granicznej liczby zębów:

b) z

1

+ z

2

 2z

g

Spełnienie w/w warunków to zastosowanie przesunięcie X –

X.

Przesunięcie X + X powoduje zmianę a – stosuje się je gdy

warunki a) i b) nie są spełnione lub gdy świadomie chcę zmienić a.

Szczególny przypadek X + 0.