PROGNOZOWANIE I SYMULACJE

> metody adaptacyjne

Stanisław Stańko

Szkoła Główna Gospodarstwa Wiejskiego

Wydział Ekonomiczno - Rolniczy

Katedra Ekonomiki Rolnictwa

i Międzynarodowych Stosunków Gospodarczych

Warszawa, 2007 r.

0

10

20

30

40

50

60

70

80

90

100

st

y-

9

0

lip

-9

0

st

y-

9

1

lip

-9

1

st

y-

9

2

lip

-9

2

st

y-

9

3

lip

-9

3

st

y-

9

4

lip

-9

4

st

y-

9

5

lip

-9

5

st

y-

9

6

lip

-9

6

st

y-

9

7

lip

-9

7

st

y-

9

8

lip

-9

8

st

y-

9

9

lip

-9

9

st

y-

0

0

lip

-0

0

0

1

-s

ty

0

1

-l

ip

0

2

-s

ty

0

2

-l

ip

0

3

-s

ty

0

3

-l

ip

0

4

-s

ty

0

4

-l

ip

zł

/h

l

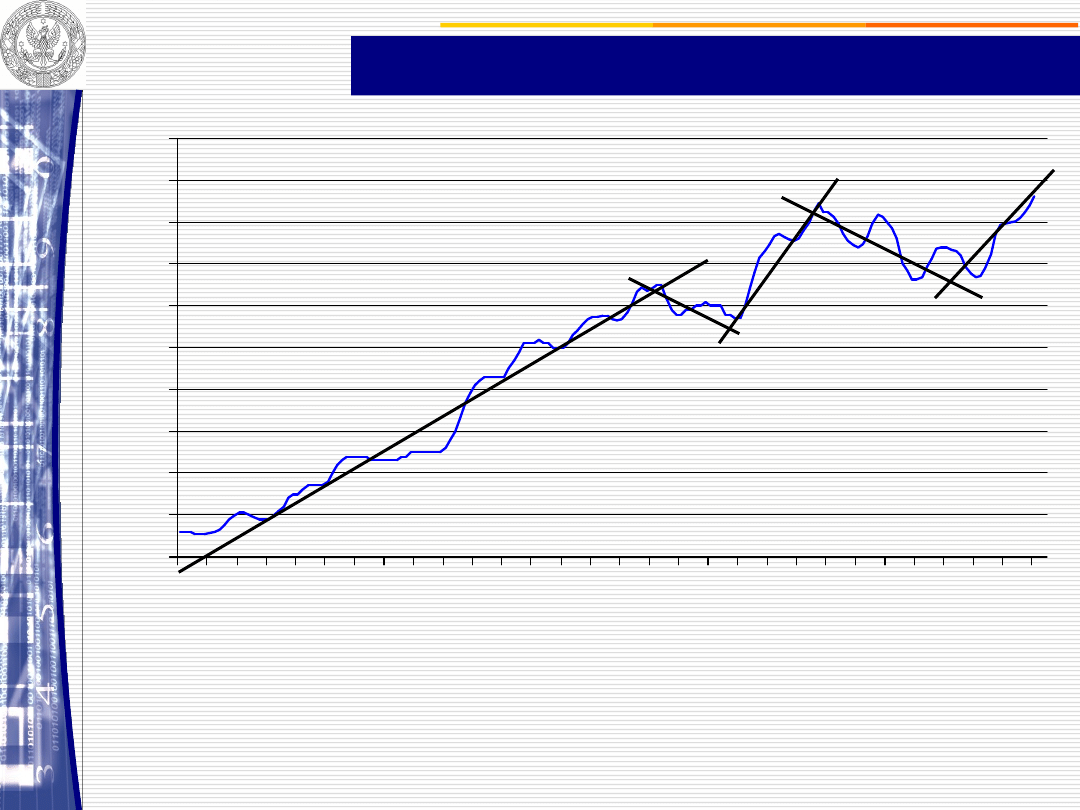
CENY SKUPU MLEKA - skorygowane sezonowo

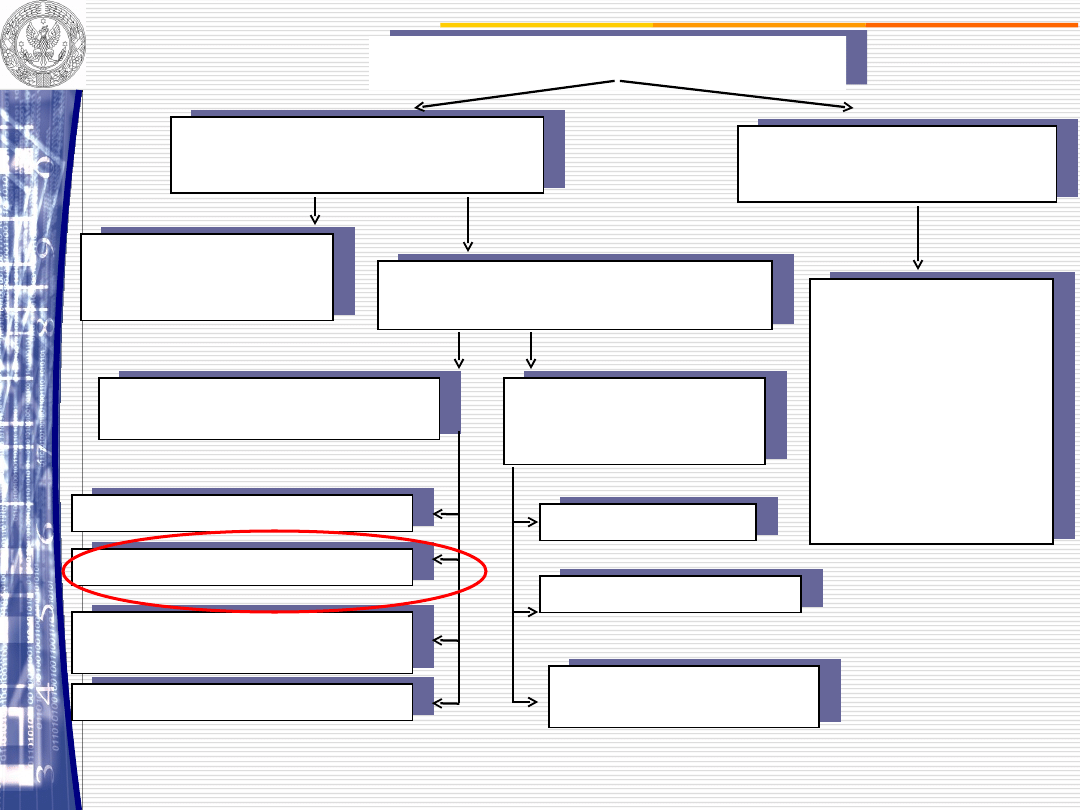
METODY PROGNOSTYCZNE

METODY PROGNOSTYCZNE

Metody matematyczno-
statystyczne

Metody matematyczno-
statystyczne

Metody
niematematyczne

Metody
niematematyczne

Metody oparte
na modelach
deterministycznych

Metody oparte
na modelach
deterministycznych

Metody oparte na modelach
ekonometrycznych

Metody oparte na modelach
ekonometrycznych

Jednorównaniowe metody
ekonometryczne

Jednorównaniowe metody
ekonometryczne

Wielorównaniowe
metody
ekonometryczne

Wielorównaniowe
metody
ekonometryczne

Klasyczne modele trendu

Klasyczne modele trendu

Adaptacyjne modele trendu

Adaptacyjne modele trendu

Modele przyczynowo-
skutkowe

Modele przyczynowo-
skutkowe

Modele autoregresyjne

Modele autoregresyjne

Modele proste

Modele proste

Modele rekurencyjne

Modele rekurencyjne

Modele o równaniach
współzależnych

Modele o równaniach
współzależnych

- ankietowe
- intuicyjne
- ekspertyz
- kol. przybliżeń
- analogowe
- modelowe
- refleksji
- inne

- ankietowe
- intuicyjne
- ekspertyz
- kol. przybliżeń
- analogowe
- modelowe
- refleksji
- inne

MODELE

PRZYCZYNOWO-

SKUTKOWE

PROGNOZOWANIE

NA PODSTAWIE

SZEREGÓW

CZASOWYCH

METODY

HEURYSTYCZNE

METODY

ANALOGOWE

METODA

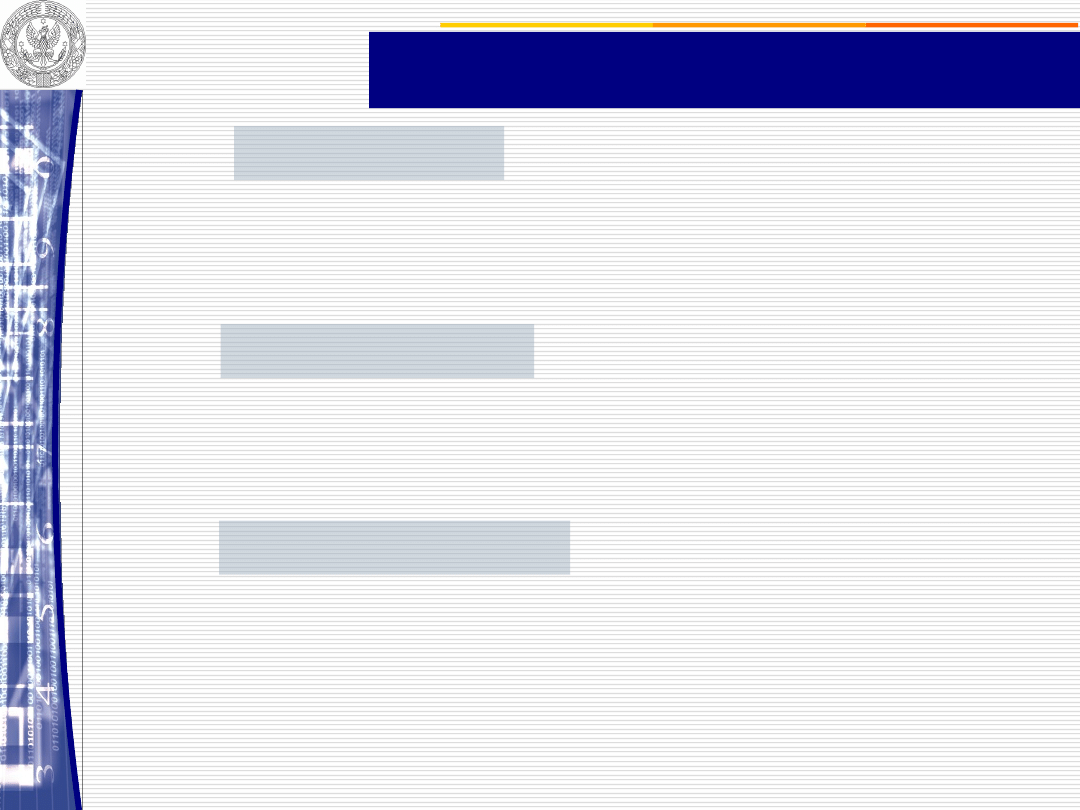
METODY PROGNOZOWANIA NA PODSTAWIE

SZEREGÓW CZASOWYCH

Modele ze

stałym poziomem

zmiennej

prognozowanej:

»

Metoda naiwna;

»

Metoda średniej ruchomej prostej i ważonej;

»

Prosty model wygładzania wykładniczego.

Modele z

tendencją rozwojową

zmiennej

prognozowanej:

»

Modele analityczne;

»

Model liniowy Holta;

»

Model trendu pełzającego z wagami harmonicznymi.

Modele z

wahaniami okresowymi

zmiennej

prognozowanej:

»

Metoda wskaźników;

»

Model Wintersa;

»

Metoda trendów jednoimiennych okresów;.

»

Analiza harmoniczna;

»

Model ARMA i ARIMA

METODY ADAPTACYJNE

METODY ADAPTACYJNE

Modele ze

stałym poziomem

zmiennej

prognozowanej:

»

Metoda naiwna;

»

Metoda średniej ruchomej prostej i ważonej;

»

Prosty model wygładzania wykładniczego.

Modele z

tendencją rozwojową

zmiennej

prognozowanej:

»

Modl Browna II i III rz;

»

Model liniowy Holta;

»

Model trendu pełzającego z wagami harmonicznymi.

Modele z

wahaniami okresowymi

zmiennej

prognozowanej:

»

Model Wintersa;

Podstawowe wyróżniki:
•

brak postulatu stałości postaci analitycznej

funkcji trendu;

•

uwzględniają zmiany kierunku trendu;

•

prognozy średnio i krótkookresowe;

•

zmienność szeregu determinowana przez I,

TI, lub TSI;

•

błędy prognoz wygasłych -korekta modelu;

•

prognoza ilościowa o charakterze

ekastrapolacyjnym;

•

wg zasady status quo, postawa pasywna;

•

prognozowanie oraz wygładzanie szeregów

czasowych;

•

brak możliwości obliczenia mierników

błędów ex ante.

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

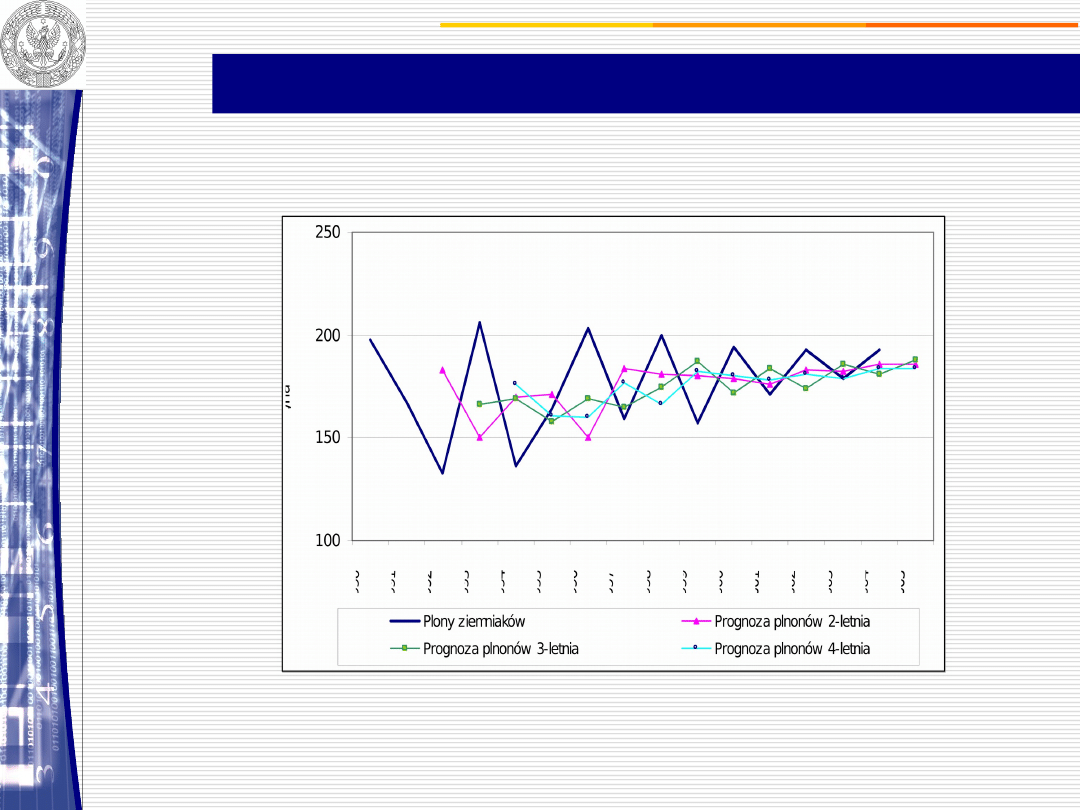
Prognozy plonów ziemniaków SR= różna

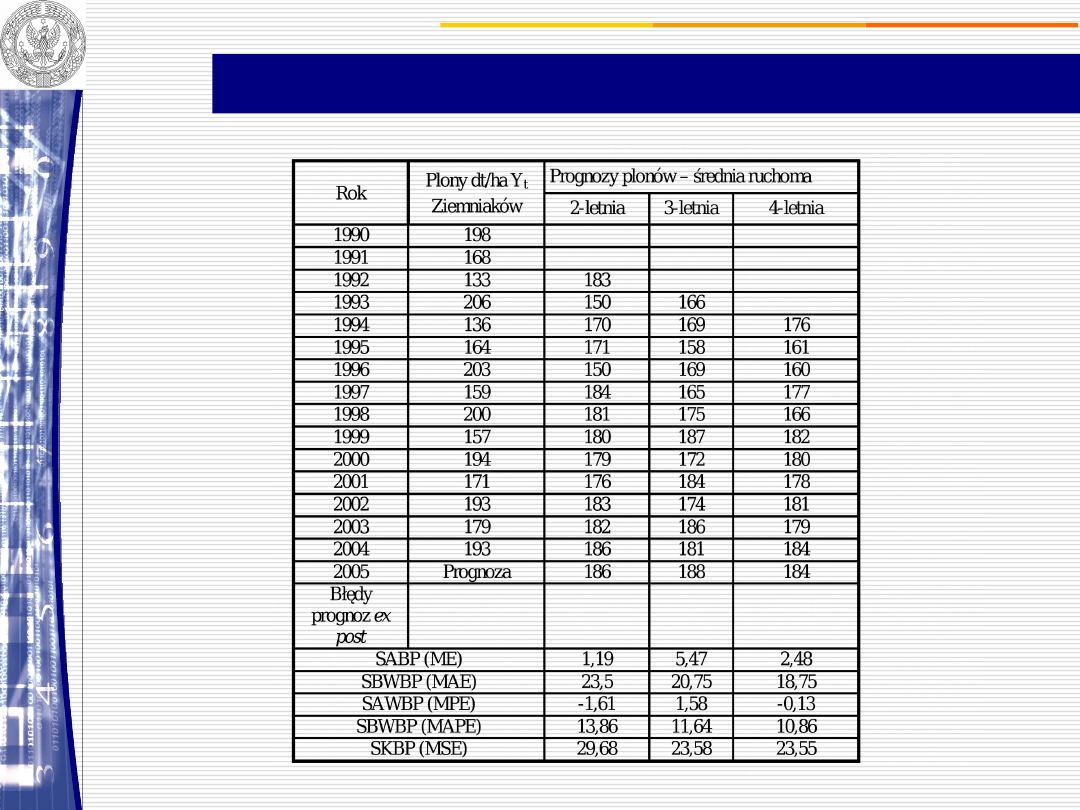
Prognozy plonów ziemniaków

gdzie:
- prognoza dla t+p okresów
- wartość zmiennej prognozowanej w okresie
l - liczba obserwacji (stała wygładzania)
p - odległość okresu prognozowanego od t (p 1)

l

Y

Y

Y

Y

l

t

t

t

p

t

1

1

...



















t

Y

p

t

Y





Średnia ruchoma

algorytm prognozowania:

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

Prognoza

- średnia z określonej liczby okresów

Średnia ruchoma

podstawowe wyróżniki:

•

prognozy krótkookresowe (max rozsądny

horyzont = 1);

•

nie uwzględnia zmian sezonowych,

cyklicznych oraz dynamiki wynikającej z

występowania tendencji;

•

zmienność szeregu determinowana jest

przez wahania przypadkowe;

•

względnie stały poziom zjawiska;

•

prognoza ilościowa o charakterze

ekastrapolacyjnym;

•

wg zasady status quo, postawa pasywna;

•

prognozowanie oraz wygładzanie szeregów

czasowych;

•

brak warzenia informacji.

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

Średnia ruchoma,

problem do rozwiązania:

•

wybór szerokości okna wygładzania l ;

•

kryterium wyboru szerokości okna

wygładzania;

»

minimalizacja błędu prognoz ex post;

»

ekspercka ocena.

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

Kryterium wyboru szerokości okna
wygładzania;

»

minimalizacja błędu prognoz ex post;

¤

średni absolutny błąd prognozy,

¤

średni kwadrat błędu,

¤

odchylenie standardowe błędu prognozy

¤

średni absolutny błąd procentowy

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

Średnia ruchoma,

uwaga:

•

wysoka wartość stałej wygładzania:

»

silny efekt wygładzania;

»

prognoza determinowana starszą informacją;

»

zatarcie krótkookresowych zmian poziomu

zjawiska;

»

brak reakcji na zmiany poziomu zmiennej

prognozowanej;

»

intensywna eliminacja wpływu wahań

przypadkowych;

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

gdzie:
- prognoza dla t+p okresów
- wartość zmiennej prognozowanej w okresie
l - liczba obserwacji (stała wygładzania)
p - odległość okresu prognozowanego od t (p 1)
w

i

- wagi dla obserwacji t - i

t

Y

p

t

Y





l

Y

w

Y

w

Y

w

Y

l

t

ik

t

i

t

i

p

t

1

1

2

1

...





































 1

0

1

,

1

k

i

p

w

Średnia ruchoma

ważona

algorytm prognozowania:

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

gdzie:
Y

t

, Y

t-1

- poziom zmiennej prognozowanej,

n - długość średniej ruchomej.

Ważenie potęgowe

:

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

1

ˆ



t

Y

=

1

...

)

2

(

)

1

(

...

)

2

(

)

1

(

2

2

2

1

2

2

2

1

2







































n

n

n

Y

n

Y

n

Y

n

Y

n

t

t

t

t

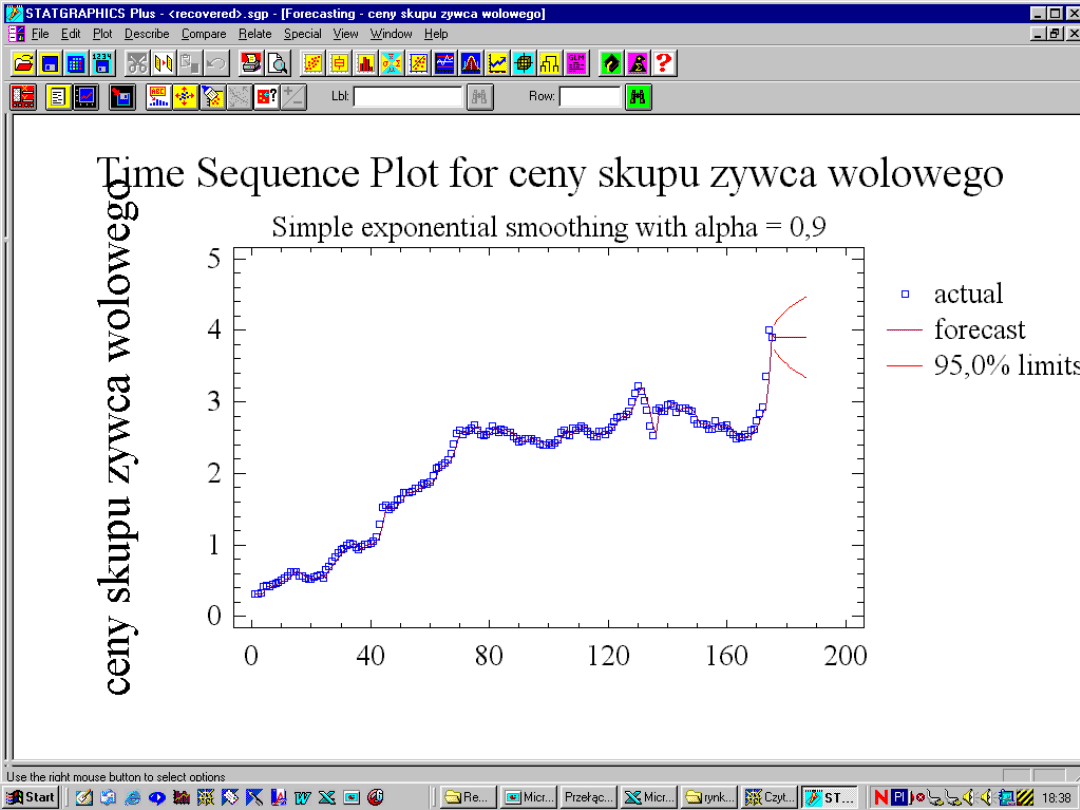
Wyrównywanie wykładnicze Browna rzędu
I

:

Budowa prognozy według wzoru:

gdzie:
- prognoza dla t+1
- poziom zmienne prognozowanej w okresie t
- prognoza dla okresu t sporządzona w t



- stała wyrównywania 0

   1

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA





t

t

t

Y

Y

Y

ˆ

1

ˆ

1

















1

ˆ



t

Y

t

Y

t

Yˆ

Wyrównywanie wykładnicze Browna rzędu
I

:

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA





t

t

t

Y

Y

Y

ˆ

1

ˆ

1

















t

t

t

t

Y

Y

Y

Y

ˆ

ˆ

ˆ

1



















t

t

t

t

Y

Y

Y

Y

ˆ

ˆ

ˆ

1











t

t

Y

e

Y

ˆ

ˆ

1









nowe oceny poziomu zjawiska otrzymujemy, dodając do poprzednich
szacunków część błędu, w kierunku którym poprawia on nowe szacunki

Problem do rozwiązania

:

•

wybór stałej wygładzania ;

•

wybór wartości początkowych

•

kryterium wyboru stałej wygładzania ;

»

minimalizacja błędu prognoz ex post;

»

ekspercka ocena.

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

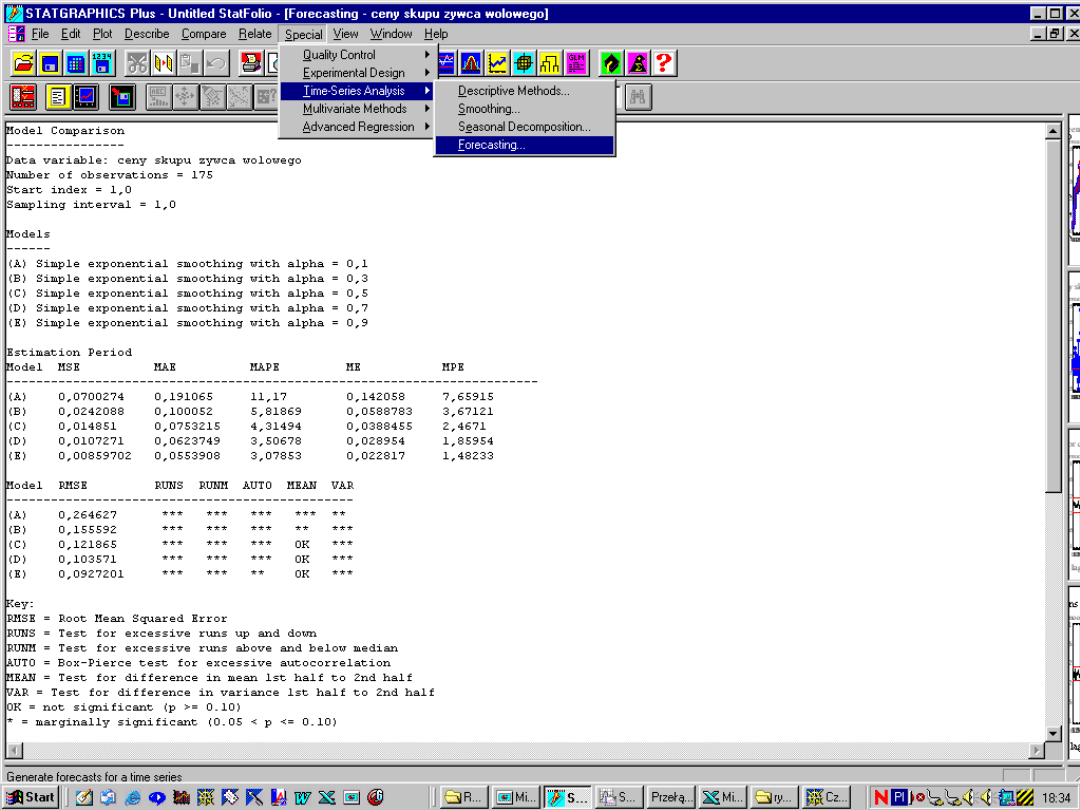
Problem do rozwiązania

:

•

wybór wartości początkowych

»

za wartość początkową bierzemy

średnią z kilku pierwszych okresów

»

metodą prognozowania "wstecz”

»

estymacja metodą najmniejszych

kwadratów

»

przyjęcie, że =Y

1

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

Stała wygładzania ,

determinuje

:

•

siłę wpływu wcześniejszych informacji na

budowane prognozy (nadaje wagi);

•

wygładzenie szeregu;

•

korektę o błędy prognoz wygasłych;

•

wysoka wartość stałej wygładzania  :

»

słaby efekt wygładzania;

»

prognoza determinowana najnowszą

informacją;

»

uwypuklenie krótkookresowych zmian

poziomu zjawiska;

»

silna reakcja na zmiany poziomu zmiennej

prognozowanej;

»

słaba eliminacja wpływu wahań

przypadkowych;

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

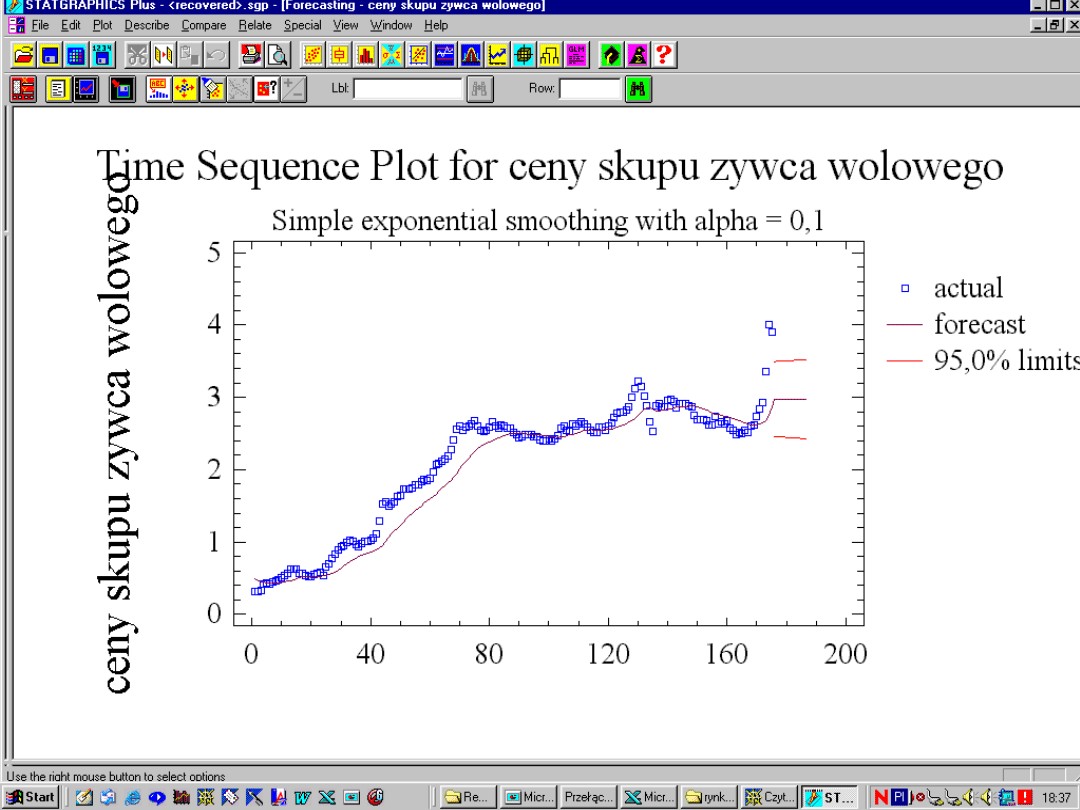
Wyrównywanie wykładnicze Browna rzędu
II

:

gdzie:

- wygładzona wartość zmiennej prognozowanej metodą

wyrównywania wykładniczego rzędu drugiego w okresie t

- wygładzona wartość zmiennej prognozowanej metodą

wyrównywania wykładniczego rzędu drugiego w okresie t-1

- wygładzona wartość zmiennej prognozowanej metodą

wyrównywania wykładniczego rzędu pierwszego w okresie t

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA









1

1

1

1

ˆ

1

ˆ

ˆ

ˆ

1

ˆ

































t

t

t

t

t

t

Y

Y

Y

Y

Y

Y









t

Y



ˆ

1

ˆ





t

Y

t

Yˆ

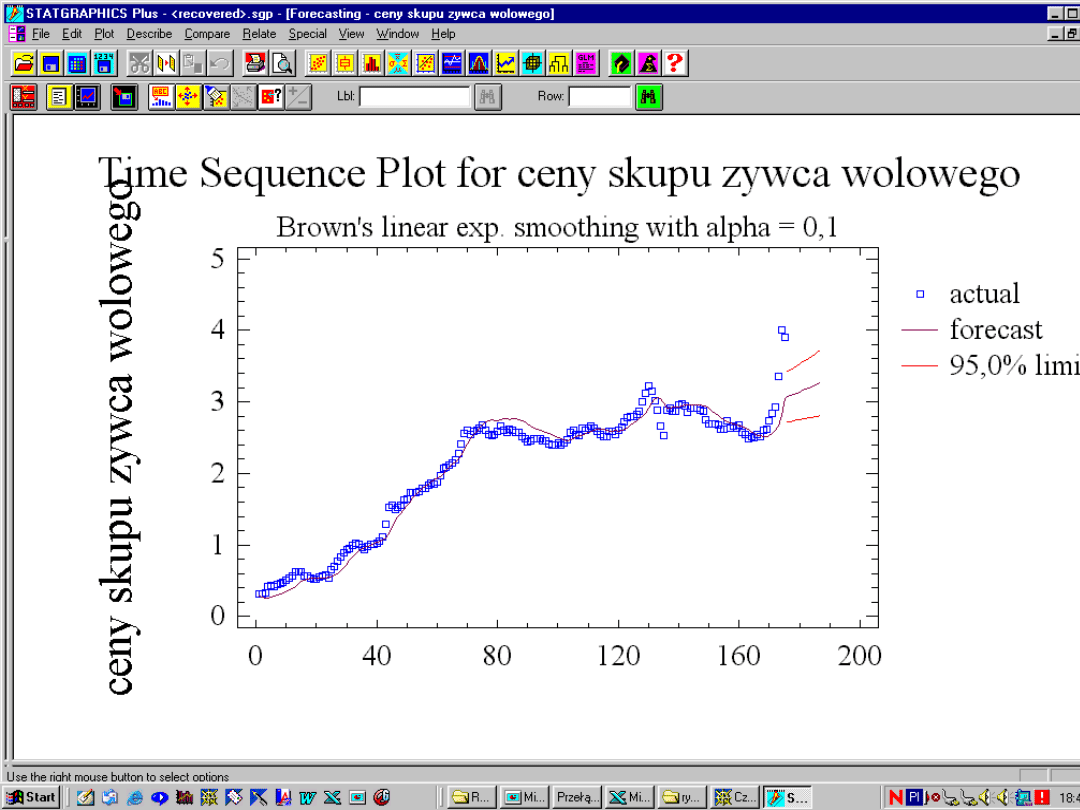
Wyrównywanie wykładnicze Browna rzędu
II

:

Budowa prognozy w okresie t dla p okresów

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA









1

1

1

1

ˆ

1

ˆ

ˆ

ˆ

1

ˆ

































t

t

t

t

t

t

Y

Y

Y

Y

Y

Y









 

t

t

t

Y

Y

t

T









ˆ

ˆ

2

ˆ

 





t

t

Y

Y

t











ˆ

ˆ

1

ˆ

1







 

 

t

p

t

T

Y

t

p

t

1

ˆ

ˆ

ˆ











- ocena poziomu trendu w okresie t

- ocena zmian trendu w okresie t

nowe oceny poziomu trendu i jego zmian otrzymujemy, dodając do poprzednich
szacunków część błędu, w kierunku którym poprawia on nowe szacunki

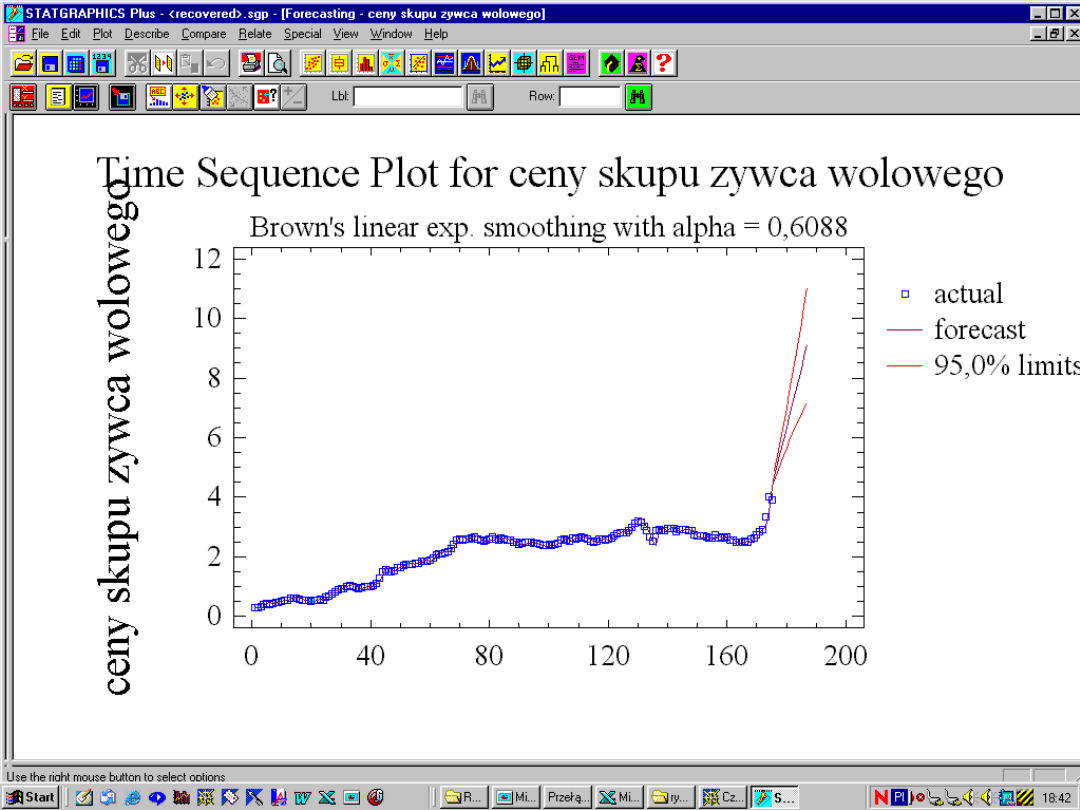
Wyrównywanie wykładnicze Browna rzędu
III

:

gdzie:
- wygładzona wartość zmiennej prognozowanej metodą
wyrównywania wykładniczego rzędu trzeciego w okresie t
- wygładzona wartość zmiennej prognozowanej metodą
wyrównywania wykładniczego rzędu trzeciego w okresie t-1

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA













1

1

1

1

1

1

ˆ

1

ˆ

ˆ

ˆ

1

ˆ

ˆ

ˆ

1

ˆ

























































t

t

t

t

t

t

t

t

t

Y

Y

Y

Y

Y

Y

Y

Y

Y













t

Y





ˆ

1

ˆ







t

Y

Wyrównywanie wykładnicze Browna rzędu

III

:

Budowa prognozy:

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

 

 





















 









t

t

t

t

t

t

t

t

t

Y

Y

Y

t

Y

Y

Y

t

Y

Y

Y

t





















































ˆ

ˆ

2

ˆ

2

1

ˆ

ˆ

3

4

ˆ

4

5

2

ˆ

5

6

1

2

ˆ

ˆ

ˆ

3

ˆ

3

ˆ

2

2

2

2

1

0





















 

 

 

t

p

t

p

t

Y

p

t

2

2

1

0

ˆ

ˆ

ˆ

ˆ



















Wyrównywanie wykładnicze Holta

:

gdzie:

- ocena zmian trendu w okresie t,

- ocena zmian trendu w okresie t-1,

- ocena poziomu trendu w okresie t-1



- stała wygładzania dla zmian trendu (0,1)



- stała wygładzania dla poziomu trendu (0,1)

Budowa prognozy:

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

  

  

  

  

 

 





1

ˆ

ˆ

1

ˆ

1

ˆ

1

ˆ

1

ˆ

1

1





























t

T

t

T

t

t

Y

t

Y

t

T

t

t

t

t

t













 

t

1

ˆ







1

ˆ

1



t







1

ˆ

1





t

T

t

 

 

t

p

t

T

Y

t

p

t

1

ˆ

ˆ

ˆ











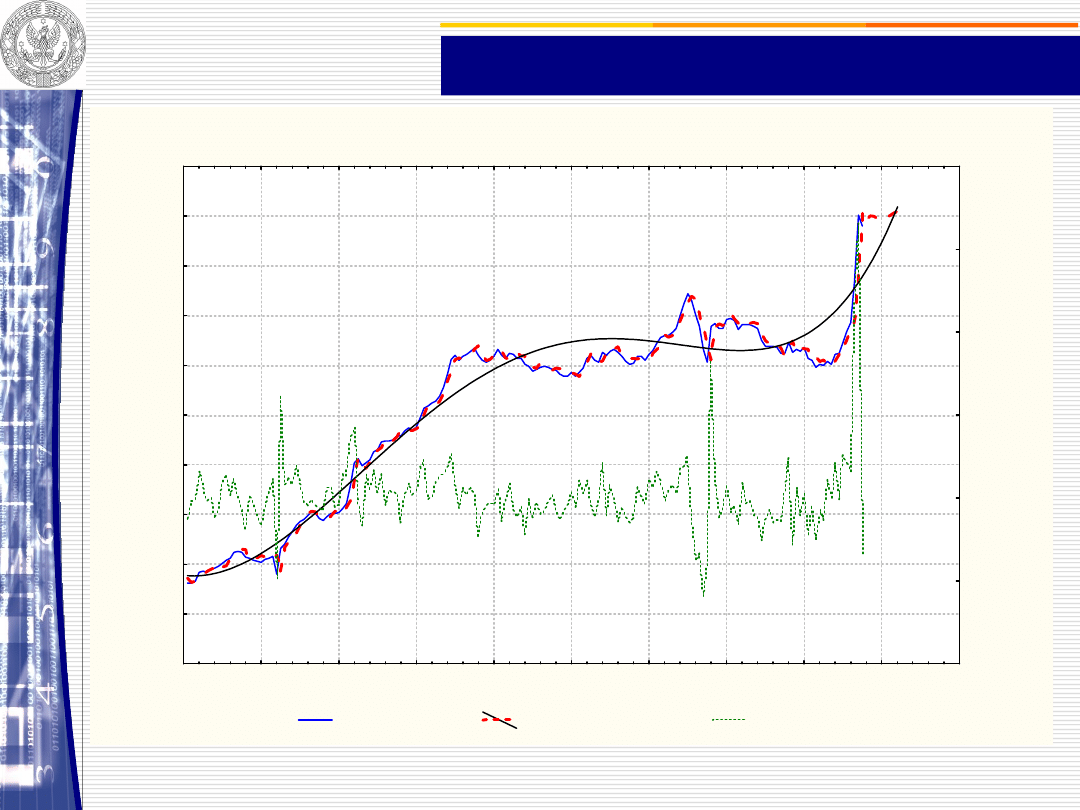
Model Holta. add.sezon.; Alfa=1,00 Delta=,116

Cena skupu(L)

Wyrówn. Szereg (L)

Reszty (R)

C

e

n

a

s

ku

p

u

R

e

sz

ty

-0,4

-0,2

0,0

0,2

0,4

0,6

0,8

-0,5

0,0

0,5

1,0

1,5

2,0

2,5

3,0

3,5

4,0

4,5

0

20

40

60

80

100

120

140

160

180

200

CENY SKUPU ŻYWCA WOŁOWEGO



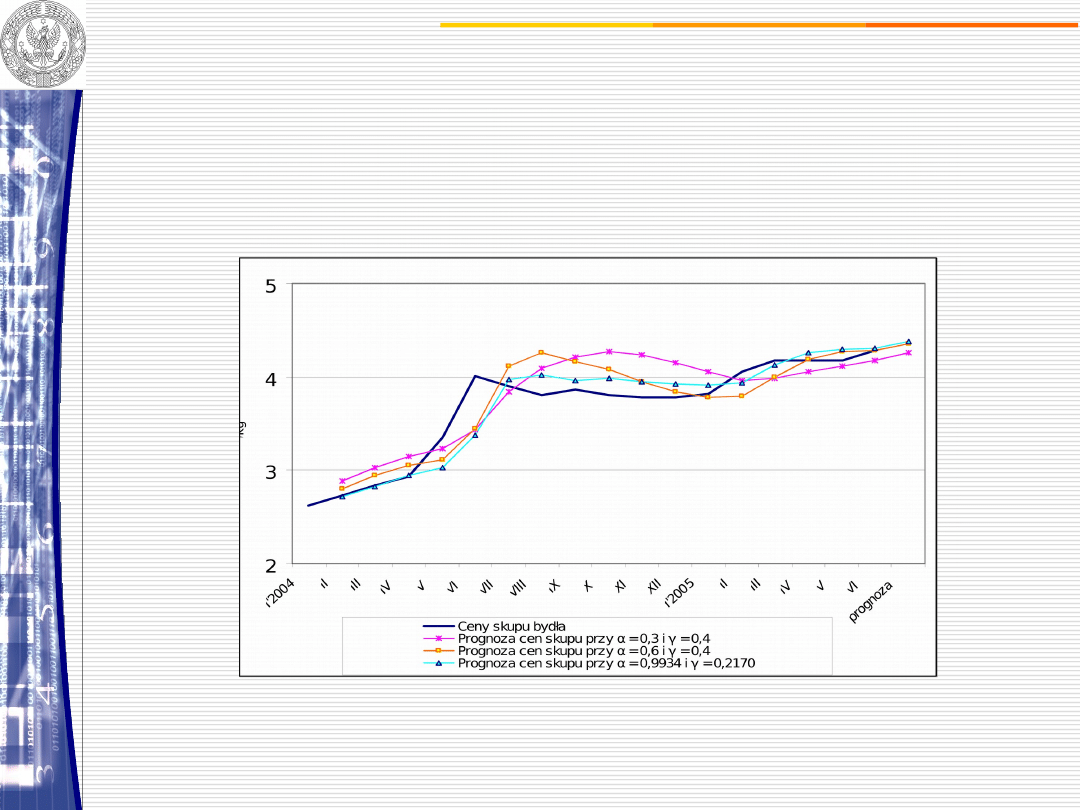
Rysunek 4.5 Empiryczne i prognozowane ceny bydła
sporządzone metodą wyrównywania wykładniczego Holta
przy różnych  i 

Wyrównywanie wykładnicze Wintersa

:

gdzie:

- ocena zmian trendu w okresie t, bez sezonowości

- ocena zmian trendu w okresie t-1, bez sezonowości

- ocena poziomu trendu w okresie t-1, bez

sezonowości

- wygładzone wielkości dla wahań sezonowych.

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

 

t

1

ˆ







1

ˆ

1



t







1

ˆ

1





t

T

t

 

 







  

1

ˆ

1

1

ˆ

ˆ

















t

T

t

S

Y

t

T

t

t





 

 











 



1

ˆ

1

1

ˆ

ˆ

ˆ

1

















t

t

T

t

T

t

t

t









 

 







 



1

ˆ

1

ˆ

ˆ















t

S

t

T

Y

t

S

i

t

t





t

Sˆ

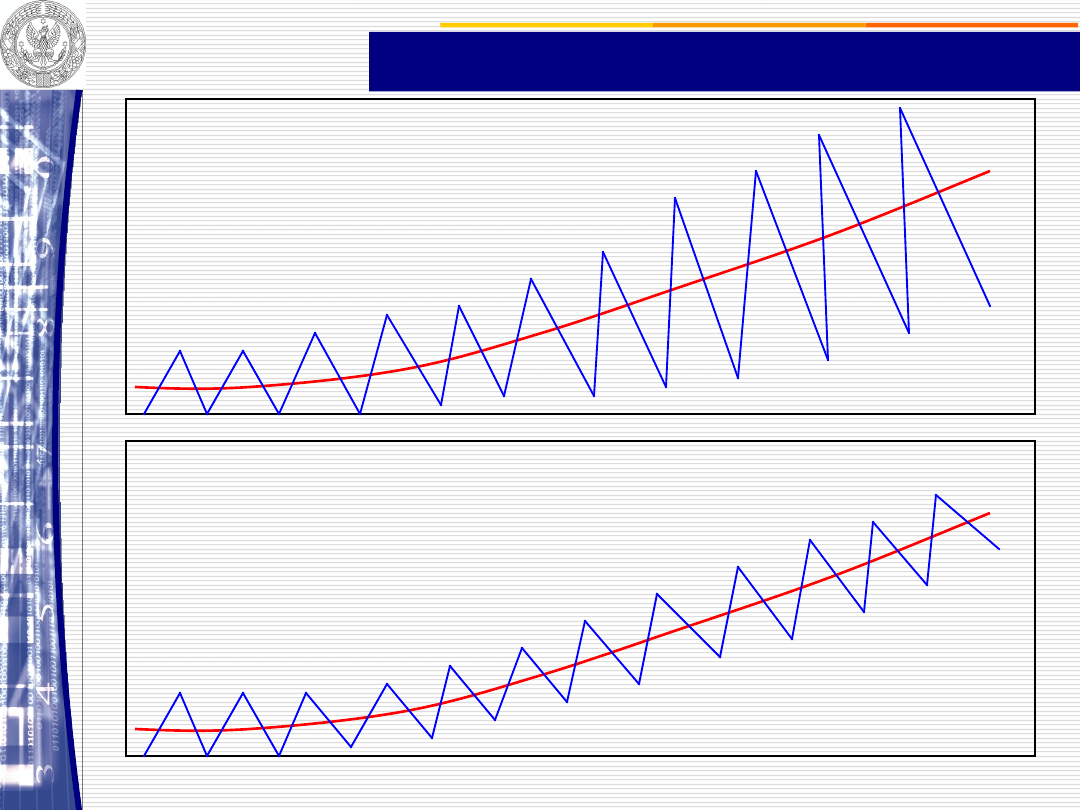
SEZONOWOŚĆ (addytywna, multiplikatywna)

Sezonowość
multiplikatywna

Sezonowość
addytywna

Y

t

= T

t

+ S

t

+ I

t

Y

t

= T

t

.

S

t

.

I

t

Wyrównywanie wykładnicze Wintersa

:

Model addytywny

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

 

 

 

 

 

 

t

S

t

p

t

T

t

S

t

T

t

Y

p

t

t

p

t

p

t

p

t





















ˆ

ˆ

ˆ

ˆ

ˆ

1







t

t

t

S

t

t

Y















1

0

)

(





t

1

0







gdzie:

- model opisujący tendencję,

S

t

-

wahania sezonowe,

 -

składnik losowy.

Budowa prognozy

Ocena poziomu trendu

Ocena zmian trendu

Sezonowość

Wyrównywanie wykładnicze Wintersa

:

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

Model multiplikatywny





t

1

0







gdzie:

- model opisujący tendencję,

S

t

-

wahania sezonowe,

 -

składnik losowy.

Budowa prognozy





t

t

t

S

t

Y

















1

0

 

 

 

 

 

 

t

S

t

p

t

T

t

S

t

T

t

Y

p

t

t

p

t

p

t

p

t





















ˆ

]

ˆ

[

ˆ

ˆ

ˆ

1



Ocena poziomu trendu

Ocena zmian trendu

Sezonowość

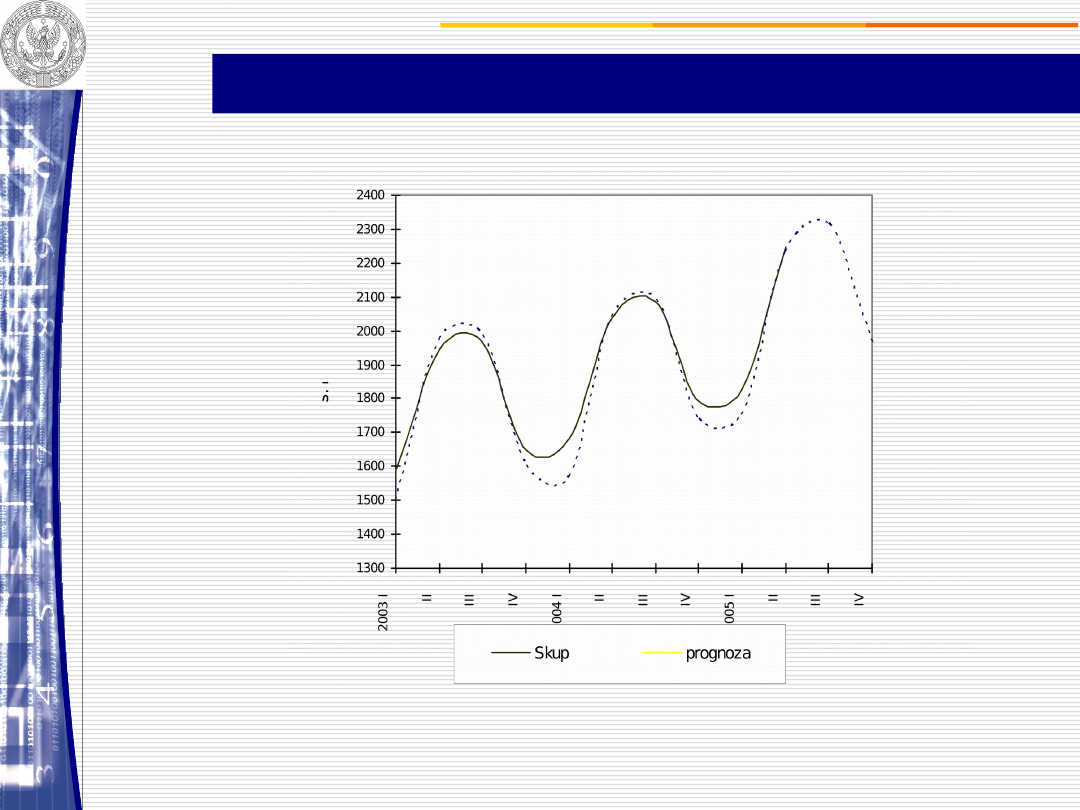
Skup mleka sporządzony metodą Wintersa

Trend pełzający z wagami harmonicznymi

:

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

Prognozowanie

wyrównanie szeregu czasowego

za pomocą trendu pełzającego

szacowanie przyszłego

kształtowania się zjawisk, prognoz

za pomocą wag harmonicznych

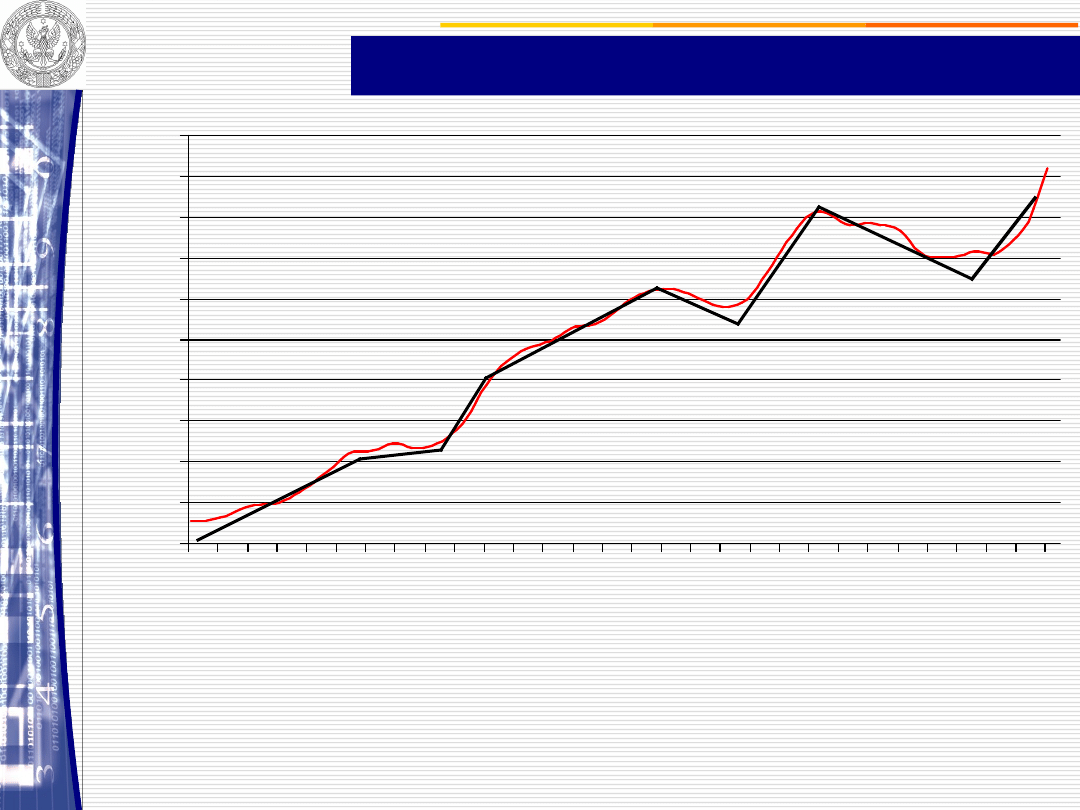
Trend pełzający z wagami harmonicznymi

:

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

wyrównanie szeregu czasowego za pomocą trendu

pełzającego

1 -

stały segment wygładzania

-

szacowanie

parametrów funkcji liniowych na podstawie kolejnych
fragmentów szeregu tej samej długości

2 -

zmienny segment wygładzania

-

szacowanie

parametrów funkcji liniowych na podstawie kolejnych
fragmentów szeregu różnej długości

Wygładzeniem jest ciąg średnich :

 







1

1

1

ˆ

m

j

ij

i

t

t

Y

m

Y

)

(t

Y

ij

- wartości teoretyczne funkcji w okresie t

Wyrównanie szeregu



Dzielimy szereg na segmenty (Y1, Y2,…,Yk)

(Y2, Y3,…Yk+1)
(Yn-k+1,…Yn)



Dla segmentów obliczamy trendy liniowe



Obliczamy wartości liczbowe z funkcji trendu



Obliczamy średnią arytmetyczną dla okresów (trend
pełzający)



Przeprowadzamy weryfikację otrzymanego trendu
łamanego

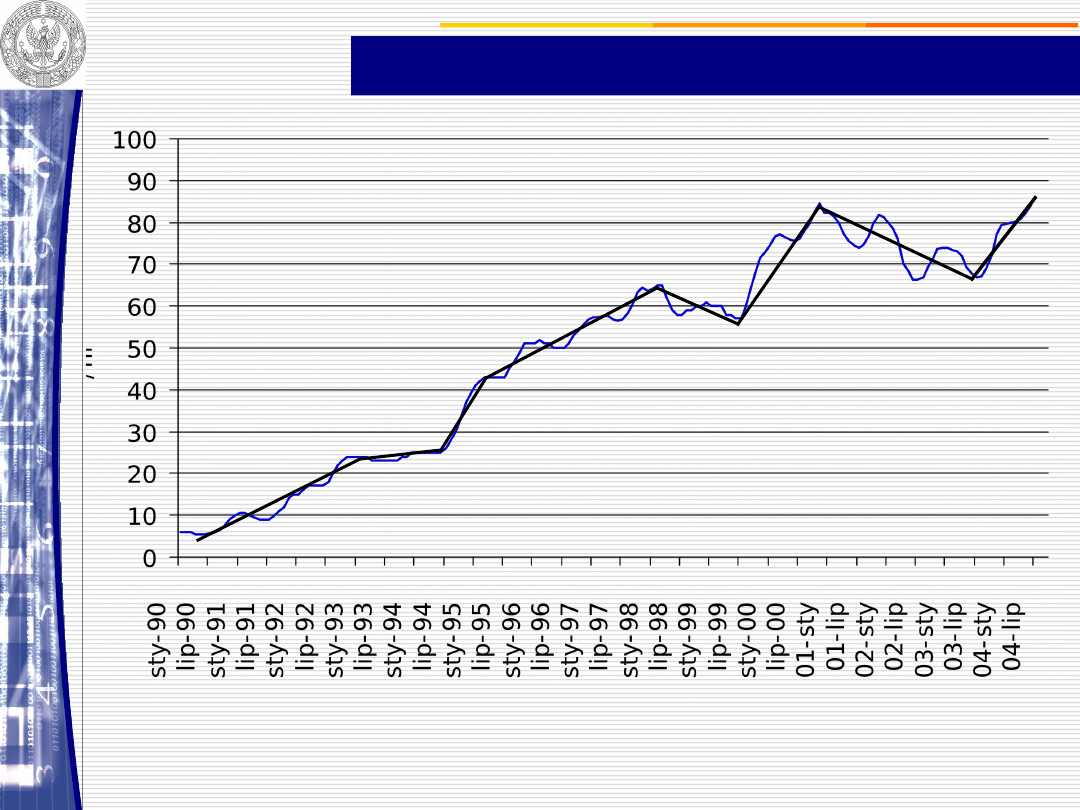
CENY SKUPU MLEKA

0

10

20

30

40

50

60

70

80

90

100

st

y

-9

0

li

p

-9

0

st

y

-9

1

li

p

-9

1

st

y

-9

2

li

p

-9

2

st

y

-9

3

li

p

-9

3

st

y

-9

4

li

p

-9

4

st

y

-9

5

li

p

-9

5

st

y

-9

6

li

p

-9

6

st

y

-9

7

li

p

-9

7

st

y

-9

8

li

p

-9

8

st

y

-9

9

li

p

-9

9

st

y

-0

0

li

p

-0

0

0

1

-s

ty

0

1

-l

ip

0

2

-s

ty

0

2

-l

ip

0

3

-s

ty

0

3

-l

ip

0

4

-s

ty

0

4

-l

ip

z

ł/

h

l

CENY SKUPU MLEKA

0

10

20

30

40

50

60

70

80

90

100

st

y

-9

0

li

p

-9

0

st

y

-9

1

li

p

-9

1

st

y

-9

2

li

p

-9

2

st

y

-9

3

li

p

-9

3

st

y

-9

4

li

p

-9

4

st

y

-9

5

li

p

-9

5

st

y

-9

6

li

p

-9

6

st

y

-9

7

li

p

-9

7

st

y

-9

8

li

p

-9

8

st

y

-9

9

li

p

-9

9

st

y

-0

0

li

p

-0

0

0

1

-s

ty

0

1

-l

ip

0

2

-s

ty

0

2

-l

ip

0

3

-s

ty

0

3

-l

ip

0

4

-s

ty

0

4

-l

ip

zł

/

h

l

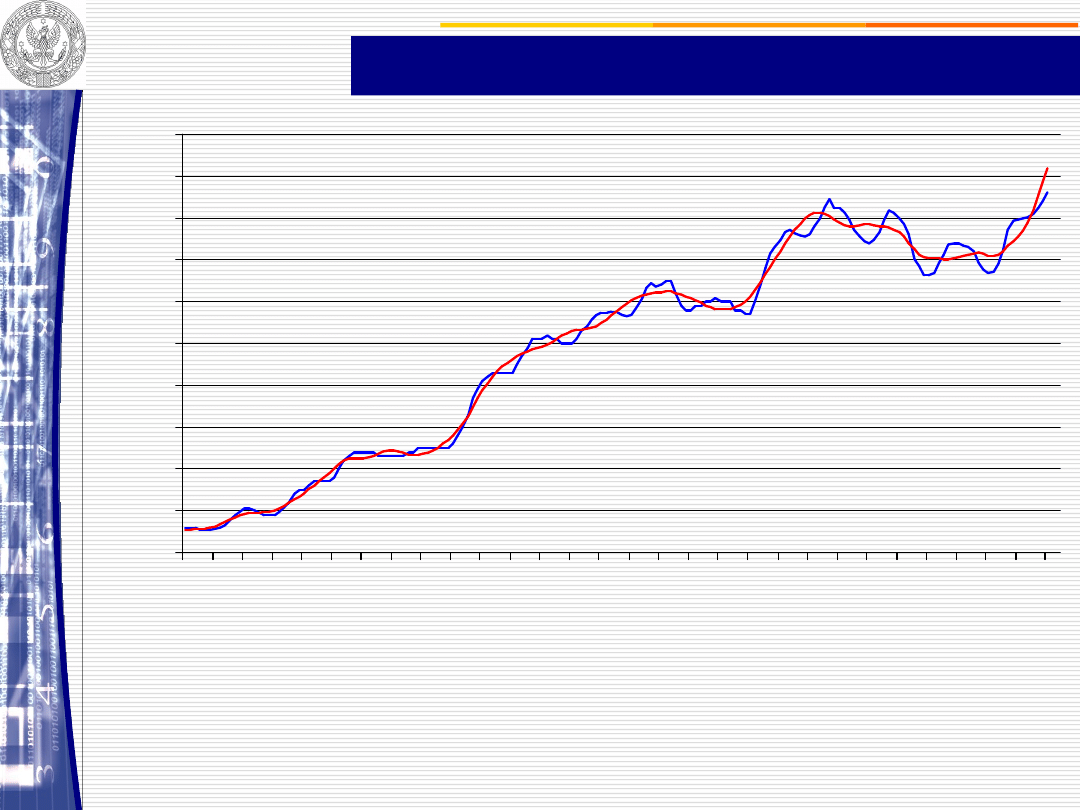
CENY SKUPU MLEKA

Trend pełzający z wagami harmonicznymi

:

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

budowa prognozy za pomocą trendu pełzającego

1 -

obliczenie przyrostów funkcji trendu

3 -

budowa prognozy

t

t

t

Y

Y

W

ˆ

ˆ

1

1









2 -

określenie tendencji (zmian) w okresie t + 1

1

1









t

t

t

W

Y

Y

1

1









t

x

t

x

t

W

Y

Y

gdzie: - prognoza dla t+1,

- prognoza dla t

x

t

Y

1



x

t

Y

Trend pełzający z wagami harmonicznymi

:

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

Problem -

obliczenie przyrostów funkcji trendu

t

t

t

Y

Y

W

ˆ

ˆ

1

1









Założenie -

jak najlepsze oszacowanie prognozy

Wskazówka -

różnicowanie wag w czasie

- wyróżnia się wagi liniowe, wykładnicze i harmoniczne

Trend pełzający z wagami harmonicznymi

:

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

Średnią przyrostu W obliczamy według wzoru:

1

1

1

1















t

n

t

n

t

W

C

W

n

t

C

1



n

t

C

1













1

1

1

1

n

t

n

t

C

- wartości współczynnika zwanego wagą harmoniczną
i spełniającego warunki:

>0

, gdzie t=1,2,3, ..., n-1, przy czym

Trend pełzający z wagami harmonicznymi

:

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

Wyprowadzenie współczynnika wag harmonicznych
oparte jest na dwóch przesłankach:

»

informacje o badanej zmiennej pochodzące z okresów

bardziej odległych od aktualnego mają mniejszą wagę,

»

przyrosty wag są odwrotnie proporcjonalne do czasu.

n

t

C

1



Trend pełzający z wagami harmonicznymi

:

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

Postulat postarzania informacji:

»

Waga jednostkowa dla najdawniejszej informacji m

2

=

»

Waga jednostkowa dla następnej informacji jest powieszona o

czyli m

3

= + itd.

»

Ogólnie ciąg wag jednostkowych obliczamy następująco:

m

t+1

= m

t

+ , gdzie t = 2, 3, 4, ..., n, przy czym

1

1



n

1

1



n

2

1


n

1

1



n

t

n

1













1

1

1

1

n

t

t

n

m

Trend pełzający z wagami harmonicznymi

:

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

Obliczenie jednostkowych

współczynników

wag harmonicznych:

n

t

C

1



Współczynniki jednostkowe wag

harmonicznych m

t+1

dzielimy przez n-1,

otrzymując współczynniki zwane wagą

harmoniczną

n

t

C

1



Trend pełzający z wagami harmonicznymi

:

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

ADAPTACYJNE METODY PROGNOZOWANIA

Średnią przyrostu W obliczamy według wzoru:

1

1

1

1















t

n

t

n

t

W

C

W

n

t

C

1



- wartości współczynnika wagi harmonicznej

Prognoza -

Do ostatniego wyrazu trendu łamanego dodajemy prostą

o nachyleniu , ekstrapolując w ten sposób trend

W

t

t

t

Y

Y

W

ˆ

ˆ

1

1









Prognoza przedziałowa



Należy obliczyć odchylenie standardowe przyrostów
trendu pełzającego ważonych wagami harmonicznymi



Do prognozy punktowej (+-) iloczyn odchylenia stand.
przyrostów i współczynnika nierówności Czebyszewa przy
danej wiarygodności

DZIĘKUJĘ ZA UWAGĘ

Szkoła Główna Gospodarstwa Wiejskiego

Wydział Ekonomiczno - Rolniczy

Katedra Ekonomiki Rolnictwa

i Międzynarodowych Stosunków Gospodarczych