Analiza produkcji

Analiza produkcji

Funkcja produkcji Cobba-Douglasa

Funkcja produkcji Cobba-Douglasa

Proces produkcyjny jest najważniejszym 

Proces produkcyjny jest najważniejszym 

elementem działalności przedsiębiorstwa 

elementem działalności przedsiębiorstwa 

produkcyjnego. Proces ten może być badany z 

produkcyjnego. Proces ten może być badany z 

różnych punktów widzenia. Jednym z nich, 

różnych punktów widzenia. Jednym z nich, 

niekoniecznie najważniejszym, jest analiza 

niekoniecznie najważniejszym, jest analiza 

ekonometryczna. Polega ona na badaniu 

ekonometryczna. Polega ona na badaniu 

ilościowych relacji między różnymi zjawiskami 

ilościowych relacji między różnymi zjawiskami 

techniczno-ekonomicznymi występującymi w 

techniczno-ekonomicznymi występującymi w 

procesie produkcyjnym. Zależności między tymi 

procesie produkcyjnym. Zależności między tymi 

zjawiskami są (powinny być) silne i 

zjawiskami są (powinny być) silne i 

wielokierunkowe.

wielokierunkowe.

Narzędziem badawczym jest model 

Narzędziem badawczym jest model 

ekonometryczny. Może to być model jedno- lub 

ekonometryczny. Może to być model jedno- lub 

wielorównaniowy, w którym przynajmniej jedną 

wielorównaniowy, w którym przynajmniej jedną 

ze zmiennych endogenicznych nieopóźnionych w 

ze zmiennych endogenicznych nieopóźnionych w 

czasie jest poziom produkcji określonego dobra.

czasie jest poziom produkcji określonego dobra.

Ograniczając się w rozważaniach do modeli 

Ograniczając się w rozważaniach do modeli 

jednorównaniowych funkcja produkcji może mieć 

jednorównaniowych funkcja produkcji może mieć 

różną postać analityczną. W takim modelu zmienną 

różną postać analityczną. W takim modelu zmienną 

objaśnianą jest wielkość produkcji, natomiast 

objaśnianą jest wielkość produkcji, natomiast 

zmiennymi objaśniającymi są tzw. czynniki 

zmiennymi objaśniającymi są tzw. czynniki 

produkcji.

produkcji.

W teorii ekonomii wyróżnia się trzy główne 

W teorii ekonomii wyróżnia się trzy główne 

czynniki produkcji:

czynniki produkcji:

-

 

 

pracę żywą,

pracę żywą,

-

 

 

pracę uprzedmiotowioną (kapitał),

pracę uprzedmiotowioną (kapitał),

-

 

 

ziemię (zwłaszcza w rolnictwie).

ziemię (zwłaszcza w rolnictwie).

W przedsiębiorstwach nierolniczych zmienia 

W przedsiębiorstwach nierolniczych zmienia 

na ogół nie odgrywa istotnej roli, dlatego ten 

na ogół nie odgrywa istotnej roli, dlatego ten 

czynnik pomijamy.

czynnik pomijamy.

Najczęściej spotykaną w praktyce postacią 

Najczęściej spotykaną w praktyce postacią 

analityczną funkcji produkcji jest funkcja potęgowa, 

analityczną funkcji produkcji jest funkcja potęgowa, 

zwana funkcją produkcji 

zwana funkcją produkcji 

Cobba-Douglasa

Cobba-Douglasa

:

:

Zasadniczo funkcja ta przybiera postać 

Zasadniczo funkcja ta przybiera postać 

dwuczynnikową:

dwuczynnikową:

jeżeli               , to:           jeżeli               , to:                  jeżeli               , to:  
  

Funkcja ta ma teoretyczne uzasadnienie i znalazła 

Funkcja ta ma teoretyczne uzasadnienie i znalazła 

potwierdzenie w praktyce.

potwierdzenie w praktyce.

.

...

ˆ

2

1

2

1

0

k

k

X

X

X

P











 

0

 

y

 

z

 

k

 

 

y

 

z

 

0

 

k

 

 

y

 

z

 

0

 

k

 

,

)

,

(





z

ak

z

k

f

y





.

0

,

,







a

1









1









1









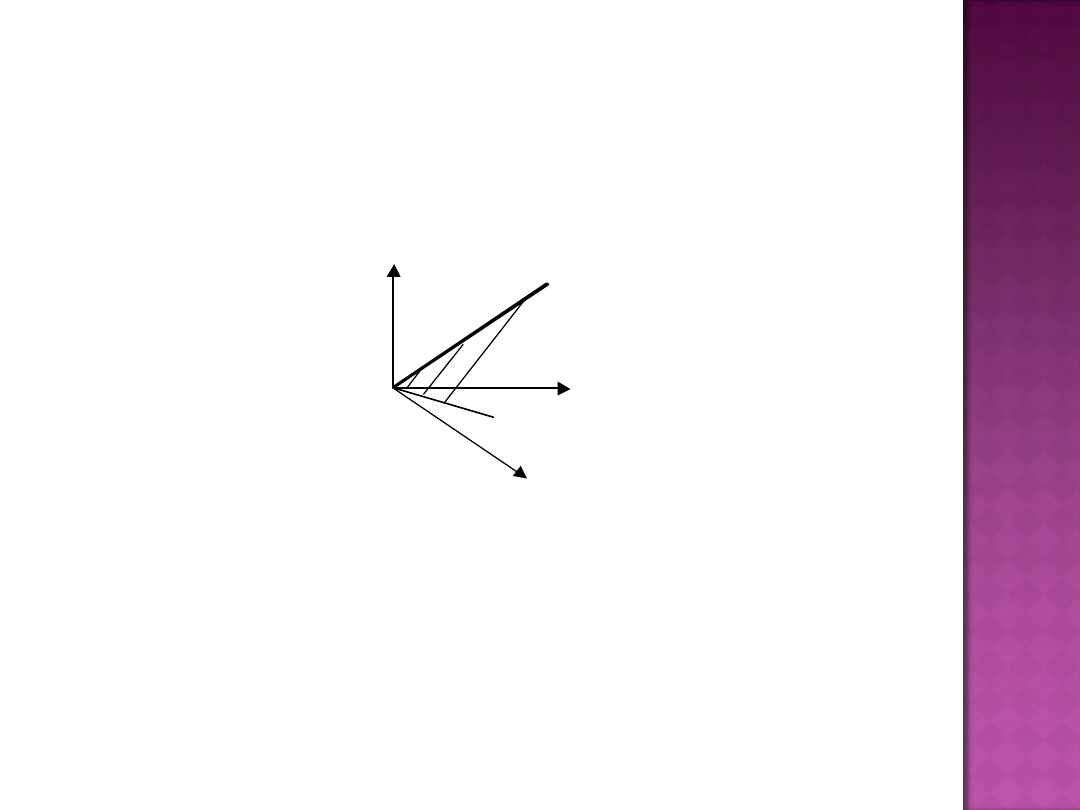
Często stosowaną postacią analityczną jest 

Często stosowaną postacią analityczną jest 

również postać liniowa:

również postać liniowa:

Różne własności i cechy funkcji 

Różne własności i cechy funkcji 

produkcji opisuje się korzystając z szeregu 

produkcji opisuje się korzystając z szeregu 

pojęć, które określa się jako 

pojęć, które określa się jako 

charakterystyki 

charakterystyki 

funkcji produkcji

funkcji produkcji

. Kolejne definicje, 

. Kolejne definicje, 

interpretacje i przykłady je pokazują.

interpretacje i przykłady je pokazują.

bz

ak

y





0

, 

b

a

 

0

 

y

 

z

 

k

 

Do ekonometrycznej analizy procesu 

Do ekonometrycznej analizy procesu 

produkcyjnego stosuje się kilka mierników 

produkcyjnego stosuje się kilka mierników 

syntetycznych.

syntetycznych.

Produkt całkowity

Produkt całkowity

 jest to teoretyczna wartość 

 jest to teoretyczna wartość 

zmiennej objaśnianej przy znanych, prognozowanych lub 

zmiennej objaśnianej przy znanych, prognozowanych lub 

ustalonych wartościach wszystkich zmiennych 

ustalonych wartościach wszystkich zmiennych 

objaśnianych, czyli:

objaśnianych, czyli:

Oznacza on taki poziom produkcji, który powinien 

Oznacza on taki poziom produkcji, który powinien 

być osiągnięty przy określonych wielkościach 

być osiągnięty przy określonych wielkościach 

wszystkich czynników produkcji występujących w 

wszystkich czynników produkcji występujących w 

modelu. Miano tego czynnika jest oczywiście takie 

modelu. Miano tego czynnika jest oczywiście takie 

samo, jak miano zmiennej objaśnianej, czyli produkcji.

samo, jak miano zmiennej objaśnianej, czyli produkcji.

Porównanie rzeczywistego poziomu produkcji z 

Porównanie rzeczywistego poziomu produkcji z 

odpowiadającym mu produktem całkowitym pozwala na 

odpowiadającym mu produktem całkowitym pozwala na 

ocenę działalności firmy w danym okresie. W sytuacji, 

ocenę działalności firmy w danym okresie. W sytuacji, 

gdy rzeczywisty poziom produkcji jest większy od 

gdy rzeczywisty poziom produkcji jest większy od 

produktu całkowitego, ocena ta jest pozytywna, w 

produktu całkowitego, ocena ta jest pozytywna, w 

sytuacji odwrotnej – negatywna, co zmusza do szukania 

sytuacji odwrotnej – negatywna, co zmusza do szukania 

przyczyn powstania takiej sytuacji.

przyczyn powstania takiej sytuacji.

.

ˆ

P

PC 

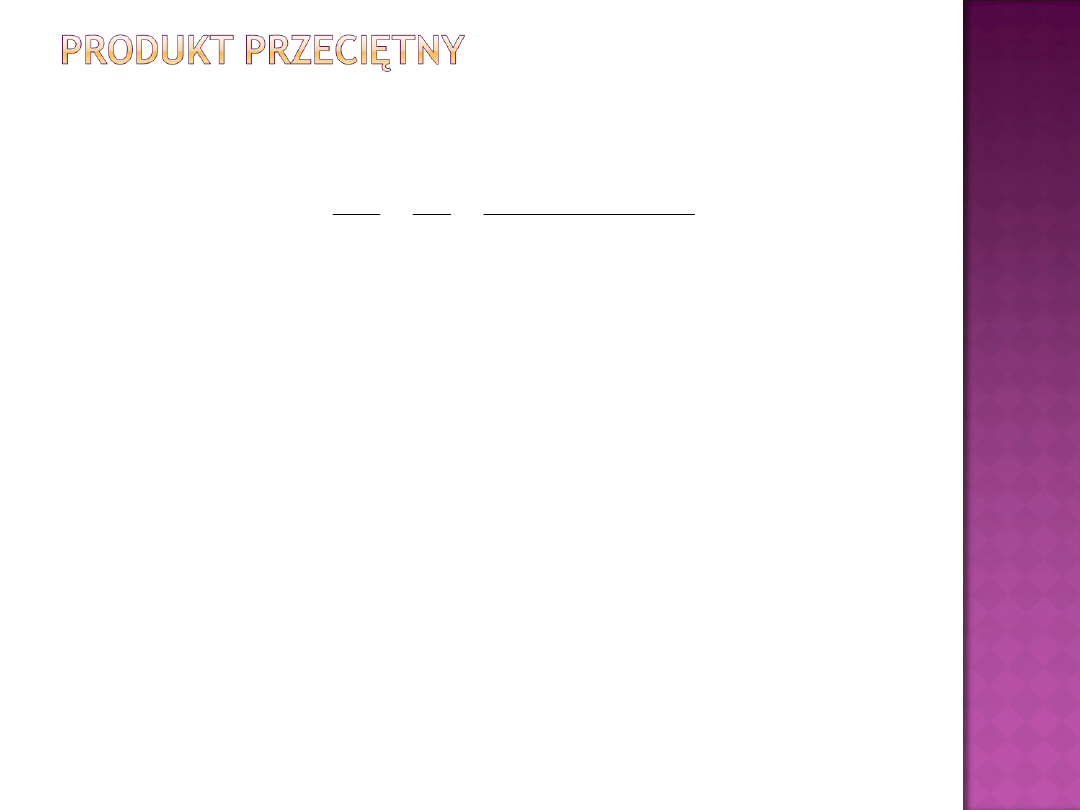
Miano produktu przeciętnego jest 

Miano produktu przeciętnego jest 

stosunkiem miana produkcji do miana 

stosunkiem miana produkcji do miana 

i-

i-

tego 

tego 

czynnika produkcji. Interpretacja produktu 

czynnika produkcji. Interpretacja produktu 

przeciętnego jest następująca: 

przeciętnego jest następująca: 

produkt 

produkt 

przeciętny jest to przeciętna wielkość 

przeciętny jest to przeciętna wielkość 

produkcji przypadająca na jednostkę 

produkcji przypadająca na jednostkę 

i

i

-tego 

-tego 

czynnika produkcji przy ustalonych 

czynnika produkcji przy ustalonych 

wartościach wszystkich czynników produkcji 

wartościach wszystkich czynników produkcji 

(czyli w ustalonym punkcie). 

(czyli w ustalonym punkcie). 

Interpretacja ta 

Interpretacja ta 

jest równoważna pojęciu przeciętnej wydajności 

jest równoważna pojęciu przeciętnej wydajności 

(produktywności) czynnika produkcji w ustalonych 

(produktywności) czynnika produkcji w ustalonych 

warunkach.

warunkach.





.

,...,

,

ˆ

2

1

i

k

i

i

i

X

X

X

X

f

X

P

X

PC

PP







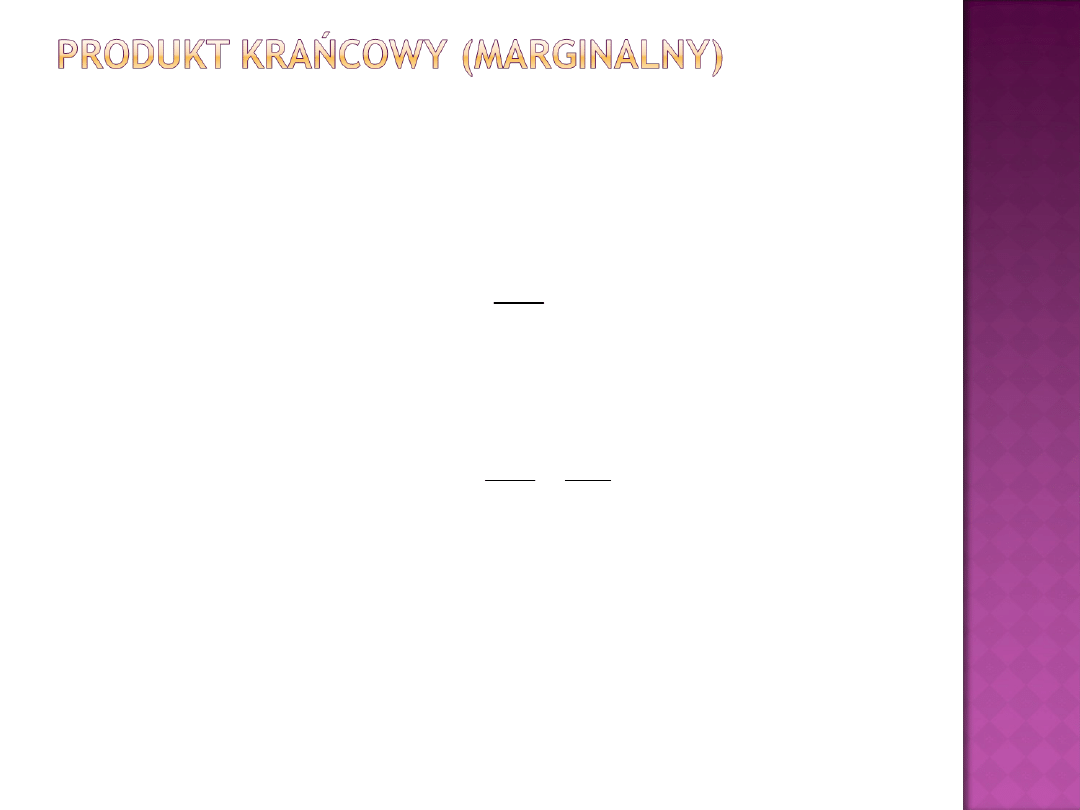
Produkt krańcowy (marginalny) 

Produkt krańcowy (marginalny) 

określa 

określa 

zmianę wielkości produkcji, spowodowaną zmianą 

zmianę wielkości produkcji, spowodowaną zmianą 

i

i

-

-

tego czynnika produkcji o jednostkę (przy ustalonym 

tego czynnika produkcji o jednostkę (przy ustalonym 

poziomie pozostałych czynników produkcji):

poziomie pozostałych czynników produkcji):

Jeśli znana jest postać analityczna funkcji produkcji, 

Jeśli znana jest postać analityczna funkcji produkcji, 

to produkt krańcowy jest pochodną cząstkową tej 

to produkt krańcowy jest pochodną cząstkową tej 

funkcji względem 

funkcji względem 

i

i

-tego czynnika produkcji:

-tego czynnika produkcji:

Miano produktu krańcowego jest takie samo jak 

Miano produktu krańcowego jest takie samo jak 

miano produktu przeciętnego. Interpretacja produktu 

miano produktu przeciętnego. Interpretacja produktu 

krańcowego jest następująca: 

krańcowego jest następująca: 

produkt krańcowy 

produkt krańcowy 

jest to oczekiwany przyrost produkcji, 

jest to oczekiwany przyrost produkcji, 

spowodowany przyrostem 

spowodowany przyrostem 

i

i

-tego czynnika 

-tego czynnika 

produkcji o jednostkę przy założeniu, że 

produkcji o jednostkę przy założeniu, że 

pozostałe czynniki produkcji nie zmieniają się. 

pozostałe czynniki produkcji nie zmieniają się. 

.

ˆ

i

i

X

P

PK







.

ˆ

ˆ

lim

0

i

i

X

i

X

P

X

P

PK

i

















Elastyczność produkcji 

Elastyczność produkcji 

względem 

względem 

i

i

-tego 

-tego 

czynnika produkcji określa względną zmianę wielkości 

czynnika produkcji określa względną zmianę wielkości 

produkcji (w procentach) spowodowaną względną 

produkcji (w procentach) spowodowaną względną 

zmianą tylko 

zmianą tylko 

i

i

-tego czynnika produkcji o jeden procent 

-tego czynnika produkcji o jeden procent 

(przy ustalonym poziomie pozostałych czynników 

(przy ustalonym poziomie pozostałych czynników 

produkcji):

produkcji):

Interpretacja elastyczności jest następująca: 

Interpretacja elastyczności jest następująca: 

elastyczność jest to oczekiwany względny przyrost 

elastyczność jest to oczekiwany względny przyrost 

produkcji (np. w procentach), spowodowany 

produkcji (np. w procentach), spowodowany 

jednostkowym względnym przyrostem 

jednostkowym względnym przyrostem 

i

i

-tego 

-tego 

czynnika produkcji (np. 1%) przy założeniu, że 

czynnika produkcji (np. 1%) przy założeniu, że 

pozostałe czynniki produkcji się nie zmieniają, 

pozostałe czynniki produkcji się nie zmieniają, 

lub: 

lub: 

elastyczność jest to oczekiwany względny przyrost 

elastyczność jest to oczekiwany względny przyrost 

produkcji (np. w procentach) spowodowany, 

produkcji (np. w procentach) spowodowany, 

ceteris 

ceteris 

paribus

paribus

, względnym przyrostem 

, względnym przyrostem 

i

i

-tego czynnika 

-tego czynnika 

produkcji o jednostkę        (np. o 1%).

produkcji o jednostkę        (np. o 1%).

,

ˆ

ˆ

:

ˆ

ˆ

i

i

i

i

i

i

i

PP

PK

X

P

X

P

X

X

P

P

E



















Definiując elastyczność, przyjmuje się założenie, 

Definiując elastyczność, przyjmuje się założenie, 

że tylko jeden czynnik produkcji wzrasta o 1%, 

że tylko jeden czynnik produkcji wzrasta o 1%, 

pozostałe zaś się nie zmieniają. Zakładając, że wszystkie 

pozostałe zaś się nie zmieniają. Zakładając, że wszystkie 

czynniki produkcji wzrastają jednocześnie o 1%, należy 

czynniki produkcji wzrastają jednocześnie o 1%, należy 

spodziewać się, że produkcja wzrośnie o 

spodziewać się, że produkcja wzrośnie o 

A

A

%:

%:

Wskaźnik ten nazywamy efektem skali produkcji 

Wskaźnik ten nazywamy efektem skali produkcji 

(oznacza się ją też symbolem 

(oznacza się ją też symbolem 

ESP

ESP

).

).

Wydaje się, że naturalne jest oczekiwanie, aby 

Wydaje się, że naturalne jest oczekiwanie, aby 

A=1

A=1

; w praktyce często tak się zdarza. Rzeczywista 

; w praktyce często tak się zdarza. Rzeczywista 

wartość efektu skali produkcji daje cenne informacje o 

wartość efektu skali produkcji daje cenne informacje o 

charakterze procesu produkcyjnego. Jeśli 

charakterze procesu produkcyjnego. Jeśli 

A<1

A<1

, oznacza 

, oznacza 

to, że efekty rosną wolniej niż nakłady i zasoby 

to, że efekty rosną wolniej niż nakłady i zasoby 

czynników produkcji. Jeśli 

czynników produkcji. Jeśli 

A>1

A>1

, to efekty rosną szybciej 

, to efekty rosną szybciej 

niż nakłady i zasoby.        I wreszcie gdy 

niż nakłady i zasoby.        I wreszcie gdy 

A=1

A=1

, wtedy 

, wtedy 

efekty rosną w takim samym tempie, jak nakłady i 

efekty rosną w takim samym tempie, jak nakłady i 

zasoby czynników produkcji.

zasoby czynników produkcji.







k

i

i

E

A

1

.

Krańcowa stopa substytucji

Krańcowa stopa substytucji

 czynników 

 czynników 

produkcji (czynnika 

produkcji (czynnika 

i

i

 przez czynnik 

 przez czynnik 

j

j

)

)

określa, jaki nakład (zasób) czynnika 

określa, jaki nakład (zasób) czynnika 

j

j

 musi być 

 musi być 

wprowadzony w miejsce wycofanej jednostki 

wprowadzony w miejsce wycofanej jednostki 

nakładów (zasobów) czynnika 

nakładów (zasobów) czynnika 

i

i

, przy założeniu, że 

, przy założeniu, że 

pozostałe czynniki się nie zmieniają, tak by poziom 

pozostałe czynniki się nie zmieniają, tak by poziom 

produkcji również nie uległ zmianie. Ponieważ 

produkcji również nie uległ zmianie. Ponieważ 

Δ

Δ

X

X

i

i

 

 

jest ujemne, więc 

jest ujemne, więc 

SS

SS

ij

ij

 jest liczbą dodatnią. 

 jest liczbą dodatnią. 

Przekształcając wzór otrzymujemy:

Przekształcając wzór otrzymujemy:

  

  

i

j

ij

X

X

SS









.

ˆ

:

ˆ

j

i

j

i

i

j

ij

PK

PK

X

P

X

P

X

X

SS























Q

1

Q

2

Q

3

X

1

X

2

Q

1

Q

2

Q

3

X

2

X

1

Q

1

Q

2

Q

3

X

2

X

1

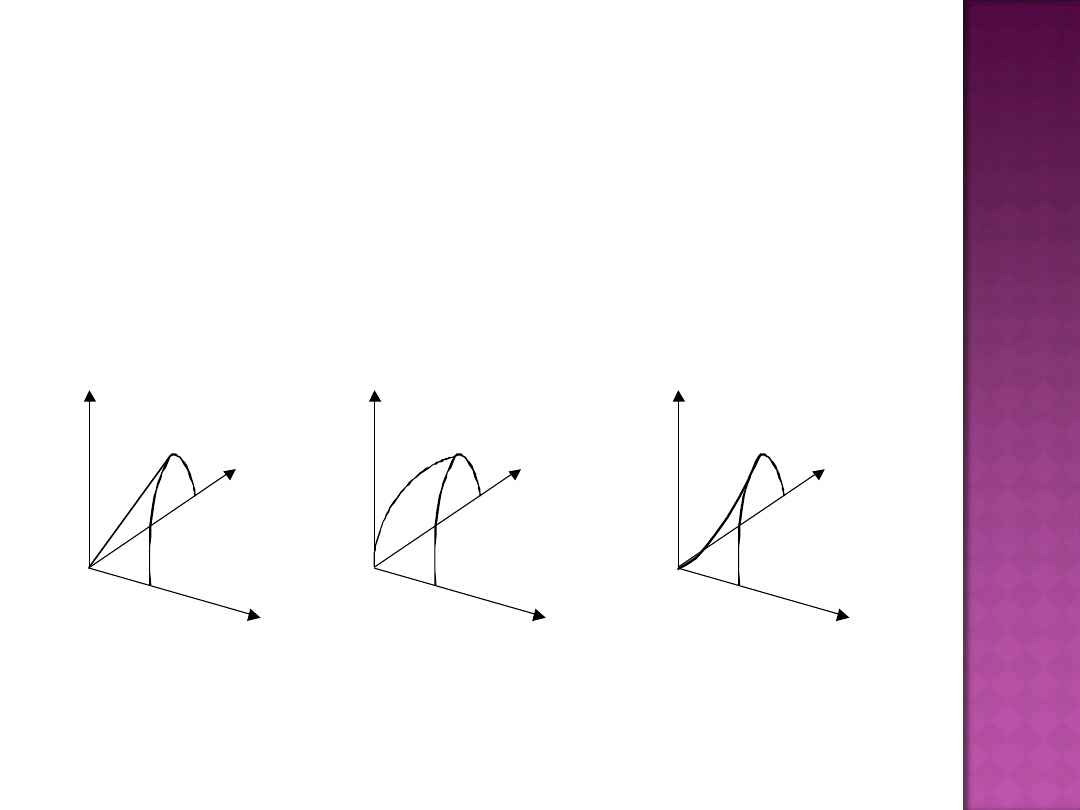
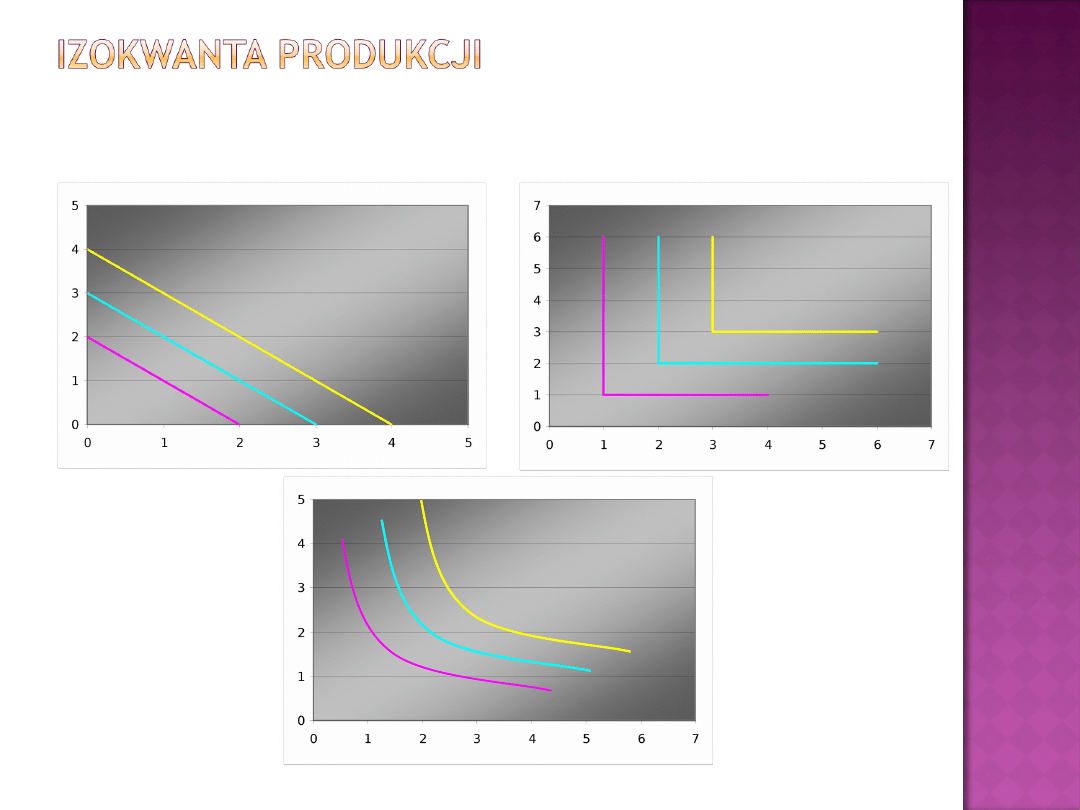
Izokwanta produkcji 

Izokwanta produkcji 

jest to krzywa jednakowego 

jest to krzywa jednakowego 

poziomu produkcji dla wszystkich możliwych kombinacji 

poziomu produkcji dla wszystkich możliwych kombinacji 

nakładów (zasobów) czynników produkcji.

nakładów (zasobów) czynników produkcji.

DOSKONAŁA SUBSTYTUCYJNOŚĆ 
(KOKS- GAZ)

KOMPLEMENTARNOŚĆ (PARA 
BUTÓW)

RZECZYWISTA SUBSTYTUCYJNOŚĆ

Oszacowano funkcję produkcji typu Cobba-

Oszacowano funkcję produkcji typu Cobba-

Douglasa

Douglasa

gdzie:

gdzie:

   

   

P – 

P – 

produkcja (w tys. zł),

produkcja (w tys. zł),

   

   

X

X

1

1

 

 

– majątek trwały (w tys. zł),

– majątek trwały (w tys. zł),

   

   

X

X

2

2

 

 

– zatrudnienie (w osobach).

– zatrudnienie (w osobach).

W pewnym okresie wartość majątku trwałego wynosiła  

W pewnym okresie wartość majątku trwałego wynosiła  

   100 000 zł, zatrudnienie 200 osób.

   100 000 zł, zatrudnienie 200 osób.

   

   

Produkt całkowity:

Produkt całkowity:

Komentarz: Przy danych nakładach obu czynników 

Komentarz: Przy danych nakładach obu czynników 

produkcji  należy się spodziewać efektów 

produkcji  należy się spodziewać efektów 

produkcyjnych na poziomie 94,3 tys. zł.

produkcyjnych na poziomie 94,3 tys. zł.

,

654

,

0

ˆ

674

,

0

2

304

,

0

1

X

X

P 

]

.

[

3

,

94

200

100

654

,

0

ˆ

674

,

0

304

,

0

zł

tys

P

PC











   

   

Produkt przeciętny:

Produkt przeciętny:

Komentarz: przy danych wartościach zmiennych 

Komentarz: przy danych wartościach zmiennych 

objaśniających z 1 tys. zł majątku trwałego można 

objaśniających z 1 tys. zł majątku trwałego można 

uzyskać przeciętnie produkcję wartości 943 zł (jest 

uzyskać przeciętnie produkcję wartości 943 zł (jest 

to więc produktywność majątku trwałego), a na 1 

to więc produktywność majątku trwałego), a na 1 

zatrudnionego przypada produkcja o wartości 

zatrudnionego przypada produkcja o wartości 

przeciętnej 471,5 zł (jest to więc wydajność pracy – 

przeciętnej 471,5 zł (jest to więc wydajność pracy – 

oczywiście teoretyczna, wynikająca z modelu).

oczywiście teoretyczna, wynikająca z modelu).



















trwalego

majatku

zł

tys

produkcji

zł

tys

X

PC

PP

_

_

_

.

_

_

.

943

,

0

100

3

,

94

1

1















osobe

produkcji

zł

tys

X

PC

PP

_

_

.

4715

,

0

200

3

,

94

2

2

   

   

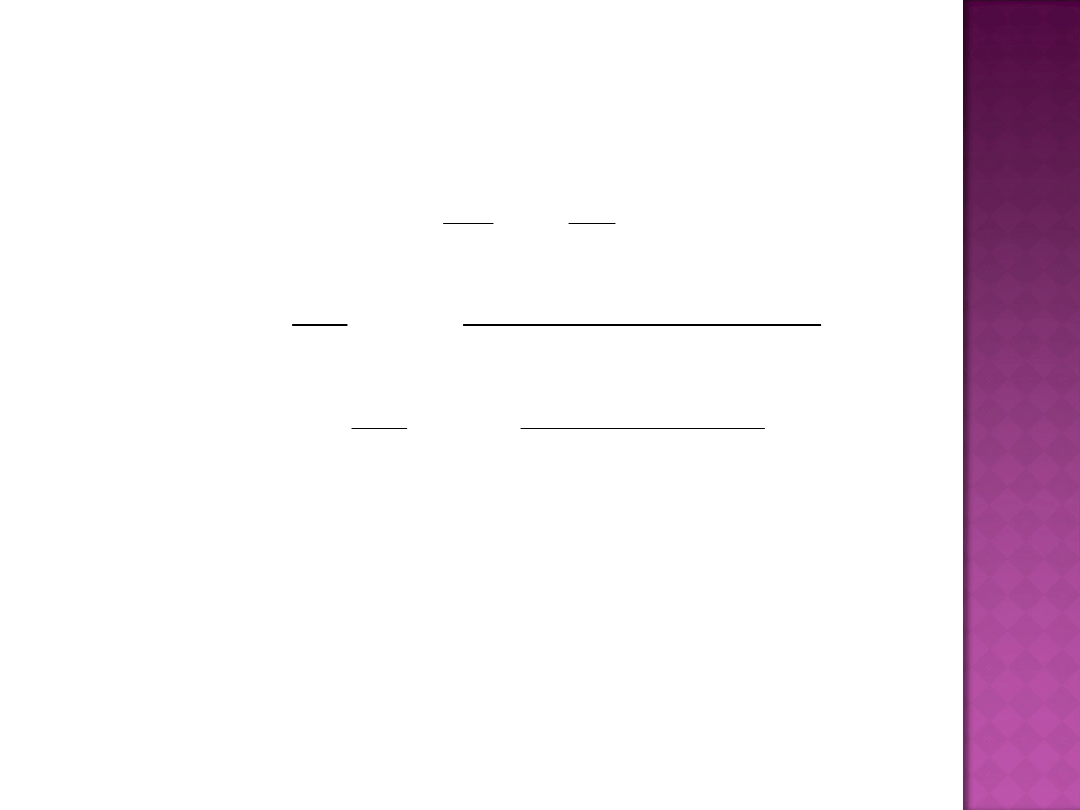
Produkt krańcowy:

Produkt krańcowy:

Komentarz: zwiększenie majątku trwałego o 1 tys. zł 

Komentarz: zwiększenie majątku trwałego o 1 tys. zł 

powinno, 

powinno, 

ceteris paribus

ceteris paribus

, spowodować wzrost 

, spowodować wzrost 

produkcji o 287 zł, a zwiększenie zatrudnienia o 1 

produkcji o 287 zł, a zwiększenie zatrudnienia o 1 

osobę o 318 zł.

osobę o 318 zł.

















trwalego

majatku

zł

tys

produkcji

zł

tys

PK

_

_

_

.

_

_

.

287

,

0

100

3

,

94

304

,

0

1

.

_

_

.

318

,

0

200

3

,

94

674

,

0

2













osobe

produkcji

zł

tys

PK

i

i

i

i

X

PC

X

P

PK













   

   

Elastyczność produkcji:

Elastyczność produkcji:

Komentarz: zwiększenie majątku trwałego o 1% 

Komentarz: zwiększenie majątku trwałego o 1% 

powinno, 

powinno, 

ceteris paribus

ceteris paribus

, spowodować wzrost 

, spowodować wzrost 

produkcji o 0,304%, a zwiększenie zatrudnienia o 1% - 

produkcji o 0,304%, a zwiększenie zatrudnienia o 1% - 

o 0,674%.

o 0,674%.

i

i

i

i

i

i

i

X

PC

X

PC

PP

PK

E











,

304

,

0

1



E

,

674

,

0

2



E

   

   

Efekt skali produkcji:

Efekt skali produkcji:

Komentarz: jednoczesne zwiększenie obu czynników 

Komentarz: jednoczesne zwiększenie obu czynników 

produkcji (majątku trwałego i zatrudnienia) o 1% 

produkcji (majątku trwałego i zatrudnienia) o 1% 

powinno dać zwiększenie produkcji o 0,978%. Ponieważ 

powinno dać zwiększenie produkcji o 0,978%. Ponieważ 

efekt skali produkcji jest prawie równy 1, można więc 

efekt skali produkcji jest prawie równy 1, można więc 

powiedzieć, że efekty (produkcja) rosną w takim samym 

powiedzieć, że efekty (produkcja) rosną w takim samym 

tempie jak nakłady obu czynników produkcji, czyli 

tempie jak nakłady obu czynników produkcji, czyli 

mamy do czynienia za stałą wydajnością czynników 

mamy do czynienia za stałą wydajnością czynników 

produkcji.

produkcji.

   

   

Krańcowa stopa substytucji:

Krańcowa stopa substytucji:

Komentarz: jednego pracownika można zastąpić 

Komentarz: jednego pracownika można zastąpić 

majątkiem trwałym wartości około 1108 zł lub majątek 

majątkiem trwałym wartości około 1108 zł lub majątek 

trwały wartości 1 tys. zł można zastąpić zwiększeniem 

trwały wartości 1 tys. zł można zastąpić zwiększeniem 

zatrudnienia o około 0,902 etatu.

zatrudnienia o około 0,902 etatu.

.

978

,

0

674

,

0

304

,

0

2

1











E

E

ESP

,

_

_

_

.

902

,

0

318

,

0

287

,

0

2

1

12



















trwalego

majatku

zł

tys

osoby

PK

PK

SS

.

_

_

_

.

109

,

1

287

,

0

318

,

0

1

2

21















osobe

trwalego

majatku

zł

tys

PK

PK

SS