Technology Related

Examples

Lecture Outline

• Introduction
• MPLS over GE Network Design
• Tunnels Optimization in MPLS Networks
• SONET/SDH Protection
• Dimensioning of Overlay Networks for P2P

Multicasting

• Access Point Location in WLANs
• Routing and Wavelegth Assignment in Optical

Networks

• Concluding Remarks

Lecture Outline

• Introduction

• MPLS over GE Network Design
• Tunnels Optimization in MPLS Networks
• SONET/SDH Protection
• Dimensioning of Overlay Networks for P2P

Multicasting

• Access Point Location in WLANs
• Routing and Wavelegth Assignment in Optical

Networks

• Concluding Remarks

Introduction (1)

• Modeling of network optimization problems is

strongly related to network technologies,
which introduce to the model various constraints

• To model network traffic various versions of

multicommodity flows are used

• Capacity of network links is mostly modeled

applying integer variables

• Construction of the model is a tradeof between

size/complexity of the model and the level of
technological details

Lecture Outline

• Introduction

• MPLS over GE Network Design

• Tunnels Optimization in MPLS Networks
• SONET/SDH Protection
• Dimensioning of Overlay Networks for P2P

Multicasting

• Access Point Location in WLANs
• Routing and Wavelegth Assignment in Optical

Networks

• Concluding Remarks

MPLS Header

L3-L7 (IP Header)

L2 (IP Data)

IP Packet

L3-L7 (IP Header)

L2 (IP Data)

MPLS Packet

MPLS

MPLS Header

0 1 2 3

0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9 0 1

Label

MPLS

MPLS

Exp S

TTL

Label identification number of the packet denoting
the FEC (Forwarding Equivalence Class) of the packet

Exp for future use

S (ang. Bottom of Stack) =1 signifies that the current
label is the last in the stack ; =0, otherwise

TTL Time to Live of the packet

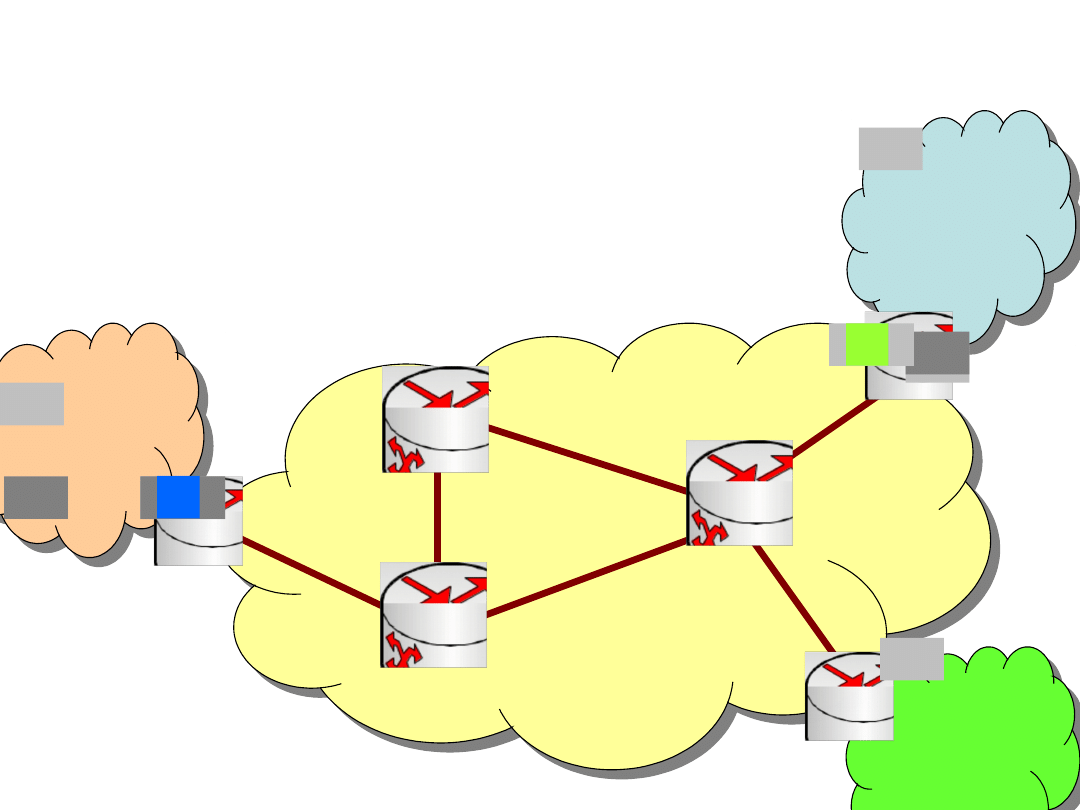
MPLS Network (1)

• The MPLS network consists of:

– Label Edge Router (LER) located on the entry

and exit points of the MPLS network

– Label Switch Routers (LSR) located inside the

MPLS network

• LER pushes an MPLS label onto an incoming

packet and pop it off the outgoing packet
according to the FEC (Forwarding Equivalence
Class)

• Packets are sent along LSP (Label Switch Paths)

between LERs and LSRs

Net IP2

Net IP2

Net IP1

Net IP1

MPLS Network

MPLS Network

MPLS Network (2)

LER2

LSR1

Net IP3

Net IP3

LSR2

LER3

LER1

LSR3

MPLS, QoS and Traffic

Engineering

• To classify a packet to FEC class IP address or

other element of the header (e.g., DSCP) can be
used

• Different FEC classes can have various QoS

parameters

• Using LSP and FEC packets between the same

pair of nodes can use diferent paths (routes)

• This enables effective traffic engineering

Network Design Problem (1)

• The network design problems includes

optimization of both routing and capacity,
therefore there are called CFA (Capacity and Flow
Assignment) problems

• Such problems are encountered by telecoms

during dimensioning the network according to
given/predicted traffic

• Usually the unicast traffic is considered
• Telecoms usually overprovision the network to

accommodate temporary traffic increase and
future clients

Network Design Problem (2)

• The network design must conform technological

constraints following from the technologies used
by the telecom (e.g., WDM, Ethernet, MPLS) as
well as business drivers (flexibility, cost,
scalability, etc.)

• Incremental network design (network

extension) problems are addressed when the
telecom is to extend the existing network to meet
growing clients’ demands considered

• Objectives of the optimization can be: cost,

survivability, QoS parameters, etc.

Objective

• How to determine network cost defined by link

capacity so that the total cost of installed links is
minimized

• Demands (traffic) are sent using MPLS

connections

• Link capacity is in modular units such as 10

Gbps links (10 Gigabit Ethernet)

• Given: network topology, demands, link module

cost

Modeling (1)

• Link-path formulation with candidate paths
• Binary variable x

dp

is 1, if demand d uses path

p; 0, otherwise

• Non-bifurcated flows and only one path can

be selected for demand d, i.e.,



p

x

dp

= 1, d = 1,2,…,D.

Modeling (2)

• Constant



edp

is 1, if link e belongs to path p

realizing demand d; 0, otherwise

• The demand volume is given by h

d

(bps)

• The flow on each link is given by formula



d



p



edp

x

dp

h

d

e = 1,2,…,E.

Modeling (3)

• The variable y

e

denotes the number of capacity

modules installed on link e

• M is the size of one module (e.g., 10 Gbps)




e

is cost of one module in link e

• The network cost is given by



e

y

e



e

• Capacity constraint - flow on each link cannot

exceed the link capacity



d



p



edp

x

dp

h

d

 y

e

M e = 1,2,…,E.

Modeling (4)

objective
minimize F = 

e



e

y

e

constraints


p

x

dp

= 1, d = 1,2,…,D



d



p



edp

x

dp

h

d

 My

e

, e = 1,2,…,E.

x

dp

binary, y

e

integer and non-negative

Optimization

• This problem has discrete (binary and integer)

variables while the constraints and the objective
function are linear

• Thus, this is an example of a integer linear

programming problem (ILP)

• Branch-and-bound or branch-and-cut algorithms

can provide optimal result

• Various heuristics can be applied

Lecture Outline

• Introduction
• MPLS over GE Network Design

• Tunnels Optimization in MPLS Networks

• SONET/SDH Protection
• Dimensioning of Overlay Networks for P2P

Multicasting

• Access Point Location in WLANs
• Routing and Wavelegth Assignment in Optical

Networks

• Concluding Remarks

Objective

• How to carry different traffic classes in an MPLS

network through the creation of tunnels in such a
way that the number of tunnels on each MPLS
router/link is minimized and load balanced?

• Given: network topology, link capacity, demands,

candidate paths

Modeling (1)

• Let identifier d=1,2,…,D denote a demand

(associated with a node pair and a traffic class)

• Demand d that requires bandwidth h

d

and is to

be routed in the network

• Demand h

d

can be carried over multiple tunnels

from ingress to egress MPLS label-edge-router
(LER) denoted by p=1,2,…,P

d

• The fraction of the demand volume for demand d

to be carried on tunnel p is denoted as x

dp

• We then have the demand constraint



p

x

dp

= 1, d = 1,2,…,D.

Modeling (2)

• Since a flow can have very small fraction, we

propose to set a lower bound on the fraction of a
flow on a path

• We use a positive quantity ε to be the lower

bound on fraction of flow on a tunnel (path)

• We use the binary variable u

dp

= 1 to denote

selection of a tunnel if the lower bound is
satisfied (and 0, otherwise)

• We introduce the following two relations

εu

dp

 x

dp

h

d

, d = 1,2,…,D p = 1,2,…,P

d

x

dp

 u

dp

, d = 1,2,…,D p = 1,2,…,P

d

.

Modeling (3)

• Capacity constraint on link e (



edp

is 1, if link

e belongs to path p realizing demand d; 0,
otherwise)



d

h

d



p



edp

x

dp

 c

e

, e = 1,2,…,E.

• The number of tunnels on link e will be



d



p



edp

u

dp

.

• Let r denote the maximum number of tunnels

on a link



d



p



edp

u

dp

 r, e = 1,2,…,E.

Modeling (4)

objective
minimize F = r
constraints


p

x

dp

= 1, d = 1,2,…,D



d

h

d



p



edp

x

dp

 c

e

, e = 1,2,…,E

εu

dp

 x

dp

h

d

, d = 1,2,…,D p = 1,2,…,P

d

x

dp

 u

dp

, d = 1,2,…,D p = 1,2,…,P

d



d



p



edp

u

dp

 r, e = 1,2,…,E.

x

dp

continuous and non-negative, u

dp

binary, r

integer

Optimization

• This problem has both continuous and discrete

variables while the constraints and the objective
function are linear

• Thus, this is an example of a mixed-integer linear

programming problem (shortly, MIP problem)

• Branch-and-bound or branch-and-cut algorithms

can provide optimal result

• Various heuristics can be applied

Lecture Outline

• Introduction
• MPLS over GE Network Design
• Tunnels Optimization in MPLS Networks

• SONET/SDH Protection

• Dimensioning of Overlay Networks for P2P

Multicasting

• Access Point Location in WLANs
• Routing and Wavelegth Assignment in Optical

Networks

• Concluding Remarks

SONET/SDH

• Synchronous Optical Networking (SONET) or

Synchronous Digital Hierarchy (SDH) are
multiplexing protocols that transmit multiple streams
over fibers

• Lower rates can also be transferred using an

electrical interface

• SONET is used in the USA and Canada and SDH in the

rest of the world

• SONET/SDH provides essential protocol neutrality

and transport-oriented features

• SONET/SDH can be used with various technologies,

e.g., ATM (Asynchronous Transfer Mode), Ethernet

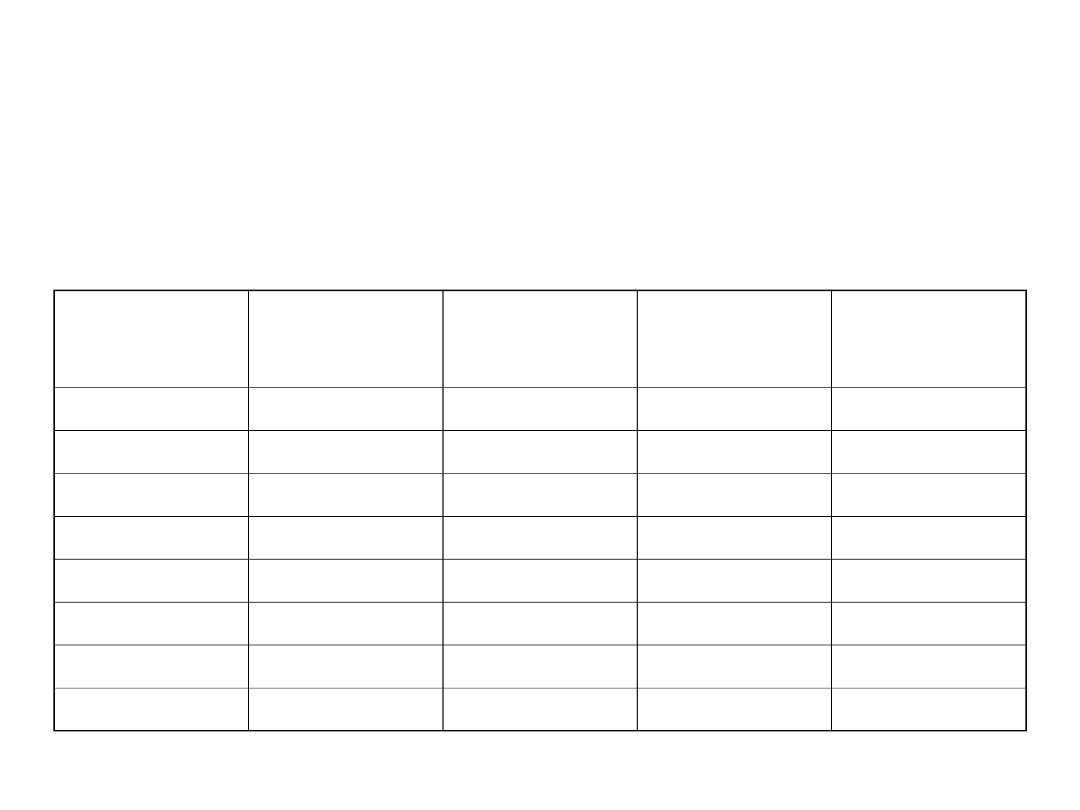
SONET/SDH Designations and

Bandwidths

SONET

Optical

Carrier Level

SONET Frame

Format

SDH level and

Frame Format

Payload

bandwidth

(kbps)

Line Rate

(kbps)

OC-1

STS-1

STM-0

50,112

51,840

OC-3

STS-3

STM-1

150,336

155,520

OC-12

STS-12

STM-4

601,344

622,080

OC-24

STS-24

–

1,202,688

1,244,160

OC-48

STS-48

STM-16

2,405,376

2,488,320

OC-192

STS-192

STM-64

9,621,504

9,953,280

OC-768

STS-768

STM-256

38,486,016

39,813,120

OC-3072

STS-3072

STM-1024

153,944,064

159,252,480

Automatic Protection

Switching

• APS (automatic protection switching), also

known as 1+1 is one of protection method used
in SDH/SONET

• The traffic is transported along both the working

and backup lightpath, then the signal quality is
then compared at the destination node and the
receiver selects the better one

• The most desirable goal of survivable networks is

to keep any interruption of carrier signal flows to
50 ms or less – APS method can assure the
duration of outage time below 50 ms

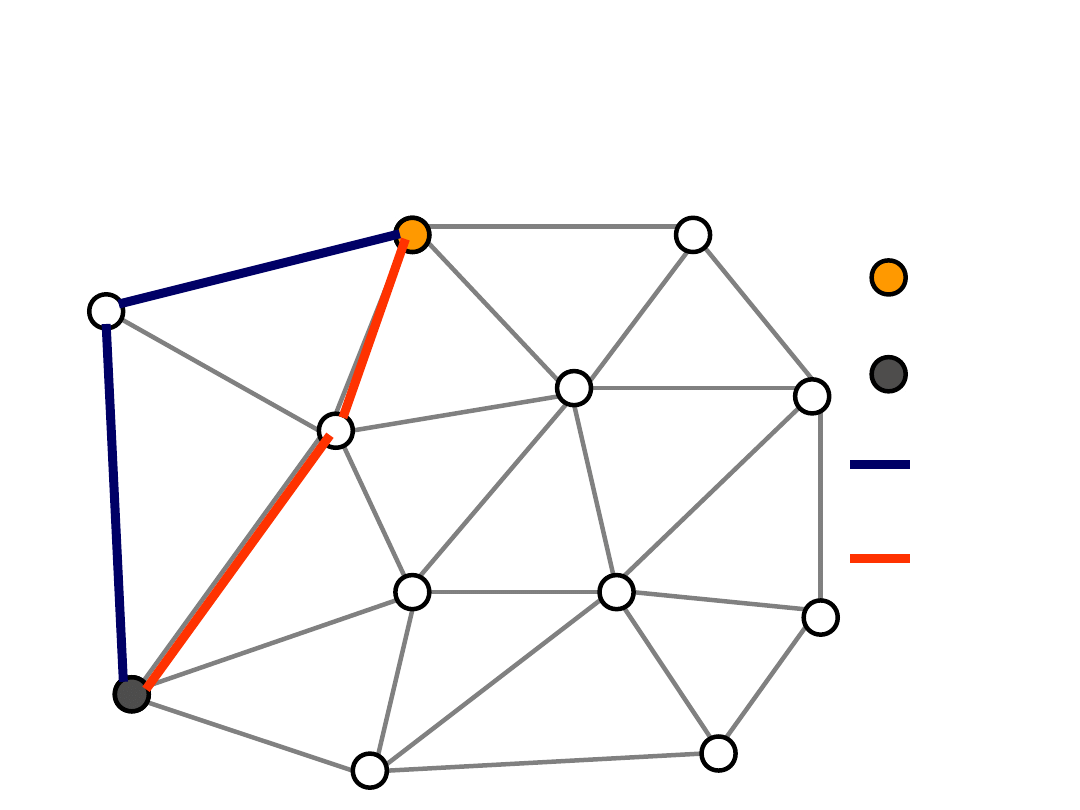
Example

2

1

3

4

12

11

10

8

7

6

9

Source
node

Destination
node

Working
path

5

1

7

Backup
path

Objective

• How to determine SDH/SONET network cost

defined by link capacity so that the total cost of
installed links is minimized

• The network is protected by APS method
• Given: network topology, demands, candidate

pairs of disjoint paths, link module cost

Modeling (1)

• Link-path formulation
• For each demand there are candidate pairs of

failure-disjoint paths p = 1,2,…,P

d

• Working path p for demand d is denoted as w

dp

,

the corresponding backup path is given by b

dp

• Constant



edp

is 1, if link e belongs to working

path w

dp

; 0, otherwise

• Constant



edp

is 1, if link e belongs to backup

path b

dp

; 0, otherwise

Modeling (2)

• Integer variable x

dp

indicates the number of

demand d circuit modules (e.g., STM-4) that
use path p; 0, otherwise

• The volume of demand d is given by h

d

, therefore



p

x

dp

= h

d

, d = 1,2,…,D.

• The flow on link e related to working paths is



d



p

 x

dp



edp

, e = 1,2,…,E.

• The flow on link e related to backup paths is



d



p

 x

dp



edp

, e = 1,2,…,E.

Modeling (3)

• The variable y

e

denotes the number of capacity

modules installed on link e

• M is the size of one module (e.g., given STM-4)




e

is cost of one module in link e

• The network cost is given by



e

y

e



e

• Capacity constraint - flow on each link cannot

exceed the link capacity



d



p

x

dp

(



edp

+



edp

)  y

e

M, e = 1,2,…,E.

Modeling (4)

objective
minimize F = 

e



e

y

e

constraints


p

x

dp

= h

d

, d = 1,2,…,D



d



p

x

dp

(



edp

+



edp

)  y

e

M, e = 1,2,…,E.

x

dp

, y

e

integer and non-negative

Optimization

• This problem has discrete (integer) variables

while the constraints and the objective function
are linear

• Thus, this is an example of a integer linear

programming problem (ILP)

• Branch-and-bound or branch-and-cut algorithms

can provide optimal result

• Various heuristics can be applied

Lecture Outline

• Introduction
• MPLS over GE Network Design
• Tunnels Optimization in MPLS Networks
• SONET/SDH Protection

• Dimensioning of Overlay Networks for P2P

Multicasting

• Access Point Location in WLANs
• Routing and Wavelegth Assignment in Optical

Networks

• Concluding Remarks

P2P Multicasting and Overlays

(1)

• Overlay is a virtual network built on the top of

an existing network (e.g., Internet)

• The underlying physical network provides

point-to-point connectivity including routing

• Overlay P2P multicasting (application-layer

multicast) uses a multicast delivery tree
constructed among peers (end hosts) of the
overlay

• Different to traditional IP multicast, the

uploading (non-leaf) nodes in the tree are
normal end hosts

P2P Multicasting and Overlays

(2)

• Peers are connected to the overlay network,

which is considered as an overprovisioned
cloud - capacity constraints are set only on access
links

• The graph is fully connected, i.e. each peer can

connect to any other peer

• The content to be distributed through P2P

multicasting can be divided into two categories:

– Elastic content (e.g. data files)
– Streaming content with specific bit rate requirements

(e.g. media streaming)

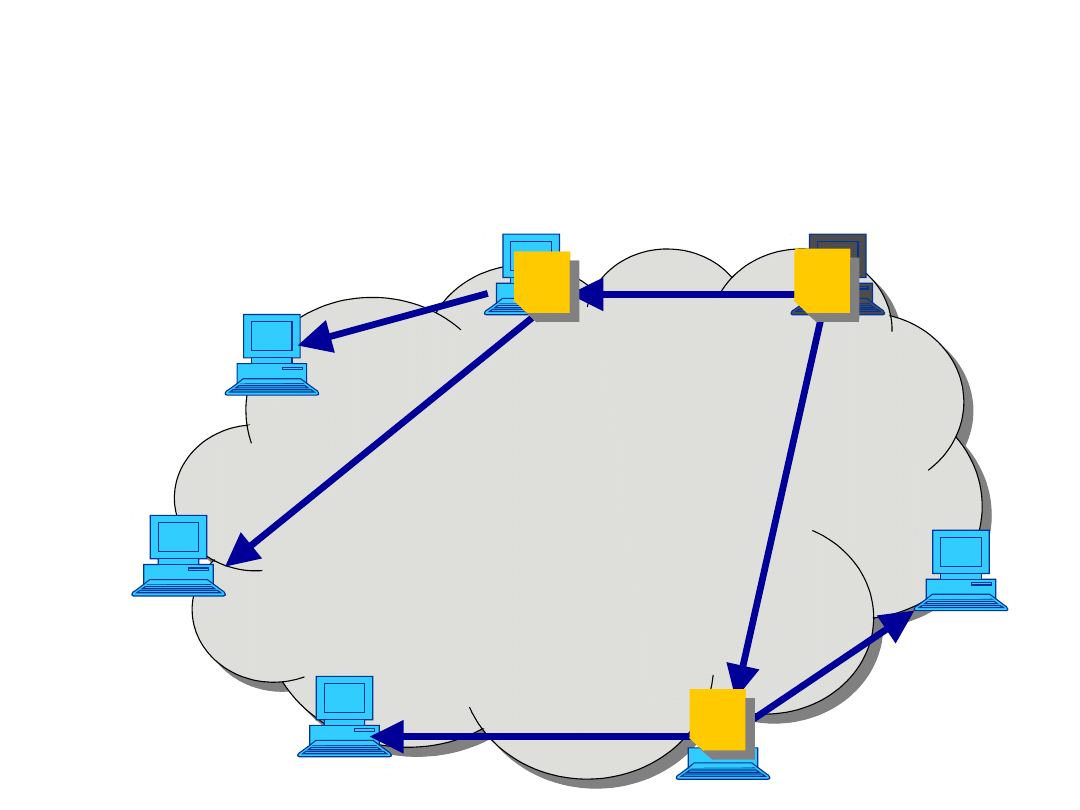
Example

1

2

3

4

5

6

7

Objective

• Minimize the overlay network cost
• The network is used for P2P multicasting of

content with a particular streaming rate

• Network cost is defined as the cost of selected

access links

• Each peer that wants to particpate in the system

has some background traffic

Modeling (1)

• The overlay network consists of V peers (nodes)

indexed by v

• For each peer we are given constants a

v

and b

v

denoting, respectively, download and upload
background traffic given in kbps

• One peer is the root of streaming and denoted

by r

v

= 1

• Each peer is connected to the network using an

access link selected from the candidate links of
a given ISP (Internet Service Provider) indexed by
k

Modeling (2)

• Let



vk

denote the cost of link type k for node v

(Euro/month)

• d

vk

is the download capacity of link type k for node

v (kbps)

• u

vk

is upload capacity of link type k for node v (kbps)

• Binary variable y

vk

is 1, if if node v is connected to the

overlay network by a link of type k; 0 otherwise
(binary)

• The download capacity of node v is 

k

 y

vk

 d

vk

• The upload capacity of node v is 

k

 y

vk

 u

vk

• The network cost is given by 

v



k

 y

vk



vk

Modeling (3)

• The volume of streaming rate is denoted by Q

(kbps)

• Each node must have enough download

capacity to receive the streaming Q and
background traffic a

v

, i.e.,



k

 y

vk

d

vk

  (a

v

 + Q),   v = 1,2,…,V.

• Each node must have enough upload capacity

to transmit background traffic b

v

, i.e.,



k

 y

vk

u

vk

  b

v

,  v = 1,2,…,V.

Modeling (4)

• The summary upload of the overlay network

should enable streaming of Q kbps to each peer

• Thus, the overall upload residual capacity

given by 

v

 (

k

 y

vk

u

vk

– b

v

)

must exceed (V – 1)Q

(we take into account the background traffic and

there are (V – 1) receiving peers)

• Let



denote a dimensioning scaling factor

• In the model we introduce the following

constraint to dimensioning the network for P2P

streaming



v

 (

k

 y

vk

u

vk

– b

v

)  



(V – 1)Q

Modeling (5)

objective
minimize F = 

v



k

 y

vk



vk

constraints


k

y

vk

= 1, v = 1,2,…,V



k

 y

vk

d

vk

  (a

v

 + Q),   v = 1,2,…,V



k

 y

vk

u

vk

  b

v

,  v = 1,2,…,V



v

 (

k

 y

vk

u

vk

– b

v

)  



(V – 1)Q.

y

vk

binary

Optimization

• This problem has binary variables while the

constraints and the objective function are linear

• Thus, this is an example of a integer linear

programming problem (ILP)

• Branch-and-bound or branch-and-cut algorithms

can provide optimal result

• Various heuristics can be applied

Lecture Outline

• Introduction
• MPLS over GE Network Design
• Tunnels Optimization in MPLS Networks
• SONET/SDH Protection
• Dimensioning of Overlay Networks for P2P

Multicasting

• Access Point Location in WLANs

• Routing and Wavelegth Assignment in Optical

Networks

• Concluding Remarks

WiFi (1)

• WiFi (Wireless Fidelity) uses standard proposed

by IEEE 802.11

• WiFi can be used in the following modes:

– IBSS (Independent Basic Service Set) ad hoc

network

– BSS (ang. Basic Service Set) infrastructure

network with one access point

– ESS (ang. Extended Service Set) infrastructure

network with multiple access point

WiFi (2)

• WiFi uses two frequency ranges:

– 2.4 Ghz, ISM (Industry, Science, Medicine)
– 5 GHz, UNII (Unlicensed National Information

Infrastucture)

• WiFi clients (laptops, smart phones, desktops) are

connected to an access point that provides the
radio connectivity

• The most popular versions of WiFi are IEEE

802.11g, 802.11a, 802.11n

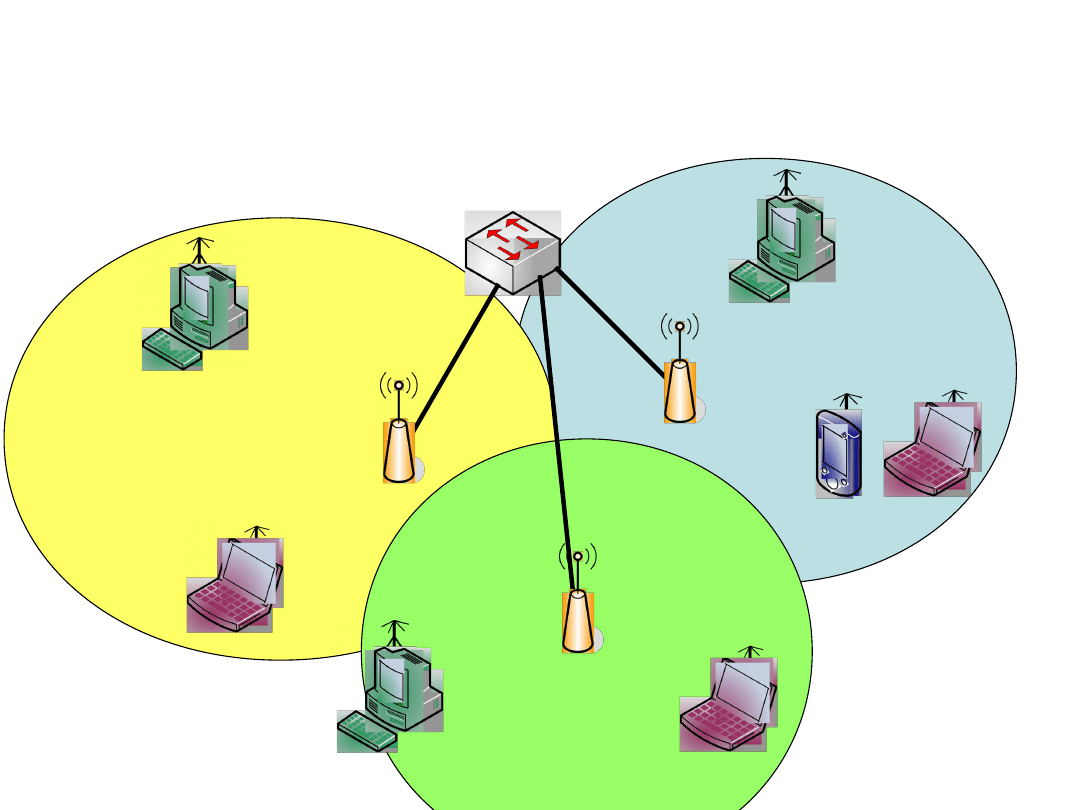
BSS1

Example

BSS2

BSS3

Objective

• Select location of WiFi access points over

candidate locations to maximize the total single-
user throughput overall all test points

• Given: candidate locations of access points, test

points, throughput for each pair of test point and
location

Modeling (1)

• Let identifier a = 1,2,…,A denote a set of

candidate AP (access point) locations

• Let index t = 1,2,…,T denote a set of TP (test

point), denoting potential users

• For each a we define a serving range, so that

TPs (test point) within the serving range of an AP,

let s = 1,2,…,S

a

be a set of of APs for which TP t is

within serving range

• Constant



at

denotes the throughput (quality of

signal) of TP t connected to AP a

Modeling (2)

• Binary variable z

a

is 1, if AP is installed in

location a; 0, otherwise

• There is a limit M on maximum number of

installed APs



a

z

a

 M.

• Binary variable x

at

is 1, if TP t is assigned to AP

installed in location a; 0, otherwise

• The TP can be assigned only to an installed AP

(i.e., z

a

= 1)

x

at

 z

a

, a = 1,2,…,A t = 1,2,…,T.

Modeling (3)

• Each TP can be assigned to maximum one AP



a

x

at

 1, t = 1,2,…,T.

• The system throughput is calculated as



a



t

x

at



at

Modeling (4)

objective
maximize F = 

a



t

x

at



at

constraints
x

at

 z

a

, a = 1,2,…,A t = 1,2,…,T



a

x

at

 1, t = 1,2,…,T



a

z

a

 M

z

a

, x

at

binary

Optimization

• This problem has binary variables while the

constraints and the objective function are linear

• Thus, this is an example of a integer linear

programming problem (ILP)

• Usually the number of candidate APs is small,

therefore branch-and-bound or branch-and-cut
algorithms can provide optimal result in
relatively small time

• Various heuristics can be applied

Lecture Outline

• Introduction
• MPLS over GE Network Design
• Tunnels Optimization in MPLS Networks
• SONET/SDH Protection
• Dimensioning of Overlay Networks for P2P

Multicasting

• Access Point Location in WLANs

• Routing and Wavelegth Assignment in Optical

Networks

• Concluding Remarks

Optical Networks

• WDM (Wavelength Division Multiplexing) is

an optical technology, which multiplexes multiple
optical signals on a single optical fiber by using
different wavelengths (colors) of laser light to
carry different signals

• WDM is a connection-oriented technique, since

the whole signal is transmitted along one path

• Optical devices mostly cannot covert the

wavelength, therefore the whole connection must
use the same color (no wavelength
conversion)

Routing and Wavelength

Assignment

• Routing and Wavelength Assignment (RWA)

the capacity of each link is given

• It has been proven to be a NP-complete

problem

• Two possible objectives:

– Maximal capacity given, i.e., maximize routed

traffic (throughput)

– Offered traffic given, i.e., minimize wavelength

requirement

Objective

• Minimize the number of wavelengths
• Given: network topology, link capacity, demands

(lightpaths), no wavelength conversion

Modeling (1)

• Let d denote a demand defined as a node pair s

d

and t

d

• Demand d that requires h

d

connections

(lightpaths) to be routed in the network

• Let a

ev

= 1, if link e originates at node v; 0,

otherwise

• Let b

ev

= 1, if link e terminates in node v; 0,

otherwise





denotes the number of wavelengths per fiber

• λ is a wavelength index (λ = 1,2,…,



)

Modeling (2)

• Single path routing (non-bifurcated flows)
• There is not wavelength conversion, i.e., the

whole path of the connection must use the same
wavelegth

• Binary variable x

dλ

is 1, if demand d uses

wavelength λ; 0, otherwise

• Binary variable x

edλ

is 1, if demand d uses

wavelength λ on link e; 0, otherwise

• Classical multicommodity formulation and

additional layer for each wavelength

Modeling (3)

• Flow conservation constraints


e

 a

ev

x

edλ

 – 

e

 b

ev

x

edλ

 =  x

dλ

,   if v = s

d

v = 1,2,…,V

d = 1,2,…,D λ = 1,2,…,





e

 a

ev

x

edλ

 – 

e

 b

ev

x

edλ

 = –x

dλ

,   if v = t

d

v = 1,2,…,V

d = 1,2,…,D λ = 1,2,…,





e

 a

ev

x

edλ

 – 

e

 b

ev

x

edλ

 = 0,  if v  s

d

,t

d

v = 1,2,…,V

d = 1,2,…,D λ = 1,2,…,



.

• The whole demand h

d

must be satisifed, i.e.,

there must h

d

ligthpaths for each demand



λ

x

dλ

= h

d

,   d = 1,2,…,D.

Modeling (3)

• Binary variable x

λ

is 1, if wavelength λ is used; 0

otherwise.

• Variable x

λ

is defined by the following constraint

x

dλ

 x

λ

, d = 1,2,…,D λ = 1,2,…,



.

• The clash constraint expresses that no two

lightpaths going through the same fiber link can
use the same wavelength



d

x

edλ

 x

λ

, e = 1,2,…,E λ = 1,2,…,



.

• The number of wavelentghs used in the network

is given by



λ

x

λ

Modeling (4)

objective
minimize F = 

λ

x

λ

constraints


e

 a

ev

x

edλ

 – 

e

 b

ev

x

edλ

 =  x

dλ

,   if v = s

d

v = 1,2,…,V

d = 1,2,…,D λ = 1,2,…,





e

 a

ev

x

edkλ

 – 

e

 b

ev

x

edkλ

 = –x

dλ

,   if v = t

d

v = 1,2,…,V

d = 1,2,…,D λ = 1,2,…,





e

 a

ev

x

edkλ

 – 

e

 b

ev

x

edkλ

 = 0,  if v  s

d

,t

d

v = 1,2,…,V

d = 1,2,…,D λ = 1,2,…,



Modeling (5)

constraints


λ

x

dλ

, = h

d

,  d = 1,2,…,D

x

dλ

 x

λ

, d = 1,2,…,D λ = 1,2,…,





d

x

edλ

 x

λ

, e = 1,2,…,E λ = 1,2,…,



.

X

edλ

, x

dλ

, x

λ

binary

Optimization

• This problem has binary variables while the

constraints and the objective function are linear

• Thus, this is an example of a integer linear

programming problem (ILP)

• Branch-and-bound or branch-and-cut algorithms

can provide optimal result

• Various heuristics can be applied, including

graph coloring methods

Lecture Outline

• Introduction
• MPLS over GE Network Design
• Tunnels Optimization in MPLS Networks
• SONET/SDH Protection
• Dimensioning of Overlay Networks for P2P

Multicasting

• Access Point Location in WLANs
• Routing and Wavelegth Assignment in Optical

Networks

• Concluding Remarks

Concluding Remarks

• Most of real network problems can be modeled

using integer and/or continuous modeling

• Details of the model follow from assumptions

and constraints of the considered technology

• The network traffic is usually modeled by

multicommodity flows

• More the model is closed to technology and

device constraints, more it becomes complicated
and harder to solve

Further Reading

• Pióro M. , Medhi D. , Routing, Flow, and Capacity Design in

Communication and Computer Networks, Morgan Kaufman Publishers

2004

• Jaumard, B., Meyer, C., Thiongane, B.: ILP formulations for the routing

and wavelength assignment problem: Symmetric systems. In: Resende,

M., Pardalos, P. (eds.) Handbook of Optimization in

Telecommunications, pp. 637-677. Springer, Heidelberg, 2006

• Grover W. , Mesh-based Survivable Networks: Options and Strategies

for Optical, MPLS, SONET and ATM Networking, Prentice Hall PTR, Upper

Saddle River, New Jersey, 2004

• Walkowiak K., Dimensioning of Overlay Networks for P2P Multicasting,

12th IEEE/IFIP Network Operations and Management Symposium NOMS

2010, pp. 805-809

• Bosio S. et al., Mathematical Optimization Models for WLAN Planning,

In: Koster A. Munoz X., (eds.) Graphs And Algorithms In

Communication Networks: Studies In Broadband, Optical, Wireless And

Ad Hoc Networks, Springer, 2010