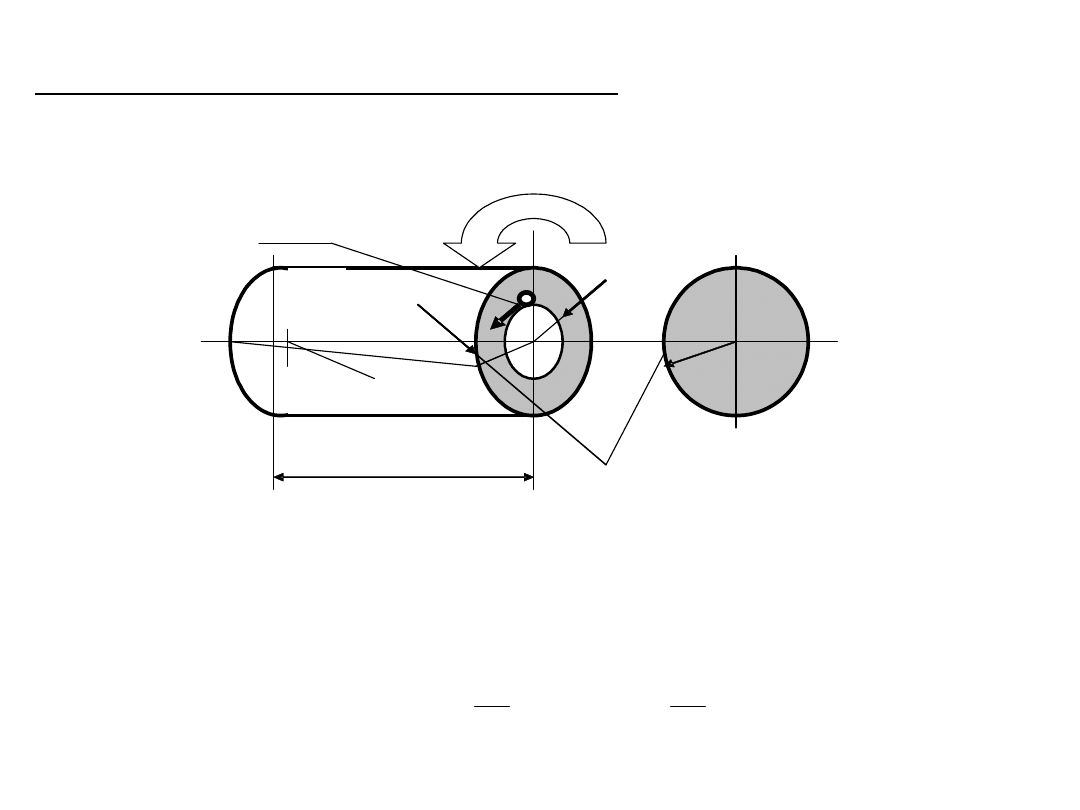
Skręcanie wałów o przekroju kołowym

ds = r d

ds =  dx

r

dx

d



M

s







dA

dM

s

=



dA

Założenia:

-Oś pręta nie podlega żadnym odkształceniom,

-Przekroje poprzeczne pozostają płaskie i nie zmieniają kształtu,

-Tworzące walca przyjmują kształt linii śrubowych o kącie nachylenia 

;

dx

d

;

dx

d

r

r

d

dx































r

0







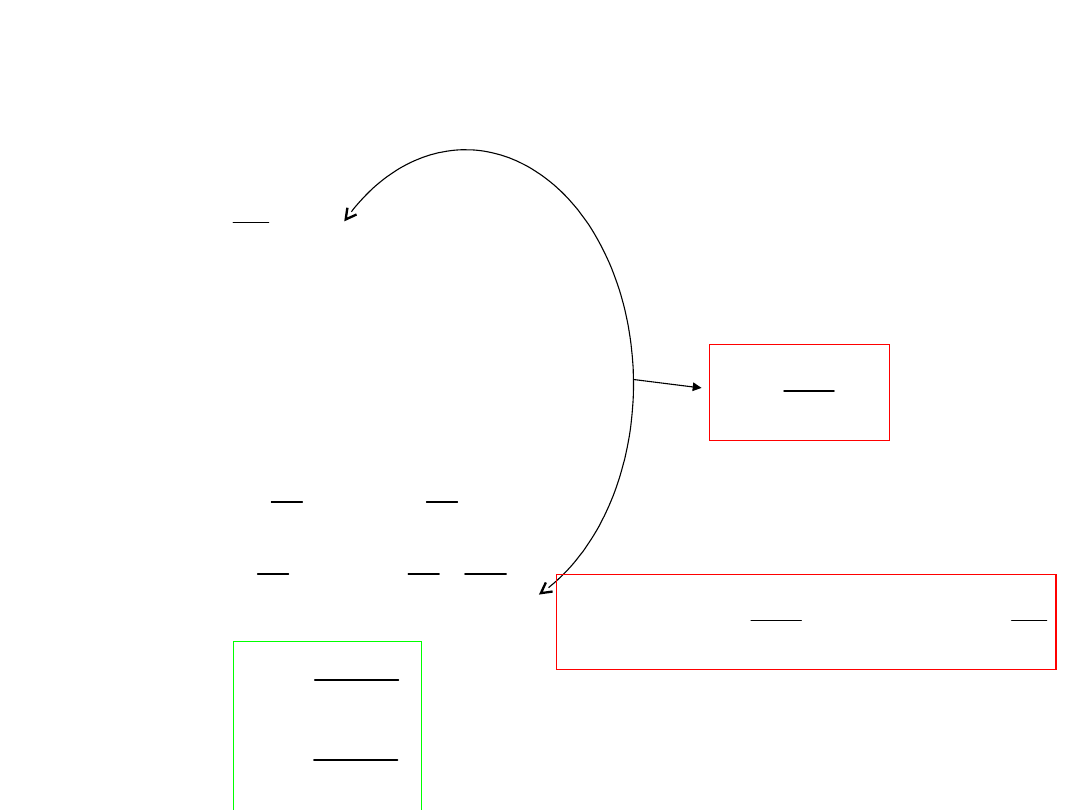
Z prawa Hooke’a dla czystego ścinania:

;

G













;

dx

d

G















Z warunku równowagi:

;

GI

M

dx

d

;

I

dx

d

G

M

;

dA

dx

d

G

dA

dx

d

G

M

;

)

dA

(

M

o

s

o

s

A

2

A

2

s

A

s



















































;

I

M

o

s











r

I

W

;

k

W

M

o

o

s

o

s

max

r

















;

GI

dx

M

;

GI

dx

M

d

i

l

o

s

o

s











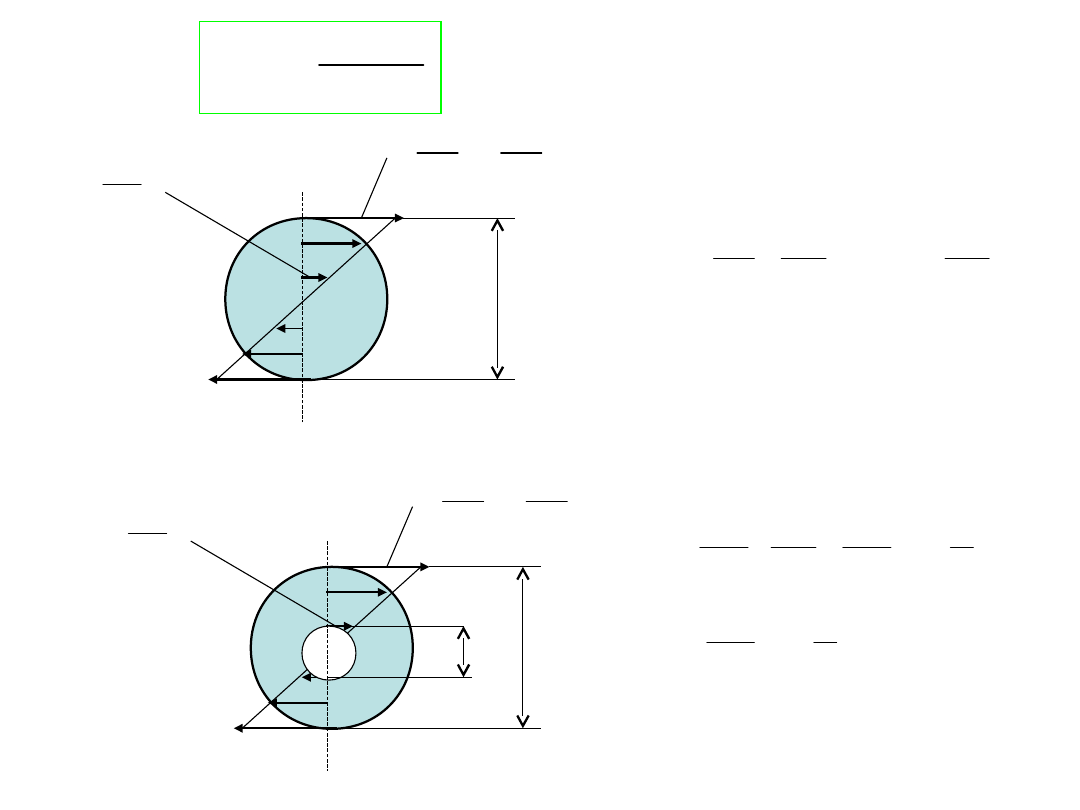
d=2r

;

I

M

o

s











o

s

o

s

max

W

M

r

I

M







16

d

W

;

32

d

2

r

I

3

o

4

4

o













Wały o przekroju drążonym

D

;

I

M

o

s











o

s

o

s

max

W

M

r

I

M







d

































































4

3

o

4

4

4

4

o

D

d

1

16

D

W

;

D

d

1

32

D

32

d

32

D

I









;

)

(





i

o

i

si

GI

l

M





Przeliczenie mocy i ilości obrotów na moment skręcający



Traktując moc jako stosunek pracy momentu skręcającego do czasu
otrzymujemy













s

s

M

t

M

N

 



















sek

J

1000

kW

N

s

/

1

60

/

n

2

]

m

N

[

M

s

















min

/

9550

obr

kW

n

N

M

s

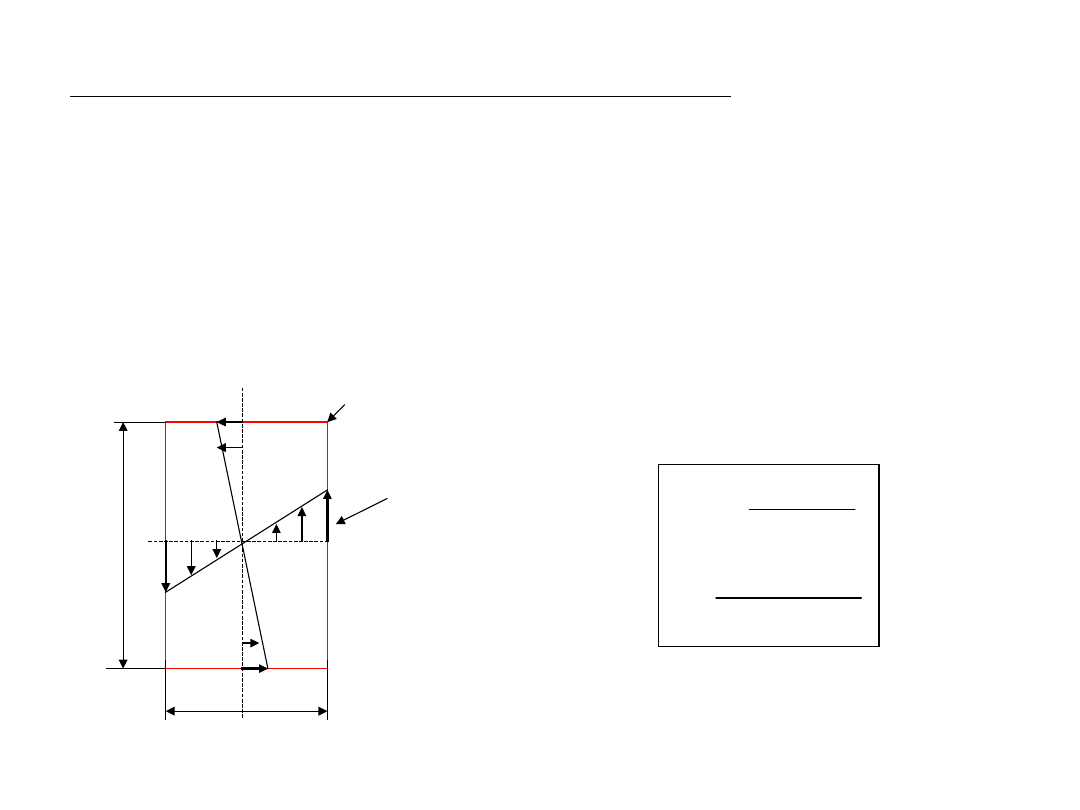
Skręcanie swobodne prętów o przekroju prostokątnym

Odkształcenie przekroju skręcanego pręta składa się z:

 obrotu dookoła osi przekroju poprzecznego jako sztywnej całości;

 przemieszczeń poszczególnych punktów przekroju w kierunkach równoległych do
osi pręta – swobodne paczenie się przekroju.

Naprężenie tnące musi mieć kierunek styczny do konturu
W narożach naprężenie jest równe zero.

;

;

3

2

max

b

a

G

M

b

a

M

s

s

























max

=

0

a

b

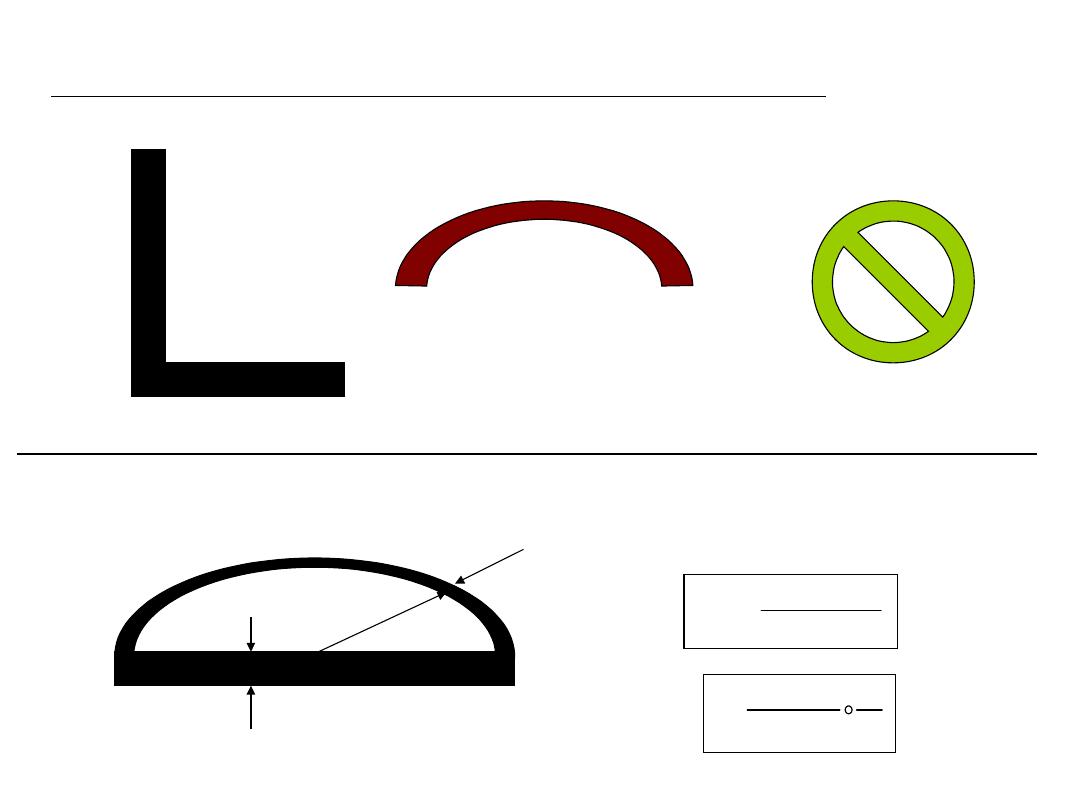
Skręcanie swobodne prętów o przekroju cienkościennym

Skręcanie swobodne prętów o przekroju cienkościennym zamkniętym – wzory Bredta

(s)



(s)

;

A

2

M

sr

min

s

max











.

)

(

)

(

const

s

s









;

ds

A

G

4

M

2

sr

s













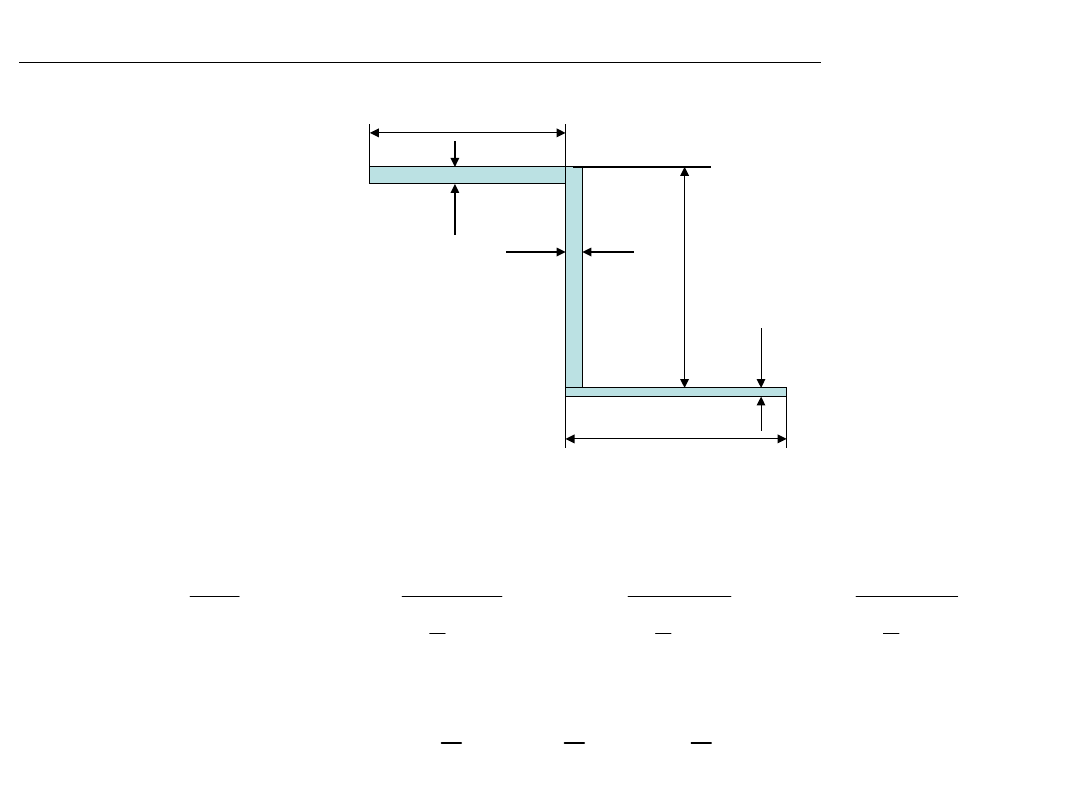
Skręcanie swobodne prętów o przekroju cienkościennym otwartym

a

1

a

2

a

3



1



2



3

;

;

1

3

2

1













n

i

si

s

s

s

s

s

M

M

M

M

M

M

Jednostkowy kąt skręcenia

.

3

2

1

const

n





















;

3

1

;

3

1

;

3

1

;

3

3

3

3

3

3

2

2

2

2

3

1

1

1

1















a

G

M

a

G

M

a

G

M

GJ

M

s

s

s

s

s









)

3

1

3

1

3

1

(

3

3

3

3

2

2

3

1

1











a

a

a

G

GJ

s







)

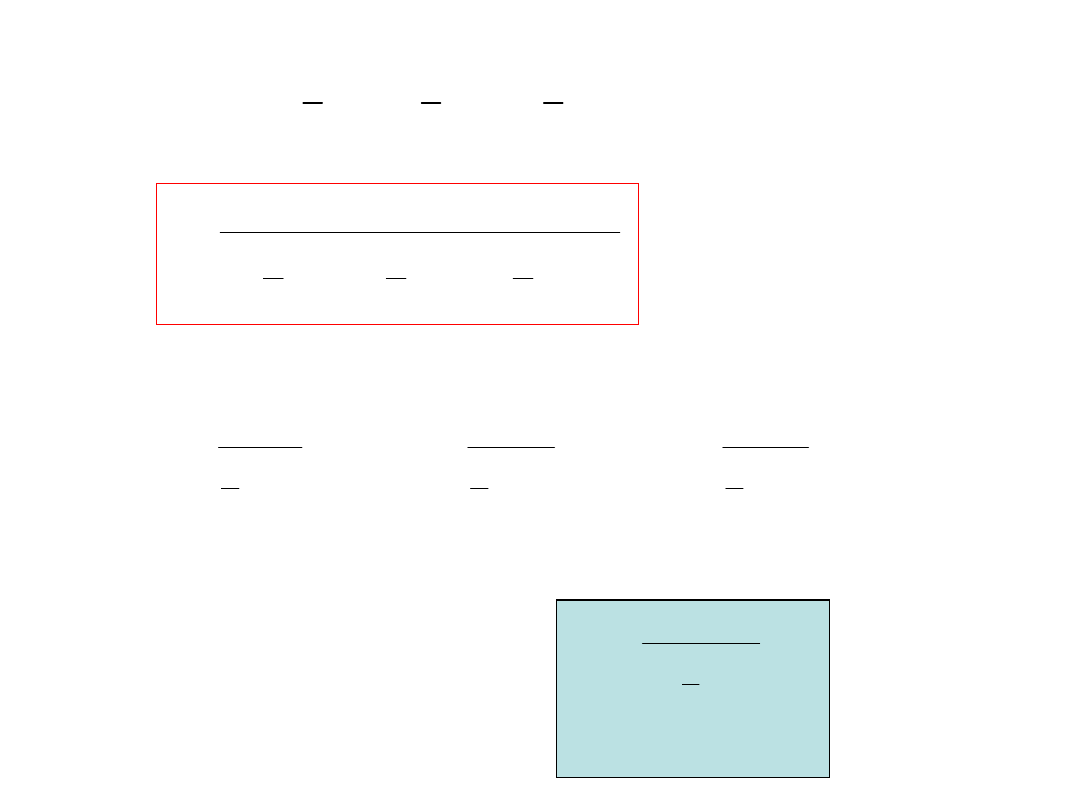
3

1

3

1

3

1

(

3

3

3

3

2

2

3

1

1







a

a

a

J

s







;

)

3

1

3

1

3

1

(

3

3

3

3

2

2

3

1

1









a

a

a

G

M

s







Jednostkowy kąt skręcenia

Naprężenia

;

;

;

;

;

3

1

;

3

1

;

3

1

max

max

3

3

2

2

1

1

3

3

3

3

3

3

2

3

2

2

2

2

1

3

1

1

1

1









































































G

G

G

G

a

M

a

M

a

M

s

s

s

s

n

i

i

i

s

k

a

M









max

max

1

3

max

;

3

1







