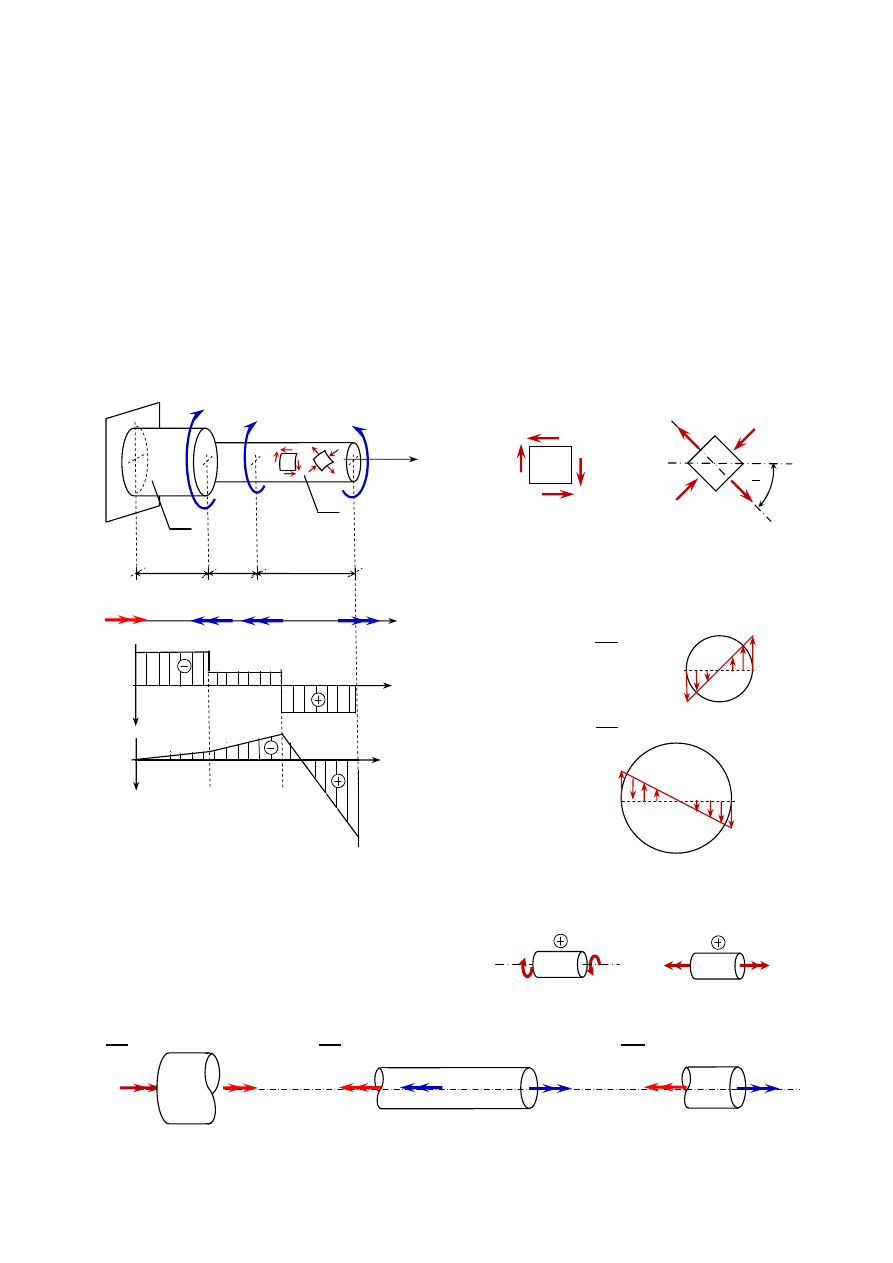
Zadanie 12.1. Pręt

o długości 3a zamocowany w lewym końcu jest obciążony jak na rysunku.

a) Sporządzić wykres momentów skręcających i kątów skręcenia oraz naprężeń stycznych w

najbardziej wytężonych przekrojach odcinków AB i BD. Określić maksymalna wartość

naprężenia stycznego. Określić wartości i kierunki naprężeń głównych oraz pokazać ich

wektory na elementarnym wycinku powierzchni pręta.

Dane: a = 1m, M

s

= 2 kNm, średnica d = 10 cm, G = 80 GPa

b) Wyznaczyć średnicę d wału przy założeniu, że naprężenie styczne w najbardziej

wytężonym przekroju wału nie może przekroczyć wartości R

t

= 75MPa. Przyjmując

obliczoną średnicę d kąt skręcenia wału

ϕ

i sprawdzić warunek

ϕ

≤

ϕ

dop

= 0,04 rad.

Ad. a)

Moment reakcji i wykres momentów skręcających:
∑

=

−1,5

− 3 +2

= 0 ,

= 2,5

= 5

Dodatni moment skręcający ma
zwrot normalnej zewnętrznej przekroju.

Momenty skręcające w przekrojach kolejnych odcinków wału:

AB

BC

CD

= −

= −5

= −

= −2

= 2

= 4

M

S

M

S

≡

M

S

M

S

τ

21

Wektory
momentów
skręcających

M

s

[kNm]

ϕ

[rad]

0,0340

d

2d

0,5a

a

1,5M

S

2M

S

1,5a

3M

S

x

1

A

B

D

C

x

1

4

5

2

1,5M

S

2M

S

3M

S

M

R

0,0023

0,0096

a)

c)

3M

S

M

BC

2M

S

2M

S

M

R

M

AB

M

CD

A

D

D

C

τ

21

τ

12=

τ

max

τ

12=

τ

max

σ

1=

τ

max

σ

2

σ

2=

τ

max

σ

1

b)

τ

max

=

20,4 MPa

20,4

CD

Naprężenia styczne

τ

[MPa]:

3,2

3,2

20,4

AB

d)

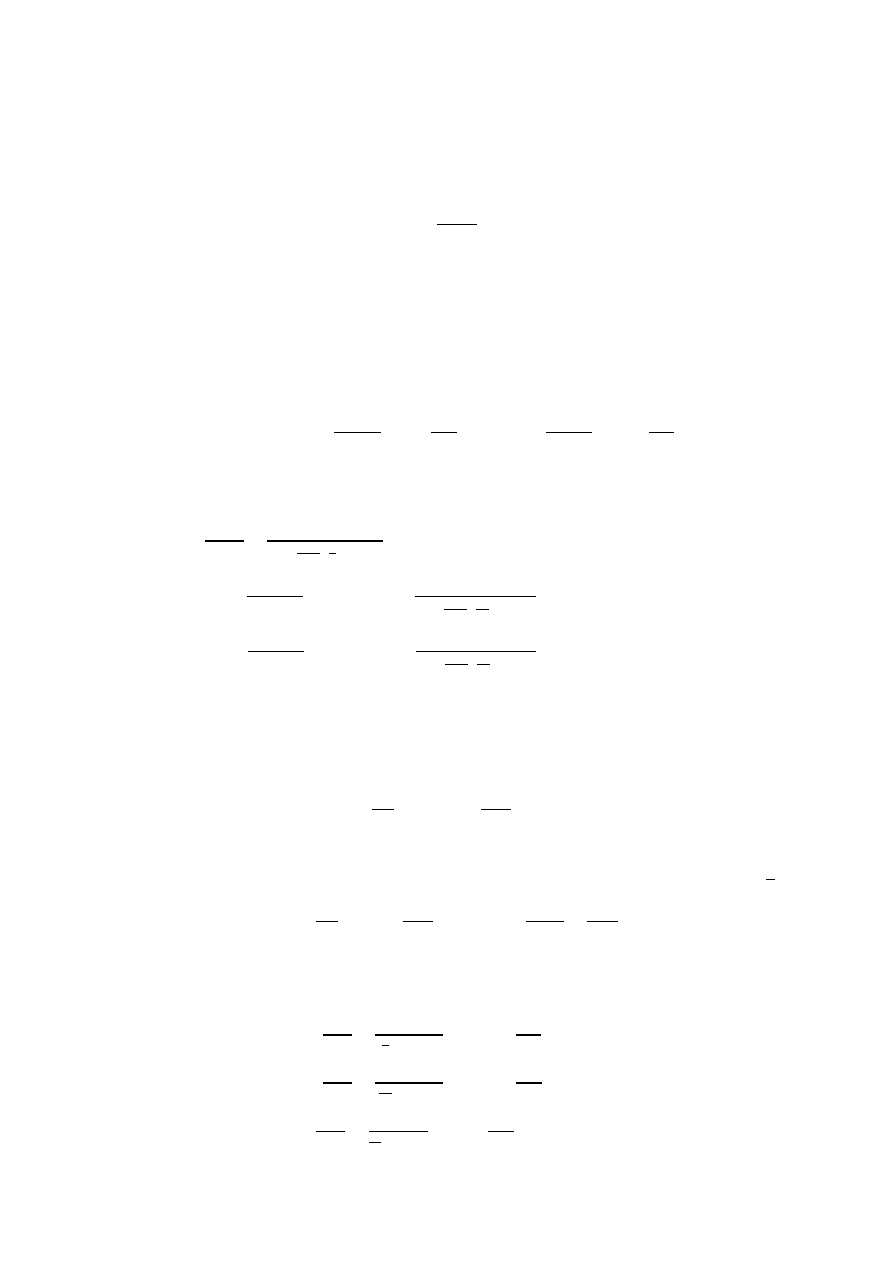
Wykres kątów skręcenia, d = 10 cm.

Względny kąt skręcenia

ϕ

skrajnych przekrojów, odcinka wału o stałym przekroju,

długości l , obciążonego momentem skręcającym M

S

jest równy

=

∙

∙ ,

gdzie G - moduł Kirchoffa, J

0

- biegunowy moment bezwładności. GJ

o

jest sztywnością

skręcania. W zadaniu wał jest utwierdzony w A, tam kąt skręcenia jest równy zeru. Kąt

skręcenia przekroju B względem przekroju A, jak również zmianę kąta skręcenia

ϕ

wzdłuż

kolejnych odcinków wału, oblicza się ze wzoru (1).

W dalszej części, obliczenia będą wykonywane w jednostkach [kN] i [cm]:

1 ! =

"

#

$%

"

&

'(

)

= 0,1

$%

'(

)

, 1 ! =

"

*

$%

"

&

'(

)

= 100

$%

'(

)

.

Wartości kątów skręcenia przekrojów:

= 0

=

,

-

./

∙0

12

3

./

=

45 $%'(∙" '(

6

78

9:)

∙

;

)

"

&

'(

&

= −0,0004 <!=

=

+

,

-

/>

∙ ,50

12

3

/>

= −0,0004 +

4? $%'(∙5 '(

6

78

9:)

∙

;

#)

"

&

'(

&

= −0,0017 <!=

=

+

,

-

>A

∙",50

12

3

>A

= −0,0017 +

$%'(∙"5 '(

6

78

9:)

∙

;

#)

"

&

'(

&

= 0,0059 <!=.

Wykres kątów skręcenia dla d = 10 cm przestawiono na rys. c).

Wykres naprężeń stycznych, d = 10 cm.

Naprężenia styczne

τ

, w punkcie wału, którego położenie określono promieniem

ρ

, 0

≤

ρ

≤

r :

gdzie M

S

jest wartością momentu skręcającego w przekroju, J

o

- biegunowym momentem

bezwładności. Największa wartość naprężenia

τ

wystąpi w skrajnym włóknie, dla

C

(0D

=

E

?

∶

G

(0D

=

H

ρ

(0D

=

I

H

, I

H

=

H

C

(0D

=

J=

K

16 ,

gdzie W

o

jest biegunowym wskaźnikiem przekroju.

Max naprężenia styczne w przekrojach kolejnych odcinków wału wynoszą:

odcinek AB:

G

(0D

=

,

./

M

N

./

=

45 $%'(

;

)

"

#

'(

#

= −0,32

$%

'(

)

= −3,2 !

odcinek BC:

G

(0D

=

,

/>

M

N

/>

=

4? $%'(

;

O*

"

#

'(

#

= −1,02

$%

'(

#

= −10,2 !

odcinek CD:

G

(0D

=

,

>A

M

N

>A

=

$%'(

;

O*

"

#

'(

#

= 2,04

$%

'(

)

= 20,4 !

(1)

G =

H

ρ

,

H

=

J=

32 ,

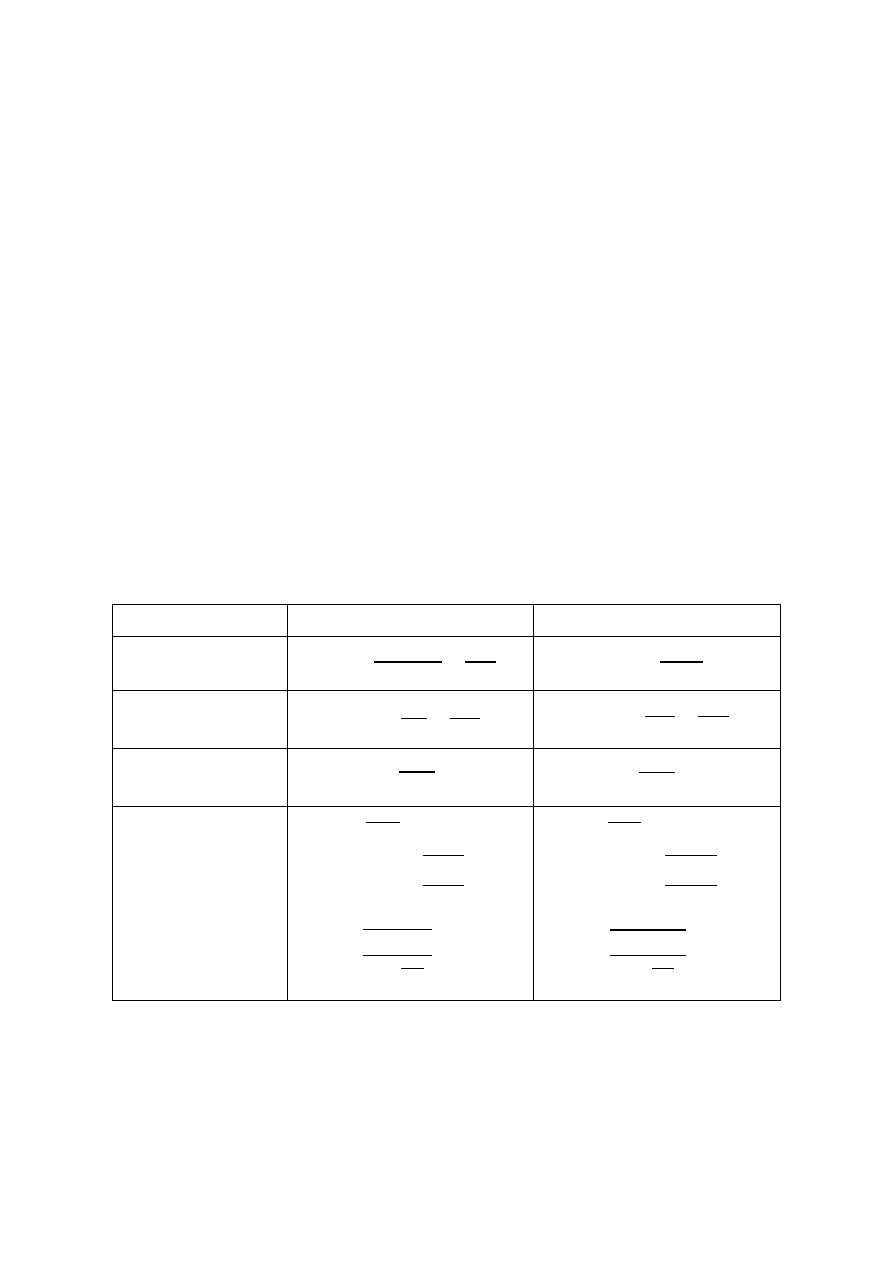
Przekroje wzdłuż odcinka CD są najbardziej wytężone, występuje tu największe naprężenie

styczne,

G = 20,4 MPa . Wektor naprężenia na powierzchni bocznej wału ma kierunek

prostopadły do osi wału. Aby spełnione były równania równowagi, sumy momentów

względem środka elementu powierzchniowego, naprężenia o tej samej wartości muszą być

również na ściankach elementu równoległych do osi walu. Na powierzchni bocznej wałka

realizowany jest stan czystego ścinania, dla którego naprężenia główne, występują w

kierunkach nachylonych do osi wału pod kątem 45° i 135

0

:

S

(TU/(0D

= ±G

(0D

= ±75MPa .

Wykresy naprężeń na rys. b) i d).

Ad. b)

Projektowanie średnicy wału.

Największa wartość momentu skręcającego występuje wzdłuż odcinka AB, jednak ze względu

na różne średnice wału, największe wartości naprężeń, przekroje najbardziej wytężone, mogą

wystąpić wzdłuż odcinków AB lub CD. W obliczeniach należy uwzględnić obydwa odcinki.

Obliczenia zestawiono w tabeli.

Odcinek AB:

Odcinek CD:

Biegunowy moment
bezwładności

H

=

J ∙ X2=Y

32

=

J=

2

H

=

J ∙ =

32

Biegunowy wskaźnik
wytrzymałości

I

H

=

H

= =

J=

K

2

I

H

=

H

=/2 =

J=

K

16

Max wartość
naprężenia stycznego

G

(0D

= I

H

≤ [

\

G

(0D

= I

H

≤ [

\

Obliczenia promienia
odcinka wału

,

./

E

./

#

2 ≤ [

\

= ≥ ^

2

J ∙ [

\

#

= ≥ ^

?∙5 $%'(

∙_,5

78

9:)

#

= 3,49 `

,

>A

E

>A

#

16 ≤ [

\

= ≥ ^

16

J ∙ [

\

#

= ≥ ^

"a∙

$%'(

∙_,5

78

9:)

#

= 6,47 `

Pomimo, że wzdłuż odcinka CD wartość momentu skręcającego jest mniejsza, wał tutaj jest

bardziej wytężony. Wymagana jest większa średnica do przeniesienia obciążenia. Przyjęto

ś

rednicę wału d = 6,47 cm,

Wartości max naprężeń stycznych, d = 6,47 cm.

odcinek AB:

G

(0D

=

,

./

M

N

./

=

45 $%'(

;

)

a, _

#

'(

#

= −1,17

$%

'(

)

= −11,7 !

odcinek BC:

G

(0D

=

,

/>

M

N

/>

=

4? $%'(

;

O*

a, _

#

'(

#

= −3,75

$%

'(

#

= −37,5 !

odcinek CD:

G

(0D

=

,

>A

M

N

>A

=

$%'(

;

O*

a, _

#

'(

#

= 7,5

$%

'(

)

= 75 !

W prawidłowo zaprojektowanym wale w najbardziej wytężonych przekrojach naprężenia

styczne są równe naprężeniom dopuszczalnym,

G = 75MPa = R

c

.

Wartości kątów skręcenia, d = 6,47cm.

Kąty skręcenia kolejnych przekrojów wału względem przekroju A :

= 0

=

,

-

./

∙0

12

3

./

=

45 $%'(∙" '(

6

78

9:)

∙

;

)

a, _

&

'(

&

= −0,0023 <!=

=

+

,

-

/>

∙ ,50

12

3

/>

= −0,0023 +

4? $%'(∙5 '(

6

78

9:)

∙

;

#)

a, _

&

'(

&

= −0,0096 <!=

=

+

,

-

>A

∙",50

12

3

>A

= −0,0049 +

$%'(∙"5 '(

6

78

9:)

∙

;

#)

a, _

&

'(

&

= 0,034 <!=.

Sztywność skręcania wału projektowanego jest mniejsza ze względu na mniejszą średnicę. Z

tego powodu całkowity kąt skręcenia wału jest większy. Obliczony max kąt skręcenia wału

jest mniejszy od kąta dopuszczalnego

ϕ

dop

= 0,04 rad.

Wniosek końcowy.

W obydwu powyższych przypadkach wartości momentów skręcających są identyczne.

Wartości kątów skręcenia wału oraz wykresy naprężeń stycznych są natomiast różne ale

proporcjonalne, zależą one od sztywności skrętnej wału. Mniejsza sztywność skrętna GJ

O

dla

wału o zaprojektowanej średnicy powoduje większe wartości kąta skręcenia.