Drgania mechaniczne

Rok II

mgr inż. Piotr Kohut

D1- IV p., p.407

Literatura



1. J. Giergiel „Drgania układów
mechanicznych”



2. J. Giergiel „Zbiór zadań z mechaniki
ogólnej”



3. W. Bogusz „Drgania mechaniczne”



4. Z. Osiński „Teoria drgań”

Program zajęć



1.

(09.10)

RDR*



2.

(23.10)

Kol. (RDR)

+ drgania nietłumione s/w**

układów o 1DOF***



3.

(06.11)

Drgania tłumione s/w układów o 1 DOF



4.

(20.11)

Laboratorium (układy z/bez tłumienia o 1 DOF)



5.

(04.12)

Kol.(układy o 1 DOF)



6

. (18.12)

Wibroizolacja



7.

(09.01)

Kol. (wibroizolacja)



8.

(23.01)

Zaliczenia



* równania dynamiczne ruchu



* * swobodne/wymuszone



*** stopień swobody

Równania dynamiczne
ruchu



1. Metoda Newtona

–

Ruch postępowy

–

Ruch obrotowy

–

Ruch płaski



2. Równania Lagrange’a II
rodzaju

Zagadnienia

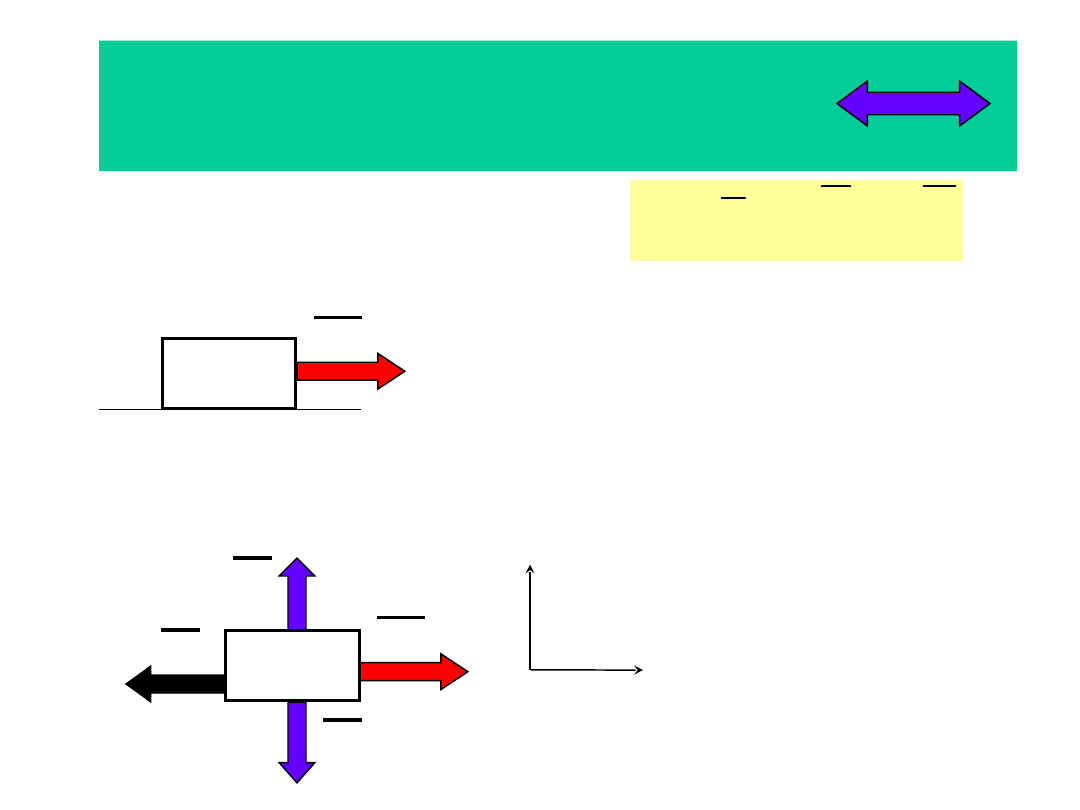
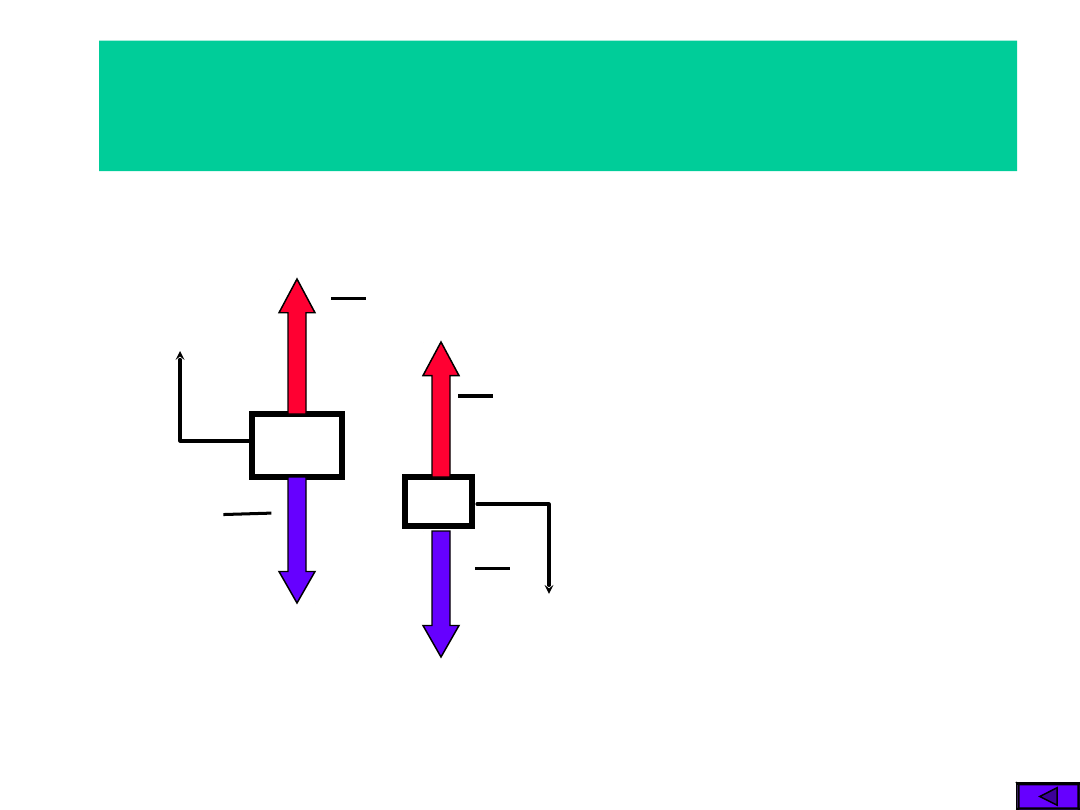
Metoda Newtona









R

P

a

m

.

1

m

P

1. Ruch postępowy

z

R

z

P

z

m

.

y

R

y

P

y

m

.

x

R

x

P

x

m

.































4

3

2

1.1. Oswobodzenie
układu

m

P

T

G

N

x

y

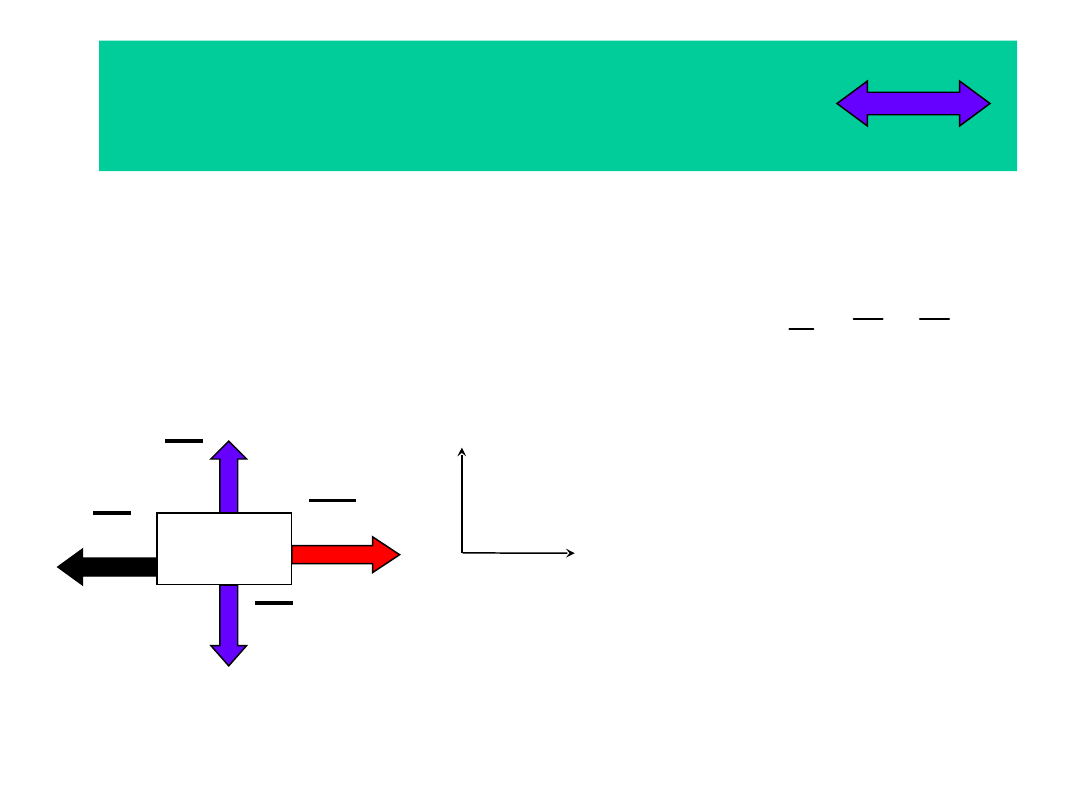
Metoda Newtona

1.2. Równania dynamiczne ruchu w
kierunku osi 0X, 0Y

N

T

.

G

N

y

m

.

T

P

x

m

.















8

0

7

6





m

P

T

G

N

x

y

T

P

a

m

.





5

G

P

x

m

.









9

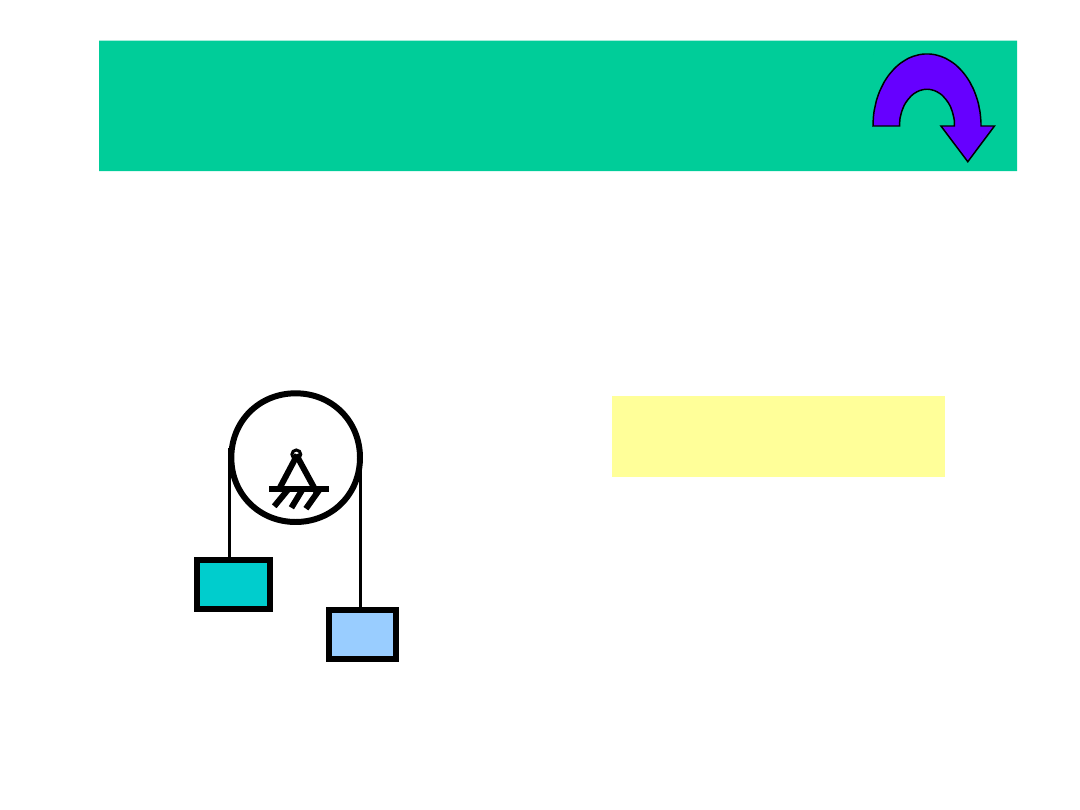
Metoda Newtona

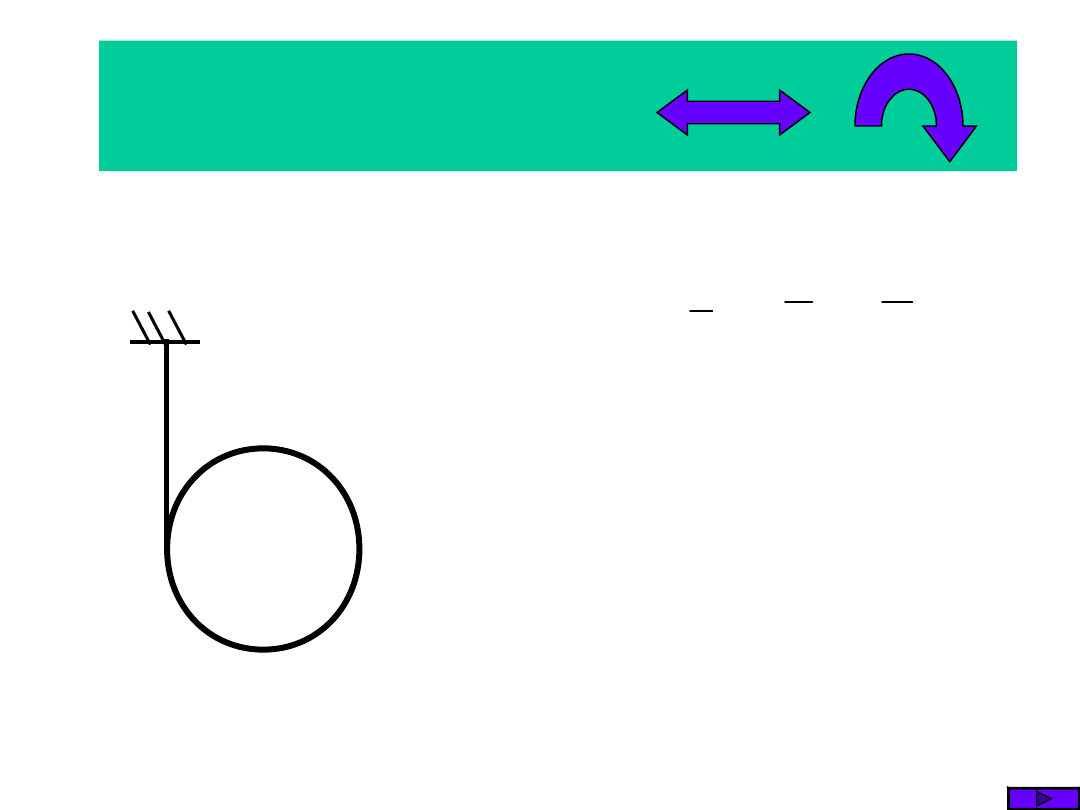
2. Ruch obrotowy





o

M

o

J

.

.

1

2



m

m1

2m,
r

Metoda Newtona

2.1. Oswobodzenie
układu

2m,
r

S

S
1

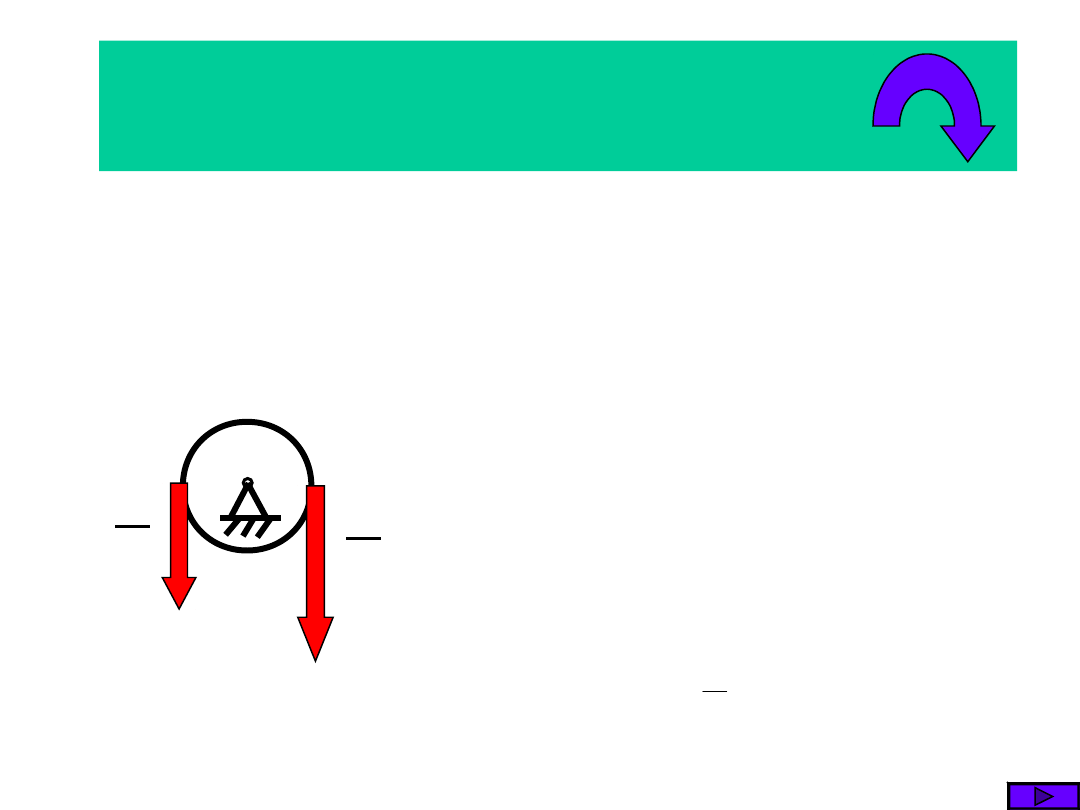
2.2. Równanie dyn.
ruchu

w ruchu obrotowym

2

2

2

1

2

2

1

1

2

r

*

m

o

J

.

.

r

*

S

r

*

S

o

J

.

.









Metoda Newtona

m

S

G

x

m1

S
1

G
1

x

1

1

1

4

2

3

2

G

S

x

m

.

.

S

G

x

m

.

.













(2.4), (2.3) --> (2.1)

Metoda Newtona

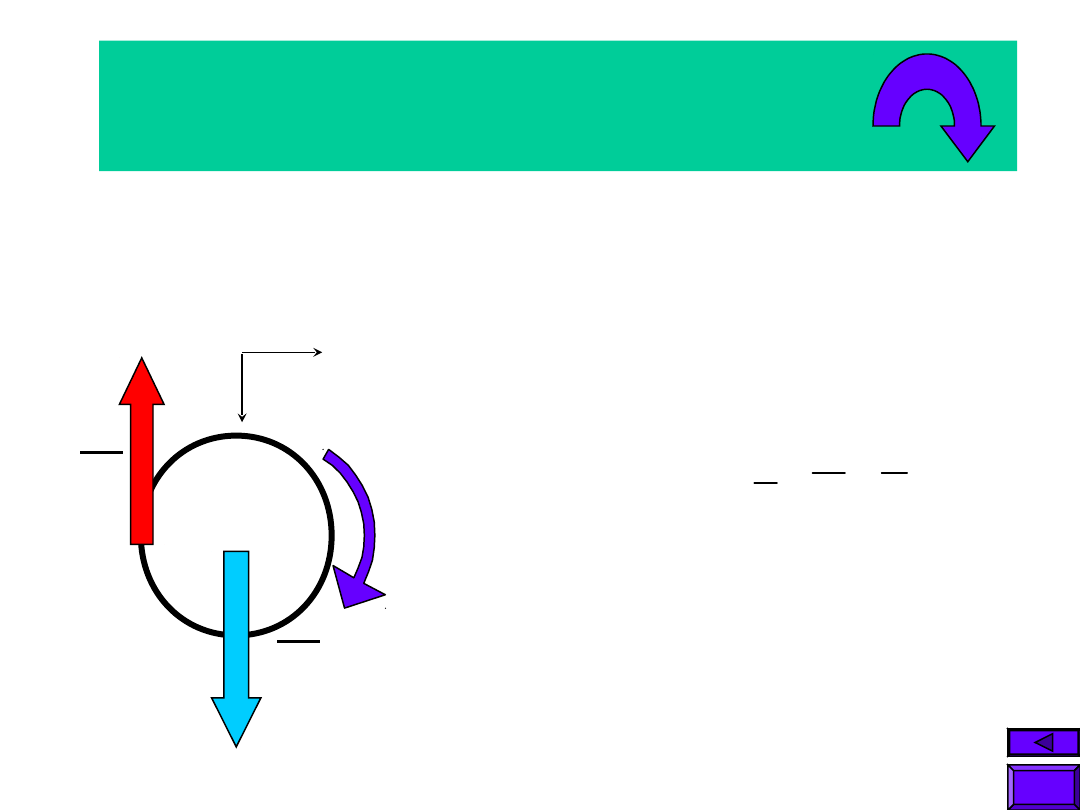
3. Ruch płaski

z

R

z

P

z

m

y

R

y

P

y

m

x

R

x

P

x

m

R

P

a

m











































o

M

o

J



o

m, r

Ruch postępowy

Ruch obrotowy

Sz:
a

Metoda Newtona

3.1.
Oswobodzenie
układu

3.1.1. RDR w
ruchu

postępowym

0

3

3

2

3

1

3











y

m

.

.

S

G

x

m

.

.

S

G

a

m

.

.





o

S

G

x

y



O

Metoda Newtona

(3.5) -->
(3.2)

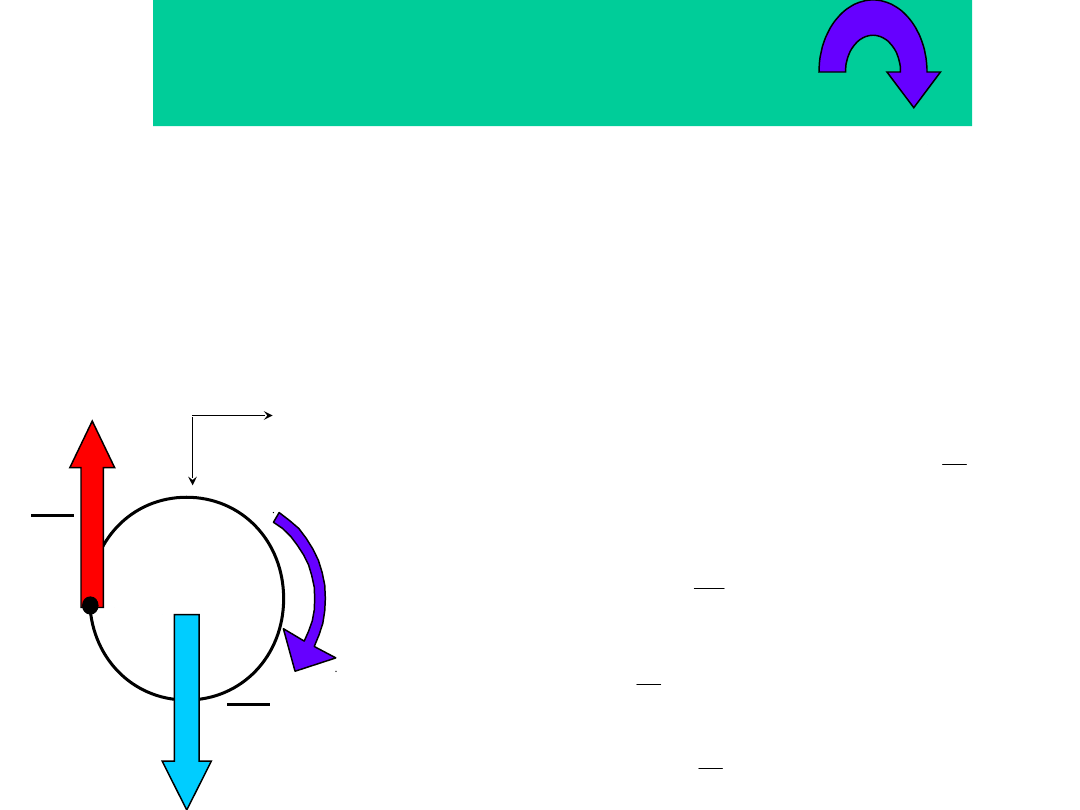
3.1.2. RDR w ruchu
obrotowym

r

x

.

.

r

*

S

o

J

.

.

o

M

o

J

.

.

















6

3

5

3

4

3

Metoda Newtona

3.1.3. RDR w ruchu obrotowym wzgl.
chwilowego środka obrotu - pkt.c

o

S

G

x

y



c

g

x

.

.

mg

x

m

.

.

r

x

.

.

r

*

m

r

*

m

o

J

c

J

.

.

r

*

G

c

J

.

.

3

2

15

3

2

3

14

3

13

3

2

2

3

2

12

3

11

3





























c

M

c

J

.

.



10

3

Równania Lagrange,a II

rodzaju

j

q

D

.

j

q

V

jp

Q

.

.

















d

E

3

4

2

4

nia).

(rozprasza

dyssypacji

Energia

.

1..s

j

1

4

























































j

Q

jp

Q

j

q

E

j

q

E

dt

d

.

.



j

Q

j

q

D

j

q

V

j

q

E

j

q

E

dt

d

.

.





































































4

4

Równania Lagrange’a II

rodzaju

Energia kinetyczna

E

E = E

p

+ E

0

E

p

= ½ mv

2

E

o

= ½ J

o



2

Energia potencjalna

sił sprężystości

V

V = ½ kx

2

Energia dyssypacji

D

D = ½ cv

2

Rozwiąz

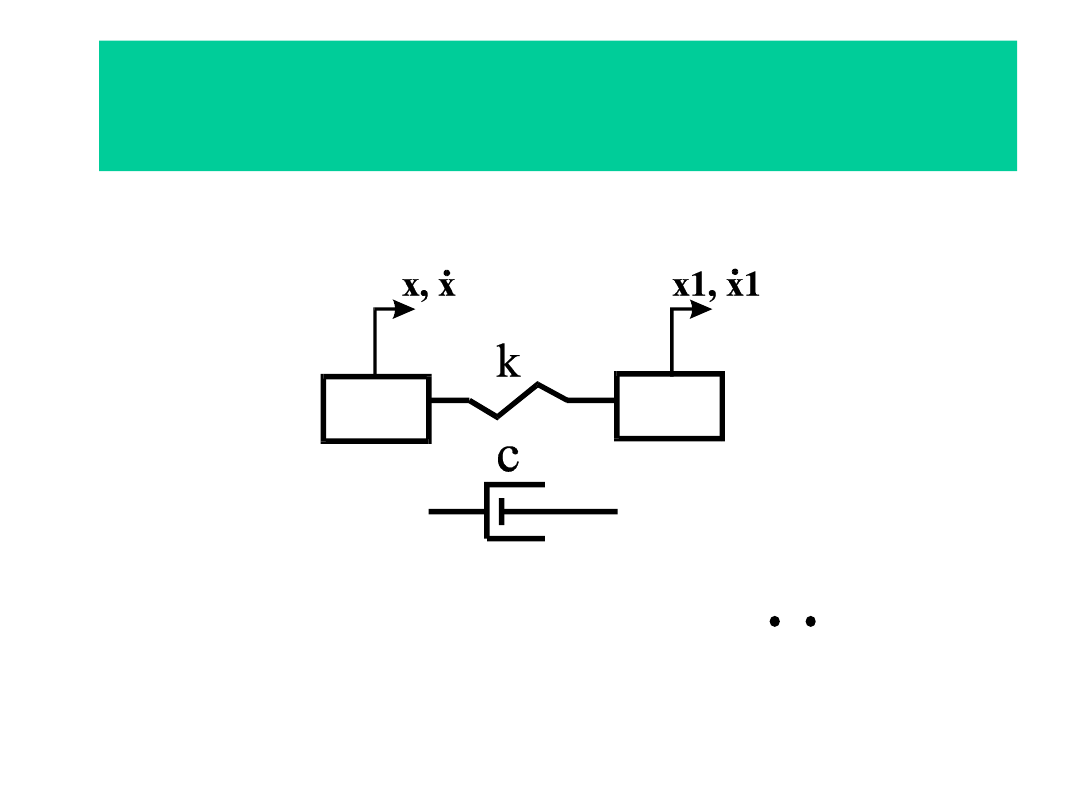
Równania Lagrange’a II

rodzaju

m

m 1

D = ½ c(x-x1)

2

V = ½ k(x-x1)

2

j

s

1

j

j

i

i

,

j

s

1

j

j

i

z

i

z

,

j

s

1

j

j

i

y

i

y

,

j

s

1

j

j

i

x

i

x

q

q

q

q

q

q

q

q





 











 











 











 







4.7.

Więzy skleronomiczne holonomiczne
(więzy geometryczne nie zależą jawnie od
czasu)























































s

1

=

j

n

1

i

n

1

i

zi

iz

P

yi

iy

P

xi

ix

P

L

j

q

j

i

i

Q

M

4.5.

1..s

=

j

n

1

i

j

i

z

iz

P

j

i

y

iy

P

j

i

x

ix

P

j

Q























































q

q

q

4.6.

Prace przygotowane



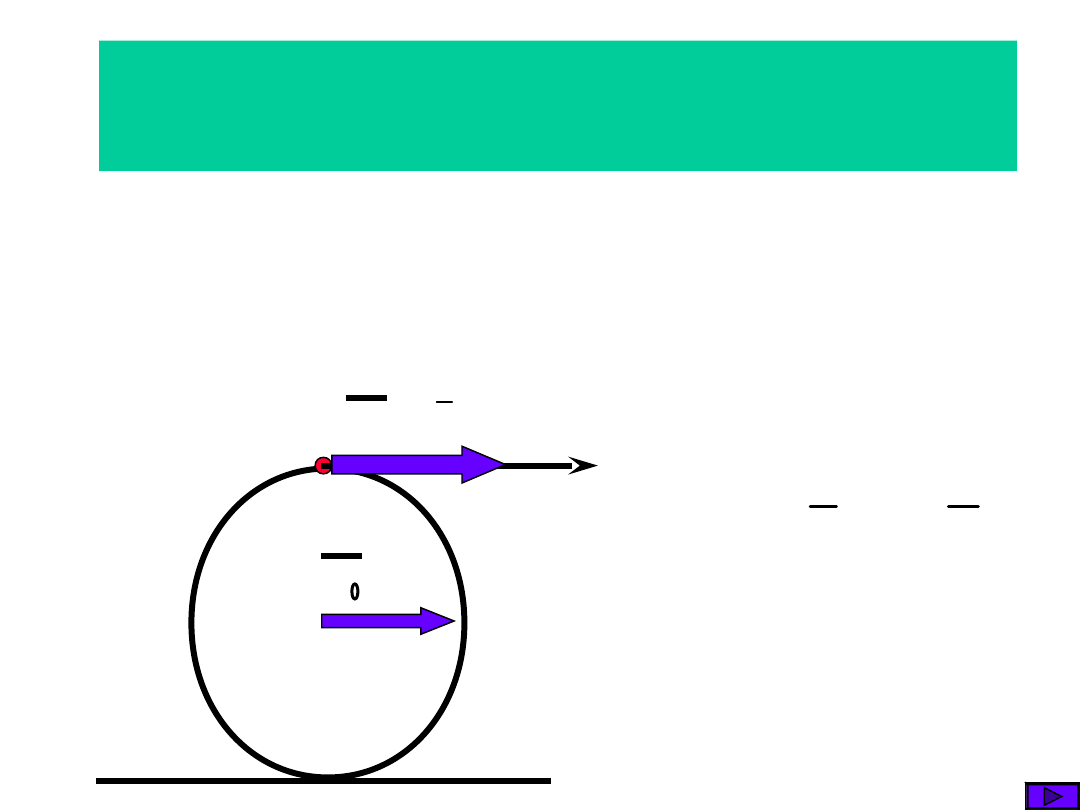
Przesunięcie możliwe -zgodne z więzami



Prędkość możliwa - zgodna z więzami

 

s v



Przesunięcia

przygotowane

A



V,

s



V

Przesunięcie

przygotowane



Przesunięcie proporcjonalne do
prędkości możliwych w pkt. A nazywamy
przesunięciami przygotowanymi lub
wirtualnymi w tym punkcie



Przesunięcia przygotowane mają
kierunek styczny do powierzchni, zwrot
zaś i wielkość dowolną



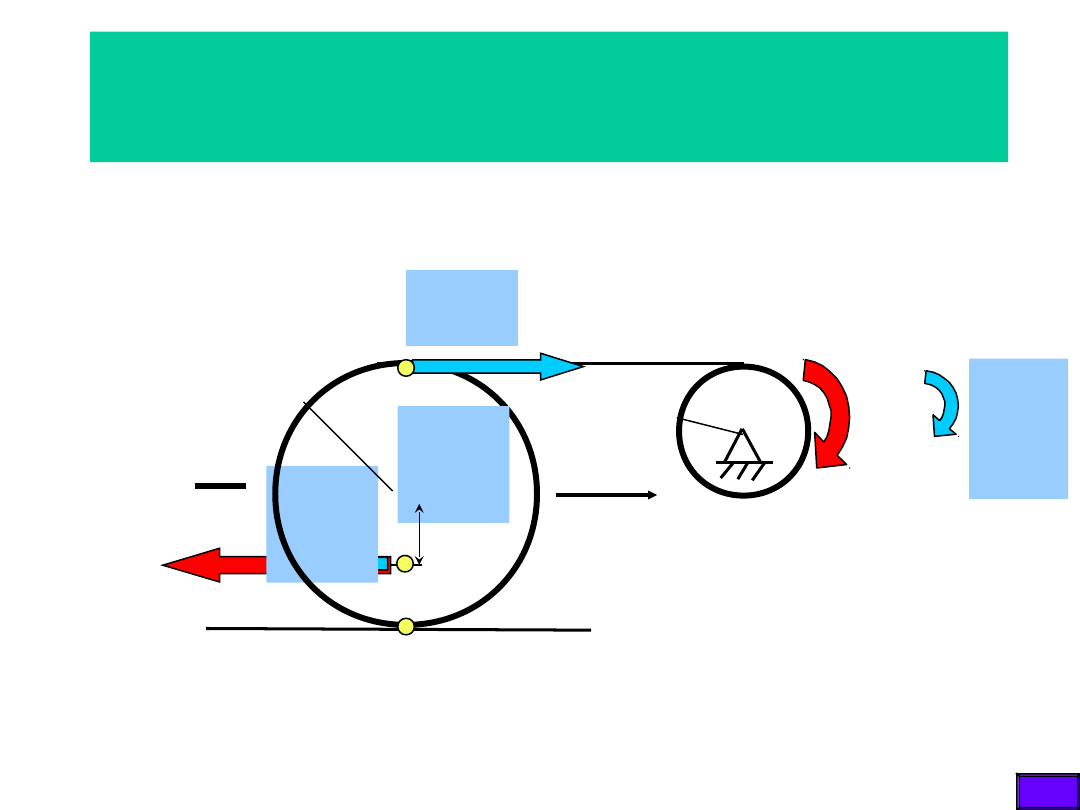
x

D

Przesunięcia

przygotowane

o

c



x

0

a

R

r

M

D

E

P



x

E









x

v



Q

J

X

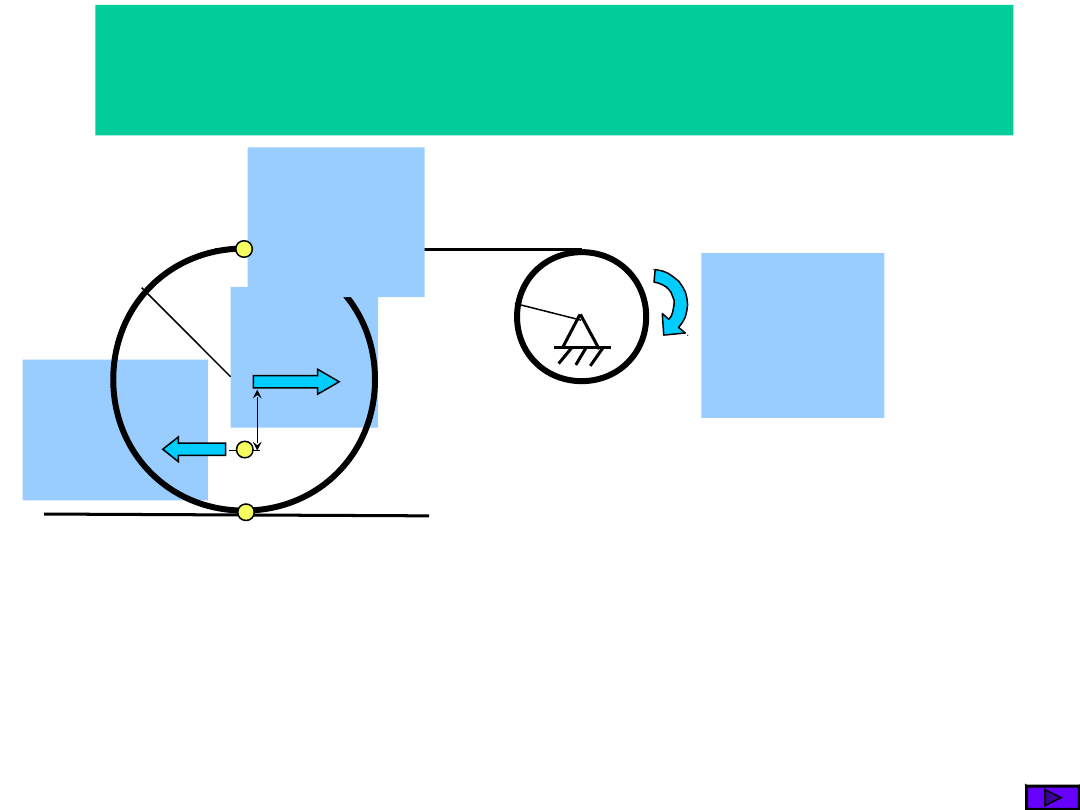
Przesunięcia

przygotowane



x

D

v

D



x

0

v

0

o

c

a

R



x

E

v

E

r

D

E











(4.8)

(4.9)









x

D

vD

x

v





0

0

(4.10)

(4.11)









x

E

vE

x

E

r



 *

Przesunięcia

przygotowane

Prędkości

Przesunięcia przygotowane

(4.12)

(4.13)

vD

R a

R

v

vE v

 



0

2 0

0

2

(4.15)

0

(4.14)

x

E

x

x

R

a

R

D

x















Siła uogólniona

Przesunięcia

przygotowane

2

(4.18)

*

M

R

a

R

*

P

Q







0

2

0

(4.17)

x

*

M

R

a

R

*

P

x

*

Q











































*

M

D

x

*

P

x

*

Q





0

(4.16)

Równania Lagrange’a II

rodzaju

x

q

j

q





Współrzędna uogólniona

Ilość stopni swobody

s=1

o

G

x

y

+

_

0

x

4.19. E

k

= E

p

+E

o

r

x

.

.

mr

o

J

.

.

o

J

o

E

.

.

x

m

p

E

.

.

















23

4

2

2

1

22

4

2

2

1

21

4

2

2

1

20

4

x

*

G

V

.

.





25

4























m

x

k

E

.

.

2

3

2

2

1

24

4



Równania Lagrange’a II

rodzaju

g

x

.

.

G

x

m

.

.

3

2

31

4

0

2

3

30

4











Równania Lagrange’a II

rodzaju

G

x

V

.

.

x

k

E

.

.















28

4

0

27

4

Równ.





























































































m

x

m

x

x

k

E

.

.

2

3

2

3

dt

d

dt

d

26

4











0

29

4



j

Q

.

.

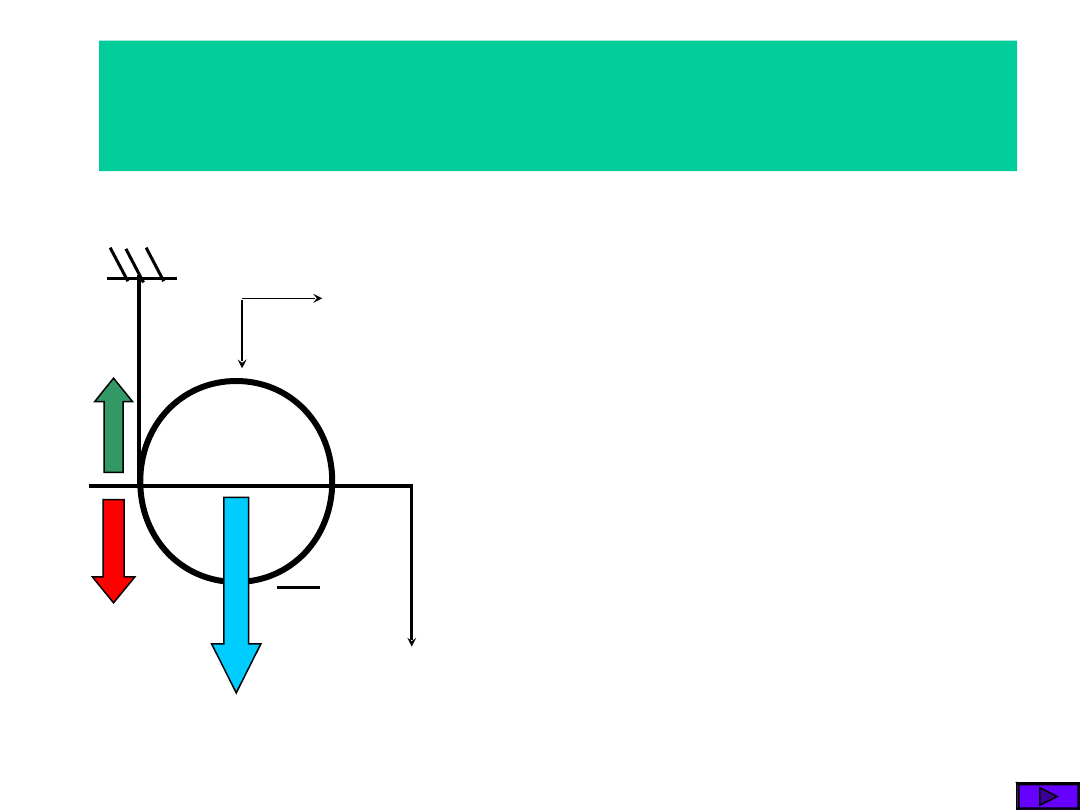
Ugięcie statyczne

0

4

5

0

3

5













kx

x

m

.

.

st

k

G

x

s

F

.

.



























st

x

k

s

F

.

.

s

F

G

x

m

.

.

2

5

1

5



x=
0

m

m

k

G=mg

x

x



st

A

x+

s

t

k

G

st

.

.

G

st

k

x

x

V

.

.





















7

5

0

0

0

6

5

2

2

1

2

2

1

5

5

st

k

st

x

G

st

x

k

V

.

.



















































2

2

1

8

5

(5.5)

(5.7)

kx

V

.

.







m

m

k

G=mg

x

x

x=0



st

A

Ugięcie statyczne

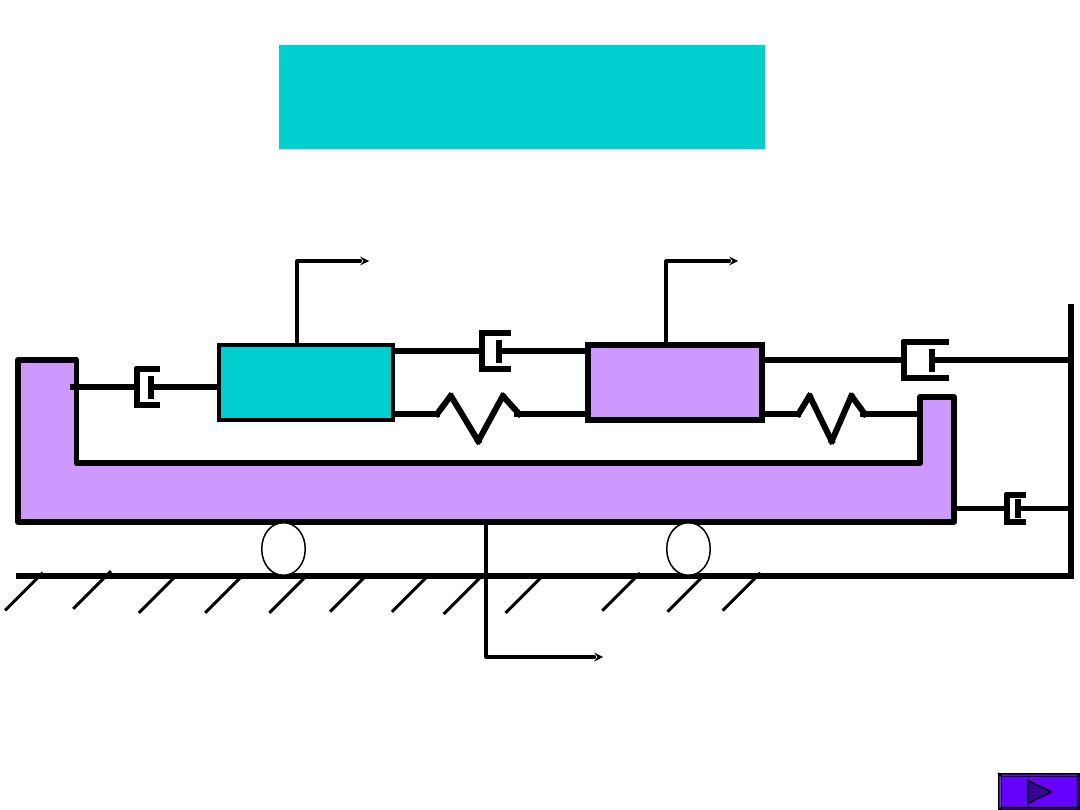
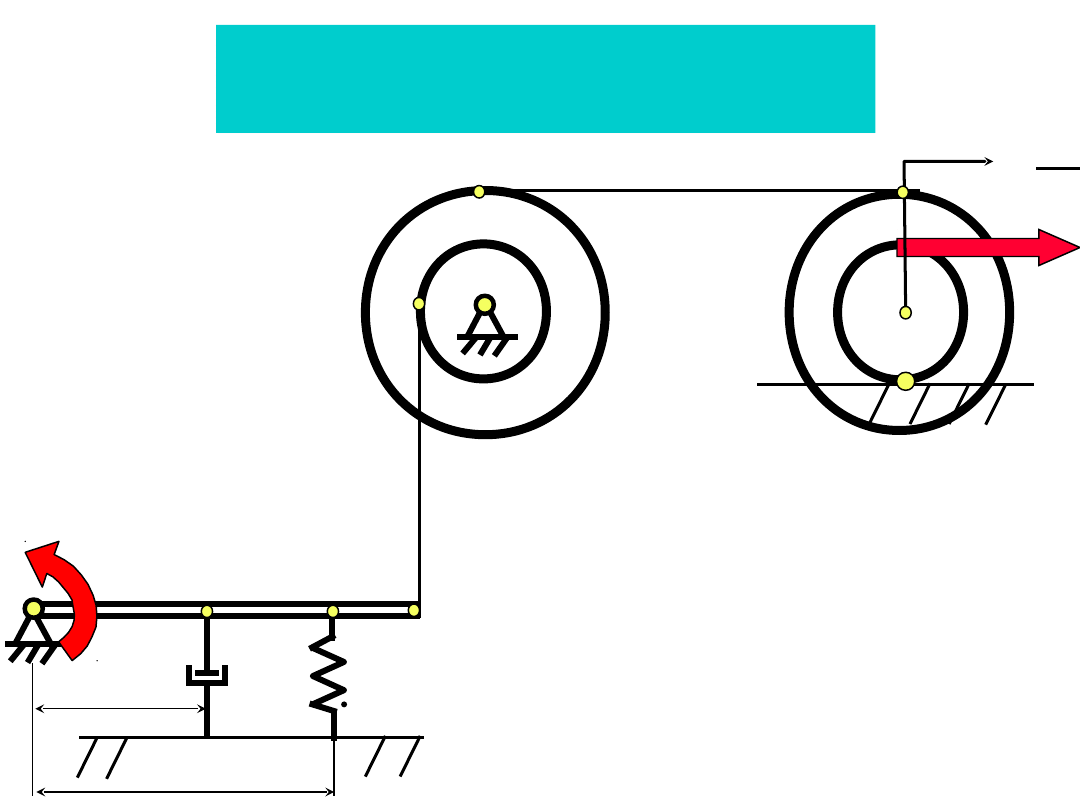
Zadanie 1

m1

m2

m3

k1

k2

c1

c2

c4

c3

x1

x3

x2

D: m1- m3, k1, k2, c1-c4
Sz: RDR

Masa m1

m1

x1

Fc

1

Fs

1

Fc

3

1. Oswobodzenie układu

2. RDR masy m1

3

1

1

1

1

(1)

c

F

s

F

c

F

x

m











(3) Fc c x x

1 1 1 2





























(2) Fs k x x

1

1 1 2

























Masa m1

(5) m x c x

x

c x

x

k x

x

1 1 1 1 2 3 1 3 1 1 2 0





















































































(4) Fc c x x

3 3 1 3





























(6) m x

c c x k x c x c x

k x

1 1

1 3 1 1 1 1 2 3 3 1 2

0











































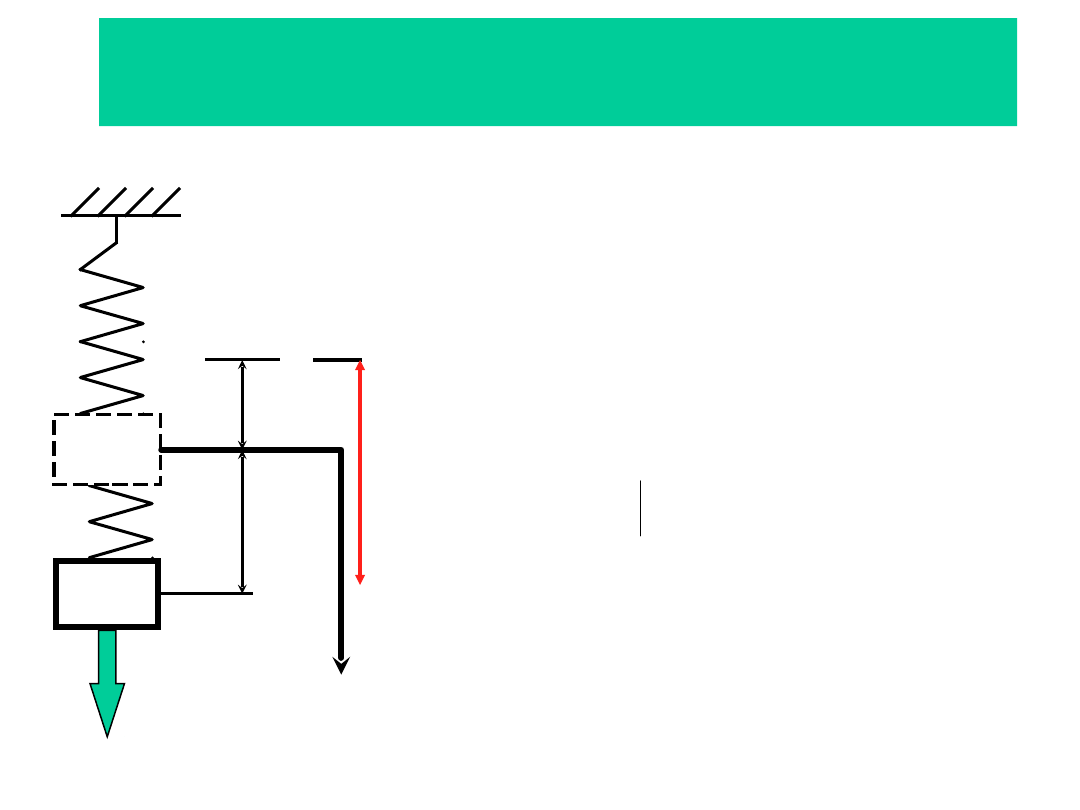
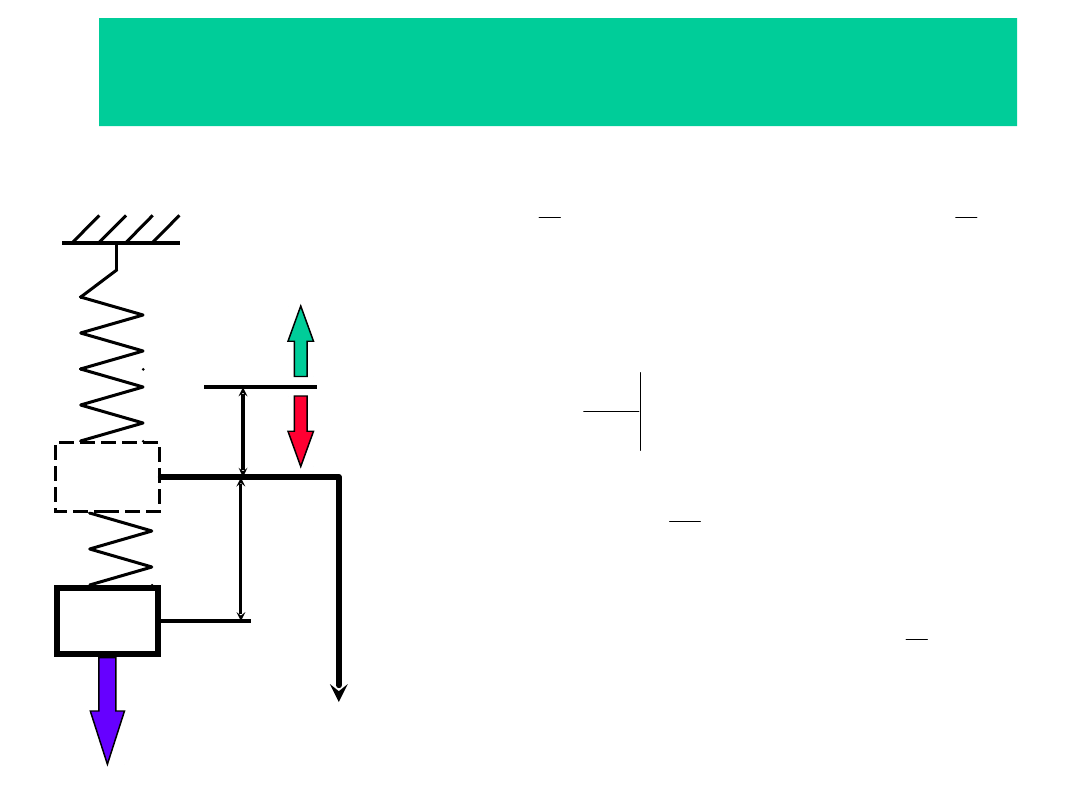
Zadanie 3

Sz: RDR ciała o masie
3m

M

c

k

r

4m, 2r

3/2 r

2m, 2r, r, 

3m, 2r, r, 

P

x

O

2

A

B

E

E

’

O

1

F

F

’

O

D