Wykład 4: Podstawy wnioskowania

statystycznego

Biometria i

Biostatystyka

Wnioskowanie
statystyczne

Dwa fundamentalne pytania dotyczące
statystyki, na które badacze muszą
niejednokrotnie odpowiadać:



Jak wiarygodne są wyniki?



Jakie jest prawdopodobieństwo, że

różnica między obserwowanymi
wynikami a spodziewanymi na podstawie
hipotezy jest dziełem przypadku?

Wnioskowanie
statystyczne



Na pytanie o wiarygodność

odpowiadamy wyznaczając przedziały

ufności dla statystyk obliczanych na

podstawie próby.



Udzielenie odpowiedzi na drugie pytanie

wymaga testowania hipotez.



Nasze wnioski są wspierane przez

rachunek prawdopodobieństwa.



Obydwa zagadnienia są elementami

wnioskowania statystycznego.

Wnioskowanie
statystyczne



Wnioskowanie odbywa się na podstawie
otrzymanej na drodze próbkowania funkcji
gęstości statystyki.



Funkcja gęstości pokazuje rozkład prawdopodobieństwa
statystyki powstały przy wielokrotnych powtórzeniach
wnioskowania na podstawie losowych próbek danych.



Wnioskowanie statystyczne zakłada, że dane
pochodziły z prostej próby losowej.



Jeśli to nieprawda, Twoje wnioski mogą zostać
zakwestionowane.

Próby losowe



Próbą (próbką) losową

nazywa się zbiór

elementów pobranych z populacji w taki
sposób, że przed jej pobraniem każdy
element populacji ma te same szanse (to
samo prawdopodobieństwo) dostania się do
próby.



Próbę losową nazywa się

prostą

, jeżeli w

trakcie losowania szanse dostania się do
próbki każdego elementu nie zmieniają się.

Próby losowe



Próbkę losową prostą otrzymuje się przez
zwracanie wylosowanych elementów do
populacji. Jako próbkę losową prostą uważa
się w praktyce próbkę, której liczność jest
znacznie mniejsza od liczby elementów w
populacji i można uważać, że wylosowane
elementy nie zmieniają składu populacji.

Estymator



Estymatorem

nazywa się statystykę służącą

za podstawę do oszacowania nieznanego
parametru.



Przykład. Nieznanym parametrem populacji jest
średnia μ, jako estymator tej średniej mogą
służyć statystyki: średnia z próbki, mediana
próbki, średnia z wartości skrajnych itp..

Estymator zgodny



Estymator U

n

parametru Q nazywa się

estymatorem zgodnym

, jeśli zachodzi

związek:

który oznacza stochastyczną zbieżność ciągu
U

n

do wartości parametru Q, gdy liczność

próbki n rośnie.





0

lim













Q

U

P

n

n

Estymator nieobciążony



Estymator U parametru Q nazywa się

estymatorem nieobciążonym

, jeśli wartość

oczekiwana E(U) jest równa wartości
parametru Q.

Q

U

E



)

(

Efektywność estymatora



Efektywnością

nieobciążonego estymatora U

parametru Q nazywa się stosunek minimalnej
wariancji w danej klasie estymatorów do
wariancji rozpatrywanego estymatora.



Efektywność wyraża się za pomocą liczby
zawartej między zerem a jednością.



Estymator najefektywniejszy to estymator U
parametru Q o wartości efektywności równej
jedności.

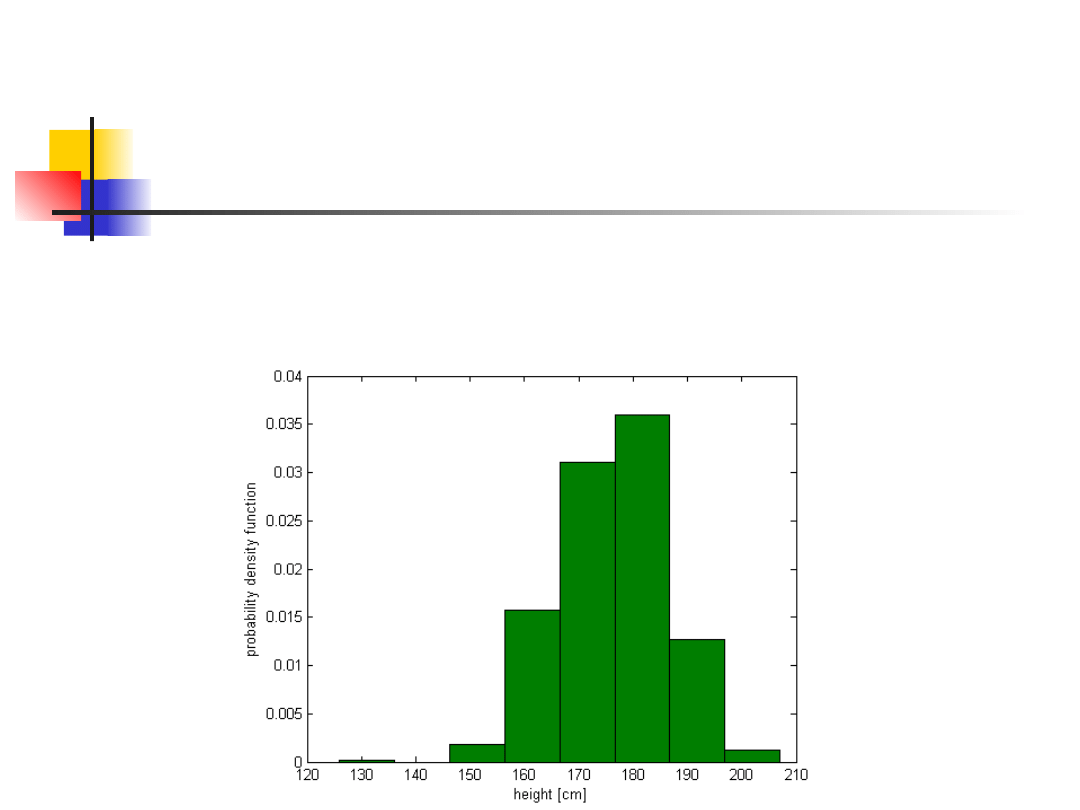
Rozkład i wariancja średniej



Dane: wzrost. Populacja: studenci AEI



Wartość średnia μ = 176.16 cm, σ =
9.86

Rozkład i wariancja średniej

Losowo wybrane próby 10 pomiarów:



x =[158 176 188 155 188
170 177 171 173 183];
średnia 173.9



y=[180 181 163 182 178
171 175 168 158 193];
średnia 174.90

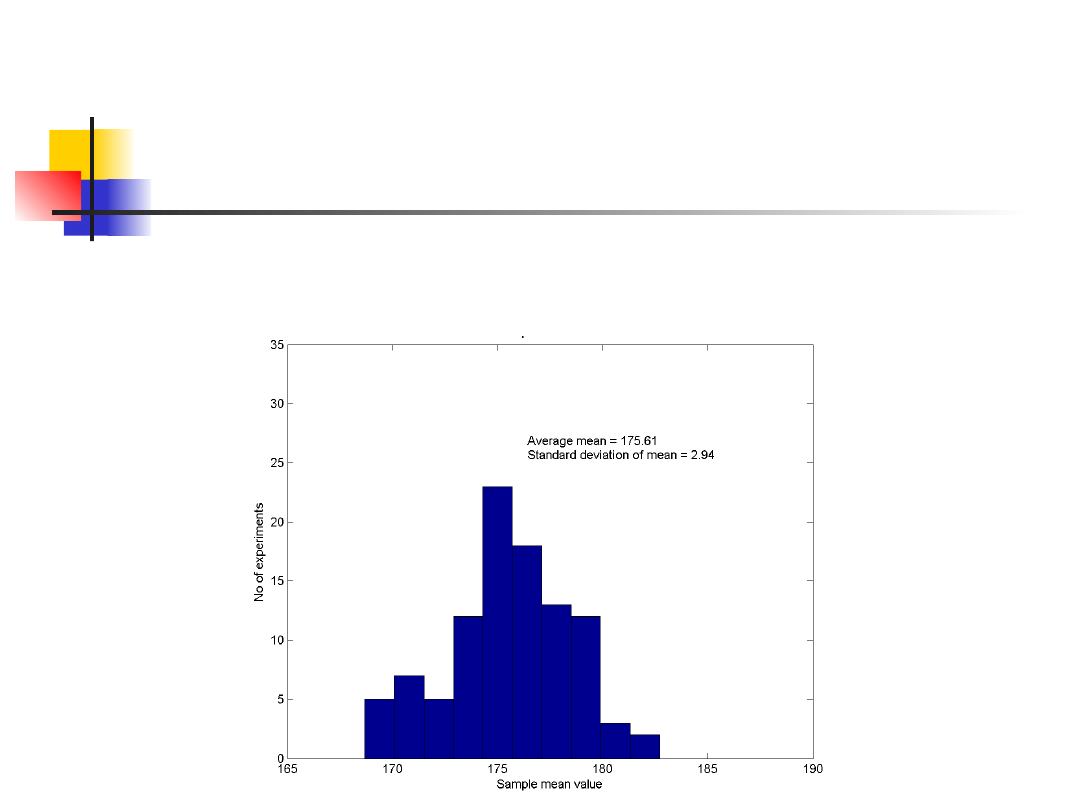
Rozkład i wariancja średniej



Histogram 100 wartości średnich wzrostu,
każdorazowo wyliczanych dla losowo wybranych
dziesięciu osób.

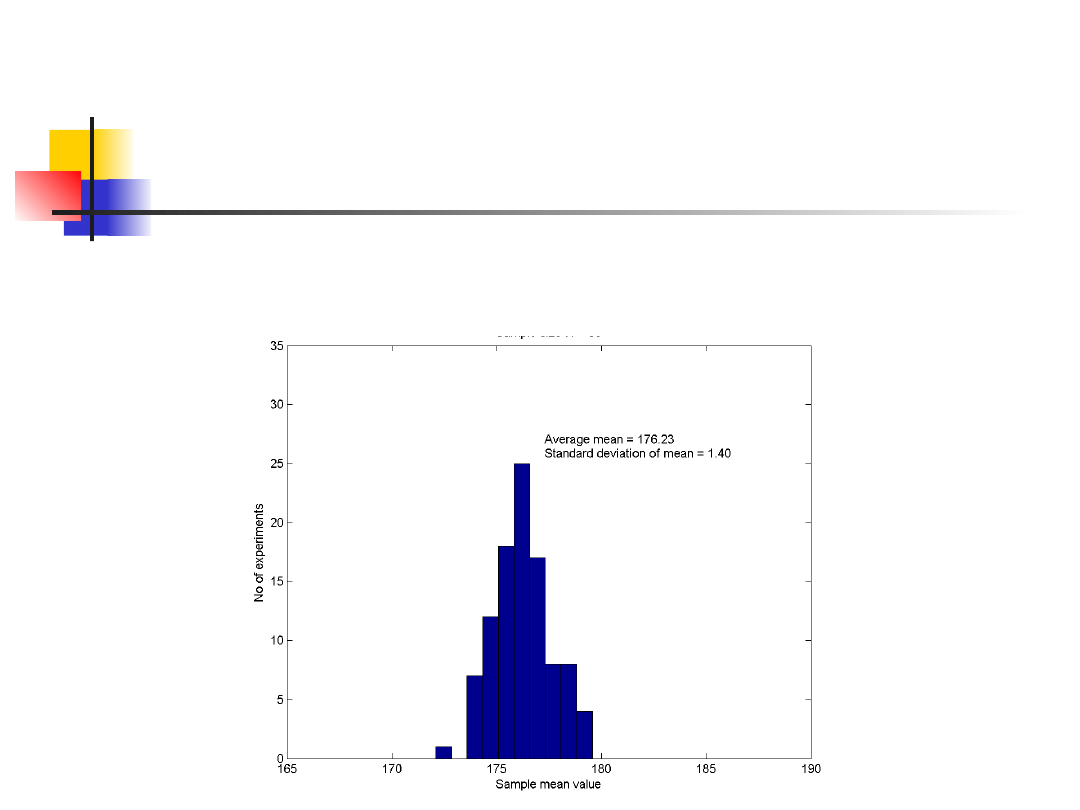
Rozkład i wariancja średniej



Histogram 100 wartości średnich wzrostu,
każdorazowo wyliczanych dla losowo wybranych
pięćdziesięciu osób.

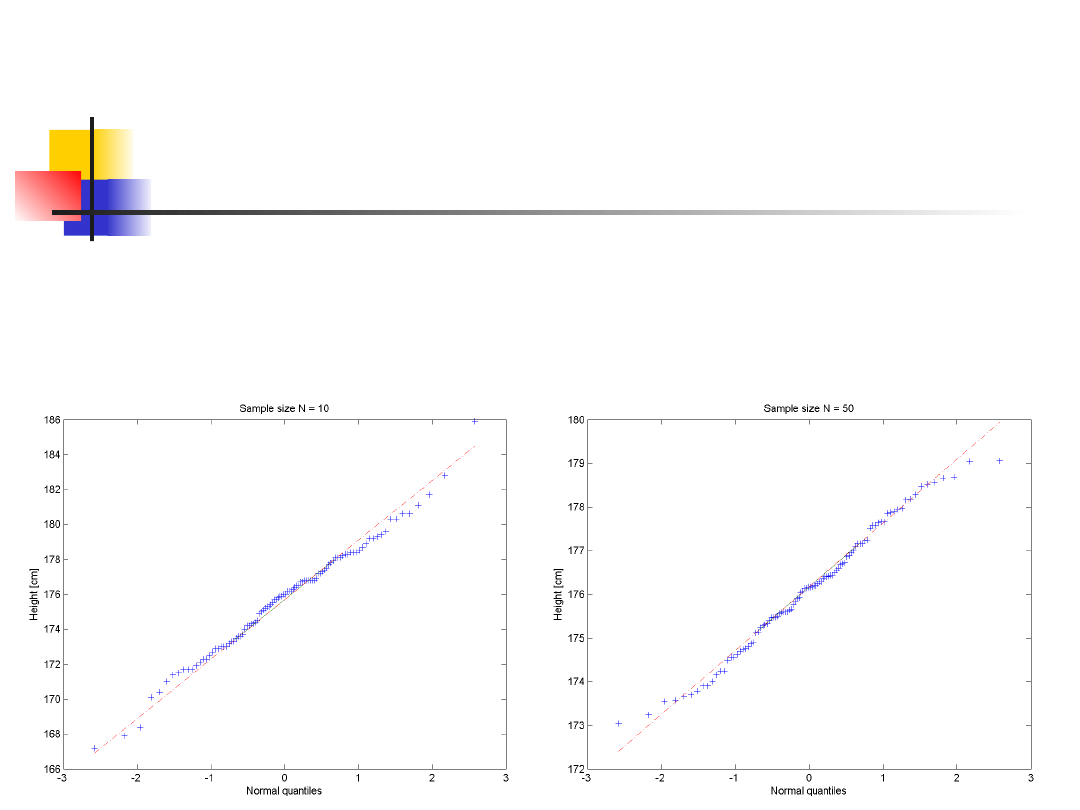
Rozkład i wariancja średniej



Średnie z próby z populacji o rozkładzie
normalnym są same z siebie normalne,
niezależnie od liczebności próby N.

Rozkład i wariancja średniej



Gdy liczebność próby wzrasta, rozkład
wartości średnich wyliczonych z prób
losowanych z populacji o dowolnym
rozkładzie zbliża się do normalnego.



Jest to

Centralne Twierdzenie Graniczne

(jedynie wtedy gdy mówimy o próbkowaniu z
populacji o skończonej wariancji)

.

Rozkład i wariancja średniej

Zakres średnich jest znacznie mniejszy niż
zakres oryginalnych danych.



Indywidualny wzrost waha się od 126 cm do
208 cm.



Średnie wzrostów wahają się od 168 cm do
183 cm w próbach N=10 i od 173 cm do 179
cm w próbach N=50.

Rozkład i wariancja średniej

Różnice w zakresach są odzwierciedlone

w różnicach w odchyleniu
standardowym tych rozkładów.

N=10

N=50

Populacja

Odchylenie

standardo

we

2.94

1.40

9.86

Rozkład i wariancja średniej



Średnie z dużych prób powinny być bliskie
parametrycznej średniej i nie będą się tak
wahały jak te z małych prób. W takim razie
wariancja średnich jest częściowo funkcją
liczności prób, z których są wyliczane.



Wariancja średniej jest także funkcją
wariancji samych danych.

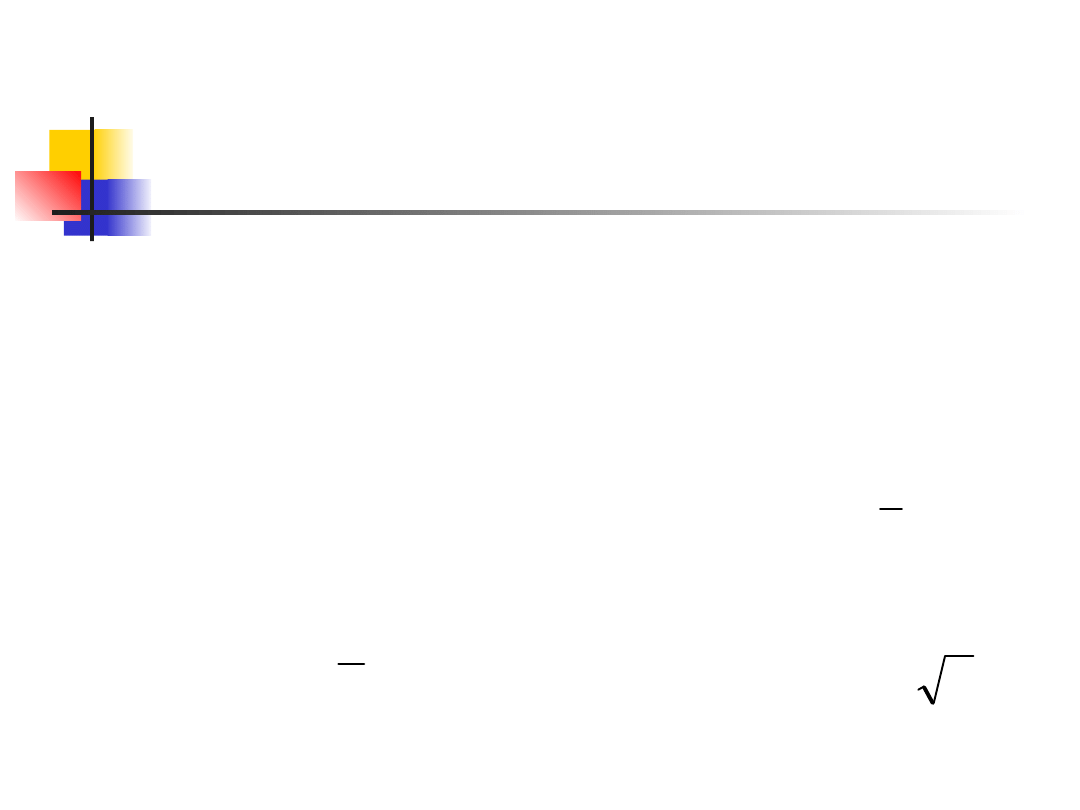
Przedział ufności



Weźmy prostą próbę losową (PPL) o

liczebności n z dowolnej populacji ze
średnią



i skończonym odchyleniem

standardowym



.



Kiedy n jest duże, rozkład średniej z

próby jest w przybliżeniu normalny:

jest w przybliżeniu

x

x





n

N

/

,





Przedział ufności



Niech n=50, σ = 9.86.



Jaki rozkład ma średnia w
powtarzanych próbach o liczności
50?



N( , 1.39) gdyż 9.86/√50 = 1.39



Co mi mówi reguła trzech sigm? (68-
95-99.7)



μ – 2.78

μ +

2.78

Przedział ufności



Średnio 95% wszystkich ocen z

próby znajduje się wewnątrz

wyznaczonego przedziału.



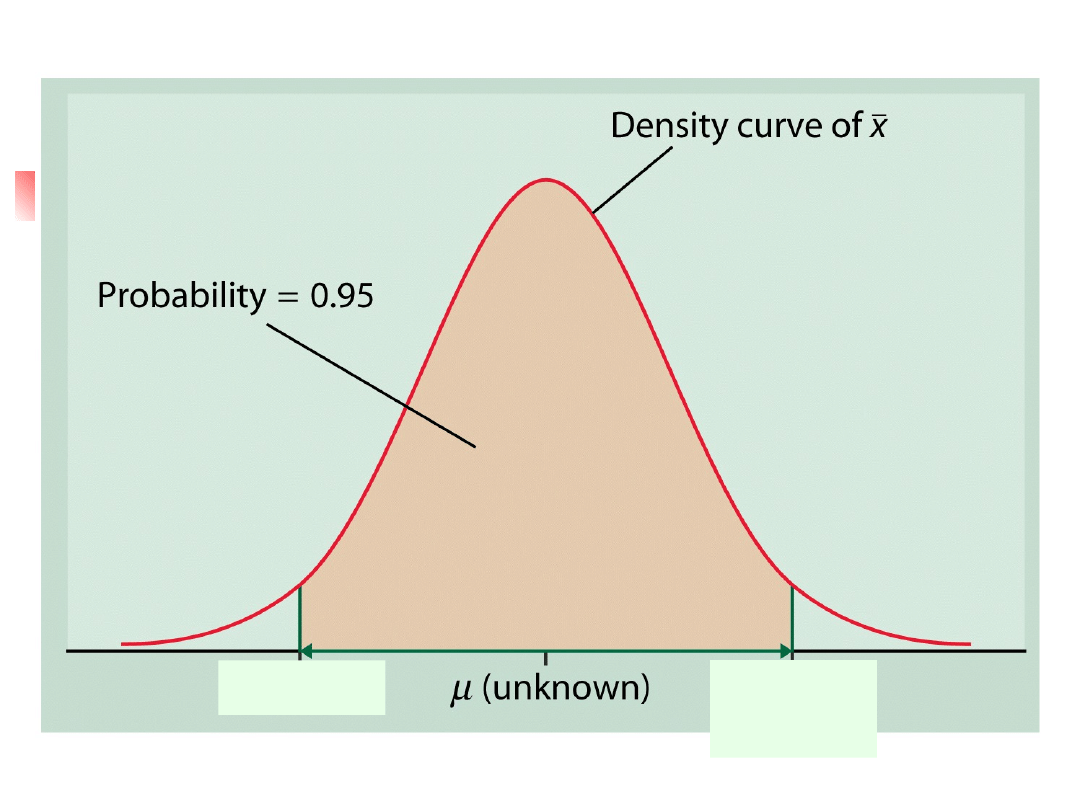
Wnioskowanie statystyczne

wykorzystuje wiedzę o tym co się

dzieje przy wielokrotnym

powtarzaniu eksperymentu do oceny

ufności wyniku w pojedynczej próbie.

x

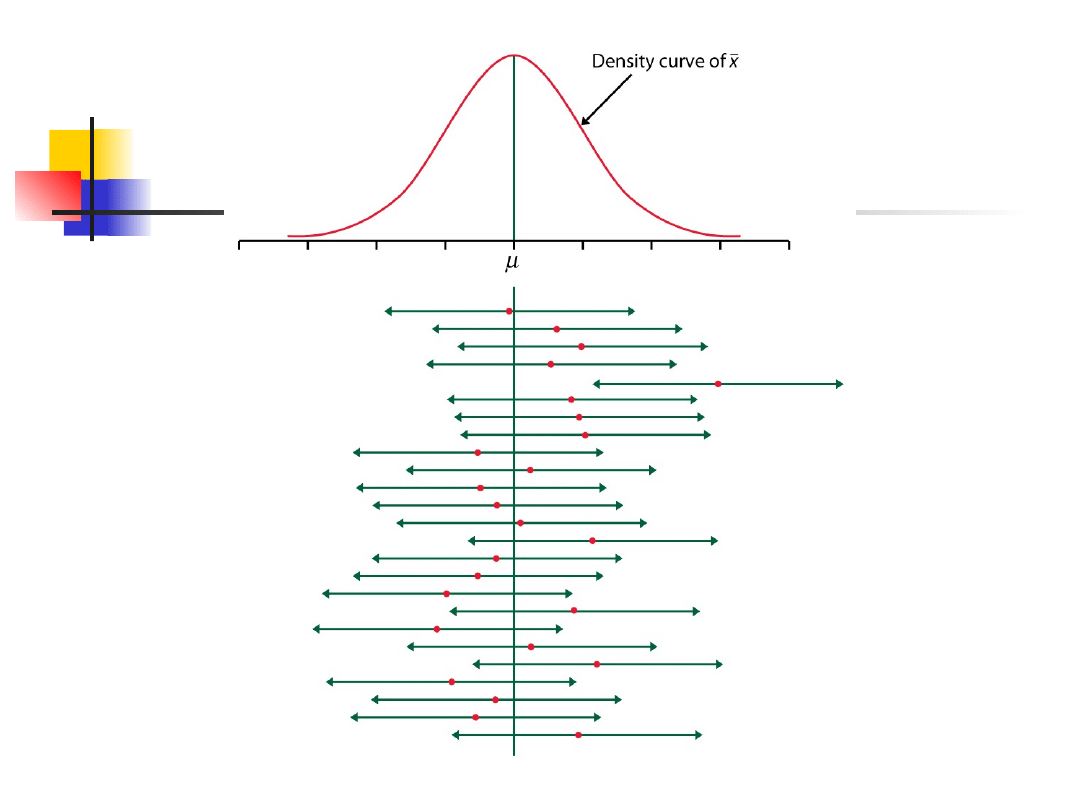
Przedziały ufności



Jest to przedział w postaci (a, b) gdzie a
i b to liczby wyliczone z danych.



Ma właściwość zwaną poziomem
ufności, która mówi o
prawdopodobieństwie, że przedział
zawiera w sobie nieznany parametr.



Najczęściej poziom ufności wynosi 90%
lub więcej, ponieważ chcemy być pewni
swoich wniosków.

Przedziały ufności, cd.



Do oznaczania poziomu ufności
stosować będziemy liczby dziesiętne C.



95%-owy poziom ufności odpowiada C=0.95



Formalna definicja



Przedział ufności na poziomie C jest
przedziałem obliczonym z danych metodą,
która z zadanym prawdopodobieństwem C
określa przedział zawierający rzeczywistą
wartość parametru.

Przedział ufności dla
średniej populacji



Przedział ufności na poziomie C dla

średniej populacji, gdy dane pochodzą z

PPL o liczności n, jest oparty na

rozkładzie próbkowania średniej próby.



Żeby zbudować przedział ufności na

poziomie C musimy najpierw znaleźć

centralne pole C pod krzywą normalną.



Musimy znaleźć takie z*, że rozkład normalny

ma prawdopodobieństwo C w zakresie ± z*

odchylenia standardowego od średniej.



x

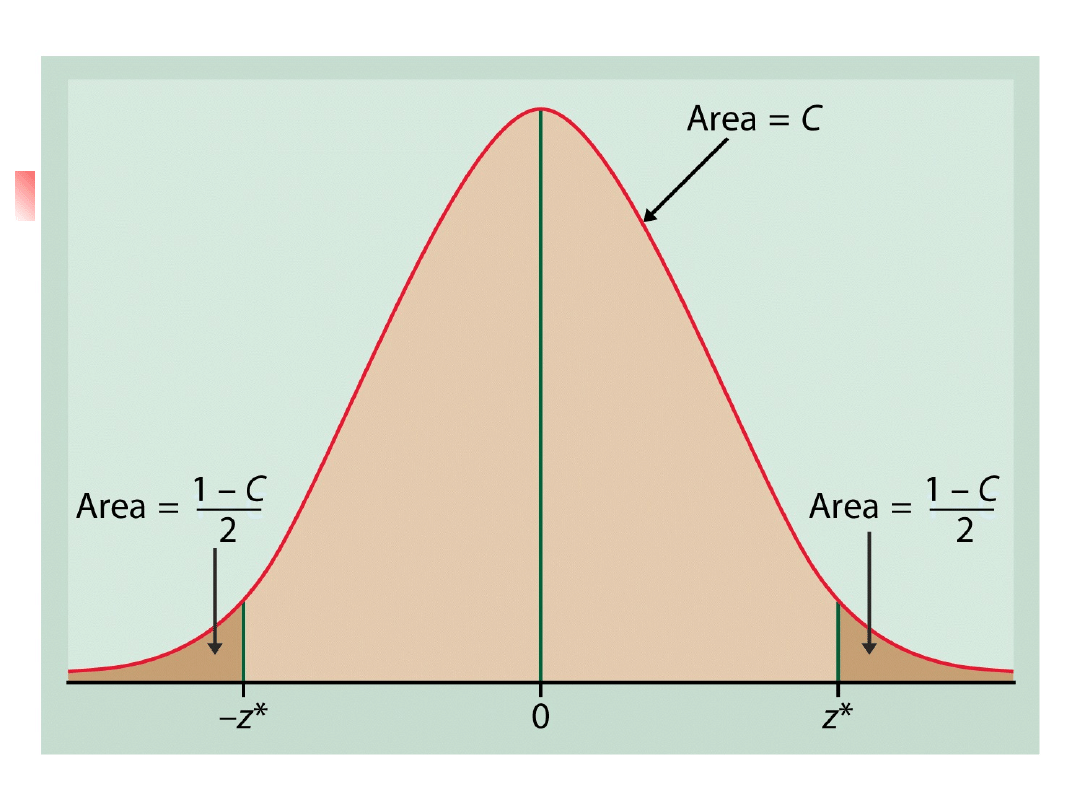
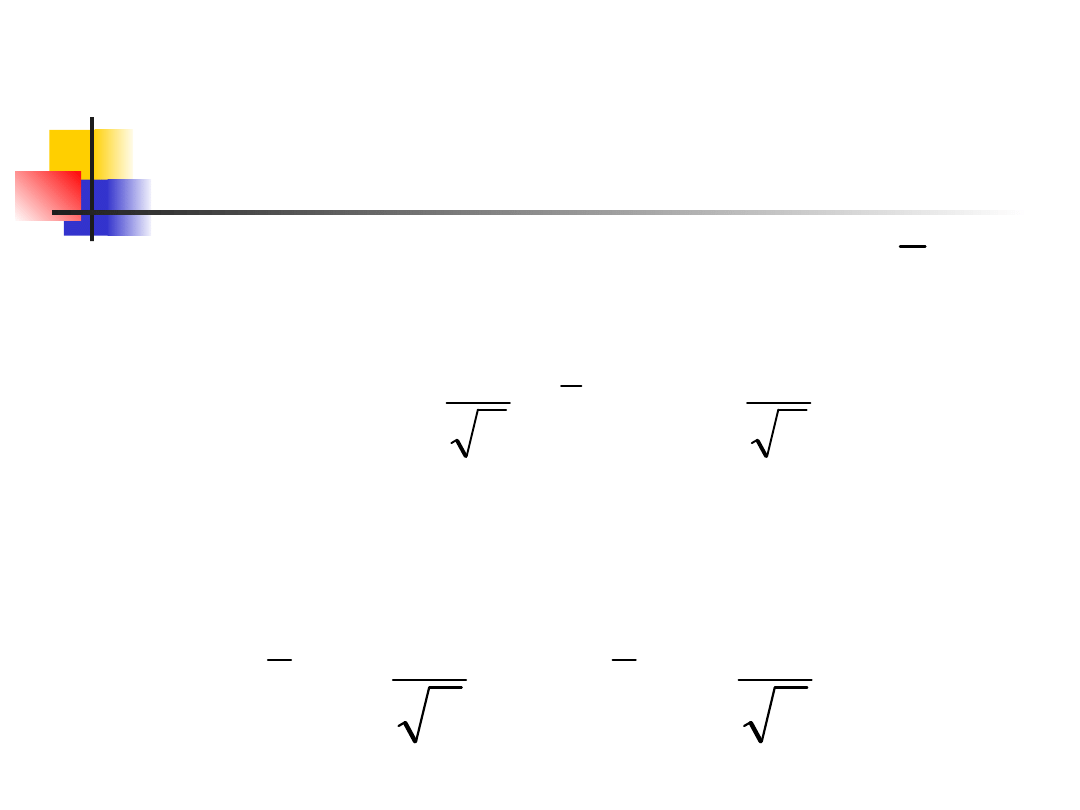
Przedział ufności dla
średniej populacji, cd.



Z zadanym prawdopodobieństwem C

leży pomiędzy



To jest dokładnie to samo co to, że nieznana

średnia populacji leży pomiędzy

x

n

z

x

n

z









*

*











n

z

x

n

z

x







*

*









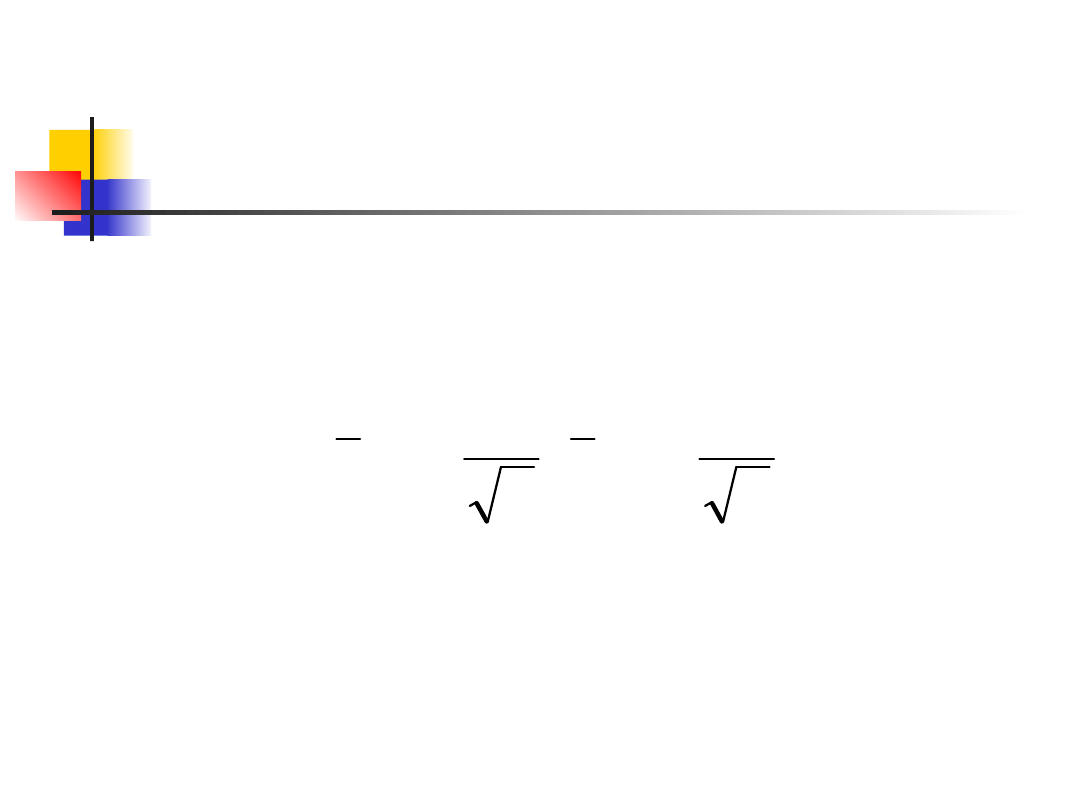
Przedział ufności dla
średniej populacji, cd.



Weźmy PPL liczności n z populacji o nieznanej

średniej i znanym odchyleniu standardowym.

Przedziałem ufności na poziomie C dla

jest



Ten przedział jest precyzyjny, kiedy rozkład

populacji jest normalny i jedynie przybliżony dla

dużych n w innych przypadkach.



n

z

x

n

z

x





*

*

, 



Przedział ufności - wzrost



Niech n=50, σ = 9.86.



Estymator wartości średniej przy
próbce losowej o liczności 50 ma
rozkład
N( , 1.39) gdyż 9.86/√50 = 1.39



Przedziały ufności



Przedział liczbowy ( -2.78, +2.78) jest

nazywany 95%-owym przedziałem ufności

dla



Ma formę (estymacja – margines błędu,

estymacja + margines błędu)



Estymacja = szacowanie: odgadywanie

wartości nieznanego parametru



Margines błędu: mówi na ile oceniamy

dokładność naszego wyniku na podstawie

zmienności estymaty parametru.

x

x



Wnioskowanie
statystyczne



Jeśli jedna średnia próby jest równa 172.9,
wtedy jedno z dwóch:



Przedział między 172.9-2.78=170.12 i
172.9+2.78=175.68 zawiera rzeczywistą średnią.

ALBO



Nasza PPL była jedną z kilku prób dla której
średnia nie jest w przedziale ±2.78 od rzeczywistej
średniej. Tylko 5% wszystkich prób daje tak
nietrafiony wynik (dla CI 95%).



Nie wiemy, w której kategorii znajduje się
nasza próbka.

x

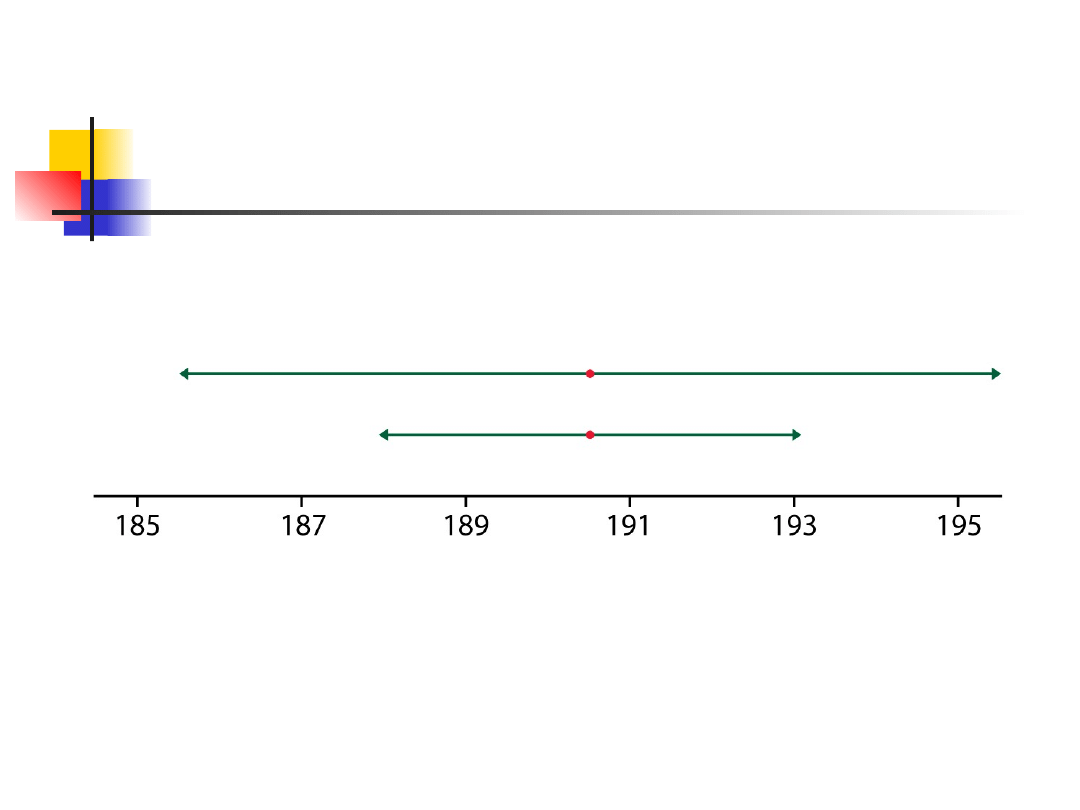
mniejsza liczność próby daje szerszy przedział

ufności

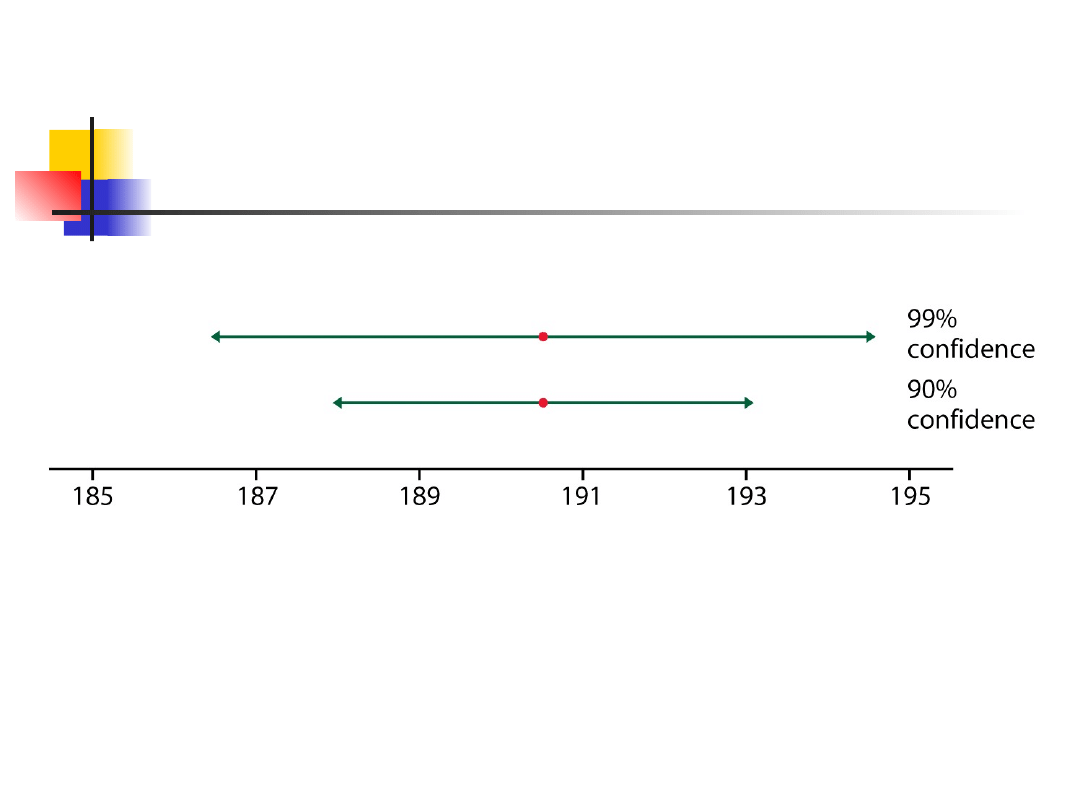
wyższy poziom ufności daje szerszy przedział

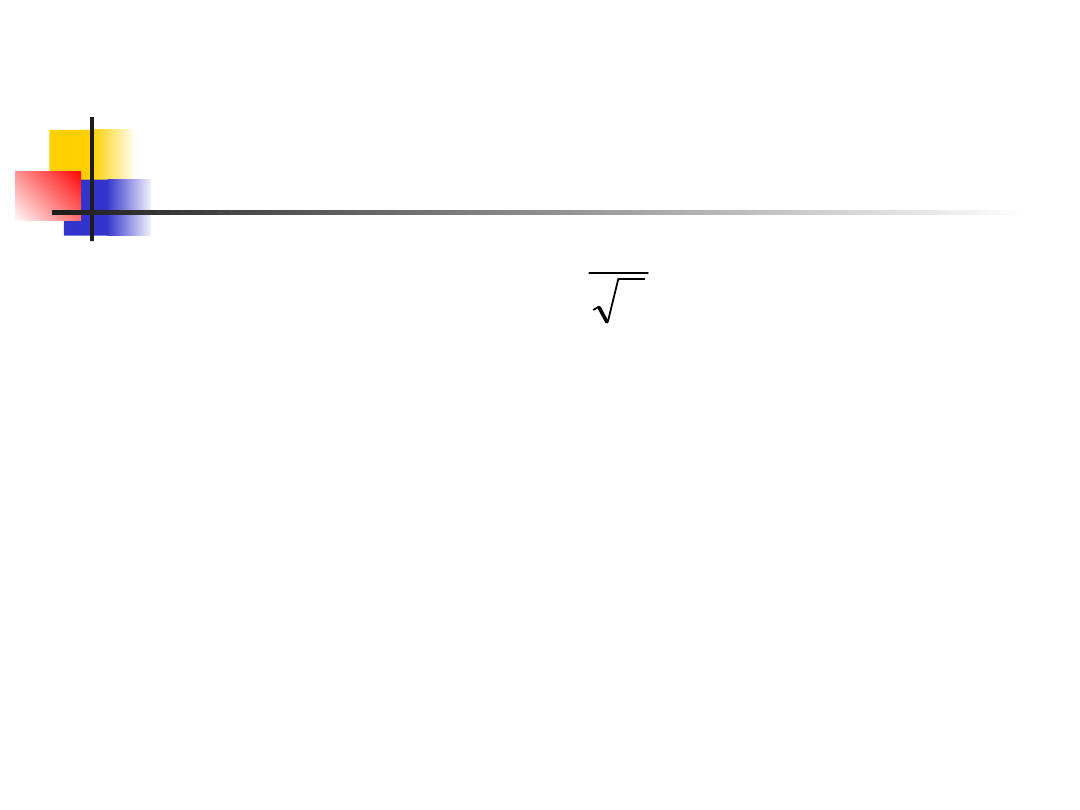
Jak się zachowują przedziały
ufności



Margines błędu



Ilustruje kilka ważnych właściwości,
które są wspólne dla wszystkich
przedziałów ufności.



Badacz wybiera poziom ufności, a
margines błędu jest efektem tego
wyboru.

n

z



*

Jeśli Twój margines błędu jest za

duży…



Zmniejsz poziom ufności (mniejsze C)



90% odpowiada z*=1.645



95% odpowiada z*=1.96



99% odpowiada z*=2.576



Zwiększ liczność próby (większe n)



Musimy pomnożyć liczbę obserwacji przez 4

żeby zmniejszyć margines błędu o połowę.



Zmniejsz σ.



Możemy czasem zmniejszyć σ przez

manipulowanie procesem pomiarów albo skupić

uwagę jedynie na części dużej populacji.

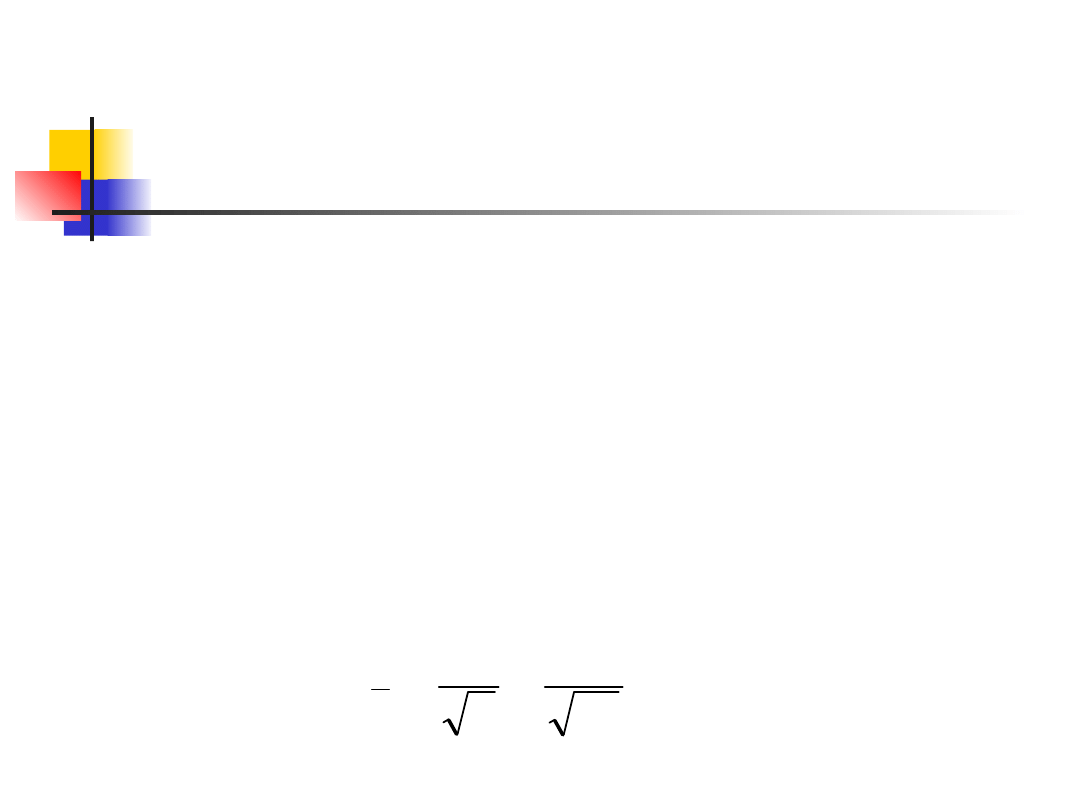
Przykład 1



Mamy próbę 35 długości skrzydełek
muchy z populacji o nieznanej średniej i
znanym odchyleniu standardowym ( =

3.90). Średnia z próby to 44.8.



Możemy się spodziewać, że odchylenie
standardowe średnich opartych na
próbkach 35 pomiarów będzie równe

6592

.

0

35

90

.

3

n

Y











Przykład 1



Granice liczymy następująco:



Z definicji

09

.

46

)

6592

.

0

(

)

960

.

1

(

8

.

44

L

51

.

43

)

6592

.

0

(

)

960

.

1

(

8

.

44

L

2

1





















95

.

0

09

.

46

51

.

43

P









Przykład 1 - cd.

Przeprowadźmy eksperyment symulacyjny:



Wartość średnia w populacji wynosi  =

45.5 a odchylenie standardowe  = 3.90.

Rozkład długości skrzydełek można

opisać rozkładem normalnym.



Wykonujemy 200 powtórzeń losowań

prób, każda po 35 wartości długości

skrzydełek. Obliczamy przedziały ufności

dla wartości średniej w populacji poprzez

zastosowanie błędu standardowego,

6592

.

0

Y





Przykład 1 - cd.



Wykres pokazuje 200 wyliczonych
95% przedziałów ufności,
wykreślonych równolegle do osi
rzędnych.

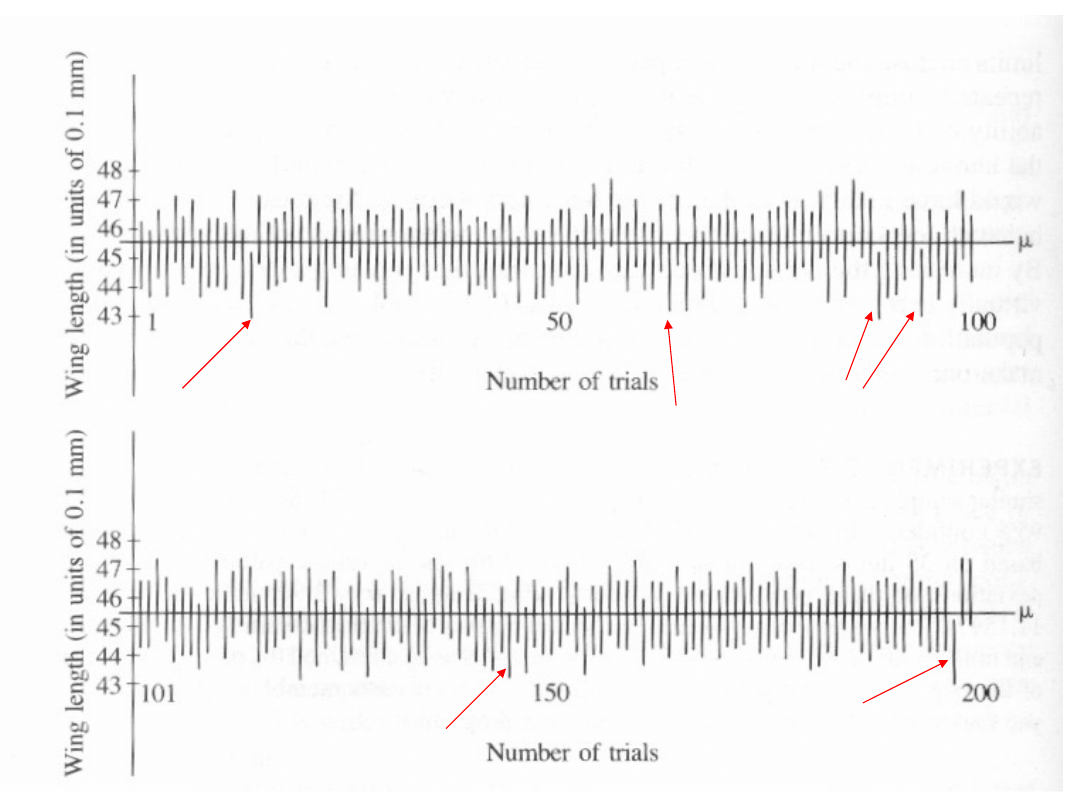
Przykład 1 - cd.



Z tych 194 (97.0%) zawiera w
sobie średnią populacji.

Uwaga

Kiedy mamy ustalone dolne i górne granice CI dla

wartości średniej, wtedy prawdopodobieństwo, że

przedział zawiera średnią z populacji jest równe

0.95 lub, innymi słowy, przeciętnie 95 ze 100

obliczonych przedziałów ufności zawiera tą średnią

populacji.

Nie możemy twierdzić

że istnieje

prawdopodobieństwo równe 0.95 że rzeczywista

średnia zawiera się w dowolnym zaobserwowanym

przedziale ufności, choć na pierwszy rzut oka może

się tak wydawać. Ostatnie stwierdzenie jest

nieprawdziwe, ponieważ rzeczywista średnia jest

parametrem, wartością stałą i jest albo w

przedziale albo poza przedziałem. Nie może być w

jakimś przedziale na 95%.

Wybór liczebności próby



Żeby otrzymać wymagany
margines błędu m, przyrównaj to
wyrażenie do m, zamień wartość z*
na Twój żądany poziom ufności i
rozwiąż równanie dla liczebności
próby n.

Przykład 2



Zgodnie z informacją podaną przez producenta,

waga paczek kawy ma rozkład normalny o

wartości średniej 100 g i odchyleniu

standardowym 5g. Aby sprawdzić tę hipotezę

dział kontroli jakości musi dokonać pomiaru

losowo wybranej partii towaru.



Co najmniej ile paczek kawy powinno być

zważonych, by oceniony na podstawie

zebranych danych przedział ufności dla średniej

wagi miał szerokość mniejszą niż 0.2 g przy

poziomie ufności równym 0.98?

Przykład 2

Liczność próby ocenić możemy

wykorzystując:

przy czym konieczna jest znajomość σ

oraz z

*

.

2

*

*

n

z



















m

z

n

m





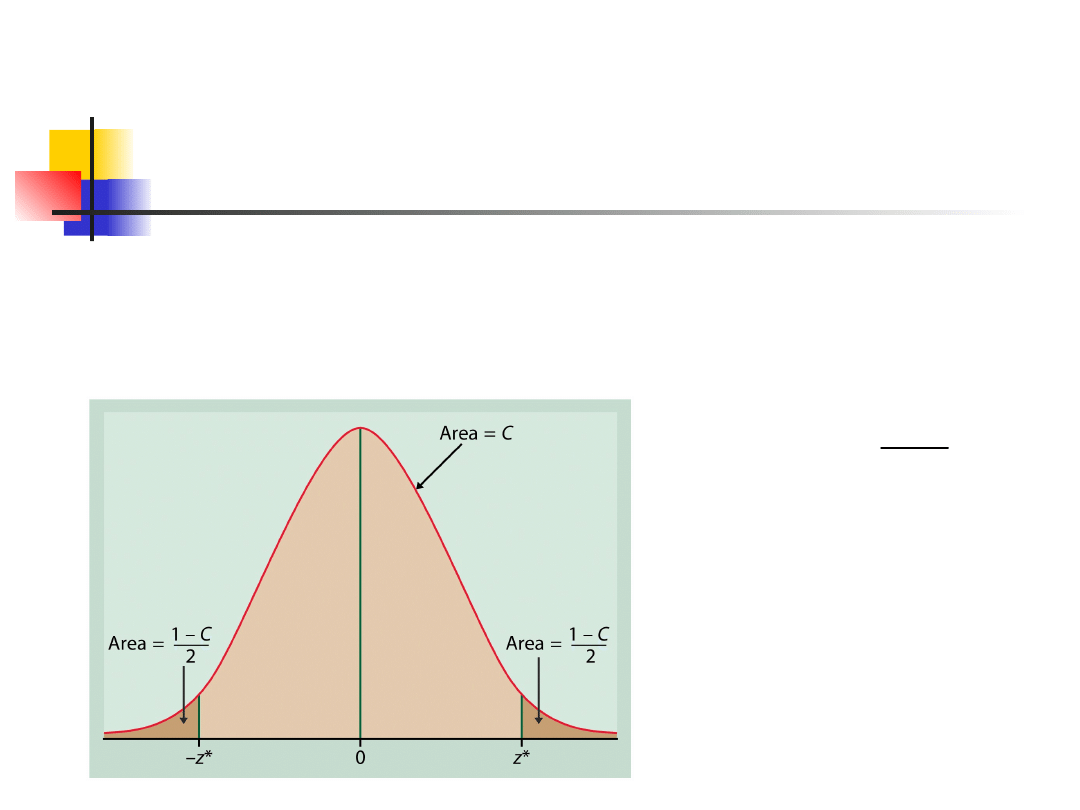
Przykład 2



Dla zadanego poziomu ufności C=0.98
wartość krytyczną z

*

znajdujemy z

zależności

99

.

0

2

1

)

(

*











C

C

z

X

P

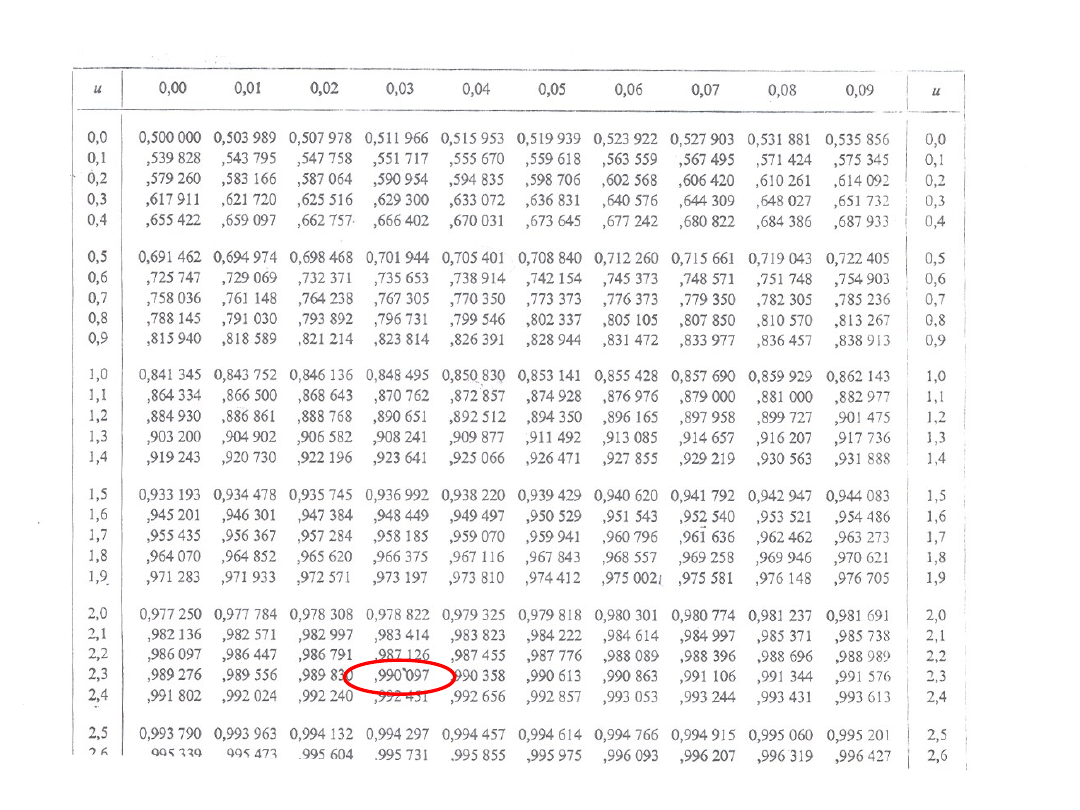
Przykład 2

Przykład 2



Dla zadanego poziomu ufności
C=0.98 wartość krytyczna z

*

wynosi 2.33.



Z danych wynika, iż σ=5g a
margines m ma być nie większy niż
0.2g

3394

06

.

3393

2

.

0

5

33

.

2

n

2

2

*



































m

z



Przykład 3



Dokonano pomiaru wagi 7 torebek cukru

i uzyskano wyniki [g]:
[985, 1015, 990, 992, 1021, 925, 1058]



Na poziomie ufności 0.97 zweryfikować

hipotezę, że średnia waga torebki cukru

to 1000g.



Zgodnie z normą wariancja wagi nie

powinna być większa niż 100.

Przykład 3



Wartość średnia z próby wynosi

998.00g.



Z danych w zadaniu wynika, że

maksymalne odchylenie standardowe

to σ=√100=10g



Poziom ufności z założenia wynosi 0.97

?

985

.

0

2

03

.

0

97

.

0

)

(

*

*











z

z

X

P

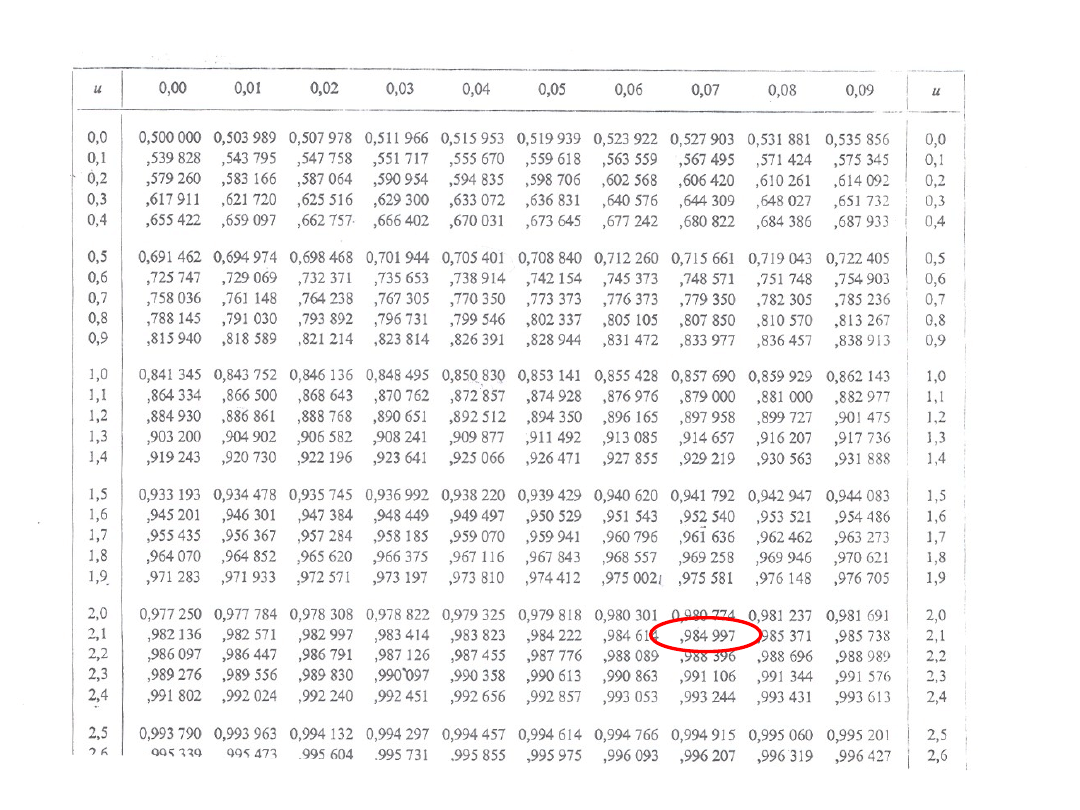
Przykład 2

Przykład 3



Z tablic odczytujemy, że z

*

=2.17



Margines błędu dla oceny wartości
średniej w populacji wynosi:



Zatem 97% przedział ufności dla wartości
średniej μ to (998.00-0.98,998.00+0.98)

98

.

0

7

10

17

.

2

*







n

z

m



Przykład 3



Wyznaczony przedział ufności to
(997.02; 998.98).



Ponieważ interesująca nas wartość
średnia w populacji (równa 1000g) nie
należy do tego przedziału, to mamy
podstawy do odrzucenia hipotezy na
poziomie
α=1-0.97=0.03

Kilka ostrzeżeń



Dane muszą być prostą próbą losową z

populacji.



Wzór nie jest poprawny dla złożonych

projektów losowań innych niż PPL. (Ale są

odpowiednie metody dla tych złożonych

projektów.)



Nie ma dobrej metody wnioskowania na

podstawie danych zebranych nieuważnie z

nieznanym błędem.



Wielkości odstające mogą mieć duży wpływ

na przedział ufności.

Kilka ostrzeżeń, cd.



Jeśli liczność próby jest mała, a

rozkład populacji nie jest normalny,

prawdziwy poziom ufności będzie inny

od C używanego w obliczeniach.



Trzeba znać odchylenie standardowe

σ populacji

.



Margines błędu w przedziale ufności

uwzględnia jedynie losowość prób.

Wnioskowanie dla średniej
populacji



Weźmy prostą próbę losową o liczności
n z populacji o rozkładzie normalnym ze
średnią μ i odchyleniem standardowym
σ. Średnia próby

ma rozkład

.



Kiedy σ jest nieznane, oceniamy je na
podstawie odchylenia standardowego
próby s, po czym szacujemy odchylenie
standardowe przez

x





n

N

/

,





x

n

s/

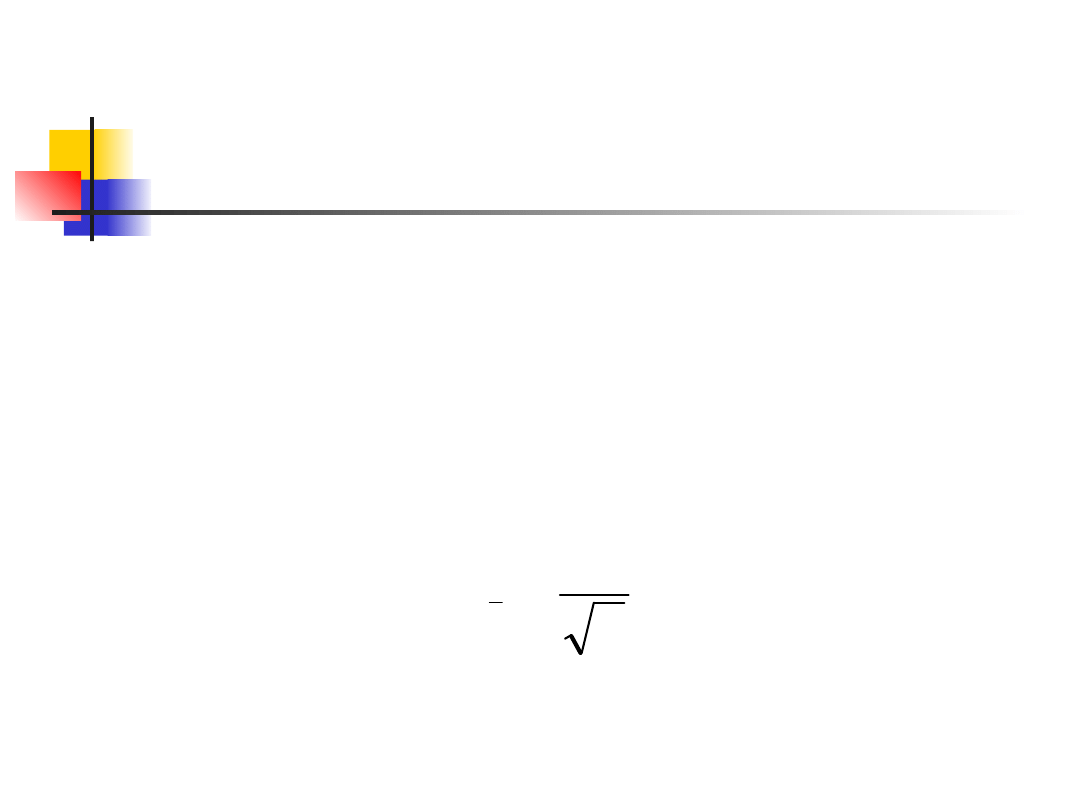
Błąd standardowy



Kiedy odchylenie standardowe
statystyki jest szacowane z
danych, wynik jest nazywany
błędem standardowym statystyki.
Błąd standardowy średniej z próby
wynosi

n

s

SE

x



Rozkład t



Kiedy zastępczo stosujemy błąd

standardowy SE zamiast odchylenia

standardowego średniej próby, wtedy

statystyka wartości średniej

NIE

ma

rozkładu normalnego.



Ma rozkład t, zwany rozkładem t-

Studenta (W.Gosset, 1908).

Rozkład t, cd.



Weźmy prostą próbę losową o liczności

n z populacji . Wtedy statystyka

t dla jednej próby

ma rozkład t z n-1 stopniami swobody.



Dla każdej liczności próby istnieje inny

rozkład t.



Poszczególne rozkłady t są określone

przez podanie stopni swobody.









,

N

n

s

x

t

/







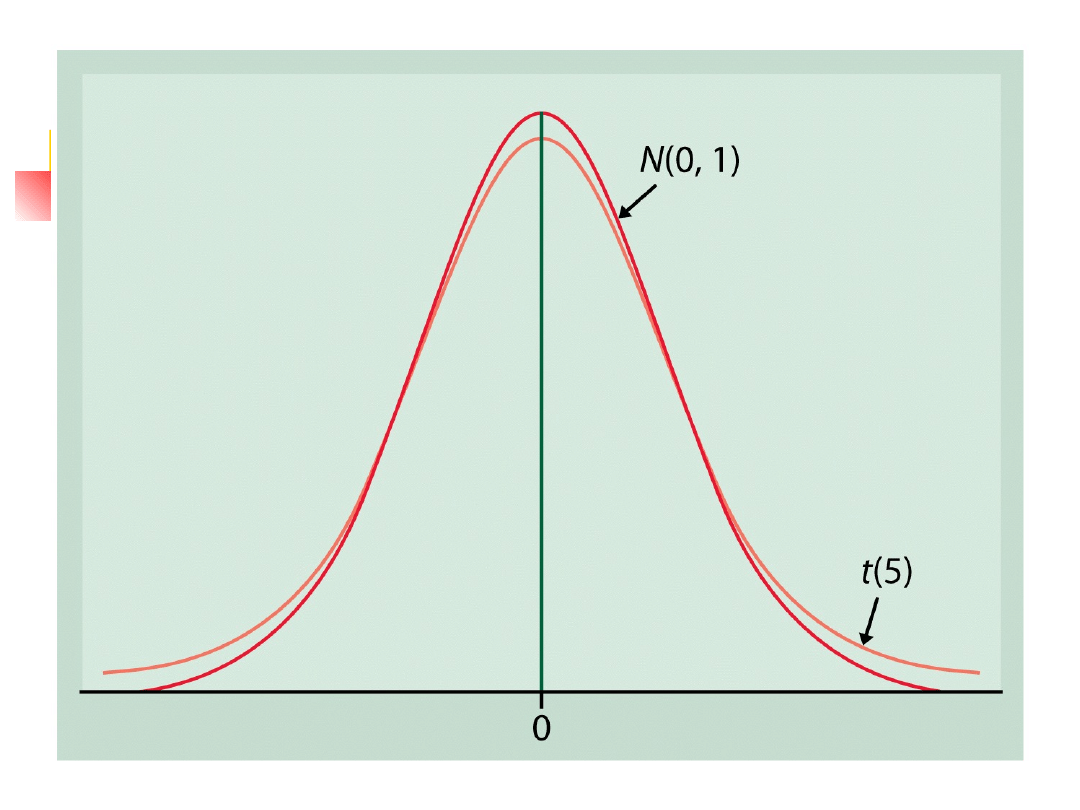
Rozkład t, cd.



Stosujemy t(k) do oznaczenia rozkładu t z k

stopniami swobody.



Krzywe gęstości rozkładów t(k) są w kształcie

podobne do standardowej krzywej normalnej.



Symetryczne względem 0



W kształcie dzwona



Rozrzut rozkładów t jest nieco większy niż

standardowego rozkładu normalnego.



Z powodu dodatkowej zmienności spowodowanej

zamianą stałego parametru σ na zmienną losową

s.

Rozkład t, cd.



Wraz ze wzrostem liczby stopni
swobody k, krzywa gęstości t(k)
dąży do rozkładu N(0,1).



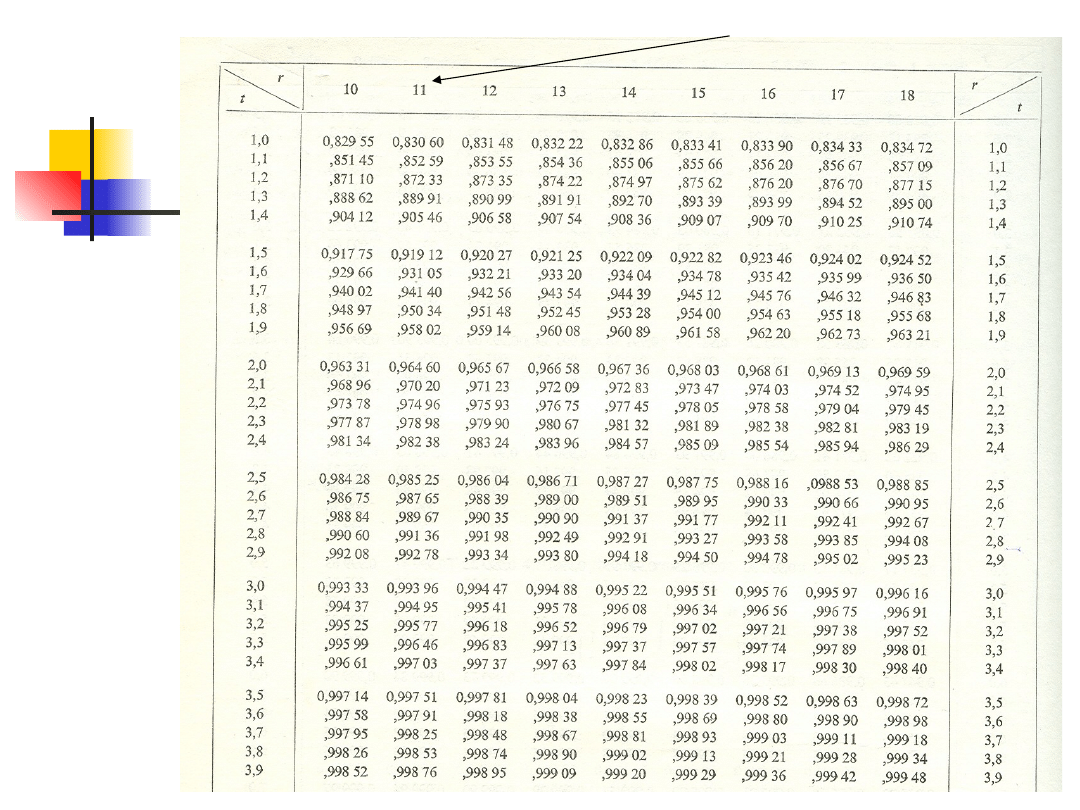
Prawie w każdej książce do
statystyki można znaleźć tablice z
wartościami krytycznymi dla
rozkładów t.

Przedział ufności t dla
jednej próby



Weźmy PPL liczności n z populacji o nieznanej

średniej μ i nieznanej wariancji σ

2

.



Przedziałem ufności na poziomie C dla μ jest

gdzie t* jest wartością dla krzywej gęstości t(n-

1) z polem C między –t* i t*. Ten przedział jest

precyzyjny kiedy rozkład populacji jest

normalny i przybliżony w innych przypadkach

dla dużych n.

n

s

t

x

n

s

t

x

*

*

, 



Stopnie swobody

Przedział ufności t dla
jednej próby - przykład



Niech PPL o liczności n=12 jest wzięta z
populacji o nieznanej średniej μ i nieznanej
wariancji σ

2

.



[114, 123.3, 116.7, 129.0, 118, 124.6, 123.1,
117.4, 111, 121.7, 124.5, 130.5]



średnia z próby = 121.15



odchylenie standardowe próby = 5.89



krytyczna t-wartość for 95% poziomu ufności
(11 stopni swobody) = 2.2010





89

.

124

;

41

.

117

12

89

.

5

*

2010

.

2

15

.

121

;

12

89

.

5

*

2010

.

2

15

.

121

n

s

t

x

,

n

s

t

x

*

*







































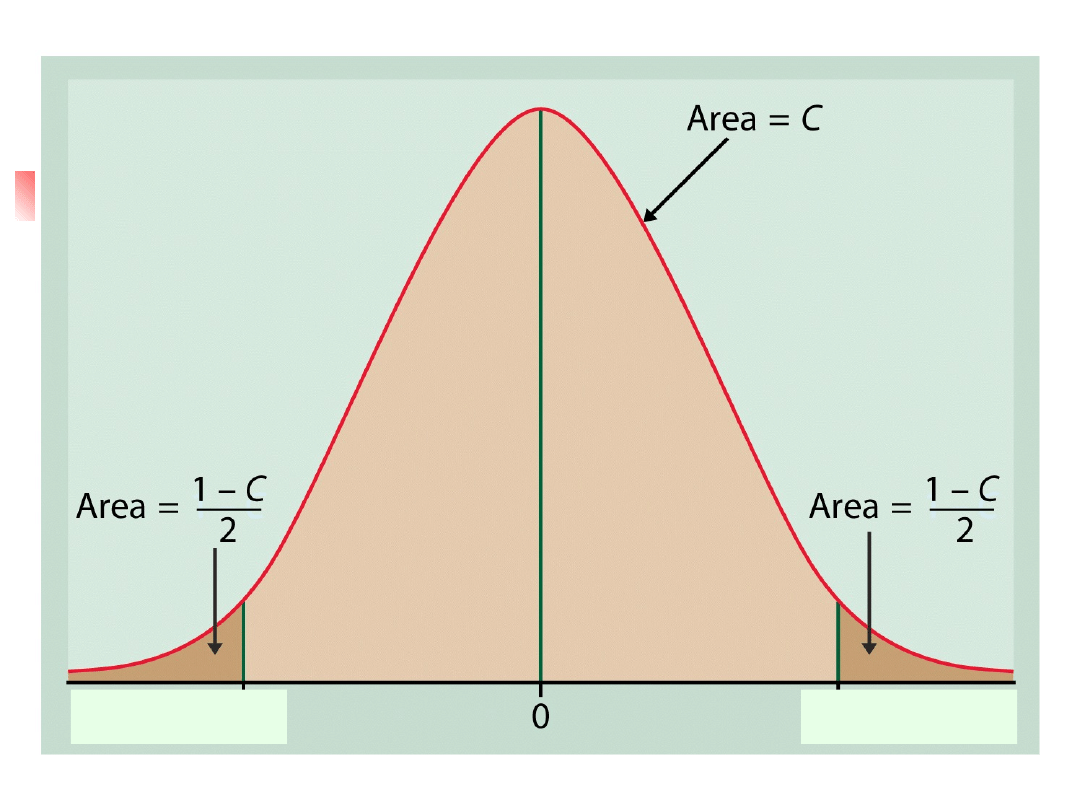
95

%

2.5%

2.5%

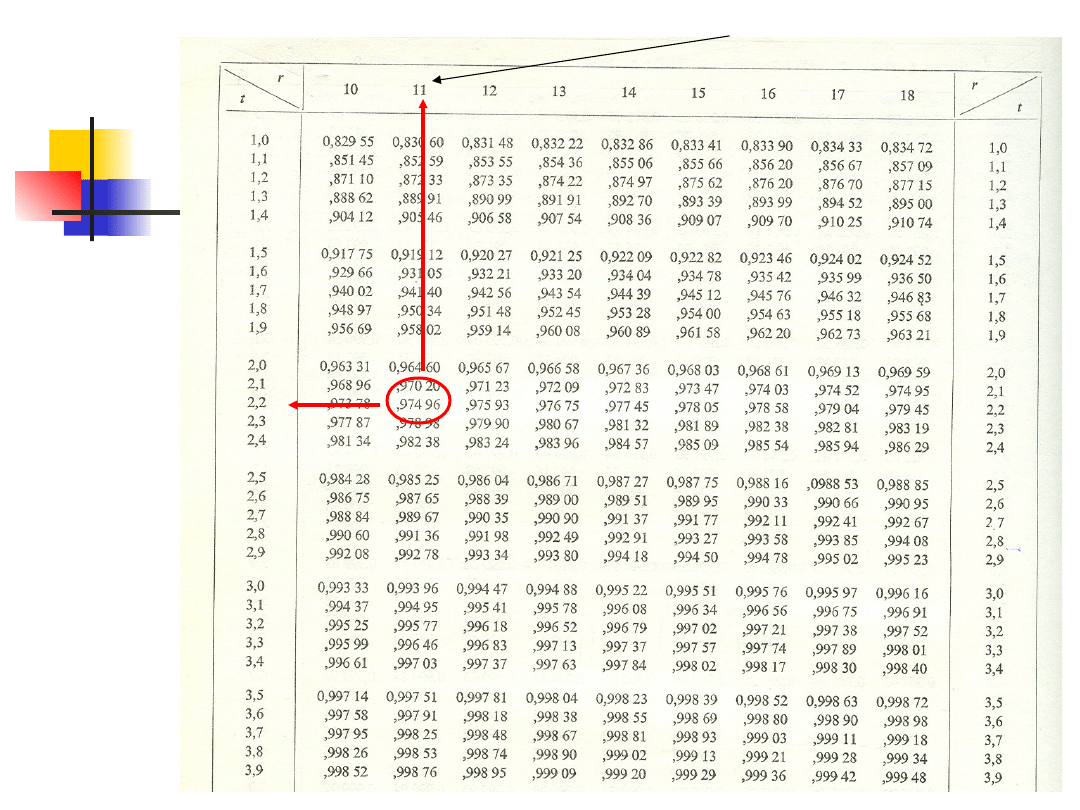
stopień swobody

Przykład 3

25 długości nóżek mszyc
Pemphigus populitransversus.
Wyniki są w mm x 10

-1.

3.8

3.6

4.3

3.5

4.3

3.3

4.3

3.9

4.3

3.8

3.9

4.4

3.8

4.7

3.6

4.1

4.4

4.5

3.6

3.8

4.4

4.1

3.6

4.2

3.9

Przykład 4



Sprawdzić na poziomie istotności
0.02 czy prawdziwe jest stwierdzenie,
że średnia długość nóżek wynosi
4x10

-1

mm.



Obliczamy (pomijamy mnożnik 10

-1

)



a z tablic rozkładu t musimy znaleźć:

25

n

;

366

.

0

s

;

004

.

4

Y







?

02

.

0

1

25

,

02

.

0









t



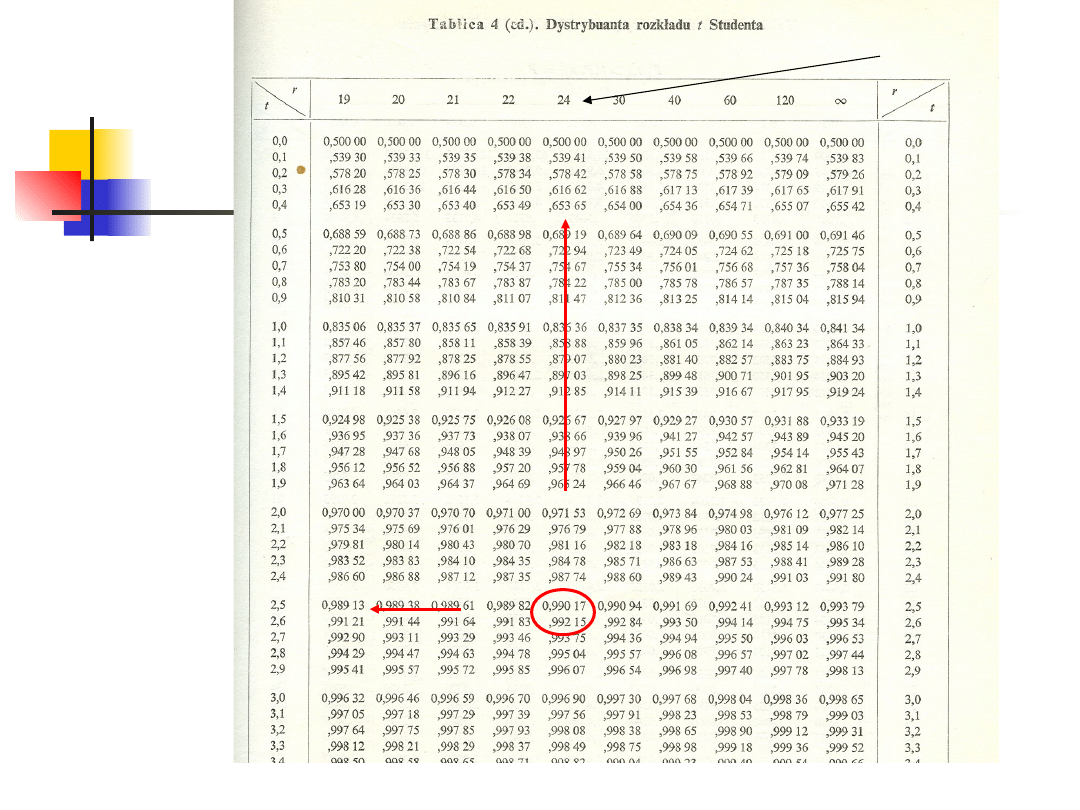
stopień swobody

Przykład 4



Granice 98% przedziału ufności dla

średniej populacji  są dane równaniami:



Ponieważ wartość 4.00 należy do

przedziału (L

1

,L

2

) to nie mamy podstaw

do odrzucenia hipotezy badawczej na

poziomie α=0.02

187

.

4

25

366

.

0

5

.

2

004

.

4

821

.

3

183

.

0

004

.

4

25

366

.

0

5

.

2

004

.

4

24

,

02

.

0

2

24

,

02

.

0

1





















































n

s

t

Y

L

n

s

t

Y

L

Granice ufności na
podstawie statystyk próby



Możemy zastosować tę samą
technikę do ustalenia granic
ufności dla dowolnej statystyki,
jeśli statystyka ma normalny
rozkład.



Ta technika dotyczy w zasadzie
wszystkich statystyk z tabeli z
następnego slajdu.

skośność

kurtoza

estymator obciążony

estymator nieobciążony

Przykład 5



W pewnym doświadczeniu

medycznym bada się czas snu

pacjentów leczonych na pewną

chorobę. Zmierzono u n=16

wylosowanych niezależnie pacjentów

czas snu i otrzymano następujące

wyniki [w minutach]: 435, 533, 393,

458, 525, 481, 324, 437, 348, 503,

383, 395, 416, 553, 500, 488.



Znaleźć 95% przedział ufności dla

mediany czasu snu.

Przykład 5



Posortowane dane są następujące:

[324 348 383 393 395 416

435 437 458 481 488 500
503 525 533 553]



Estymator punktowy mediany w
populacji wynosi 447.5



Do wyznaczenia przedziału ufności
potrzebna jest wartość błędu
standardowego dla wartości średniej

Przykład 5



Ponieważ odchylenie standardowe z
próby wynosi s=68.04 to błąd
standardowy dla oceny średniej



Błąd standardowy dla oceny mediany
to

01

.

17

16

04

.

68







n

s

s

Y

32

.

21

01

.

17

2533

.

1

2533

.

1











Y

M

s

s

Przykład 5



Wartość krytyczna t

*

dla C=0.95 i 15

stopni swobody wynosi

tinv(0.975,15)=2.1314



Zatem 95% przedział ufności dla
oceny mediany to (L

1

;L

2

) gdzie

94

.

492

32

.

21

1314

.

2

5

.

447

06

.

402

32

.

21

1314

.

2

5

.

447

2

1

















L

L

Przykład 6

Strukturę zarobków w pewnej firmie przedstawia

tabela.

Na poziomie 0.96 oszacować przedziałowo

odchylenie standardowe zarobków w tej firmie.

Pensja

Liczba

osób

(1000;2000]

10

(2000; 4000]

25

(4000; 6000]

12

(6000;8000]

8

(8000;10000]

4

(10000;20000]

2

Przykład 6

Wyliczona już wcześniej wartość średnia z próby

to 4459. Odchylenie standardowe z próby
wyliczymy jako

6

.

2888

68

.

8344125

1

)

2

4

25

10

(

)

4459

15000

(

2

)

4459

3000

(

25

)

4459

1500

(

10

2

2

2



































s

s





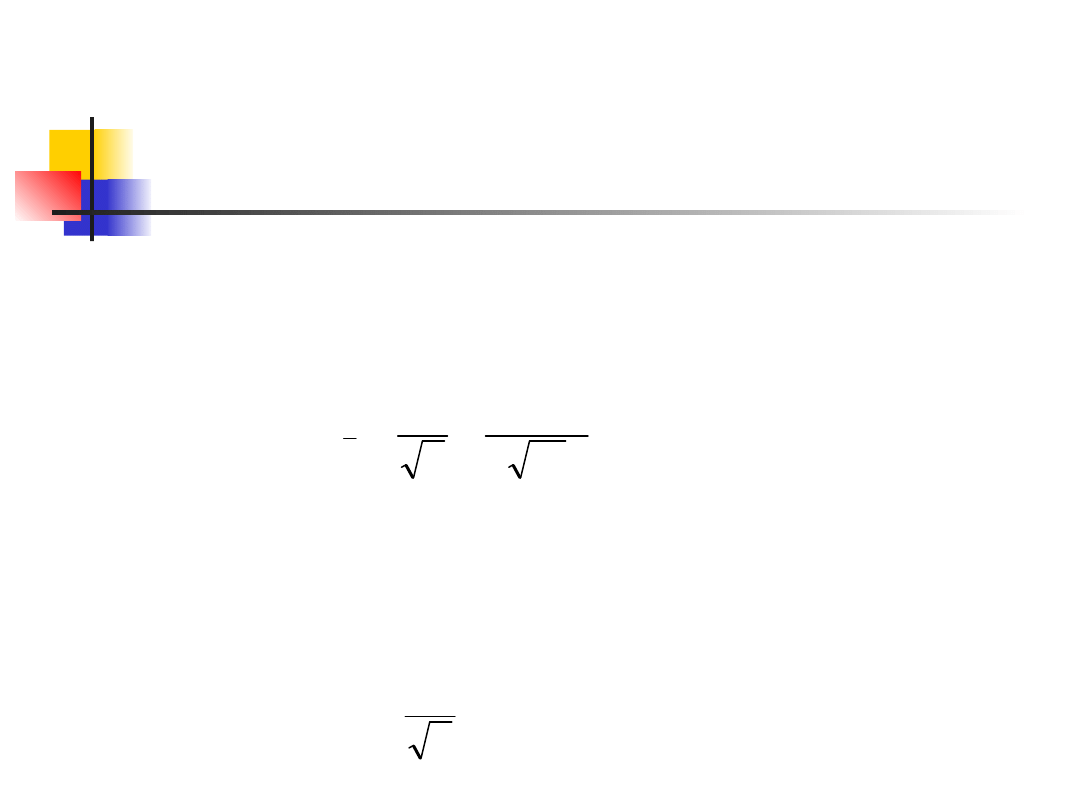
Przykład 6

Błąd standardowy średniej to

Zatem przybliżony błąd standardowy

odchylenia standardowego wynosi:

85

.

369

61

6

.

2888







n

s

s

X

52

.

261

85

.

369

7071068

.

0

7071068

.

0









n

s

s

s

Przykład 6

Wartość krytyczną t

*

dla C=0.96 znajdujemy

jako tinv(0.98,60) i wynosi ona 2.0994

Wobec tego granice 96% przedziału ufności

dla odchylenia standardowego to
odpowiednio:

6

.

3437

6

.

2339

52

.

261

0994

.

2

6

.

2888

2

1











L

L

Rozkład chi-kwadrat



Rozkład chi-kwadrat jest funkcją
prawdopodobieństwa gęstości, która
zwraca wartości od zera do plus
nieskończoności.



W ten sposób, w przeciwieństwie do
rozkładu normalnego lub t, funkcja
zbliża się do osi 

2

asymptotycznie

tylko w prawym końcu krzywej.

Rozkład chi-kwadrat



Tak jak w przypadku t, nie ma
jedynie jednego rozkładu 

2

, ale

wiele różnych funkcji gęstości dla
kolejnych wartości stopni swobody.



Funkcja opisująca rozkład 

2

jest

skomplikowana i nie będzie tutaj
zamieszczona.

Rozkład chi-kwadrat



Możemy wygenerować rozkład
zbliżony do 

2

z populacji

standardowych odchyleń
normalnych.



Standaryzujemy zmienną X

i

przez:









i

'
i

X

X

Rozkład chi-kwadrat



Wyobraźmy sobie powtarzane próby

losowe n zmiennych X

i

z populacji o

rozkładzie normalnym ze średnią  i

odchyleniem standardowym .



Dla każdej próby standaryzujemy

zmienną X

i

do X

i’

.



Wartości obliczane są dla każdej

próby i będą w przybliżeniu miały

rozkład 

2

z n stopniami swobody.



2

'
i

n

X

Rozkład chi-kwadrat



Możemy przepisać



Kiedy zastąpimy nieznaną średnią
w populacji  średnią z próby,

wyrażenie przyjmuje postać:

2

i

n

n

2

2

2

i

n

2

'
i

)

X

(

1

)

X

(

X























2

2

2

i

n

2

s

)

1

n

(

)

X

X

(

1













Rozkład chi-kwadrat



Gdybyśmy wielokrotnie próbkowali
n pomiarów z populacji o rozkładzie
normalnym i wyliczali każdorazową
tę wartość to uzyskali byśmy z dużą
dokładnością rozkład 

2

z

n-1

stopniami swobody.



Straciliśmy jeden poziom swobody,
ponieważ stosujemy średnią próby
zamiast średniej populacji.

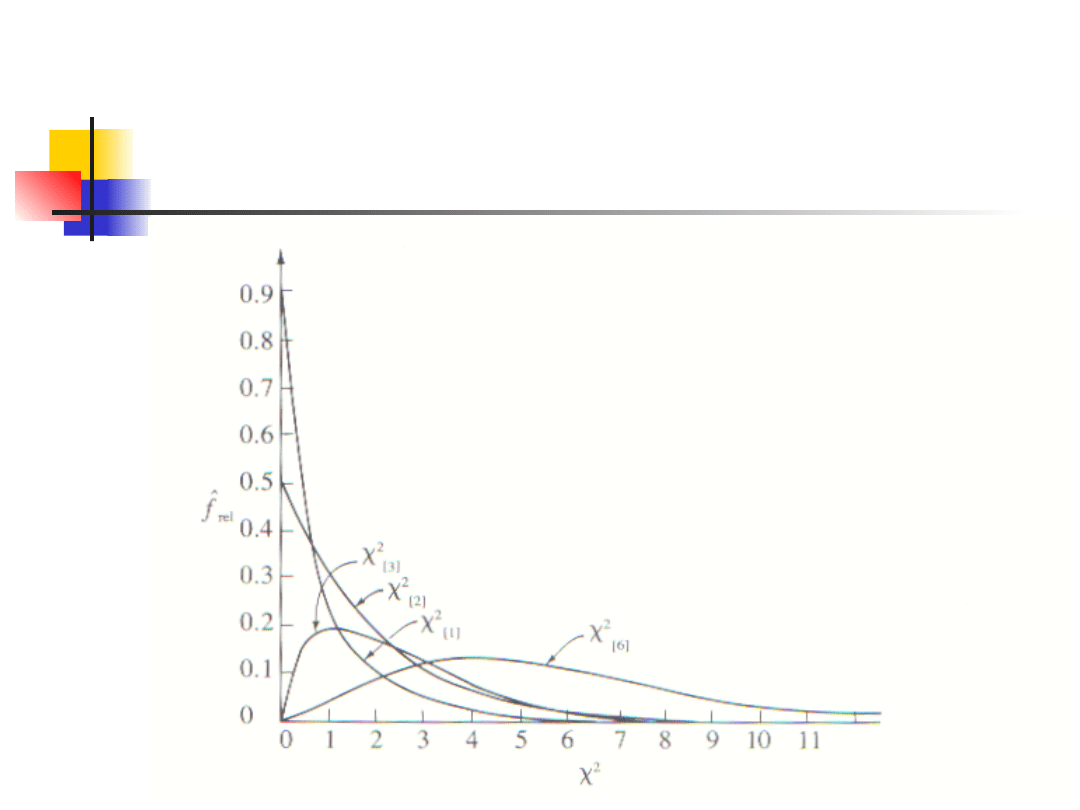
Rozkład chi-kwadrat

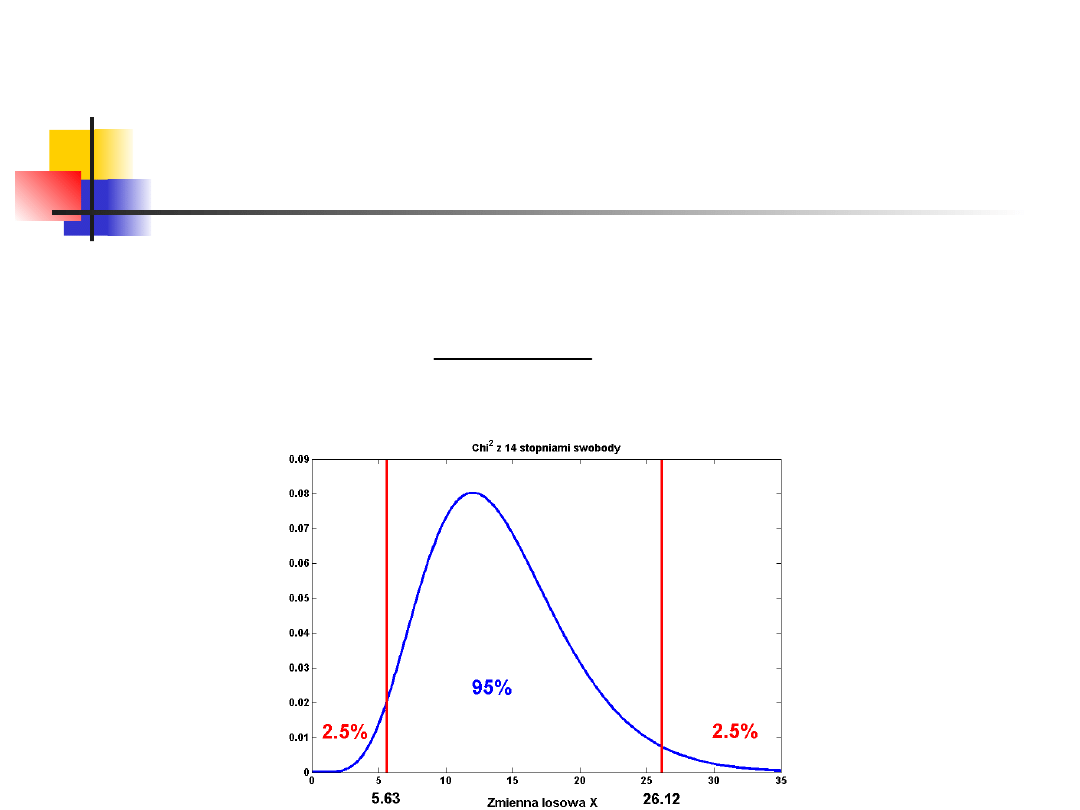
Granice ufności dla
wariancji



Możemy stwierdzić, że









































1

)

1

(

2

]

1

[

),

2

/

1

(

2

2

2

]

1

[

),

2

/

(

n

n

s

n

P

05

.

0





Granice ufności dla
wariancji

2

2

]

1

[

),

2

/

1

(

2

1

2

]

1

[

),

2

/

1

(

2

2

2

]

1

[

),

2

/

1

(

2

2

2

2

]

1

[

),

2

/

(

2

2

2

2

]

1

[

),

2

/

(

2

2

2

2

]

1

[

),

2

/

(

)

1

(

)

1

(

)

1

(

)

1

(

)

1

(

)

1

(



































































































n

n

n

n

n

n

s

n

L

s

n

s

n

L

s

n

s

n

s

n

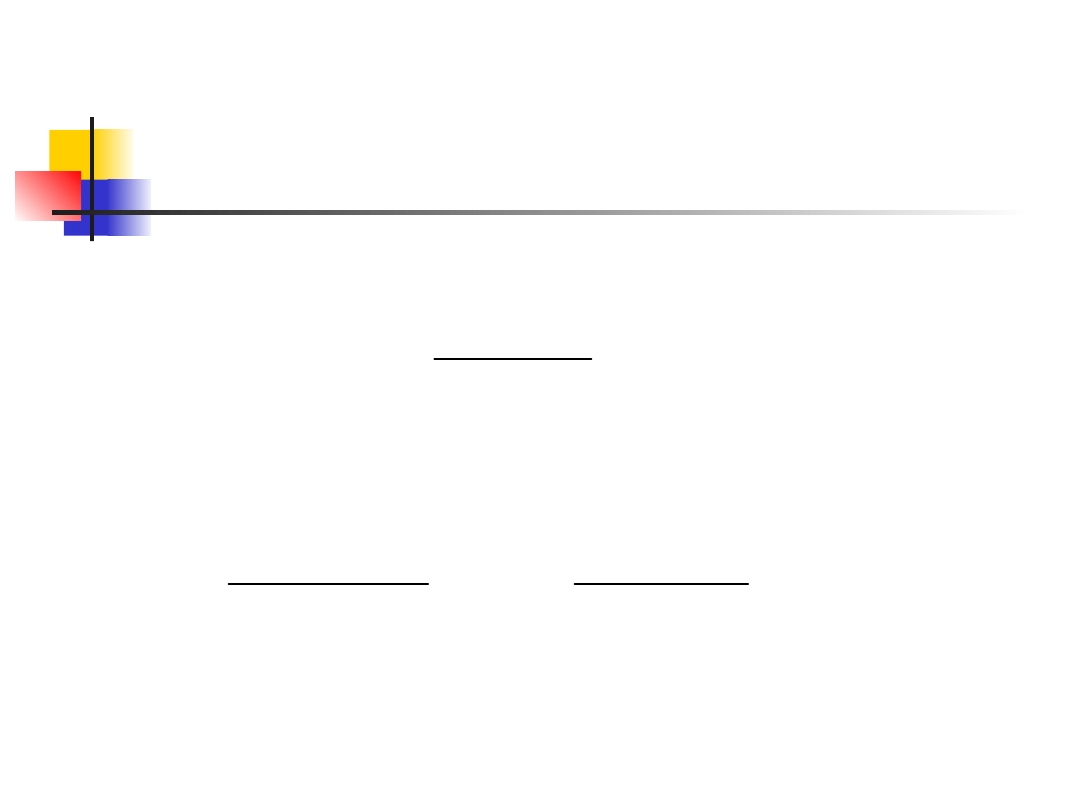
Granice ufności dla
wariancji



Możemy stwierdzić, że



Co daje w konsekwencji









































1

)

1

(

2

]

1

[

),

2

/

1

(

2

2

2

]

1

[

),

2

/

(

n

n

s

n

P















































1

)

1

(

)

1

(

2

]

1

[

),

2

/

(

2

2

2

]

1

[

),

2

/

1

(

2

n

n

s

n

s

n

P

Przykład 7



Weźmy próbę 15 długości
skrzydełek muchy z wariancją
próby s

2

=13.52



Jeśli chcemy ustalić 95% granice
ufności dla wariancji w populacji,
szukamy wartości



Wynoszą odpowiednio 5.63 i 26.12.

2

]

14

[

,

975

.

0

2

]

14

[

,

025

.

0

oraz





Przykład 7



Wtedy granice mają postać



A poszukiwany przedział ufności

68

.

33

5.62

189.28

52

.

13

14

25

.

7

26.12

189.28

52

.

13

14

2

]

14

[

,

025

.

0

2

2

]

14

[

,

975

.

0

1





















L

L





95

.

0

68

.

33

25

.

7

2









P

Przykład 7



Czy prawdą jest, że odchylenie

standardowe wynosi 6?



Skoro hipotetyczne odchylenie

standardowe wynosi 6, to wariancja

36.



Ponieważ , gdzie L

1

=7.25

oraz L

2

=33.68, to odrzucamy hipotezę

na poziomie α=1-C=0.05

)

;

(

36

2

1

L

L



Przykład 8

By ocenić klasę dwóch urządzeń mierzących

średnicę rur, przeprowadzono eksperyment

i uzyskano następujące wyniki:



dla urządzenia A, 20 pomiarów, odchylenie

standardowe 2.65;



dla urządzenia B, 16 pomiarów, odchylenie

standardowe 4.80.



Przyjmując α=0.01 zweryfikować hipotezę,

że urządzenie A ma taką samą wariancję

pomiarów.

Przykład 8

Wyznaczamy przedział ufności dla

wariancji dla urządzenia A





99

.

0

50

.

19

46

.

3

99

.

0

8440

.

6

65

.

2

19

5823

.

38

65

.

2

19

2

2

2

2

































P

P

Przykład 8



By zweryfikować hipotezę o braku

różnic

musimy

sprawdzić,

czy

estymata

punktowa

z

drugiego

eksperymentu mieści się we wnętrzu

przedziału ufności dla wariancji

pierwszej populacji.

)

,

(

80

.

4

)

50

.

19

;

46

.

3

(

)

,

(

2

1

2

2

1

L

L

L

L



