Wykład 3

Wybór w sytuacji

niepewności

Wybór w sytuacji

niepewności

• Podstawowy model wyboru w

sytuacji ryzykownej

• Przekształcenia psychologiczne

na wartościach

• Paradoksy Allaisa

PODSTAWOWY MODEL

WYBORU W WARUNKACH

RYZYKA

Racjonalne zachowanie

Maksymalizacja wartości oczekiwanej

(XVII wiek - Pascal)

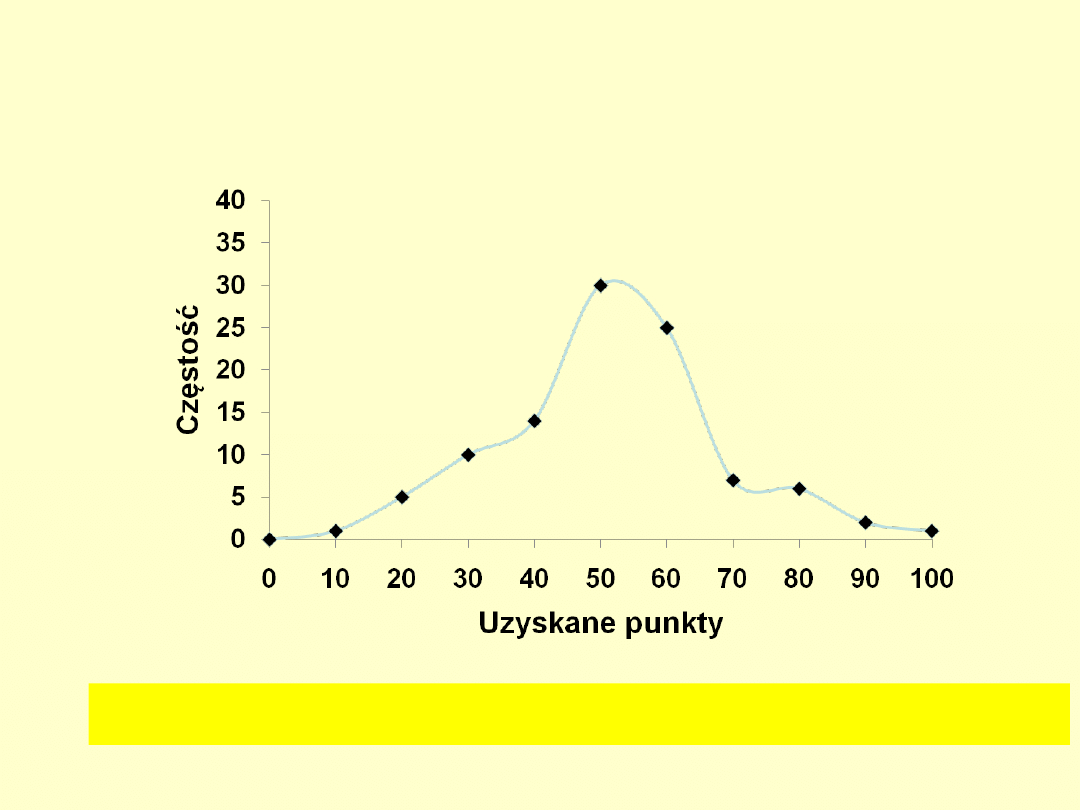
Średni wynik w tescie IQ

Średnia: (0 * 0 + 10 * 1 + ....+ 100 * 1)/N

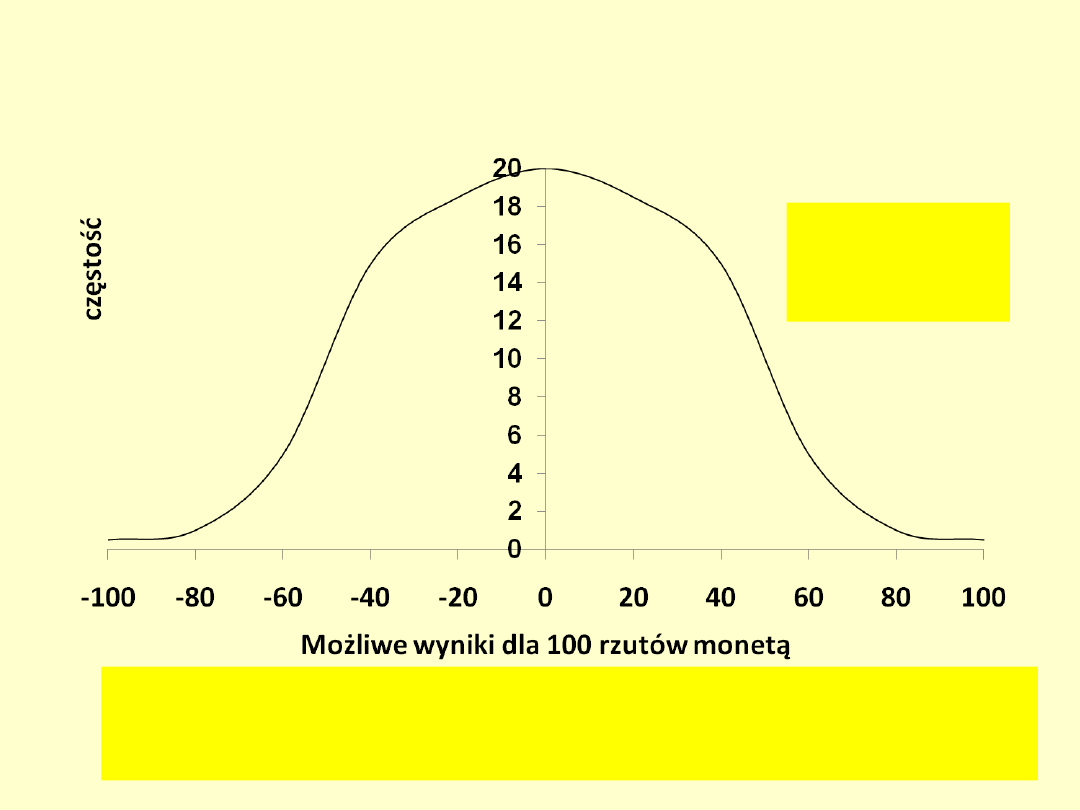
Maksymalizacja średniego

zysku (EV)

(decyzje wielokrotne, np. gry hazrdowe)

100 rzutów
Orzeł +1 zł
Reszka -1 zł

Średnia:[(-100 * 0.01) + (-80 * 0.05)... + ....+ ....(+ 100 *
0.01)]/N=100

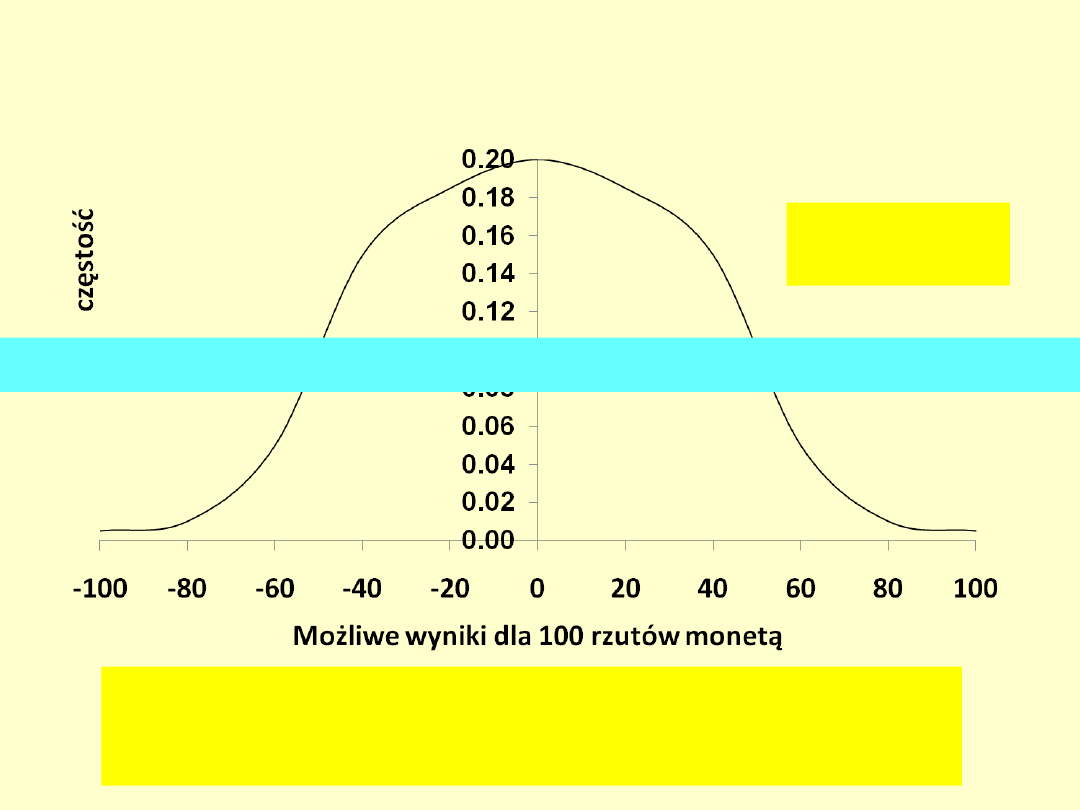
Maksymalizacja średniego

zysku

(decyzje wielokrotne, np. gry hazrdowe)

Orzeł +1 zł
Reszka -1 zł

Średnia:[(-100 * 0.01) + (-80 * 0.05)... + .... +...
(+ 100 * 0.01)]

EV = (WARTOŚĆ WYNIKU * PRAWDOPODOBIEŃSTWO)

Maksymalizacja wartości

oczekiwanej (EV)

(wybór jednorazowy)

• Gra 1: [orzeł, +1pln; reszka, -1pln] 

EV(G1) = [(1/2 * +1) + (1/2 * -1)] = 0

• Gra 2: [orzeł, +2pln; reszka, -2pln] 

EV(G2) = [(1/2 * +2) + (1/2 * -2)] = 0

• Gra 3: [orzeł, +2pln; reszka, -1pln] 

EV(G3) = [(1/2 * +2) + (1/2 * -1)] = +0.5

EV = (WARTOŚĆ WYNIKU * PRAWDOPODOBIEŃSTWO)

MODEL WARTOŚCI

OCZEKIWANEJ

WARTOŚĆ =
OCZEKIWANA

 (WARTOŚĆ WYNIKU *
PRAWDOPODOBIEŃSTWO)

- Dla każdego możliwego wyniku obliczmy taki

iloczyn

- Iloczyny sumujemy

Wybór w sytuacji

niepewności

•

Podstawowy model wyboru w sytuacji

Podstawowy model wyboru w sytuacji

ryzykownej

ryzykownej

• Przekształcenia psychologiczne na

wartościach

• Paradoksy Allaisa

• Próba wyjaśnienia paradoksów Allaisa

Przekształcenia

psychologiczne na

wartościach

• Paradoks petersburski

• Wyjaśnienie Bernoulli’ego –

pojęcie użyteczności

• Użyteczność pieniędzy

Paradoks Petersburski

• Rzucamy monetą, aż do momentu

wypadnięcia orła

• Wypłata to 2

n

• n – liczba rzutów do momentu

wypadniecia orła

• Np. orzeł wypadł za pierwszym razem,

n=1,
wypłata 2

1

=2,

za drugim razem n=2, wypłata 2

2

=4, itd.

Paradoks Petersburski

• Suma (p

1

*2PLN + p

2

*4PLN + p

3

*8PLN + ... +

p

n

*2

ⁿ

PLN)

od 1 do nieskończonosci

• Każdy iloczyn jest równy 1
• Ilość iloczynów jest nieskończona

p

1

= 0.50, czyli 0.50*2 + 0.50*0 = 1

p

2

= 0.25, czyli 0.25*4 + 0.75*0 = 1 ... itd.

• EV tej gry jest wobec tego wartością nieskończoną
• Eksperymentalnie wykazano, że ludzie chcą płacić za

udział w tej grze około 2.50

Wyjaśnienie Bernoulliego –

przekształcenia psychologiczne na

wartości

•

Ludzie nie posługują się wartością obiektywną,

ale jej subiektywną oceną - użytecznością

•

Ocena subiektywna zależy od stanu posiadania

-

dla biednego 100PLN jest warte więcej niż dla

bogatego

-

apetyt rośnie w miarę jedzenia

•

Takie przekształcenia psychologiczne na

wartości opisuje funkcja logarytmiczna

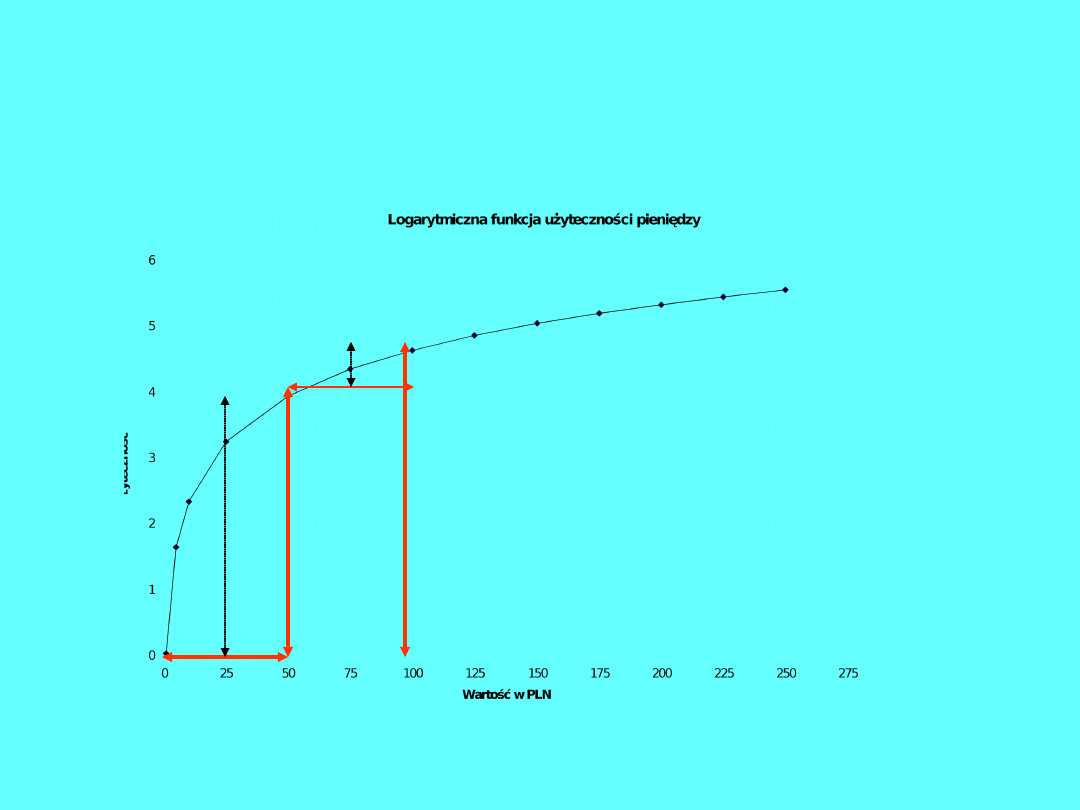
Wyjaśnienie Bernoulliego (1738) –

przekształcenia psychologiczne na

wartości

Pojęcie użyteczności

WARTOŚĆ

=  (

WARTOŚĆ

WYNIKU *

PRAWDOPODOBIEŃSTWO)

OCZEKIWANA

przekształcenia psychologiczne

UŻYTECZNOŚĆ

=

 (

UŻYTECZNOŚĆ

WYNIKU*PRAWDOPODOBIEŃSTWO)

OCZEKIWANA

Bernoulli (1954)

Zastosowanie obserwacji

Bernoulliego do percepcji

• Zmniejszająca się wrażliwość na zmiany w

natężeniu bodźca:

- promyk światła w ciemności
- dodatkowa 100-watowa żarówka na sali

balowej

• Prawo Webera-Fechner (1860): odczuwana

zmiana w stosunku do rzeczywistej zmiany
jest opisywana przez funkcję logarytmiczną

• Prawo Stevensa

Malejąca użyteczność a

stosunek do ryzyka

Oczekiwana

użyteczność w

sytuacji pewnej

• +100, 100%

• EV = 100 * 1=100

• EU = u(100)*1

Oczekiwana

użyteczność zakładu

o tym samym EV

• +200, 50%, vs 0,50%

• EV = 200*½ + 0* ½

=
100

• EU = u(200)* ½

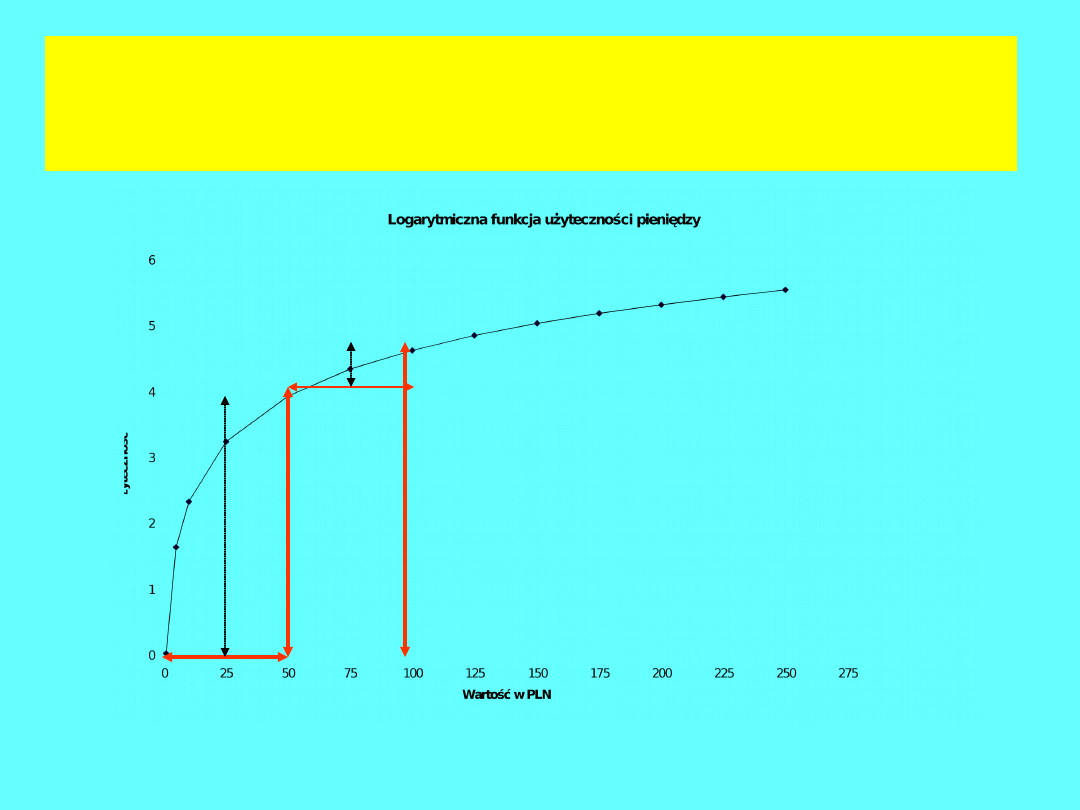
u(100)*1=a większe niż
u(200)*½= ½ b

a

b

Malejąca użyteczność a

stosunek do ryzyka

Oczekiwana

użyteczność w

sytuacji pewnej

EU = u(100)*1=a

Oczekiwana

użyteczność zakładu

o tym samym EV

EU = u(200)* ½= ½b

Zgodnie z ogólnym prawem – malejącej wrażliwości na zmianę bodżca
wraz ze wzrostem wartości:

użyteczność wyniku pewnego jest zawsze wyższa niż

użyteczność zakładu

Prawo zmniejszającej się

wrażliwości na zmianę bodzca

a ryzyko

Zgodnie z ogólnym prawem

malejącej wrażliwości na zmianę bodżca

wraz ze wzrostem wartości

użyteczność wyniku pewnego

jest zawsze wyższa niż

użyteczność zakładu

racjonalne
zachowanie
to maksymalizacja
oczekiwanej
użyteczności

wybór pewności
unikanie ryzyka

MODYFIKACJE MODELU

WARTOŚCI OCZEKIWANEJ

(1)

WARTOŚĆ

=  (

WARTOŚĆ

WYNIKU *

PRAWDOPODOBIEŃSTWO)

OCZEKIWANA

przekształcenia psychologiczne

(prawo Fechnera-Webera)

UŻYTECZNOŚĆ

=

 (

UŻYTECZNOŚĆ

WYNIKU*PRAWDOPODOBIEŃSTWO)

OCZEKIWANA

Bernoulli (1954); Stevens (1959)

Wybór w sytuacji

niepewności

•

Podstawowy model wyboru w sytuacji

Podstawowy model wyboru w sytuacji

ryzykownej

ryzykownej

•

Przekszta

Przekszta

łcenia psychologiczne na

łcenia psychologiczne na

wartściach

wartściach

• Paradoksy Allaisa

• Próba wyjaśnienia paradoksów Allaisa

Co byś wybrał?

A: +4000, 80%, B: +3000, 100%

0, 20%

Co byś wybrał?

C: +4000, 20%,

D: +3000, 25%

0, 80%

0, 75%

Paradoksy Allaisa (1953)-

ł

amanie zasady common ratio

A: +4000, 80%,

B: +3000, 100%

0, 20%

• Ludzie wybierają B

C: +4000, 20%,

D: +3000, 25%

0, 80%

0, 75%

• Ludzie wybierają C

Paradoksy Allaisa (1953)-

ł

amanie zasady common ratio

A: +4000, 80%

0, 20%

B: +3000,

100%

C: +4000, 20%

0, 80%

D: +3000, 25%

0, 75%

u(3000) * 1.00 większe niż u(4000) * 0.80

Wybór B

Wybór C

u(3000) * 0.25 mniejsze niż u(4000) * 0.20

Paradoksy Allaisa - ł

amanie

zasady common ratio

• Wybór B

u(3000) * 1.00 większe u(4000)

* 0.80

• Wybór C

u(3000) * 0.25 mniejsze u(4000)

* 0.20

obie strony mnożymy przez 4

Paradoksy Allaisa - ł

amanie

zasady common ratio

• Wybór B

u(3000) * 1.00 większe u(4000) *

0.80

• Wybór C

u(3000) * 0.25 mniejsze u(4000) *

0.20

obie strony mnożymy przez 4

u(3000) * 0.25 * 4 mniejsze u(4000) * 0.20 * 4

u (3000) * 1.00 mniejsze u(4000) * 0.80 !!!!

Paradoksy Allaisa - ł

amanie

zasady common ratio

•

Wybór B

u(3000) * 1.00 większe u(4000)

* 0.80

•

Wybór C

u(3000) * 0.25 mniejsze u(4000) *

0.20

obie strony mnożymy przez 4

u(3000) * 0.25 * 4 mniejsze u(4000) * 0.20 * 4

u (3000) * 1.00 mniejsze u(4000) * 0.80 !!!!

Uproszczony przykład - łamanie

zasady common ratio

u(Paryż, 6 dni) większa niż (Berlin, 6

dni)

• powinno być:

u(Paryż, 3 dni) większa niż (Berlin, 3 dni)

• pardoks Allaisa jest:

u(Paryż, 3 dni) mniejsza niż (Berlin, 3

dni)

Co byś wybrał?

A: +5000, 10%

B: +1000,

100%
+1000, 89%

0, 1%

Co byś wybrał?

C: +5000, 10%

D: +1000, 11%

0, 90%

0, 89%

Paradoksy Allaisa (1953) -

ł

amanie zasady wspólnych

konsekwencji

A: +5000, 10%

B: +1000, 100%

+1000, 89%
0, 1%

• Większość ludzi wybiera B, ze względu na 1%

na wynik 0 w przypadku A
C: +5000, 10%

D: +1000, 11%

0, 90% 0, 89%

• Większość ludzi wybiera C, lekceważąc fakt,

że prawdopodobieństwo wygrania jest

mniejsze o 1%, ponieważ tutaj kierują się

wielkością wygranej

Paradoksy Allaisa - ł

amanie

zasady wspólnych

konsekwencji

A: +5000, 10%

+1000, 89%
0, 1%

C: +5000, 10%
0, 89%

0, 1%

B: +1000, 10%
+1000, 89%
+1000, 1%

D: +1000, 10%
0, 89%
+1000, 1%

Paradoksy Allaisa - ł

amanie

zasady wspólnych

konsekwencji

A: +5000, 10%

+1000, 89%

0, 1%

C: +5000, 10%

0, 89%

0, 1%

B: +1000, 10%

+1000, 89%

+1000, 1%

D: +1000, 10%

0, 89%

+1000, 1%

Uproszczony przykład - ł

amanie

zasady wspólnych

konsekwencji

A:

Paryż, 10%

Berlin, 89%

0, 1%

C:

Paryż, 10%

0, 89%

0, 1%

B: Berlin, 10%

Berlin,

89%

Berlin, 1%

D: Berlin, 10%

0, 89%

Berlin, 1%

Pytania i ćwiczenia do

paradoksów Allaisa

Proszę uważnie przeczytać

przykład

VACATION PACKAGES

Which do you choose?

• A1: A lottery ticket

that gives you:

- a 50% chance of

winning a 3-week

trip to England,

France, and Italy

• 50% chance of

getting nothing

• A2: Simply a

guaranteed one-

week trip to England

Now which do you choose?

• B1: A lottery ticket that

gives you:

- a 5% chance of winning a

3-week trip to England,

France, and Italy

- a 95% chance of getting

nothing

• B2: A lottery ticket that

gives you:

- a 10% chance of winning

a one-week trip to

England

- a 90% chance of getting

nothing

Teraz proszę go zapisać

symbolicznie,

tj. zostawić tylko nagrody i

szanse

Proszę się uważnie przyjrzeć

temu zapisowi – co można

zaobserwować?

VACATION PACKAGES

• A1:
-

50%, 3 tyg. A, F,

W

- 50%, 0

• A2:
-

100%, 1 tydz. A

• B1:

- 5%, 3 tyg. A, F, W

- 95%, 0

• B2:

- 10%, 1 tydz. A

- 90%, 0

VACATION PACKAGES

Większość ludzi wybiera:
- 1-tygodniową wycieczkę do Anglii,

która jest pewna (A2) – pierwszy
wybór,

- ale 3-tygodnie w Anglii, Francji i

Włoszech (B1) – drugi wybór

Czy patrząc na swój symboliczny

zapis rozumiesz, gdzie jest
problem?

VACATION PACKAGES

• This choice pattern simply contradicts

any application of Decision Theory and
the Rational Expectations Principle

- see if you can find any numbers to

represent your desires for each
outcome (e.g., 0 for nothing, 1 for the
1-week tour, 3 for the 3-week tour) and
could explain these choices.

- You can't.

Independence Axiom

Kolejny slajd ilustruje znany

aksjomat (zasadę) – podaj na

podstawie wykładu jej polską

nazwę oraz przykład niezgodnych

z tym aksjomatem wyborów

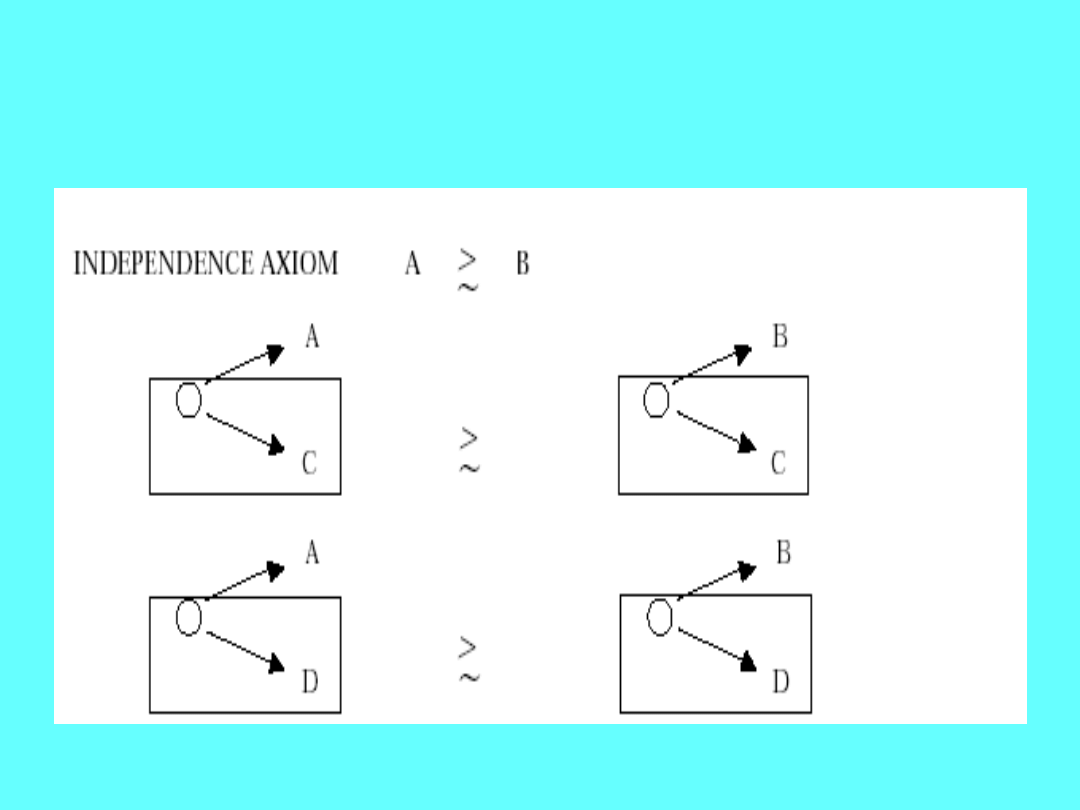
Proszę podać przykład wyborów

niezgodnych z tym aksjomatem

Paradoks Allaisa i

Ellsberga

Dwa kolejne slajdy ilustrują

dwa słynne paradoksy

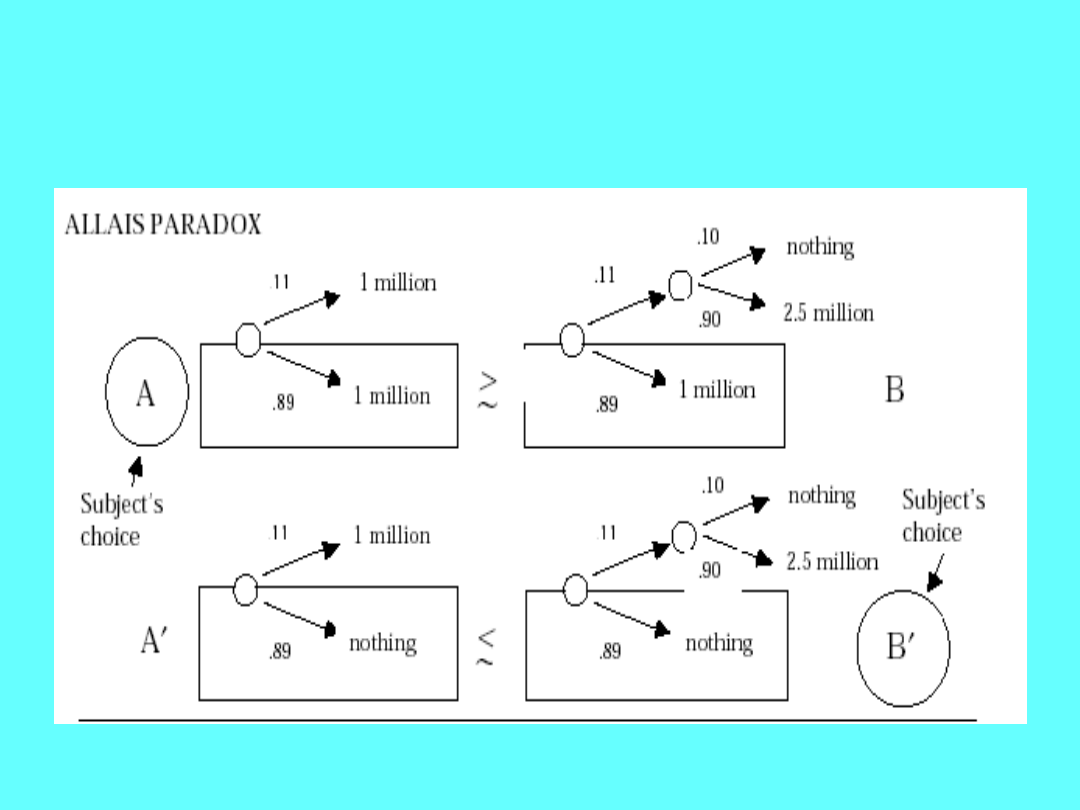
Dlaczego wybory badanych są

paradoksalne?

Paradoksy Allaisa - ł

amanie

zasady wspólnych

konsekwencji

A:

1 milion, 89%

1 milion, 11%

C:

0, 89%

1 milion, 11%

B:

1 milion, 89%

11%

_________________________

0 10%
2.5 mil. 90%

D:

0,

89%

11%

__________________________

0 10%
2.5 mil. 90%

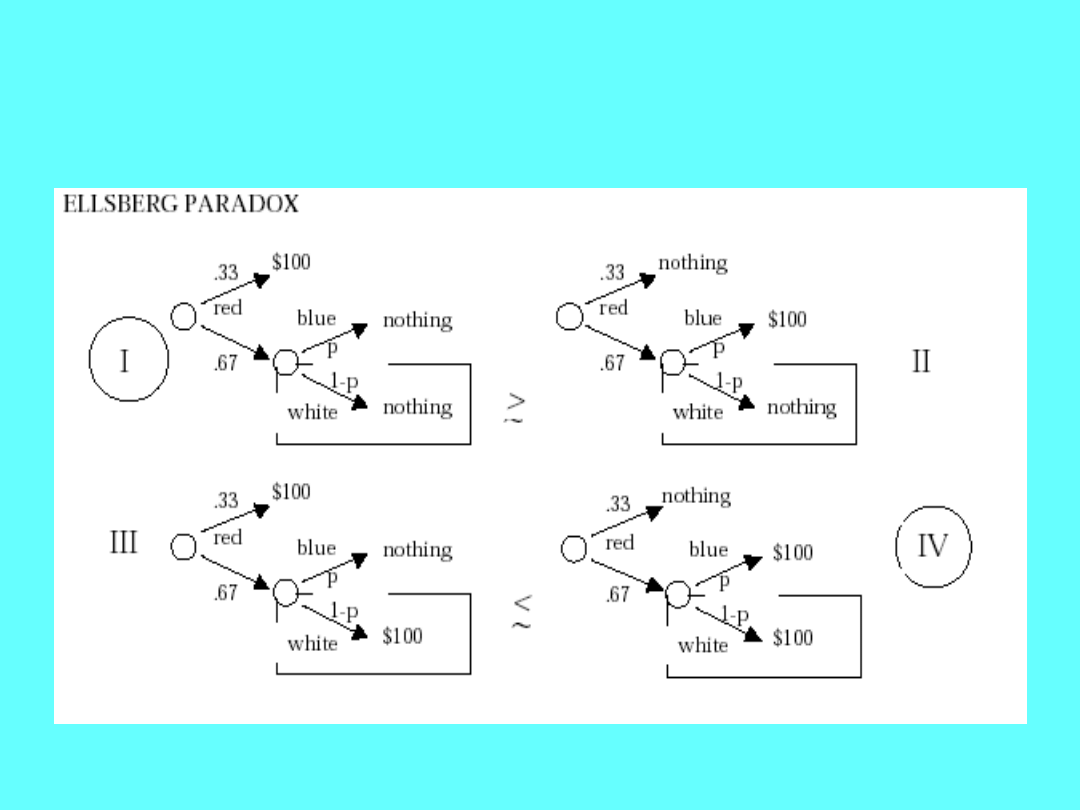
Dlaczego wybór I i IV uznajmemy za

paradoks?

Jeśli odpowiedziałeś(aś) na

poprzednie pytania, to:

Zastanów się czy te dwa

paradoksy iluustrują łamanie

tej samej zasady, czy dwóch

różnych zasad?