
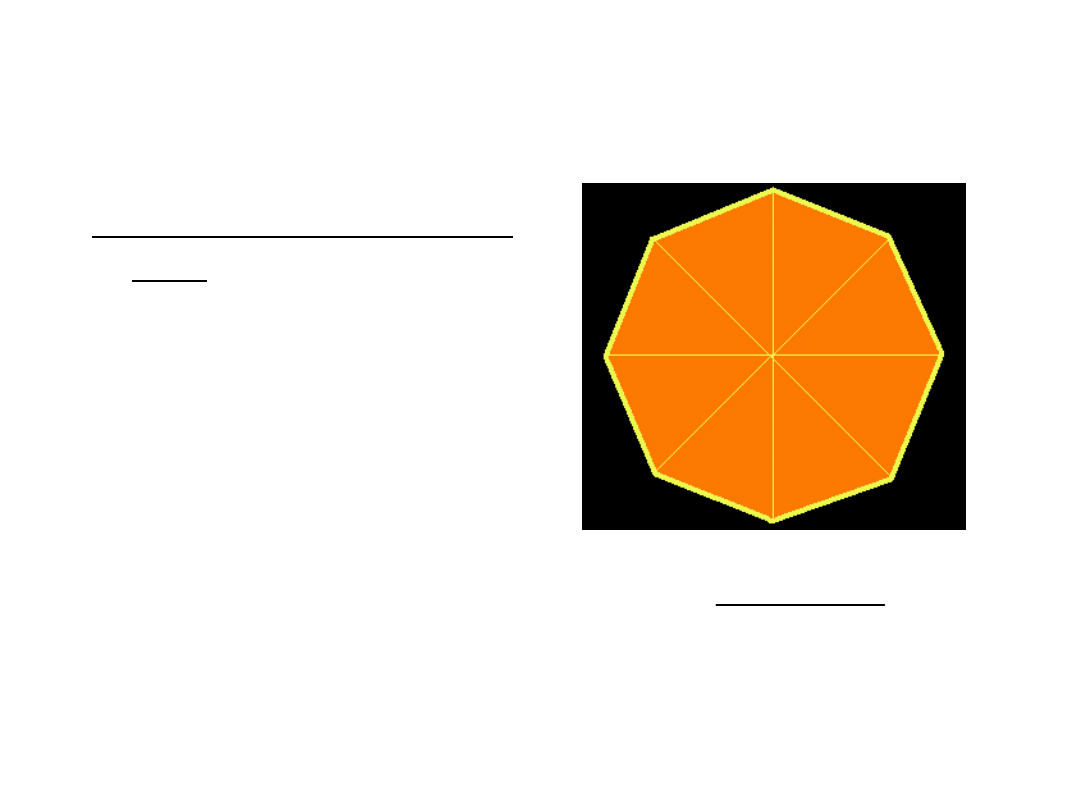
OŚMIOKĄT FOREMNY
OŚMIOKĄT FOREMNY
MA:
• BOKI JEDNAKOWEJ
DŁUGOŚCI.
• ŚRODEK SYMETRII.
• 8 OSI SYMETRII.
• KĄTY WEWNĘTRZNE
PRZYSTAJĄCE.
• 20 PRZEKĄTNYCH.
a
Ob
rw
a
P
8
2
8
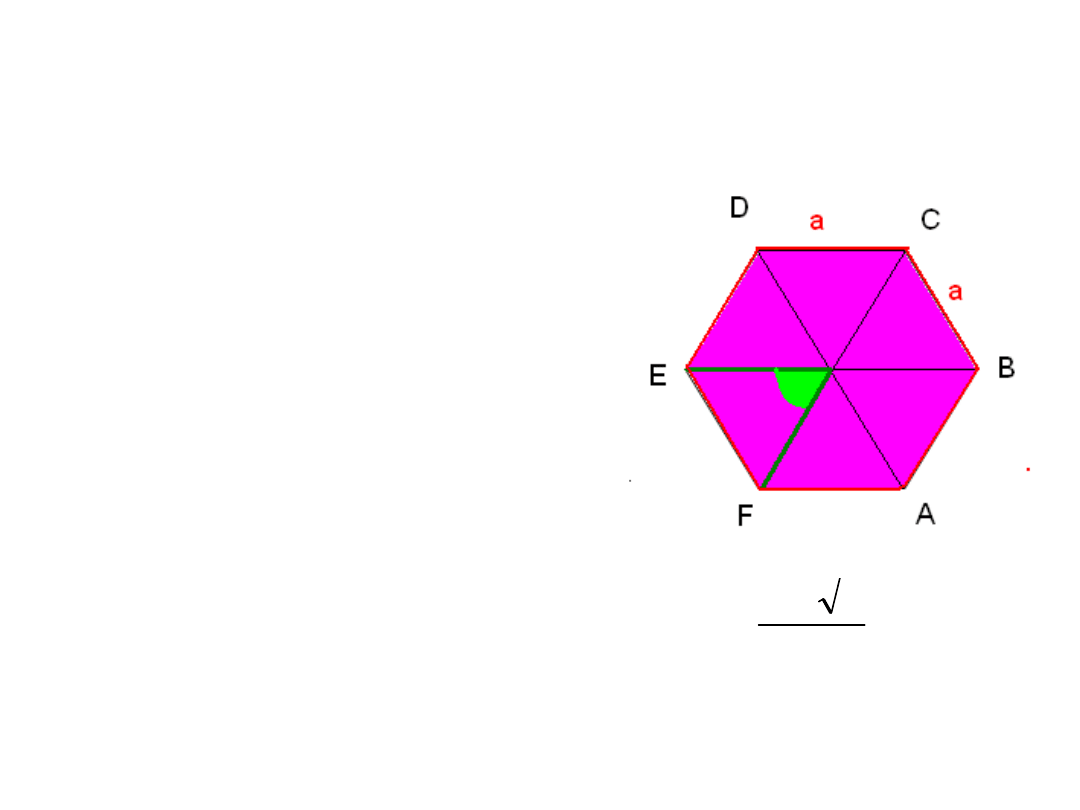
SZEŚCIOKĄT
FOREMNY
• BOKI JEDNAKOWEJ
DŁUGOŚCI.
• ŚRODEK SYMETRII.
• 6 OSI SYMETRII.
• KĄTY WEWNĘTRZNE
JEDNAKOWEJ MIARY.
• 9 PRZEKĄTNYCH.
a
Ob
a
P
6
4
3
6
2
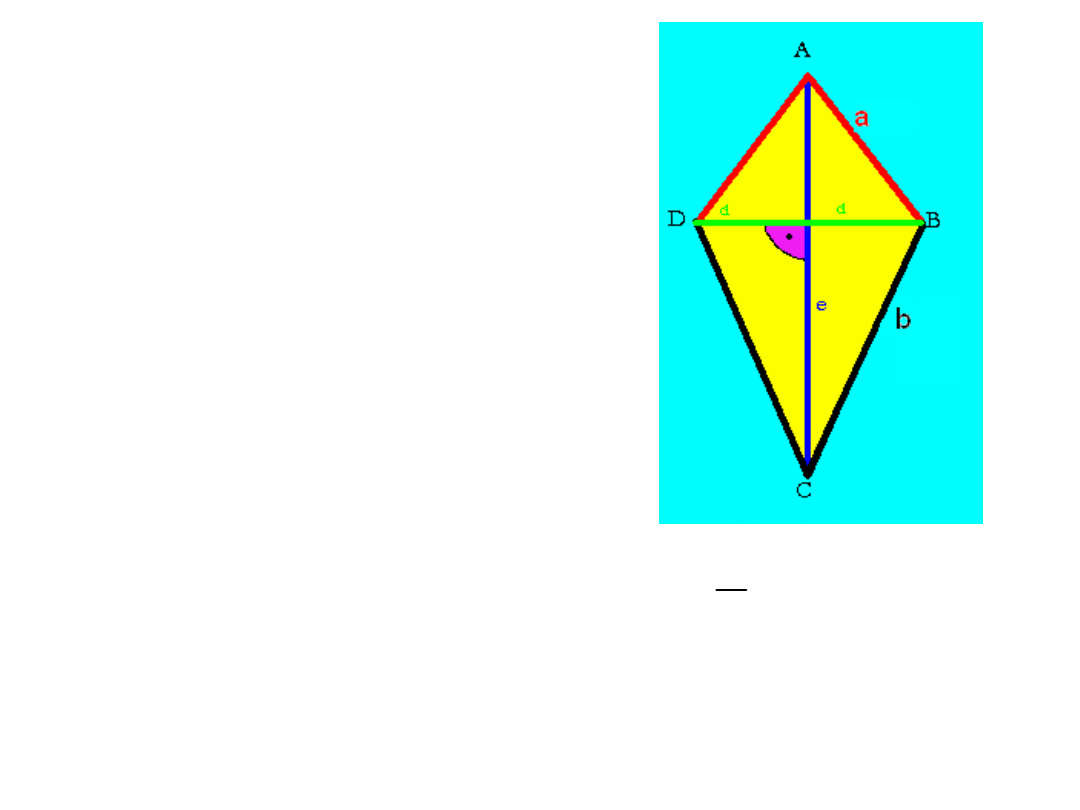
DELTOID
• RÓWNE 2 PARY
SĄSIEDNICH BOKÓW.
• 1 OŚ SYMETRII.
• KĄTY PRZYLEGŁE DO
KRÓTSZYCH BOKÓW-
PRZYSTAJĄCE.
• SUMA MIAR KĄTÓW
WEW.- 360
0
• PRZEKĄTNE
PRZECINAJĄ SIĘ POD
KĄTEM 90
0
• DŁUŻSZA PRZEKĄTNA
DZIELI KRÓTSZĄ NA
POŁOWY.
b
a
Ob
f
e
P
2
2
2
1
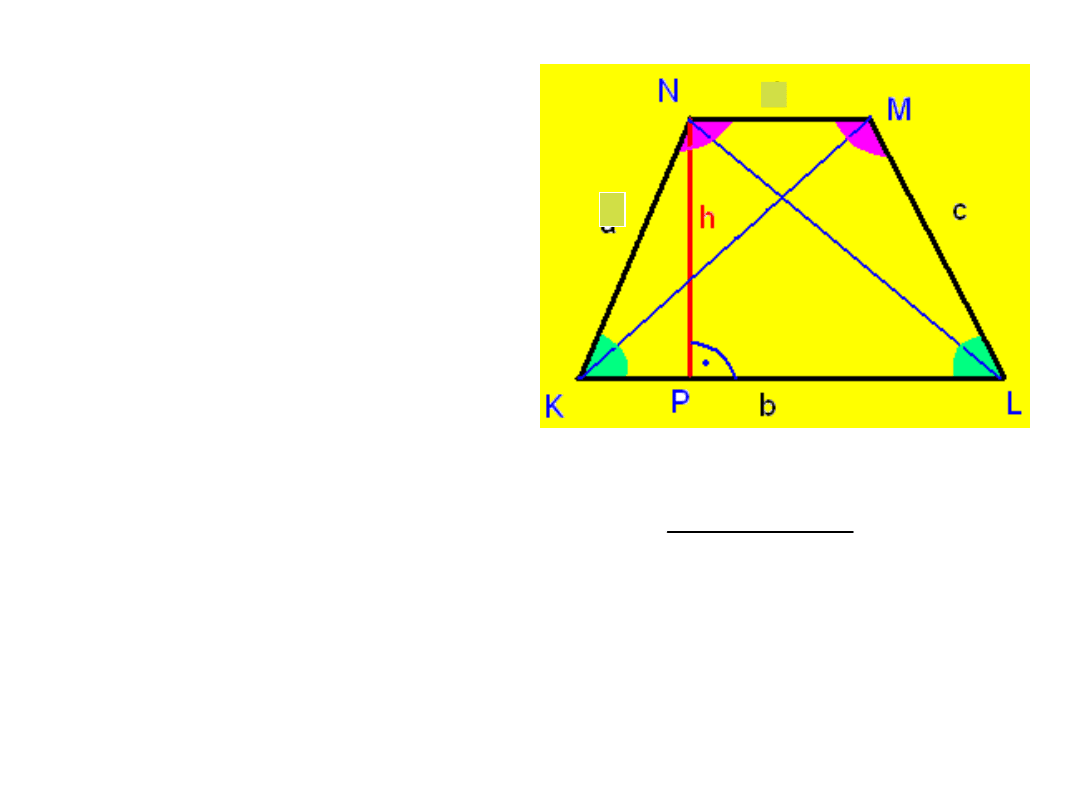
TRAPEZ
• CO NAJMNIEJ 1
PARA BOKÓW
RÓWNOLEGŁYCH
TZW. PODSTAWY.
• SUMA MIAR
KĄTÓW LEŻĄCYCH
PRZY TYM SAMYM
RAMIENIU- 180
0
• SUMA MIAR
KĄTÓW
WEWNĘTRZNYCH
-360
0
• PRZEKĄTNE
RÓŻNEJ DŁUGOŚCI.
d
c
b
a
Ob
h
b
a
P
2
d
a
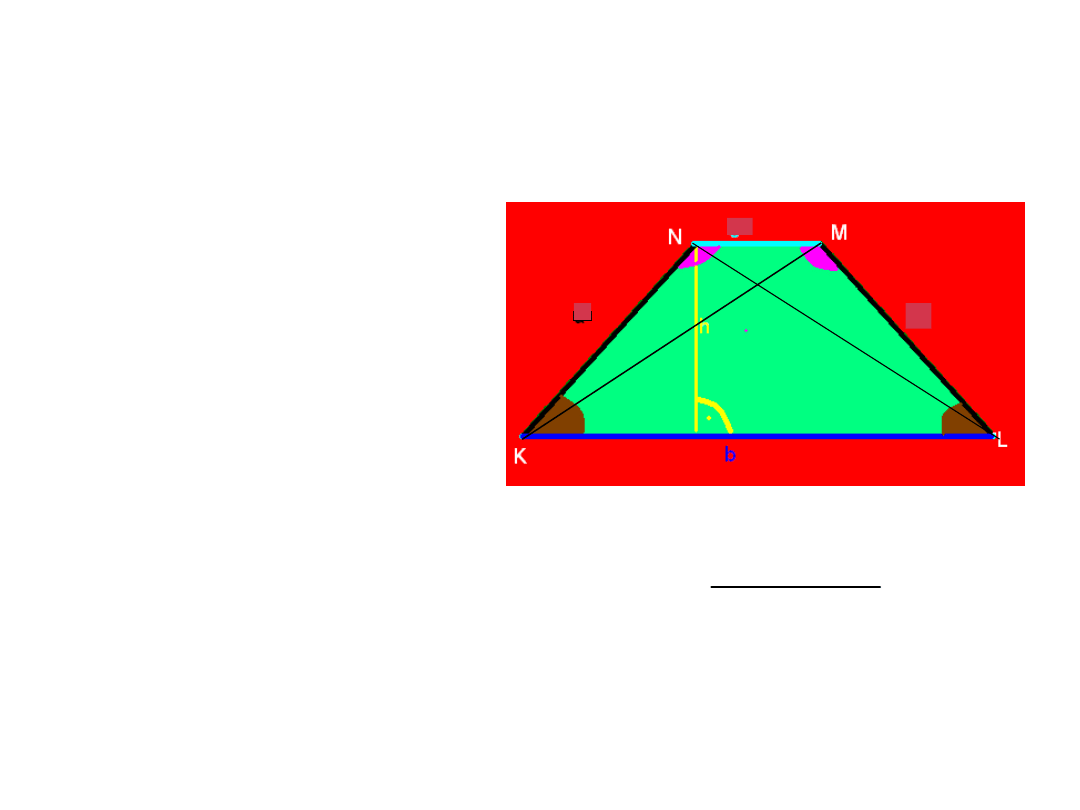
TRAPEZ
RÓWNORAMIENNY
• RAMIONA RÓWNEJ
DŁUGOŚCI.
• 1 OŚ SYMETRII.
• KĄTY PRZY
PODSTAWACH MAJĄ
RÓWNE MIARY.
• SUMA MIAR KĄTÓW
WEWNĘTRZNYCH –
360
0
• PRZEKĄTNE SĄ
RÓWNEJ DŁUGOŚCI.
d
c
b
a
Ob
h
b
a
P
2
a
c
c
c
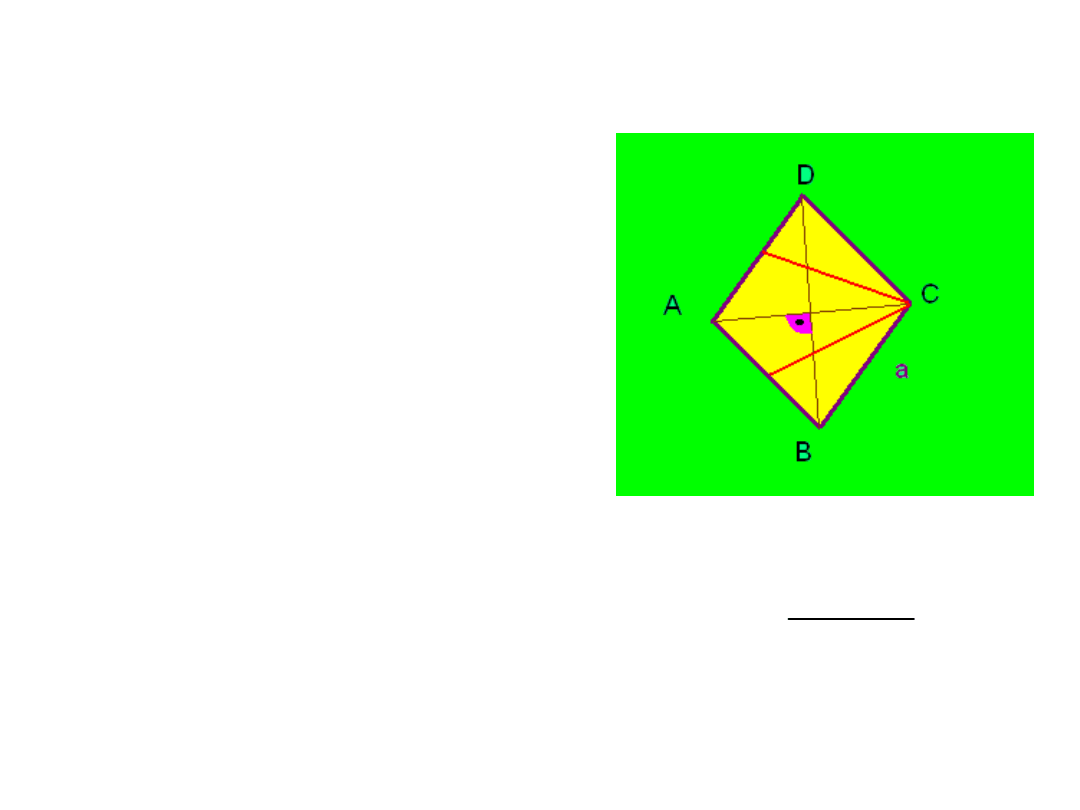
ROMB
• PRZECIWLEGŁE BOKI SĄ
RÓWNOLEGŁE.
• WSZYSTKIE BOKI SĄ
JEDNAKOWEJ DŁUGOŚCI .
• 2 OSIE SYMETRII .
• PRZECIWLEGŁE KĄTY SĄ
PRZYSTAJĄCE .
• DWA PRZECIWLEGŁE
KĄTY SĄ ROZWARTE A
DWA NASTĘPNE SĄ
OSTRE.
• PRZEKĄTNE DZIELĄ SIĘ
NA POŁOWY I
PRZECINAJĄ POD KĄTEM
PROSTYM.
• PRZEKĄTNE DZIELĄ
KĄTY NA POŁOWY.
a
Ob
d
d
P
4
2
2
1
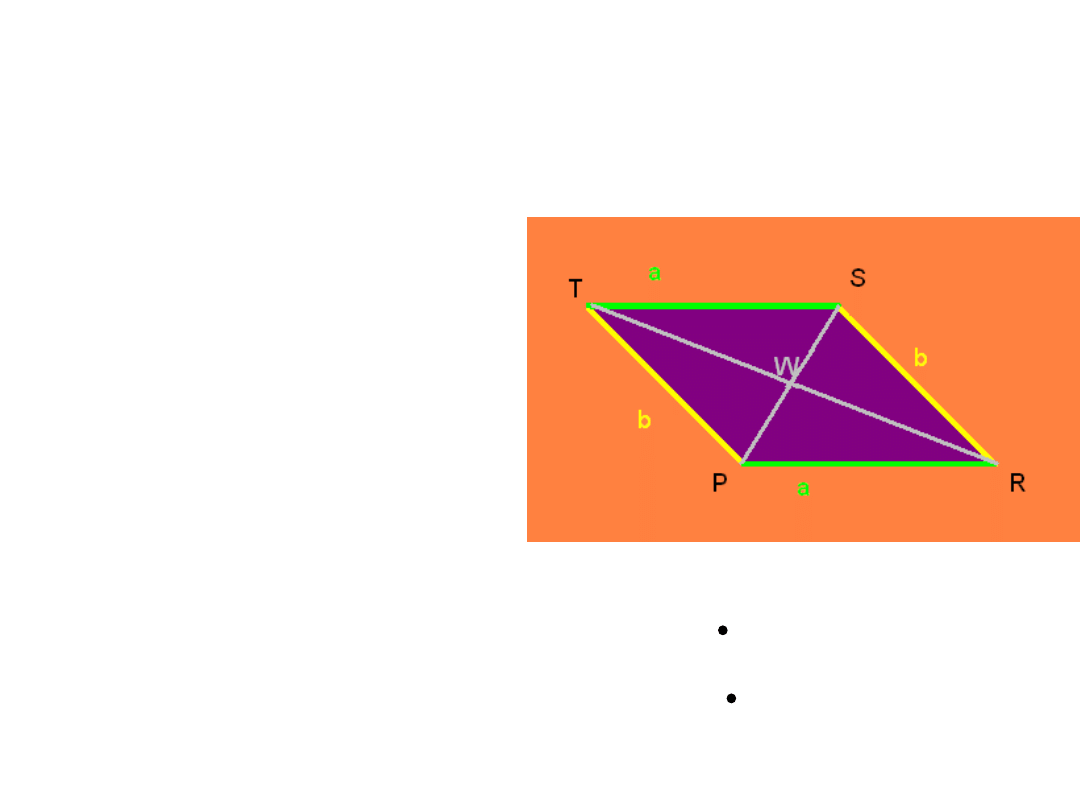
RÓWNOLEGŁOBOK
• DWIE PARY
PRZECIWLEGŁYCH
BOKÓW SĄ RÓWNE I SĄ
DO SIEBIE
RÓWNOLEGŁE.
• SUMA MIAR KĄTÓW
WEWNĘTRZNYCH –
360
0
.
• PRZECIWLEGŁE KĄTY SĄ
DO SIEBIE
PRZYSTAJĄCE.
• PRZEKĄTNE PRZECINAJĄ
SIĘ W POŁOWIE.
• PUNKT PRZECIĘCIA SIĘ
PRZEKĄTNYCH JEST
ŚRODKIEM SYMETRII.
P = a h
Ob=2 (a+b)
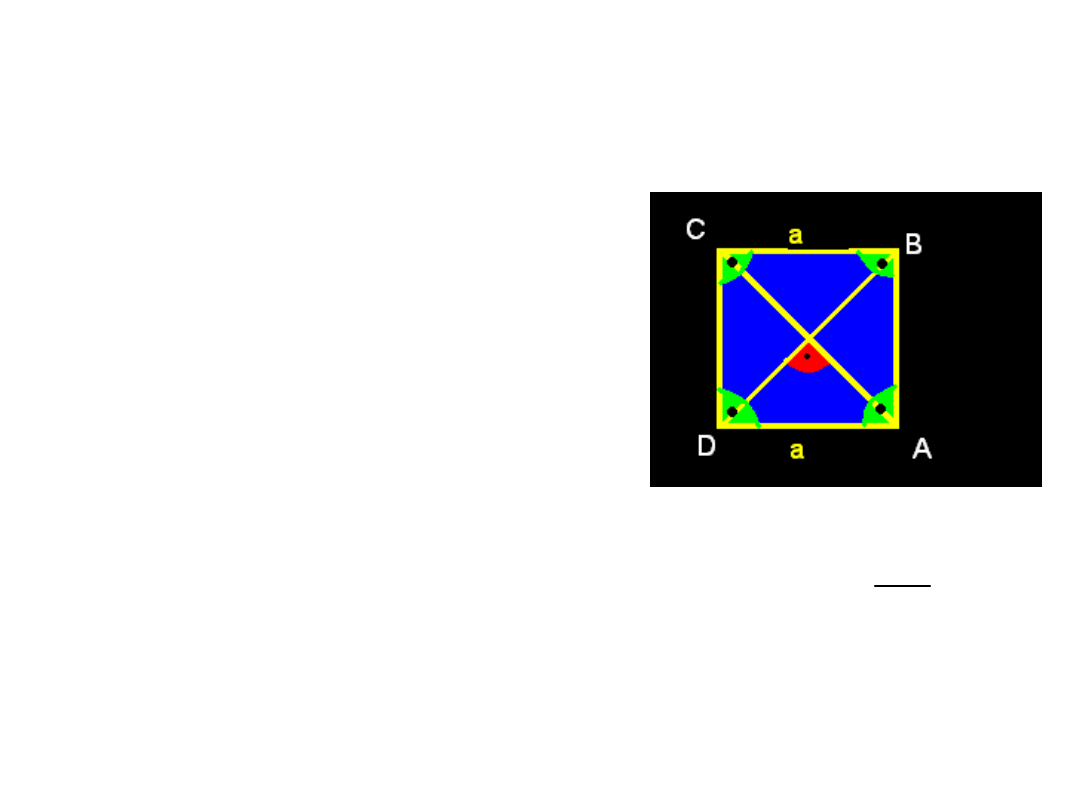
KWADRAT
• WSZYSTKIE BOKI SĄ
JEDNAKOWEJ
DŁUGOŚCI.
• SUMA MIAR KĄTÓW
WEWNĘTRZNYCH – 360
0
• WSZYSTKIE KĄTY
WEWNĘTRZNE SĄ
KĄTAMI PROSTYMI.
• PRZEKĄTNE MAJĄ
JEDNAKOWĄ DŁUGOŚĆ,
PRZECINAJĄ SIĘ W
POŁOWIE I SĄ DO
SIEBIE PROSTOPADŁE.
• PRZEKĄTNE DZIELĄ
KĄTY NA POŁOWY.
a
Ob
d
a
P
4
2
2
2
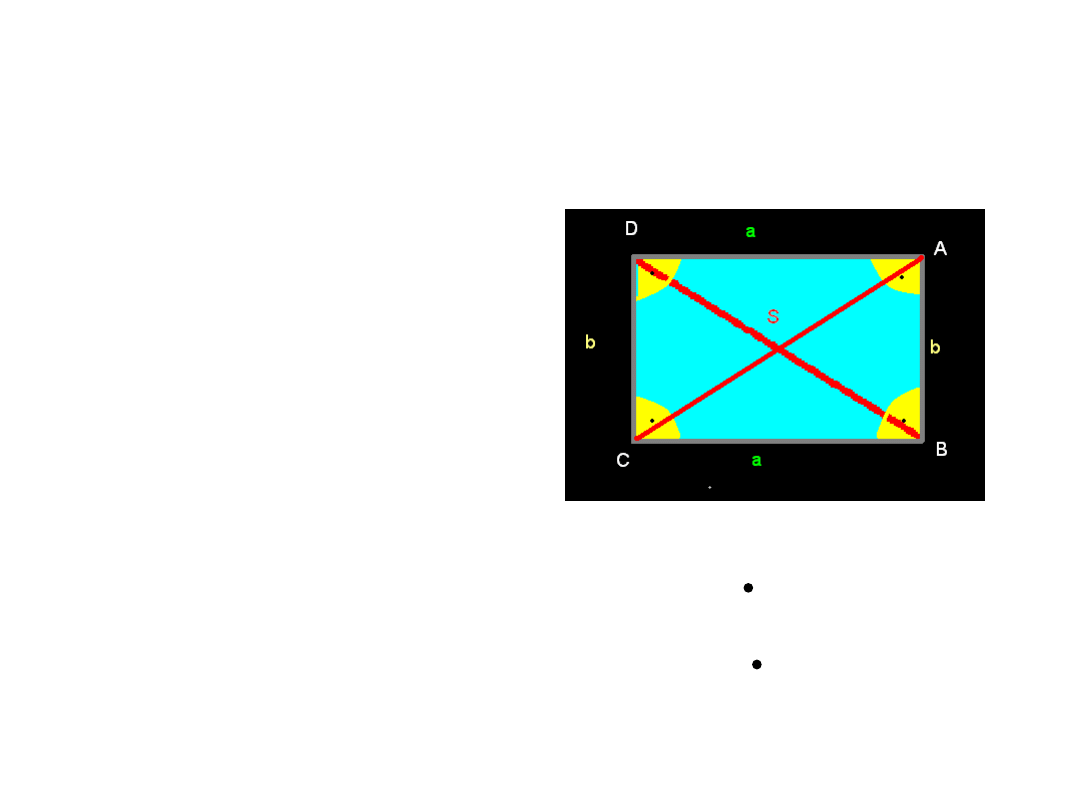
PROSTOKĄT
• BOKI SĄ PARAMI RÓWNE
I RÓWNOLEGŁE.
• SUMA MIAR KĄTÓW
WEWNĘTRZNYCH – 360
0
.
• WSZYSTKIE KĄTY SĄ
PROSTE.
• PRZEKĄTNE MAJĄ
JEDNAKOWĄ DŁUGOŚĆ,
PRZECINAJĄ SIĘ W
POŁOWIE.
• PUNKT PRZECIĘCIA
PRZEKĄTNYCH JEST
ŚRODKIEM OKRĘGU
OPISANEGO NA
PROSTOKĄCIE.
P = a b
Ob=2 (a+b)

TRÓJKĄT RÓŻNOBOCZNY
• KAŻDY BOK MA
INNĄ DŁUGOŚĆ.
• KAŻDY KĄT MA
INNĄ MIARĘ.
c
b
a
Ob
h
a
P
2
h
h
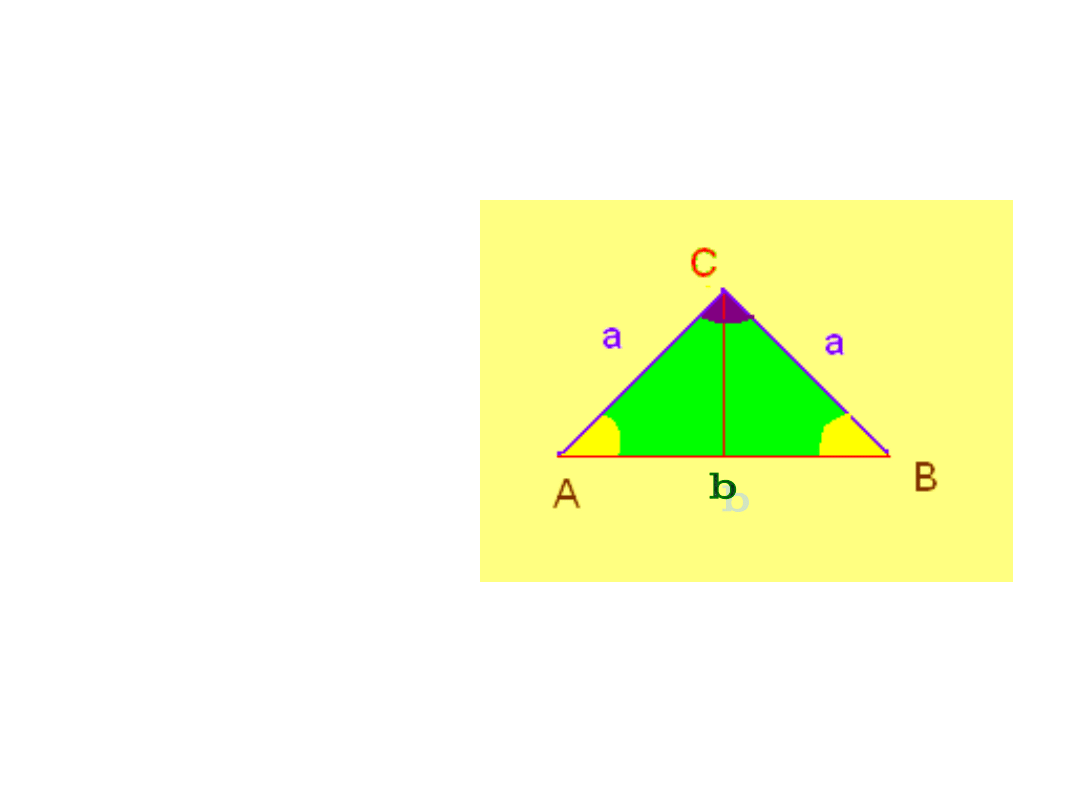
TRÓJKĄT
RÓWNORAMIENNY
• RAMIONA SĄ
RÓWNEJ
DŁUGOŚCI.
• KĄTY PRZY
PODSTAWIE
MAJĄ RÓWNE
MIARY.
Ob = 2a +
b
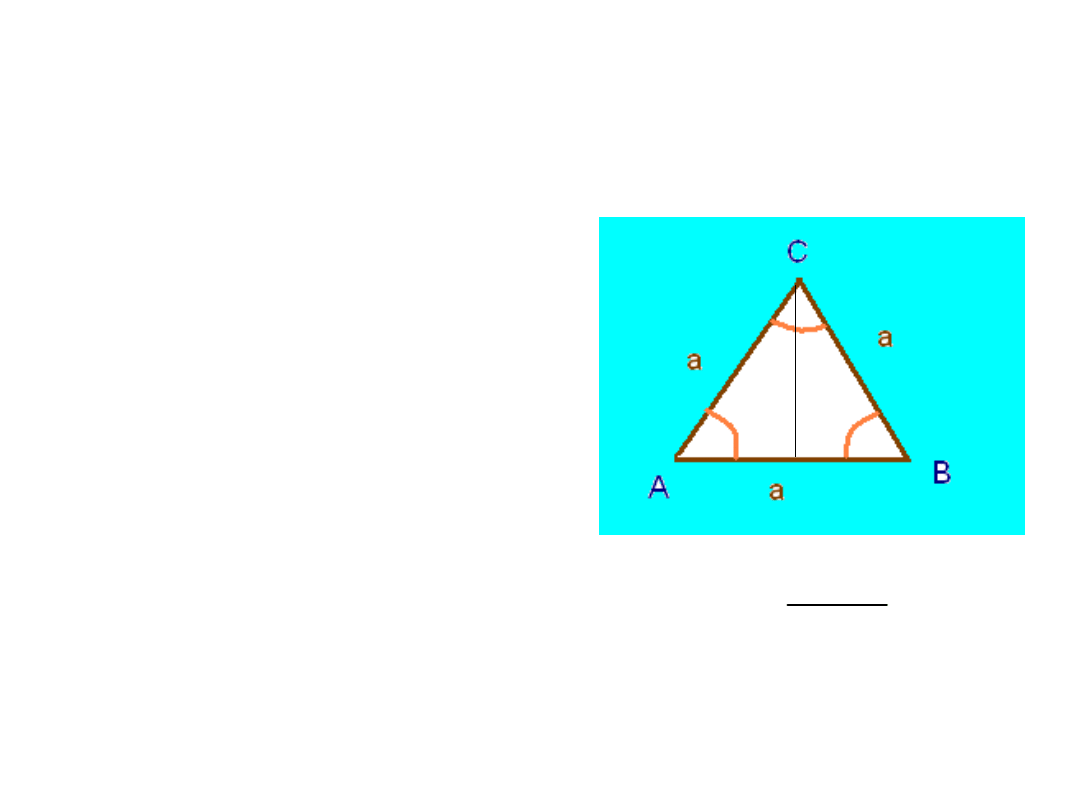
TRÓJKĄT
RÓWNOBOCZNY
• WSZYSTKIE BOKI SĄ
RÓWNEJ DŁUGOŚCI.
• WSZYSTKIE KĄTY
MAJĄ RÓWNE
MIARY.
• SUMA MIAR KĄTÓW
WEWNĘTRZNYCH W
KAŻDYM TRÓJKĄCIE
WYNOSI 180
0
.
a
Ob
h
a
P
3
2
h
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
Wyszukiwarka
Podobne podstrony:
Sprawdzian wiadomości z własności figur płaskich dla kl6
Wlasnosci figur plaskich
Wlasności figur plaskich 6a
Geometria analityczna i podstawowe własności figur płaskich
wzory figur płaskich
Podstawowe wzory i tablice geometria figur płaskich
Zestaw6 trygonometria i własności figur
Momenty bezwładności figur płaskich
4 Momenty Figur Płaskich
Pola figur płaskich - ćwiczenia, materiały szkolne, wielokąty
Odpowiedzi do testu z figur płaskich
Współrzędne środków ciężkości figur płaskich
charakterystyki geometryczne figur plaskich czesc I
Momenty bezwładności figur płaskich (1)
charakterystyki geometryczne figur plaskich czesc II (1)
Charakterystyki geometryczne figur płaskich
więcej podobnych podstron