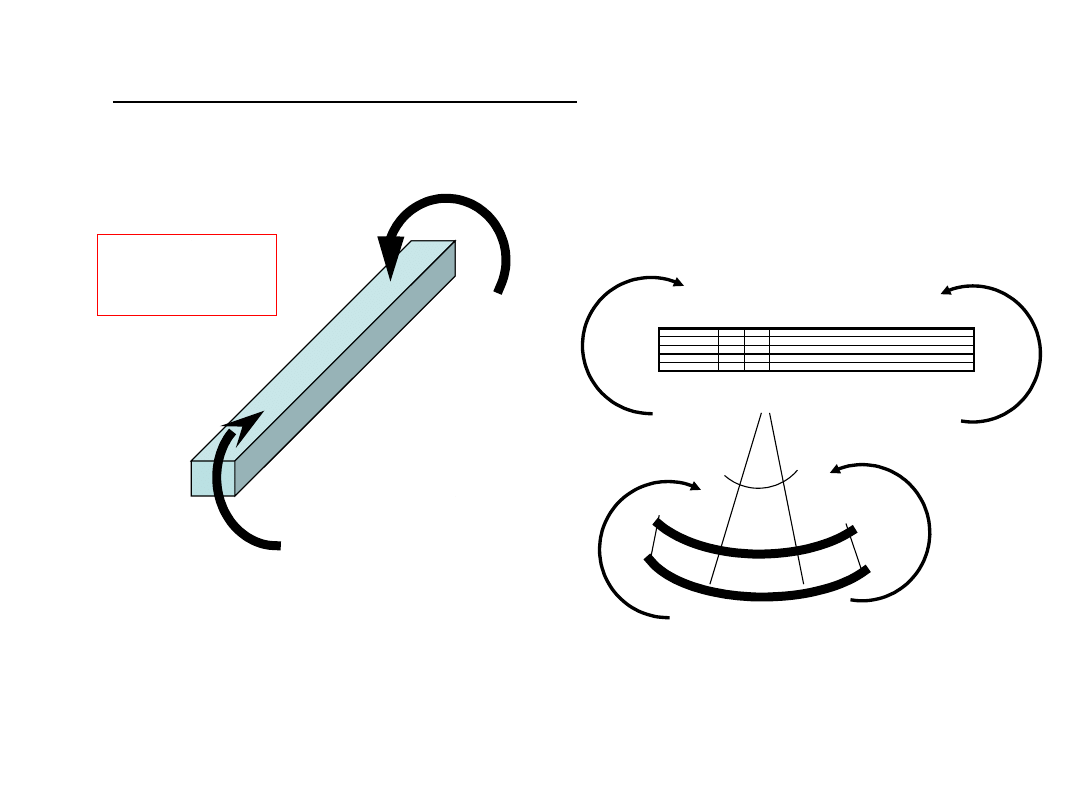
Naprężenia przy czystym zginaniu

M

g

M

g

T=0
M

g

=const.

Założenia:

-Przekroje poprzeczne pozostają płaskie,
- Warstwy nie oddziałują na siebie wzajemnie,

-Warstwy poddane są jedynie rozciąganiu bądź ściskaniu (jednokierunkowy stan
naprężenia).



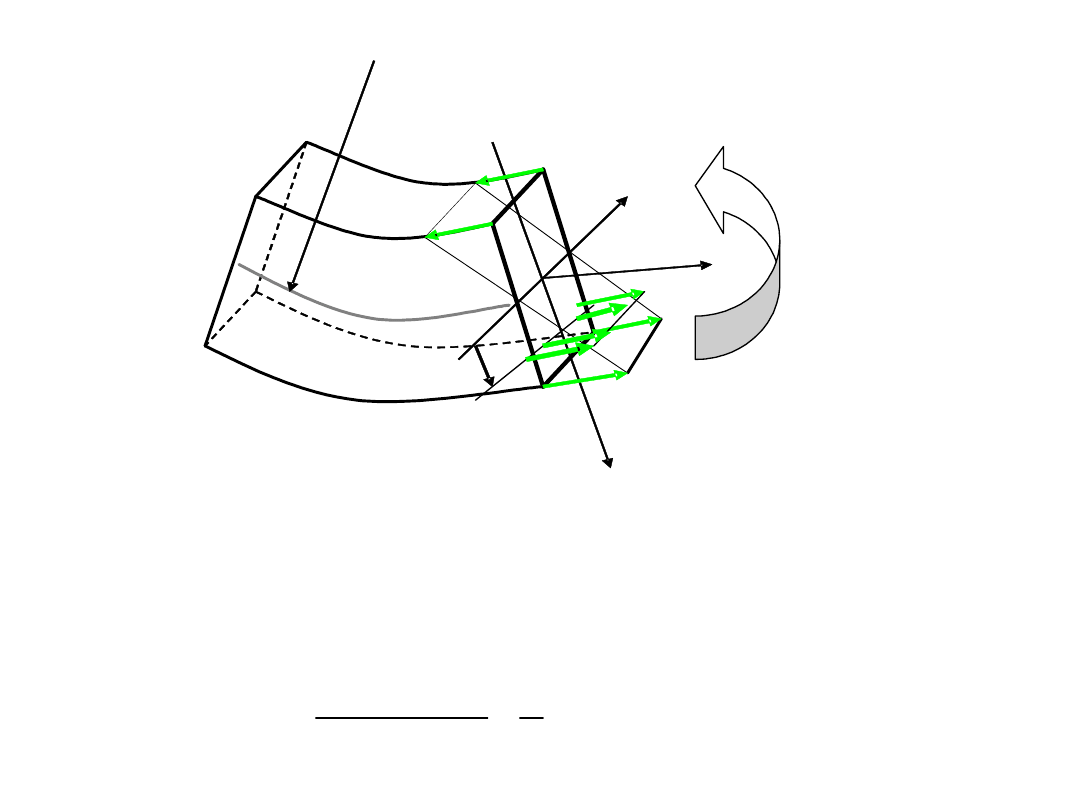
x

z

y

y



M

g





 - promień krzywizny warstwy obojętnej

)

(

)

(

y

E

y

x

x









;

)

(

)

(













y

y

y

x









Wydłużenie warstwy odległej o y od warstwy obojętnej

)

(

)

(

)

(

y

y

y

x

z

y

















;

)

(





y

E

y

x





z

y

y

y

x

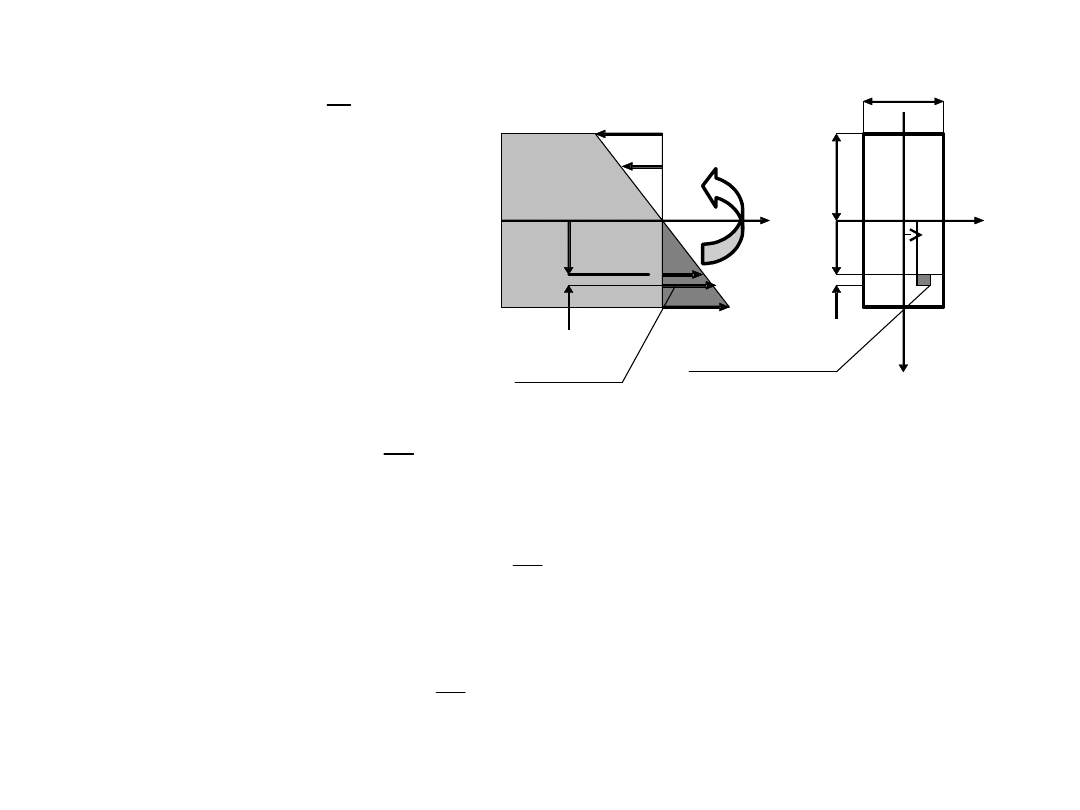
dy

dA

M

g



x

=E

b

h/2















A

A

x

ix

ydA

E

dA

F

0

0





Warstwa obojętna zawiera środek

ciężkości

przekroju poprzecznego (Oz=Oz

c

)

Warunki równowagi



















A

g

2

A

g

x

iz

M

dA

y

E

;

0

M

dA

y

M























A

A

x

iy

;

0

ydA

z

E

;

0

dA

z

M





E=const., =const.

;

I

ydA

z

;

I

dA

y

A

z

y

A

z

2

C

C

C











Moment bezwładności przekroju
poprzecznego względem osi z

c

Moment bezwładności przekroju
poprzecznegowzględem układu
osi y

c

z

c

Wprowadzając oznaczenia

Mamy:

;

0

I

E

;

M

I

E

C

C

C

z

y

g

z









;

0

I

C

C

z

y



;

)

(





y

E

y

x





;

)

(

y

I

M

y

C

z

g

x







z

g

max

z

g

max

W

M

y

J

M

C









max

y

J

W

zc

z



Wskaźnik przekroju

2

2

2

/

3

2

2

2

dx

w

d

dx

dw

1

dx

w

d

1









































z

g

J

M

E





z

g

2

2

EJ

M

dx

w

d





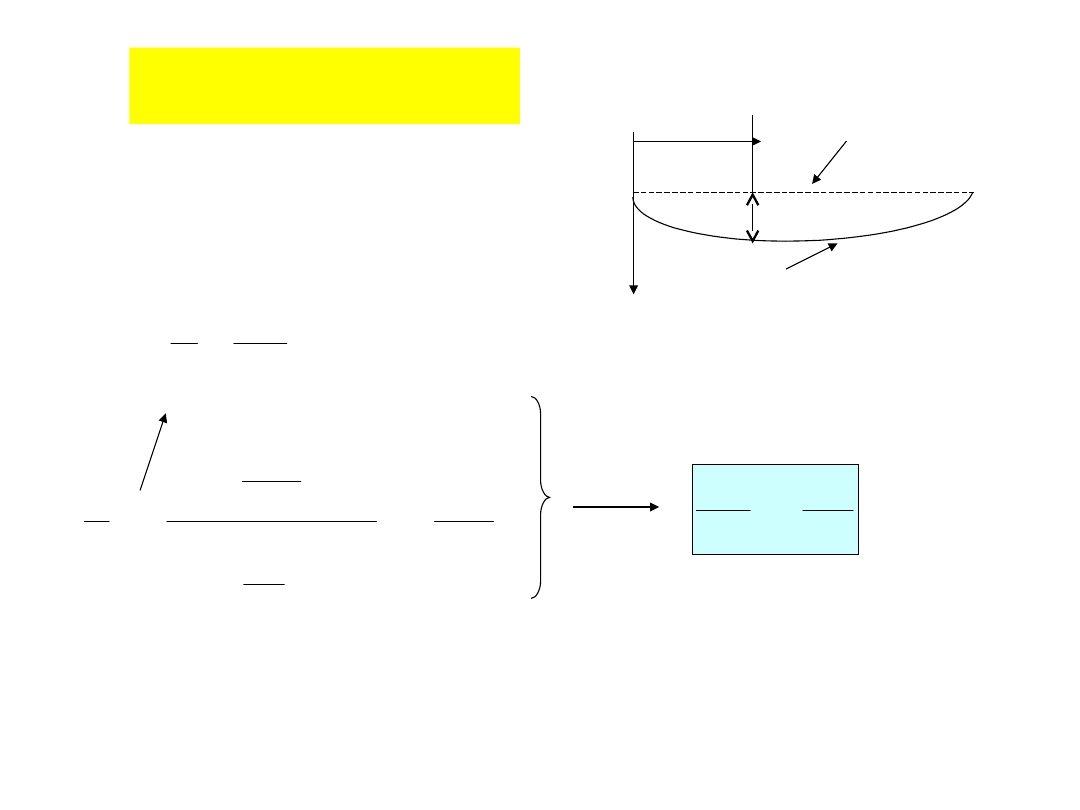
w – przemieszczenie warstwy obojętnej

Równanie różniczkowe linii
ugięcia

w

x

w(x)

nieodkształcona warstwa
obojętna

Warstwa obojętna
po odkształceniu

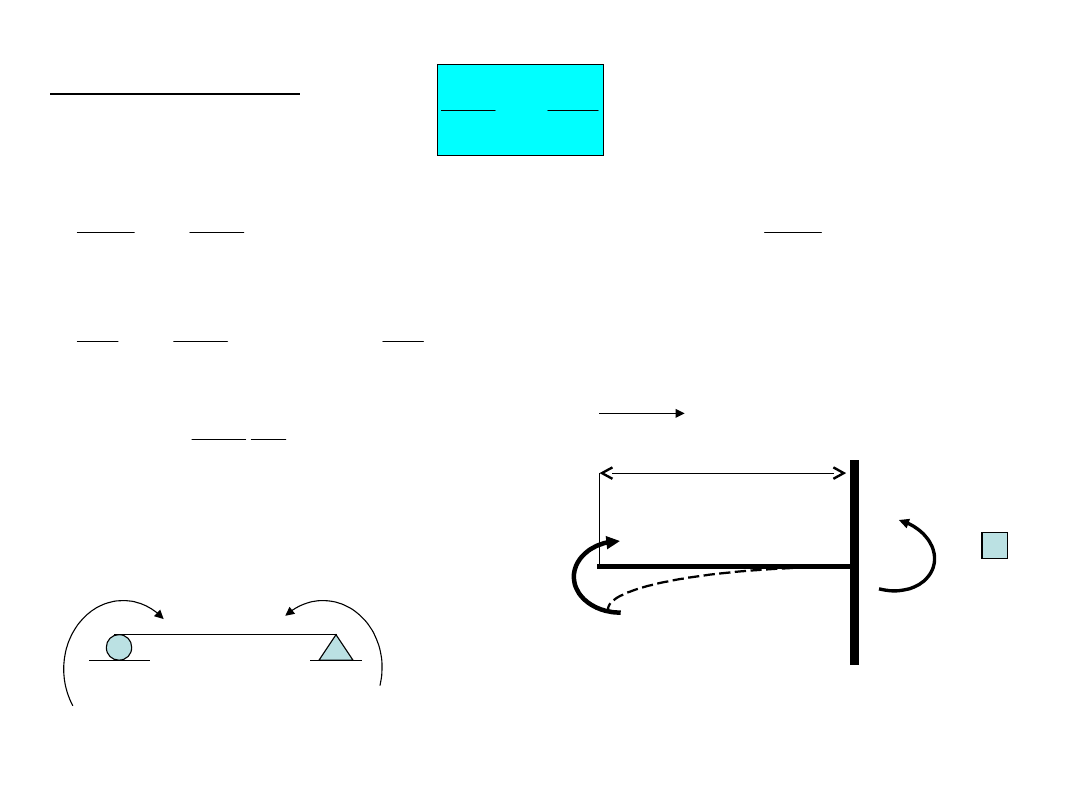
Warunki brzegowe

z

g

2

2

EJ

M

dx

w

d





''

.

.

;

2

2

2

2

w

dx

w

d

const

EJ

const

M

EJ

M

dx

w

d

z

g

z

g











;

2

)

(

'

;

2

1

2

1

C

x

C

x

EJ

M

x

w

w

dx

dw

C

x

EJ

M

dx

dw

z

g

z

g

















C

1

i C

2

– stałe całkowania

x

M

u

l

x=l w(l)=0
x=l w’(l)=0

M

g

M

g

M

g

x=0 w(0)=0
x=l w(l)=0

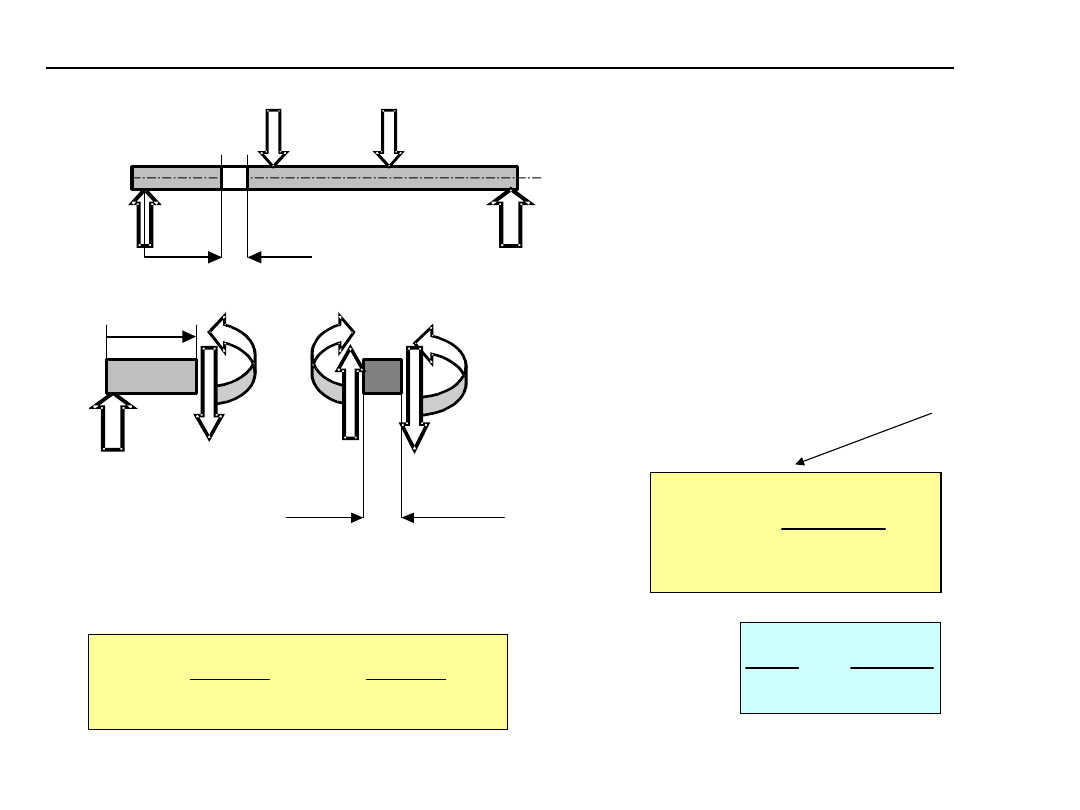
Naprężenia od zginania w belkach obciążonych poprzecznie

dx

x

dx

T

x

+dT

x

T

x

M

gx

R

1

M

g

+dM

gx

R

2

P

1

T

x

P

2

x

R

1

a)

.

;

0

const

M

T

g

x





;

)

(

)

(

y

I

x

M

y

C

z

g

x







Uogólnienie wzorów wyprowadzonych
dla czystego zginania

gdy k

r

=k

c

g

g

z

g

g

k

W

M

y

J

M

C









min

max

max

max

max



z

g

EJ

x

M

dx

w

d

)

(

2

2





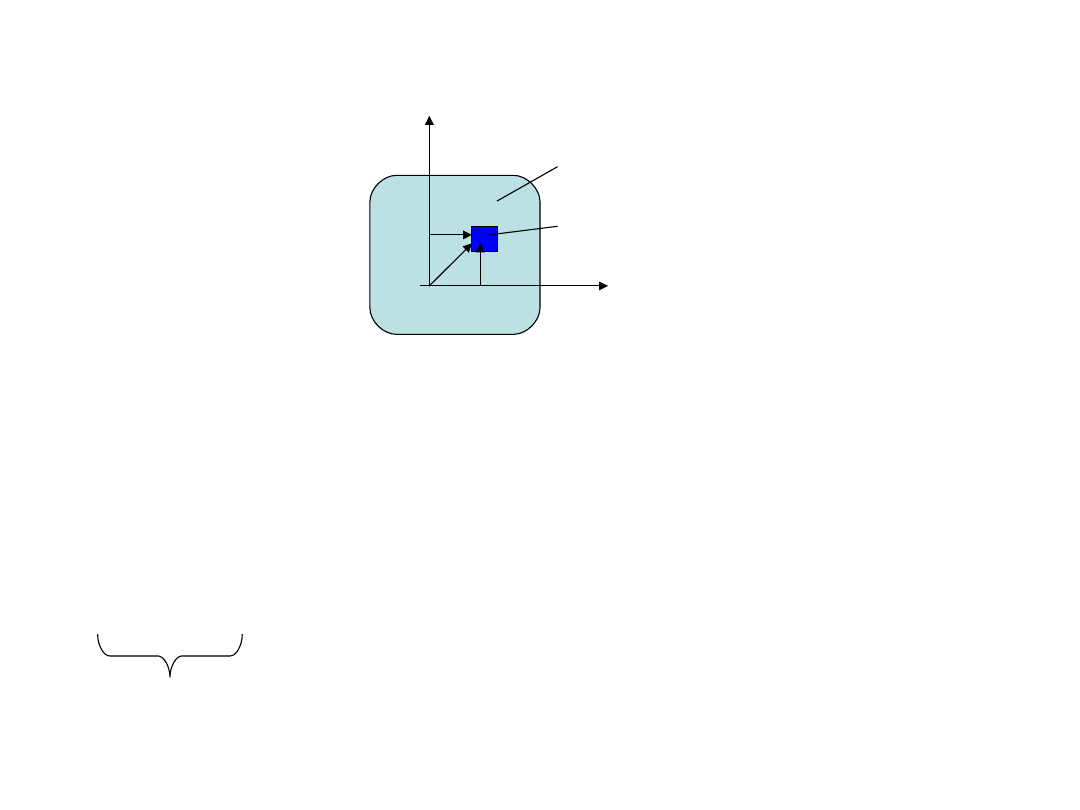
Teoria bezwładności figur płaskich

A

dA

z

y

;

;

2

2

dA

z

I

dA

y

I

A

y

A

z









r

O

Moment bezwładności względem osi

;

;

2













A

zy

y

A

z

O

yzdA

I

I

I

dA

r

I

Moment bezwładności względem punktu O

Moment bezwładności względem układu osi
Moment dewiacyjny

=0, gdy jedna z osi jest osią symetrii

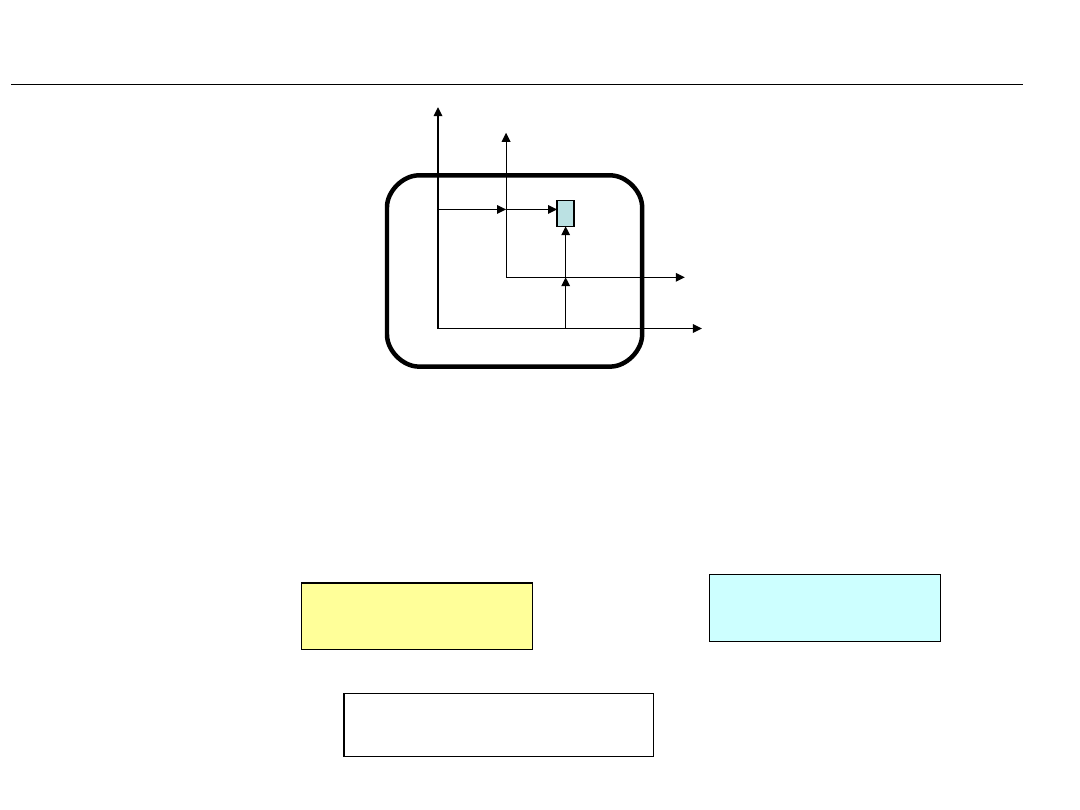
Twierdzenie Steinera (momenty bezwładności względem osi równoległych)

C

O

z

y

z

C

y

C

dA

z

C

y

C

a

b

0

;

2

)

(

2

2

2

2

























A

c

A

c

A

C

A

c

A

z

dA

y

A

a

dA

y

a

dA

y

dA

a

y

dA

y

I

A

a

I

I

C

z

z

2





A

b

I

I

C

y

y

2





A

b

a

I

I

C

C

y

z

zy









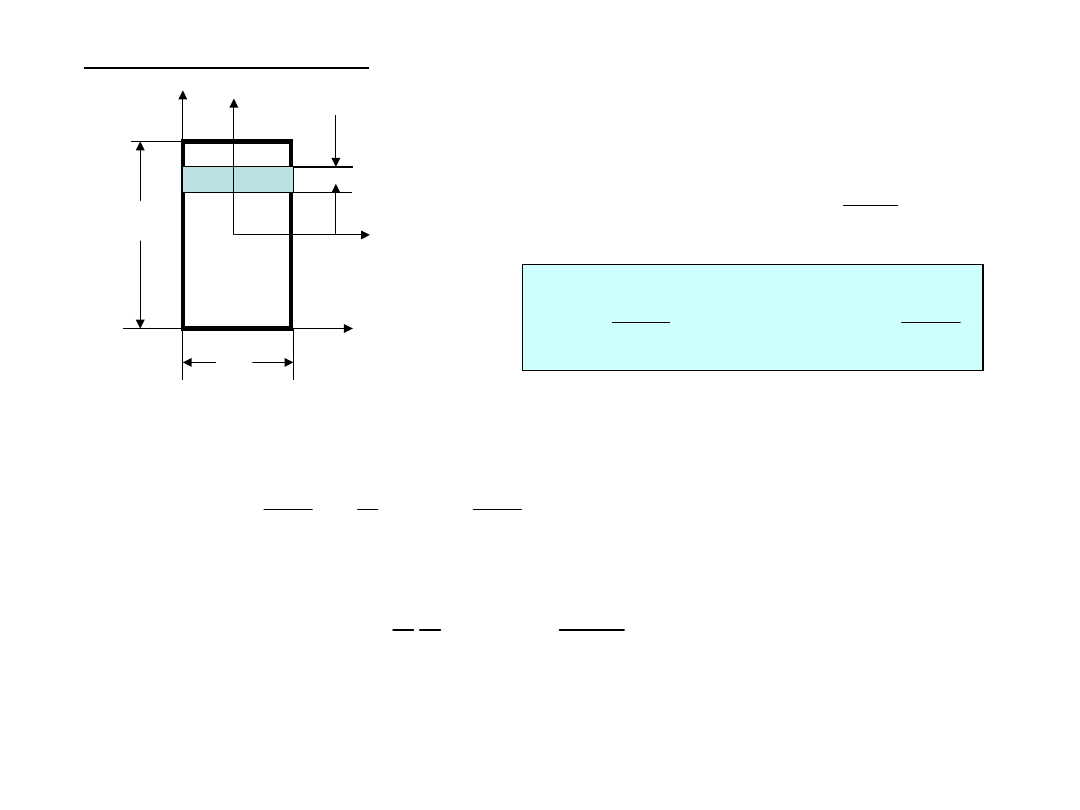
Podstawowe kształty

b

h

dy

y

C

z

C

y

C

12

;

3

2

/

2

/

2

bh

dy

b

y

I

bdy

dA

h

h

z

C













z

;

12

;

12

3

3

hb

I

bh

I

C

C

y

z





Zgodnie z twierdzeniem Steinera

;

3

2

12

3

2

3

bh

bh

h

bh

I

z



















y

;

4

0

2

2

2

2

h

b

bh

h

b

I

I

C

C

y

z

zy









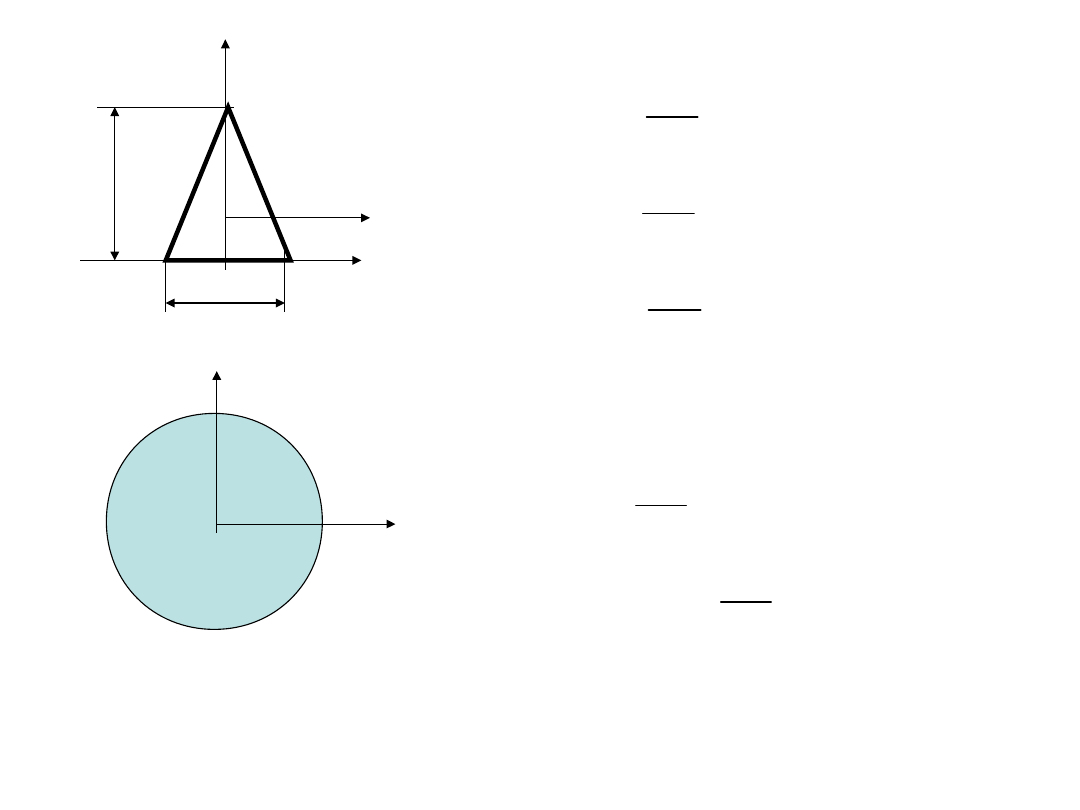
y=y

C

z

z

C

b

h

;

48

;

12

;

36

3

3

3

hb

I

bh

I

bh

I

C

C

y

z

z







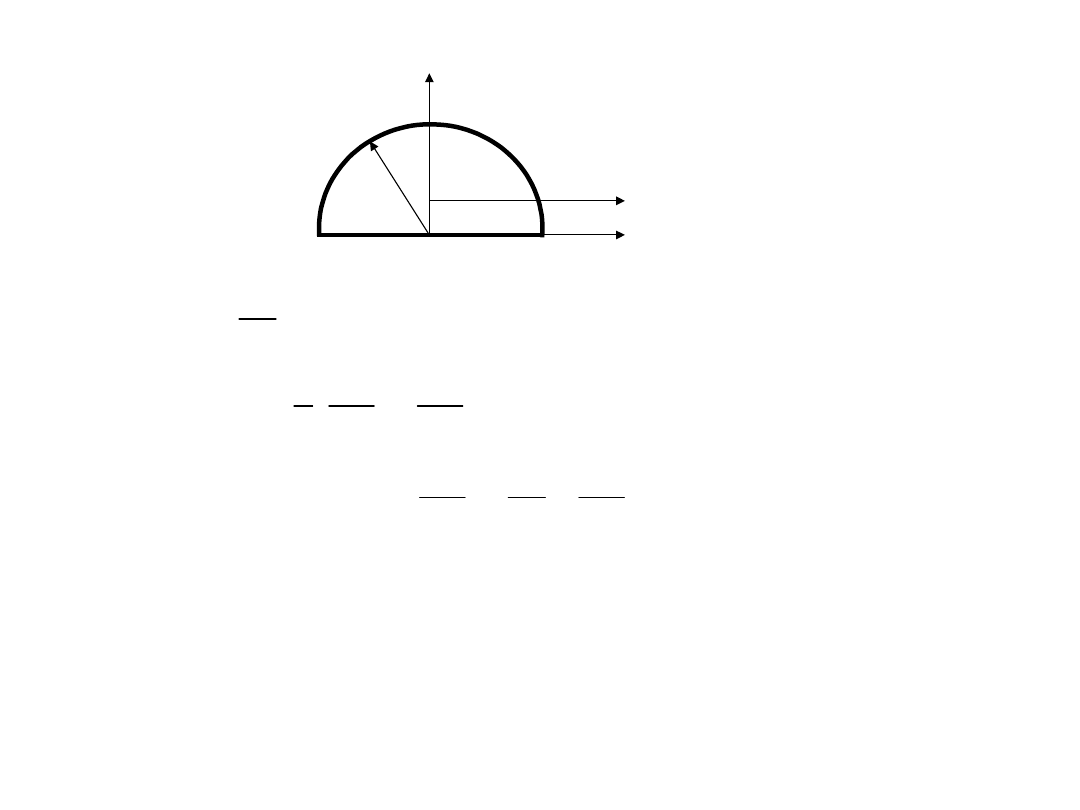
O

z

C

y

C

;

4

;

2

4

4

r

I

I

r

I

C

C

y

z

O











z

z

C

y=y

C

r

;

11

,

0

2

3

4

8

)

(

;

8

)

4

(

2

1

;

3

4

4

2

2

4

2

4

4

r

r

r

r

A

y

I

I

r

r

I

I

r

y

C

z

z

y

z

c

C











































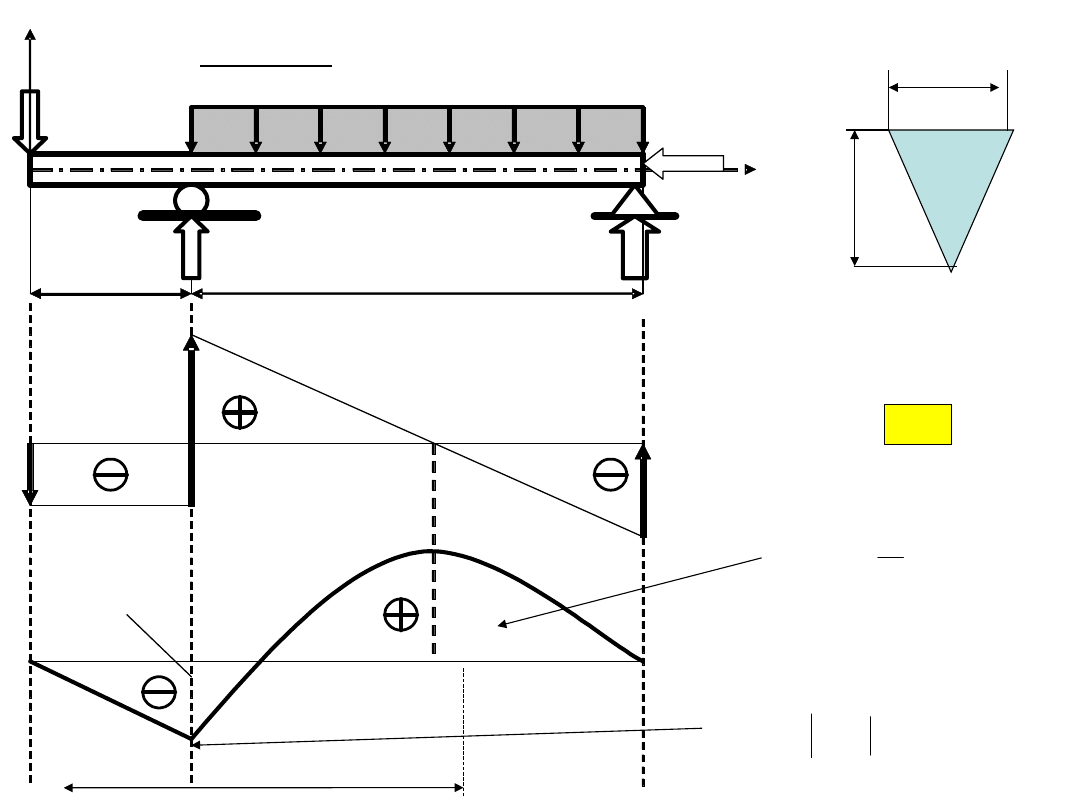
R

BY

R

A

P=ql

x

2 l

q kN/m ]

l/2

R

BX

y

P

R

A

R

BY

T

x

M

gx

-Pl

7l /
4

2

32

9

ql

M

gekstr



Przykład

20

30

l=0.5m
k

g

=160MP

a

?



q

2

max

ql

Pl

M

g







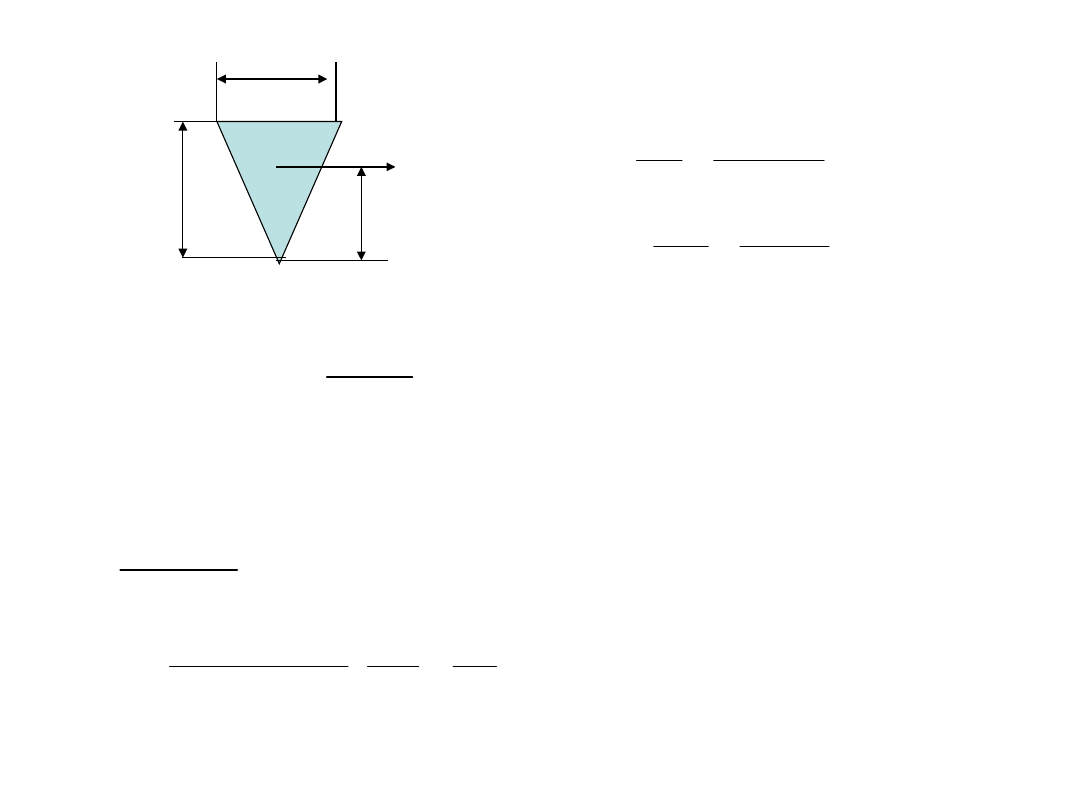
20

30

z

C

y

max

=20

;

10

75

,

0

20

10

5

,

1

;

10

5

,

1

36

)

30

(

20

36

3

3

4

max

min

4

4

3

3

mm

y

I

W

mm

bh

I

C

C

z

z





















g

g

g

k

W

M





min

max

max

























m

kN

mm

N

q

ql

ql

M

g

2

3

3

2

2

max

500

10

75

,

0

160

;

160

10

75

,

0

;

m

kN

q

/

48

,

0



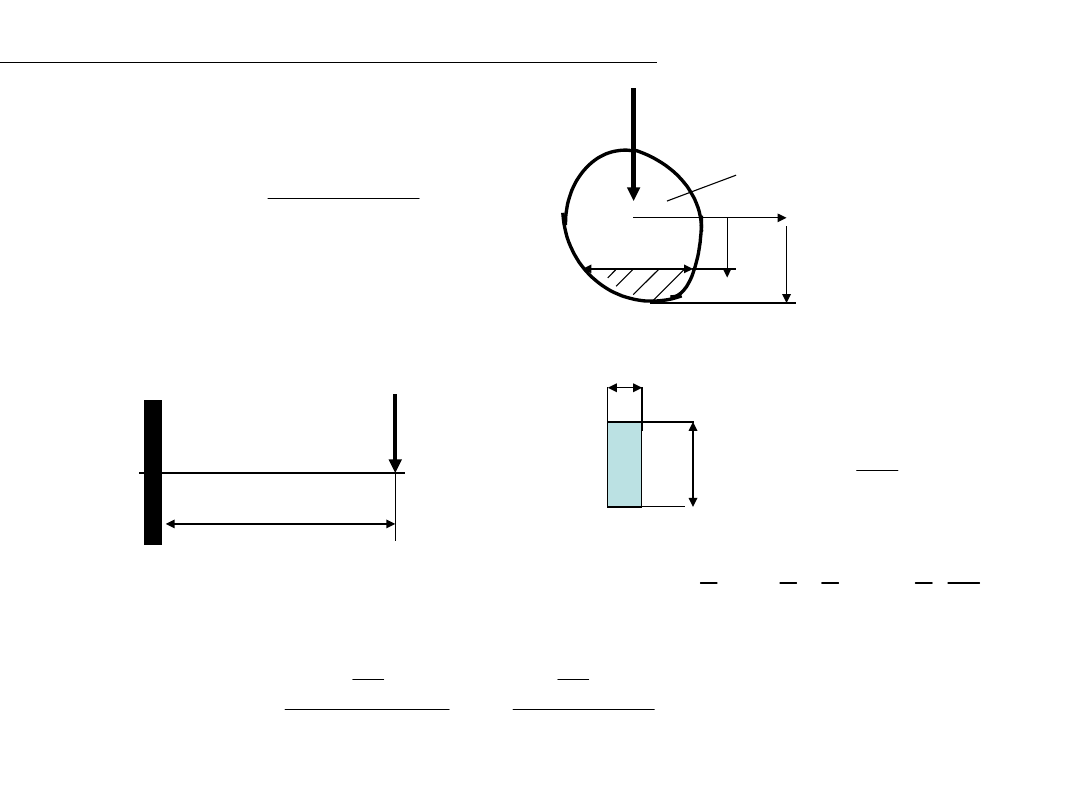
Naprężenia tnące przy zginaniu – wzór Żurawskiego

P

l

h

b

zc

y

y

x

I

)

y

(

b

S

T

)

y

,

x

(

max









T

x

z

C

b(y)

A

y

y

max

Przykład

T=const.=P

b(y)=const.=b

;

12

bh

I

3

zc



);

y

4

h

(

2

b

)

y

2

h

(

2

1

)

y

2

h

(

b

S

2

2

y

y

max

















;

bh

)

y

4

h

(

P

6

12

h

b

b

2

)

y

4

h

(

b

P

)

y

(

3

2

2

3

2

2























;

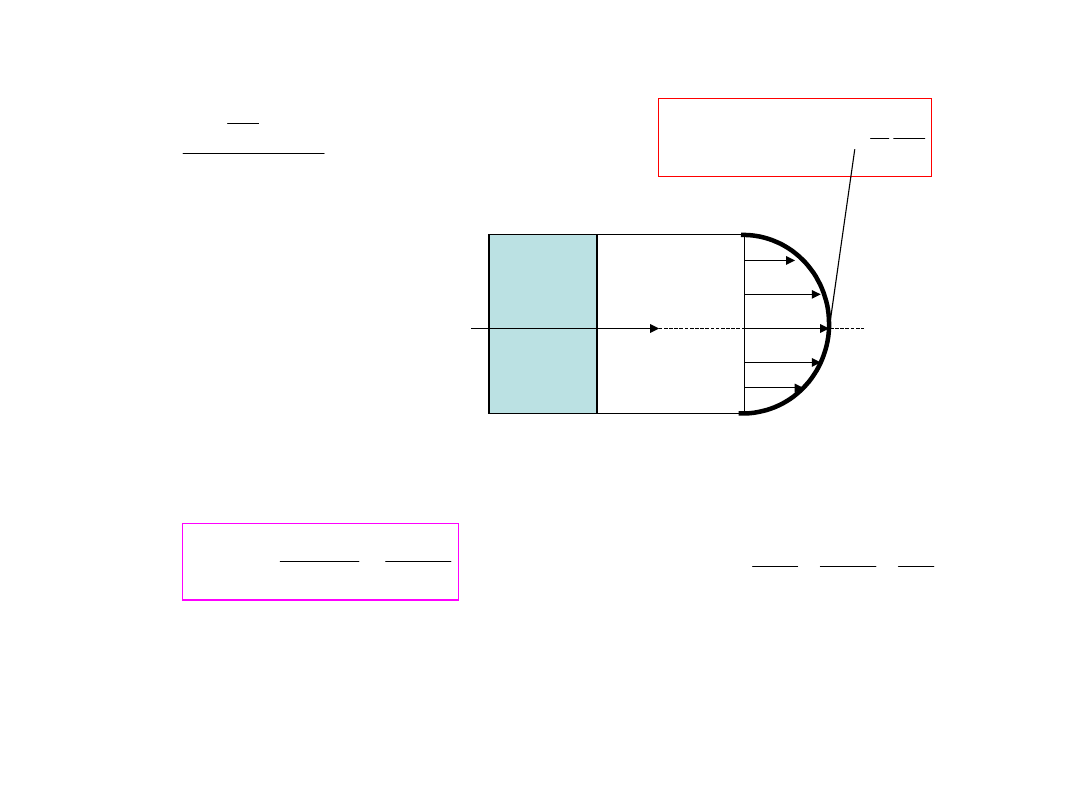
bh

)

y

4

h

(

P

6

)

y

(

3

2

2







bh

P

2

3

)

0

y

(

max











;

0

)

2

/

h

y

(









Maksymalne naprężenia gnące w rozważanej belce

2

min

max

g

max

g

bh

l

P

6

W

M











;

6

bh

h

12

2

bh

y

I

W

2

3

max

zc

min









Gdy l=h

max

max

g

4







Gdy l=5h

max

max

g

20







