„Księga natury pisana jest w 

matematycznym języku.”

Galileusz

DŁUGOŚĆ OKRĘGU.

Wyobraź sobie, że trzymasz w rękach okrąg 
wykonany np. z drutu. Jeśli rozetniemy ten 
okrąg i wyprostujemy, otrzymany drut będzie 
miał taką samą długość jak okrąg. Kiedy 
chcemy zmierzyć obwód okrągłego 
przedmiotu, np. słoika, najłatwiej to zrobić 
przy pomocy sznurka – opasamy nim słoik, 
zaznaczamy miejsce spotkania dwóch końców 
a następnie prostujemy i mierzymy np. linijką. 
Obwód koła i długość okręgu to analogiczne 
pojęcia.

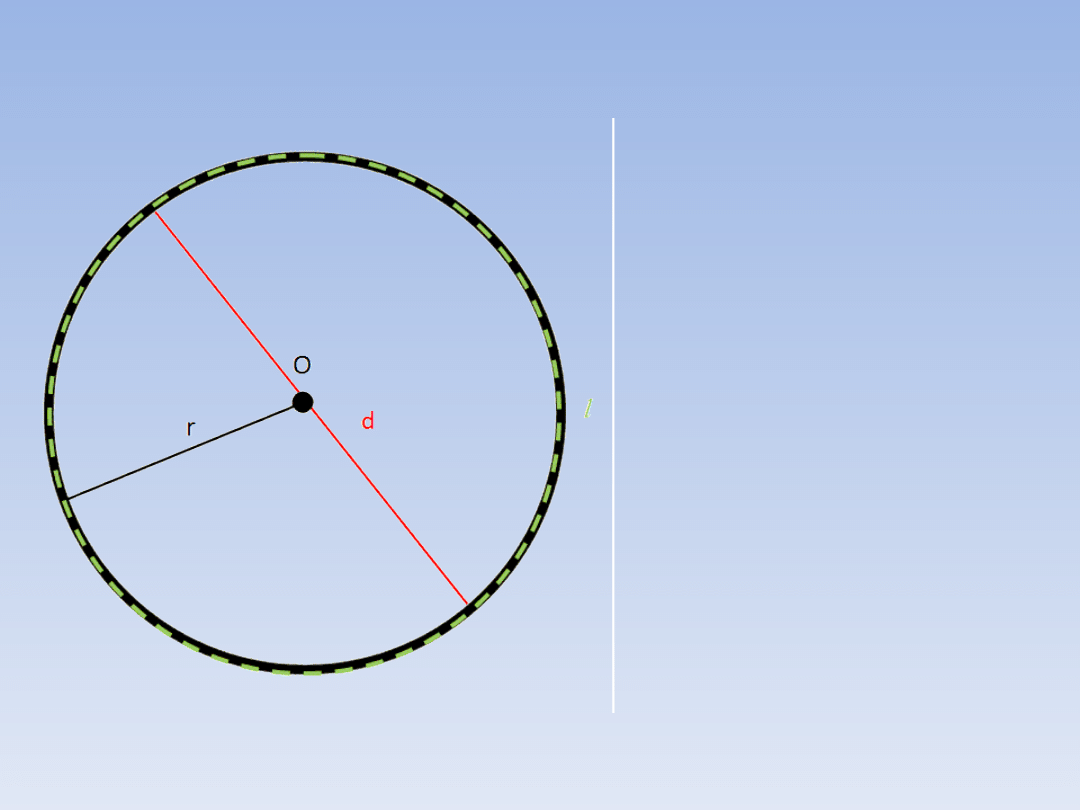
OZNACZENIA.

Przyjmujemy 
następujące 
oznaczenia:
r – długość 
promienia

d

 – długość 

średnicy

l

 – długość okręgu 

(obwód koła)
O – środek okręgu 
(koła)

Ważne:

d = 2r

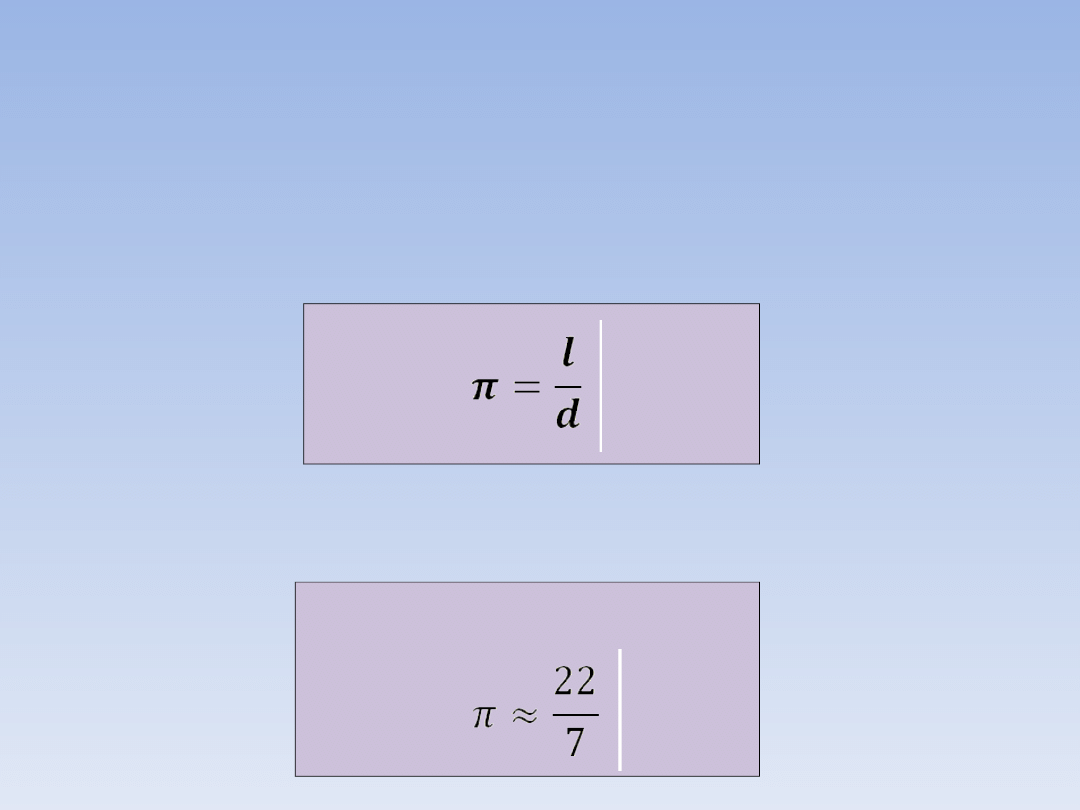
LICZBA π.

Przypomnijmy (dokładne informacje 
znajdziesz w lekcji „Koło. Okrąg. Liczba π”):

Najczęściej stosowane przybliżenia:

   π ≈ 3,14

DŁUGOŚĆ OKRĘGU.

Skoro

łatwo więc wyznaczyć wzór na obliczenie 
długości okręgu - l 

l = πd

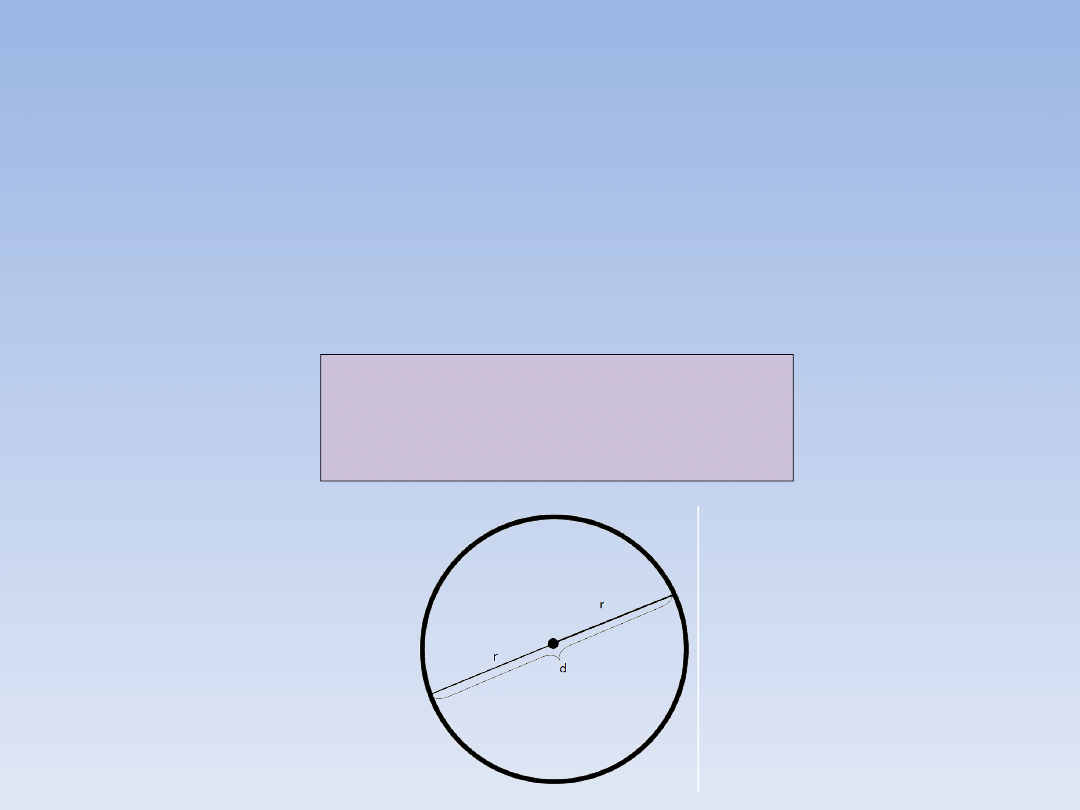
DŁUGOŚĆ OKRĘGU.

Pamiętając o związku między długością 
średnicy a długością promienia: d = 2r , wzór 
na długość okręgu możemy zapisać tak:

l = 2πr

PRZYKŁADY.

PRZYKŁAD 1.
Podaj długość okręgu o promieniu 3,14.
r = 3,14
l = 2πr
l = 2π ∙ 3,14 = 6,28π

PRZYKŁAD 2.
Podaj długość okręgu o średnicy 4,2.
d = 4,2
l = πd
l = π ∙ 4,2
l = 4,2π

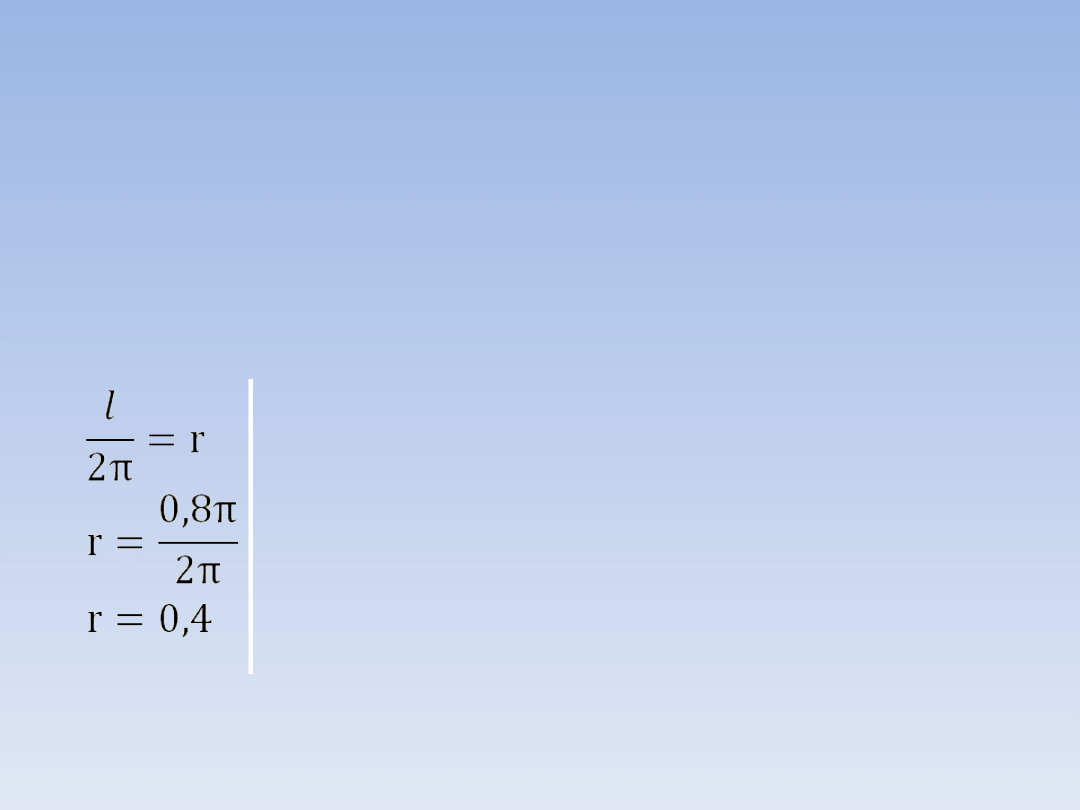
PRZYKŁADY.

PRZYKŁAD 3.
Podaj długość promienia koła o obwodzie 
0,8π.
l = 0,8π
l = 2πr /: 2π

PRZYKŁADY.

PRZYKŁAD 4.
Podaj przybliżoną długość okręgu o 
promieniu 10 km.
r = 10 km
l = 2πr
π ≈ 3,14
l ≈ 2 ∙ 3,14 ∙ 10 km
l ≈ 62,8 km

PRZYKŁADY.

PRZYKŁAD 5.
Podaj przybliżoną długość okręgu o 
średnicy 5 m.
d = 5 m
l = πd
π ≈ 3,14
l ≈ 3,14 ∙ 5 m
l ≈ 15,7 m

UWAGA

Przybliżenie π stosujemy tylko kiedy 
wymaga tego zadanie. W pozostałych 

przypadkach podajemy wartość dokładną 

– stosując symbol π.

PRZYKŁADOWE ZADANIA.

ZADANIE 1.
Każda z 4 osób ma rozpiętość ramion równą 140 
cm. Czy zdołają objąć pień drzewa o średnicy 180 
cm?
Obliczamy najpierw obwód drzewa:
d = 180 cm
π ≈ 3,14
l = πd
l ≈ 3,14 ∙ 180 cm = 565,2 cm.
4 osoby o danej rozpiętości ramion mogą objąć 
drzewo o obwodzie 4 ∙ 140 cm = 560 cm. Jak 
widać z obliczeń to mniej niż obwód danego 
drzewa.

PRZYKŁADOWE 

ZADANIA.

ZADANIE 2.
Tomek wybrał się do wesołego miasteczka i 
wsiadł na karuzelę. W ciągu minuty karuzela 
obraca się 5 razy. Tomek siedzi na krzesełku 
w odległości 5 m od środka karuzeli. Jaką 
drogę pokonuje chłopiec w ciągu 10 minut?
Najpierw obliczymy jaką drogę pokonuje 
krzesełko w czasie 1 obrotu.
r = 5 m
l = 2πr
l = 2π ∙ 5 m = 10π m

PRZYKŁADOWE ZADANIA.

ZADANIE 2 – ciąg dalszy.
W takim razie w ciągu minuty karuzela 
pokonuje drogę:
5 ∙ 10π m = 50π m,
a więc w ciągu 10 minut:
10 ∙ 50π m = 500π m.
W przybliżeniu (wstawiając π ≈ 3,14) jest to: 
500 ∙ 3,14 m = 1570 m = 1,57 km

PRZYKŁADOWE ZADANIA.

ZADANIE 3. 
Koło skutera ma średnicę 40 cm. Ile pełnych 
obrotów wykona to koło na drodze 100 m?
W ciągu jednego pełnego obrotu koło 
pokonuje drogę równą swemu obwodowi.
d = 40 cm
l = πd
l = π ∙ 40 cm = 40π cm
l ≈ 40 ∙ 3,14 cm = 125, 6 cm = 1,256 m
Aby obliczyć ile pełnych obrotów wykona to 
koło na danej drodze wystarczy podzielić tę 
drogę przez obwód koła.

PRZYKŁADOWE ZADANIA.

ZADANIE 3 – ciąg dalszy.
100 m : 1,256 m = 79,61 …
W takim razie na drodze 100 m koło o 

średnicy 40 cm wykona 79 pełnych 
obrotów (zaokrąglamy w dół, gdyż chodzi 
nam jedynie o pełne obroty na danej 
drodze).

PRZYKŁADOWE 

ZADANIA.

ZADANIE 4. 
Ania jedzie na rowerze z tak ustawioną 

przerzutką, że jeden pełny obrót pedałów 
powoduje trzy obroty każdego koła roweru. 
Koła te mają średnicę 70 cm. Ile pełnych 
obrotów pedałami musi wykonać Ania, aby 
przejechać 1 kilometr? W obliczeniach 
przyjmij                .

Zadanie jest podobne do poprzedniego. 

Najpierw obliczymy „długość kół” roweru.

d = 70 cm

PRZYKŁADOWE 

ZADANIA.

ZADANIE 4 – ciąg dalszy.

Jeden obrót pedałów powoduje trzy obroty kół, 

więc aby dowiedzieć się jaką drogę pokonuje 
Ania po jednym obrocie napędu musimy nasz 
wynik pomnożyć przez 3.

220 cm ∙ 3 = 660 cm
660 cm = 6,6 m
1 km = 1000 m

PRZYKŁADOWE 

ZADANIA.

ZADANIE 4 – ciąg dalszy.
Zamiana jednostek była niezbędna do 

przeprowadzenia dalszych  obliczeń (możemy 

działać jedynie na wielkościach wyrażonych w 

tych samych jednostkach). Aby obliczyć ilość 

obrotów pedałów na drodze 1 km, dzielimy tę 

drogę przez obwód koła roweru x3 (tyle obrotów 

przypada na jeden obrót pedałów).

1000 m : 6,6 m = 151,(51)
Pytanie brzmiało tak: „ Ile pełnych obrotów 

pedałami musi wykonać Ania, aby przejechać 1 

kilometr? „ a więc wynik musimy zaokrąglić w 

górę, gdyż chodzi nam o pełne obroty pedałów 

potrzebne to pokonania danej trasy – potrzeba 

ich 152 (151 nie wystarczy do przejechania 1 

km.