Geometria
Czworokąty
Geometria
Czworokąty
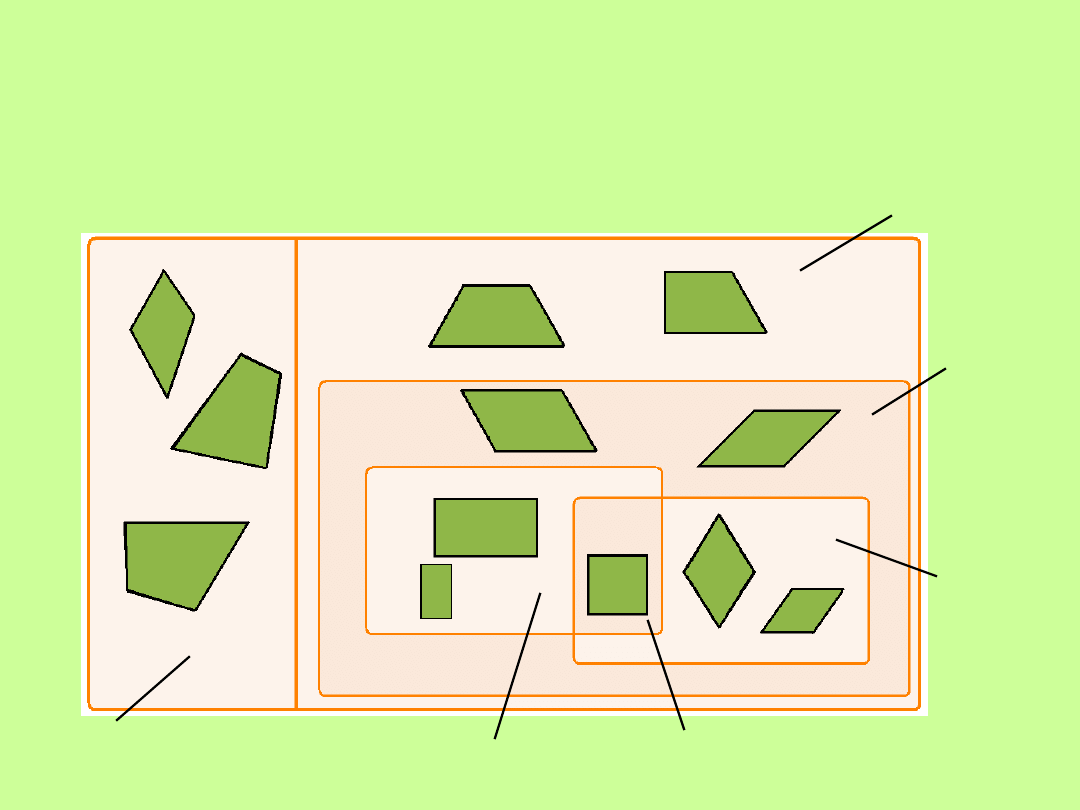
Podział czworokątów
TRAPEZOIDY
PROSTOKĄTY
KWADRATY
ROMBY
RÓWNOLEGŁOBOKI
TRAPEZY
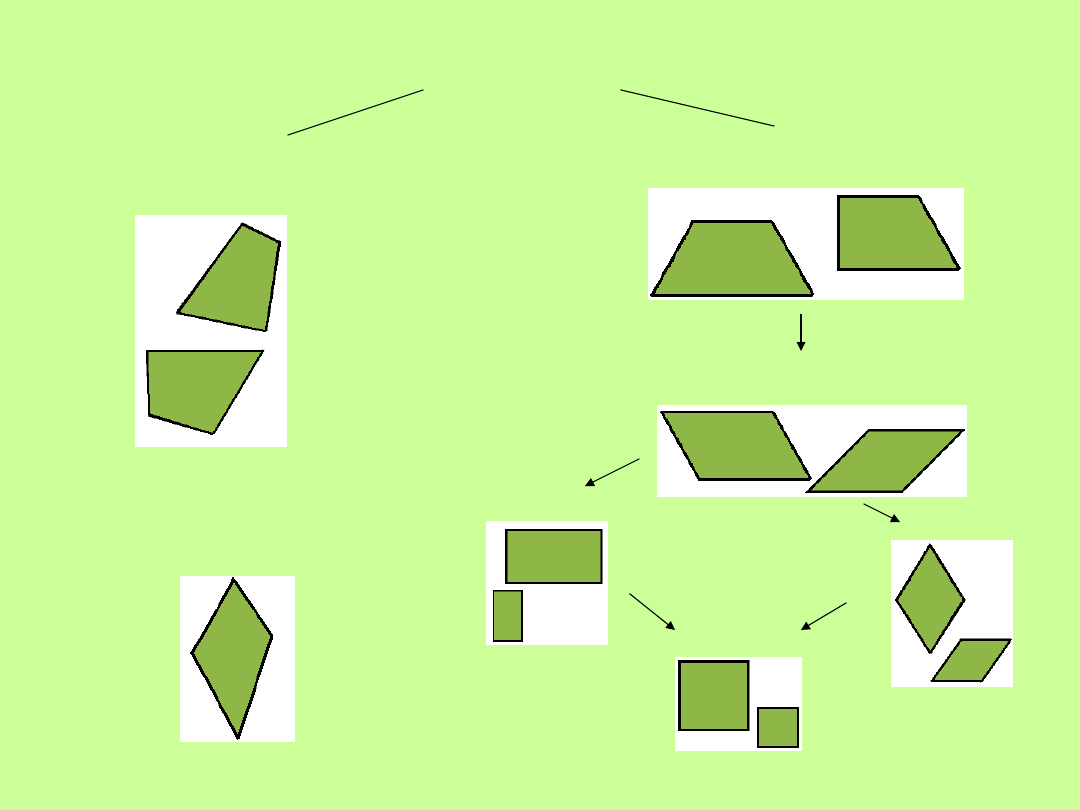
CZWOROKĄT
Y
TRAPEZOIDY
TRAPEZ
Y
CO NAJMNIEJ JEDNA PARA BOKÓW RÓWNOLEGŁYCH
RÓWNOLEGŁOBO
K
PROSTOKĄT
Y
ROMB
Y
KWADRATY
DWIE PARY BOKÓW RÓWNOLEGŁYCH
M.IN.:
-DELTOID (LATAWIEC)
NIE MA PAR BOKÓW RÓWNOLEGŁYCH
Trapezoidy
1.
Suma miar kątów dowolnego czworokąta jest równa 360º
2.
Deltoid
– czworokąt wypukły, będący trapezoidem.
Posiada tylko jedną oś symetrii.
Własności:
a) przekątne są prostopadłe
b) miary kątów między bokami różnej długości są równe
c) przekątna łącząca wierzchołki kątów o różnych miarach zawiera się
w ich dwusiecznych
d) punkt przecięcia przekątnych dzieli przekątną – łączącą na wierzchołki kątów
o równych miarach – na połowy
S
D
C
B
A
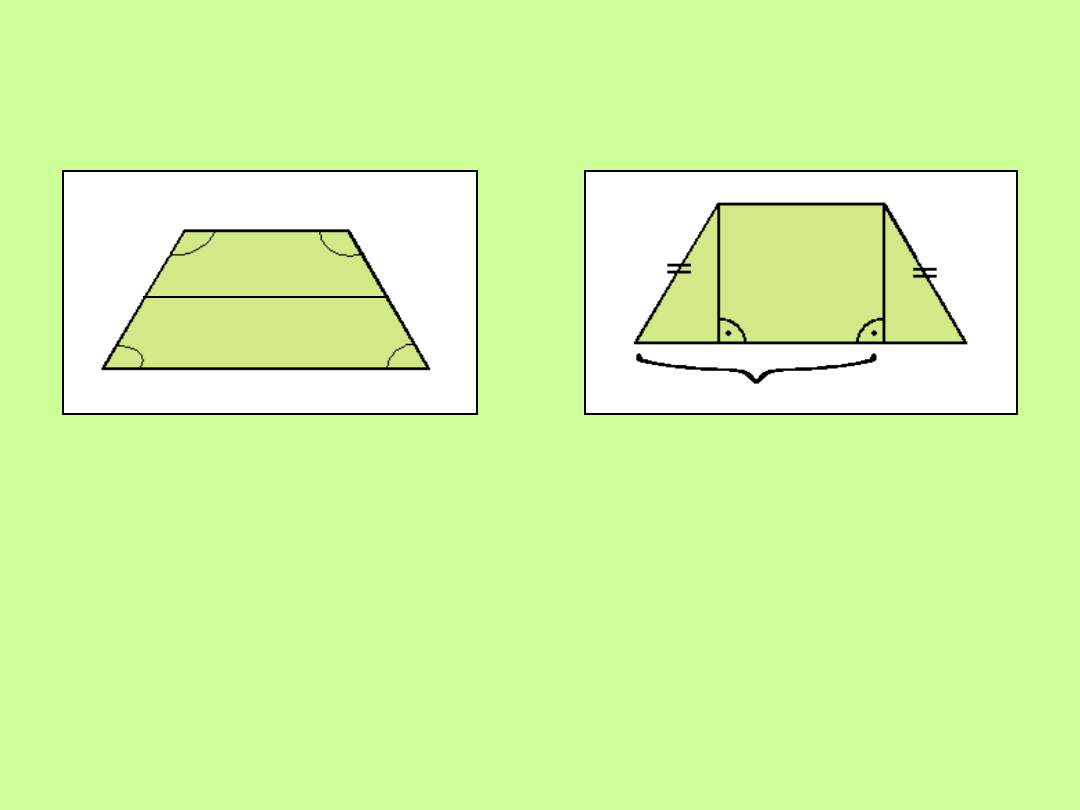
Trapezy
Własności trapezu:
1.
α + β + γ + δ = 360
º
2.
α + β = γ + δ = 180
º
3.
E- środek AB
F- środek CD
to EF || AB ∧ EF ||DC
4.
W dowolnym trapezie
odcinek łączący środki
ramion jest równoległy do
podstaw trapezu i jego
długość jest połową sumy
długości podstaw
5.
x = (a+b)/2
α
β
γ
δ
B
A
C
D
F
E
b
a
x
Własności trapezu równoramiennego:
1.
Ramiona mają taką samą
długość
2.
W trapezie równoramiennym o
podstawach a , b (a>b)
wysokość poprowadzona z
wierzchołka kąta rozwartego
dzieli dłuższą podstawę na
odcinki długości
x = (a-b)/2
y = (a+b)/2
b
C
D
B
A
a
x
y
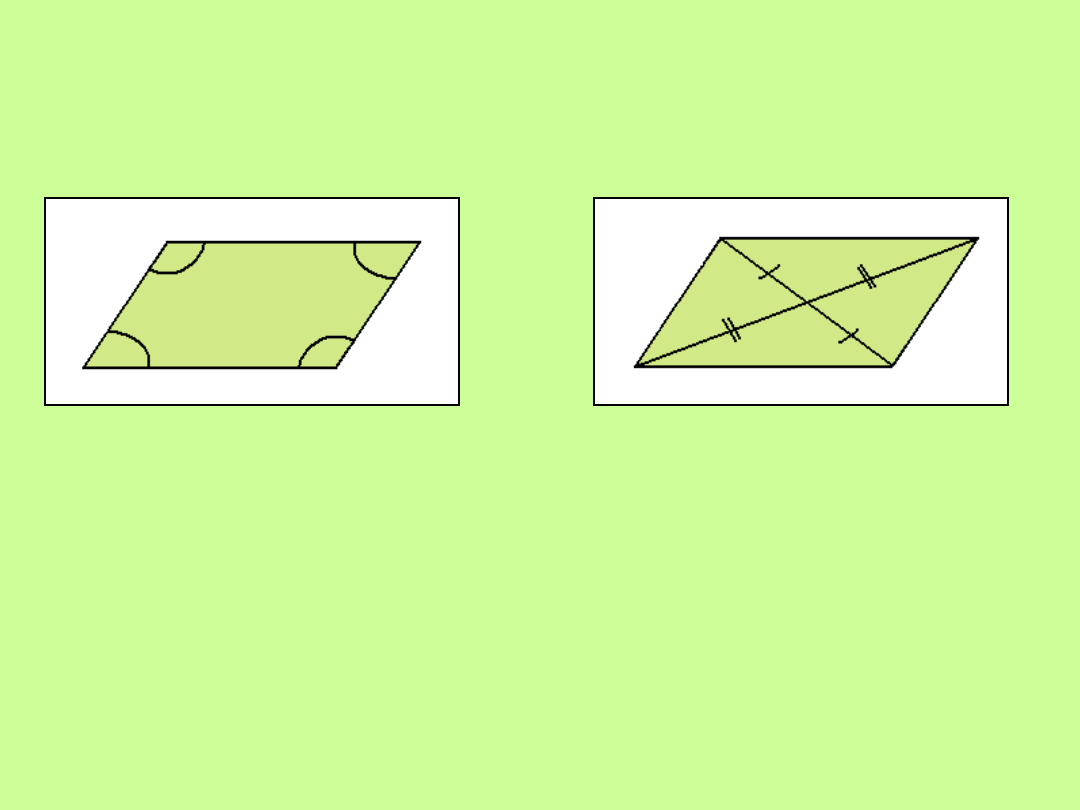
Równoległoboki
Własności:
1.
Każde dwa przeciwległe boki są sobie równe
2.
Przeciwległe kąty są równe
3.
Punkt przecięcia dzieli przekątne na połowy
4.
Suma miar kątów leżących przy każdym boku równoległoboku jest
równa sumie 180 º
A
B
C
D
α
β
a
b
A
B
C
D
a
b
α
β
S
d/2
d/2
c/2
c/2
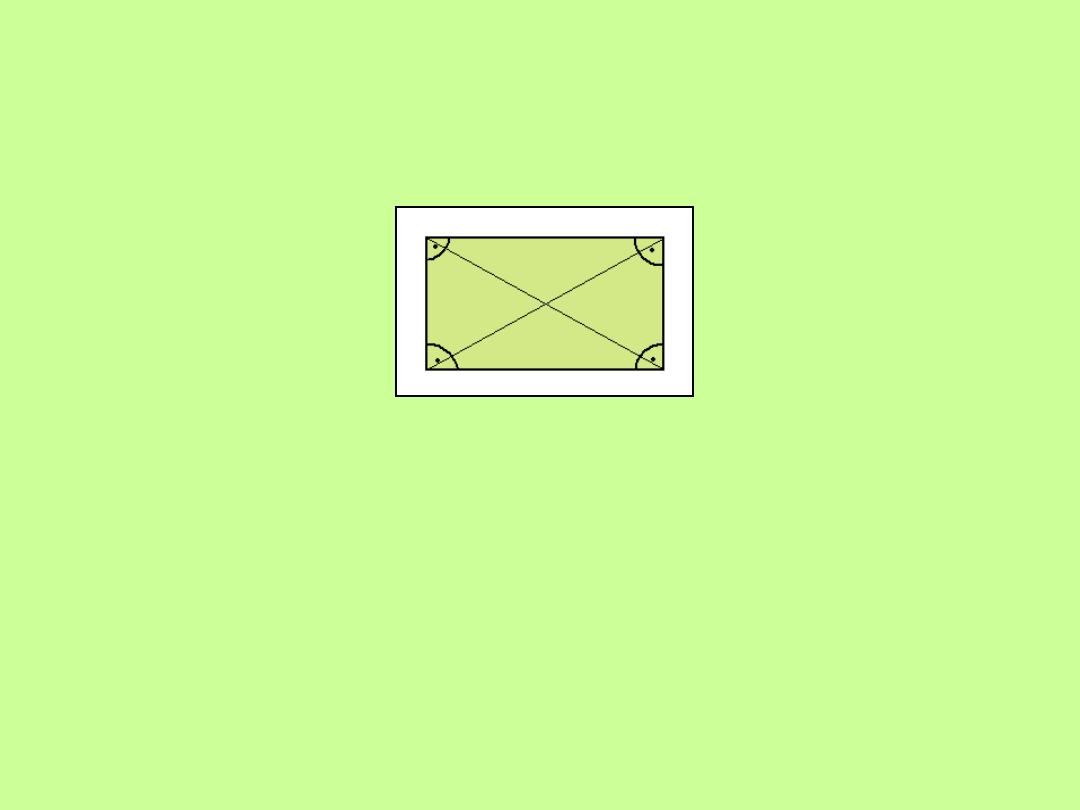
Prostokąty
Własności:
1. Każdy jego kąt jest kątem prostym.
2. Zachowuje własności 1-4 równoległoboków
3. Jego przekątne mają tę samą długość, lecz nie są dwusiecznymi
kąta
A
D
C
B
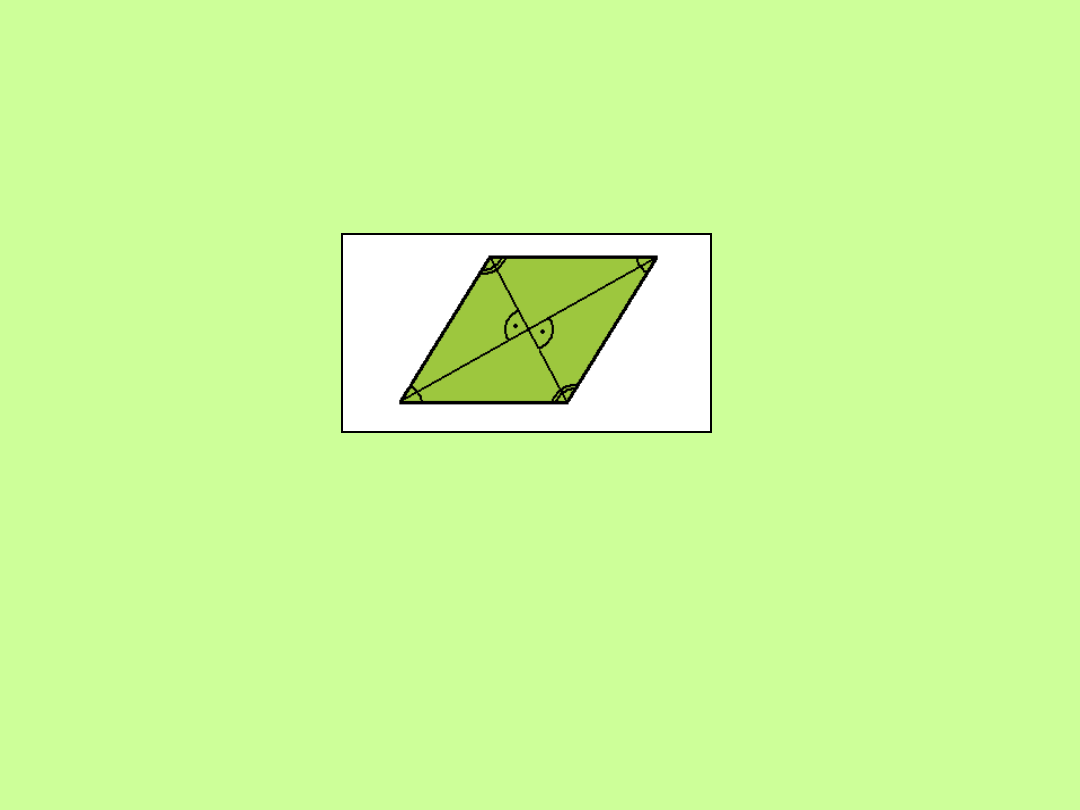
Romby
A
D
C
B
a
a
