HALINA KLIMCZAK
INSTYTUT GEODEZJ I
GEOINFORMATYKI
halina.klimczak@up.wroc.pl
ANALIZA DANYCH
PODZIAŁ NA KLASY
HALINA KLIMCZAK
INSTYTUT GEODEZJ I
GEOINFORMATYKI
halina.klimczak@up.wroc.pl
ANALIZA DANYCH
PODZIAŁ NA KLASY
DANE
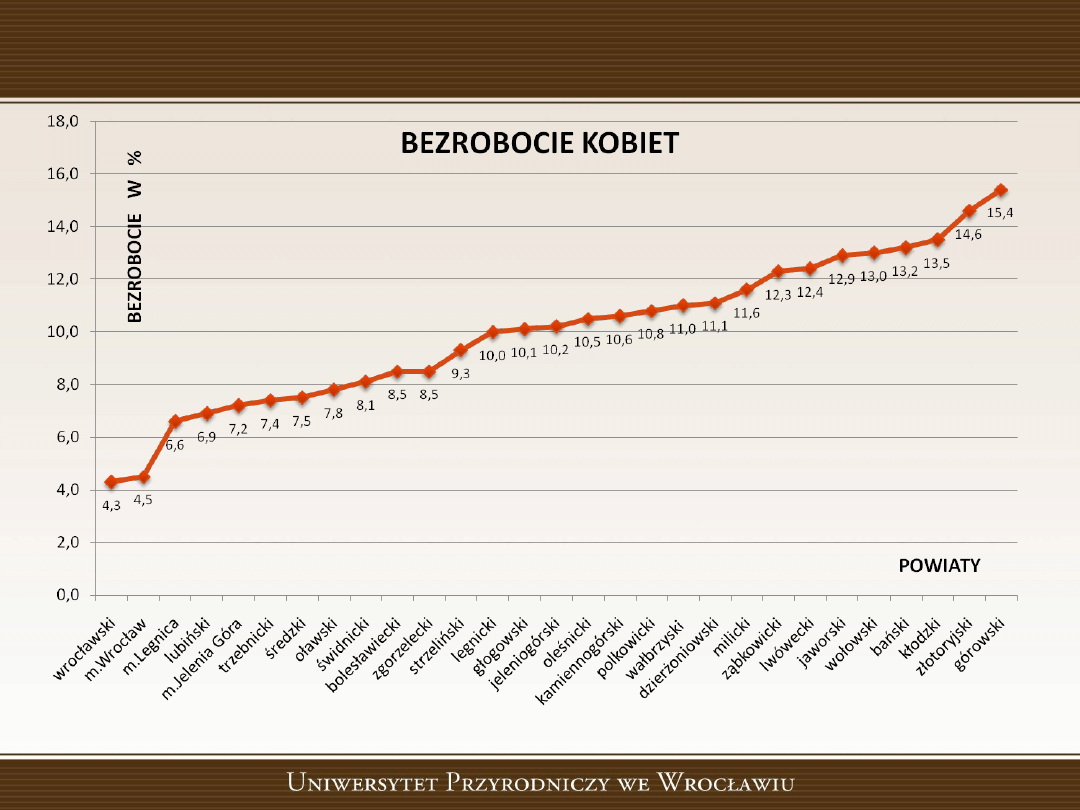
Kod
Jednostka terytorialna
Powiat
2010
1.
[%]
5020423000
wrocławski
4,3
5020564000
m.Wrocław
4,5
5020262000
m.Legnica
6,6
5020211000
lubiński
6,9
5020161000
m.Jelenia Góra
7,2
5020420000
trzebnicki
7,4
5020418000
średzki
7,5
5020415000
oławski
7,8
5020319000
świdnicki
8,1
5020101000
bolesławiecki
8,5
5020125000
zgorzelecki
8,5
5020417000
strzeliński
9,3
5020209000
legnicki
10,0
5020203000
głogowski
10,1
5020106000
jeleniogórski
10,2
5020414000
oleśnicki
10,5
5020107000
kamiennogórski
10,6
5020216000
polkowicki
10,8
5020321000
wałbrzyski *
11,0
5020302000
dzierżoniowski
11,1
5020413000
milicki
11,6
5020324000
ząbkowicki
12,3
5020112000
lwówecki
12,4
5020105000
jaworski
12,9
5020422000
wołowski
13,0
5020110000
lubański
13,2
5020308000
kłodzki
13,5
5020126000
złotoryjski
14,6
5020204000
górowski
15,4
15,4 max
4,3 min
10,2 mediana
10,0 śred. artm.
2,788762
odch.stand
.
Podstawowe statystyki
Uporządkowany zbiór danych
Udział zarejestrowanych
bezrobotnych kobiet w liczbie
ludności
w wieku produkcyjnym
WYKRES FUNKCJI
WYKRES FUNKCJI
14,
0
8,
9
12,
0
5,
6
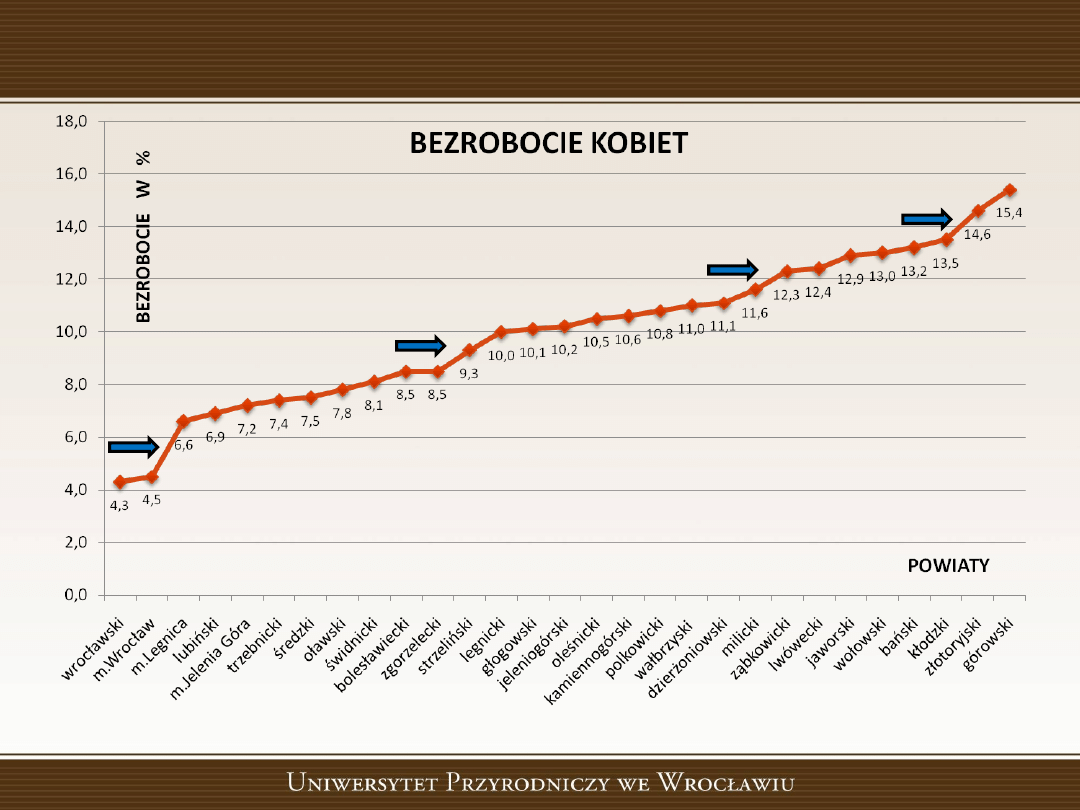
PODZIAŁ GRAFICZNY
Jednostka terytorialna
Powiat
2010
1.
[%]
wrocławski
4,3
m.Wrocław
4,5
m.Legnica
6,6
lubiński
6,9
m.Jelenia Góra
7,2
trzebnicki
7,4
średzki
7,5
oławski
7,8
świdnicki
8,1
bolesławiecki
8,5
zgorzelecki
8,5
strzeliński
9,3
legnicki
10,0
głogowski
10,1
jeleniogórski
10,2
oleśnicki
10,5
kamiennogórski
10,6
polkowicki
10,8
wałbrzyski *
11,0
dzierżoniowski
11,1
milicki
11,6
ząbkowicki
12,3
lwówecki
12,4
jaworski
12,9
wołowski
13,0
lubański
13,2
kłodzki
13,5
złotoryjski
14,6
górowski
15,4
14,0 – 15.3 %
(2)
12.0 – 13,9
(6)
8,9 – 11,9
(10)
5,6 – 8,8
(9)
4,3 – 5,5
(2)
Podział graficzny
na podstawie wykresu funkcji
RÓWNA LICZBA OBSERWACJI
Ogólną liczbę jednostek odniesienia dzieli się na ustaloną
liczbę klas. Następnie dane uszeregowane w kolejności
rosnącej lub malejącej przydziela się do odpowiednich
klas.
W sytuacji, gdy liczba danych jest niepodzielna przez
założoną liczbę klas, należy tak wyznaczyć klasy, aby
zawierały one wartości możliwie podobne. W wyniku
takiego podziału rozpiętość klas będzie różna i praktycznie
niemożliwe jest zachowanie jakiejkolwiek prawidłowości
rozpiętości.
W naszym przykładzie ustalona, ze sposobu graficznego,
liczba klas wynosi 5, przedziały zostały określony w
następujący sposób:
Liczba obserwacji ( powiatów) w kalsie 29 / 5 = 5,8
W badanym przypadku większość (4) przedziałów będzie miała 6 obserwacji
a jeden przedział 5 obserwacji.
RÓWNA LICZBA OBSERWACJI
Jednostka terytorialna
Powiat
2010
1.
[%]
wrocławski
4,3
m.Wrocław
4,5
m.Legnica
6,6
lubiński
6,9
m.Jelenia Góra
7,2
trzebnicki
7,4
średzki
7,5
oławski
7,8
świdnicki
8,1
bolesławiecki
8,5
zgorzelecki
8,5
strzeliński
9,3
legnicki
10,0
głogowski
10,1
jeleniogórski
10,2
oleśnicki
10,5
kamiennogórski
10,6
polkowicki
10,8
wałbrzyski *
11,0
dzierżoniowski
11,1
milicki
11,6
ząbkowicki
12,3
lwówecki
12,4
jaworski
12,9
wołowski
13,0
lubański
13,2
kłodzki
13,5
złotoryjski
14,6
górowski
15,4
13.0 – 15.3 % (5)
10,9 – 12,9 (6)
9,6 – 10,8 (6)
7,5 – 9,5 (6)
4,3 – 7,4 (6)
Granice klas
Przedziały o równej rozpiętości wartości
W tej metodzie wszystkie klasy mają jednakową
rozpiętość.
Różnicę maksymalnej i minimalnej wartości dzieli się
przez liczbę klas. W naszym przykładzie dla pięciu
przedziałów można obliczyć wartość stałą
C
:
C = (15,4 – 4,3) / 5 = 2,25
Uzyskana wartość jest interwałem, stałą różnicą miedzy
granicami klas.
Wykorzystuje się ją do określenia przedziałów klasowych wg
wzoru:
minimalna wartość + C + C + C + C + C = maksymalna
wartość
Przedziały o równej rozpiętości wartości
Jednostka terytorialna
Powiat
2010
1.
[%]
wrocławski
4,3
m.Wrocław
4,5
m.Legnica
6,6
lubiński
6,9
m.Jelenia Góra
7,2
trzebnicki
7,4
średzki
7,5
oławski
7,8
świdnicki
8,1
bolesławiecki
8,5
zgorzelecki
8,5
strzeliński
9,3
legnicki
10,0
głogowski
10,1
jeleniogórski
10,2
oleśnicki
10,5
kamiennogórski
10,6
polkowicki
10,8
wałbrzyski *
11,0
dzierżoniowski
11,1
milicki
11,6
ząbkowicki
12,3
lwówecki
12,4
jaworski
12,9
wołowski
13,0
lubański
13,2
kłodzki
13,5
złotoryjski
14,6
górowski
15,4
13.2 – 15.4 % (4)
11,0 – 13,1 (7)
8,8 – 10,9 (7)
6,6 – 8,7 (9)
4,3 – 6,5 (2)
Granice klas
CIĄG ARYTMETYCZNY
CIĄG ARYTMETYCZNY
Ciąg arytmetyczny jest to seria liczb, w której każda następna
wartość może być określona na podstawie poprzedniej przez
dodanie stałej wartości.
Granice klas mogą być obliczone z poniższego wzoru, przy
założeniu, że liczba klas wynosi pięć:
minimalna wartość + C + 2C + 3C + 4C + 5C = maksymalna
wartość
W przykładzie stała
C
została obliczona w następujący sposób:
maksymalna wartość minus minimalna wartość podzielona przez
liczbę stałych
C
według wzoru:
C = (15,4 – 4,3) / 15 = 0,74
W przypadku danych w rozpatrywanym przykładzie występuje jedna
klasa pusta
CIĄG ARYTMETYCZNY
CIĄG ARYTMETYCZNY
Jednostka terytorialna
Powiat
2010
1.
[%]
wrocławski
4,3
m.Wrocław
4,5
m.Legnica
6,6
lubiński
6,9
m.Jelenia Góra
7,2
trzebnicki
7,4
średzki
7,5
oławski
7,8
świdnicki
8,1
bolesławiecki
8,5
zgorzelecki
8,5
strzeliński
9,3
legnicki
10,0
głogowski
10,1
jeleniogórski
10,2
oleśnicki
10,5
kamiennogórski
10,6
polkowicki
10,8
wałbrzyski *
11,0
dzierżoniowski
11,1
milicki
11,6
ząbkowicki
12,3
lwówecki
12,4
jaworski
12,9
wołowski
13,0
lubański
13,2
kłodzki
13,5
złotoryjski
14,6
górowski
15,4
11,8 – 15.4 % (8)
8,8 – 11,7 (10)
6,6 – 8,7 (9)
5,1 – 6,5 (0)
4,3 – 5,0 (2)
Granice klas
CIĄG GEOMETRYCZNY
CIĄG GEOMETRYCZNY
W tej metodzie każdą kolejną wartość można uzyskać z
poprzednich wartości przez pomnożenie jej przez stałą
C
,
współczynnik ciągu. Aby określić granice klas za pomocą tej
metody, należy obliczyć logarytmy maksymalnej i minimalnej
wartości. Te wartości są następnie odejmowane od siebie i dzielone
przez liczbę klas, co daje logarytm stałej
C
, którą można obliczyć w
następujący sposób:
C = (log 15,4 – log 4,3) / 5= (1,1875 – 0,6334)/5 = 0,11
C
jest następnie wykorzystane we wzorze:
log maksymalnej wartości – C = log drugiej najwyższej
wartości
log drugiej najwyższej wartości – C = log trzeciej najwyższej
wartości
itd.
Antylogarytmy uzyskanych w ten sposób wartości dają w
rezultacie granice klas.
CIĄG GEOMETRYCZNY
CIĄG GEOMETRYCZNY
Jednostka terytorialna
Powiat
2010
1.
[%]
wrocławski
4,3
m.Wrocław
4,5
m.Legnica
6,6
lubiński
6,9
m.Jelenia Góra
7,2
trzebnicki
7,4
średzki
7,5
oławski
7,8
świdnicki
8,1
bolesławiecki
8,5
zgorzelecki
8,5
strzeliński
9,3
legnicki
10,0
głogowski
10,1
jeleniogórski
10,2
oleśnicki
10,5
kamiennogórski
10,6
polkowicki
10,8
wałbrzyski *
11,0
dzierżoniowski
11,1
milicki
11,6
ząbkowicki
12,3
lwówecki
12,4
jaworski
12,9
wołowski
13,0
lubański
13,2
kłodzki
13,5
złotoryjski
14,6
górowski
15,4
12,0 – 15.4 % (8)
9,3 – 11,9 (10)
7,3 – 9,2 (6)
5,7 – 7,2 (3)
4,3 – 5,6 (2)
Granice klas
1,19 - 1,08
1,07 - 0,97
0,96 - 0,86
0,85 - 0,74
0,73 - 0,63
CIĄG HARMONICZNY
W klasyfikacji tego typu określa się serię harmoniczną, w której ciąg jest
definiowany na podstawie odwrotności wartości. Granice klas określa
się przez obliczenie różnicy między odwrotnościami najwyższej i
najniższej wartości i podzielenie wyniku przez liczbę klas.
.
W rezultacie
otrzymuje się współczyn nik ciągu
C
.
C = (1 / 15,28 – l / 3,93) / 5 = -0,04
Do wyznaczania granic klas stosuje się wzór podobny do tego, który
służy do obliczenia granic klas według ciągu geometrycznego:
odwrotność maksymalnej wartości - C = (odwrotność
maksymalnej wartości – C) – C = ((odwrotność
maksymalnejwartości - C) – C) – C itd.
Odwrotności uzyskanych wartości są przyjmowane jako granice
klas.
Ta metoda pozwala uwypuklić cechy rozkładu niskich wartości w
szeregu statystycznym.
W przypadku naszych danych ta metoda nie może być wykorzystana
skutecznie, ponieważ określa jedną klasę pustą.
CIĄG
CIĄG
HARMINICZNY
HARMINICZNY
Jednostka terytorialna
Powiat
2010
1.
[%]
wrocławski
4,3
m.Wrocław
4,5
m.Legnica
6,6
lubiński
6,9
m.Jelenia Góra
7,2
trzebnicki
7,4
średzki
7,5
oławski
7,8
świdnicki
8,1
bolesławiecki
8,5
zgorzelecki
8,5
strzeliński
9,3
legnicki
10,0
głogowski
10,1
jeleniogórski
10,2
oleśnicki
10,5
kamiennogórski
10,6
polkowicki
10,8
wałbrzyski *
11,0
dzierżoniowski
11,1
milicki
11,6
ząbkowicki
12,3
lwówecki
12,4
jaworski
12,9
wołowski
13,0
lubański
13,2
kłodzki
13,5
złotoryjski
14,6
górowski
15,4
10,3 – 15.4 % (14)
7,7 – 10,2 (8)
6,1 – 7,6 (5)
5,1 – 6,0 (0)
4,3 – 5,0 (2)
Granice klas
0,06 - 0,10
0,11 - 0,13
0,14 - 0,17
0,18 - 0,20
0,21 - 0,23
ŚREDNIE ZAGNIEŻDŻONE
Aby określić granice klas tą metodą, należy najpierw
obliczyć średnią ze wszystkich obserwowanych wartości.
W przykładzie jest to
w =10,0
.
Następnie oblicza się średnią dla wszystkich wartości
powyżej i poniżej tej średniej, a potem kolejno dla
wszystkich wartości powyżej i poniżej kolejnych średnich
(w przykładzie będą to
w
1
=
7,4
i
w
2
=
12,1
).
Te trzy wartości mogą być użyte jako granice klas. W tej
metodzie liczba klas musi być podzielna przez dwa.
W przykładzie użyto jej do określenia czterech klas.
ŚREDNIE ZAGNIEŻDŻONE
Jednostka terytorialna
Powiat
2010
1.
[%]
wrocławski
4,3
m.Wrocław
4,5
m.Legnica
6,6
lubiński
6,9
m.Jelenia Góra
7,2
trzebnicki
7,4
średzki
7,5
oławski
7,8
świdnicki
8,1
bolesławiecki
8,5
zgorzelecki
8,5
strzeliński
9,3
legnicki
10,0
głogowski
10,1
jeleniogórski
10,2
oleśnicki
10,5
kamiennogórski
10,6
polkowicki
10,8
wałbrzyski *
11,0
dzierżoniowski
11,1
milicki
11,6
ząbkowicki
12,3
lwówecki
12,4
jaworski
12,9
wołowski
13,0
lubański
13,2
kłodzki
13,5
złotoryjski
14,6
górowski
15,4
12,1 – 15.4 % (8)
10,0 – 12,0 (9)
7,4 – 9,9 (7)
4,3 – 7,3 (5)
Granice klas
12 obserwacji
17 obserwacji
ODCHYLENIE STANDARDOWE
ODCHYLENIE STANDARDOWE
Jest to modyfikacja poprzedniej metody oparta na odchyleniu
standardowym. Rozpiętość klas równa jest wartości
odchylenia standardowego, zaś granice klas to kolejne
wielokrotności odchylenia, dodawane i odejmowane od
średniej arytmetycznej zbioru, do momentu sklasyfikowania
wszystkich danych. Najniższa i najwyższa klasa mają różną
rozpiętość, ponieważ dolna granica najniższej klasy i górna
granica najwyższej klasy równają się odpowiednio najniższej i
najwyższej wartości szeregu kartowanych danych.
Aby określić granice klas tą metodą, należy najpierw
obliczyć średnią (dla danych w przykładzie =
10,0
) oraz
odchylenie standardowe (=
2,8
) ze wszystkich
obserwowanych wartości .
Dodając i odejmując wartości odchylenia od średniej
otrzymamy kolejne liczby, które można wykorzystać jako
granice przedziałów:
7,2 (=10,0-2,8) oraz 13,0
(=10,2+2,8).
Można też operować liczbami równymi ½, ¼, itp. wielkości
odchylenia standardowego.
ODCHYLENIE STANDARDOWE
ODCHYLENIE STANDARDOWE
Jednostka terytorialna
Powiat
2010
1.
[%]
wrocławski
4,3
m.Wrocław
4,5
m.Legnica
6,6
lubiński
6,9
m.Jelenia Góra
7,2
trzebnicki
7,4
średzki
7,5
oławski
7,8
świdnicki
8,1
bolesławiecki
8,5
zgorzelecki
8,5
strzeliński
9,3
legnicki
10,0
głogowski
10,1
jeleniogórski
10,2
oleśnicki
10,5
kamiennogórski
10,6
polkowicki
10,8
wałbrzyski *
11,0
dzierżoniowski
11,1
milicki
11,6
ząbkowicki
12,3
lwówecki
12,4
jaworski
12,9
wołowski
13,0
lubański
13,2
kłodzki
13,5
złotoryjski
14,6
górowski
15,4
13,1 – 15.4 % (4)
10,1 – 13,0 (12)
7,2 – 10.0 (9)
4,3 – 7,1 (4)
Granice klas
DOBÓR METODY PODZIAŁU
Która z tych metod jest najlepsza?
Najlepszy efekt, czyli najdokładniejszy obraz, uzyskamy
dobierając taką krzywą funkcji, która jest najlepiej
dopasowana do charakteru mapowanych danych.
Przedziały o równej rozpiętości zalecane są, gdy krzywa na
wykresie wartości zbliża się do linii prostej, natomiast
przedziały określone na zasadach ciągów arytmetycznego,
geometrycznego lub harmonicznego stosuje się, gdy rozkład
wartości zbliża się do kształtu krzywych odpowiednich
funkcji. Uniwersalny charakter ma zastosowanie punktów
charakterystycznych czy średnich zagnieżdżonych.
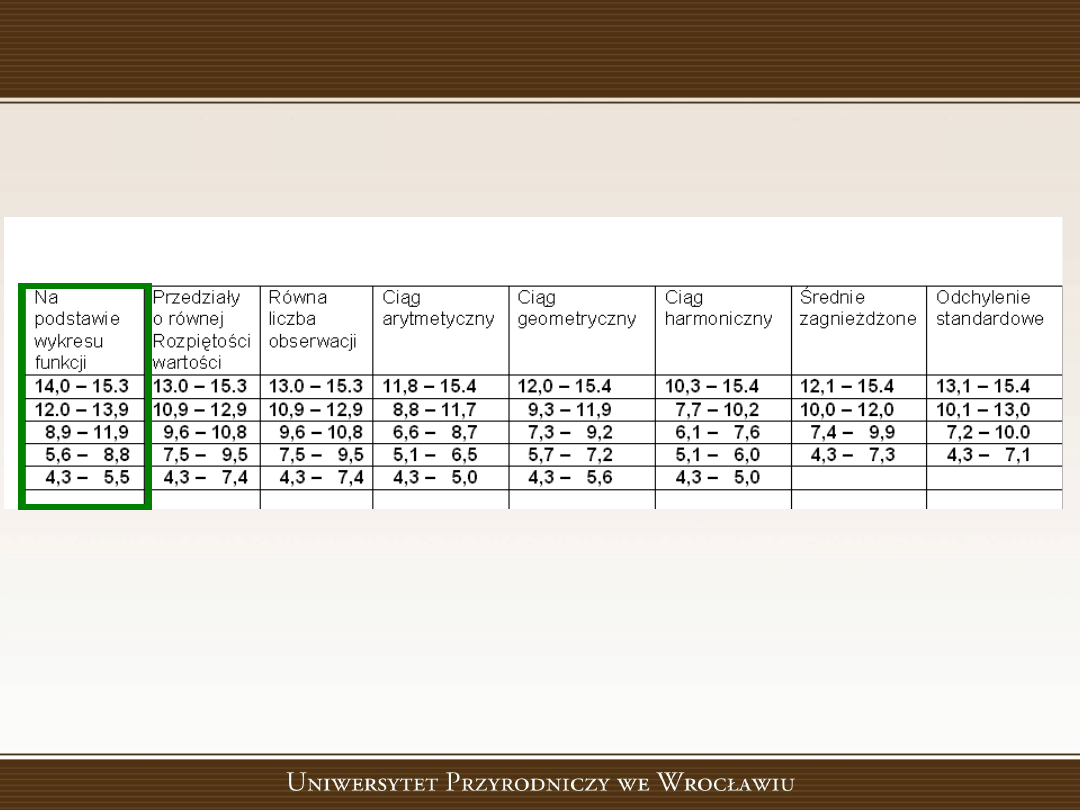
ZESTAWIENIE GRANIC KLAS OPRACOWANYCH
RÓZNYMI METODAMI
Udział zarejestrowanych bezrobotnych kobiet w liczbie ludności
w wieku produkcyjnym stan w 2010 r (w %)
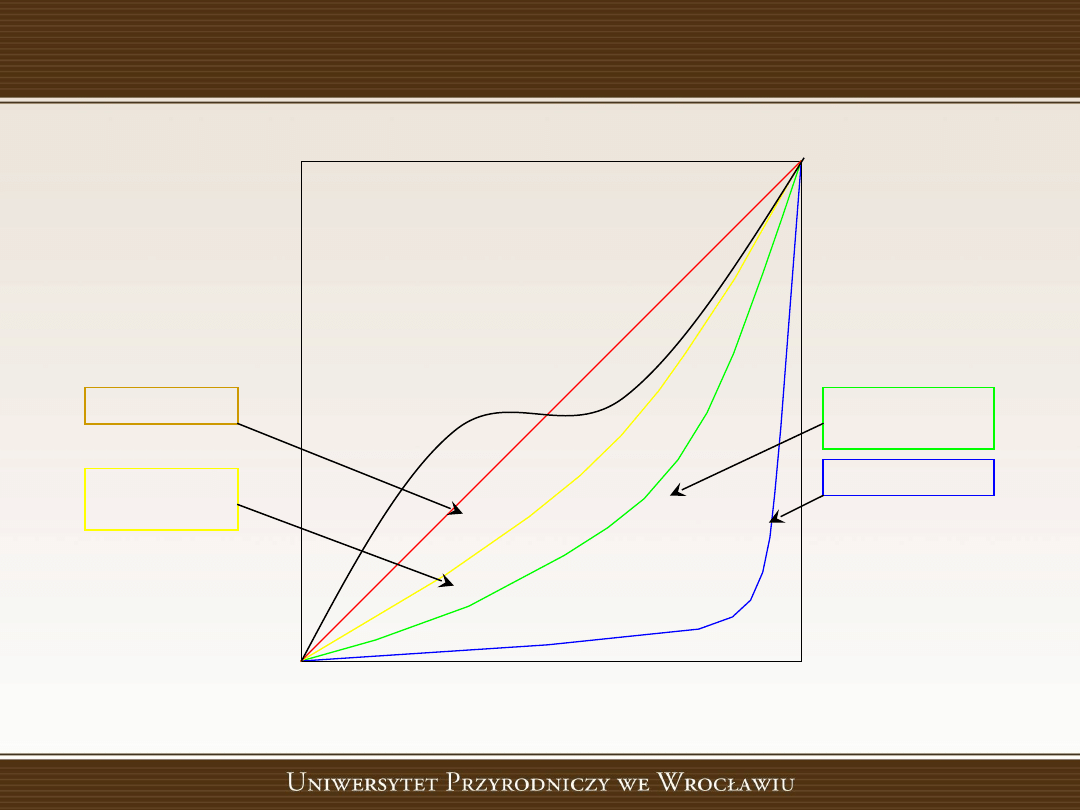
DOBÓR METODY PODZIAŁU
liniowe
arytmetycz
ne
geometryczn
e
harmoniczne
normalna
SPOSOBY ITERACYJNE
Sposoby iteracyjne są skomplikowane i nie można je prowadzić
tradycyjnie, dlatego wykorzystuje się technikę komputerową.
Przed podziałem należy ustalić pewne logiczne kryterium
statystyczne, a następnie komputer dokonuje iteracji w ten sposób,
że dane są grupowane tak, aby możliwie najdokładniej spełnić
założone kryterium.
System wyznaczania przedziałów klasowych wykorzystujący
sposoby iteracyjne na podstawie kryteriów statystycznych,
bazujących na teorii kartografii, po raz pierwszy zastosował George
F. Jenks (1967)
Nowszymi opracowaniami są dwa kryteria statystyczne, które
można wykorzystać w iteracji komputerowej:
Pierwszy z nich, to tzw. współczynnik GVF (goodness of variance
fit), który minimalizuje kwadraty odchyleń od wartości średnich dla
klas. Spełnienie kryterium polega na maksymalizacji wielkości GVF,
gdzie:
nego
statystycz
szeregu
całego
średniej
wartosci
od
odchyleń
kwadratów
suma
całkowita
klasami
między
odchyleń
kwadratów
suma
GVF
SPOSOBY ITERACYJNE
Stosując to kryterium należy najpierw przyjąć pewne grupowanie
danych uporządkowanego szeregu statystycznego. Oblicza się
średnia dla każdej utworzonej klasy oraz sumę kwadratów odchyleń
miedzy każda obserwacją a ta wartością. Następny etap polega na
przeniesieniu obserwacji z jednej klasy do drugiej w celu
zmniejszenia sumy kwadratów odchyleń od średniej i tym samym
zwiększenia wartosci wskaźnika GVF.
Drugie
kryterium wykorzystuje mediany w celu konstrukcji wskaźnika
GADF
(goodness of absolute devation fit)
nego
statystycz
szeregu
całego
mediany
od
ych
bezwzgledn
odchyleń
suma
klasach
kolejnych
w
mediany
od
odchyleń
suma
1
GADF
SPOSOBY ITERACYJNE
Główną zaletą tych sposobów jest to, że
można maksymalizować jednolitość
każdej klasy jednocześnie
maksymalizując różnice miedzy klasami –
co jest podstawową zasdą poprawnego
agregowania danych w klasy