C 01

1

Zadanie 1.4

Dana jest funkcja
skalarna

a) , b)

, c)

,

f

F

F

���Ѵ

r

r

( , , )

f x y z

x y z

= + +

oraz pole wektorowe

( , , ) (

)

x

y

z

F x y z

x y i

yi

zi

= +

+

+

r

r

r

r

Obliczyć:

2

2

d)

, e)

, f) ( ),

f

F

fF

�

�

��

r

r

( )

( )

2

2

g)

, h)

e

.

x

f

�

�

Wskazówki:

 obliczając punkt

f

skorzystać z tożsamości

( )

;

fF

f

F

f F

��

= �� +� �

r

r

r

( )

2

2

.

f

f

�

= �

 obliczając punkt

g

skorzystać z równości

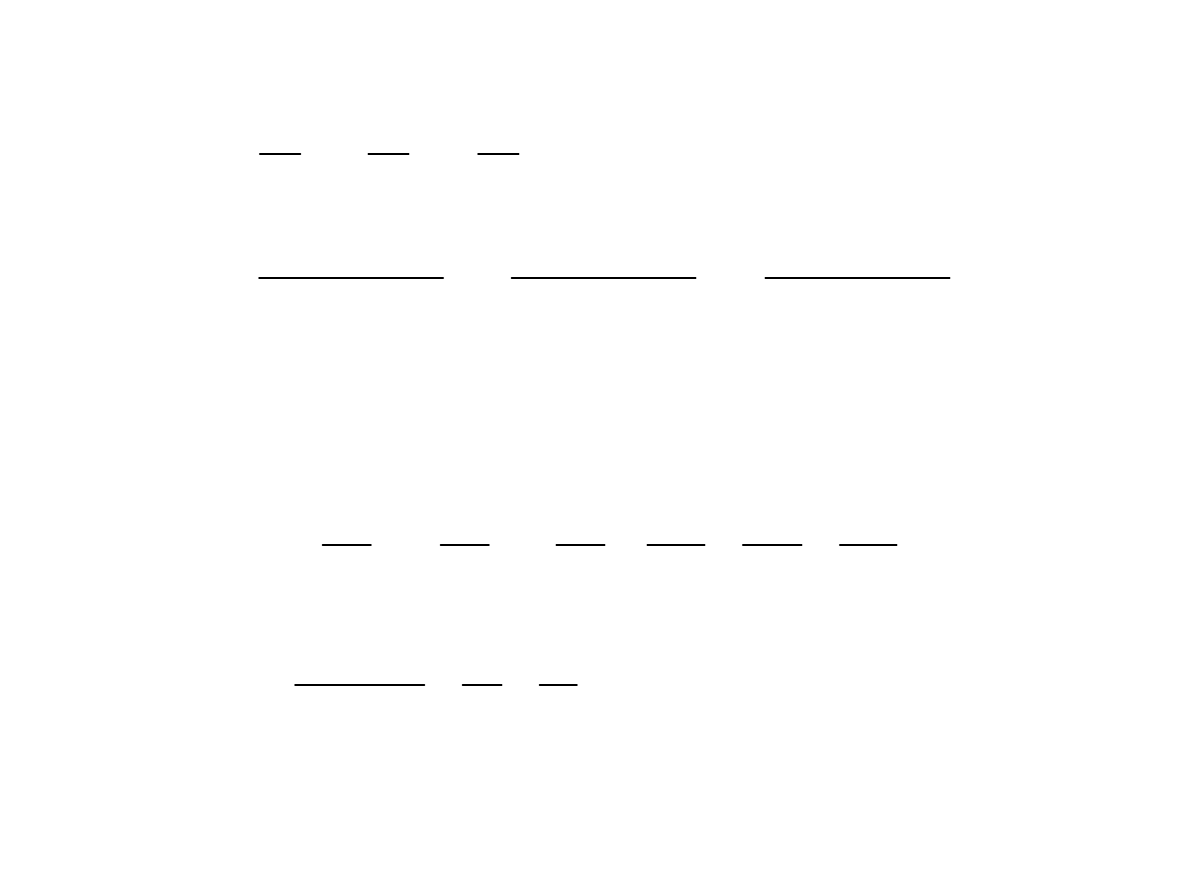
C 01

2

Zadanie 1.4 (2)

a)

x

y

z

f

f

fi

i

i

x

y

z

�

�

�

� =

+

+

=

�

�

�

r

r

r

(

)

(

)

(

)

x

y

z

x y z

x y z

x y z

i

i

i

x

y

z

� + +

� + +

� + +

=

+

+

=

�

�

�

r

r

r

x

y

z

i

i

i

= + +

r r r

b)

y

x

z

x

y

z

F

F

F

F

F

F

F i

i

i

x

y

z

x

y

z

�

�

�

�

�

�

�� =

+

+

=

+

+

=

�

�

�

�

�

�

r

r

r

r r

r

r

(

)

1 1 1 3

x y

y

z

x

y

z

� +

� �

=

+ + = + + =

�

� �

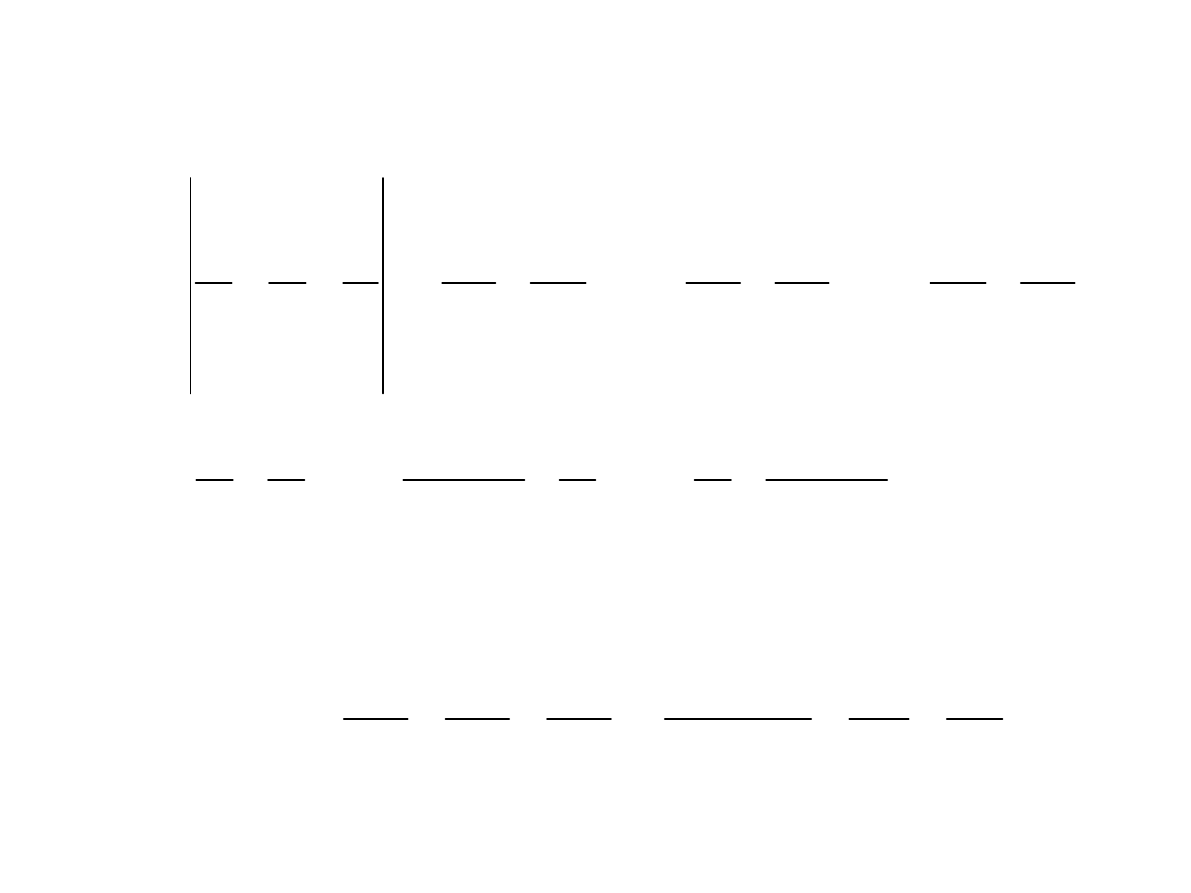
C 01

3

Zadanie 1.4 (3)

c)

d)

2

2

2

2

2

2

(

)

0

x y

y

z

x

y

z

� +

�

�

+

+

=

�

�

�

x

y

z

y

y

x

x

z

z

x

y

z

x

y

z

i

i

i

F

F

F

F

F

F

F

i

i

i

x

y

z

y

z

z

x

x

y

F

F

F

�

�

�

�

�

�

�

�

�

�

� � �

�

�

Ѵ

=

=

-

+

-

+

-

=

�

�

�

�

�

�

� � �

�

�

�

�

�

�

�

�

�

�

�

�

r

r

r

r

r

r

r

(

)

(

)

x

y

z

z

z

y

x y

z

y

x y

i

i

i

i

y

z

z

x

x

y

� �

� +

�

� � +

�

�

�

�

�

�

=

-

+

-

+

-

=-

�

�

�

�

�

�

� �

�

�

�

�

�

�

�

�

�

�

r

r

r

r

2

2

2

2

2

2

2

f

f

f

x

y

y

�

�

�

D�Ѻ++=

�

�

�

C 01

4

Zadanie 1.4 (4)

e)

f)

(

)

2

2

2

2

2

2

2

y

x

z

x

y

z

F

F

F

F

F

F

F

i

i

i

x

y

z

�

�

�

D��=���-ѴѴ=++=

�

�

�

r

r

r

r

r

r

r

2

2

2

2

2

2

(

)

0

x

y

z

x y

y

z

i

i

i

x

y

z

� +

�

�

=

+

+

=

�

�

�

r

r

r

( )

fF

f

F

f F

��

= �� +� � =

r

r

r

(

)3 (

) (

)

x

y

z

x

y

z

x y z

i

i

i

x y i

yi

zi

�

�

= + +

+ + + � +

+

+

=

�

�

r r r

r

r

r

(

)3

x y z

x y y z

= + +

+ + + +

4

5

4

x

y

z

= + +

g)

( )

2

2

f

f

�

= � =2(

)(

)

x

y

z

x y z i

i

i

+ +

+ +

r r r

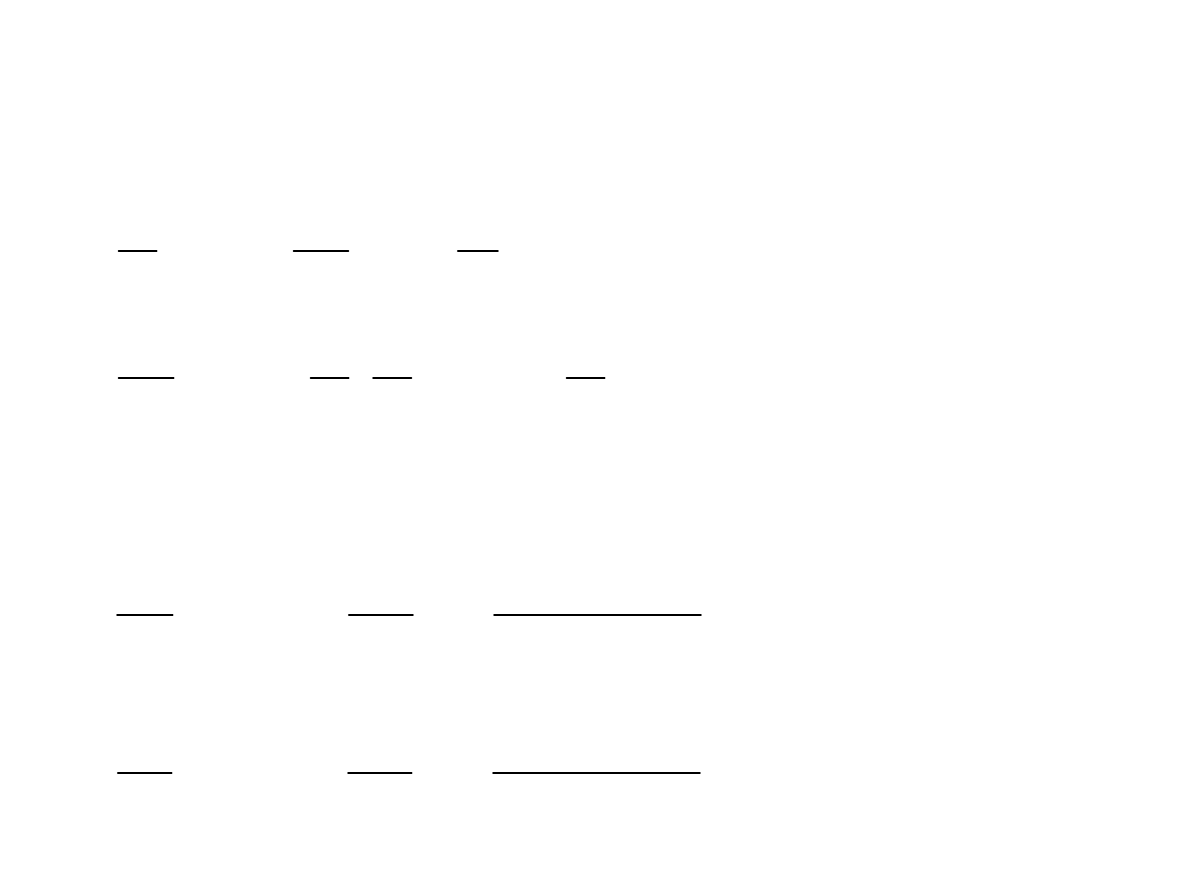
C 01

5

Zadanie 1.4 (5)

h)

( )

(

)

2

2

x

x

e f

e x y z

�

�

�

=�

+ +

�

�

( )

(

)

(

)

e

e

e

e

e

e

1

x

x

x

x

x

x

f

f

x y z

x y z

x

x

x

�

�

�

=

+

=

+ + + =

+ + +

�

�

�

( )

( )

(

)

2

2

e

e

e

1

x

x

x

f

x y z

x

x x

x

�

� �

�

�

�

�

�

=

=

+ + +

=

�

�

�

�

�

� �

�

�

�

(

)

(

)

e

1 e

e

2

x

x

x

x y z

x y z

=

+ + + + =

+ + +

( )

(

)

2

2

2

2

2

2

e

e

e

0

x

x

x

x y z

f

f

y

y

y

� + +

�

�

=

=

=

�

�

�

( )

(

)

2

2

2

2

2

2

e

e

e

0

x

x

x

x y z

f

f

z

z

z

� + +

�

�

=

=

=

�

�

�

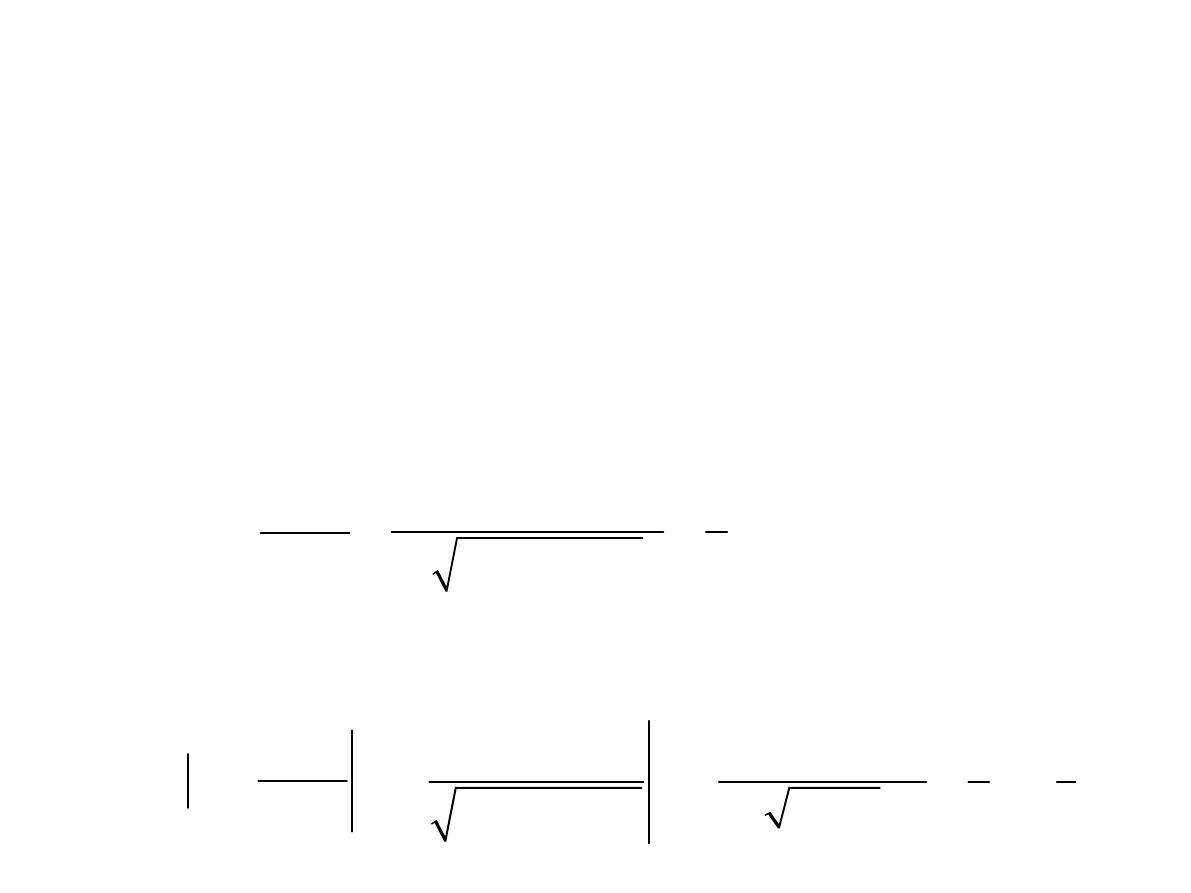
C 01

6

Zadanie 1.5

Wyznaczyć kierunek najszybszego
wzrostu

2

2

2

.

U x

y

z

= + +

pola skalarnego

Wykonać obliczenia dla punktu P

0

(4, 3,

0).

Wersor wskazujący najszybszy wzrost pola jest wersorem gradientu

|

|

grad

U

i

U

�

=

=

�

r

Wersor gradientu w punkcie P

0

(4,3,0):

0

0

P

P

|

|

grad

U

i

U

�

=

=

�

r

0

2

2

2

P

4

3

0

4

3

5

5

16 9

x

y

z

x

y

z

x

y

xi

yi

zi

i

i

i

i

i

x

y

z

+

+

+

+

=

=

+

+

+ +

r

r

r

r

r

r

r

r

2

2

2

2

2

2

2

x

y

z

xi

yi

zi

r

r

x

y

z

+

+

=

+ +

r

r

r

r

C 01

7

Zadanie 1.6

Obszar pewnego pokoju opisano we współrzędnych
kartezjańskich. W punkcie P

0

(20 m, 15 m, 2 m)

zmierzono temperaturę T(P

0

) = 312 K, oraz jej

gradient

Wyznaczyć przybliżoną wartość temperatury w punkcie
P

1

(21 m, 14 m, 3 m).

Temperatura w punkcie P

1

(21 m, 14 m,

3 m):

[

]

0

(P )

K m .

x

z

T

i

i

�

= +

r r

1

0

0

0 1

(P)

(P )

(P )

T

T

T

P P

@

+�

�

uuur

0

0 1

(P )

(

) (

) [K] 2 K

x

z

x

y

z

T

P P

i

i

i

i

i

�

�

= + � -

+

=

uuur

r r

r r r

1

(P) 312 K 2 K 314 K

T

=

+

=

C 01

8

Zadanie 1.7

Obliczyć strumień wektora pozycji przez
sferę
o promieniu r

0

= 5.

Strumień wektora przez powierzchnię
zamkniętą S ograniczającą obszar V:

Wektor pozycji we współrzędnych

sferycznych:

rr

S

A ds

F =

�

�

�

r r

�

A

r

r

r ri

=

r

r

Wektor elementu

powierzchni

we współrzędnych

sferycznych:

2

sin d d

r

ds i r

q q j

=

r

r

Prawo

Gaussa:

d

d ,

V

S

A V

A s

��

=

�

�

�

�

�

�

r

r r

�

C 01

9

Zadanie 1.7 (2)

Strumień wektora pozycji przez sferę o
promieniu r

0

:

2

2

0

0

S

0 0

sin d d

r

r

r ds

r i i r

p p

q q j

F =

� =

�

=

�

�

��

r r

r r

�

2

3

3

0

0

0 0

sin d d

4

500

r

r

p p

q q j

p

p

=

=

��

Strumień wektora pozycji przez sferę o
promieniu r

0

z wykorzystaniem twierdzenia Gaussa:

0

2

2

V

0 0 0

d

3 sin d d d

r

r v

r

r

p p

q q j

F =

��

=

=

�

�

�

���

r

3

2

1

3

r

r

r

r

�

��=

=

�

r

V

d

r v

F =

��

�

�

�

r

2

d

sin d d d

v r

r

q q j

=

(

)

2

2

(sin

)

1

1

1

sin

sin

r

A

r A

A

A

r

r

r

r

j

q

q

q

q

q j

�

�

�

�� =

+

+

�

�

�

r

2

3

3

0

0

0 0

sin d d

4

500

r

r

p p

q q j

p

p

=

=

=

��

C 01

10

Zadanie 1.8

Obliczyć strumień wektora pozycji przez
powierzchnię
sześcianu o boku a = 5, jeżeli wiadomo, że trzy
jego
krawędzie pokrywają się z dodatnimi półosiami
układu
współrzędnych 0xyz.

rr

Korzystając z prawa Gaussa otrzymuje

się:

{

3

3

V

V

d

3 d 3

375

r v

v a

=

F =

��

=

=

=

�

�

�

�

�

�

r

C 01

11

Zadanie 1.9

Obliczyć strumień wektora
przez
powierzchnię sfery o promieniu r

0

= a.

S

A ds

F =

�

�

�

r r

�

3

4

d

d

3

V

V

A v

v

a

=

��

=

=

�

�

�

�

�

�

r

2

3

5(3

)

x

y

z

A xi

x i

y i

=

+

+

+

r

r

r

r

2

(3 )

5(3

)

1

x

x

y

A

x

y

z

� �

� +

�� = +

+

=

�

�

�

r

0

0

2

2

2

3

0

V

0 0 0

0 0 0

1

d

sin d d d

sin d d d

3

r

r

v

r

r

r

r

p p

p p

q q j

q q j

=

=

�

�

� ���

���

2

d

sin d d d

v r

r

q q j

=

[

]

2

3

3

0

0

0

0

1

4

cos

d

3

3

r

r

p

p

q

j

p

=

-

=

�

C 01

12

Zadanie 1.10

Obliczyć cyrkulację wektora po
ścieżce
wyznaczonej przez boki kwadratu o długości a, z
których dwa leżą na osiach x i y. Należy wybrać
prawoskrętną
cyrkulację względem osi z.

(2

)

x

A

y i

= +

r

r

1

2

3

4

1

2

3

4

d

d

d

d

d

L

L

L

L

L

A l

A l

A l

A l

A l

� =

� +

� +

� +

� =

�

�

�

�

�

r

r

r

r

r

r

r

r

r

r

�

Metoda 1 W oparciu o definicję cyrkulacji

x

y

a

z

0

a

1

L

3

L

2

L

4

L

0

0

0

0

0

0

d

d

( d )

( d )

a

a

x

y

x

y

y

x a

y a

x

a

a

A

xi

A

yi

A

xi

A

yi

=

=

=

=

=

� +

� +

�-

+

�-

=

�

�

�

�

r

r

r

r

r

r

r

r

0

0

0

0

2

d

(2

)

d

(2

)

d

(2

)

d

a

a

a

a

x

x

x

y

x

x

x

y

i i x

y i i y

a i i x

y i i y

=

� +

+

� -

+

� -

+

� =

�

�

�

�

r r

r r

r r

r r

2

2

0

0

2 d

(2

) d

2

2

a

a

x

a

x

a

a a

a

=

-

+

= -

-

=-

�

�

C 01

13

Zadanie 1.10 (2)

W oparciu o twierdzenie

Stokes’a

Metoda 2

d

(

) d

L

S

A l

A

s

�=Ѵ�

�

�

�

r

r

r

r

�

d(2

)

d

2

0

0

x

y

z

z

z

i

i

i

y

A

i

i

x

y

z

y

y

�

� �

+

Ѵ

=

=-

=-

�

� �

+

r

r

r

r

r

r

(2

)

x

A

y i

= +

r

r

d

d d

z

s

x yi

=

r

r

2

0 0

d

(

) d

(

) d d

a a

z

z

L

S

A l

A

s

i i x y

a

�=Ѵ�=-�=-

�

�

�

�

�

r

r

r

r r

r

�