Pojęcie statystycznej

próby losowej

Populacja generalna

(zbiorowość statystyczna)

Populacja statystyczna (skończona lub nieskończona)
badana jest ze względu na pewne cechy(zmienne).
Rozkładem populacji generalnej będziemy nazywać
rozkład badanej cechy w tej populacji. Modelem
matematycznym rozkładu populacji jest rozkład
prawdopodobieństwa pewnej zmiennej losowej skokowej
lub ciągłej. Odpowiednie prawdopodobieństwa w
modelowym rozkładzie zmiennej losowej interpretujemy
jako częstości względne w populacji elementów o
określonych wartościach badanej cechy.
 
Interesujemy się jedynie badaniami statystycznymi
częściowymi. Tak więc, by orzec coś o rozkładzie
populacji, pobieramy z niej do badania częściowego
pewną próbkę statystyczną. Ze względu na
reprezentacyjny charakter próby statystycznej
pozwalający uogólnić jej wyniki na całą zbiorowość,
dopuszczamy jedynie taki dobór próby, który jest

beztendencyjny

(losowy).

Losowość próby oznacza, że wyniki jej można traktować
jako realizację zmiennych losowych o rozkładzie
identycznym z rozkładem populacji.
 
Losową próbę statystyczną z nieskończonej,
hipotetycznej populacji możliwych wyników
eksperymentów (pomiarów) w badaniach przyrodniczych
lub technicznych uzyskuje się drogą obserwacji
niezależnych powtórzeń eksperymentu wykonywanego w
określonych warunkach uwzględniających różne czynniki
wpływające na wynik eksperymentu.
 
Próba prosta ze skończonej populacji jest uzyskiwana
przy zastosowaniu losowania ze zwracaniem.
Dla nieskończonej populacji uzyskuję się próbę prostą
zakładając niezmienne warunki powtarzalnego
doświadczenia i dokonując powtórzeń niezależnych tego
doświadczenia.

Próba prosta

Próba prosta,

może być zdefiniowana jako n-

wymiarowa zmienna losowa (wektor losowy)
X = (X

1

,X

2

,…,X

n

) o własnościach:

 
        X

1

,X

2

,…,X

n

są niezależnymi zmiennymi

losowymi
        Każda zmienna losowa X

i

(i-ty wynik w

próbie) ma rozkład identyczny z rozkładem
populacji.

 

Prezentacja wyników próby

Szeregi rozdzielcze

x

i

n

i

x

1

x

2

x

3

.
.

x

k

 

n

1

n

2

n

3

  

 

n

k

 

 
 

[x

0j

, x

1j

)

n

i

[x

01

, x

11

)

[x

02

, x

12

)

[x

03

, x

13

)

.
.
.

[x

0k

, x

1k

)

 

n

1

n

2

n

3

 

 

 

n

k

 

[x

0j

,

x

1j

)

n

i

15-25
25-35
35-45
45-55
55-65
65-75

10
25
48
30
10

5

 

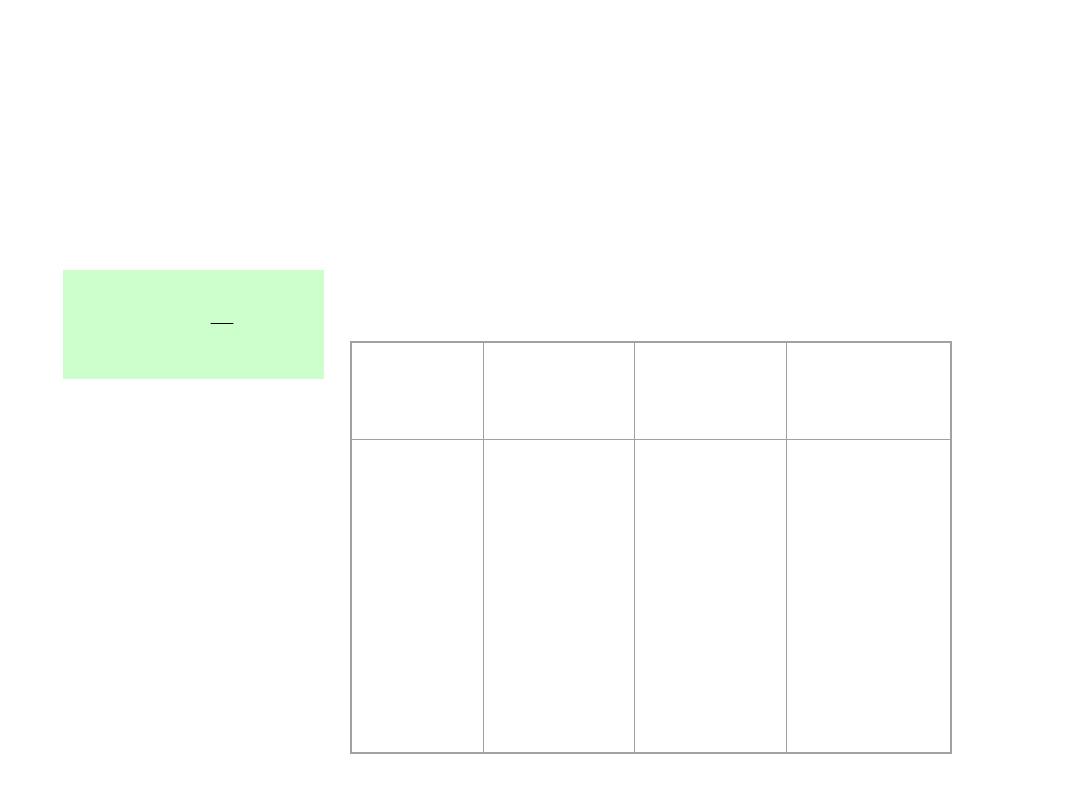
Szereg rozdzielczy wyników próby nazywa się też
często rozkładem empirycznym, gdyż można z
niego uzyskać rozkład procentowy (tzw. Rozkład
częstości). Wyników próby rozdzielonych na k klas,
tzw. szereg skumulowanych liczebności, będący
podstawą tzw. dystrybuanty empirycznej określonej
jako







r

j

j

r

n

n

n

x

F

1

1

1

)

(

dla r = 1,2,…,k.

 

j

x

1j

n

j

/n

F

n

(x

1j

)

1
2
3
4
5
6

25
35
45
55
65
75

0,083

3

0,208

4

0,333

3

0,250

0

0,083

3

0,041

7

0,0833
0,2917
0,6250
0,8750
0,9583
1,0000

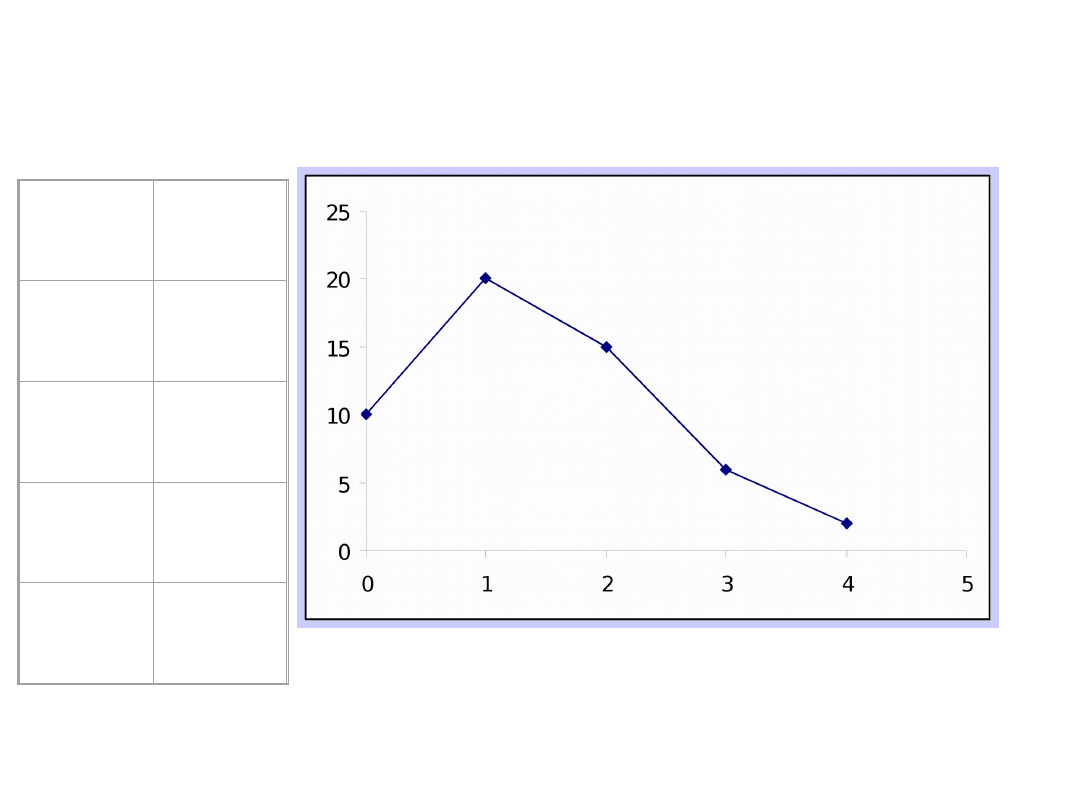
Graficzna prezentacja wyników

próby

 
 

0

10

1

20

2

15

3

6

4

2

 

Wielobok liczebności

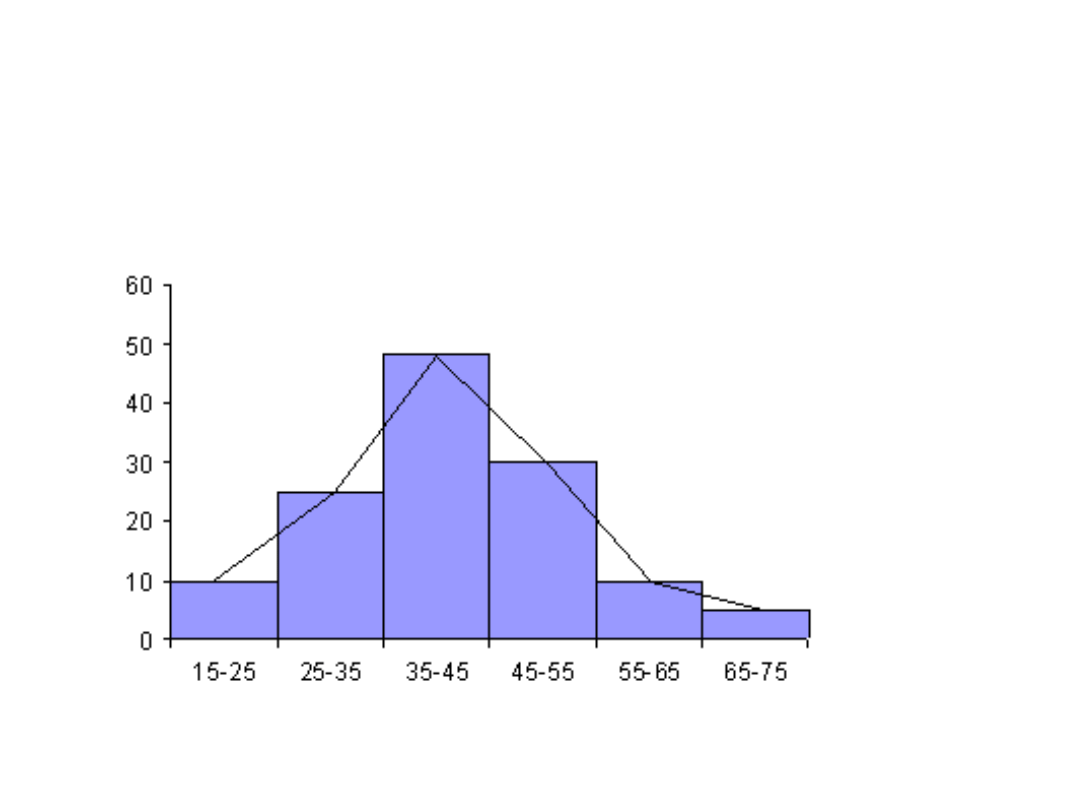
Histogram i diagram

 

 
 

Dwie cechy w populacji

Jeżeli w populacji generalnej bada się jednocześnie dwia
cechy X i Y , to matematycznym modelem rozkładu
populacji jest rozkład prawdopodobieństwa
dwuwymiarowej zmiennej losowej ( X, Y) . Wyniki n-
elementowej próby stanowią wtedy pary liczb (x

i

, y

i

)

dla i=1,2,…,n .
Dla dużych liczebności prób prezentacji wyników próby z
dwuwymiarowej populacji dokonuje się w postaci tzw.
tablicy korelacyjnej, stanowiącej dwudzielną kombinację
dwóch szeregów rozdzielczych – cechy X oraz Y . Tablica
korelacyjna
(dla cech ciągłych ) ma postać

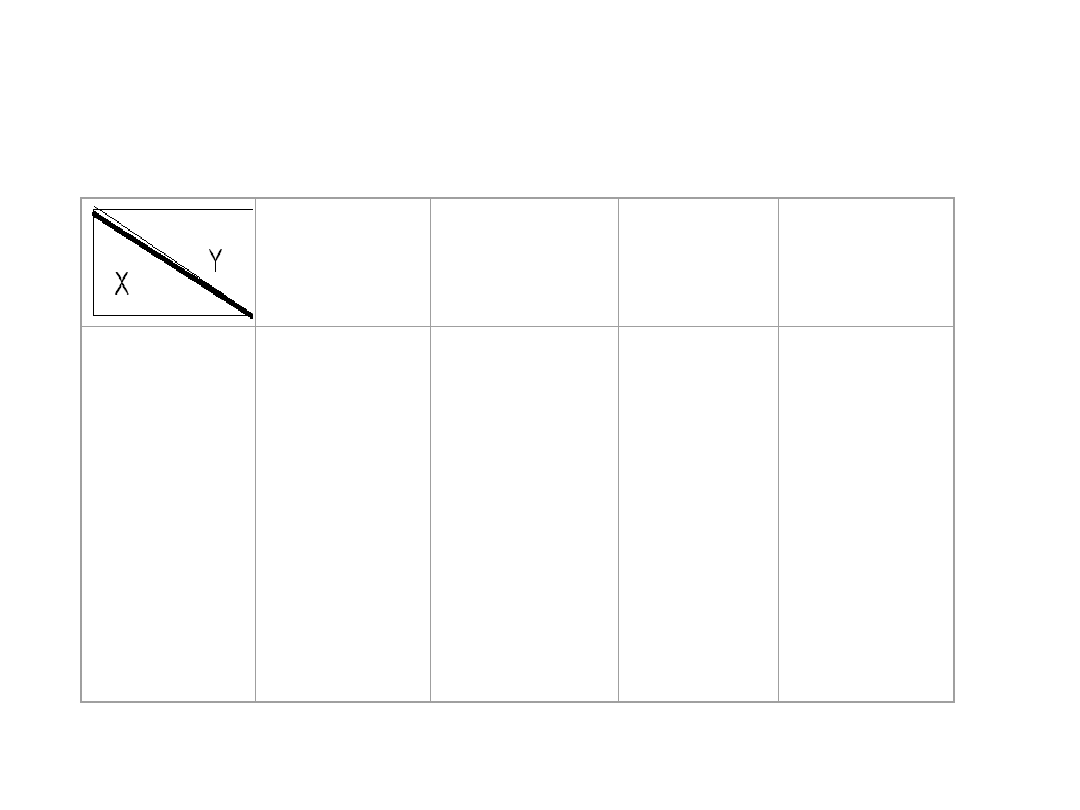
Tablica korelacyjna

 

 

[y

01

,

y

11

)

 

[y

0 2

, y

1 2

)

 

 

[y

0 l

, y

1l

)

 

[x

01

, x

11

)

[x

02

, x

12

)

[x

03

, x

13

)

.
.
.

[x

0k

, x

1k

)

 

n

11

n

21

n

31

 

 

 

n

k1

 

n

1 2

n

2 2

n

3 2

 

 

 

n

k 2

 

 

n

1 l

n

2 l

n

3 l

 

 

 

n

k l

 

 

Obliczanie wartości statystyk z

próby

 

Jeżeli przez X = (X

1

,X

2

,…X

n

) oznaczymy n-elementową

próbę losową a realizację próby (wektor liczbowych
wyników próby) przez x = (x

1

,x

2

,…x

n

) to statystyką Z

n

nazywamy dowolną funkcję próby X
o wartościach rzeczywistych Z

n

= g(X)

 
Z

n

jest zmienną losową ma więc swój rozkład

prawdopodobieństwa.
 
Realizację zmiennej losowej Z

n

będącej statystyką

nazywamy wartością statystyki i oznaczamy
symbolem z

n

= g(x)

 
Statystyki z próby dzielimy na miary skupienia
(tendencji centralnych), miary rozproszenia (rozrzutu,
dyspersji), miary współzależności (korelacji).

Miary skupienia









n

i

r

i

r

r

X

n

X

A

1

1

Moment zwykły rzędu r









n

i

i

X

n

X

A

1

1

1









n

i

i

X

n

X

A

1

2

2

2

1

 

Dla r = 1 średnia arytmetyczna z próby.

Dla r = 2 średnia kwadratowa z próby.

średnia arytmetyczna z

próby

Dla konkretnych wyników próby x = (x

1

,x

2

,…x

n

)







n

i

i

x

n

x

1

1

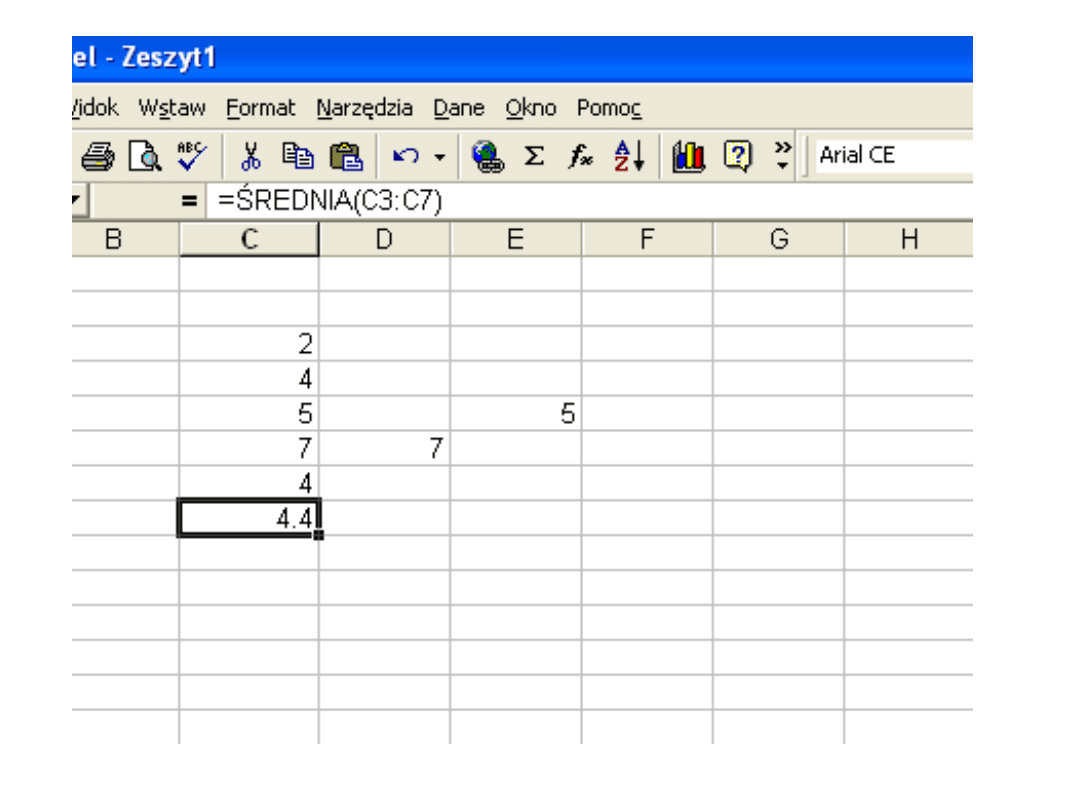
Jeżeli mamy dla dużych prób, których wyniki
pogrupowano w szereg rozdzielczy o k klasach.

 
 

 

Wartość średniej wygodniej jest obliczać jako
średnią ważoną







k

j

j

j

n

x

n

x

1

0

1

 

 

[x

0j

,

x

1j

)

n

i

x

o

j

x

o

j

n

j

15-25
25-35
35-45
45-55
55-65
65-75

10
25
48
30
10

5

20
30
40
50
60
70

200
750

1600
1500

600
350



120

 

5000

(x

o

j

jest środkiem

klasy)

Odchylenia od średniej

arytmetycznej

Ważną własnością wartości średniej arytmetycznej z
próby jest, że suma odchyleń od niej dla wszystkich
wyników x

i

w próbie wynosi zero :

 

 

























n

i

n

i

i

i

n

i

i

n

i

i

x

x

x

n

x

x

x

1

1

1

1

0

)

(

statystyki pozycyjne

Jako miarę tendencji centralnej empirycznego rozkładu
uzyskanego w próbie występują też, statystyki
pozycyjne. Wyniki z próby należy uporządkować w
niemalejący ciąg liczb.

)

(

)

2

(

)

1

(

...

n

x

x

x







Statystyką pozycyjną rzędu k nazywamy taką zmienną
losową Z

(k)

n

,

której wartości zajmują k-te miejsce w uporządkowanym,
niemalejącym ciągu wyników n-elementowej próby.

Liczbę k nazywamy rzędem lub rangą statystyki
pozycyjnej Z

(k)

k

statystyki pozycyjne cd.

Statystyki pozycyjne dzielimy na skrajne oraz na
środkowe (kwantyle z próby). Statystykę Z

(k)

k

nazywamy

skrajną jeżeli:
 

Statystykę Z

(k)

k

nazywamy środkową jeżeli:

 

Środkowe statystyki pozycyjne zwane kwantylami z
próby rzędu p
Rząd k statystyki pozycyjnej będącej kwantylem rzędu p
określa się
 
k =[np] lub k =[np] + 1 .

1

lub

0

lim

lim













n

k

n

k

n

n

}

1

,

0

{

lim









p

n

k

n

Mediana

Statystyka pozycyjna szczególna

)

(

2

n

n

Z

)

(

2

1

n

n

Z



dla parzystej liczby
obserwacji

dla nieparzystej liczby obserwacji

Środkowa statystyka pozycyjna –
mediana z próby (kwantyl z próby rzędu
½).

n

n

n

n

n

n

2

1

2

1

2

lim

lim















Mediana_2

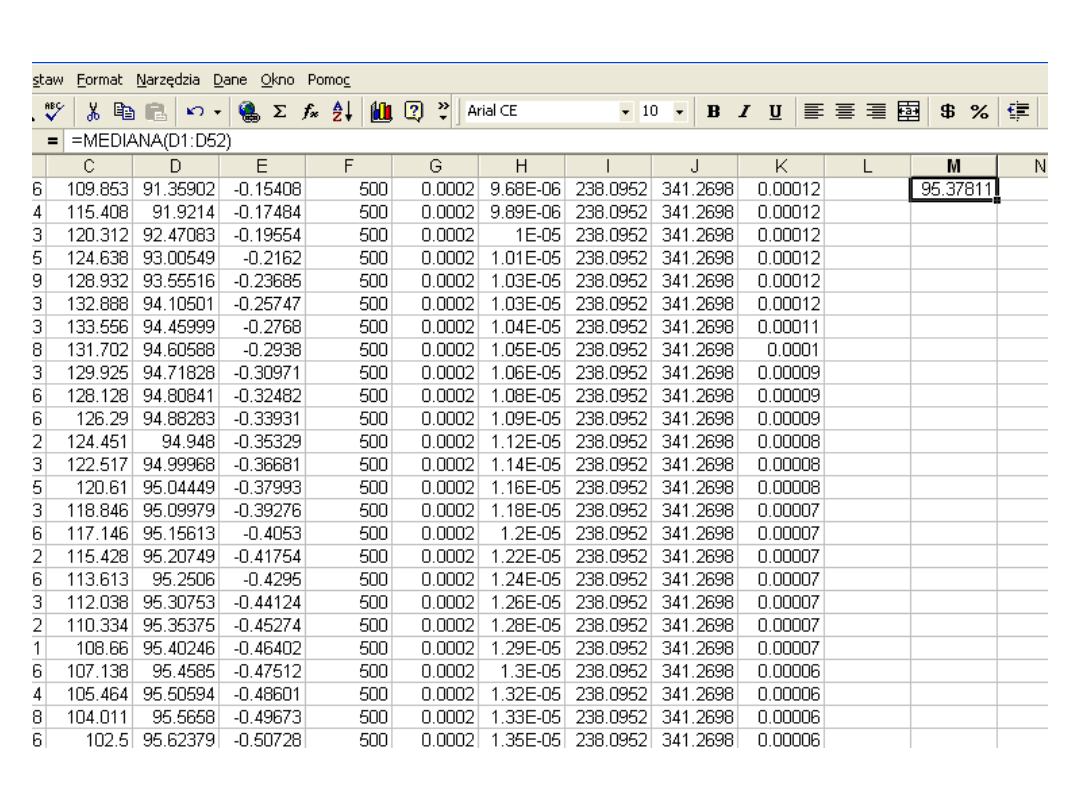
Dla dużych prób, których wyniki pogrupowano w szereg
rozdzielczy o k klasach medianę z próby wyznacza się ze
wzoru interpolacyjnego:

 
gdzie r

m

oznacza numer przedziału klasowego, w którym

znajduje się me (jest to przedział, w którym skumulowana
liczebność n

j

osiąga n/2 , x

om

– początek przedziału

klasowego, w którym znajduje się me ; n

m

– liczebność

przedziału r

m

, h – rozpiętość (długość) przedziałów

klasowych w szeregu rozdzielczym.



























1

1

2

2

m

r

j

j

om

n

n

h

x

me

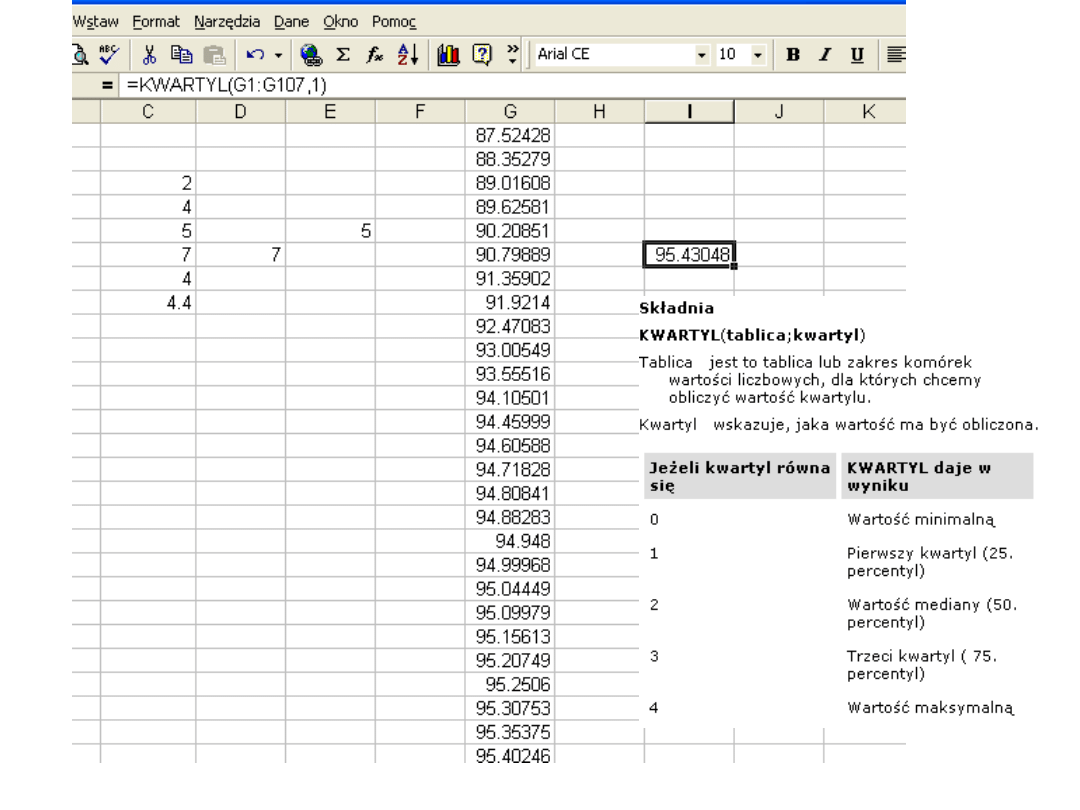
Kwantyle

Dla dowolnej liczby p ( 0 < p < 1 ) kwantylem rzędu p
rozkładu zmiennej losowej X nazywamy liczbę x

p

spełniającą nierówności:
 

 
Jeżeli istnieje (dla zmiennej losowej skokowej) więcej niż
jedna taka liczba x

p

, to przyjmuje się najmniejszą z nich.

Dla zmiennej ciągłej mamy równość p=F(x

p

).

Podstawowymi

kwantylami

ważnymi zmiennej losowej X

w praktyce statystycznej są:
Centyle (p = 0.01 i 99 wielokrotności tej liczby )
Decyle (p = 0.1 i 9 wielokrotności tej liczby )
Kwartyle (p = 0.25 i 3 wielokrotności tej liczby )
 
Najczęściej używanym kwantylem jest x

0.5

mediana









1

oraz

p

x

X

P

p

x

X

P

p

p











Miary rozproszenia

Rozstęp

Wariancja z próby

Odchylenia standardowe
z próby

min

max

)

(

1

)

(

X

X

Z

Z

R

n

n

n







































n

i

i

n

i

i

X

X

X

n

X

n

S

S

1

___

2

1

2

__

2

2

1

1

)

(

Dla małych
prób



























n

i

X

X

n

S

n

n

S

1

2

___

2

2

1

1

1

ˆ

Miary rozproszenia 2













n

i

m

X

n

S

1

2

2

*

1

Jeżeli znana jest wartość średniej populacji
generalnej m





















k

j

j

j

n

x

n

s

x

1

2

__

0

2

1

Dla danych z szeregu rozdzielczego

[x

0j

,

x

1j

)

n

i

15-25
25-35
35-45
45-55
55-65
65-75

10
25
48
30
10

5

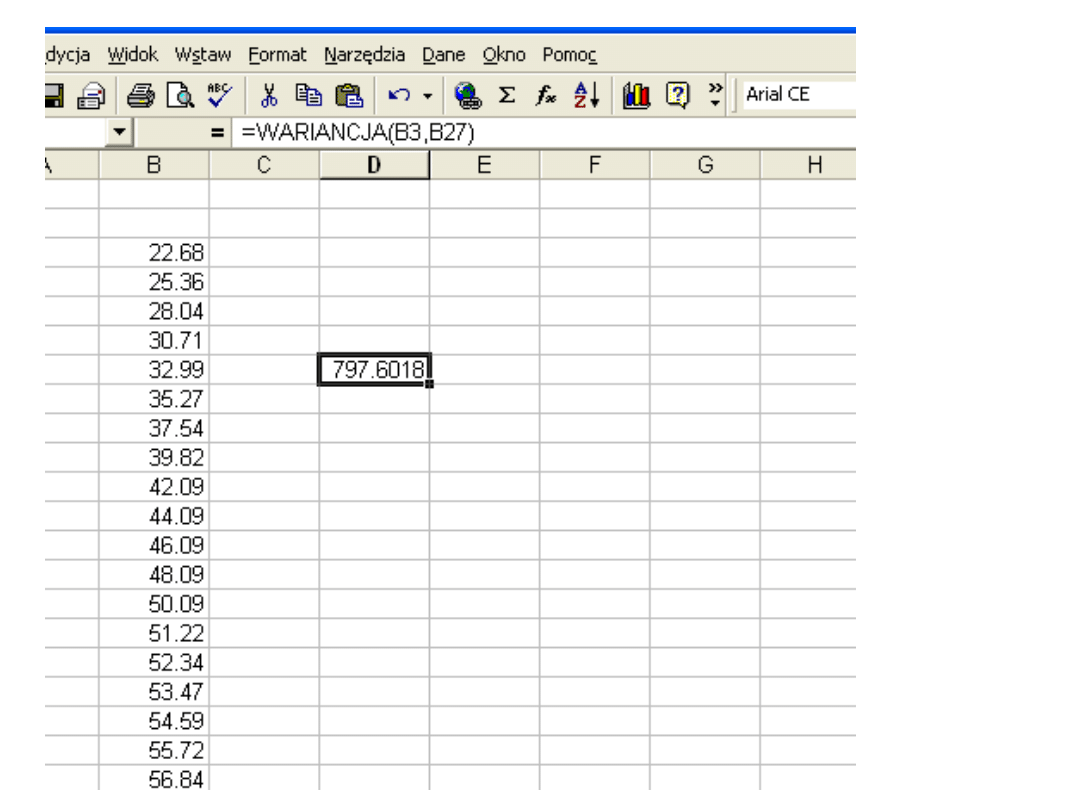
WARIANCJA

Ocenia wariancję na podstawie próbki.

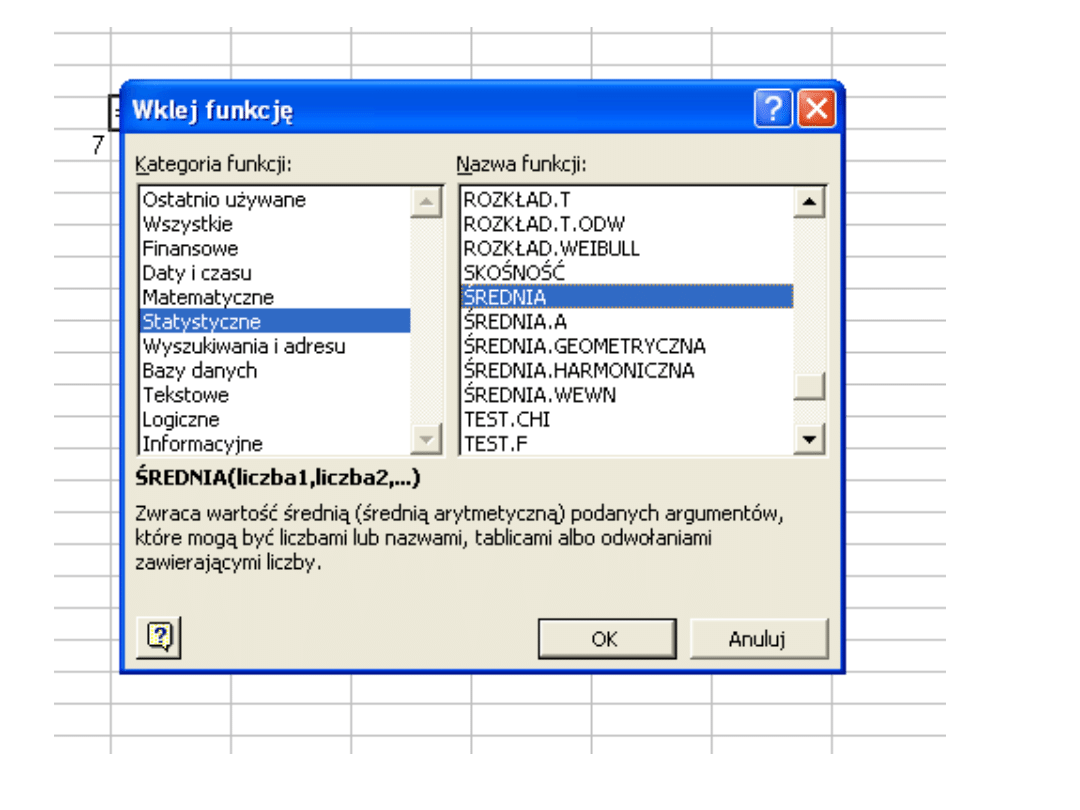
Składnia

WARIANCJA(liczba1;liczba2;...)

Liczba1;liczba2;...   to od 1 do 30 argumentów liczbowych odpowiadających
próbce z populacji.

Uwagi

•Funkcja WARIANCJA przyjmuje, że jej argumenty są próbką z populacji.
Jeżeli nasze dane reprezentują całą populację, należy obliczyć wariancję
stosując funkcję WARIANCJA.POPUL.

•Wartości logiczne, takie jak PRAWDA i FAŁSZ oraz tekst są ignorowane. Jeśli
wartości logiczne i tekst nie mają być ignorowane, użyj funkcji arkusza
WARIANCJA.A.

•Funkcja WARIANCJA używa następującego wzoru:

Excel - help

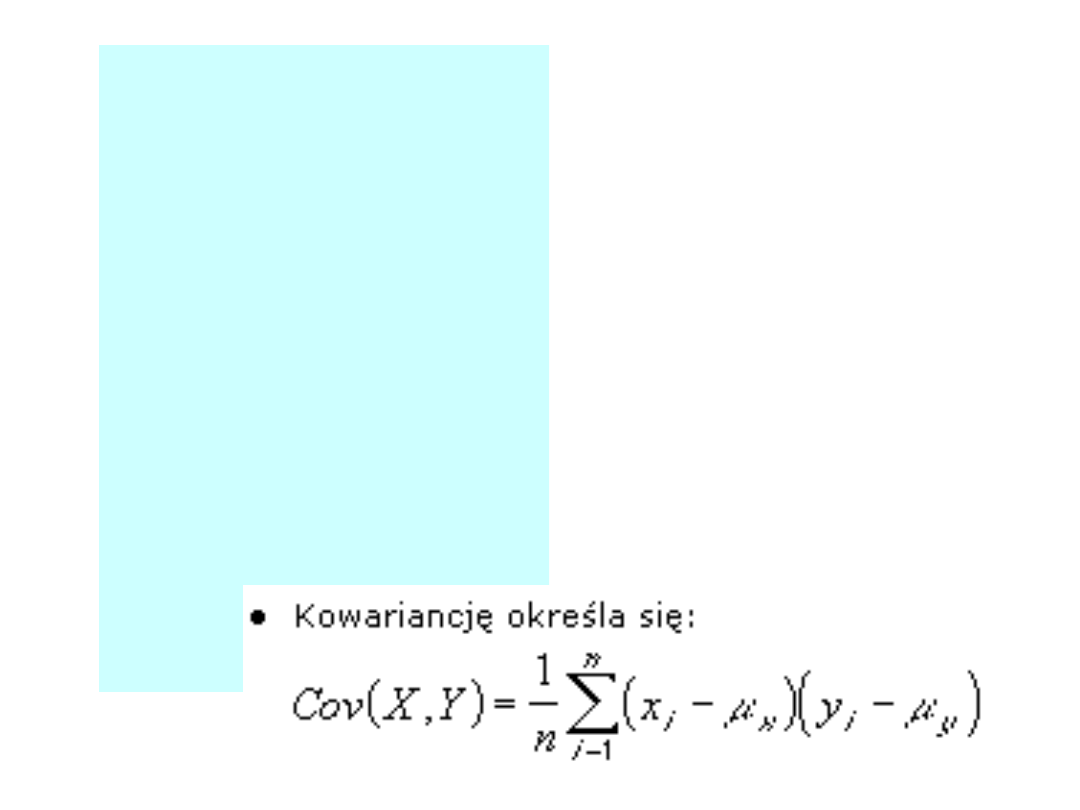
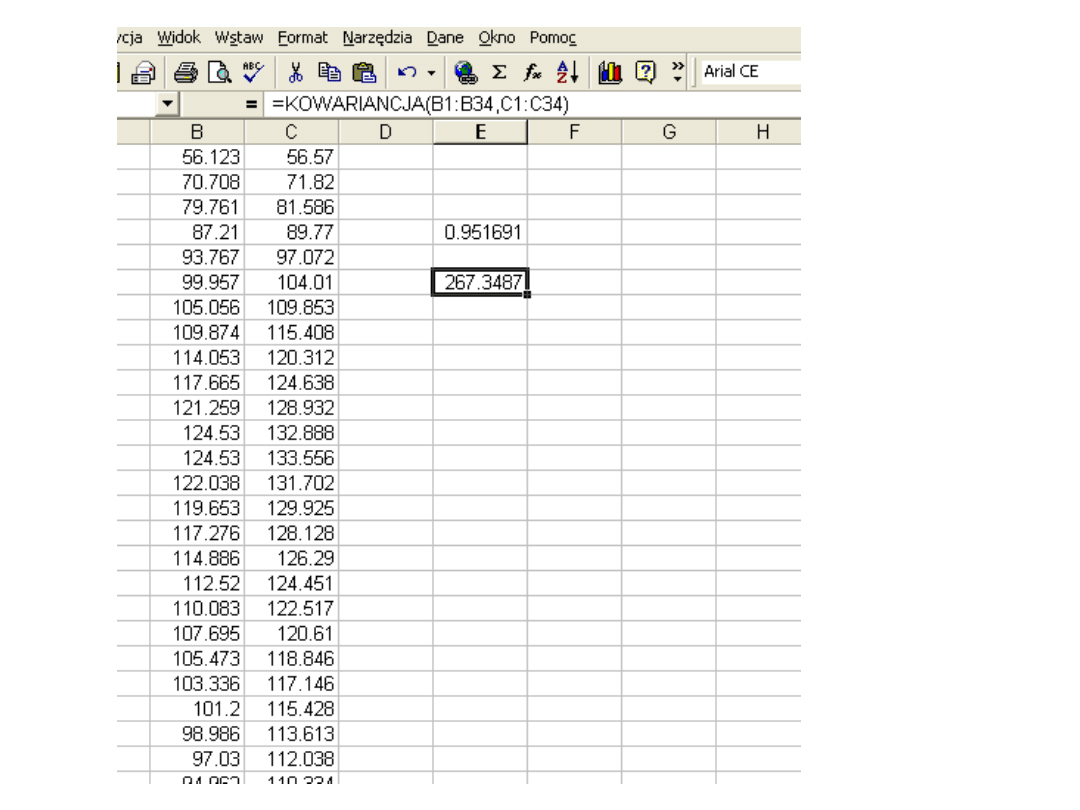
KOWARIANCJA

Podaje wartość kowariancji, tzn.

średniej z iloczynów odchyłek

każdej pary punktu danych. Należy

używać kowariancji w celu

określenia zależności pomiędzy

dwoma zbiorami danych. Na

przykład można sprawdzić, czy

większe przychody związane są z

wyższym poziomem wykształcenia.

Składnia

KOWARIANCJA(tablica1;tablica
2)

Tablica1   jest pierwszą komórką
zakresu liczb.

Tablica2   jest drugą komórką
zakresu liczb.

Współczynnik korelacji z

próby















 



































n

i

n

i

i

i

n

i

i

i

y

x

n

i

i

i

y

y

x

x

y

y

x

x

s

s

y

y

x

x

n

r

1

1

2

2

1

1

1



 























n

i

n

i

i

i

n

i

i

i

y

y

x

x

y

x

n

y

x

1

1

2

2

1

Współczynnik korelacji cd.

y

x

k

s

l

sl

l

s

s

ns

n

y

y

x

x

r



 







1

1

0

0

)

)(

(

 

 
 

 

 

 

 

 

 

18
15
13
14
16
14

42
56
61
49
50
42

3
0
-2
-1
1
-1

-8
6
11
-1
0
-8

-24
0
-22
1
0
8

9
0
4
1
1
1

64
36
121
1
0
64

90

300

 

 

 

 

 

i

x

i

y

x

x

i



y

y

i



)

)(

(

y

y

x

x

i

i





2

)

(

y

y

i



2

)

(

x

x

i



-37

16

286

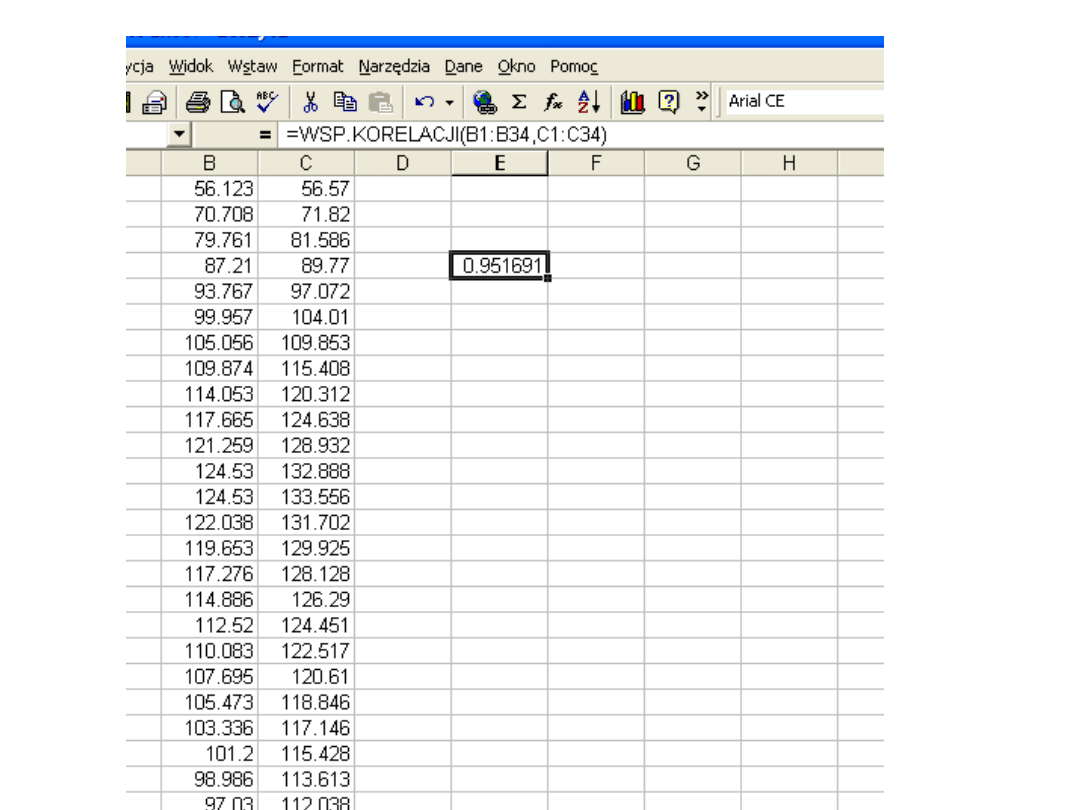
WSP.KORELACJI

Podaje wartość współczynnika korelacji zakresów

komórek tablica1 i tablica2 . Współczynnik korelacji

jest wykorzystywany do wyznaczania zależności

pomiędzy dwoma własnościami. Na przykład, można

sprawdzić zależność między średnią temperaturą

danej miejscowości, a używaniem klimatyzatorów.

Składnia

WSP.KORELACJI(tablica1;tablica2)

Tablica1   jest to zakres komórek zawierających
wartości.

Tablica2   jest to drugi zakres komórek zawierających
wartości.

Uwagi

•Argumenty powinny być liczbami, nazwami, tablicami
lub adresami zakresów zawierających liczby.

•Jeśli argument w postaci tablicy lub zakresu zawiera
tekst, wartości logiczne lub komórki puste, to wartości
takie są pomijane, jednakże uwzględnia się komórki z
wartościami zerowymi.

•Jeśli zakresy tablica1 i tablica2 mają różne liczby
punktów danych, to funkcja WSP.KORELACJI zwraca
wartość błędu.