Teoria Obwodów
dr inż. Stanisław Hałgas
p.103 al.Politechniki 11
tel. 631-25-22
stanislaw.halgas@p.lodz.pl
GP wtorek 12-13
Teoria Obwodów
dr inż. Stanisław Hałgas
p.103 al.Politechniki 11
tel. 631-25-22
stanislaw.halgas@p.lodz.pl
GP wtorek 12-13
Literatura
• Tadeusiewicz M.: Teoria obwodów. Część I.
Wydawnictwo Politechniki Łódzkiej, Łódź 2000.
• Tadeusiewicz M. i inni: Teoria obwodów.
Zadania. Wydawnictwo Politechniki Łódzkiej,
Łódź 1999
• Osiowski J., Szabatin J.: Podstawy teorii
obwodów. T.I, II WNT, Warszawa 1995.
• Krakowski M.: Elektrotechnika teoretyczna.
T.I, PWN Warszawa, 1999.
• Osowski S. i inni: Teoria obwodów.
Politechnika Warszawska – podręcznik
multimedialny
Program wykładu
•
Stan nieustalony w obwodach drugiego rzędu w ujęciu
klasycznym.
•
Równania stanu obwodów.
•
Przekształcenie Laplace’a. Analiza obwodów metodą
operatorową.
•
Czwórniki. Równania opisujące właściwości czwórników.
Czwórniki odwracalne i symetryczne, połączenia
czwórników.
•
Transmitancja operatorowa i widmowa (interpretacja zer
i biegunów). Odpowiedź jednostkowa i impulsowa układu.
•
Układy trójfazowe symetryczne. Układy trójfazowe
niesymetryczne. Składowe symetryczne.
•
Podstawy topologii obwodów elektrycznych.
Zaliczenie
• trwa 1.5 godziny i obejmuje 3
pytania teoretyczne oraz 3
zadania rachunkowe.
• Aby zdać należy rozwiązać 50%
pytań teoretycznych i 50% zadań.
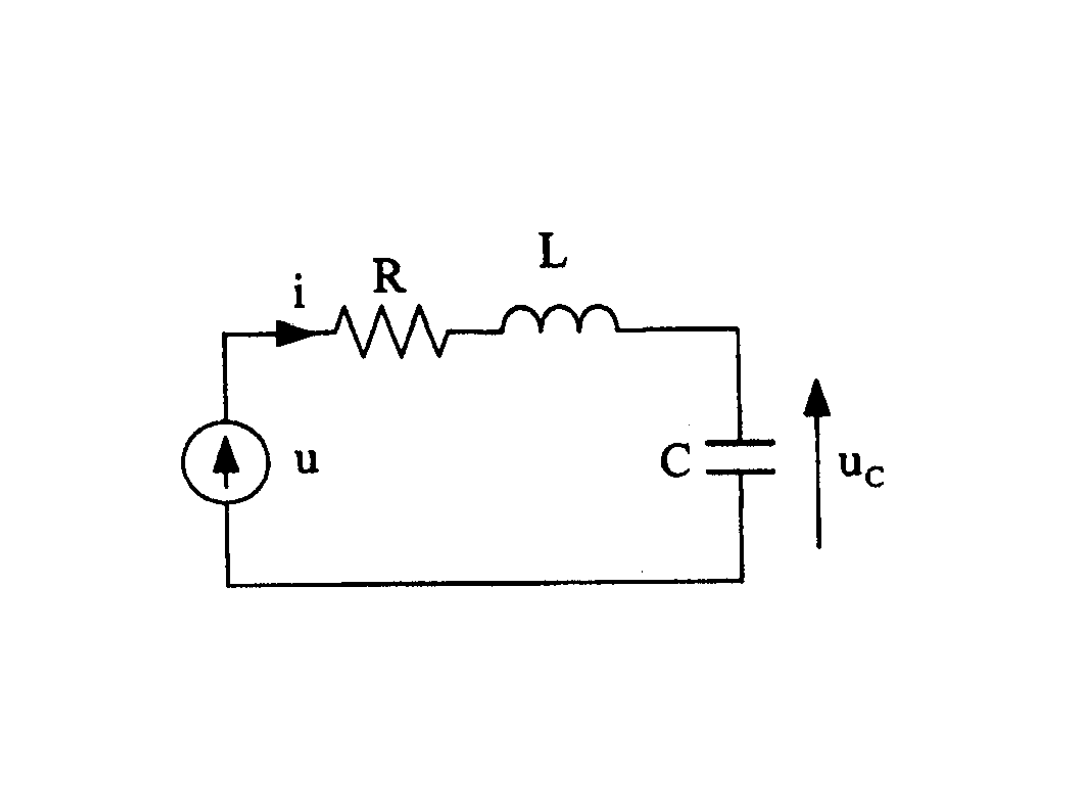
Stan nieustalony w
szeregowym obwodzie
RLC
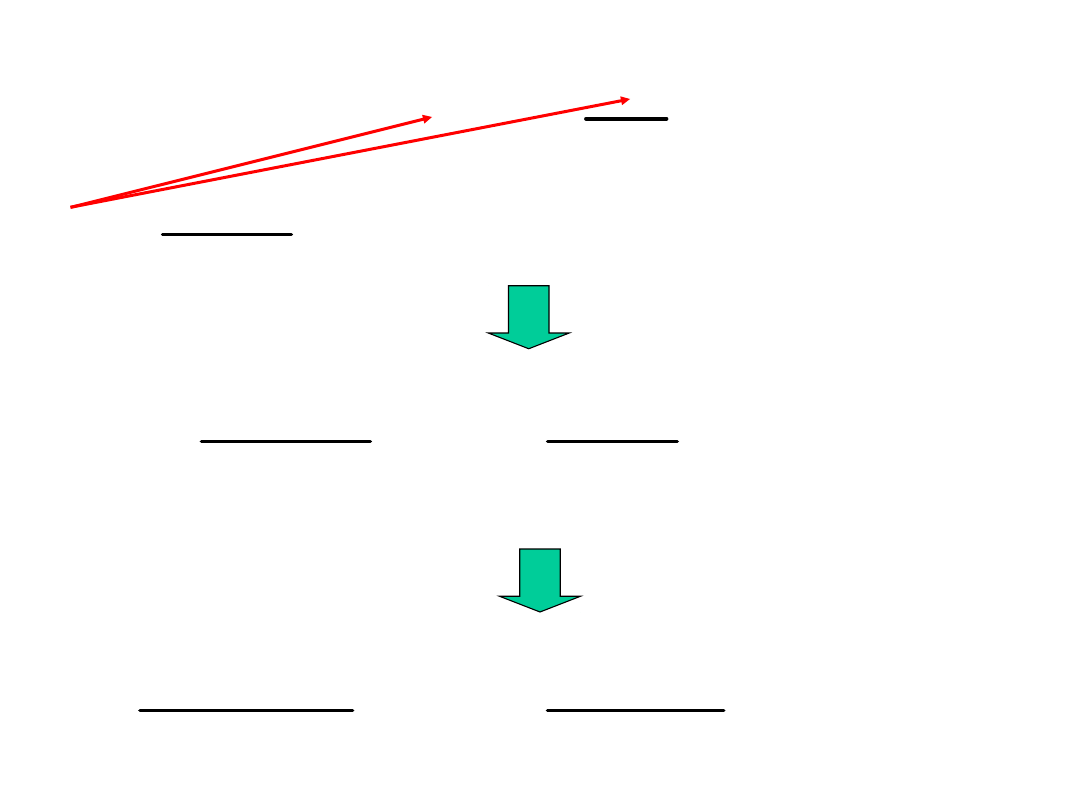
NP
K
u
u
t
i
L
Ri
C
d
d
t
u
C
i
C
d
d
0
d
d
d
d
2
2
S
S
S
C
C
C
u
t
u
RC
t
u
LC
RJ
RN
u
u
dt
du
RC
dt
u
d
LC
C
C
C
2
2
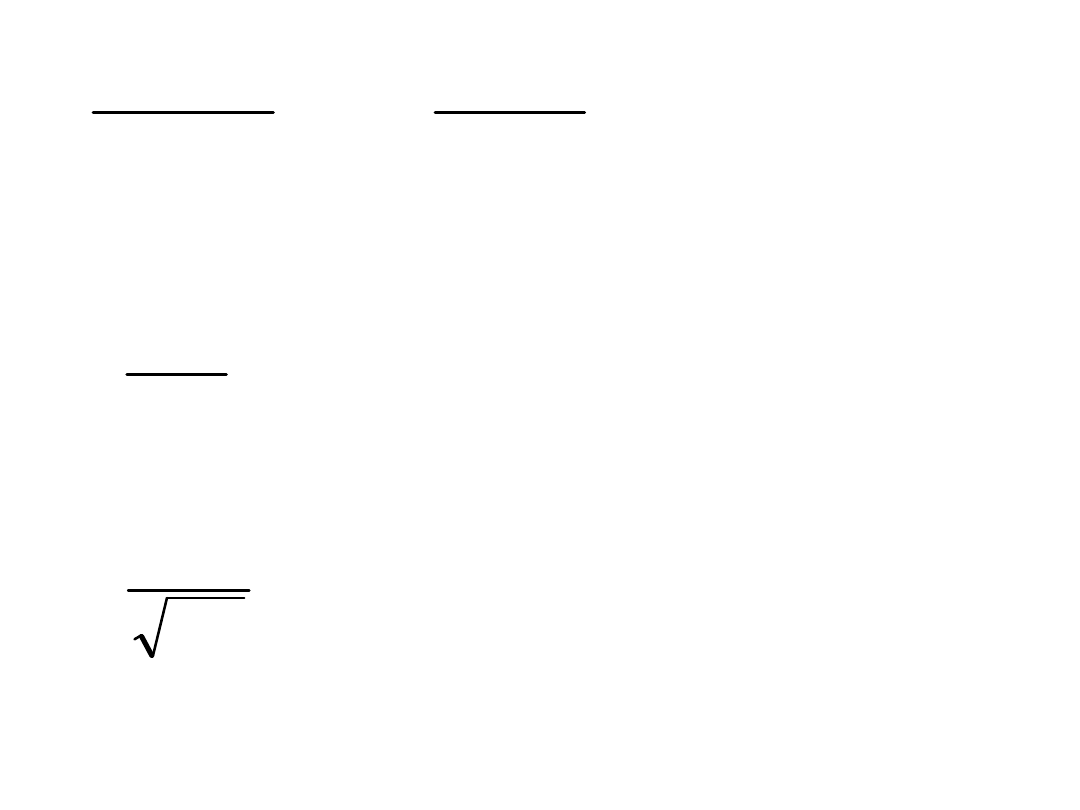
0
d
d
2
d
d
2
2
2
S
S
S
C
n
C
C
u
t
u
t
u
L
R
2
C
1
L
n
- stała tłumienia
[1/s]
- pulsacja drgań
nietłumionych [1/s]
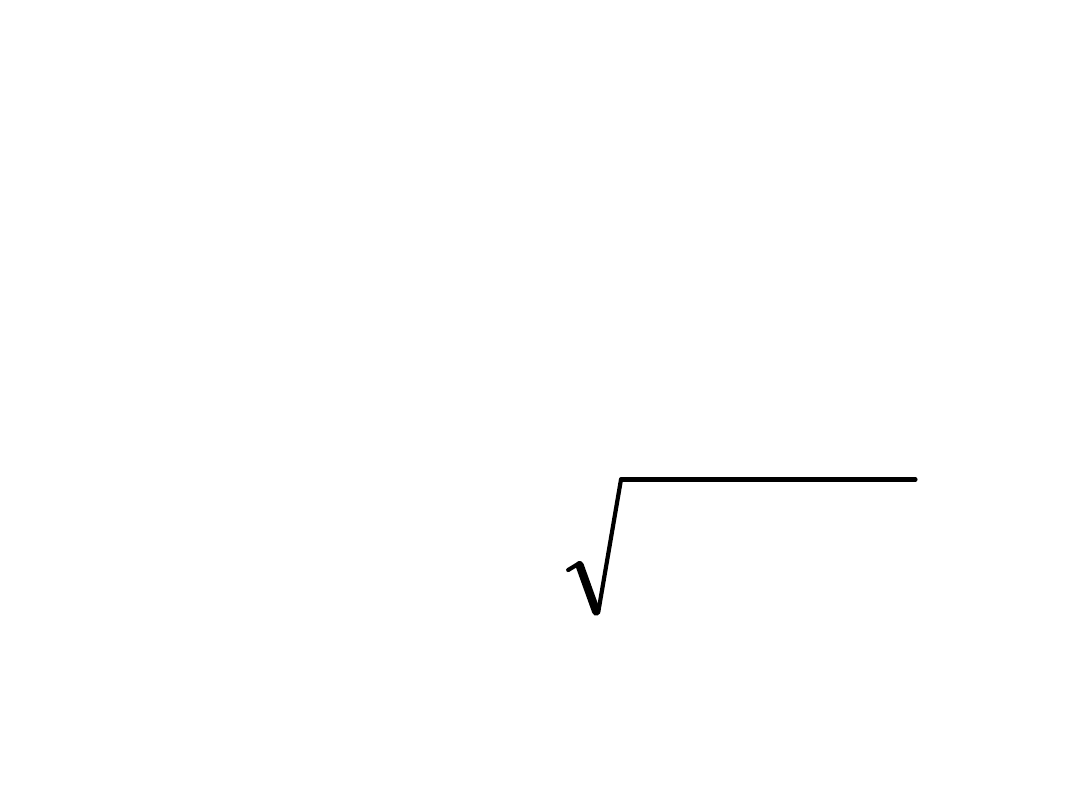
Rozwiązanie RJ zależy od
pierwiastków równania
charakterystycznego
0
s
2
s
2
n
2
2
2
2
1
n
,
s
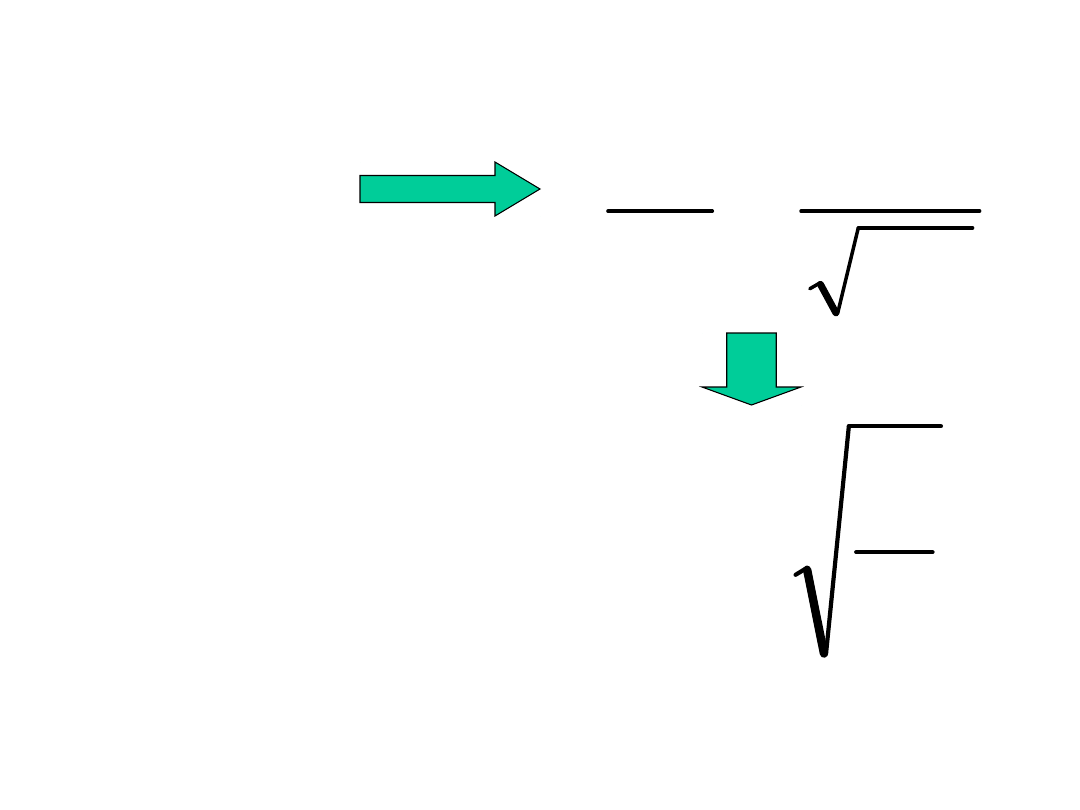
Rozróżniamy trzy przypadki
n
C
L
R 2
LC
1
L
2
R
- dwa różne pierwiastki
rzeczywiste, ujemne
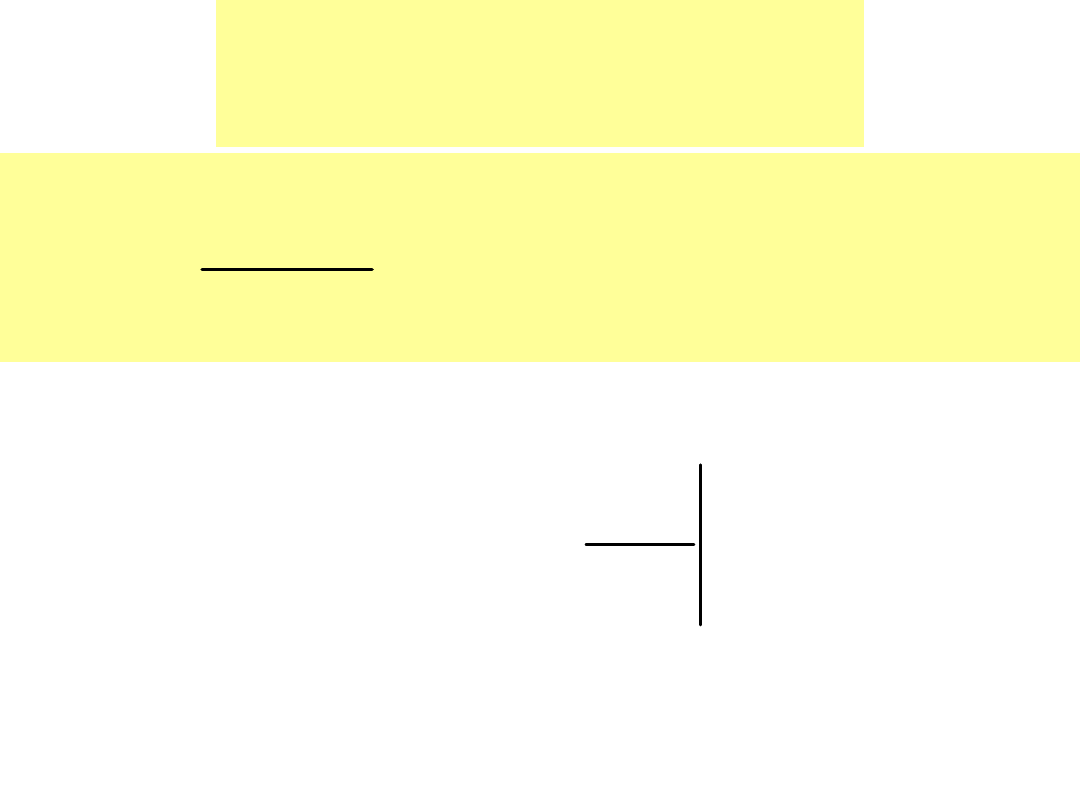
t
s
t
s
C
A
A
u
S
2
1
e
e
2
1
t
s
t
s
C
s
s
A
s
A
C
t
u
C
i
S
2
1
e
e
d
d
2
2
1
1
A
1
i A
2
- stałe zależne od w.
początkowych
0
t
c
c
dt
du
oraz
0
u
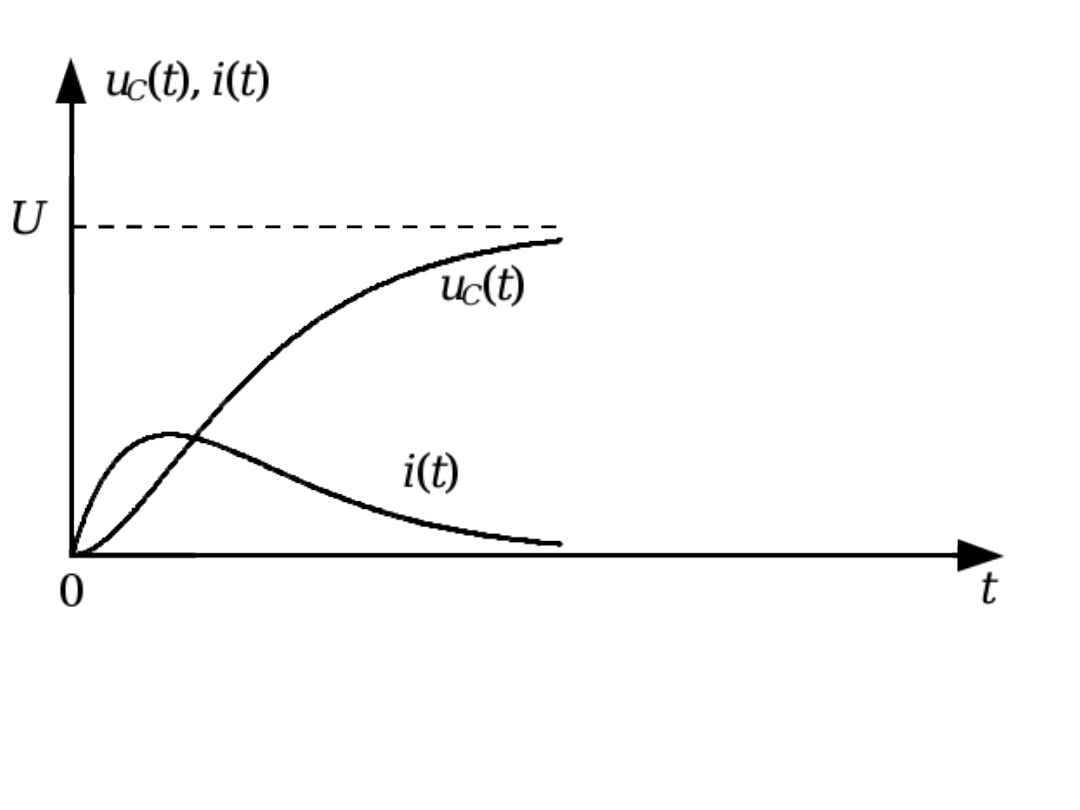
Przebiegi napięcia i prądu mają
charakter aperiodyczny
i zanikają
do zera dla
t
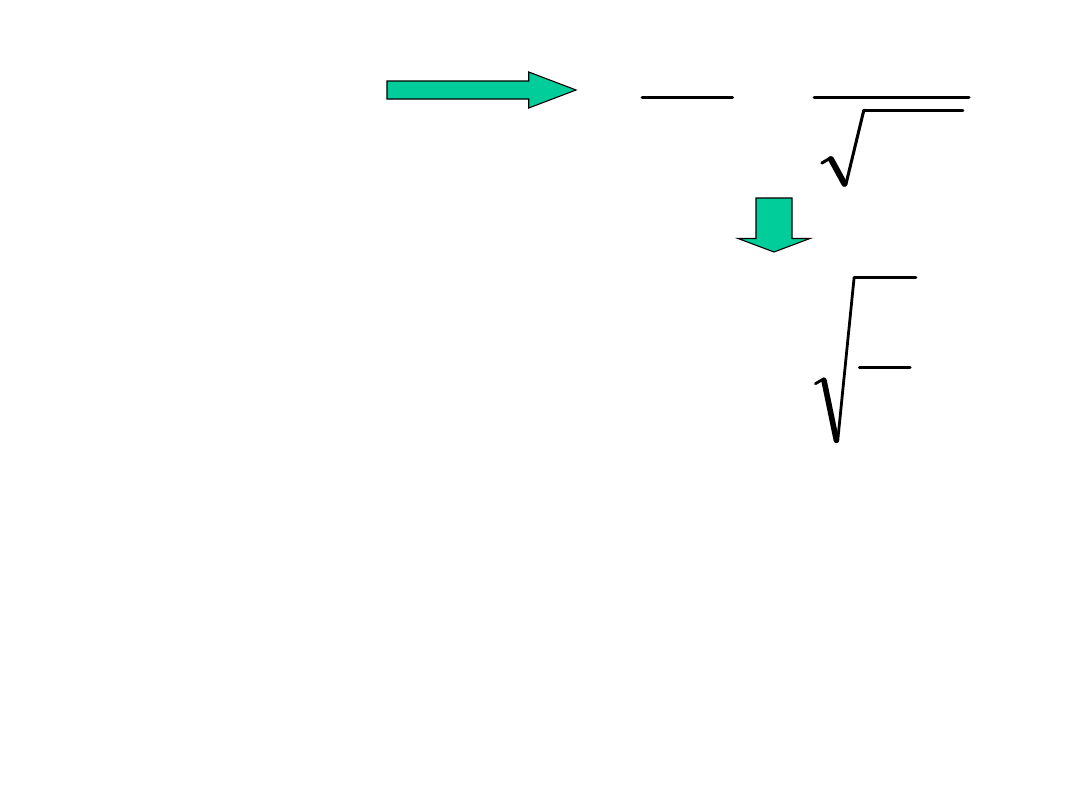
n
LC
1
L
2
R
C
L
2
R
obydwa pierwiastki równania
charakterystycznego są jednakowe,
rzeczywiste i ujemne
2
1
s
s
t
C
t
A
A
u
S
2
1
e
)
(
t
C
S
t
A
A
A
C
t
u
C
i
S
2
1
2
e
)
(
d
d
Przebiegi napięcia i prądu mają
charakter aperiodyczny graniczny
i zanikają do zera dla
t
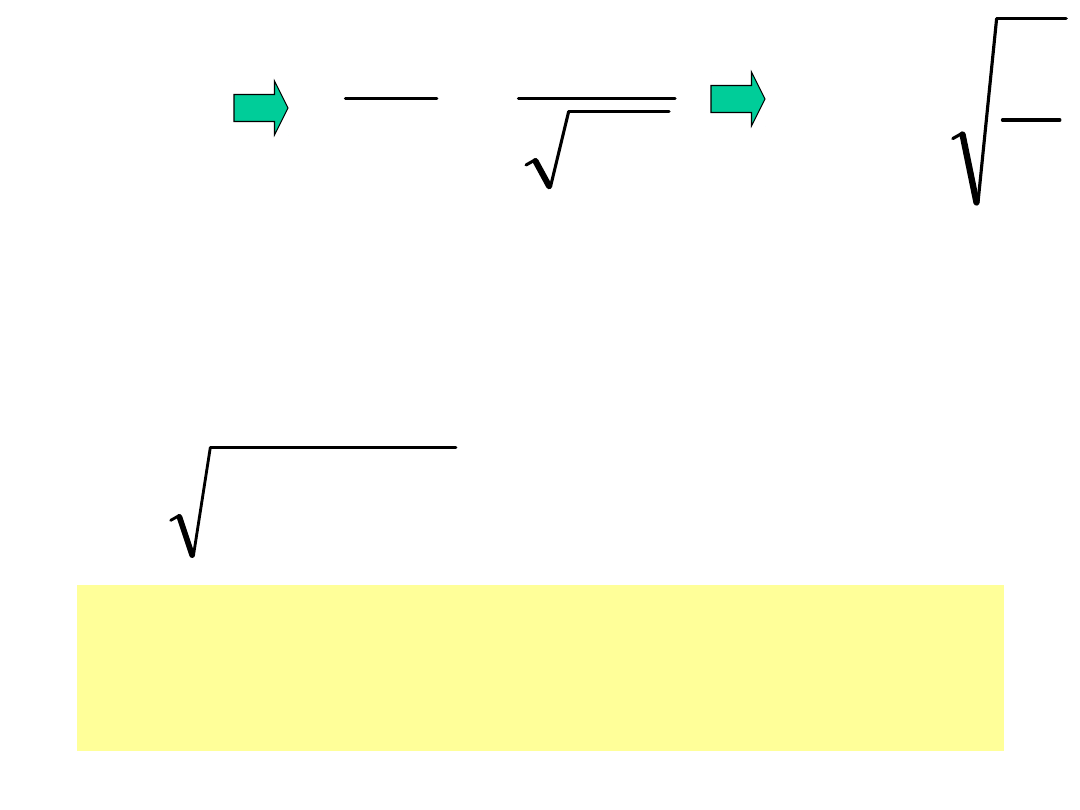
n
LC
1
L
2
R
C
L
2
R
- dwa pierwiastki zespolone
sprzężone
0
2
,
1
j
s
2
2
n
0
- pulsacja drgań
własnych
)
t
A
u
t
C
S
0
(
sin
e
A i - stałe
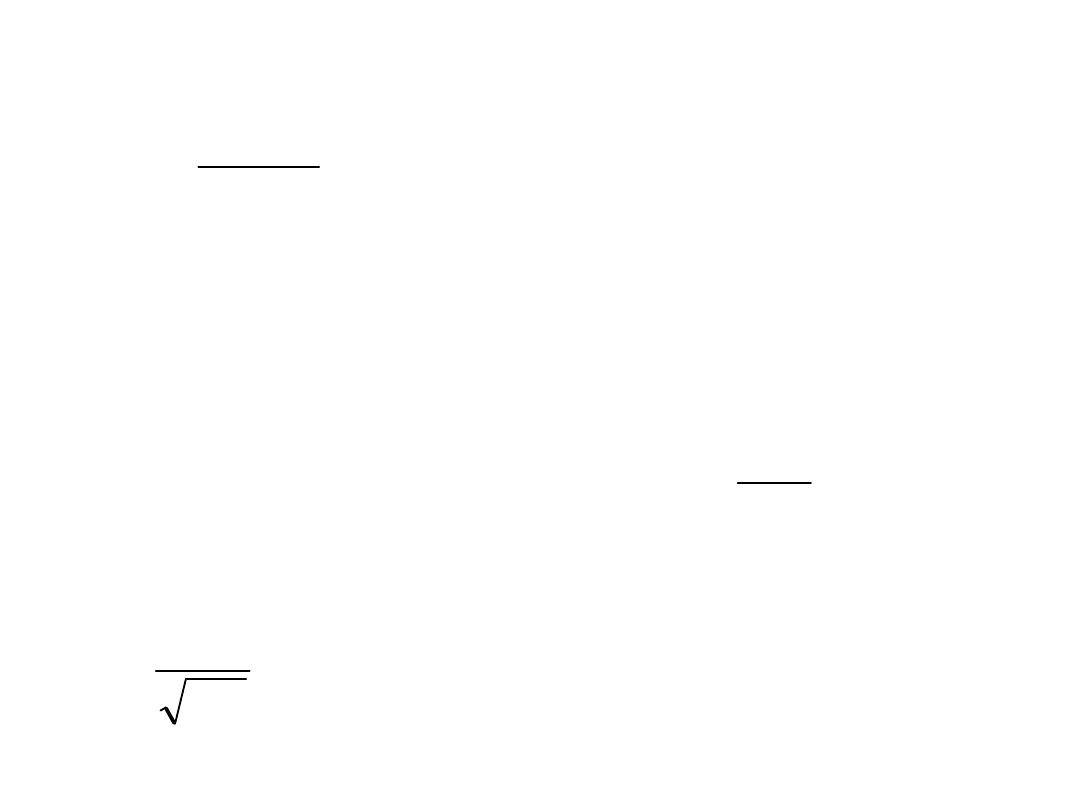
t
0
0
0
C
e
)
(
cos
)
(
sin
-
A
t
d
u
d
S
t
t
C
C
i
S
0
tg
arc
t
0
0
s
e
t
cos
cos
t
sin
sin
LC
1
CA
i
ozn.
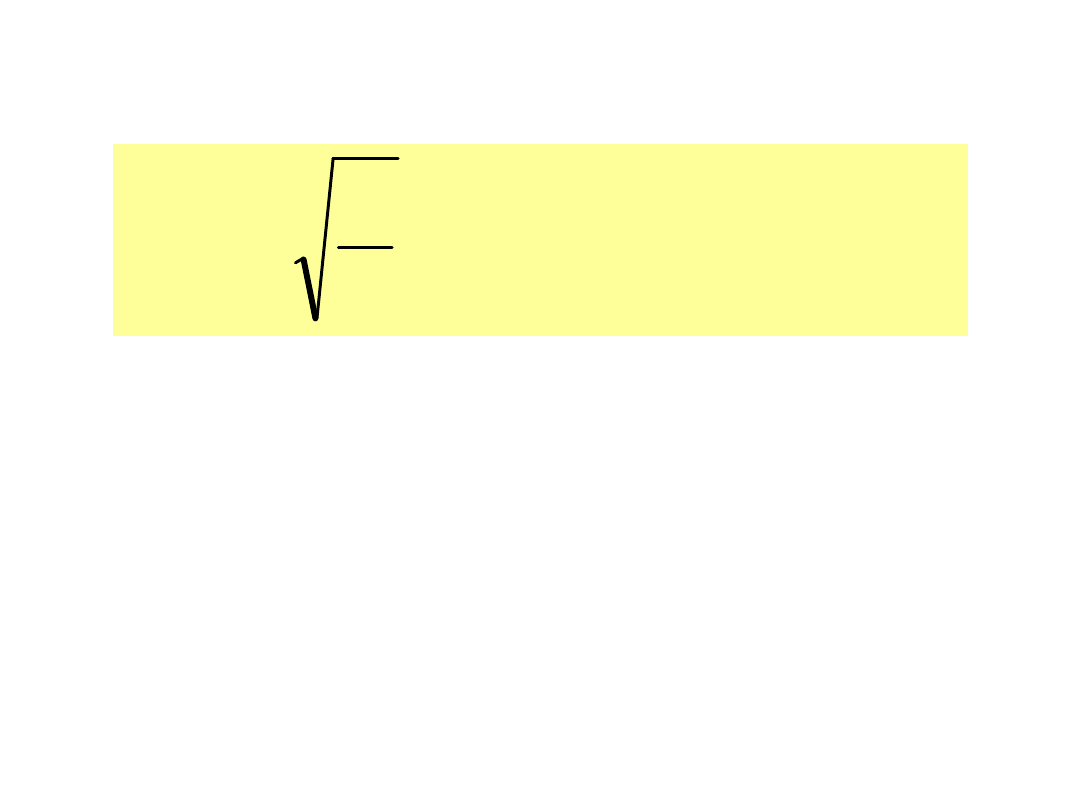
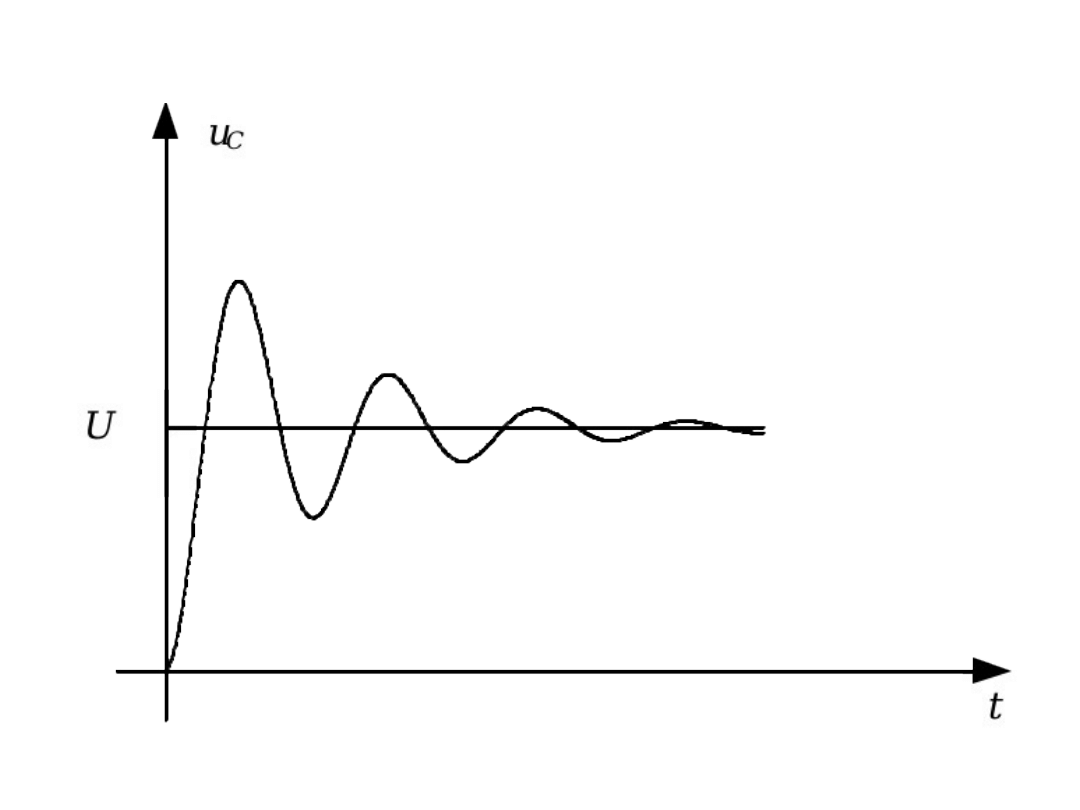
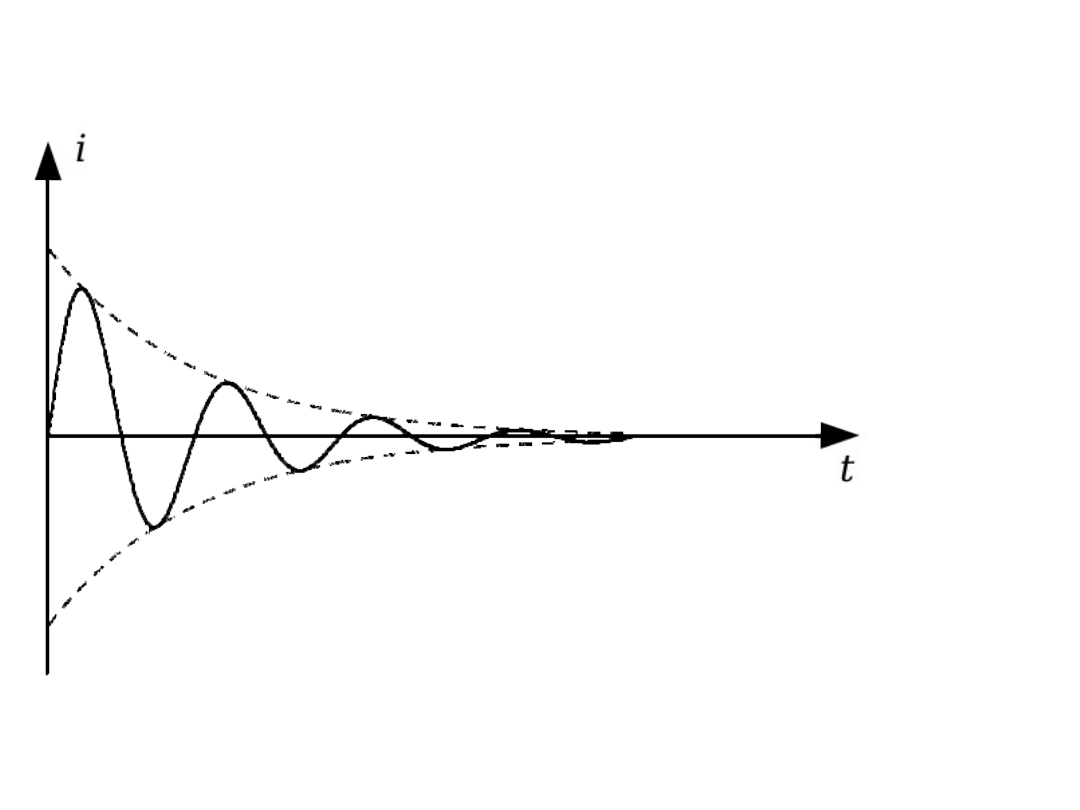
Przebiegi mają
charakter
drgający
Składowe swobodne funkcjami
sinusoidalnymi o pulsacji
0
,
tłumionymi wykładniczo dla
i nietłumionymi dla
0
0
)
(
cos
e
0
t
L
C
A
i
t
S
sin
sin
cos
cos
cos
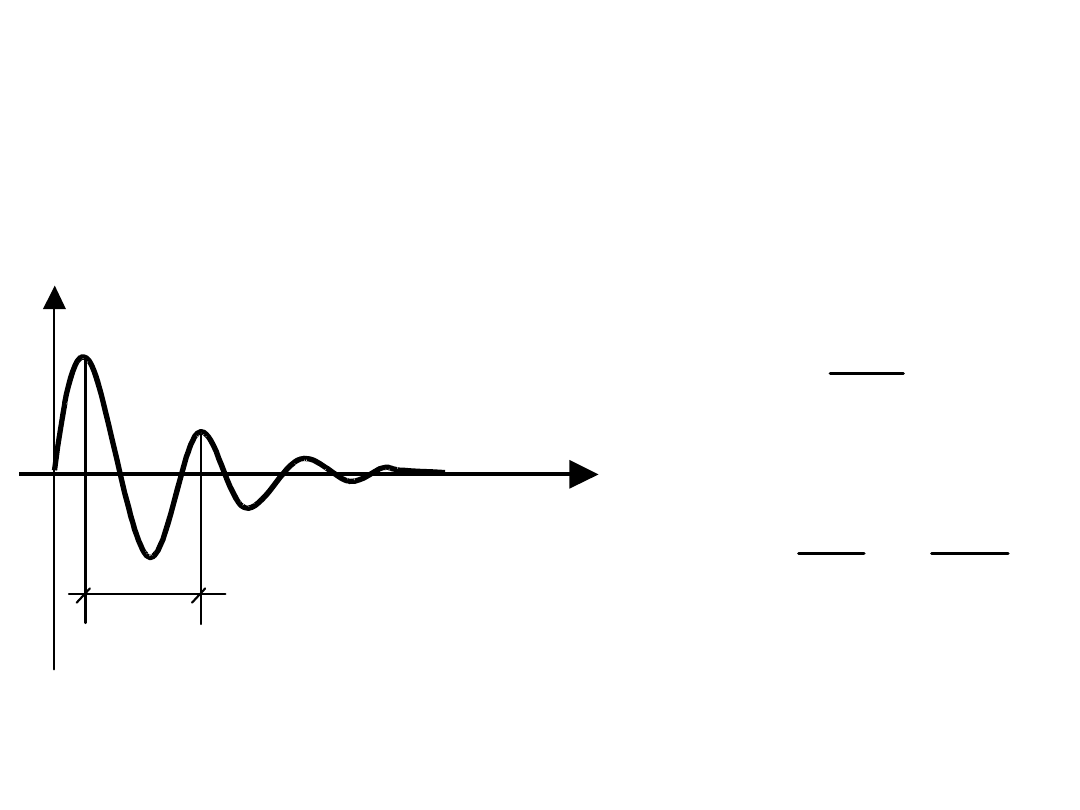
Stopień tłumienia określa
dekrement tłumienia
, - iloraz
wielkości drgającej w chwili t do
tej samej wielkości w chwili t+T
0
,
0
0
2
T
0
0
0
T
0
0
0
)
(
0
t
0
0
)
(
0
t
0
e
)
2
(
sin
e
)
(
sin
e
)
)
(
(
sin
e
)
(
sin
e
)
(
)
(
T
T
t
A
t
A
T
t
A
t
A
T
t
u
t
u
T
t
T
t
C
C
S
S
Dekrement logarytmiczny tłumienia
0
ln
T
u
Cs
t
A
1
A
2
T
0
2
1
0
0
0
ln
1
2
A
A
T
T
Algorytm obliczania układów 2 rzędu
• wybieramy zmienną (u
c
, i
L
)
• układamy równanie różniczkowe
• ustalamy warunki początkowe:
0
0
,
,
0
,
0
t
L
t
C
L
C
dt
di
dt
du
i
u
• obliczamy składową wymuszoną
• obliczamy składową swobodną:
- formułujemy równanie charakterystyczne
- znajdujemy pierwiastki
- wyznaczamy stałe całkowania
• sumujemy obie składowe i
wyznaczamy
u
C
lub i
L
• wyznaczamy inne wielkości obwodowe