Laboratorium Elektrotechniki i elektroniki LABORATORIUM © AMD2012

Temat ćwiczenia:

STANY NIEUSTALONE W OBWODACH ELEKTRYCZNYCH

Wprowadzenie

Przejście od jednego stanu pracy układu elektrycznego złożonego z elementów R, L, C do innego stanu

pracy, wywołany np. zmianą parametrów układu, jego struktury lub też zmianą rodzaju i charakteru wymuszeń
nie odbywa się skokowo, ale trwa pewien przedział czasu. Teoretycznie ten przedział czasu rozciąga się od
momentu początkowego aż do nieskończoności. Stan ten nazywamy stanem nieustalonym. Przejście od jednego
stanu pracy do drugiego obejmujemy wspólną nazwą – komutacja, przy czym zakłada się, że sam fakt
komutacji odbywa się w czasie nieskończenie krótkim. Każdemu stanowi pracy układu odpowiada określony
zapas energii pola elektrycznego i pola magnetycznego (w modelach obwodowych indukcyjności i pojemności
reprezentowany przez tzw. warunki początkowe, tj. prąd i

0

w indukcyjności i napięcie u

0

na pojemności.

Zarówno energia pola magnetycznego zgromadzona w indukcyjności oraz energia pola elektrycznego
zgromadzona w pojemności mogą zmieniać się tylko w sposób ciągły (nie skokowo), gdyż w przeciwnym
przypadku moc jako pochodna energii (szybkość jej zmian) osiągała by wartość nieskończenie dużą, co
fizycznie nie jest możliwe.

Wspomniano wyżej, że przejście od jednego stanu pracy do drugiego wymaga teoretycznie nieskończenie

dużego czasu. Praktycznie ten przedział czasu przejścia od jednego do drugiego stanu (stan przejściowy) może
być bardzo krótki, po upływie którego prądy i napięcia zbliżają się na tyle blisko wartości ustalonych, że bez
popełnienia błędu można taki stan uznać za ustalony.

Jeśli układ elektryczny nie zawiera indukcyjności oraz pojemności (jest obwodem rezystancyjnym, czyli

składa się tylko z oporności), wtedy przejście od jednego do drugiego stanu ustalonego odbywa się skokowo,
bez żadnych opóźnień ponieważ rezystancje nie posiadaja zdolności gromadzenia energii.

Obwód składający się z elementów R, L, C może być traktowany jako obwód tylko rezystancyjny, jeśli

wymuszenia w nim działające są stałe (niezależne od czasu) oraz gdy pominiemy stan przejściowy obwodu.

Występowanie stanów przejściowych w układach elektrycznych z jednej strony jest niepożądane, czasem

niebezpieczne (np. przy zwarciach występujących w systemach energetycznych), a z drugiej strony – stan
przejściowy może być normalnym stanem pracy układu, jak to ma miejsce np. w systemach radiotechnicznych,
układach automatycznego sterowania itp.

Do analizy stanów nieustalonych zachodzących w układach elektrycznych złożonych z liniowych

i skupionych elementów R, L, C można stosować różny aparat matematyczny. W instrukcji posługujemy się
tzw. metodą klasyczną, która polega na ułożeniu (na podstawie praw Kirchhoffa i zleżności prądowo
napięciowych na elementach) równań obwodu elektrycznego. Równania te są równaniami różniczkowo-
całkowymi z czasową zmienną niezależną t. W ćwiczeniu będziemy się zajmować układami R, L, C opisanymi
liniowymi równaniami różniczkowymi drugiego rzędu. Rozwiązanie równania różniczkowego jest sumą dwóch
części. Jedną z nich jest całka szczególna równania niejednorodnego (ogólnie nazywaną składową
wymuszoną), druga zaś – całką ogólną równania różniczkowego jednorodnego (składowa ta nosi nazwę
składowej swobodnej). Wartości początkowe umożliwiają wyznaczenie stałych całkowania występujących
w rozwiązaniu.

)

(

)

(

)

(

t

x

t

x

t

x

w

s





gdzie: x

s

(t) – składowa swobodna (odpowiedź na warunki początkowe)

x

u

(t) – składowa wymuszona (odpowiedź na wymuszenie)

Rozwiązanie równania różniczkowego można również przedstawić jako sumę składowej przejściowej
i składowej ustalonej

)

(

)

(

)

(

t

x

t

x

t

x

u

p





gdzie: x

p

(t) – składowa przejściowa

x

u

(t) – składowa ustalona

Składowa przejściowa ma taką własność, że dla czasu dążącego do nieskończoności zanika.

0

)

(

lim







t

x

p

t

Natomiast składowa ustalona ma charakter wymuszenia.

AMD

2

Badanie obwodów II-go rzędu - pomiary w obwodzie RLC

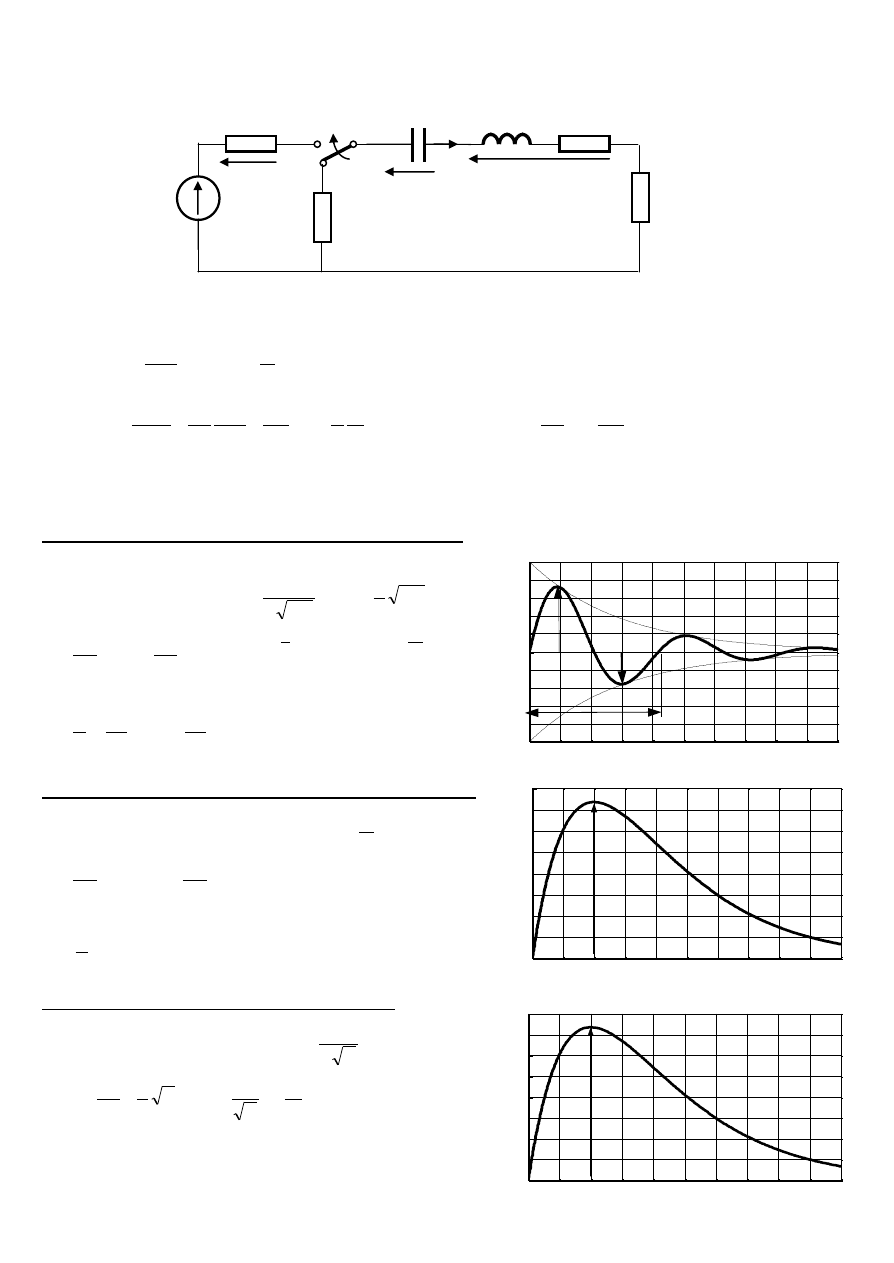
Obwód RLC II-go rzędu przedstawia poniższy rysunek

.

.

Rys. 1. Schemat obwodu elektrycznego R, L, C drugiego rzędu

Równanie obwodu

)

(

)

(

4

d

d

1

1

d

d

d

d

0

d

d

R

2

Z

Z

2

2

0

Z

t

i

R

t

u

LC

L

R

e(t)

t

L

i(t)

LC

t

i(t)

L

R

t

i(t)

e(t)

)

(

u

i(t)dt

C

1

i(t)

R

t

i(t)

L

t

C











































Przyjmujemy:

e(t) = E = const, u(0)= 0, i(0) = 0, R

Z

=R+R

L

+R

G

Rozwiązanie dla



< 0 przebieg oscylacyjnie tłumiony

Wielkości obliczone teoretycznie.

4

3

2

4

1

2

Δ

T

m

T

m

Z

m

t

α

m

e

I

A

e

I

A

ω

T

2L

R

α

2

1

ω

L

2E

I

t)

sin(ω

e

I

i(t)











































Wielkości obliczone z pomiarów oscyloskopem

amplitudy

2

1







i

A

T

2π

ω

A

A

ln

T

2

α

Rozwiązanie dla



= 0 przebieg aperiodyczny krytyczny

max

max

1

max

,

2

i

R

U

e

R

E

i

,

2L

R

α

L

E

C

0

C

e

t

C

e

C

i(t)

Z

Z

2

1

t

α

2

t

α

1

































Wielkości obliczone z pomiarów oscyloskopem

1

1

t





Rozwiazanie dla



> 0 przebieg aperiodyczny

)

(

ln

1

)

(

1

max

1

2

1

2

1

2

1

2

1

2

1

t

i

R

U

s

s

t

2

1

2L

R

s

L

E

C

C

e

C

e

C

t

i

Z

,

t

s

t

s

















































0

1

2

3

4

5

6

7

8

9

1 0

-1

-0 . 8

-0 . 6

-0 . 4

-0 . 2

0

0 . 2

0 . 4

0 . 6

0 . 8

1

u

R

[V]

T

t[ms]

A

1

A

2

0

1

2

3

4

5

6

7

8

9

1 0

0

0 . 1

0 . 2

0 . 3

0 . 4

0 . 5

0 . 6

0 . 7

0 . 8

t

1

U

max

u

R

[V]

t

[ms]

0

1

2

3

4

5

6

7

8

9

1 0

0

0 . 1

0 . 2

0 . 3

0 . 4

0 . 5

0 . 6

0 . 7

0 . 8

t

1

U

max

u

R

[V]

t

[ms]

C

R

e(t)

i(t)

u

C

u

R

u=u

L

+ u

RL

L

R

L

R

G

R

G

t

0

= 0

K

AMD

3

Przebieg ćwiczenia

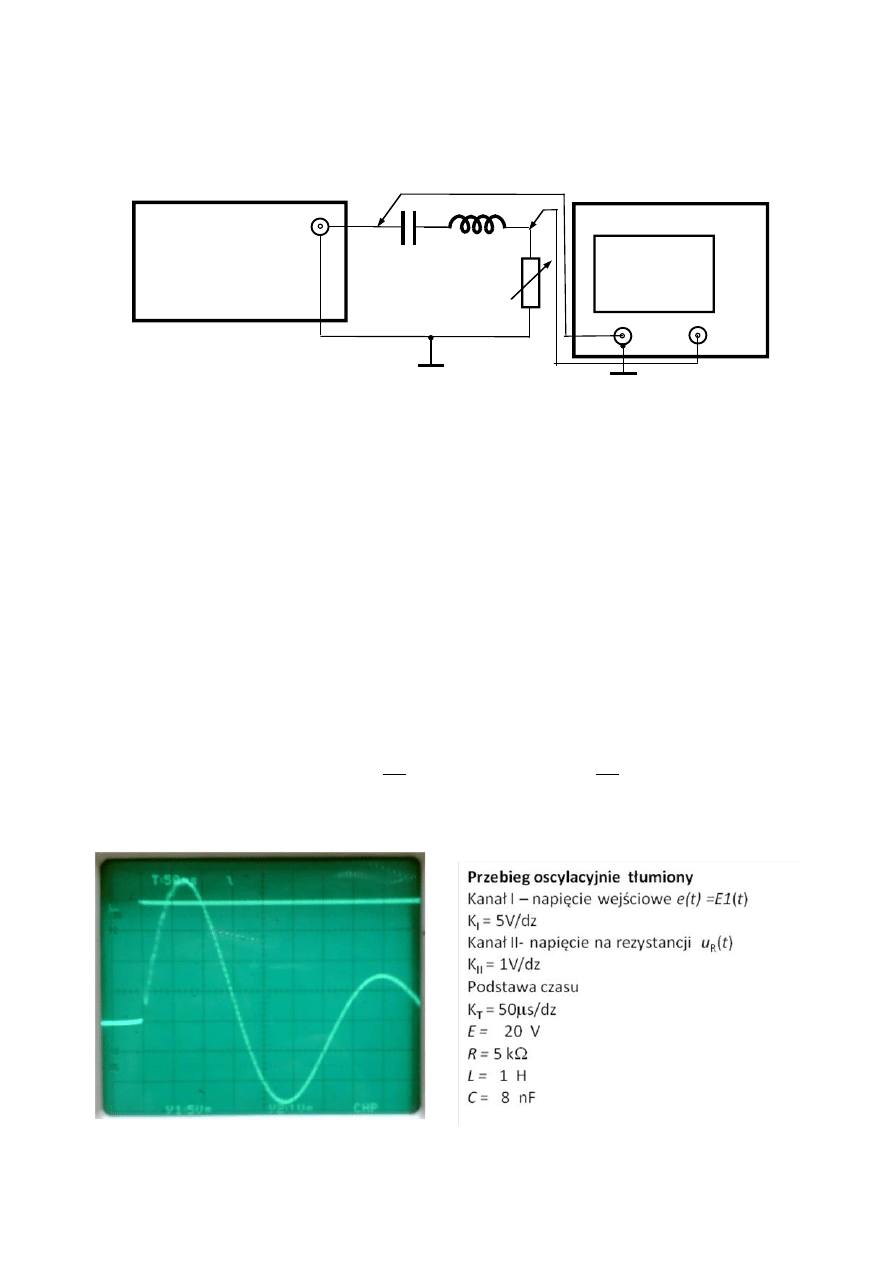
Układ pomiarowy należy połączyć zgodnie ze schematem przedstawionym na rysunku 2. W układzie
pomiarowym zamiast przełącznika „K” zastosowano generator fali prostokątnej. Na ekranie oscyloskopu należy
zaobserwować przebiegi czasowe w ciągu jednego okresu a następnie rozciągnąć skalę czasu na stan przejścia
napięcia wejściowego z jednego stanu do drugiego (skok napięcia).

We I

We II

Oscyloskop

Wy

Generator

fali prostokątnej

R

G

=50



Rys. 2. Schemat układu pomiarowego obwodu RLC

Na wyjściu generatora funkcyjnego należy ustawić napięcie:
- o kształcie impulsów prostokątnych i wypełnieniu 1/2,
- częstotliwości f =120 [Hz],
- amplitudzie E = 10 [V],
Zmierzyć omomierzem rezystancję cewki indukcyjnej R

L

[



] przy L = 1[H],

Wstępnie ustawić wartość:
Rezystancji R = 5 [k



indukcyjności L = 1[H], pojemności C = 5 [nF].

Po skorygowaniu wartości R i C należy wykonać zdjęcie aparatem cyfrowym ekranu oscyloskopu oraz dokonać
pomiarów odpowiednich wielkości w zależności od badanych przebiegów.

Odczyt z oscyloskopu

Wielkości z ekranu oscyloskopu odczytuje się w działkach, najczęściej w [cm]. W celu otrzymania wartości
napięcia mierzonego sygnału należy przemnożyć wartość wyrażoną w cm przez wzmocnienie właściwe dla
danego kanału. Podobnie dla określenia czasu, odcinek odpowiadający określonemu przedziałowi czasowemu
należy pomnożyć przez podstawę czasu oscyloskopu dla danego przebiegu.

























cm

ms

]

[

]

[

cm

V

]

cm

[

]

V

[

m

m

T

K

cm

T

ms

T

K

E

E

(*)

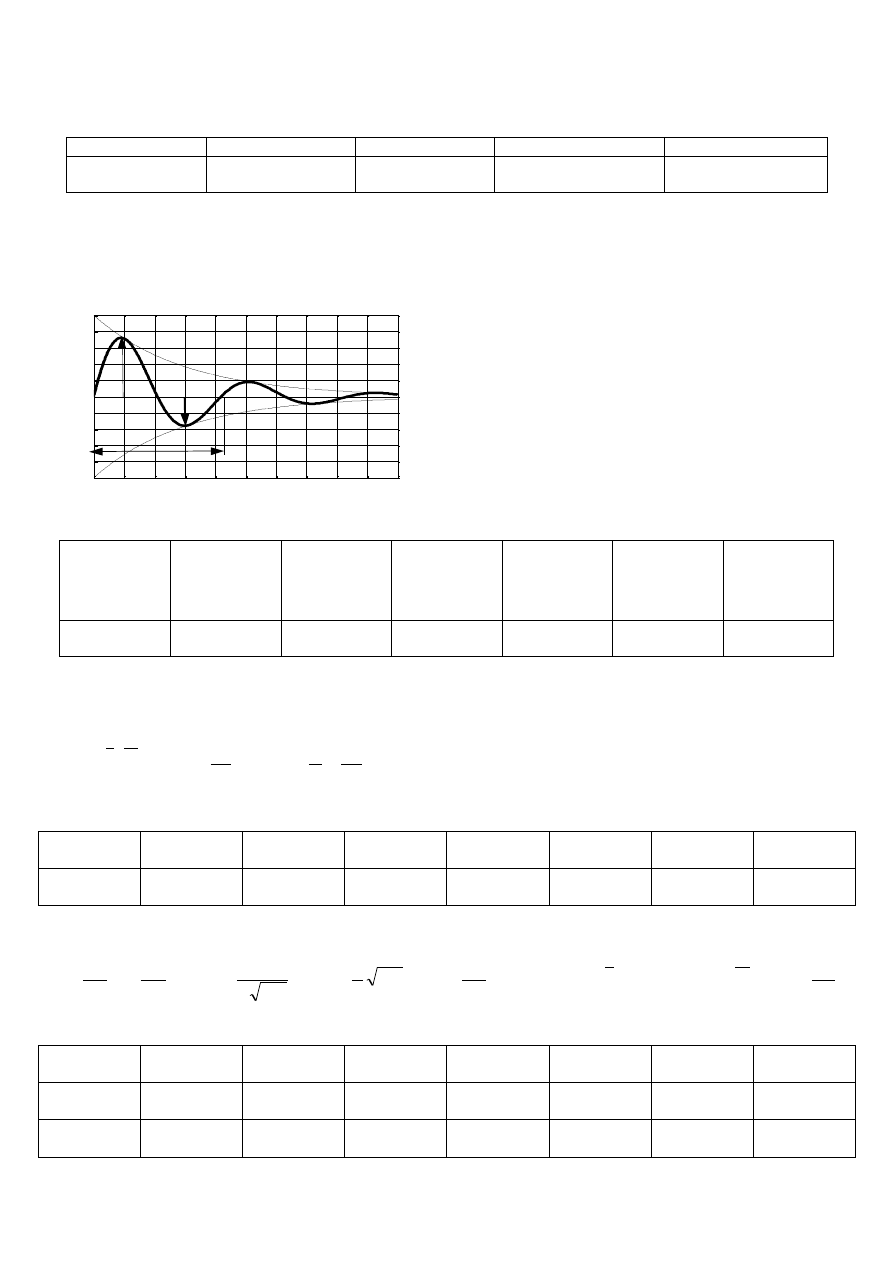
Przykładowy ekran oscyloskopu wraz z opisem przedstawia rysunek 3.

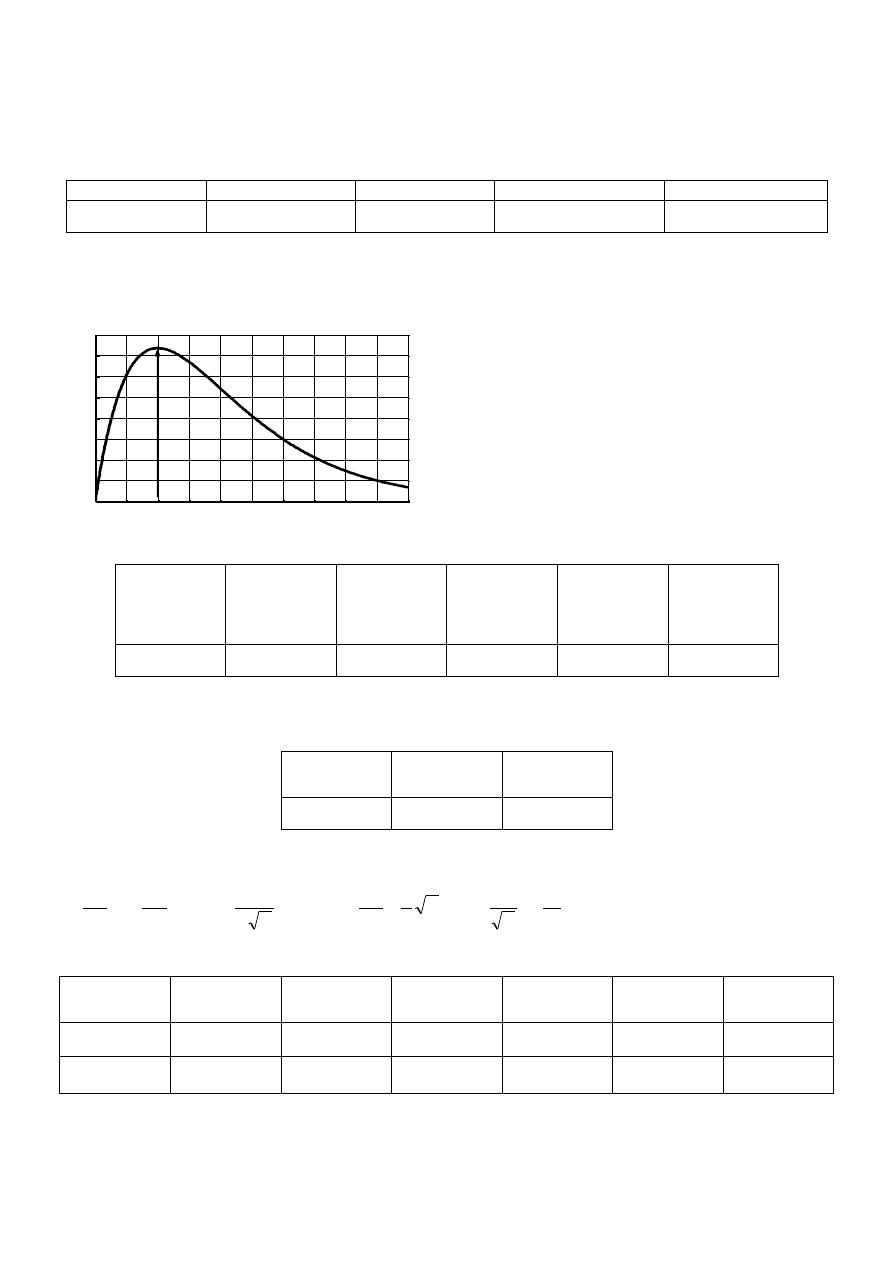
Rys. 3. Odpowiedź szeregowego obwodu RLC na skok napięcia wejściowego

AMD

4

Pomiary dla przebiegu oscylacynie tłumionego

W tabeli 1 wpisujemy nastawy wartości parametrów elementów badanego obwodu.

Tabela 1. Wartości elementów obwodu odczytane z nastaw lub zmierzone.

R[k



]

R

G

[



]

L[H]

R

L

[



]

C[nF]

Pomiar oscyloskopem

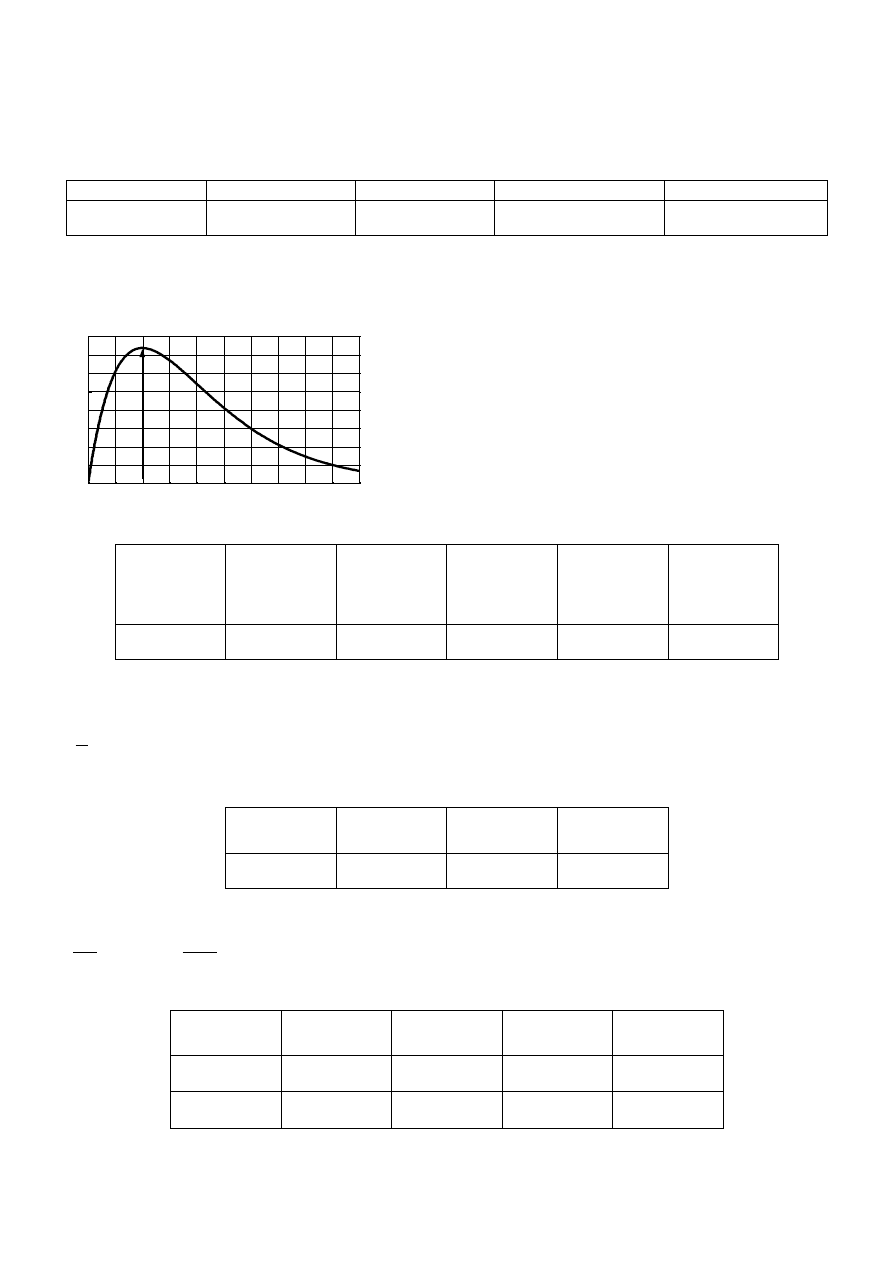
Na kanale I oscyloskopu obserwujemy skok napięcia e(t), natomiast na kanale II oscyloskopu obserwujemy
napięcie u

R

(t)

na rezystancji R. Pomiary sygnału oscylacyjnego nieco upraszczamy przyjmując,że ekstrema

przebiegu występują dla ¼ oraz ¾ okresu T.

0

1

2

3

4

5

6

7

8

9

1 0

-1

-0 . 8

-0 . 6

-0 . 4

-0 . 2

0

0 . 2

0 . 4

0 . 6

0 . 8

1

u

R

[V]

T

t[ms]

A

1

A

2

Tabela 2. Wartości sygnałów odczytane z ekranu oscyloskopu

Wzmocnienie

napięciowe

kanał "I"

KI[V/cm]

Wzmocnienie

napięciowe

kanał "II"

KII[V/cm]

Podstawa czasu

oscyloskopu

KT[ms/cm]

Skok napięcia

E[cm]

Amplituda

A1[cm]

Amplituda

A2[cm]

Okres
T[cm]

Opracowanie pomiarów
Wzory do obliczeń na podstawie pomiarów oscyloskopem.

2

1

2

1

1

e

2

1

A

A

ln

T

2

α

T

2π

ω

A

I

A

A

ln

m







Tabela 3. Wartości wyznaczone na podstawie pomiarów oscyloskopem

Wyróżnik

∆

I

m

[mA]

Pulsacja



[rad/s]

Stała tłumienia



Skok napięcia

E[V]

Amplituda

A1[V]

Amplituda

A2[V]

Okres
T [



s]

∆

<0



Wzory do obliczeń teoretycznych:

ω

T

e

I

A

e

I

A

2L

R

α

2

1

ω

L

2E

I

LC

L

R

T

m

T

m

Z

Z







2

,

,

,

,

,

Δ

,

4

4

3

2

4

1

m

2













































Tabela 4. Wartości zadane i obliczone teoretycznie

Wyróżnik

∆

I

m

[mA]

Pulsacja



[rad/s]

Stała tłumienia



Skok napięcia

E[V]

Amplituda

A1[V]

Amplituda

A2[V]

Okres
T [



s]



Błąd względny



%



AMD

5

Pomiary dla przebiegu aperiodycznego krytycznego

Przebieg aperiodyczny krytyczny uzyskamy z przebiegu oscylacyjnie tłumionego przy niezmienionej wartości L
zwiększając rezystancję R o



R od 2 do 4 k



i obliczając



C z warunku



= 0.

W tabeli 5 wpisujemy nastawy wartości parametrów elementów badanego obwodu.

Tabela 5. Wartości elementów obwodu odczytane z nastaw lub zmierzone.

R[k



]

R

G

[



]

L[H]

R

L

[



]

C[nF]

Pomiar oscyloskopem

Na kanale I oscyloskopu obserwujemy skok napięcia e(t), natomiast na kanale II oscyloskopu obserwujemy
napięcie u

R

(t)

na rezystancji R.

0

1

2

3

4

5

6

7

8

9

1 0

0

0 . 1

0 . 2

0 . 3

0 . 4

0 . 5

0 . 6

0 . 7

0 . 8

t

1

U

max

u

R

[V]

t

[ms]

Tabela 6. Wartości sygnałów odczytane z ekranu oscyloskopu

Wzmocnienie

napięciowe

kanał "I"

KI[V/cm]

Wzmocnienie

napięciowe

kanał "II"

KII[V/cm]

Podstawa czasu

oscyloskopu

KT[ms/cm]

Skok napięcia

E[cm]

Wartość max

U

max

[cm]

Czas

t

1

[cm]

Opracowanie pomiarów
Wzory do obliczeń na podstawie pomiarów oscyloskopem:

1

1

t





Tabela 7. Wartości wyznaczone na podstawie pomiarów oscyloskopem

stała tłumienia



[



s

-1

]

Skok napięcia

E[V]

Wartość max

U

max

[V]

Czas

t

1

[



s]

Wzory do obliczeń teoretycznych:

1

max

2







e

R

ER

U

,

2L

R

α

Z

Z

Tabela 8. Wartości zadane i obliczone teoretycznie

Wyróżnik



stała tłumienia



[



s

-1

]

Skok napięcia

E[V]

Wartość max

U

max

[V]

Czas

t

1

[



s]

0

Błąd względny



%

AMD

6

Pomiary dla przebiegu aperiodycznego

Przebieg aperiodyczny uzyskamy z przebiegu aperiodyczny krytyczny przy niezmienionej wartości L
zwiększając rezystancję R o



R = 1 k



oraz zwiększając



pojemność



C o



C = 10 nF.

W tabeli 9 wpisujemy nastawy wartości parametrów elementów badanego obwodu.

Tabela 9. Wartości elementów obwodu odczytane z nastaw lub zmierzone.

R[k



]

R

G

[



]

L[H]

R

L

[



]

C[nF]

Pomiar oscyloskopem

Na kanale I oscyloskopu obserwujemy skok napięcia e(t), natomiast na kanale II oscyloskopu obserwujemy
napięcie u

R

(t)

na rezystancji R.

0

1

2

3

4

5

6

7

8

9

1 0

0

0 . 1

0 . 2

0 . 3

0 . 4

0 . 5

0 . 6

0 . 7

0 . 8

t

1

U

max

u

R

[V]

t

[ms]

Tabela 10. Wartości sygnałów odczytane z ekranu oscyloskopu

Wzmocnienie

napięciowe

kanał "I"

KI[V/cm]

Wzmocnienie

napięciowe

kanał "II"

KII[V/cm]

Podstawa czasu

oscyloskopu

KT[ms/cm]

Skok napięcia

E[cm]

Wartość max

U

max

[cm]

Czas

t

1

[cm]

Opracowanie pomiarów

Tabela 11. Wartości wyznaczone na podstawie pomiarów oscyloskopem

Skok napięcia

E[V]

Wartość max

U

max

[V]

Czas

t

1

[



s]

Wzory do obliczeń teoretycznych:

)

(

,

ln

1

,

,

,

4

1

max

1

2

1

2

1

1

2

t

i

R

U

s

s

t

2

1

2L

R

s

L

E

C

LC

L

R

Z

,

Z



















































Tabela 12. Wartości zadane i obliczone teoretycznie

Wyróżnik



C

1

[mA]

s

1

[s

-1

]

s

2

[s

-1

]

Skok napięcia

E[V]

Wartość max

U

max

[V]

Czas

t

1

[



s]

Błąd względny



%

X

X

X

Dla badanych obwodów należy ułożyć równanie różniczkowe. Rozwiązać równanie dla właściwych wartości
parametrów R, L, C i wymuszenia E. Otrzymane rozwiązania przedstawić w postaci analitycznej i graficznej.
Porównać przebiegi otrzymane z oscyloskopu (zdjęcia ekranu oscyloskopu) z rozwiązaniami teoretycznymi.

AMD

7

Przykładowe obliczenia numeryczne obwodu w programie Matlab
Równania stanu badanego obwodu mają postać:

i(t)

C

(t)

u

t

e(t)

L

(t)

u

L

i(t)

L

R

i(t)

t

1

d

d

1

1

d

d

C

C

Z











Plik funkcyjny równań stanu obwodu:

function dy=row_stanu(t,y)

global Rz L C E

dy=zeros(2,1);

dy(1)=-R/L*y(1)-1/L*y(2)+1/L*E;

dy(2)=1/C*y(1);

Plik skyptowy rozwiązań numerycznych obwodu :

global Rz L C E

Rz=4000;L=1;C=7*10^-9;E=10;

[t,y]=ode45('row_stanu',[0 0.002],[0;0]);

subplot(3,1,1)

plot(t,y(:,1)),grid on

title('przebiegi czasowe prad i(t)')

subplot(3,1,2)

plot(t,y(:,2)),grid on

title('przebiegi czasowe napiecie uc(t)')

subplot(3,1,3)

plot(y(:,1),y(:,2)),grid on

title('trajektoria')

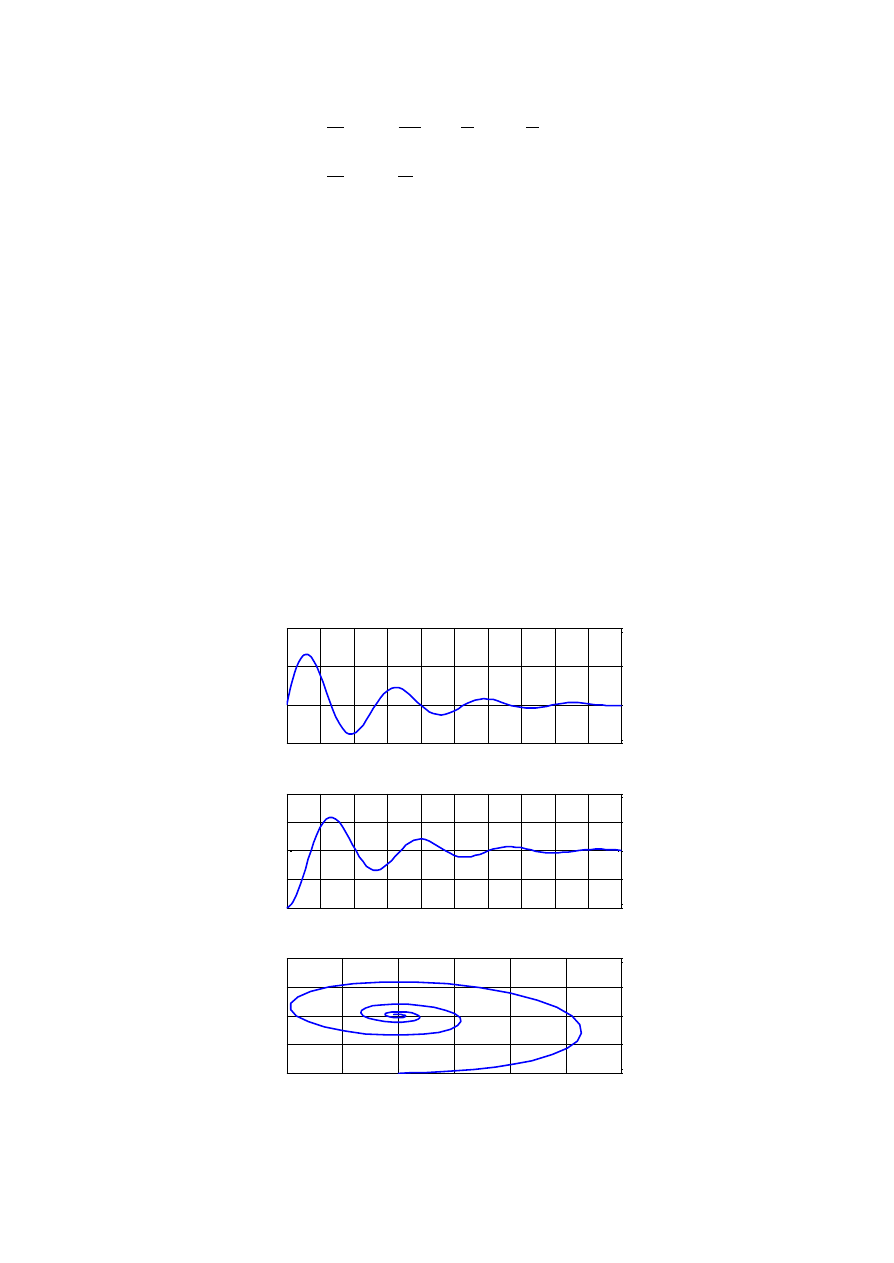
Rozwiązanie graficzne

0

0.2

0.4

0.6

0.8

1

1.2

1.4

1.6

1.8

2

x 10

-3

-5

0

5

10

x 10

-4

przebiegi czasowe prad i(t)

0

0.2

0.4

0.6

0.8

1

1.2

1.4

1.6

1.8

2

x 10

-3

0

5

10

15

20

przebiegi czasowe napiecie uc(t)

-4

-2

0

2

4

6

8

x 10

-4

0

5

10

15

20

trajektoria

AMD

8

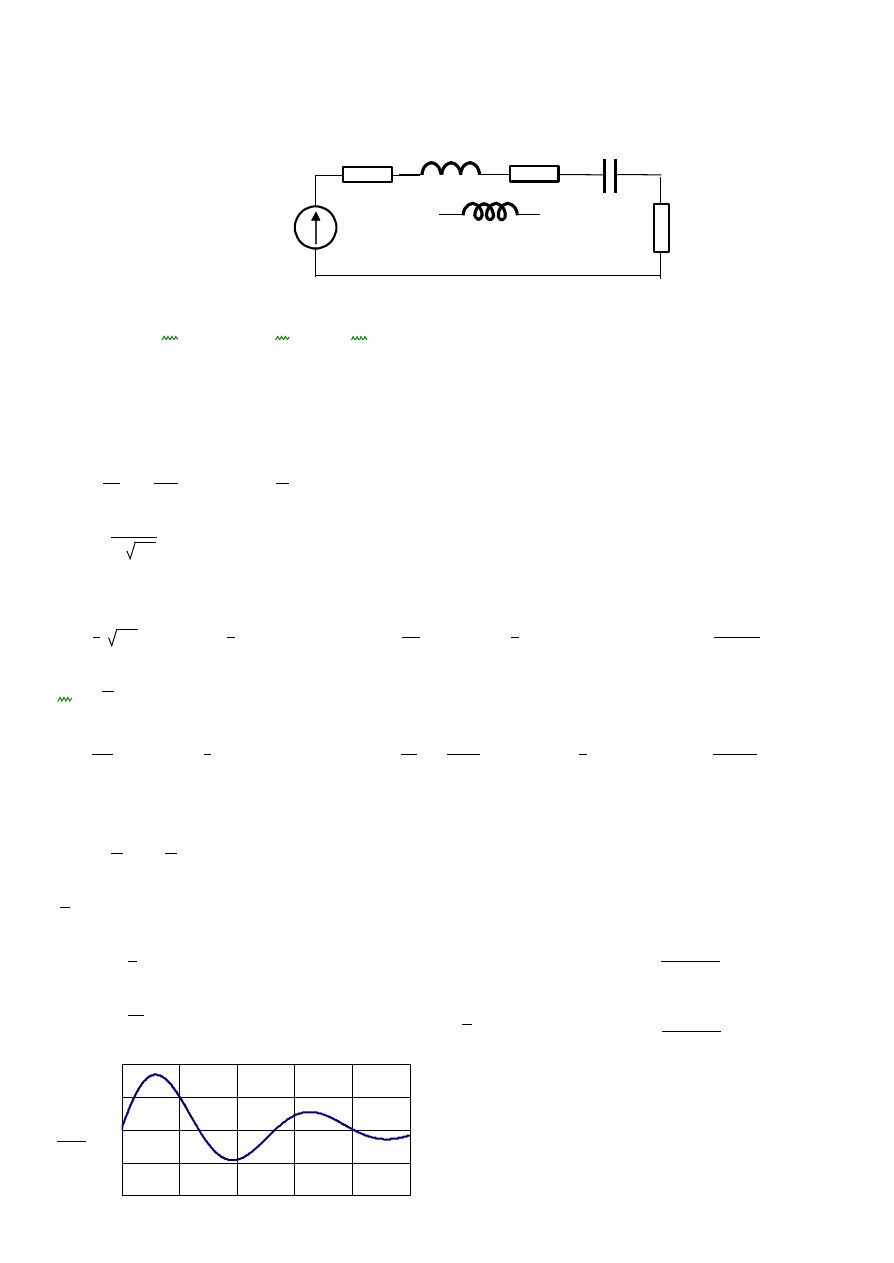
Przykładowe obliczenia obwodu w programie Mathcad

Stan nieustalony w obwodzie RLC

L

C

R

R

L

R

g

e(t)=E

Przebieg oscylacyjny

Dane z odczytu i pomiaru

Rg

50







R

4000







L

1 H





C

7

10

9





F





RL

229







Rz

Rg

R



RL





Pomiary oscyloskopowe

E

8 V





A1p

2100 mV





A2p

1100



mV





Tp

550 10

6





s





Obliczenia teoretyczne



Rz

L









2

4

L C





5.531



10

8



1

s

2





Imax

2 E



L







6.803

10

4





A





Obliczenia z pomiarów

Różnice względne

Umax

R Imax



2.721V







1

2







1.176

10

4



1

s







p

2



T p

1.142

10

4



1

s







 

p





100



2.851





T

2






5.343

10

4





s







Rz

2 L



2.139

10

3



1

s







p

2

T p

ln

A1p

A2p













2.351 10

3



1

s







 

p





100



9.903







uR t

( )

R Imax



e





t





sin



t



(

)





- napięcie na rezystancji R

tmax

1



atan














1.183 10

4





s





T

4

1.336 10

4





s



A1

uR

T

4









2.045V





A1max

uR tmax

(

)

2.079V







A1

A1

A1p



A1

100



2.699







A2

uR

3T

4









1.155



V





A2max

uR tmax

T

2











1.174



V







A2

A2

A2p



A2

100



4.725





0

2 10

4





4 10

4





6 10

4





8 10

4





2.5



1.25



0

1.25

2.5

uR t

( )

t

AMD