Ćwiczenie 8

Temat:

BADANIE STANÓW NIEUSTALONYCH

W OBWODACH RC I RLC

I. ZAGADNIENIA

1.

Badanie przebiegów napięć i prądów podczas ładowania i rozładowania
kondensatora w obwodzie RC

2.

Obserwacja na oscyloskopie przebiegu napięcia na kondensatorze
w obwodzie szeregowym RLC, zasilanym z generatora fali prostokątnej

II. WIADOMOŚCI PODSTAWOWE

Stanem nieustalonym lub stacjonarnym obwodu elektrycznego liniowego

nazywamy taki stan, w którym prądy, napięcia i energia zmieniają się okresowo
lub są niezmienne w czasie.

Stanem nieustalonym obwodu elektrycznego liniowego nazywa się stan,

który charakteryzuje przejście od stanu ustalonego początkowego do ustalonego
stanu końcowego.

Każda zmiana konfiguracji lub zmiana parametrów obwodu elektrycznego

powoduje występowanie w nim stanu nieustalonego. W obwodach
elektrycznych liniowych, do których stosuje się zasadę superpozycji, stan
nieustalony można uważać za wynik superpozycji dwóch stanów: stanu
ustalonego, zależnego od źródeł wymuszających i stanu przejściowego,
zależnego od różnic energii w elementach L C obwodu.

Taką metodę analizy stanów nieustalonych nazywamy klasyczną.

1. Obwód szeregowy RC w stanie nieustalonym

Jeżeli do obwodu złożonego z szeregowego połączenia kondensatora C

i rezystancji R (Rys. 8.1) przyłożymy stałe napięcie zasilania U

o

, to korzystając

z bilansu napięć w oczku, otrzymujemy równanie:

U

0

=

Ri + u

C

i

=

dq

dt

=

d (Cu )

dt

C

=

C

du

dt

C

RC

du

dt

C

+ u

C

=

U

0

u

C

=

u

cu

+ u

cp

u

cp

=

A e

− α

t

α

=

1

RC

=

1

T

, czyli

T

=

RC

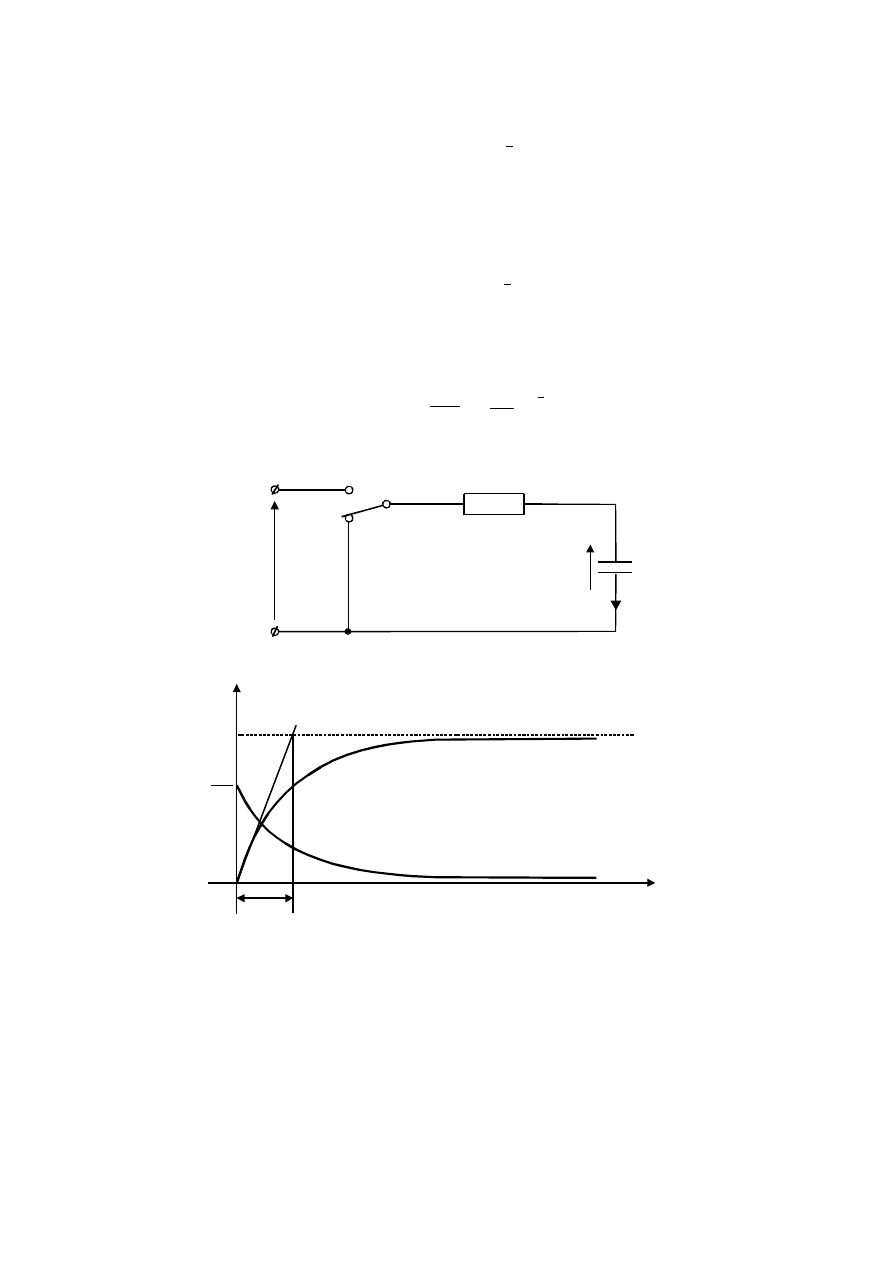
u

cu

=

U

0

u

C

=

U

0

+ A e

t

T

−

W celu wyznaczenia stałej A korzystamy z warunków początkowych dla t = 0,

u

c

= 0:

0

=

U

0

+ A

, stąd

A

=

- U

0

Ostatecznie:

u

C

=

U

0

(1 - e

)

t

T

−

(8.1)

Prąd ładowania kondensatora:

i

=

C

du

dt

C

=

U

R

e

o

−

t

T

(8.2)

Rys. 8.1

Rys. 8.2

Przebieg napięcia na kondensatorze oraz przebieg prądu ładowania

przedstawia rys. 8.2. Przy rozładowaniu kondensatora przez rezystancję R
(klucz k - rys. 8.1 w poz. 2) korzystamy z tych samych równań ogólnych, z tym,
że zwarciu kondensatora odpowiada napięcie U

o

= 0.

Obwód, w którym kondensator się rozładowuje (rys. 8.1) nie zawiera

napięcia źródłowego, wobec czego w obwodzie w stanie ustalonym nie może

R

C

u

c

i

1

2

k

U

o

T

i

u

c

t

U

o

U

o

u

c

i

,

R

0

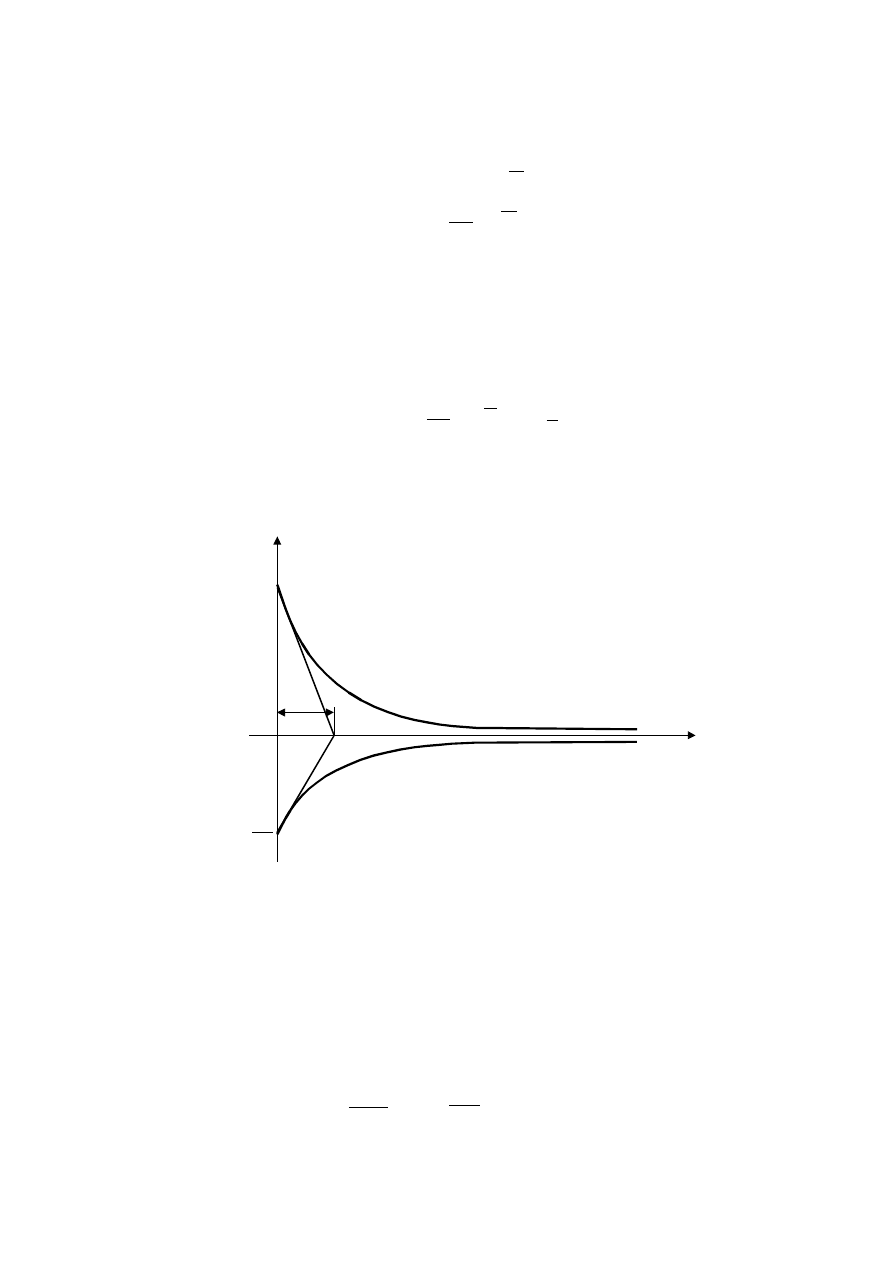
płynąć prąd, ani istnieć napięcie na kondensatorze. Stan nieustalony w obwodzie
jest, więc równy stanowi przejściowemu:

u

C

=

u

cp

=

U

0

e

t

RC

−

i

=

i

p

=

U

0

R

e

t

RC

−

Znak minus oznacza, że przy rozładowaniu kondensatora zwrot prądu jest
przeciwny, niż przy ładowaniu. Przebieg napięcia podczas rozładowania
kondensatora oraz przebieg prądu przedstawia rys. 8.3.

Energia pola elektrycznego kondensatora przy rozładowaniu zamienia się

w ciepło wydzielone na rezystancji R przez przepływający prąd i. Wartość tej
energii A można wyliczyć ze wzoru:

A

=

i

0

2

R dt

∞

∫

=

U

R

o

2

e dt

-2t

T

0

∞

∫

=

1
2

CU

0

2

Taka sama ilość energii wydziela się na rezystancji R przy ładowaniu
kondensatora, a więc całkowita energia pobrana ze źródła wyniesie:

A

=

CU

0

2

Rys. 8.3

2. Obwód szeregowy RLC w stanie nieustalonym

Jeżeli do obwodu złożonego z szeregowego połączenia rezystancji R,

indukcyjności L i pojemności C (rys. 8.4) doprowadzimy napięcie U

o

= const, to

przebieg prądu w obwodzie i napięcie na kondensatorze przy zerowych
warunkach początkowych opisują następujące równania:

C

L

d u

dt

C

2

2

+

RC

du

dt

C

+

u

C

=

U

0

a) gdy:

T

i

u

c

t

U

o

U

o

u

c

i

,

R

0

-

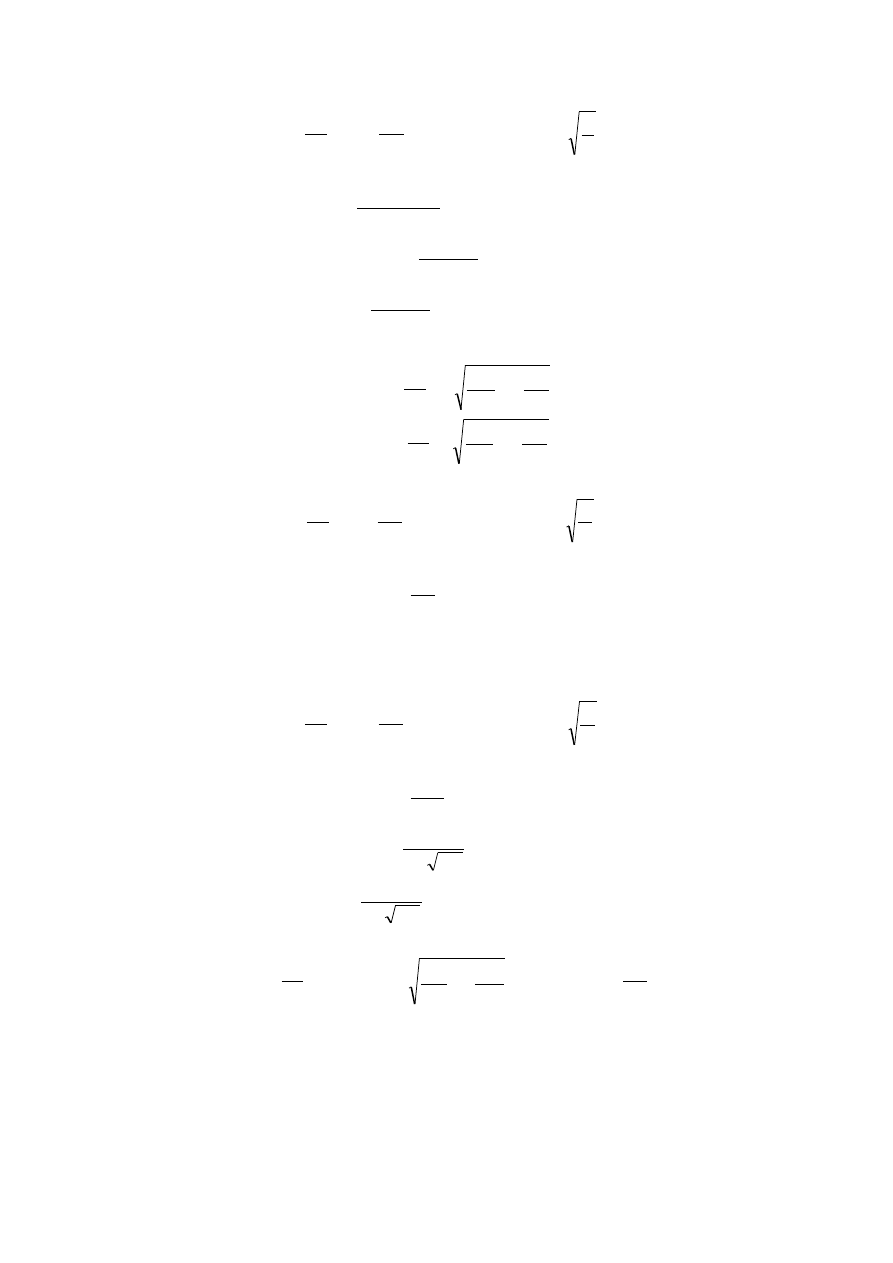
R

L

2

2









>

1

LC

lub

R

>

L

C

2

to:

i

=

U

L(p

e

o

p t

p t

1

1

2

- p

- e

2

)

(

)

(8.3)

u

C

=

U

0

+

U

p

p e

e

o

p t

p t

1

2

1

2

- p

- p

2

1

(

)

(8.4)

u

L

=

U

p

p e

e

o

p t

p t

1

1

1

2

- p

- p

2

2

(

)

(8.5)

gdzie:

p

1

=

−

R

2L

+

R

4L

-

1

LC

2

2

p

2

=

−

R

2L

-

R

4L

-

1

LC

2

2

b) gdy:

R

L

2

2









=

1

LC

lub

R

=

2

L

C

to:

i

=

U

L

te

o

pt

(8.6)

u

C

=

U

pt

0

- U

- 1) e

0

pt

(

(8.7)

u

L

=

U

- 1) e

0

pt

(pt

(8.8)

c) gdy:

R

L

2

2









<

1

LC

lub

R

<

L

C

2

to:

i

=

U

L

e

t

o

o

ω

ω

α

−

t

o

sin

(8.9)

u

C

=

U

0

-

U

LC

e

t

o

o

ω

ω

ψ

α

−

+

t

o

(

)

sin

(8.10)

u

L

=

U

LC

e

t

o

o

ω

ω

ψ

α

−

−

t

o

(

)

sin

(8.11)

gdzie:

α

=

R

2L

,

ω

o

L

=

1

LC

-

R

2

4

2

,

tg

ψ

ω

α

=

o

Przebiegi prądu i napięć w obwodzie RLC po włączeniu napięcia stałego

dla przypadku aperiodycznego przedstawione są na rys. 8.5, zaś dla przypadku
oscylacyjnego na rys. 8.6.

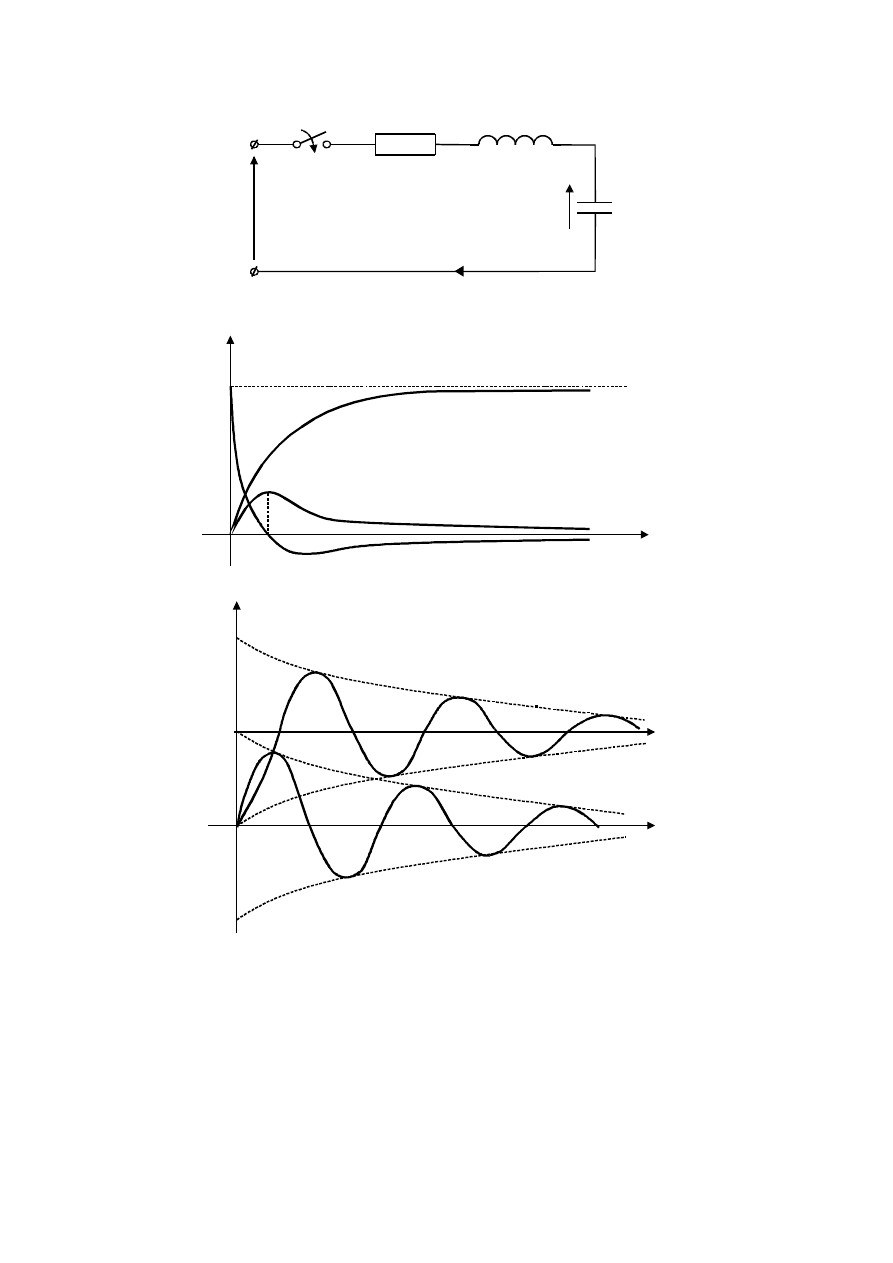
Rys.8.4

Rys.8.5

Rys. 8.6

C

u

c

i

k

U

o

R

L

i

u

c

t

u

c

i

,

0

u

L

u

L

i

u

c

t

u

c

i

,

0

U

III. POMIARY

1.

Obwód szeregowy RC w stanie nieustalonym

1.1. Schemat pomiarowy

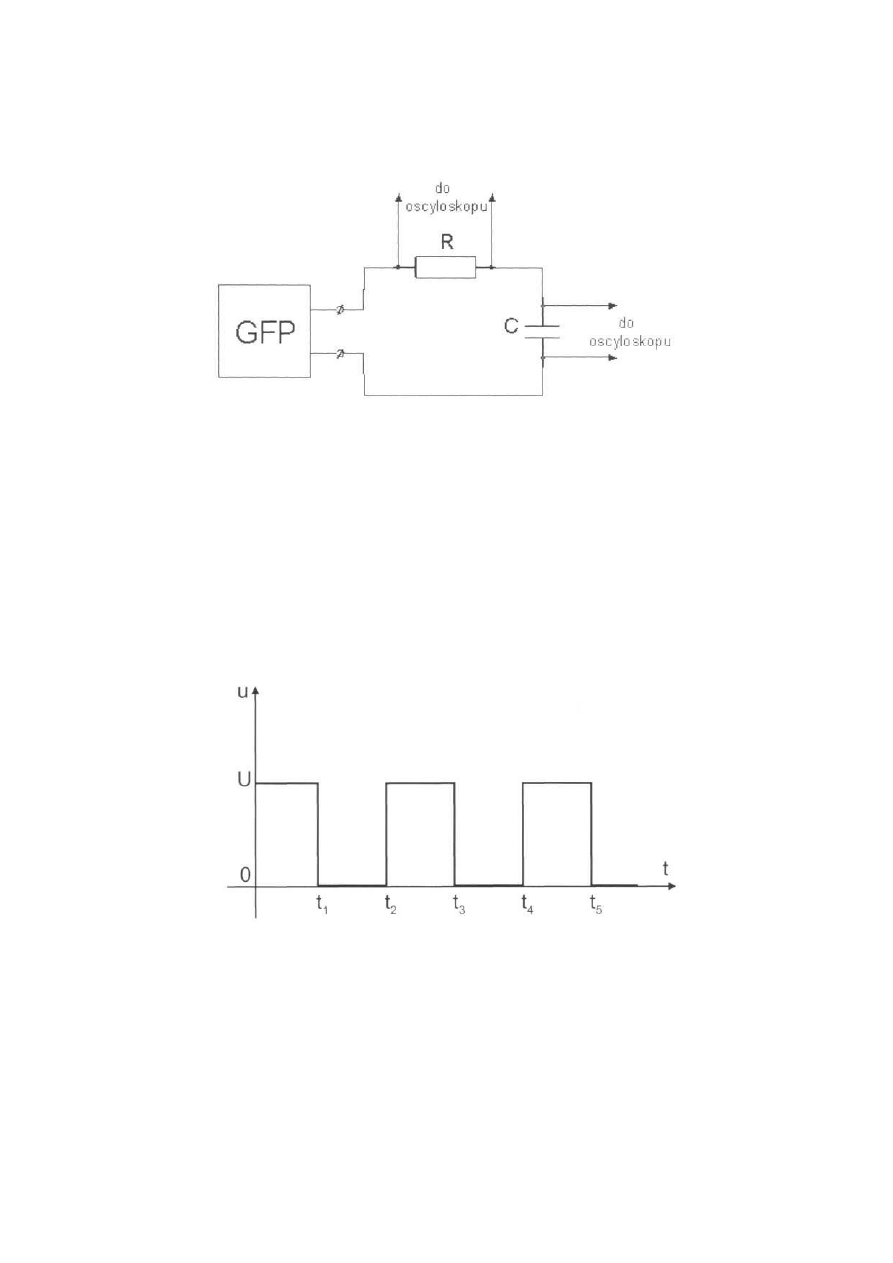
Rys. 8.7. Obwód szeregowy R C

1.2 Zmontować układ RC według rys. 8.7 i zasilić z generatora fali

prostokątnej. Generator fali prostokątnej wytwarza napięcie jak na rys.
8.8. W czasie 0 < t < tj układ jest załączony do stałego napięcia U. W
czasie tj < t < t2 układ nie posiada zasilania (jest zwierany przez
wewnętrzną rezystancję generatora). W obwodzie powstają przebiegi
nieustalone, powtarzające się z częstotliwością przebiegów prądu
generatora.
Po zsynchronizowaniu oscyloskopu z generatorem przebiegi można
obserwować na ekranie oscyloskopu.

Rys. 8.8. Sygnał z generatora fali prostokątnej (GFP)

1.3

Dla dwóch rezystancji R i pojemności C zaobserwować na oscyloskopie
zmianę kształtu przebiegu napięcia u

c

(t) i prądu i(t), przerysować

otrzymane przebiegi.

1.4

Wyznaczyć z u

c

(t) przebiegów stałe czasowe τ i porównać z obliczonymi

.

2.

Obwód szeregowy RLC w stanie nieustalonym

2.1

Schemat pomiarowy

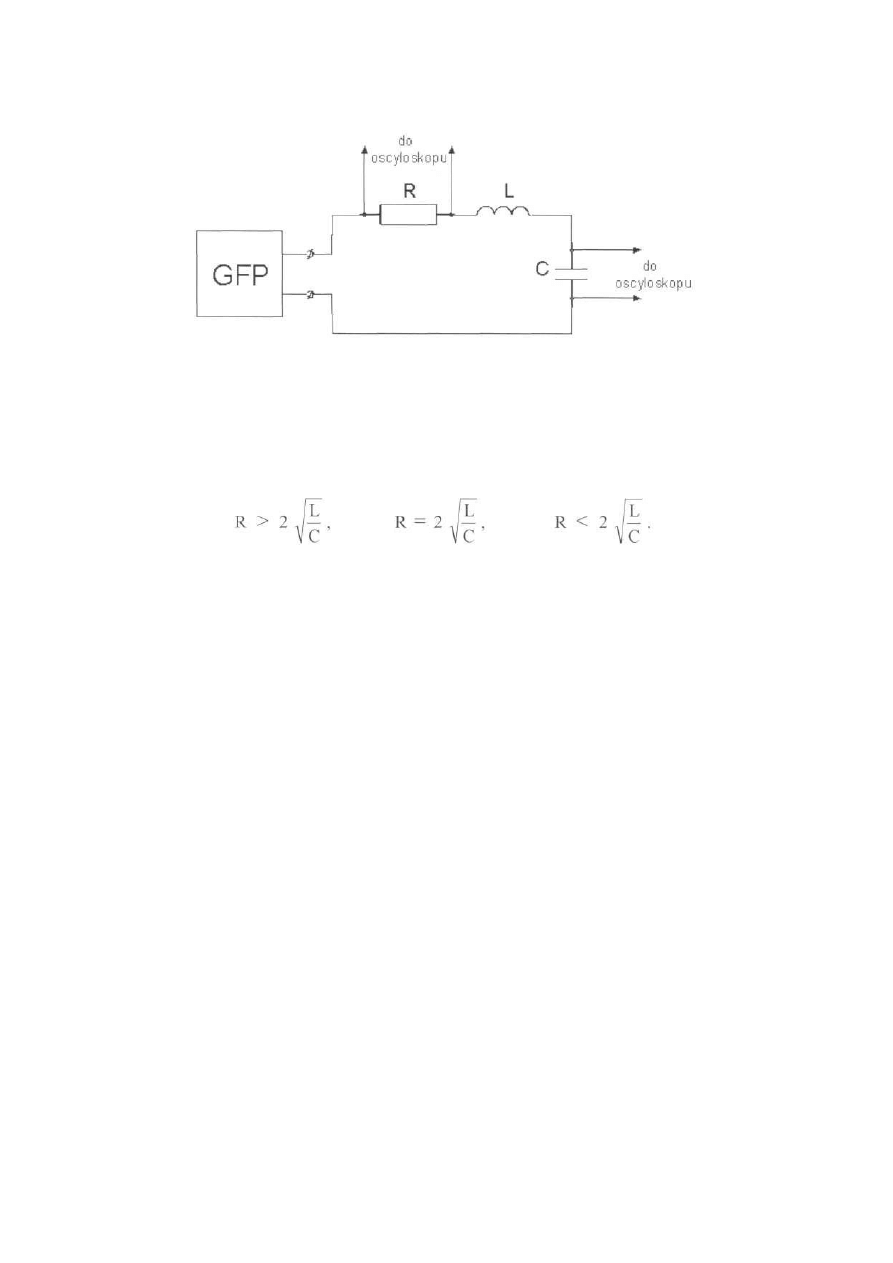
Rys. 8.9 Obwód szeregowy RLC

2.2

Zmontować układ RLC według rys.8.9 i zasilić z generatora fali
prostokątnej.

2.3

Zmieniać parametry R, L i C i zaobserwować na oscyloskopie zmianę
kształtu przebiegów napięcia uc(t) i prądu i(t) dla trzech przypadków, tj.

2.4

Zaobserwować wpływ parametrów R, L, C na współczynnik α i pulsację
drgań własnych ω

0

dla przypadku oscylacyjnego.