
Uniwersytet Wrocławski
Wydział Fizyki i Astronomii
Opracował:
Andrzej Koźmic
I rok mgr
Wrocław 2010

2
Spis treści:

3
1.
Abstrakt
Niniejsza praca jest przeznaczona dla osób, które interesują się oraz chcą zgłębić
swoją wiedzę związaną z obwodami LC i RLC. W tekście znajduje się opis matematyczny
opisywanych obwodów, dlatego zaleca się, aby przed przystąpieniem do lektury, zapoznać się
z podstawowymi metodami rozwiązywania równań różniczkowych.
2. Wstęp
Przed przystąpieniem do mówienia tytułowego zagadnienia, powinniśmy się
zastanowić nad samym tematem pracy, otóż: Jak rozumieć „drgania obwodów”? Osoby, które
miały kiedykolwiek do czynienia z obwodami elektrycznymi wiedzą, że w pracowni nikt
nigdy nie zawiesza opornika na przewodzie przyczepionym do statywu i nie mierzy okresu
drgań tak zbudowanego wahadła. Proponuję jednak, aby to pytanie pozostało bez odpowiedzi,
którą poznamy na końcu.
3. Drgania obwodu LC
3.1. Drgania własne układu
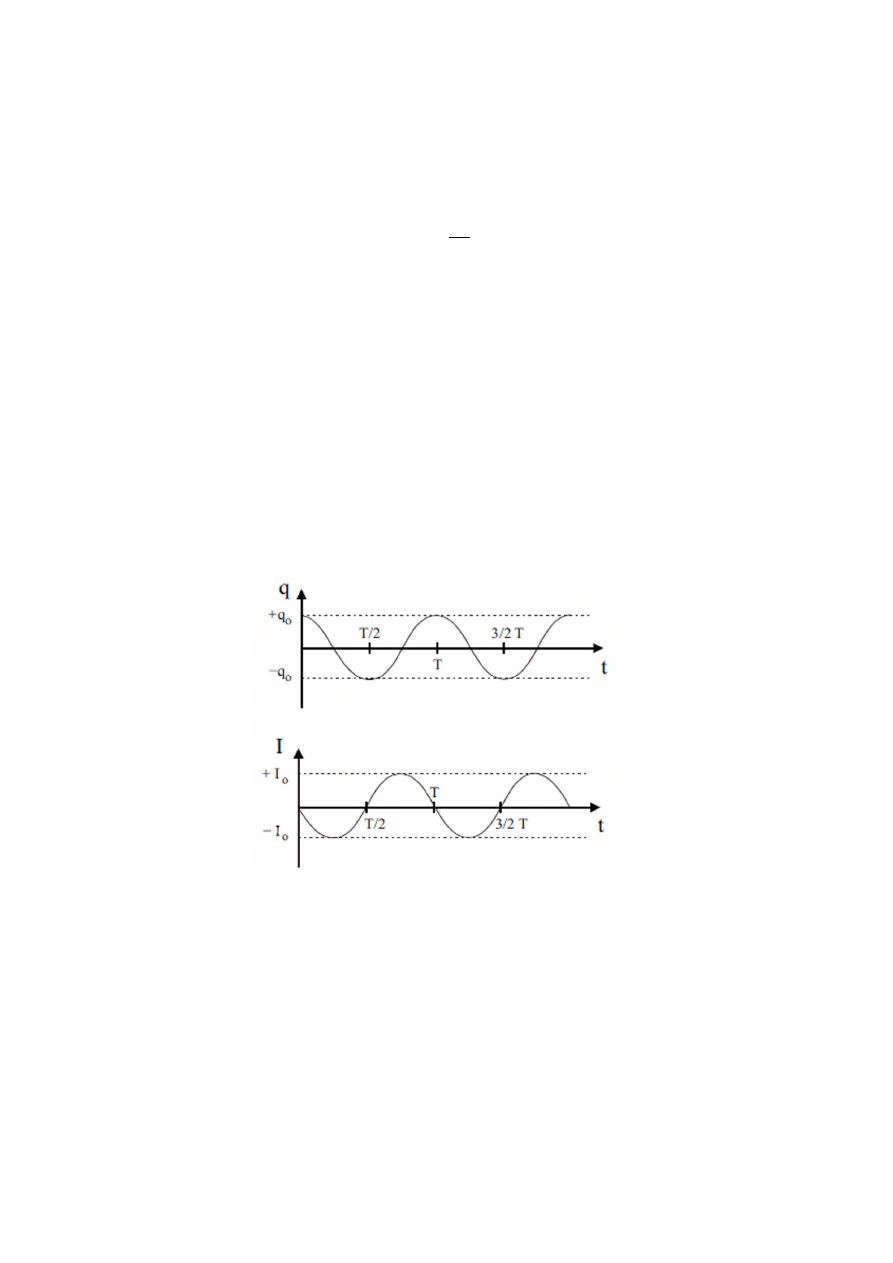
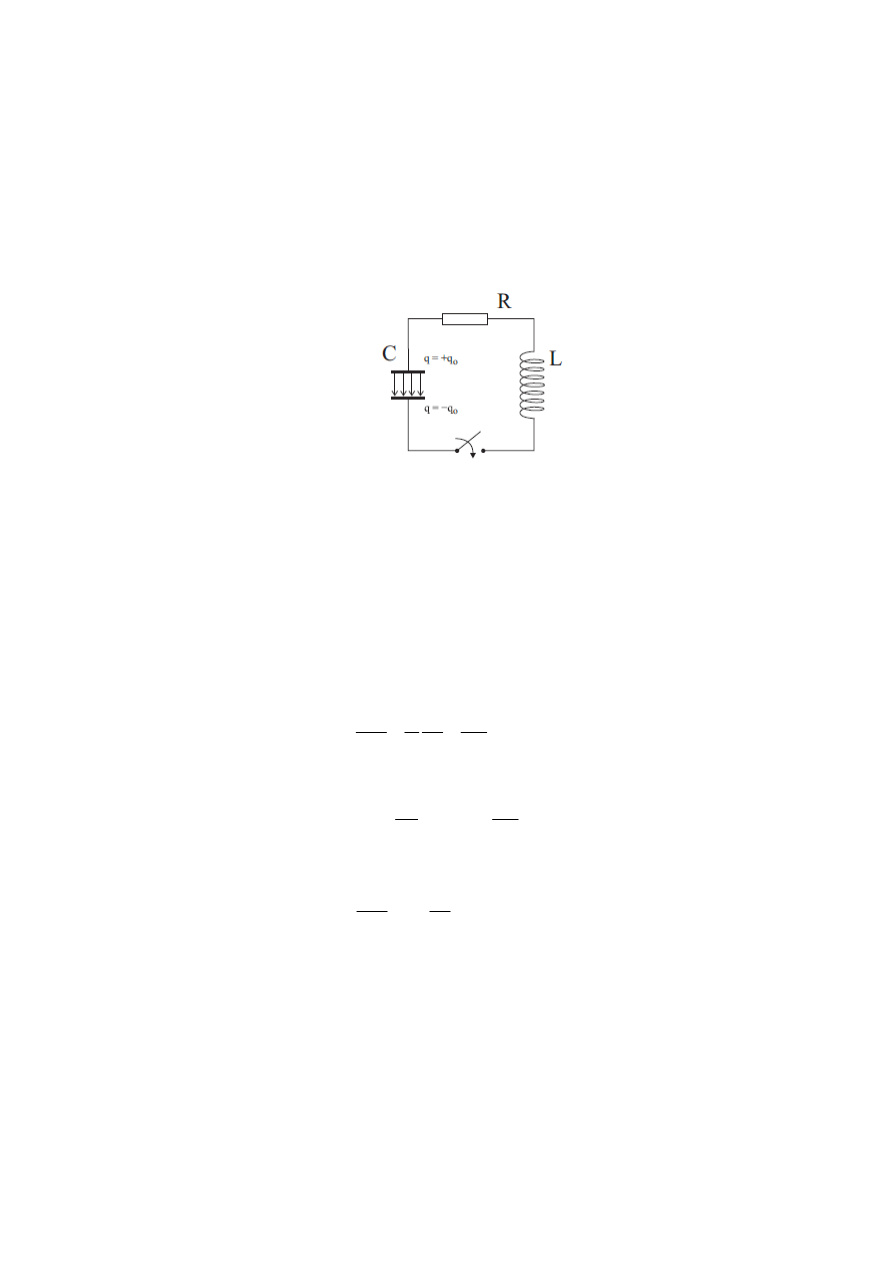
Na początku warto się zastanowić nad układem przedstawionym na rysunku 1.
Widzimy na nim kondensator scharakteryzowany pojemnością C oraz cewkę opisywaną
indukcyjnością L. W obwodzie pomijamy opory pochodzące od przewodów oraz
przyjmujemy, że zaczynamy rozważania w chwili, w której kondensator jest naładowany
ładunkiem początkowym
0
q .
W celu znalezienia funkcji opisującej, jak zmienia się w czasie ładunek na okładkach
kondensatora musimy przypomnieć sobie treść II prawa Kirchhoffa, które mówi, że suma
napięć na wszystkich elementach układu musi dać zero. Ponieważ nasz obwód składa się
z dwóch elementów możemy zapisać równość:
L
C
U
U
=
.
(3.1)
Rys. 1 Schemat obwodu LC
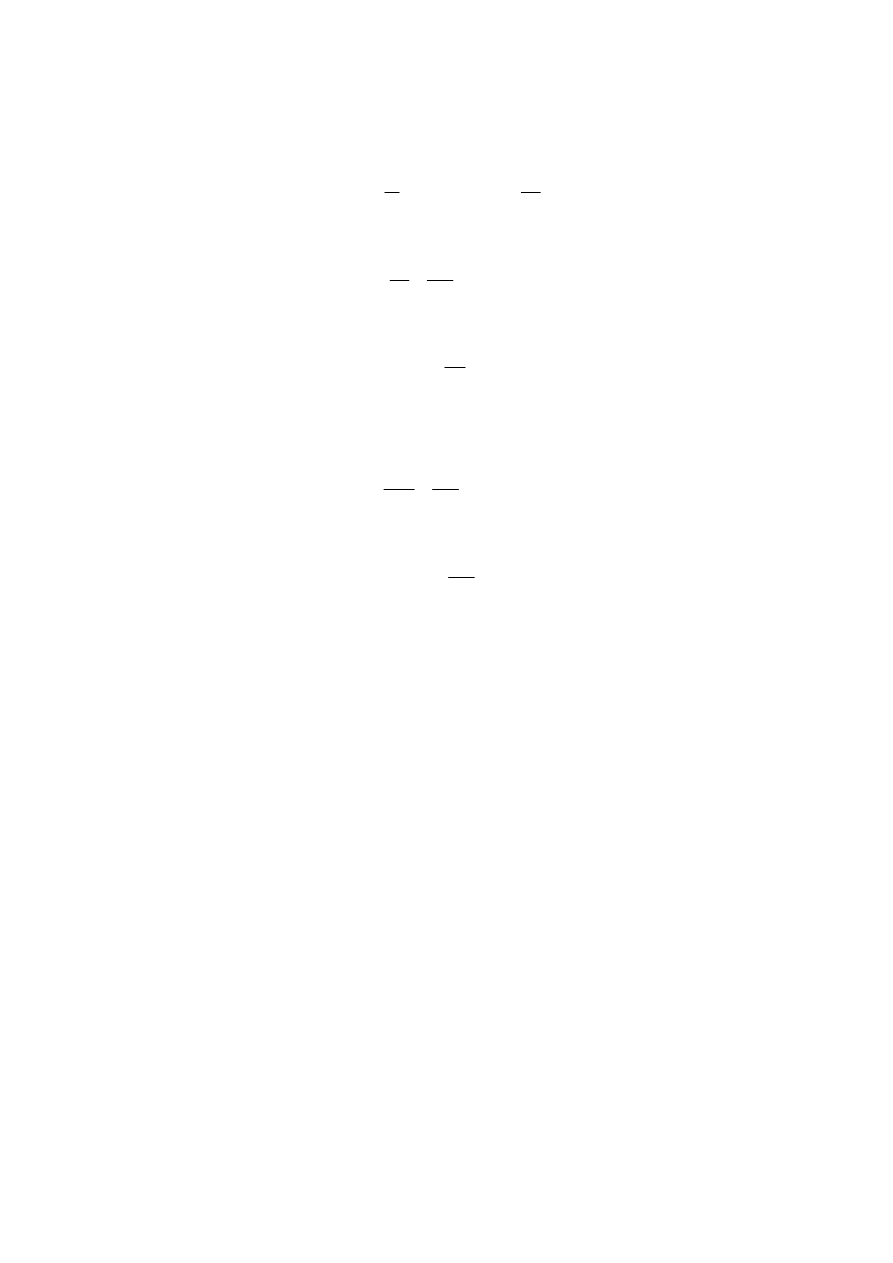
4
Teraz musimy jedynie przypomnieć sobie, jak wyrażamy napięcia na kondensatorze i na
cewce. Otóż:
dt
dI
L
U
C
q
U
L
C
-
=
=
,
.
(3.2)
Jeśli teraz wstawimy wzory (3.2) do równości (3.1) oraz uporządkujemy otrzymamy równane:
0
1
=
+
q
LC
dt
dI
.
(3.3)
Pamiętając, że:
dt
dq
I
=
,
(3.4)
i wstawiając tą zależność do (3.3) otrzymujemy szukane równanie opisujące wartość ładunku
elektrycznego na okładkach kondensatora:
0
1
2
2
=
+
q
LC
dt
q
d
.
(3.5)
Dla ułatwień obliczeń wygodnie jest wprowadzić nową stałą, taką, że:
LC
1
2
0
=
w
,
(3.6)
wielkość
0
w
nazywać będziemy częstością własną układu.
Równanie (3.5) jest równaniem różniczkowym drugiego rodzaju, liniowym, jednorodnym,
dlatego rozwiązania będziemy szukać w postaci wykładniczej, jako:
( )
t
e
t
q
a
=
.
(3.7)
Tę funkcję i jej drugą pochodną wstawiamy do (3.5), co daje równanie algebraiczne:
0
2
0
2
=
+
w
a
,
(3.8)
które ma dwa pierwiastki
0
w
a
i
±
=
. Rozwiązaniem równania (3.5) jest, więc kombinacja
liniowa funkcji wykładniczych, co daje ogólne rozwiązanie w postaci:
( )
t
i
t
i
e
c
e
c
t
q
0
0
2
1
w
w
-
+
=
.
(3.9)
Otrzymane rozwiązanie może być niepokojące ze względu na fizyczny sens funkcji (3.9),
ponieważ pojawia się tam jednostka zespolona i. Dlatego korzystając ze wzoru Eulera
j
j
j
sin
cos
i
e
i
±
=
±
można to rozwiązanie przedstawić w innej postaci:
( )
(
)
(
)
(
) (
)
,
sin
cos
sin
cos
sin
cos
0
2
1
0
2
1
0
0
2
0
0
1
t
c
c
i
t
c
c
t
i
t
c
t
i
t
c
t
q
w
w
w
w
w
w
-
+
+
=
=
-
+
+
=
( )
t
A
t
A
t
q
0
2
0
1
sin
cos
w
w
+
=
.
(3.10)
5
Ostatnia postać jest dobra, bo nie zawiera jednostki urojonej i stałe
2
1
A
i
A
możemy
traktować, jako rzeczywiste:
Â
Î
2
1
, A
A
.
Wyznaczmy teraz wartości stałych
2
1
A
i
A
. W tym celu użyjmy warunków początkowych:
( )
( )
0
0
,
0
0
=
=
dt
dq
q
q
.
(3.11)
Po wykorzystaniu powyższych warunków dostajemy rozwiązanie szczególne równania (3.5):
( )
( )
t
q
t
q
0
0
cos
w
=
.
(3.12)
Jednak wartość ładunku elektrycznego na okładkach kondensatora jest trudno mierzalna i nie
praktyczna, dlatego wygodniej jest zróżniczkować powyższy wzór, aby otrzymać zależność
na wartość natężenia prądu elektrycznego. Pamiętając o zależności (3.4) otrzymujemy:
( )
( )
t
q
t
I
0
0
0
sin
w
w
-
=
,
(3.13)
wygodnie jest przyjąć, że
0
0
0
w
q
I
=
, wówczas równanie (3.13) możemy przepisać w postaci:
( )
( )
.
sin
0
0
t
I
t
I
w
-
=
.
(3.14)
Przeanalizujmy teraz na rysunkach zależności opisane wzorami (3.12) oraz (3.14).
Analizując wykresy widzimy, że w momencie rozładowywania się kondensatora w układzie
pojawia się przepływ prądu elektrycznego w kierunku zgodnym z ruchem wskazówek zegara.
W momencie, gdy kondensator jest rozładowany w obwodzie możemy zmierzyć maksymalną
wartość natężenia prądu elektrycznego. W następnej fazie prąd jest wytwarzany przez cewkę,
która ładuje kondensator w sposób przeciwny do początkowego. Po czym cykl zaczyna się od
nowa tyle, że w przeciwną stronę. Widzimy również, że wartość natężenia prądu
Rys. 2
a) Wykres ładunku elektrycznego na okładkach kondensatora w funkcji czasu
b) Zależność natężenia prądu elektrycznego w obwodzie od czasu
a)
b)
6
elektrycznego w ciągu czasu T zmienia wartość z dodatniej na ujemną, dlatego mówimy, że
mamy tu do czynienia z przemiennym prądem elektrycznym.
3.2. Drgania obwodu LC z zewnętrzną siłą elektromotoryczną
Teraz
rozpatrzmy
układ
LC,
do
którego
podłączymy
zewnętrzną
siłę
elektromotoryczną, co ilustruje rysunek 3.
Przyjmijmy, że napięcie zewnętrznej siły elektromotorycznej z częstością wymuszającą
w
w
opisane będzie wzorem:
( )
( )
t
U
t
U
w
w
sin
max
=
.
(3.15)
Korzystając z II prawa Kirchhoffa można zapisać równość:
( )
t
U
U
U
L
C
+
=
,
(3.16)
uwzględniając zależności (3.2), (3.4) oraz (3.15) można zapisać równanie różniczkowe
opisujące zmianę ładunku elektrycznego na okładkach kondensatora:
t
U
q
dt
q
d
w
w
w
sin
0
2
0
2
2
=
+
,
(3.17)
gdzie:
L
U
U
LC
max
0
2
0
,
1
=
=
w
.
(3.18)
Jest to równanie liniowe niejednorodne. Wiemy, że rozwiązaniem takiego równania jest suma
równania jednorodnego oraz szczególnego. Rozwiązanie równania jednorodnego jest takie
samo jak równania (3.5), czyli:
( )
(
)
j
w
+
=
t
q
t
q
jed
0
0
cos
.
(3.19)
Natomiast rozwiązania szczególnego równania (3.17) szukamy w rytmie zewnętrznej siły
elektromotorycznej w możliwie najprostszej postaci:
Rys. 3
Schemat obwodu LC z zewnętrzną siłą elektromotoryczną

7
( )
( )
t
h
t
q
w
sz
w
sin
=
.
(3.20)
Stałą h wyznaczamy wstawiając tę funkcję do równania (3.17)
t
U
t
h
t
h
w
w
w
w
w
w
w
w
w
sin
sin
sin
0
2
0
2
=
+
-
,
0
2
0
2
U
h
h
w
=
+
-
w
w
,
skąd
2
2
0
0
w
U
h
w
w
-
=
,
(3.21)
oraz
( )
t
U
t
q
w
w
sz
w
w
w
sin
2
2
0
0
-
=
.
(3.22)
Ogólne rozwiązanie jest postaci:
( )
(
)
t
U
t
q
t
q
w
w
w
w
w
j
w
sin
cos
2
2
0
0
0
0
-
+
+
=
.
(3.23)
Otrzymaliśmy rozwiązanie, które nie można nazwać harmonicznym, gdyż jest to suma dwóch
drgań o różnych częstościach. Niepokojący jest przypadek, gdy
0
w
w
=
w
, gdyż wówczas
w mianowniku drugiego składnika sumy mamy w rezultacie zero, czyli amplituda tego
drgania staje się nieskończona. „Przyjrzyjmy się temu jednak bliżej. Powołując się na wzór
(3.10) możemy zapisać równanie (3.23), jako:
( )
t
U
t
A
t
A
t
q
w
w
w
w
w
w
w
sin
sin
cos
2
2
0
0
0
2
0
1
-
+
+
=
.
(3.24)
Wprowadzając warunki początkowe w najbardziej ogólnej formie:
( )
( )
0
0
0
,
0
I
q
q
q
=
=
&
,
(3.25)
wyliczamy stałe
2
1
A
i
A
:
0
2
2
0
0
0
0
2
0
1
,
w
w
w
w
w
w
w
U
I
A
q
A
-
-
=
=
(3.26)
i wstawiamy do rozwiązania (3.24):
( )
t
U
t
U
I
t
q
t
q
w
w
w
w
w
w
w
w
w
w
w
w
w
w
sin
sin
cos
2
2
0
0
0
0
2
2
0
0
0
0
0
0
-
+
÷÷
ø
ö
çç
è
æ
-
-
+
=
.
Grupujemy wyrazy zawierające osobliwy mianownik:
( )
÷÷
ø
ö
çç
è
æ
-
-
+
+
=
t
t
U
t
I
t
q
t
q
w
w
w
0
0
2
2
0
0
0
0
0
0
0
sin
sin
sin
cos
w
w
w
w
w
w
w
w
w
.
Korzystamy z równości
(
)(
)
w
w
w
w
w
w
w
w
w
+
-
=
-
0
0
2
2
0
:
8
( )
0
sin
sin
0
0
0
0
0
0
0
0
0
sin
cos
w
w
w
w
w
w
w
w
w
w
w
w
-
-
+
-
+
=
w
t
t
w
w
w
w
U
t
I
t
q
t
q
.
Interesuje nas granica rezonansu
0
w
w
®
w
:
( )
( )
0
sin
sin
0
0
0
0
0
0
0
0
0
0
lim
2
sin
cos
lim
w
w
w
w
w
w
w
w
w
w
w
w
w
-
-
-
+
=
=
®
®
w
t
t
rez
w
w
w
w
U
t
I
t
q
t
q
t
q
.
W ostatnim wyrazie rozpoznajemy pochodną funkcji
( )
w
w
w
t
f
sin
=
w punkcie
0
w
w
=
.
Pochodna ta wynosi
2
sin
cos
w
w
w
w
w
t
t
t
d
df
-
=
,
Więc możemy napisać
( )
(
)
t
t
t
U
t
I
t
q
t
q
rez
0
0
0
2
0
0
0
0
0
0
0
sin
cos
2
sin
cos
w
w
w
w
w
w
w
-
-
+
=
.
Grupujemy wyrazy przy cosinusie i sinusie:
( )
t
U
I
t
t
U
q
t
q
rez
0
2
0
0
0
0
0
0
0
0
sin
2
cos
2
w
w
w
w
w
÷÷
ø
ö
çç
è
æ
+
+
÷÷
ø
ö
çç
è
æ
-
=
.
(3.27)”
1
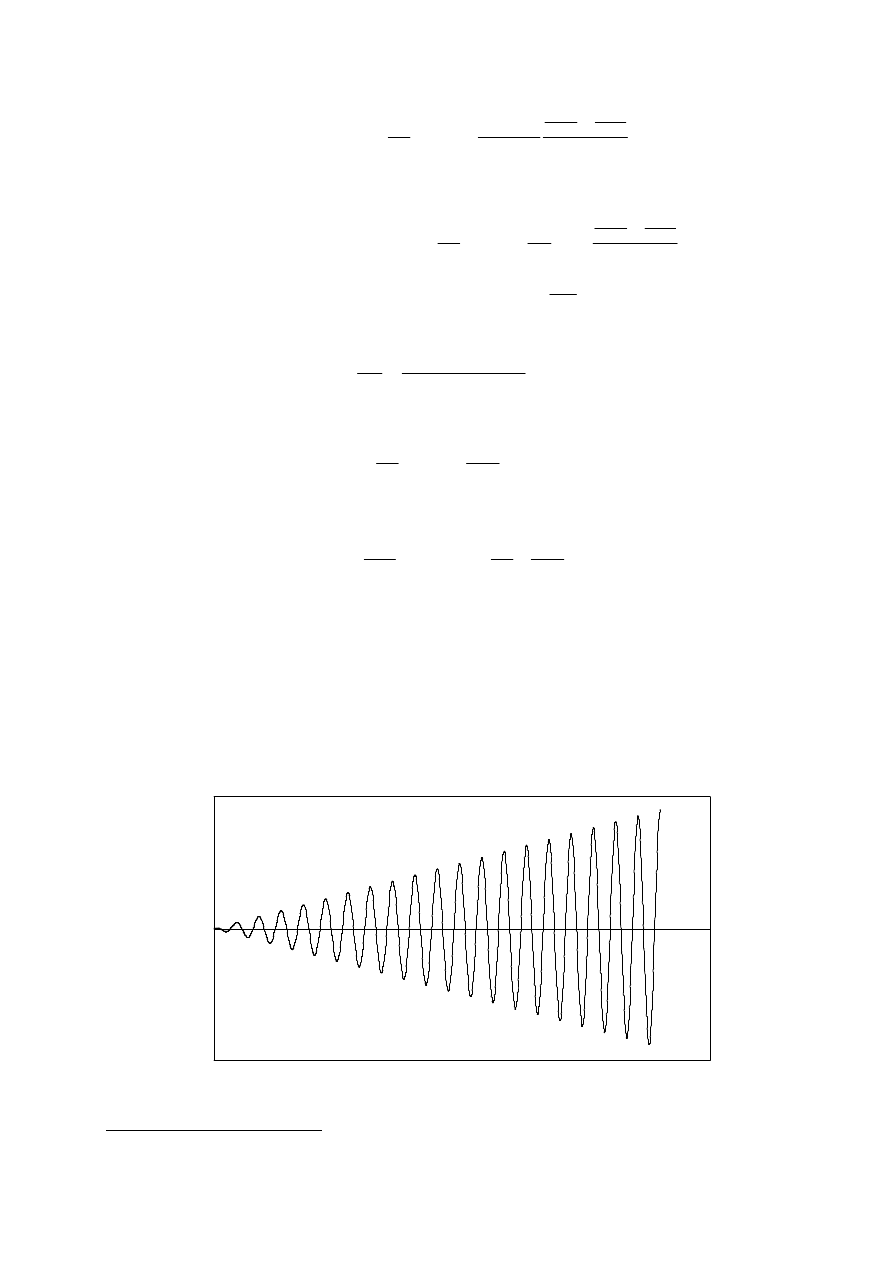
Widzimy, że w przypadku rezonansu amplituda nie staje się od razu nieskończona, ale rośnie
liniowo z czasem, co jest niebezpieczne dla układu. Ponieważ na kondensatorze będzie
utrzymywać się duże napięcie o coraz większej wartości, dla pewnej granicznej wartości
dielektryk będący umieszczony między okładkami kondensatora zacznie zachowywać się jak
przewodnik i przestanie spełniać swoje zadanie, będziemy mieli do czynienia z tzw.
przebiciami na kondensatorze. Sytuację opisaną wzorem (3.27) dobrze obrazuje rysunek 4.
czas
warto
ść
ł
adunku elektrycznego na ok
ładkach
kondensatora
1
Rozumowanie powtórzone za prof. B. Jancewiczem, Mechanika klasyczna – notatki z wykładu 2010 r., s.15
Rys. 4
Wartość ładunku elektrycznego na kondensatorze podczas rezonansu w obwodzie LC
9
4. Drgania obwodu RLC
4.1 Drgania własne obwodu
Teraz proponuję rozpatrzeć przypadek bardziej realny, tzn. do obwodu układu LC
włączymy szeregowo opornik, którego interpretacją może być opór przewodów użytych
w układzie lub rzeczywisty opornik, którego opór jest dużo większy od oporu przewodów
łączących.
Patrząc na rysunek 5, możemy zapisać dla tego układu równość wynikającą z II prawa
Kirchhoffa:
L
R
C
U
U
U
=
+
,
(4.1)
wiedząc, że
IR
U
R
=
oraz korzystając z zależności (3.2) i (3.4) możemy powyższą równość
zapisać, jako:
0
1
2
2
=
+
+
q
LC
dt
dq
L
R
dt
q
d
.
(4.2)
Dla ułatwień obliczeniowych warto jest wprowadzić stałe:
LC
L
R
1
,
2
2
0
=
=
w
b
.
(4.3)
Po ich wprowadzeniu otrzymujemy równanie tożsame z równaniem (4.2):
0
2
2
0
2
2
=
+
+
q
dt
dq
dt
q
d
w
b
.
(4.4)
Mamy do czynienia z równaniem różniczkowym liniowym, jednorodnym, więc rozwiązań
szukamy w postaci (3.7), co daje na równanie algebraiczne:
0
2
2
0
2
=
+
+
w
ba
a
.
(4.5)
Naszym zadaniem jest wyznaczyć
,
a
w tym celu policzmy wyróżnik równania (4.5):
2
0
2
4
4
w
b
-
=
D
.
(4.6)
Rys. 5
Schemat obwodu RLC
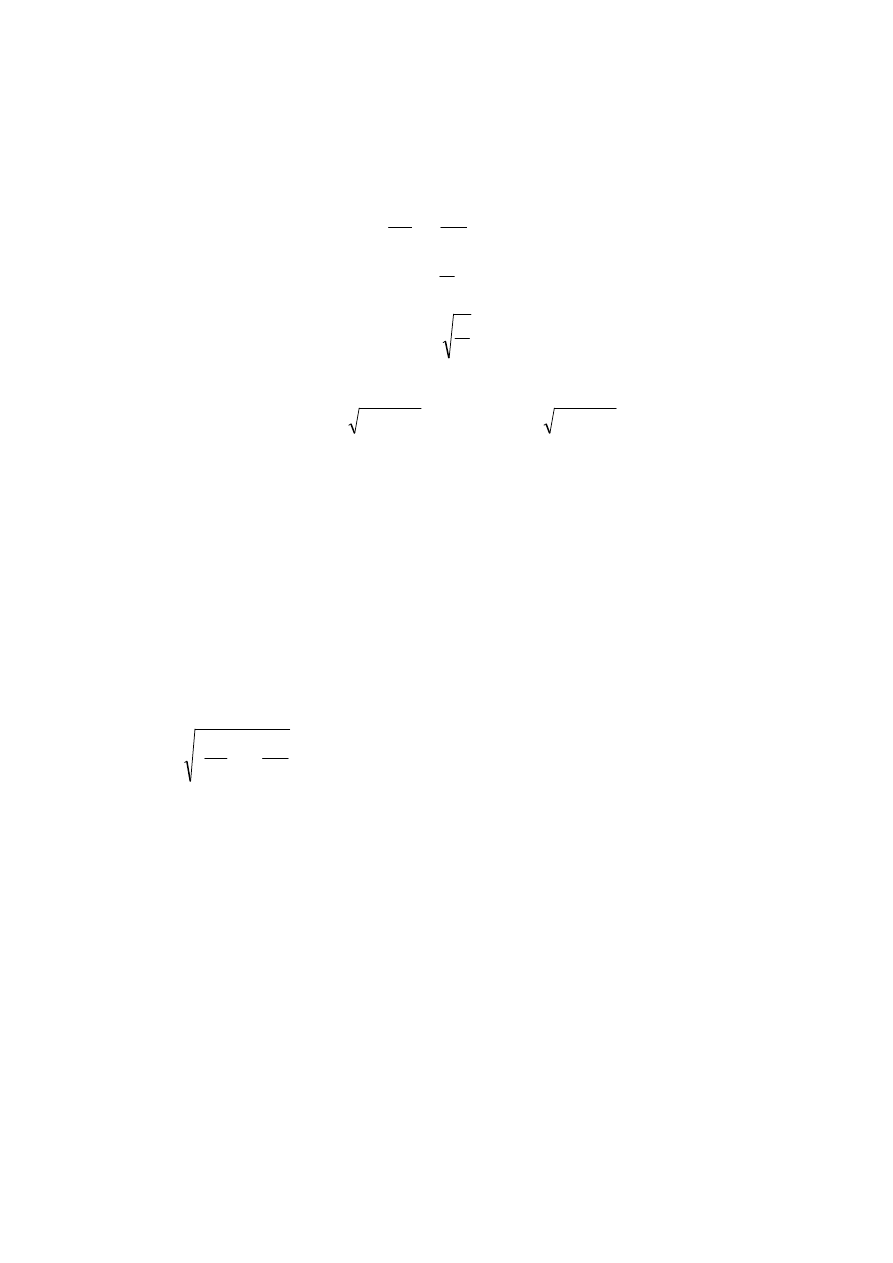
10
Przypadek najczęściej spotykany w pracowniach odpowiada wartościom, dla których
0
<
D
,
dlatego zajmijmy się szczegółowo tym przypadkiem.
Korzystając z zależności (4.3) możemy wyznaczyć warunek, dla którego
0
<
D
:
,
4
,
0
1
4
2
2
2
C
L
R
LC
L
R
<
<
-
C
L
R
<
.
(4.7)
Zatem rozwiązaniem równania (4.5) spełniającym warunek (4.7) jest:
2
0
2
2
2
0
2
1
,
w
b
b
a
w
b
b
a
-
+
-
=
-
-
-
=
i
i
.
(4.8)
Teraz możemy zapisać całkę ogólną równania (4.4) jako:
( )
t
t
e
c
e
c
t
q
2
1
2
1
a
a
+
=
.
(4.9)
Wygodnie jest wprowadzić stałą:
2
0
2
2
w
b
w
-
=
,
(4.10)
wówczas rozwiązanie (4.9) możemy zapisać z uwzględnieniem (4.8), jako:
( )
(
)
.
2
1
t
i
t
i
t
e
c
e
c
e
t
q
w
w
b
+
=
-
-
(4.11)
Wiemy, że korzystając z wzoru Eulera można przejść do postaci:
( )
(
)
j
w
b
+
=
-
t
e
q
t
q
t
cos
0
,
(4.12)
gdzie
.
1
2
2
LC
L
R
-
÷
ø
ö
ç
è
æ
=
w
Wyrażenie (4.12) jest jednak niepraktyczne ze względu no to, że opisuję jak zmienia się
ładunek na kondensatorze, dlatego dobrze jest wyznaczyć na jego podstawie jak zmienia się I.
Pamiętając o zależności (3.4) otrzymujemy:
( )
(
)
(
)
[
]
j
w
w
j
w
b
b
+
+
+
-
=
-
t
t
e
q
t
q
t
sin
cos
0
.
(4.13)
Pierwszy składnik w nawiasie jest do pominięcia ze względu na (4.7), możemy zapisać:
( )
(
)
,
sin
0
j
w
w
b
+
-
»
-
t
e
q
t
q
t
(4.14)
a korzystając z warunku
w
0
0
q
I
=
otrzymujemy:
( )
(
)
.
sin
0
j
w
b
+
-
»
-
t
e
I
t
q
t
(4.15)
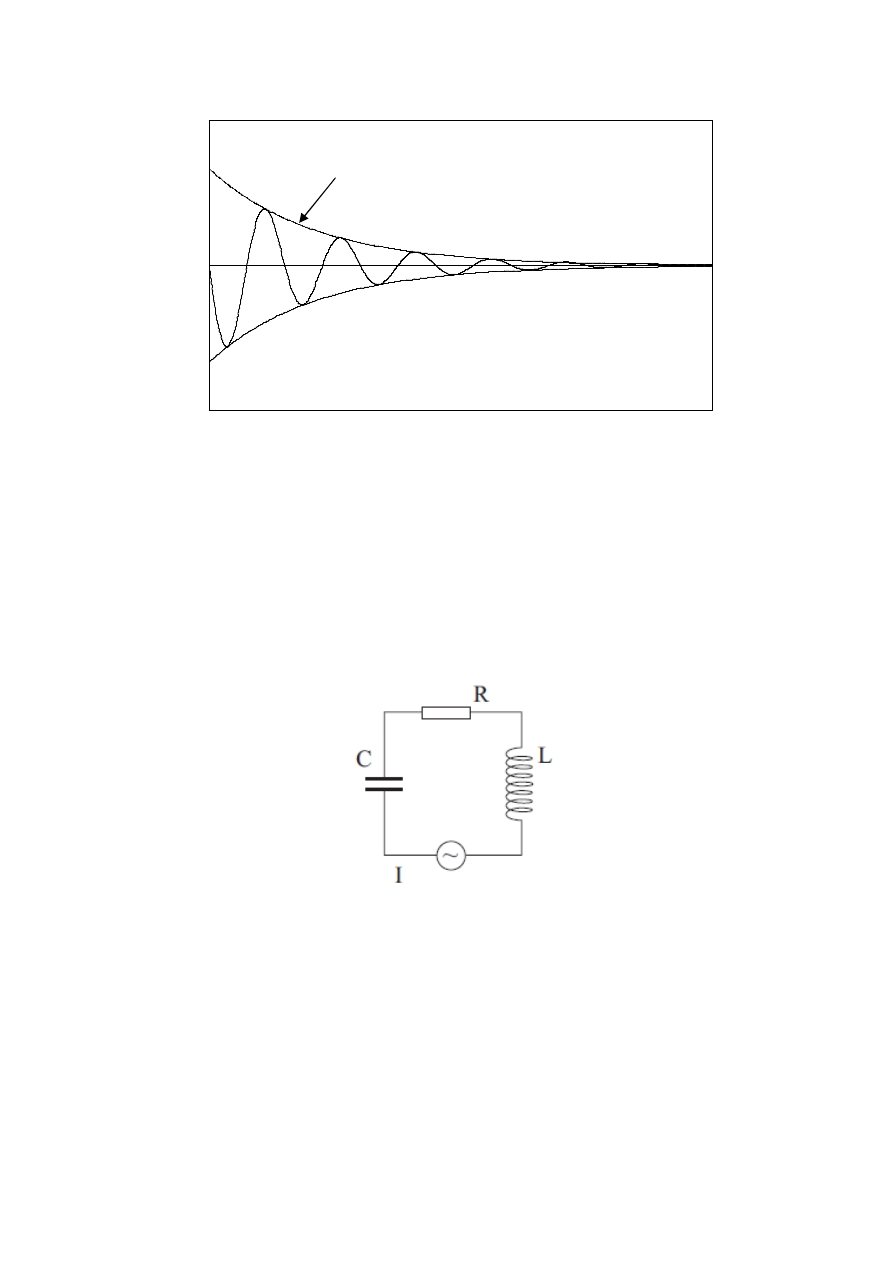
Rozwiązanie to w sposób graficzny przedstawia rysunek 6.
11
Na powyższym rysunku widzimy, że wartość natężenia prądu dla
¥
®
t
maleje do
zera, jeśli do układu włączyć szeregowo galwanometr, to obserwowalibyśmy wahania
wskazówki wokół zera na skali z malejącymi wychyleniami.
4.2 Drgania obwodu RLC z zewnętrzną siłą elektromotoryczną
Teraz do naszego układu RLC włączamy szeregowo zewnętrzne źródło napięcia.
W tym przypadku z II prawa Kirchhoffa wynika równość:
e
+
=
+
L
R
C
U
U
U
.
(4.16)
Załóżmy, jak poprzednio, że:
t
w
w
e
e
sin
0
=
,
(4.17)
wówczas otrzymujemy równanie:
czas
Warto
ść
nat
ęż
enia pr
ądu
t
e
I
b
-
0
Rys. 6
Wartość natężenia prądu w układzie RLC
Rys. 7
Schemat układu RLC z zewnętrzną siłą elektromotoryczną
e

12
t
L
q
LC
I
L
R
dt
dI
w
w
e
sin
1
0
=
+
+
,
(4.18)
po zróżniczkowaniu i wykorzystaniu zależności (4.3) mamy:
t
L
I
dt
dI
dt
I
d
w
w
w
w
e
w
b
cos
2
0
2
0
2
2
=
+
+
.
(4.19)
Otrzymaliśmy równanie, które od razu pozwoli nam wyznaczyć, jak zmienia się natężenie
prądu elektrycznego w obwodzie bez zastanawiania się nad wartościami ładunku
elektrycznego. Rozwiązania równania (4.19) będziemy szukać w możliwie najprostszej
postaci:
(
)
j
w
-
=
t
I
I
w
sin
0
.
(4.20)
Musimy tak dobrać stałe
0
I oraz
j
, aby funkcja (4.20) była rozwiązaniem równania (4.19).
W tym celu wyliczmy jej pierwszą i drugą pochodną:
(
)
(
)
.
sin
,
cos
2
0
2
2
0
j
w
w
j
w
w
-
-
=
-
=
t
I
dt
I
d
t
I
dt
dI
w
w
w
w
Teraz funkcję (4.20) oraz jej pochodne wstawmy do równania (4.19), po uporządkowaniu
równania otrzymujemy równość:
(
)
(
)
t
t
R
I
t
L
C
I
w
w
w
w
w
w
e
j
w
j
w
w
w
cos
cos
sin
1
0
0
0
=
-
+
-
÷÷
ø
ö
çç
è
æ
-
,
(4.21)
jeśli wprowadzić stałą
j
a
w
j
w
a
+
=
Þ
-
=
t
t
w
w
, to po wykorzystaniu wzoru na cosinus
sumy kątów możemy zapisać równość (4.21), jako:
( )
( )
( ) ( )
( ) ( )
a
j
e
a
j
e
a
a
w
w
sin
sin
cos
cos
cos
sin
1
0
0
0
0
-
=
+
÷÷
ø
ö
çç
è
æ
-
R
I
L
C
I
w
w
.
(4.22)
Wiemy, że funkcje sinus i cosinus są liniowo niezależne, dlatego równość otrzymamy
wówczas, gdy odpowiednie współczynniki stojące przy funkcjach trygonometrycznych będą
sobie równe.
( )
( )
.
sin
1
,
cos
0
0
0
0
j
e
w
w
j
e
=
÷
ø
ö
ç
è
æ
-
=
C
L
I
R
I
(4.23)
Jeżeli wzory (4.23) podniesiemy do kwadratu i dodamy stronami otrzymamy:
2
0
2
2
2
0
1
e
w
w
=
ú
ú
û
ù
ê
ê
ë
é
÷
ø
ö
ç
è
æ
-
+
C
L
R
I
,
(4.24)
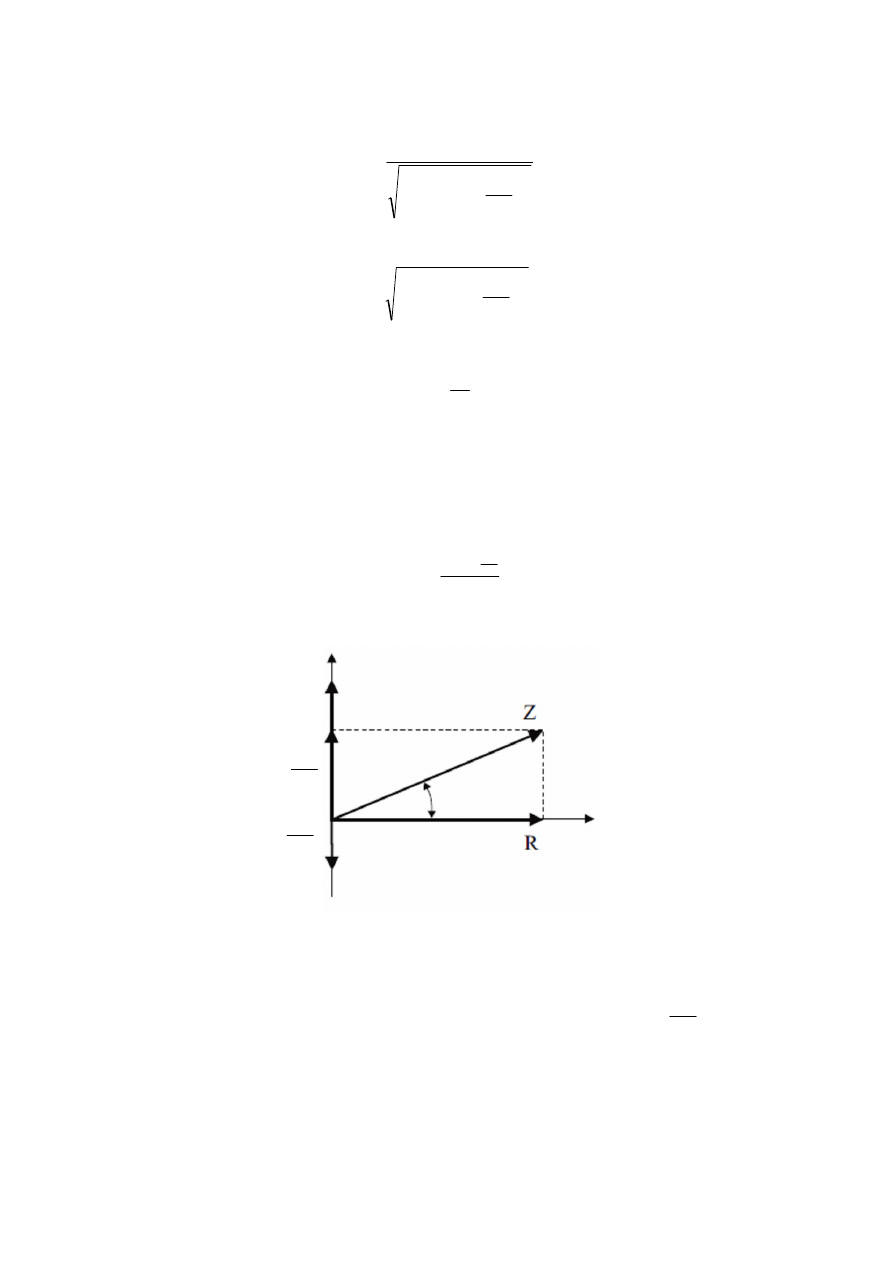
13
po przekształceniu:
2
2
0
0
1 ÷
ø
ö
ç
è
æ
-
+
=
C
L
R
I
w
w
e
.
(4.25)
Jeżeli wielkość znajdującą się w mianowniku zapisać, jako:
2
2
1 ÷
ø
ö
ç
è
æ
-
+
=
C
L
R
Z
w
w
,
(4.26)
wówczas wzór (4.25) możemy zapisać prościej:
Z
I
0
0
e
=
.
(4.27)
Wzór ten jest odpowiednikiem prawa Ohma (które dotyczy obwodu prądu stałego), przy
czym
Z
jest odpowiednikiem oporu. Wielkość
Z
nazywamy impedancją (oporem pozornym,
zawadą).
Jeśli natomiast wzory (4.23) podzielimy stronami otrzymamy warunek na stałą
j
:
( )
R
L
tg
C
w
w
j
1
-
=
.
(4.28)
Wzory (4.26) oraz (4.28) mają łatwą interpretację geometryczną:
Narysujmy w kierunku dodatnim osi odciętych wektor o długości
R
, w dodatnim
kierunku osi rzędnych wektor o długości
L
w
, a ujemnym kierunku wektor
C
w
1
. Wtedy jak
łatwo stwierdzić, długość wypadkowego wektora jest równa impedancji
Z
obwodu, a kąt
między tym wektorem a osią odciętych jest równy przesunięciu fazowemu
j
.
C
w
1
L
w
C
L
w
w
1
-
j
Rys. 8
Interpretacja geometryczna zawady i przesunięcia fazowego
14
Można się jeszcze zastanowić, kiedy
0
I osiąga wartość największą. Najłatwiej jest to
obliczyć korzystając z wzoru (4.27). Widać z niego, że
0
I osiągnie wartość największą
w przypadku, gdy
Z
będzie mieć wartość najmniejszą. Jest tak tylko wtedy, gdy:
,
0
1 =
-
C
L
w
w
(4.29)
wynika stąd, że:
.
1
LC
r
=
w
(4.30)
Wielkość
r
w
nazywamy częstością rezonansową obwodu RLC.
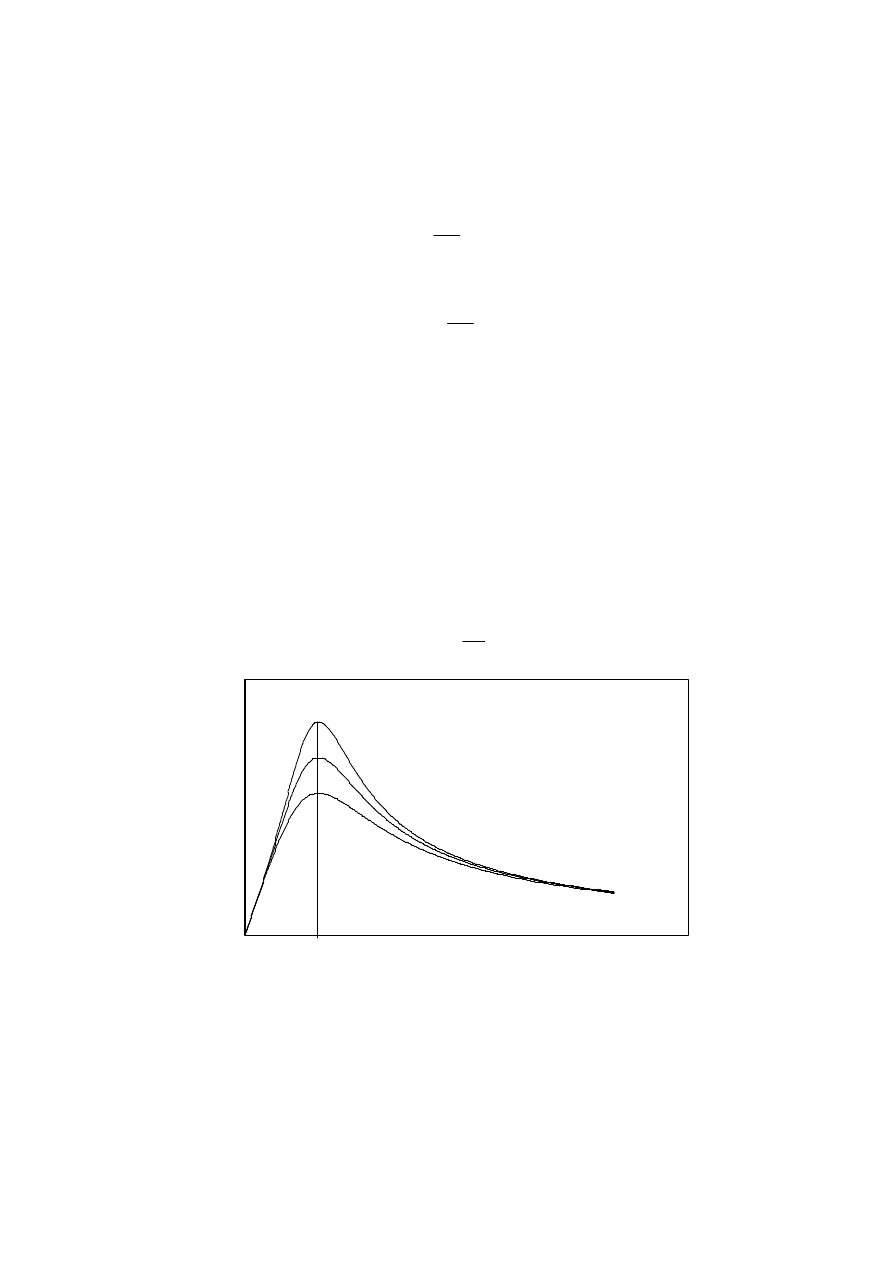
Rysunek 9 przedstawia, w jaki sposób zależy amplituda natężenia prądu w funkcji
częstości zewnętrznej siły elektromotorycznej. Widać z niego, że w przypadku małych
wartości oporów krzywa rezonansowa staje się bardziej strzelista, natomiast dla dużych
oporów staje się rozmyta. Rozpatrywany przypadek jest bardzo ważny zwłaszcza
w radiotechnice, gdyż opisuje schemat działania prostego radia. W przypadku tego urządzenia
źródłem zewnętrznej siły elektromotorycznej jest wektor indukcji magnetycznej B
r
,
pochodzący od fali radiowej. Wartość takiej siły jest ściśle określona przez prawo Faradaya:
t
B
E
rot
¶
¶
-
=
r
r
.
(4.31)
cz
ęstości
Warto
ść
nat
ęż
enia pr
ądu
3
2
1
R
R
R
<
<
1
R
2
R
3
R
r
w
Rys. 9
Zależność amplitudy natężenia prądu od częstości zewnętrznego źródła

15
Podsumowanie
Niniejsza praca została skierowana do osób, które zaczynają dopiero swoją przygodę
z obwodami prądu zmiennego. Jestem przekonany, że zawarte w niej treści są zrozumiałe i są
dobrym fundamentem do dalszej nauki w tym kierunku.
Na samym początku swojej pracy postawiłem pytanie. Jak rozumieć zwrot: „drgania
obwodów”? Być może, dla niektórych czytelników (zwłaszcza dla tych, którzy z uwagą
śledzili równania), odpowiedź nasuwa się sama. Otóż: otrzymane przeze mnie rozwiązania
równań różniczkowych, jak i one same są odpowiednikiem zapisów, jakie możemy spotkać
podczas zajmowania się matematyką związaną z oscylatorem harmonicznym. Dlatego
właśnie, ze względu na to podobieństwo mówi się o drganiach obwodów elektrycznych.

16
Literatura
• Halliday, Resnick, Podstawy Fizyki 3, Wydawnictwo Naukowe PWN, Warszawa 2007
• Prof. B. Jancewicz, Mechanika klasyczna – notatki z wykładu 2010, WFiA UWr
• Dr hab. R. Kucharczyk, Podstawy fizyki 2 – notatki z wykładu 2008, WFiA UWr
• Rys. 4, 6, 9 wykonane w programie Excel 2003
• Rys. 1, 2,3, 5, 7, 8 pobrane z wykładu Drgania w obwodach RLC i fale
elektromagnetyczne, Politechnika Gdańska 2009
Wyszukiwarka
Podobne podstrony:
Cw2 Stany nieustalone RC RLC id Nieznany
Badanie odbiornikow RLC id 7741 Nieznany (2)
Elementy RLC 1 id 160161 Nieznany
Badanie odbiornikow RLC id 7741 Nieznany (2)
Mostek RLC MT4080 2 id 308095 Nieznany
Cw5 Drganie relaksacyjne id 123 Nieznany
Drgania 4 id 141931 Nieznany
ORZ drgania id 340792 Nieznany
IMIC przyklady drgania id 21180 Nieznany
2005 UI RLC czas id 25392 Nieznany (2)
MF12 drgania id 297511 Nieznany
ARKUSZ GM P1 142 wersja A id 68 Nieznany (2)
stany nieustalone, Politechnika Poznańska, Elektrotechnika, Teoria obwodów, Laboratoria, 12. Stany n
GOTOWE, Politechnika Poznańska, Elektrotechnika, Teoria obwodów, Laboratoria, 12. Stany nieustalone
lop drgania w03 id 273123 Nieznany
drgania belka id 141945 Nieznany
6 RLC mostki cw6 id 612202 Nieznany
!231 UI RLC czas id 504 Nieznany (2)
7 Drgania i fale id 45166 Nieznany
więcej podobnych podstron