Ćwiczenie 7

Temat:

STANY NIEUSTALONE W OBWODACH RL I RC

PRZY WYMUSZENIU STAŁYM

I.

ZAGADNIENIA

1.

Doświadczalna obserwacja czasowych przebiegów przejściowych przy
załączaniu i wyłączaniu napięcia stałego w obwodach RL, RC

2.

Porównanie obserwowanych przebiegów z przebiegami otrzymanymi za
pomocą obliczeń analitycznych.

II.

WIADOMOŚCI PODSTAWOWE

Stanem nieustalonym w obwodzie nazywa się stan pośredni, jaki występuje
między dwoma kolejnymi stanami ustalonymi. Stan nieustalony może powstać
pod wpływem zmiany konfiguracji obwodu, zmiany parametrów wchodzących
w jego skład, bądź zmiany wielkości wymuszających. Stany nieustalone można
opisać za pomocą równań różniczkowych lub różniczkowo-całkowych. Aby w
sposób jednoznaczny określić rozwiązanie takiego układu równań, konieczna
jest znajomość warunków początkowych. Przez warunki początkowe rozumie
się wartości zmiennych w stanie początkowym, czyli w chwili, w której
rozpoczyna się badanie zjawisk w danym obwodzie. Warunki początkowe mogą
być zerowe, jeżeli w chwili t=0 obwód jest w stanie bezenergetycznym (napięcia
i prądy mają wartość zero). W przeciwnym razie warunki początkowe są
niezerowe.
Zmiany zachodzące w obwodzie w określonej chwili i powodujące powstanie
stanów nieustalonych (np. zamykanie i otwieranie łącznika) nazywamy
komutacją. Cewka L i kondensator C są elementami zachowawczymi w
obwodzie i z nimi związane są tzw. Prawa komutacji, wynikające z zasady
zachowania energii. Energia pola magnetycznego cewki i pola elektrycznego
kondensatora nie może zmieniać się skokowo. Zasada ciągłości w chwili
komutacji strumienia Ψ skojarzonego z cewką o indukcyjności L jest
równoznaczna z zasadą ciągłości napięcia na jego zaciskach. Powyższe zasady
ciągłości strumienia i prądu w cewce oraz ładunku i napięcia kondensatora
nazywane są prawami komutacji. Prawa te można zapisać

a) gałąź z cewką:

( ) ( ) ( ) ( )

+

−

+

−

=

≡

Ψ

=

Ψ

0

0

0

0

L

L

i

i

b)

gałąź z kondensatorem:

( ) ( )

( )

( )

+

−

+

−

=

≡

=

0

0

0

0

C

C

u

u

q

q

W przeprowadzanym ćwiczeniu prawdziwe jest założenie (dla wszystkich
układów), że przed przełączeniem przełącznika w układzie panował stan
ustalony.

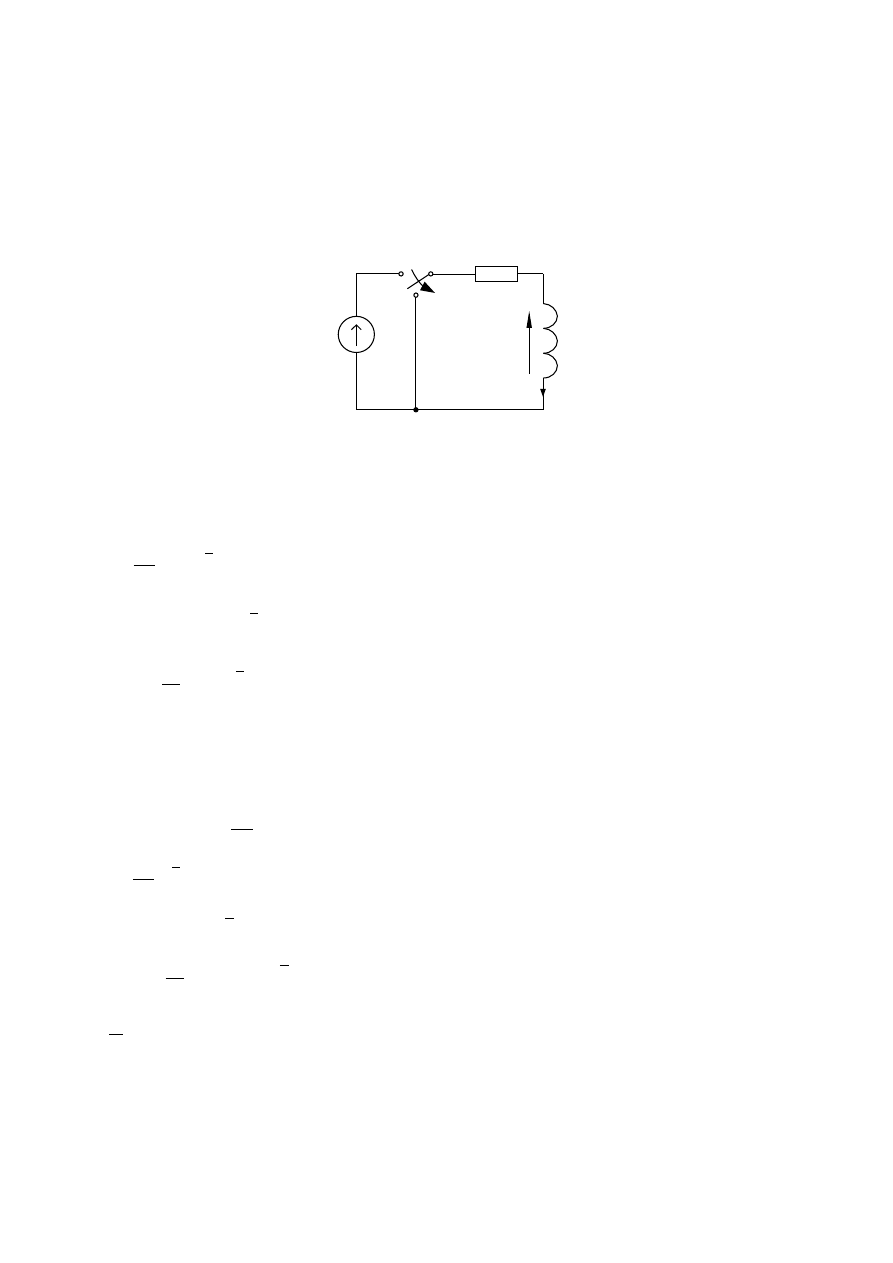
1.

Stan nieustalony w obwodzie RL przy wymuszeniu stałym

L

R

e

P

1

2

t=0

0

E

L

u

i

W chwili t=0 doprowadzono napięcie stałe E

0

do gałęzi RL (pozycja 1

przełącznika P

e

)

Warunki początkowe zakładamy zerowe

( ) ( )

0

0

0

=

=

+

−

L

L

i

i









−

=

−

t

L

R

e

R

E

i

1

0









−

=

=

−

t

L

R

R

e

E

Ri

u

1

0

t

L

R

L

e

E

dt

di

L

u

−

=

=

0

W chwili t=0 dokonano operacji łączeniowej, tj. zmiany położenia przełącznika
P

e

z pozycji 1 na 2. Gałąź RL zostaje zwarta.

Warunki początkowe w obwodzie są niezerowe

( ) ( )

R

E

i

i

L

L

0

0

0

=

=

+

−

t

L

R

e

R

E

i

−

=

0

t

L

R

R

e

E

Ri

u

−

=

=

0









−

=

=

−

t

L

R

L

e

E

dt

di

L

u

1

0

τ

=

R

L

(stała czasowa)

t

0

E

0

0

E

−

R

u

L

u

t

0

E

0

L

u

R

u

τ

t

0

E

R

0

i

τ

t

0

u

E

i

R

=

0

i

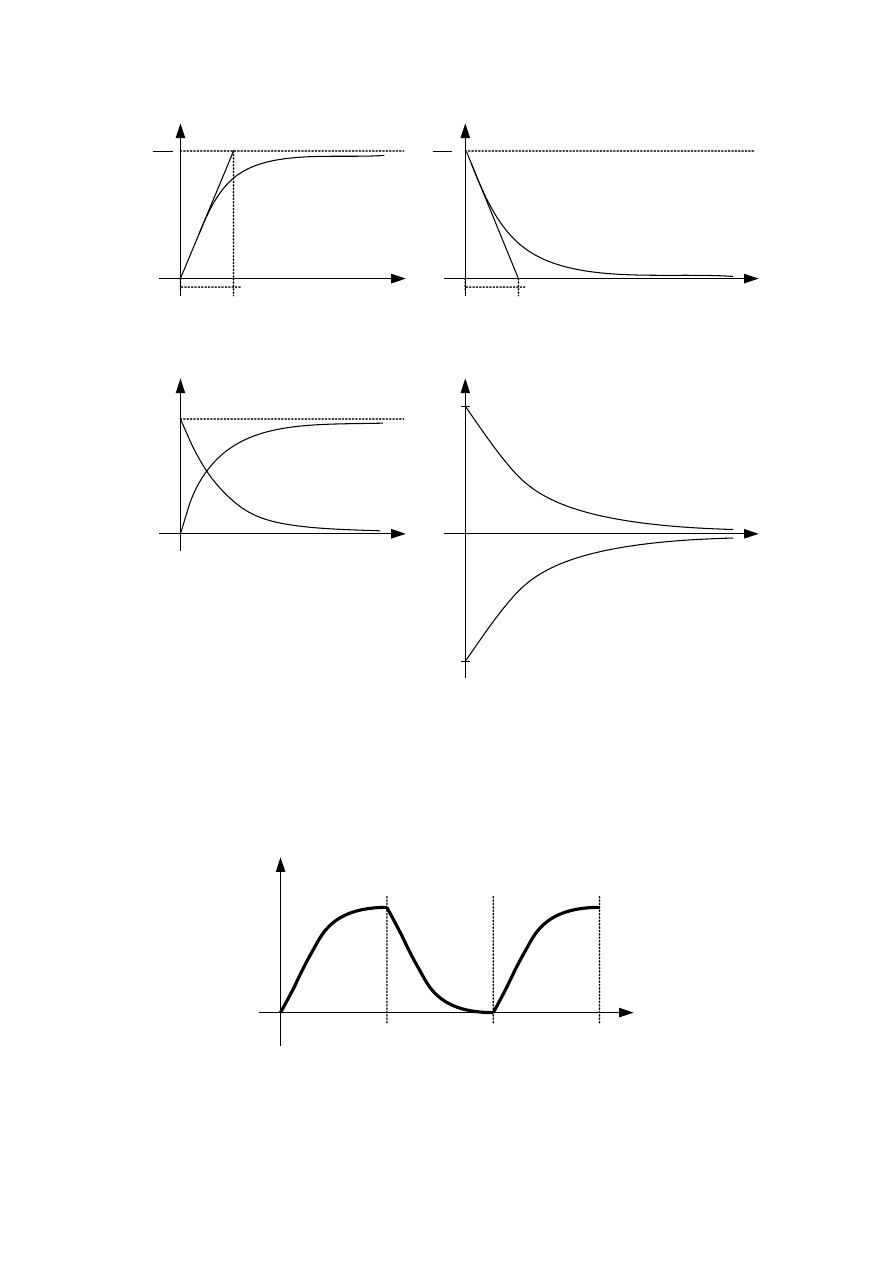
Gałąź RL przy załączaniu napięcia
stałego

Gałąź RL przy zwarciu

Czasowe przebiegi dla obu powyższych przypadków (przełącznik odpowiednio
w pozycjach 1 i 2) przedstawiono na rysunku:

t

( )

R

u t

II

I

→

I

II

→

II

I

→

poz.1

poz.2

0

E

u

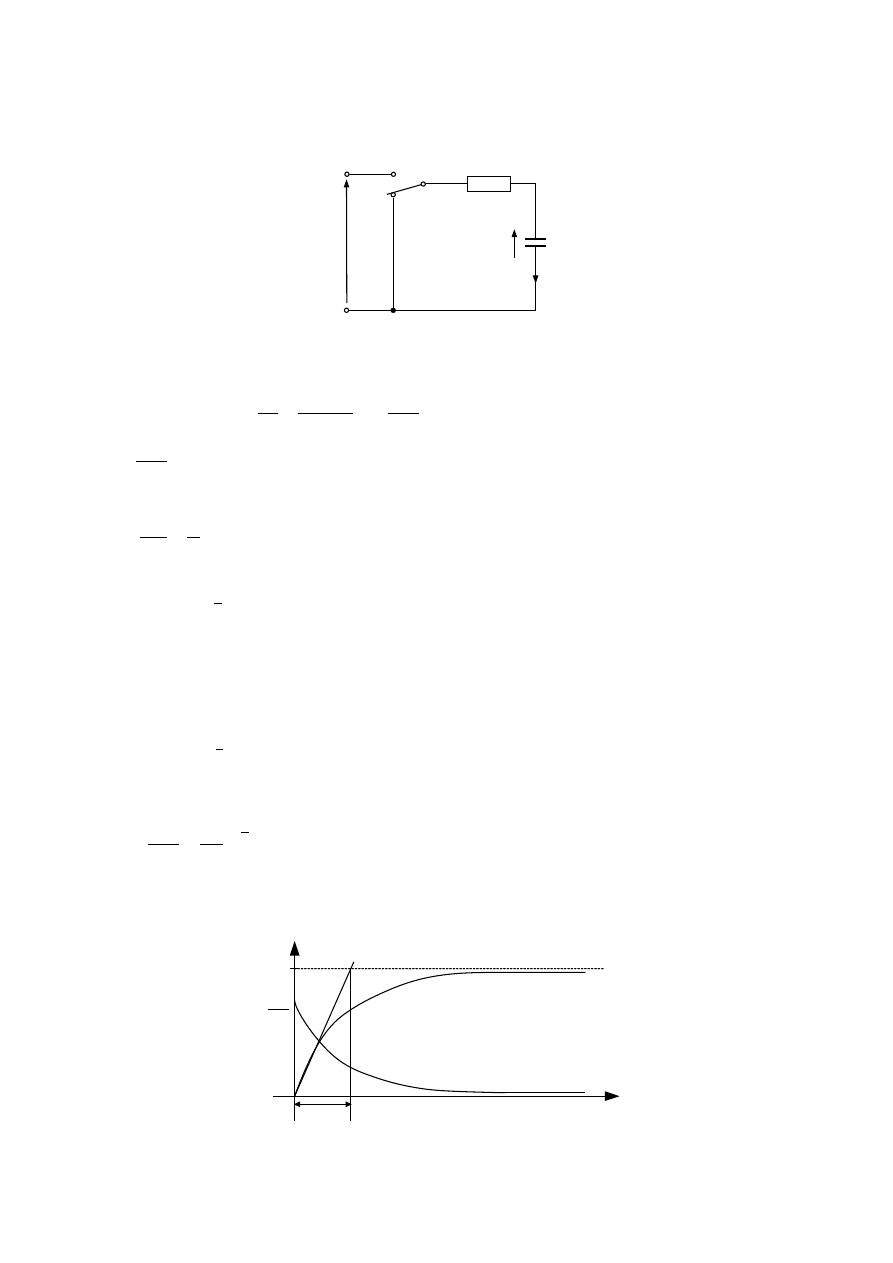
2.

Stan nieustalony w obwodzie RC przy wymuszeniu stałym

C

R

1

2

0

U

c

u

i

e

P

Jeżeli do obwodu złożonego z szeregowego połączenia kondensatora C i
rezystancji R przyłożymy napięcie stałe U

0

, to korzystając z bilansu napięć w

oczku, otrzymujemy równanie:

C

u

Ri

U

+

=

0

;

(

)

dt

du

C

dt

Cu

d

dt

dq

i

C

C

=

=

=

0

U

u

dt

du

RC

C

C

=

+

Cp

Cu

C

u

u

u

+

=

,

t

Cp

Ae

u

α

−

=

T

RC

1

1

=

=

α

, czyli

RC

T

=

0

U

u

Cu

=

T

t

C

Ae

U

u

−

+

=

0

W celu wyznaczenia stałej A korzystamy z warunków początkowych dla t=0,

0

=

C

u

:

A

U

+

=

0

0

, stąd

0

U

A

−

=

Ostatecznie:









−

=

−

T

t

C

e

U

u

1

0

Prąd ładowania kondensatora

T

t

C

e

R

U

dt

du

C

i

−

=

=

0

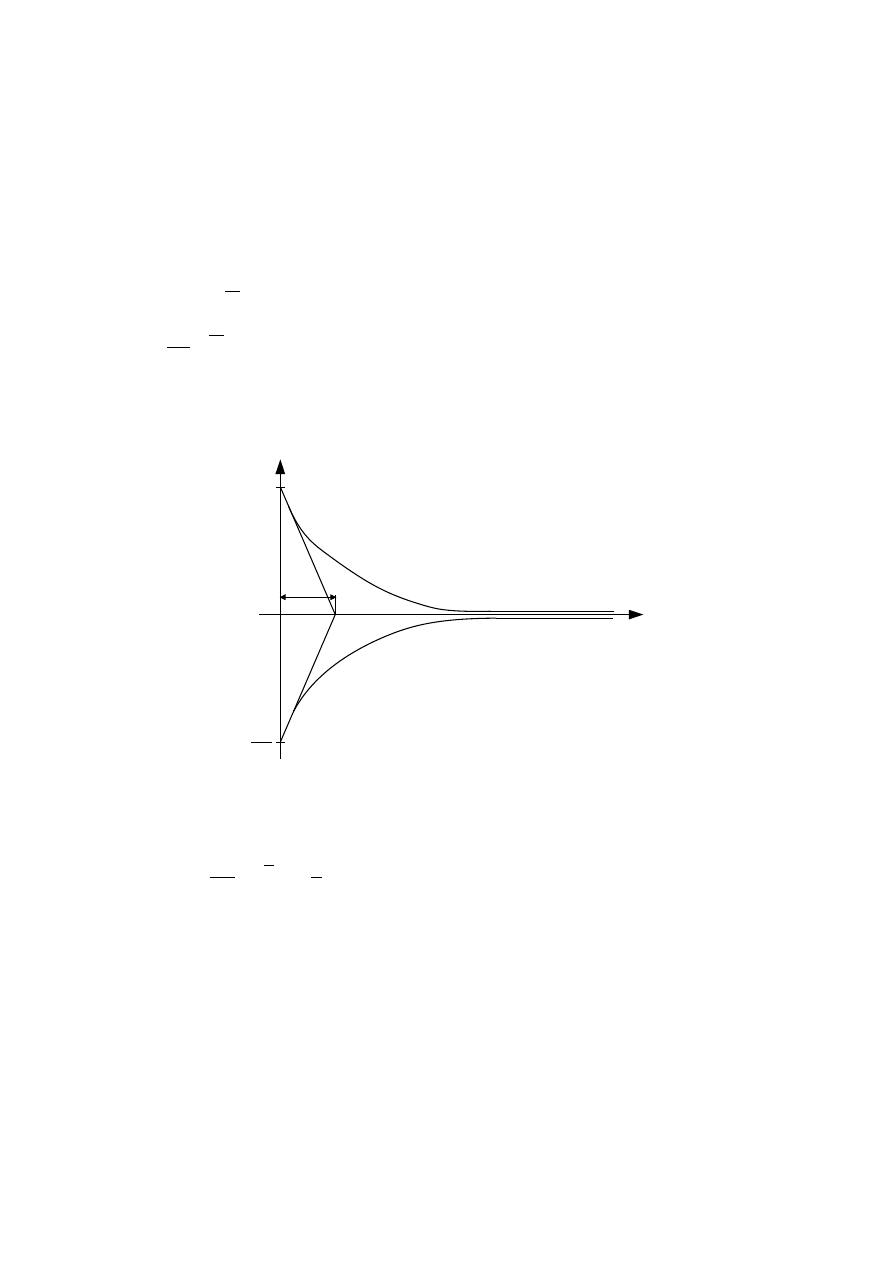
Przebieg napięcia na kondensatorze oraz przebieg prądu ładowania przedstawia
rysunek:

t

0

U

0

0

U

R

c

u

i

c

u

i

T

Przy rozładowaniu kondensatora przez rezystancję R korzystamy z tych samych
równań ogólnych, z tym, że zwarciu kondensatora odpowiada napięcie U

0

=0.

Obwód, w którym kondensator się rozładowuje nie zawiera napięcia
źródłowego, wobec czego w obwodzie w stanie ustalonym nie może płynąć prąd
ani istnieć napięcie na kondensatorze. Stan nieustalony w obwodzie jest więc
równy stanowi przejściowemu:

RC

t

cp

C

e

U

u

u

−

=

=

0

RC

t

p

e

R

U

i

i

−

=

=

0

Znak minus oznacza, że przy rozładowaniu kondensatora zwrot prądu jest
przeciwny niż przy ładowaniu. Przebieg napięcia podczas rozładowania
kondensatora oraz przebieg prądu przedstawia rysunek:

t

0

U

0

0

U

R

−

c

u

i

c

u

i

T

Energia pola elektrycznego kondensatora przy rozładowaniu zamienia się w
ciepło wydzielone na rezystancji R przez przepływający prąd i. Wartość tej
energii A można wyliczyć ze wzoru:

2

0

0

2

2

0

0

2

2

1

CU

dt

e

R

U

Rdt

i

A

T

t

=

=

=

∫

∫

∞

−

∞

Taka sama ilość energii wydziela się na rezystancji R przy ładowaniu
kondensatora, a więc całkowita energia pobrana ze źródła wyniesie:

2

0

CU

A

=

III.

Przebieg ćwiczenia

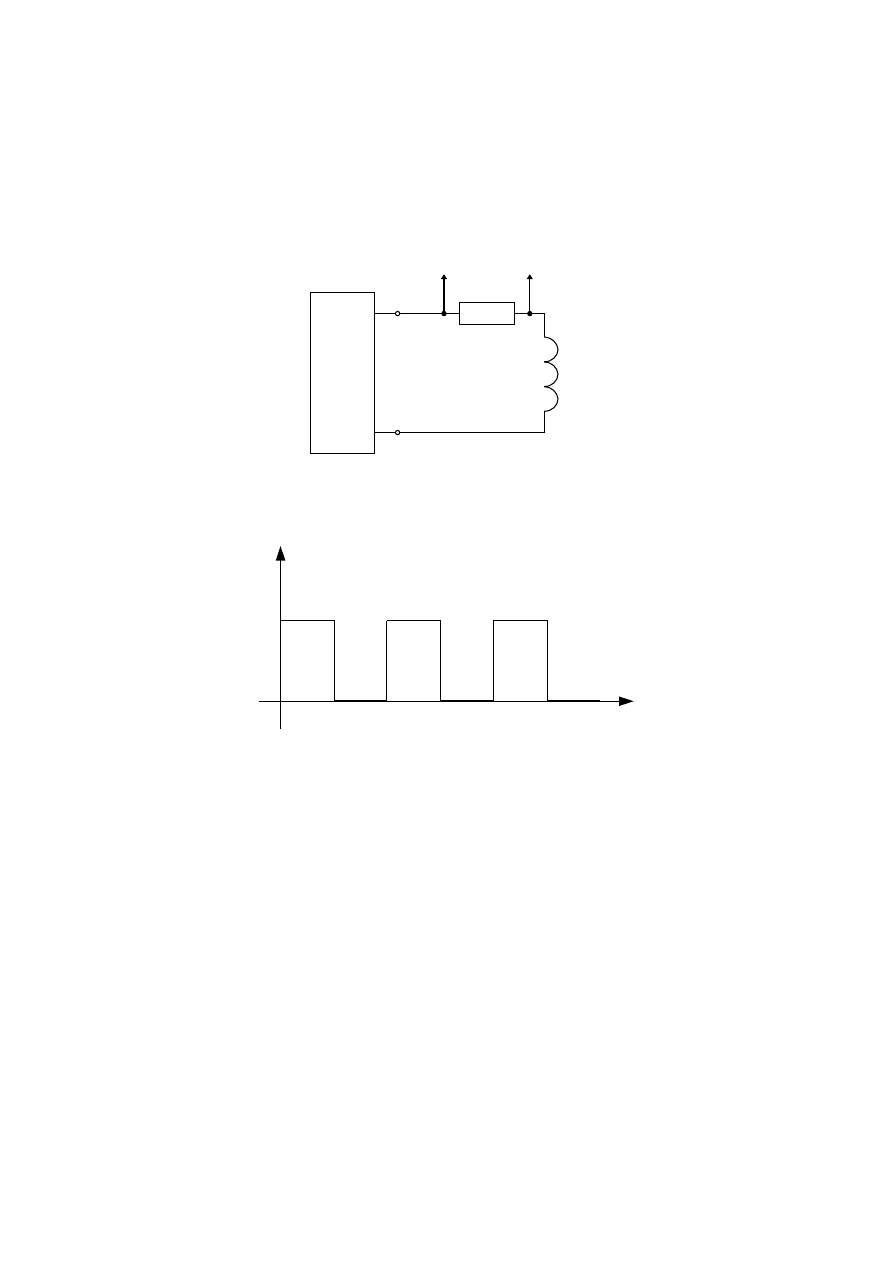
1.

Obserwacja oraz zapis przebiegów napięć przy

załączaniu i odłączaniu napięcia stałego w układzie RL

a)

Schemat połączeń

GFP

R

L

Do oscyloskopu

b)

Przebieg pomiarów

Sygnał z generatora fali prostokątnej (GFP):

u

U

0

t

1

t

2

t

3

t

4

t

5

t

Połączyć układ według schematu. Podłączyć oscyloskop w odpowiednie punkty
układu (jak na schemacie), tak aby można było obserwować przebieg napięcia
u

R

(t). Obserwacje prowadzić dla różnych wartości rezystora R (0; 100; 200; 300

Ω). Dobrać odpowiednio zakres obserwowanych napięć i zapisać wybrane
przebiegi.
c)

Obliczenia

i.

Zaznaczyć na otrzymanych przebiegach podziałkę czasową i
amplitudową.

ii.

Wyprowadzić, stosując metodę klasyczną, postać czasową napięcia
(u

R

(t) oraz i(t)) wskazanego przez prowadzącego zajęcia. Podstawić

wartości liczbowe i narysować przebieg wybranego napięcia i prądu.

iii.

Obliczyć stałą czasową układu dla różnych wartości rezystora R i
cewki L.

iv.

Wyznaczyć graficznie z przebiegów stałe czasowe rzeczywistych
układów i porównać je z wyznaczonymi teoretycznie.

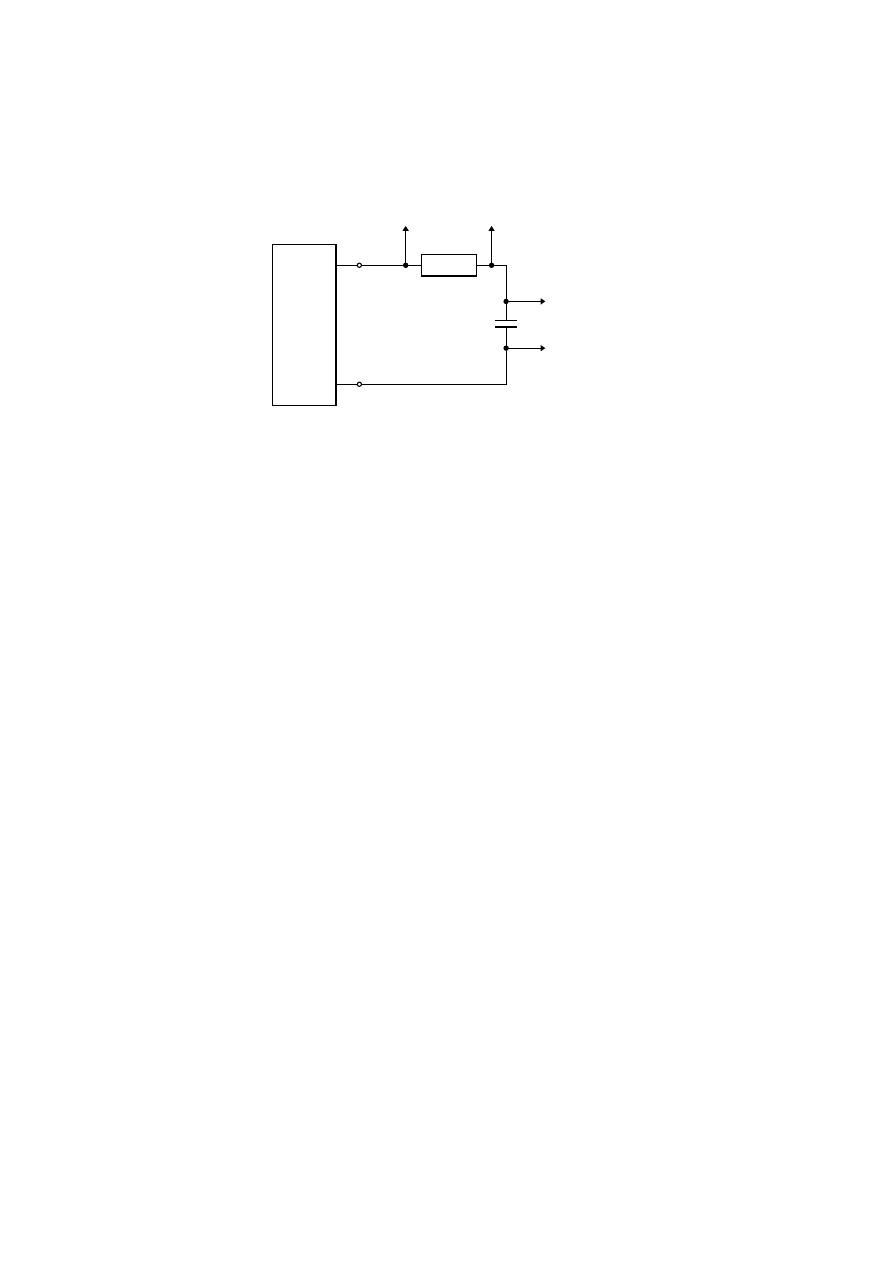
2.

Obserwacja oraz zapis przebiegów napięć przy

załączaniu i załączaniu napięcia stałego w układzie RC
a)

Schemat połączeń

GFP

R

Do oscyloskopu

Do

oscyloskopu

b)

Przebieg pomiarów

Połączyć układ według schematu. Podłączać oscyloskop w odpowiednie punkty
układu (jak na schemacie), tak aby można było obserwować przebiegi napięć
u

R

(t) oraz u

C

(t). Obserwacje prowadzić dla różnych wartości rezystancji R (0;

100; 200; 300 Ω) i C (10; 20; 30 μF). Dobrać odpowiednio zakres
obserwowanych napięć i narysować wybrane przebiegi.
c)

Obliczenia

i. Zaznaczyć na otrzymanych przebiegach podziałkę czasową i

amplitudową.

ii.

Wyprowadzić, stosując metodę klasyczną, postać czasową napięcia (u

R

(t),

u

C

(t) oraz i(t)) wskazanego przez prowadzącego zajęcia. Podstawić

wartości liczbowe i narysować przebieg wybranego napięcia i prądu.

iii. Obliczyć stałą czasową układu dla różnych wartości rezystora R i

kondensatora C.

iv. Wyznaczyć graficznie z przebiegów stałe czasowe rzeczywistych

układów i porównać je z wyznaczonymi teoretycznie.