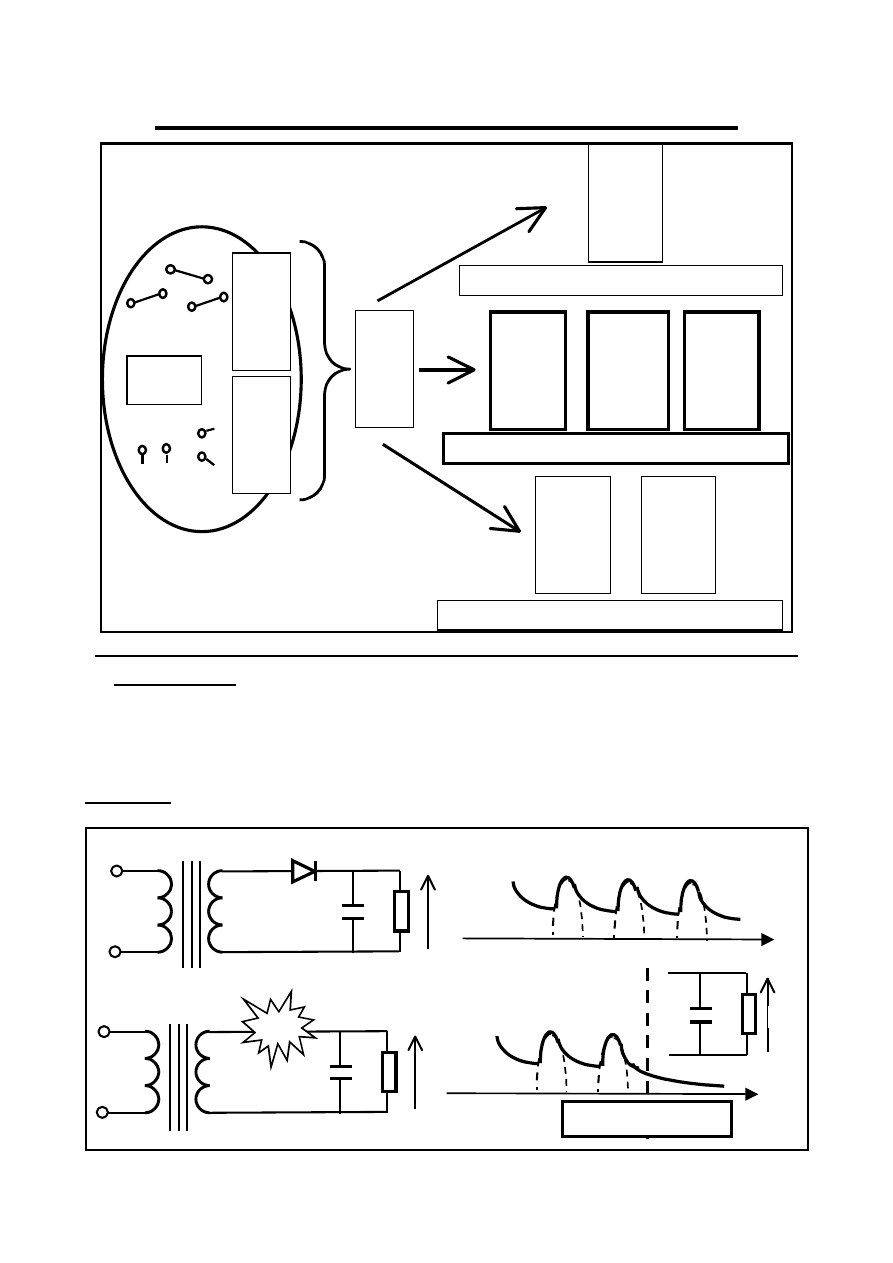
SD ( stany dynamiczne) obwodów

SLS

i

1

(t)

i

2

(t)

……
i

N

(t)

u

1

(t)

u

2

(t)

……
u

N

(t)

W

e1

(t)

W

e2

(t)

……
W

eo

(t)

p

1

(t)

p

2

(t)

……
p

N

(t)

W

L1

(t)

W

L2

(t)

……
W

Ln

(t)

W

M1

(t)

W

M2

(t)

……
W

Mm

(t)

W

C1

(t)

W

C2

(t)

……
W

Cp

(t)

W

R1

(t)

W

R2

(t)

……
W

Rk

(t)

W

j1

(t)

W

j2

(t)

……
W

jr

(t)

Energia „stracona” w elementach dyssypatywnych

Energia „zgromadzona” w elementach konserwatywnych

Energia „przetworzona” w elementach źródłowych

Stany Dynamiczne w obwodzie SLS związane są z zaistnieniem KOMUTACJI.

Komutacja – jakakolwiek zmiana czegokolwiek w obwodzie !

– Zwarcie lub rozwarcie gałęzi;
– Włączenie ( wyłączenie ) autonomicznego napięciowego ( prądowego ) źródła energii;
– Zmiana parametrów własnych lub wzajemnych gałęzi ;

–

itd.

Przykłady
1). Komutacja typu rozwarcie gałęzi ( uszkodzenie elementu ):

≈

u

o

(t)

≈

u

o

(t)

Chwila komutacji

u

o

(t)

C

R

D

Ts

C

R

C

R

Komutacja !

Ts

Dr inż. Jacek Czosnowski

Katedra Elektrotechniki AGH Wydział EAIiE

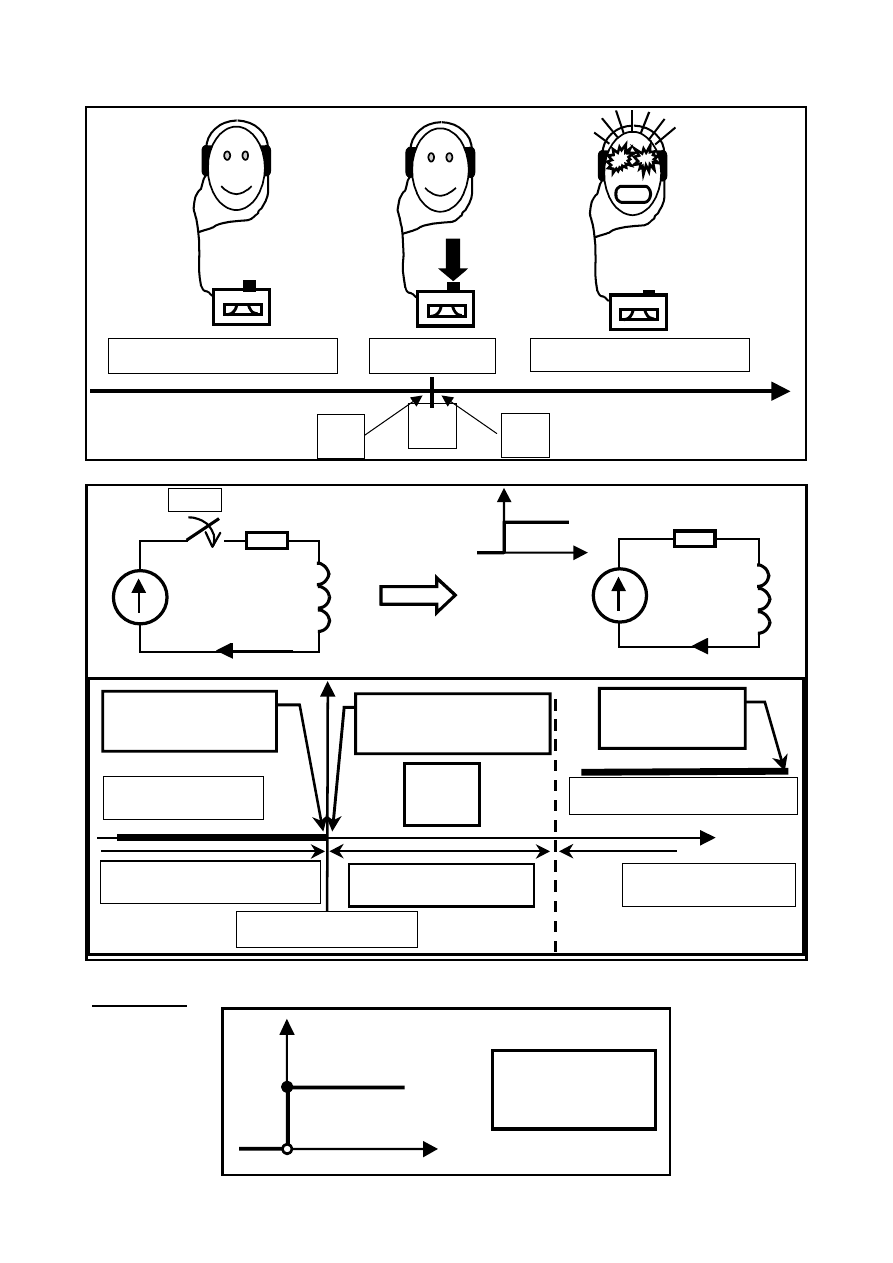
2). Włączenie zasilania ( autonomicznego źródła napięcia ) w obwodzie:

Chwila przed komutacją

Chwila po komutacji !

ON !

Komutacja

t

0–

t

0

t

0+

t

3).

t

0

= 0

R

L

E

i(t)

t < 0, i(t)

≡ 0 A

t

>> 0, i(t) ≡ G

⋅E [A]

?

Stan przed komutacją

Stan ustalony

Stan dynamiczny

Chwila komutacji

t

R

L

e(t)=E⋅1(t)

i(t)

i(0

–

)

– dana początkowa

i(0

+

)

– warunek początkowy

i(∞)

– stan ustalony

e(t)

t

E

Definicja: Funkcja Heaviside’a ( skok jednostkowy, funkcja jednostkowa)

1(t)

t

⎩

⎨

⎧

≥

<

=

0

,

1

0

,

0

)

(

x

x

x

1

1

Dr inż. Jacek Czosnowski

Katedra Elektrotechniki AGH Wydział EAIiE

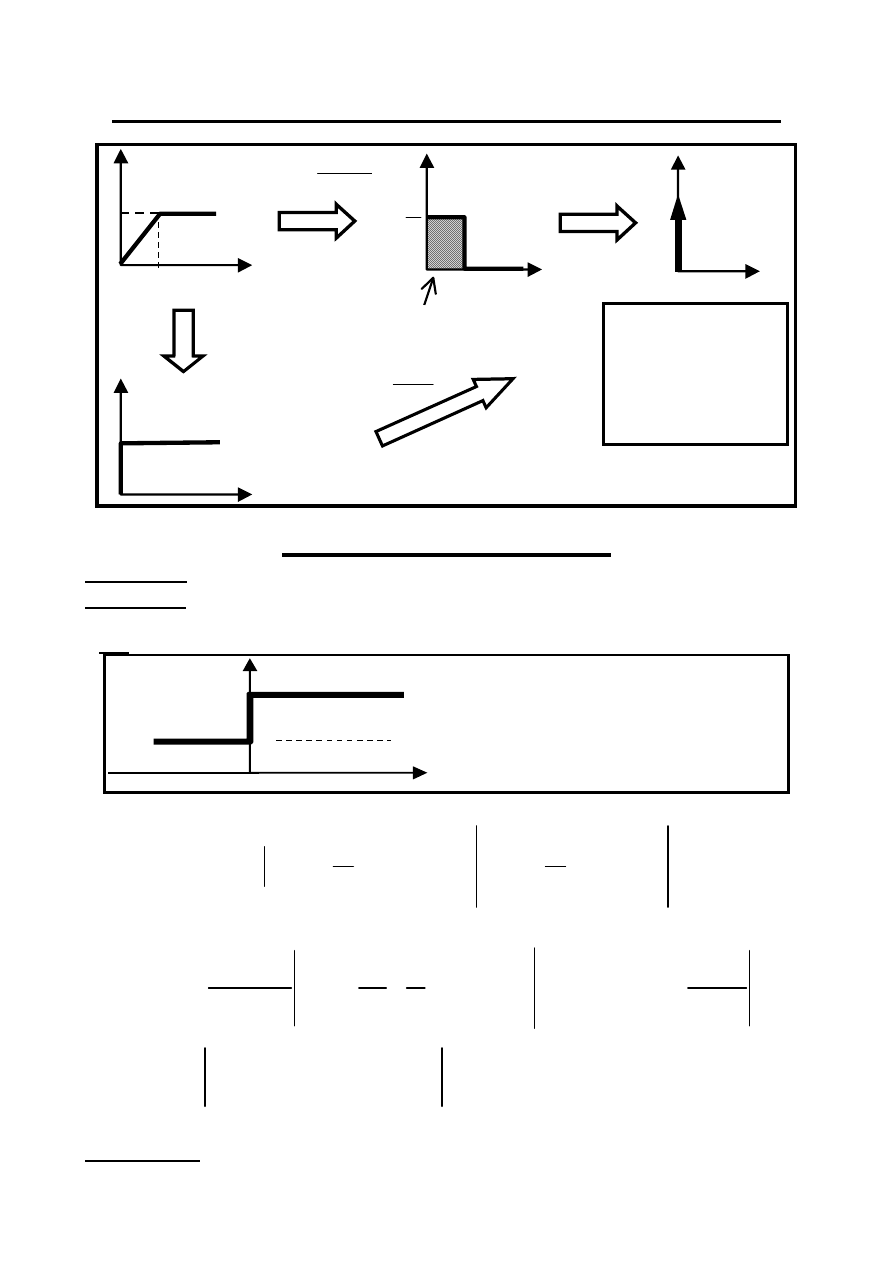
Pseudo Funkcja Impulsowa – Delta Dirac’a

δ(t)

1

ε

t

1(t,

ε)

ε

t

δ(t,ε)

1

ε

t

δ(t)

)

ε

,

δ(

lim

)

δ(

0

ε

t

t

→

=

t

t

t

d

)

ε

,

(

d

)

ε

,

δ(

1

=

1

d

)

δ(

=

∫

+∞

∞

−

t

t

A= 1

⎩

⎨

⎧

=

∞

+

≠

=

0

dla

0

dla

0

)

δ(

t

t

t

)

ε

,

(

1

lim

)

(

1

0

ε

t

t

→

=

t

t

t

d

)

(

d

)

δ(

1

=

1

1(t,

ε)

Prawa Komutacji

Element R – możliwa skokowa zmiana napięcia i prądu;
Element L – musi być zachowana ciągłość prądu (strumienia skojarzonego)

Dowód

( przez negację )

:

Zał. – w chwili komutacji

t

= 0 następuje skokowa zmiana prądu płynącego w elemencie L:

t

I

0–

I

0+

i(t)

t = 0

i(t)|

t=0+

= I

0+

i(t)= I

0–

+ ( I

0+

– I

0–

) ⋅1(t)

Energia zgromadzona w elemencie L w chwili komutacji:

0

2

0

0

)

(

L

2

1

)

(

)

(

ψ

2

1

)

(

=

=

=

⋅

=

⋅

=

t

t

t

L

t

i

t

i

t

t

w

Moc chwilowa przetwarzania energii w elemencie L w chwili komutacji:

0

0

2

0

)

(

)

(

L

)

(

L

2

1

)

(

)

(

=

=

=

∂

∂

⋅

⋅

=

⎟

⎠

⎞

⎜

⎝

⎛

⋅

∂

∂

=

∂

∂

=

t

t

t

L

L

t

t

i

t

i

t

i

t

t

t

w

t

p

?

!

!

)

(

δ

A

)

(

0

0

∞

+

→

⋅

=

=

=

t

t

L

t

t

p

qed.

Element C – musi być zachowana ciągłość napięcia ( ładunku ).

Dr inż. Jacek Czosnowski

Katedra Elektrotechniki AGH Wydział EAIiE

Prawa komutacji dla niezdegenerowanych obwodów SLS

i

L

(0

–

)

≡ i

L

(0

+

)

u

C

(0

–

)

≡ u

C

(0

+

)

Jeśli znamy wartości prądów i napięć bezpośrednio przed komutacją,

to znamy je także bezpośrednio po komutacji.

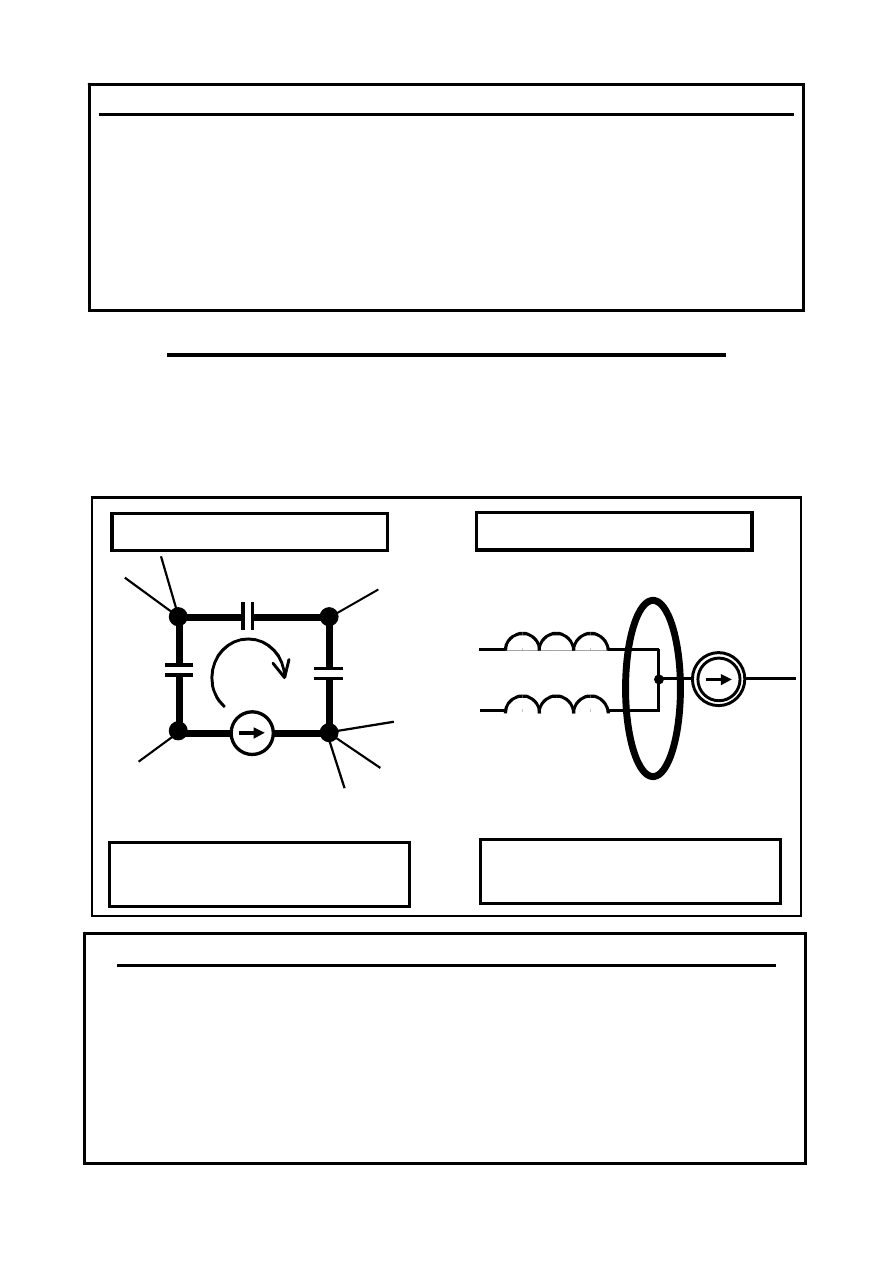
Degeneracje w obwodach SLS

są to obwody w których występują:

–

Oczka pojemnościowe ( OC );

–

Pęki indukcyjne ( PL )

i mogące generować odpowiedzi zawierające delty Dirac’a.

C

1

C

2

C

3

e

!

NPK (!): u

C1

+ u

C2

+ u

C3

+ e = 0

Oczko Pojemnościowe

L

1

L

2

j

Pęk Indukcyjny

!

PPK (!): i

L1

+ i

L2

+ j = 0

W OC elementy: C, e
– są zależne ( NPK ) !

W PL elementy: L, j

– są zależne ( PPK )!

Prawa komutacji dla zdegenerowanych obwodów SLS

i

L

(0

–

)

→ i

L

(0

+

)

u

C

(0

–

)

→ u

C

(0

+

)

Jeśli znamy wartości prądów i napięć bezpośrednio przed komutacją,

to musimy wyliczyć ich wartości bezpośrednio po komutacji.

Dr inż. Jacek Czosnowski

Katedra Elektrotechniki AGH Wydział EAIiE

Rząd obwodu SLS: r = ( n

C

– n

OC

) + ( n

L

– n

PL

)

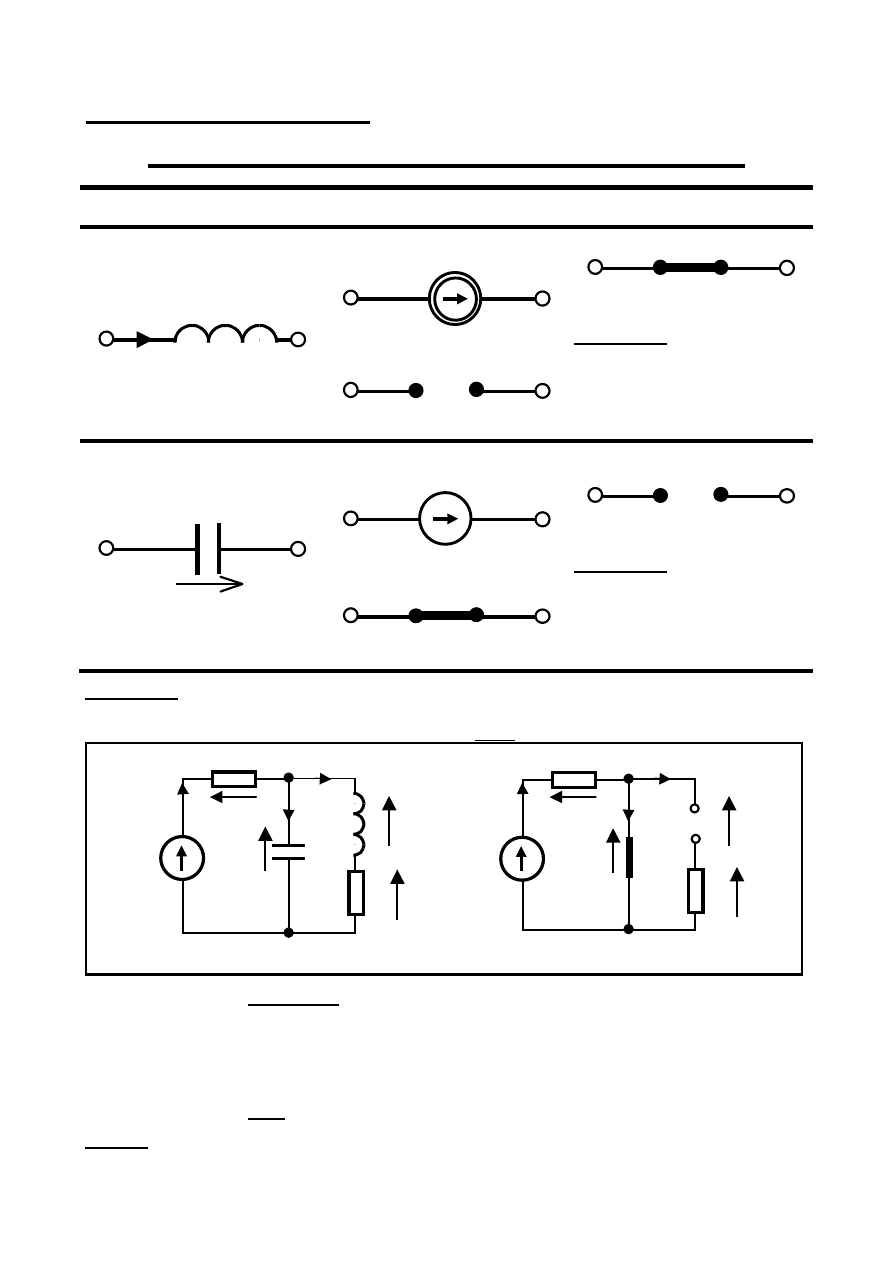
Modele elementów konserwatywnych

T

→0

–

T

→0

+

t

→ + ∞

L

i(0

–

)

A

B

J = i(0+) ≠ 0

A

B

A

B

J = i(0+) = 0

A

B

U = 0

UWAGA !!!

Jeśli wszystkie wymuszenia są
postaci:

w(t)= A

⋅1(t) i w

obwodzie nie powstaną drgania
samowzbudne.

C

u(0

–

)

A

B

A

B

U = u(0+) ≠ 0

A

B

U = u(0+) = 0

A

B

J = 0

UWAGA !!!

Jeśli wszystkie wymuszenia są
postaci:

w(t)= A

⋅1(t) i w

obwodzie nie powstaną drgania
samowzbudne.

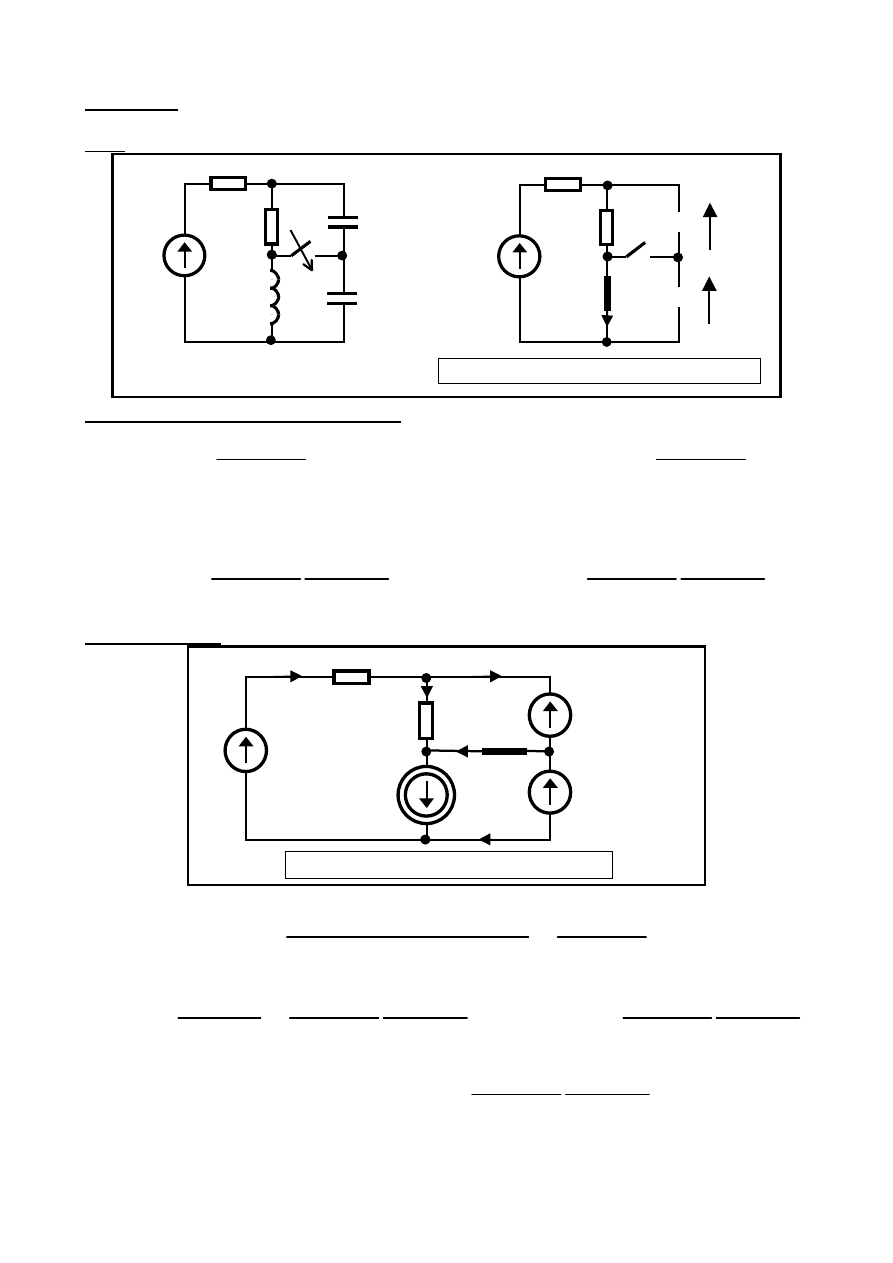
Przykład

W pokazanym na rysunku obwodzie SLS nie jest zgromadzona energia. W

chwili

t = 0 zostaje włączone autonomiczne źródło napięcia stałego. Wyznaczyć wartości

początkowe prądów i napięć oraz ich pochodnych. Dane: E, R

1

, R

2

, L, C.

e(t)=E1(t)

R

1

R

2

L

C

E

R

1

R

2

L

C

i(t)

i

C

(t)

u

C

(t)

i

RL

(t)

u

L

(t)

u

2

(t)

u

1

(t)

i(0

+

)

i

C

(0

+

)

u

C

(0

+

)

i

RL

(0

+

)

u

L

(0

+

)

u

2

(0

+

)

u

1

(0

+

)

Chwila: t = 0

–

Chwila: t = 0

+

Bezpośrednio PRZED komutacją ( włączeniem źródła e(t) ):

e(0

–

)= 0 [V];

i(0

–

)= i

C

(0

–

)= i

RL

(0

–

)= 0 [A];

u

1

(0

–

)= u

C

(0

–

)= u

R

(0

–

)= u

L

(0

–

)= 0 [V];

Bezpośrednio PO komutacji ( włączeniu źródła e(t) ):

Prądy: i(0

+

)= i

C

(0

+

)= G

1

⋅E

i

RL

(0

+

)= 0

Dr inż. Jacek Czosnowski

Katedra Elektrotechniki AGH Wydział EAIiE

Napięcia:

u

1

(0

+

)= R

1

⋅

i(0

+

)= R

1

⋅

G

1

⋅E = E

u

2

(0

+

)= R

2

⋅

i

RL

(0

+

)= R

2

⋅

0= 0

0

)

0

(

)

(

C

1

)

0

(

0

0

=

+

=

∫

+

→

−

+

t

C

C

C

u

dt

t

i

u

u

L

(0

+

)= u

C

(0

+

) – u

2

(0

+

)= 0

Pochodne:

0

d

)

0

(

d

L

)

0

(

RL

L

=

=

+

+

t

i

u

→

0

d

)

0

(

d

RL

=

+

t

i

0

0

R

d

)

0

(

d

R

d

)

0

(

d

2

RL

2

2

=

⋅

=

⋅

=

+

+

t

i

t

u

→

0

d

)

0

(

d

2

=

+

t

u

u

L

(0

+

) = u

C

(0

+

) – u

2

(0

+

)

)

0

(

C

1

d

)

0

(

d

d

)

0

(

d

d

)

0

(

d

d

)

0

(

d

C

C

2

C

L

+

+

+

+

+

=

=

−

=

i

t

u

t

u

t

u

t

u

→

E

G

t

u

⋅

⋅

=

+

1

L

C

1

d

)

0

(

d

⎥

⎦

⎤

⎢

⎣

⎡

+

=

∂

∂

∫

t

t

i

t

t

i

d

i

t

0

RL

2

RL

C

)

(

R

d

)

(

d

L

)

(

C

1

τ

τ

t

t

i

t

t

i

t

i

d

)

(

d

R

d

)

(

d

L

)

(

C

1

RL

2

2

RL

2

C

+

=

→

1

2

RL

2

R

E

LC

1

d

)

0

(

d

=

+

t

i

t

i

t

u

2

RL

2

2

2

2

2

d

)

0

(

d

R

d

)

0

(

d

+

+

⋅

=

→

1

2

2

2

2

R

E

LC

1

R

d

)

0

(

d

⋅

=

+

t

u

Dr inż. Jacek Czosnowski

Katedra Elektrotechniki AGH Wydział EAIiE

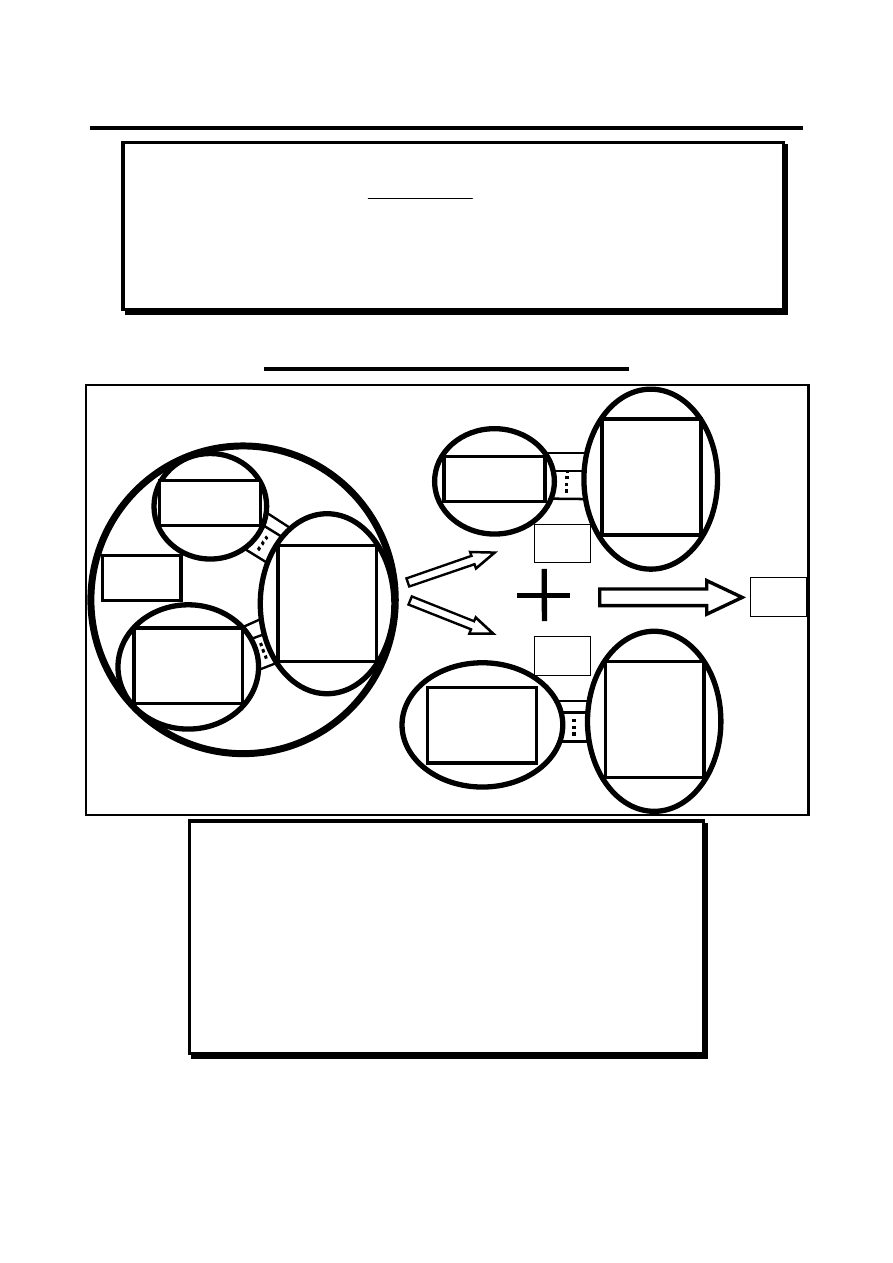
Przykład

Obwód SLS pokazany na rysunku znajduje się w stanie ustalonym. W chwili t=

0 zamknięto wyłącznik W. Wyznaczyć wartości początkowe prądów.
Dane:

u

(

t

)= E 1(

t

), R

1

, R

2

, L, C

1

, C

2

.

R

2

C

1

C

2

L

R

1

W

E

⋅1(t)

t=0

R

2

C

1

L

R

1

W

E

C

2

Stan ustalony – przed komutacją

i

L

u

C1

u

C2

Stan ustalony – przed komutacją:

2

1

L

R

R

E

)

0

(

+

=

−

i

;

E

R

R

R

)

0

(

)

0

(

2

1

1

C

C

2

1

+

=

+

−

−

u

u

Ładunki w kondensatorach połączonych szeregowo:

)

0

(

C

)

0

(

C

2

1

C

2

C

1

−

−

⋅

=

⋅

u

u

E

C

C

C

R

R

R

)

0

(

2

1

2

2

1

1

C

1

+

+

=

−

u

,

E

C

C

C

R

R

R

)

0

(

2

1

1

2

1

1

C

2

+

+

=

−

u

Po komutacji:

R

2

R

1

W

E

Bezpośrednio po komutacji

u

C1

(0

+

) = u

C1

(0

–

)

u

C2

(0

+

) = u

C2

(0

–

)

i

L

(0

+

) = i

L

(0

–

)

i

2

(0

+

)

i

C1

(0

+

)

i

C2

(0

+

)

i

W

(0

+

)

i

1

(0

+

)

(

)

2

1

2

C

C

2

R

R

E

R

)

0

(

)

0

(

E

)

0

(

2

1

+

=

+

−

=

+

+

+

u

u

i

;

2

1

2

2

1

1

C

1

C

C

C

R

R

E

R

)

0

(

)

0

(

1

+

+

=

=

+

+

u

i

;

2

1

1

2

1

C

C

C

C

R

R

E

)

0

(

1

+

+

=

+

i

2

1

1

2

1

1

L

W

C

C

C

R

R

E

)

0

(

)

0

(

)

0

(

+

+

=

−

=

+

+

+

i

i

i

;

0

)

0

(

)

0

(

)

0

(

L

2

C

1

=

−

=

+

+

+

i

i

i

Dr inż. Jacek Czosnowski

Katedra Elektrotechniki AGH Wydział EAIiE

Liniowe Równanie Różniczkowe ( LRR )

( )

[

]

tkowe

począ

warunki

-

)

1

(

1

0

dla

),

0

(

;

)

(

)

(

)

(

1

0

)

(

−

=

⋅

=

⎥

⎦

⎤

⎢

⎣

⎡

⋅

∑

∑

=

=

r

,

,

,

k

f

t

w

b

dt

t

df

a

k

m

n

n

n

r

k

k

k

k

K

Rozwiązanie ogólne

Źródła

autonomiczne

Pseudo źródła

związane z

warunkami

początkowymi

R, C,

L (M),

ZS

Źródła

autonomiczne

R, C,

L (M),

ZS

Pseudo źródła

związane z

warunkami

początkowymi

R, C,

L (M),

ZS

SLS

f

w

(t)

f

p

(t)

f(t)

)

,

0

dla

)

(

)

(

)

(

0

m

p

+∞

∈<

+

=

+

=

∑

t

t

f

t

f

t

f

n

m

W

f

p

(t)

– składowa przejściowa odpowiedzi ( RRJ );

f

W

•

(t) –

składowa wymuszona odpowiedzi ( RRN );

Dr inż. Jacek Czosnowski

Katedra Elektrotechniki AGH Wydział EAIiE

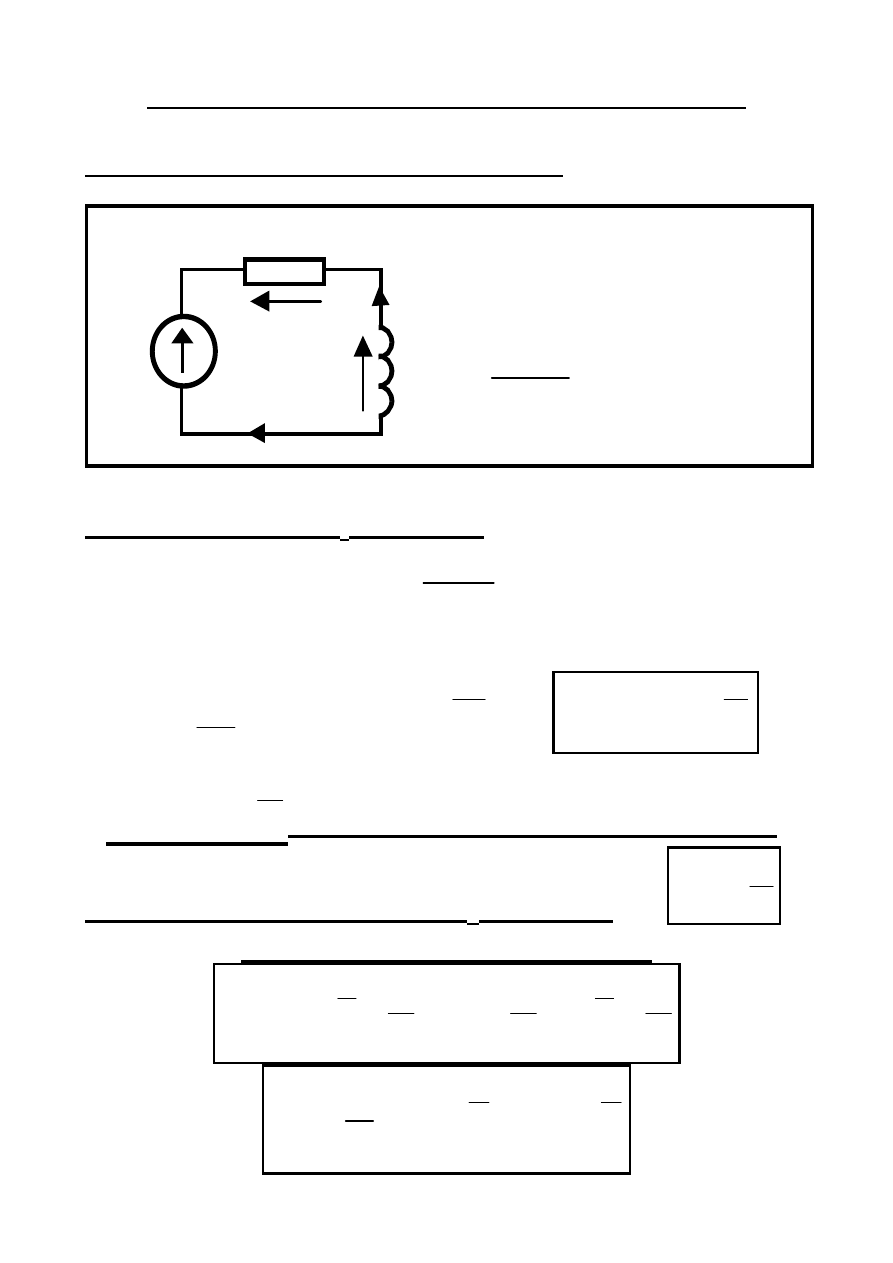
Stany dynamiczne (nieustalone, przejściowe) w obwodach SLS

Obwód RL (o

bwód rzędu pierwszego )

R

L

e(t)

u

R

u

L

i

u

L

(t) + u

R

(t) = e(t)

)

(

)

(

R

t

d

)

(

d

L

t

e

t

i

t

i

=

⋅

+

I

0

1). e(t) = E

⋅1(t); I

0

≠ 0

( przed komutacją w elemencie L jest energia ).

Składowa przejściowa i

p

(t) prądu i(t):

0

)

(

R

t

d

)

(

d

L

p

p

=

⋅

+

t

i

t

i

RRJ:

Równanie charakterystyczne:

L

⋅s + R = 0

GL

1

−

=

s

→

GL

e

e

t

t

s

−

⋅

=

→

GL

e

)

(

p

t

A

t

i

−

=

[ ]

R

L

GL

s

T

=

=

– stała czasowa obwodu RL.

Składowa wymuszona ( ustalona ) i

w

(t) prądu i(t):

R

E

)

(

w

=

t

i

Pełna odpowiedź obwodu RL

R

E

e

R

E

I

R

E

e

)

(

GL

GL

0

+

⋅

⎟

⎠

⎞

⎜

⎝

⎛ −

=

+

=

−

−

t

t

A

t

i

( )

GL

GL

e

I

e

1

R

E

)

(

0

t

t

t

i

−

−

⋅

+

−

⋅

=

Dr inż. Jacek Czosnowski

Katedra Elektrotechniki AGH Wydział EAIiE

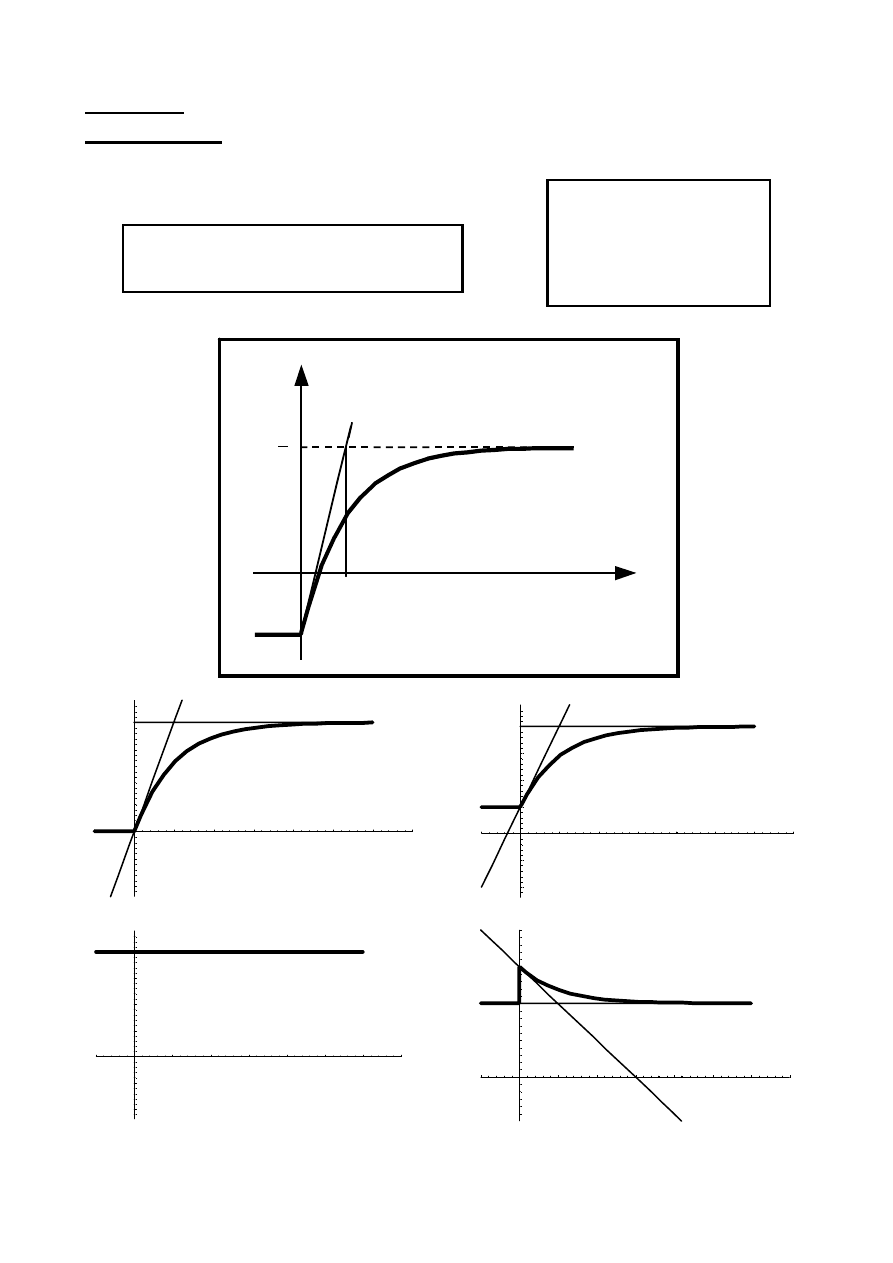
Przykład E= 10 V, R= 1

Ω, L= 1 H, I

0

= –5 A

Rozwiązanie:

T = GL = 1 s; E/R = 10 A

[A]

0

1

e

15

)

(

+

⋅

−

=

−t

t

i

→

[A]

10

)

(

[A]

5

)

0

(

+

=

∞

−

=

i

i

T

I

0

E
R

t

i(t)

-1

1

2

3

4

5

6

7

-5

-2.5

2.5

5

7.5

10

-1

1

2

3

4

5

6

7

-5

-2.5

2.5

5

7.5

10

-1

1

2

3

4

5

6

7

-5

5

10

15

20

-1

1

2

3

4

5

6

7

-5

-2.5

2.5

5

7.5

10

Dr inż. Jacek Czosnowski

Katedra Elektrotechniki AGH Wydział EAIiE

Obwód RC (o

bwód rzędu pierwszego )

R

C

e(t)

u

R

u

i

R

t

u

t

e

t

u

)

(

)

(

t

d

)

(

d

C

−

=

U

0

)

(

t

d

)

(

d

C

t

i

t

u

=

1). e(t) = E

⋅1(t); U

0

≠ 0

( przed komutacją w elemencie C jest energia

).

Składowa przejściowa u

p

(t) napięcia u(t):

0

)

(

t

d

)

(

d

RC

p

p

=

+

t

u

t

u

RRJ:

Równanie charakterystyczne:

RC

⋅s + 1 = 0

RC

1

−

=

s

→

RC

e

e

t

t

s

−

⋅

=

→

RC

e

)

(

p

t

A

t

u

−

=

[ ]

RC

s

T

=

– stała czasowa obwodu RC.

Składowa wymuszona ( ustalona ) i

w

(t) prądu i(t):

E

)

(

w

=

t

u

Pełna odpowiedź obwodu RC

(

)

E

e

E

U

E

e

)

(

GL

RC

0

+

⋅

−

=

+

=

−

−

t

t

A

t

u

( )

GL

RC

e

U

e

1

E

)

(

0

t

t

t

u

−

−

⋅

+

−

⋅

=

Dr inż. Jacek Czosnowski

Katedra Elektrotechniki AGH Wydział EAIiE

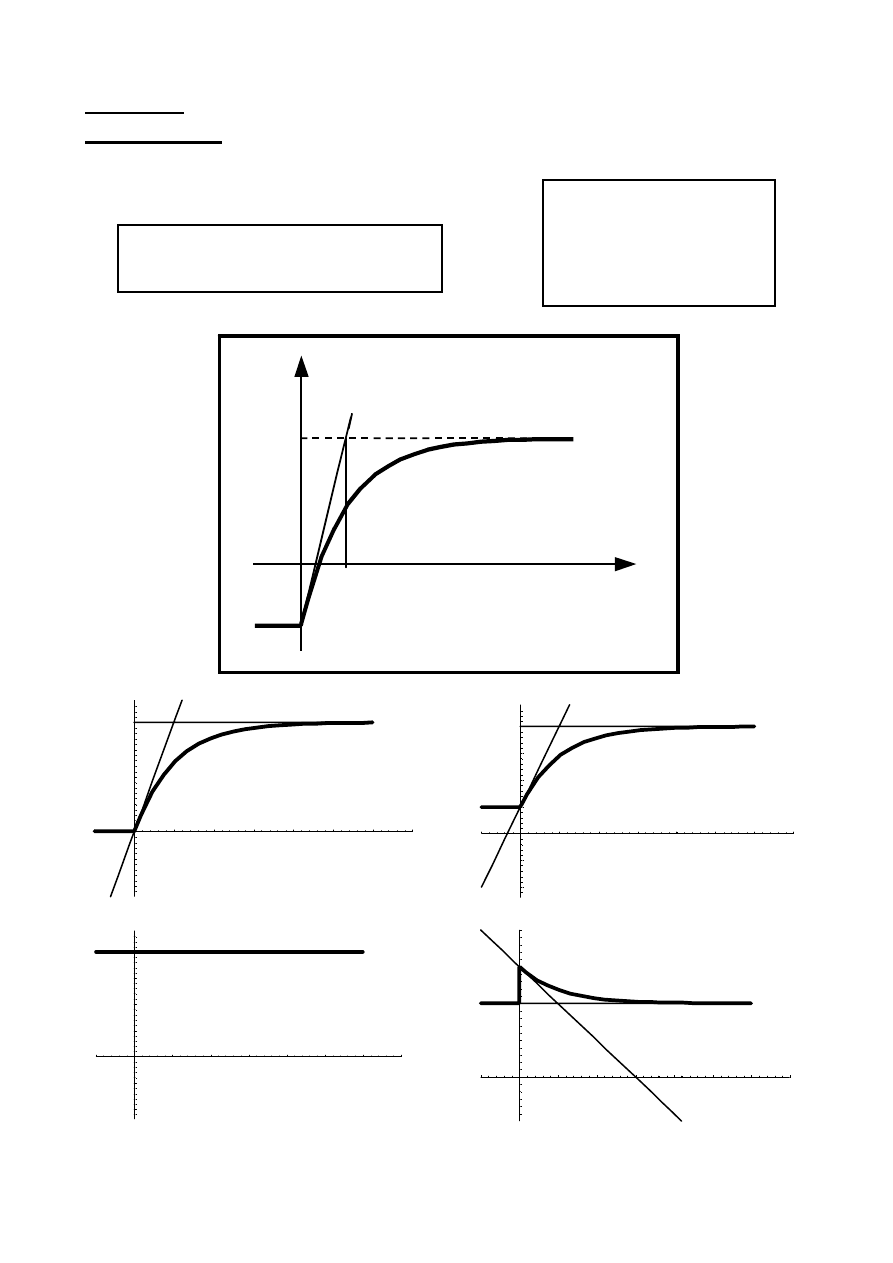
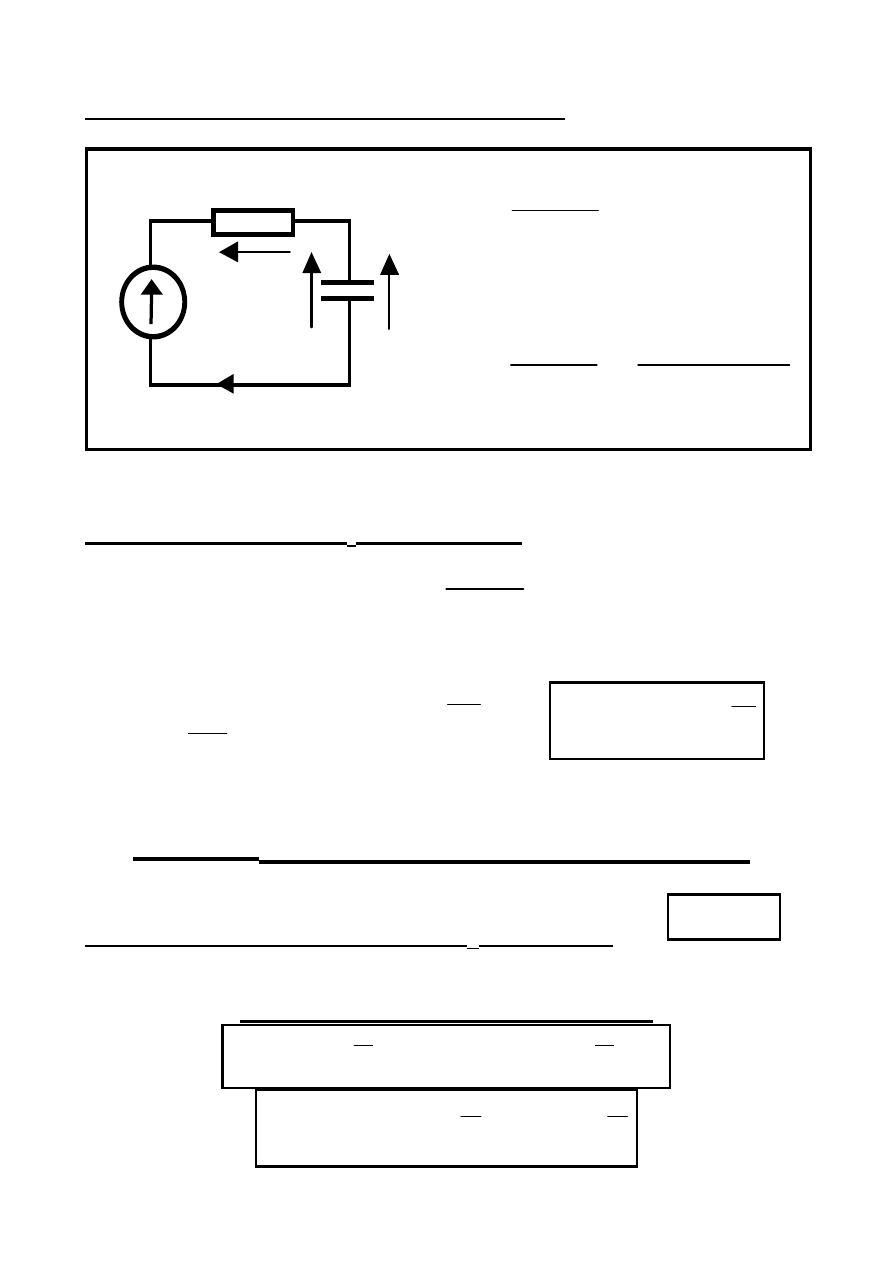
Przykład E= 10 V, R= 1

Ω, C= 1 F, U

0

= –5 V

Rozwiązanie:

T = RC = 1 s; E = 10 V

[V]

e

15

0

1

)

(

t

t

u

−

⋅

−

=

→

[V]

10

)

(

[V]

5

)

0

(

+

=

∞

−

=

u

u

T

U

0

E

t

u(t)

-1

1

2

3

4

5

6

7

-5

-2.5

2.5

5

7.5

10

-1

1

2

3

4

5

6

7

-5

-2.5

2.5

5

7.5

10

-1

1

2

3

4

5

6

7

-5

5

10

15

20

-1

1

2

3

4

5

6

7

-5

-2.5

2.5

5

7.5

10

Dr inż. Jacek Czosnowski

Katedra Elektrotechniki AGH Wydział EAIiE

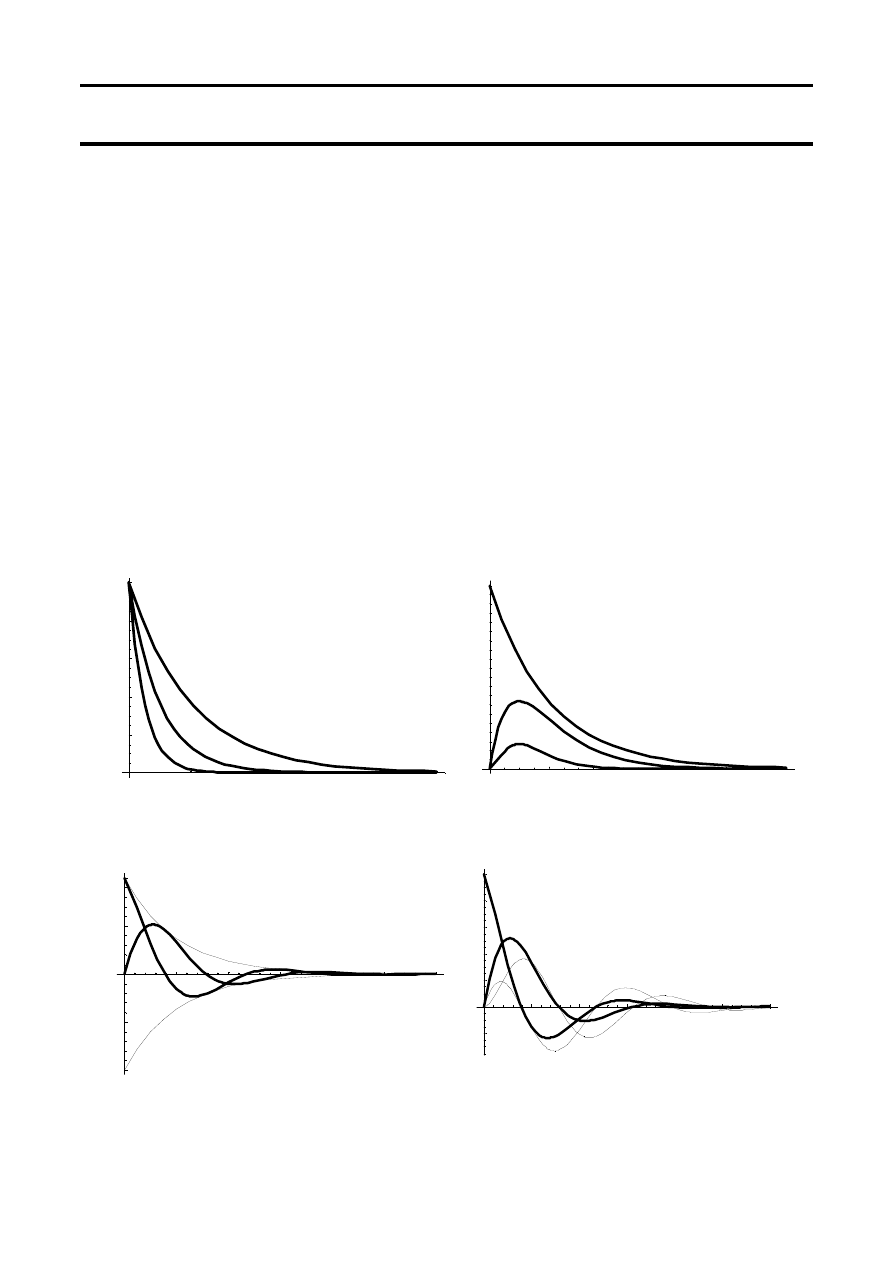
Pierwiastki równania

charakterystycznego

Funkcje należące do układu

podstawowego rozwiązań

s= –

α

,

α∈

ℜ

e

–

αt

s

k

= –

α

, k=1,2,…m,

α∈

ℜ

e

–

αt

, te

–

αt

, t

2

e

–

αt

, …, t

(m-1)

e

–

αt

s= –

α

±

j

ω

,

α∈

ℜ

,

ω∈

ℜ

+

e

–

αt

cos

ω

t, e

–

αt

sin

ω

t

s

k

= –

α

k

±

j

ω

k

, k=1,2,…,m,

α

k

∈

ℜ

,

ω

k

∈

ℜ

+

e

–

αt

cos

ω

t, te

–

αt

cos

ω

t,…, t

(m-1)

e

–

αt

cos

ω

t,

e

–

αt

sin

ω

t, te

–

αt

sin

ω

t,…, t

(m-1)

e

–

αt

sin

ω

t,

2

4

6

8

10

0.2

0.4

0.6

0.8

1

e

- a

t

2

4

6

8

10

0.2

0.4

0.6

0.8

1

e

- a

t

,

te

- a

t

,

t

2

e

- a

t

1

2

3

4

5

6

-0.2

0.2

0.4

0.6

0.8

1

ă

-

a t

Cos

@

w

t

D

,

ă

-

a t

Sin

@

w

t

D

,t

ă

-

a t

Cos

@

w

t

D

,t

ă

-

a t

Sin

@

D

w

t

1

2

3

4

5

6

-1

-0.5

0.5

1

ă

-

a t

Cos

@

w t

D

,

ă

-

a t

Sin

@

w t

D

Dr inż. Jacek Czosnowski

Katedra Elektrotechniki AGH Wydział EAIiE