Stany nieustalone

2

STANY NIEUSTALONE

Poj cie stanu ustalonego i nieustalonego

Stan nieustalony wyst puje w dwóch przypadkach: w sytuacji, gdy obwód został

doł czony do ródła zasilania oraz, gdy zmienia si jego struktura, przy czym dotyczy to
zarówno obwodów pr du stałego, jak i zmiennego.

Warunki pocz tkowe. Prawa komutacji

Pierwsze prawo komutacji.

Pr d w obwodzie z indukcyjno ci nie mo e zmienia si skokowo i w chwili tu

przed komutacj ma tak sam warto , jak w chwili tu po komutacji.

Ze wzgl du na wyst puj cy w cewce strumie magnetyczny skojarzony zasada

niezmienno ci pr du w chwili komutacji jest równowa na zasadzie niezmienno ci
strumienia magnetycznego skojarzonego z cewk , st d nazywana jest czasami zasad
ci gło ci pr du i strumienia magnetycznego w cewce.

Drugie prawo komutacji

Napi cie na kondensatorze nie mo e si zmieni skokowo i w chwili tu przed

komutacj posiada tak sam warto jak w chwili tu po komutacji.

Stany nieustalone

3

Stan nieustalony w dwójniku szeregowym RL

Wł czenie napi cia stałego

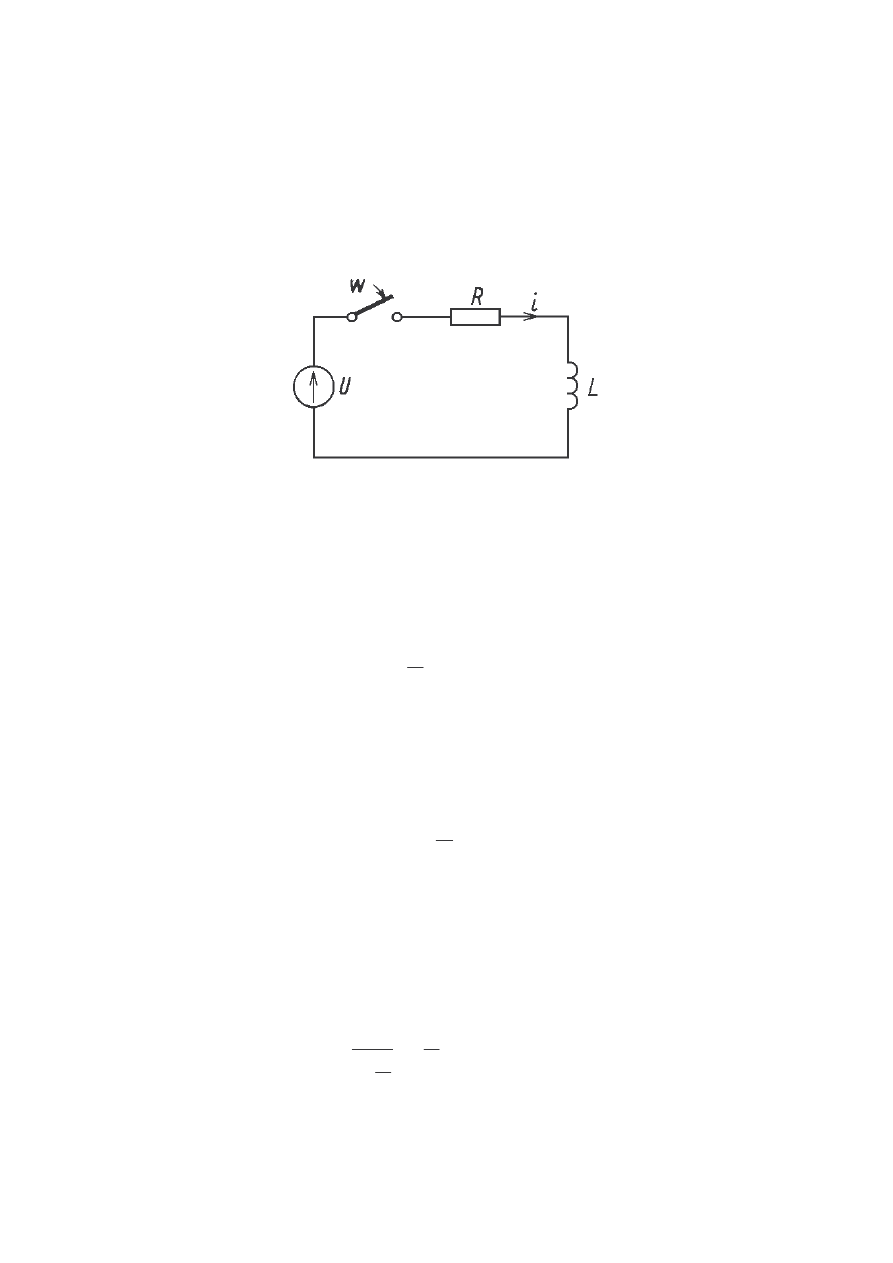
Do szeregowego układu RL doł czono ródło napi cia stałego o warto ci U. W

chwili t = 0 zamkni to wył cznik powoduj c, e w obwodzie płynie pr d.

Układ szeregowy RL wł czony do ródła napi cia stałego

Ze wzgl du na wyst puj cy po zamkni ciu wył cznika stan nieustalony, warto

pr du narasta od zera do warto ci ustalonej danej wzorem (nale y pami ta , i napi cie na
indukcyjno ci w stanie ustalonym wynosi zero):

R

U

i

=

(1)

Wyznaczenie przebiegu zmienno ci pr du i napi cia w stanie nieustalonym jest

bardziej skomplikowane. W my l drugiego prawa Kirchhoffa bilans w oczku b dzie miał
nast puj c posta :

dt

di

L

Ri

U

+

=

(2)

Pierwszy składnik prawej strony równania opisuje napi cie na rezystancji, drugi

napi cie indukcji własnej indukowane przez przepływaj cy przez cewk pr d zmienny i.

W celu okre lenia warto ci pr du konieczne jest rozdzielenie zmiennych

wyst puj cych w nim:

dt

L

R

R

U

i

di

−

=

−

(3)

Po scałkowaniu obustronnym równanie przybiera nast puj c posta :

Stany nieustalone

4

A

t

L

R

R

U

i

ln

+

−

=

−

(4)

Przekształcaj c:

t

L

R

Ae

R

U

i

−

=

−

(5)

Przy czym w powy szym równaniu A jest stał całkowania, która b dzie wyznaczona

poni ej z warunku pocz tkowego (dla chwili pocz tkowej zgodnie z prawami komutacji
pr d nie zmieni skokowo swojej warto ci):

dla t = 0 pr d i = 0

(6)

Podstawiaj c powy sze warto ci do zale no ci (5) i wykonaniu przekształce pr d

b dzie dany nast puj cym równaniem:

−

=

− t

L

R

e

1

R

U

i

(7)

We wzorze wyst puj dwie składowe: składowa ustalona (pierwsza) oraz składowa

przej ciowa (druga). Pr d wypadkowy i jest sum składowej ustalonej iu oraz składowej
przej ciowej ip:

e

przejsciow

ustalone

i

i

i

+

=

(8)

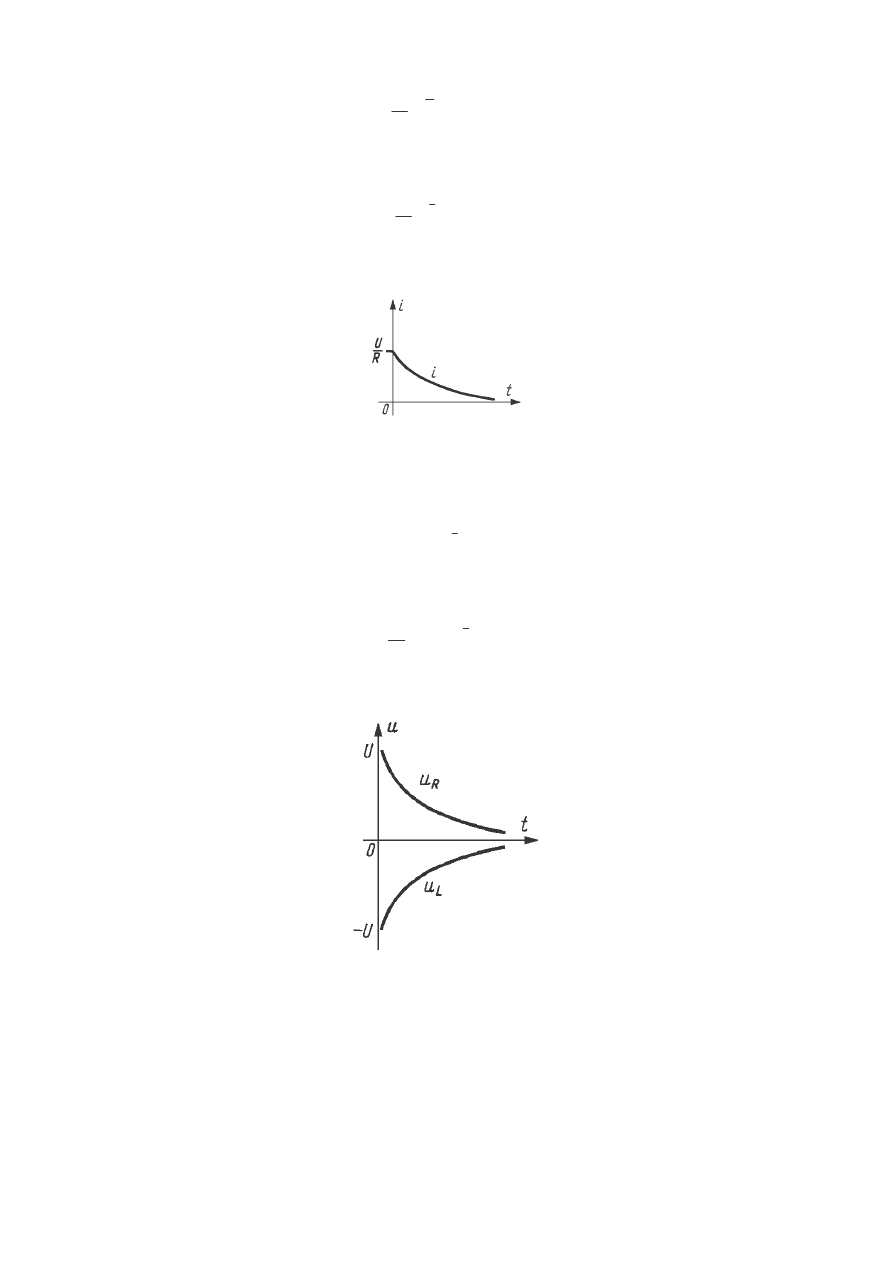
Przebiegi czasowe obu wielko ci przedstawia poni szy rysunek:

Przebiegi czasowe pr dów w układzie szeregowym RL z rysunku

Stany nieustalone

5

Napi cie na rezystancji:

t

L

R

R

Ue

U

Ri

u

−

−

=

=

(9)

Napi cie na indukcyjno ci:

t

L

R

L

Ue

dt

di

L

u

−

=

=

(10)

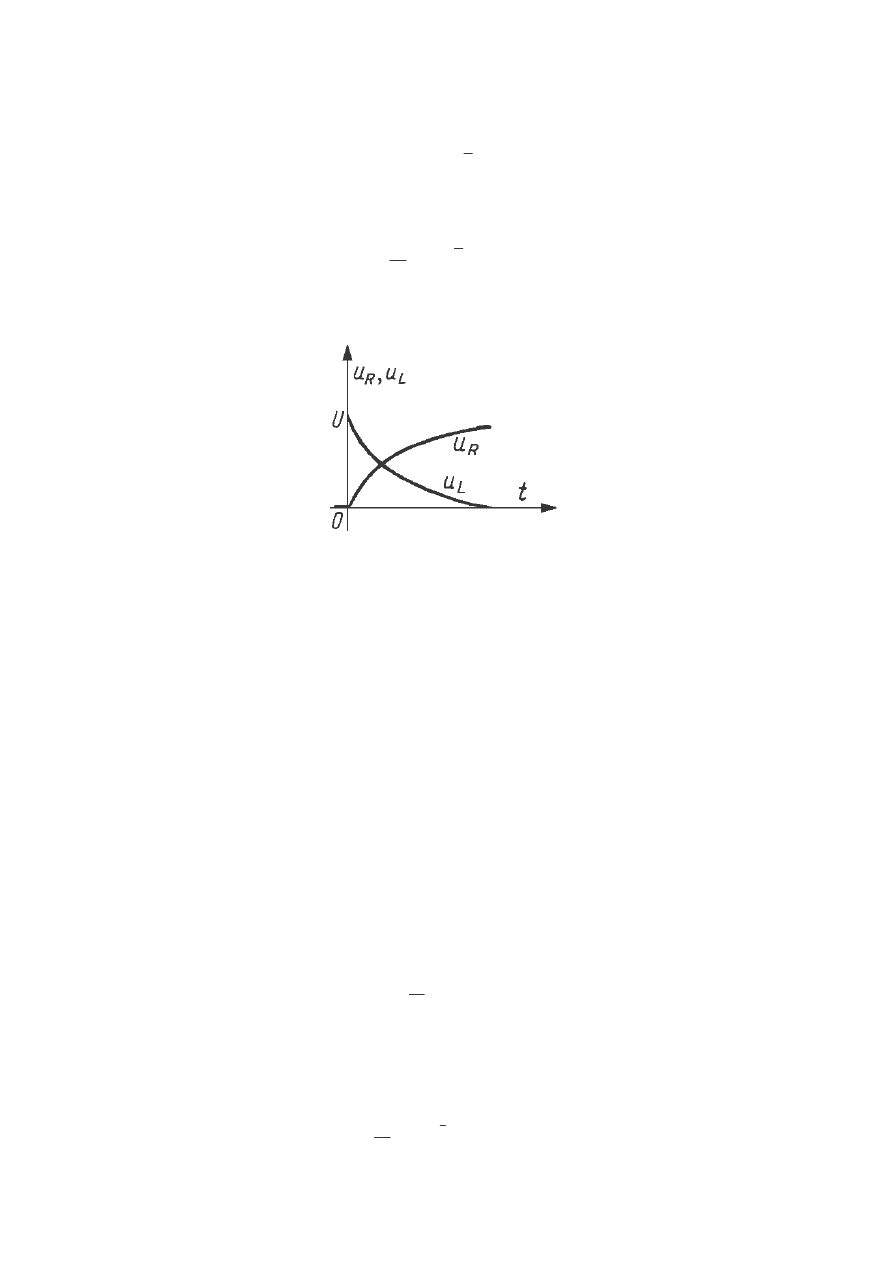
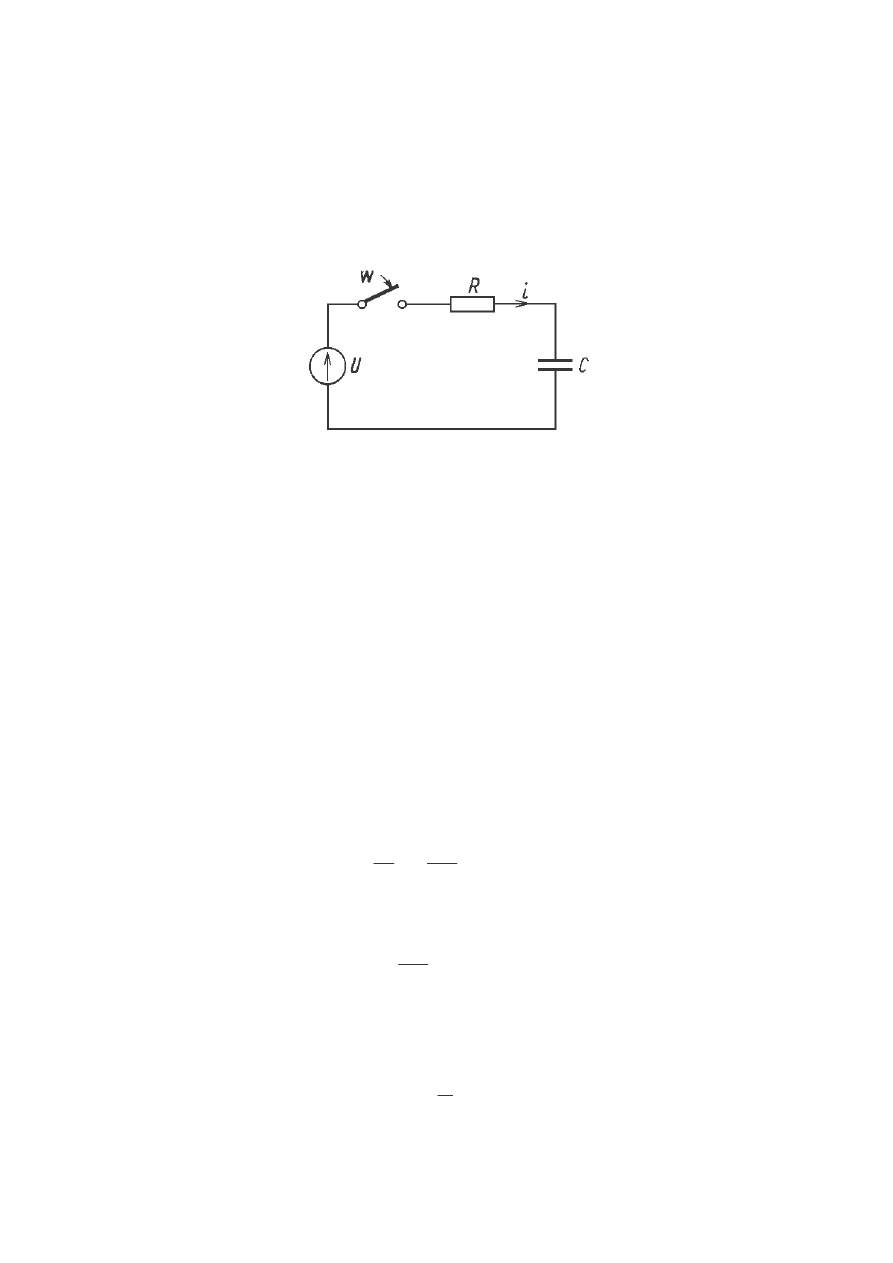
Poni szy rysunek przedstawia przebiegi napi w układzie:

Przebiegi czasowe napi w układzie szeregowym RL wł czonym na napi cie

stałe.

Stała czasowa

Jak wynika z analizy powy szego wzoru (7) na warto pr du przepływaj cego w

układzie, mo liwe jest wpływanie na szybko zaniku składowej przej ciowej poprzez
zmian warto ci rezystancji i indukcyjno ci. Aby scharakteryzowa szybko zmian
zachodz cych w układzie wprowadzono wielko fizyczn nosz c nazw stałej czasowej
układu.

Stała czasowa układu

τ jest to czas, po upływie którego warto bezwzgl dna

składowej przej ciowej maleje e razy.

W przypadku tego układu dana jest ona wzorem:

R

L

=

τ

(11)

Wielko ta mierzona jest w sekundach.
Podstawiaj c stał czasow do wyznaczonej wy ej warto ci pr du mo na zapisa :

−

=

τ

−

t

e

1

R

U

i

(12)

Stany nieustalone

6

Stał czasow danego układu mo na zdefiniowa równie w oparciu o konstrukcj

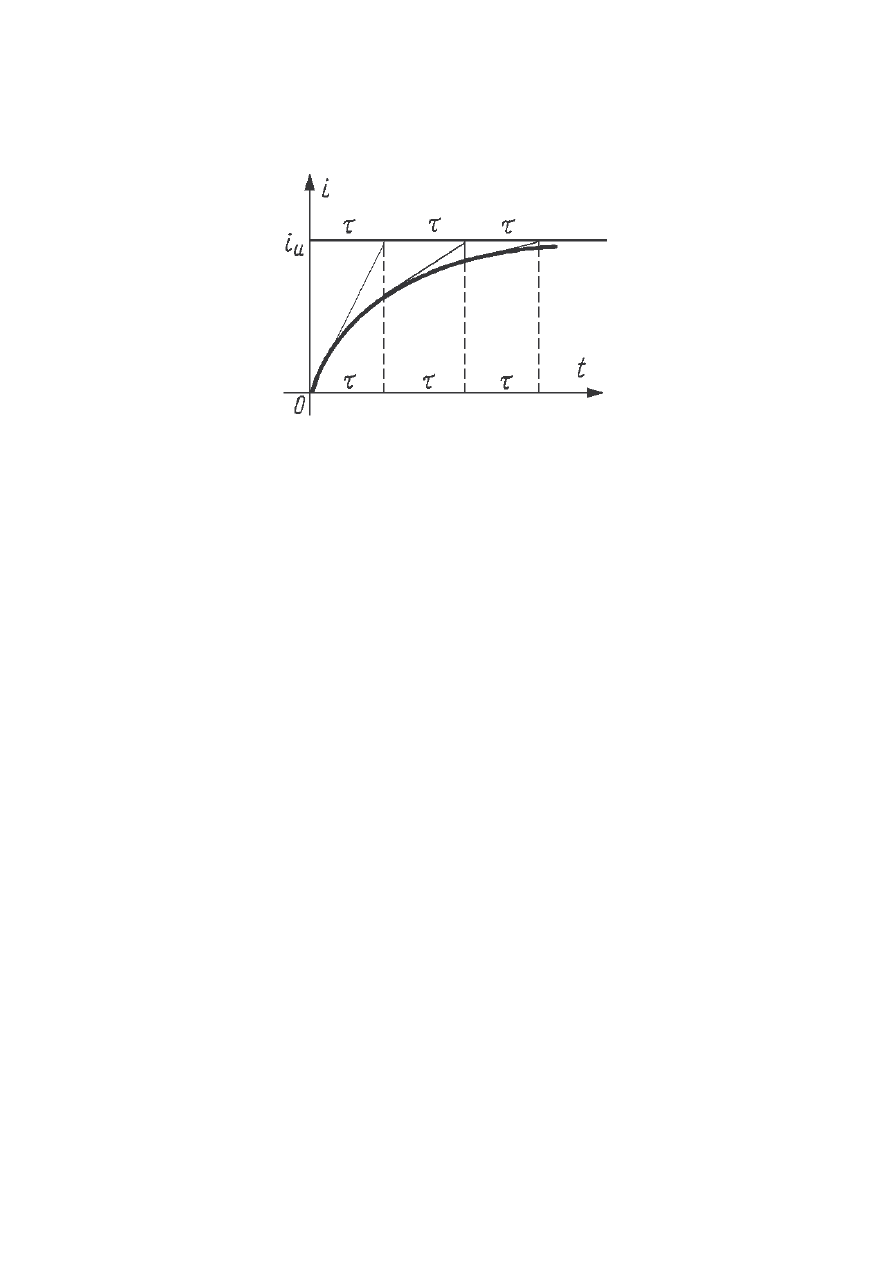
graficzn , przedstawion na poni szym rysunku:

Wyznaczanie stałej czasowej układu w sposób graficzny

Styczna poprowadzona na wykresie pr du do krzywej w chwili czasowej t = 0

przecina asymptot pr du po czasie

τ, ponadto dzieje si tak bez wzgl du na to, w którym

punkcie krzywej styczna b dzie prowadzona. Na tej podstawie mo na sformułowa
nast puj c definicj :

Stała czasowa

τ jest to czas, po upływie którego pr d nieustalony osi gn łby warto

ustalon , gdyby narastanie miało charakter liniowy, czyli przy stałej pr dko ci narastania
pr du i równa pr dko ci narastania w chwili zerowej.

Z reguły po okresie czasu wynosz cym cztery do pi ciu stałych czasowych pr d

praktycznie osi ga warto ustalon . Warto pr du mo na wyznaczy w oparciu o
zale no (12). Dla czasu t =

τ, i = 0,632iu; dla t = 2τ, i = 0,864iu; t = 3τ, i = 0,95iu;

t = 4

τ, i = 0,981iu; t = 5τ, i = 0,993iu.

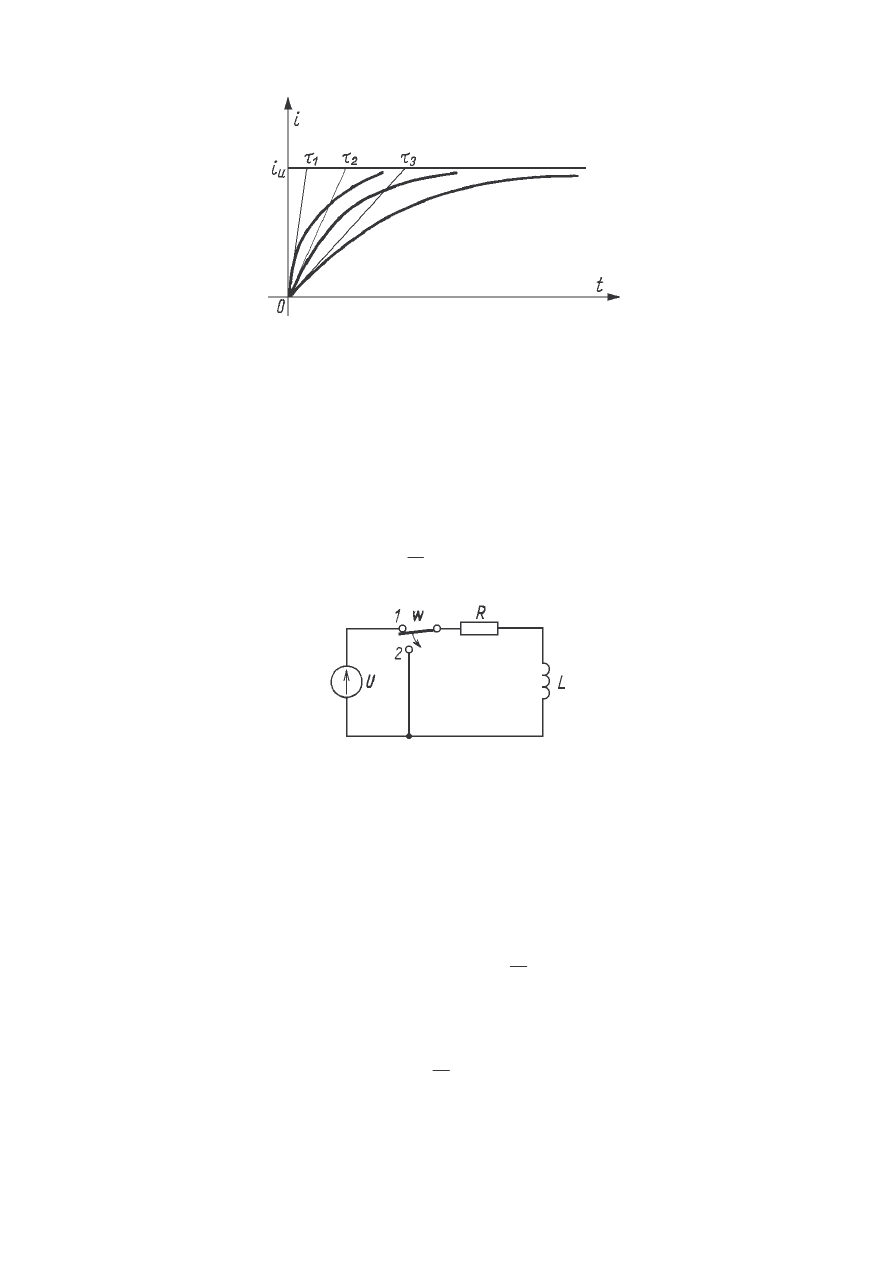
Jak wynika z powy szych rozwa a czas trwania stanu nieustalonego zale y od stałej

czasowej układu, a tym samym warto ci parametrów obwodu. Przykładowy przebieg
narastania pr du w układach o ró nych stałych czasowych przedstawiono poni ej:

Stany nieustalone

7

Zwi zek pomi dzy stał czasow układu, a przebiegiem pr du w stanie

nieustalonym.

Zwarcie przy niezerowym warunku pocz tkowym

Analogiczny dwójnik RL wł czony jest do ródła napi cia stałego. W układzie

panuje ju stan ustalony i przez obwód przepływa pr d stały o nat eniu:

R

U

i

=

(13)

Zwarcie dwójnika szeregowego RL przy niezerowym warunku pocz tkowym

W chwili t = 0 wył cznik odł cza dwójnik od zasilania, przy czym jednocze nie

zwiera jego zaciski. Zgodnie z pierwszym prawem komutacji, tu po przeł czeniu pr d w
obwodzie posiada warto równ warto ci z chwili poprzedzaj cej t zmian . W zwartym
obwodzie równie musi by spełnione drugie prawo Kirchhoffa, wi c w chwili komutacji

na elemencie indukcyjnym powstaje napi cie

dt

di

L

u

L

=

przeciwnie skierowane do napi cia

na rezystancji R. W tej sytuacji bilans napi wygl da nast puj co:

dt

di

L

Ri

0

+

=

(14)

Z równania tego po odpowiednich przekształceniach oraz scałkowaniu i wyznaczeniu

warto ci stałej całkowania otrzymuje si wyra enie opisuj ce przebieg pr du:

Stany nieustalone

8

t

L

R

e

R

U

i

−

=

(15)

Uwzgl dniaj c stał czasow układu:

τ

−

=

t

e

R

U

i

(16)

Przebieg zmienno ci pr du przedstawia rysunek:

Przebieg czasowy pr du w dwójniku szeregowym podczas zwarcia.

Napi cie na rezystancji zmienia si według wzoru:

τ

−

=

=

t

R

Ue

Ri

u

(17)

za na indukcyjno ci:

τ

−

−

=

=

t

L

Ue

dt

di

L

u

(18)

Warto ci obu napi pokazano na rysunku:

Przebiegi czasowe napi cia w dwójniku szeregowym RL podczas zwarcia

Stany nieustalone

9

Stan nieustalony w dwójniku szeregowym RC

Wł czenie napi cia stałego

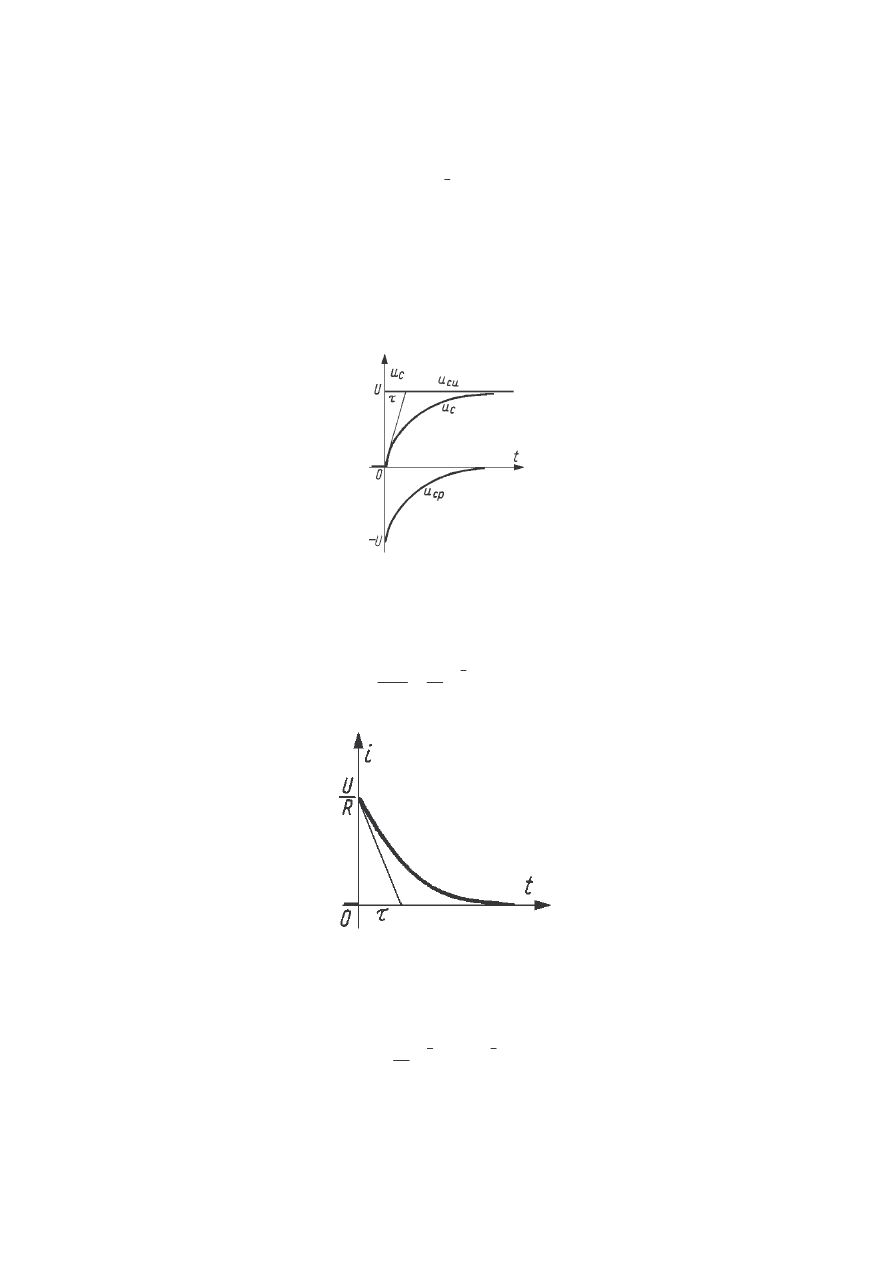
Do dwójnika szeregowego RC przedstawionego na poni szym schemacie doł czono

ródło napi cia stałego U.

Dwójnik szeregowy RC wł czony na napi cie stałe

W chwili czasu t = 0 zamkni to obwód przy u yciu wył cznika, zakładamy przy tym,

e układ był w chwili pocz tkowej w stanie zerowym. Po zamkni ciu wył cznika wyst pi

stan nieustalony, w którym zarówno pr d, jak i napi cia na poszczególnych elementach
b d zmienne w czasie. Warto ci tych wielko ci zostan wyznaczone poni ej. Napi cie
kondensatora zmienia si od zera do warto ci ustalonej uCu, równej napi ciu
przyło onemu, co zachodzi w procesie ładowania ze ródła napi cia stałego przez rezystor
R. Z drugiego prawa Kirchhoffa otrzymuje si nast puj ce równanie:

C

U

Ri

U

+

=

(19)

przy czym i okre lane jest mianem pr du ładowania kondensatora:

dt

du

C

dt

dq

i

C

=

=

(20)

Podstawiaj c warto pr du do równania:

C

C

U

dt

du

RC

U

+

=

(21)

Po rozdzieleniu zmiennych i scałkowaniu wzór okre laj cy napi cie na

kondensatorze:

−

=

−

t

RC

1

C

e

1

U

u

(22)

W przypadku układu RC stała czasowa wyra ona jest nieco innym wzorem:

Stany nieustalone

10

RC

=

τ

(23)

Po jej uwzgl dnieniu we wzorze na napi cie kondensatora:

−

=

τ

− t

C

e

1

U

u

(24)

Napi cie to posiada dwie składowe: składow ustalon (pierwsza) oraz składow

przej ciow . Napi cie wypadkowe jest ich sum . Znajduj cy si ni ej rysunek przedstawia
przebiegi czasowe obu napi :

Przebiegi czasowe napi na poszczególnych elementach dwójnika

Pr d ładowania:

τ

−

=

=

t

C

e

R

U

dt

du

C

i

(25)

Przebieg pr du w dwójniku szeregowym RC wł czonym na napi cie stałe.

Napi cie na rezystancji:

τ

−

τ

−

=

=

=

t

t

R

Ue

e

R

U

Ri

u

(26)

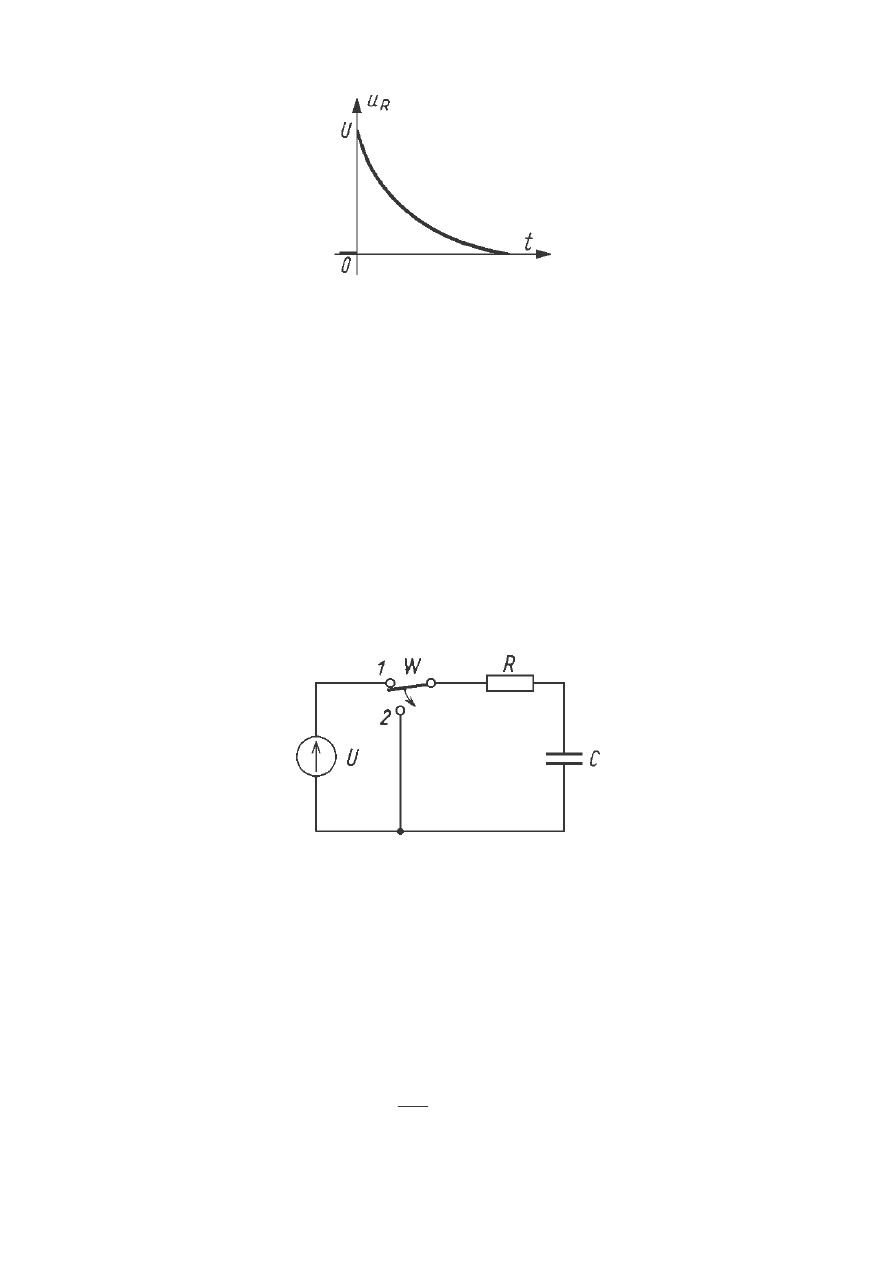
Przedstawia go poni szy przebieg:

Stany nieustalone

11

Przebieg czasowy napi cia na rezystancji

Jak wynika ze wzoru okre laj cego stał czasow dla układu szeregowego RC

przebieg ładowania zale y od pojemno ci kondensatora i warto ci rezystancji wł czonej w
obwód. Zale no ta jest wprost proporcjonalna, im wi ksze R i C tym wolniej przebiega
ładowanie.

Zwarcie przy warunku pocz tkowym niezerowym

Ten sam dwójnik wł czony jest do ródła napi cia stałego, przy czym panuje w nim

stan ustalony. Pr d w obwodzie nie płynie, gdy kondensator stanowi przerw w
obwodzie, natomiast napi cie na nim równe jest napi ciu ródła.

Zwarcie dwójnika szeregowego RC przy niezerowym warunku pocz tkowym

W zerowej chwili pocz tkowej (t = 0) przeł cznik zostaje przestawiony powoduj c

odł czenie układu od ródła i zwarcie jego zacisków. Wynikiem tego jest powstanie stanu
nieustalonego, a nagromadzona w polu elektrycznym kondensatora energia ulega
przemianie w ciepło w wyniku przepływu pr du przez rezystor. Proces ten nazywa si
wyładowaniem kondensatora przez rezystor. Bilans napi w obwodzie:

C

C

u

dt

du

RC

0

+

=

(27)

Stany nieustalone

12

Po odpowiednich przekształceniach i scałkowaniu uzyskuje si zale no opisuj c

napi cie na kondensatorze w stanie nieustalonym:

t

RC

1

C

Ue

u

−

=

(28)

Uwzgl dniaj c stał czasow :

τ

−

=

t

C

Ue

u

(29)

Z kolei pr d wyładowania kondensatora:

τ

−

−

=

=

t

C

e

R

U

dt

du

C

i

(30)

Napi cie na rezystancji:

τ

−

−

=

=

t

R

Ue

Ri

u

(31)

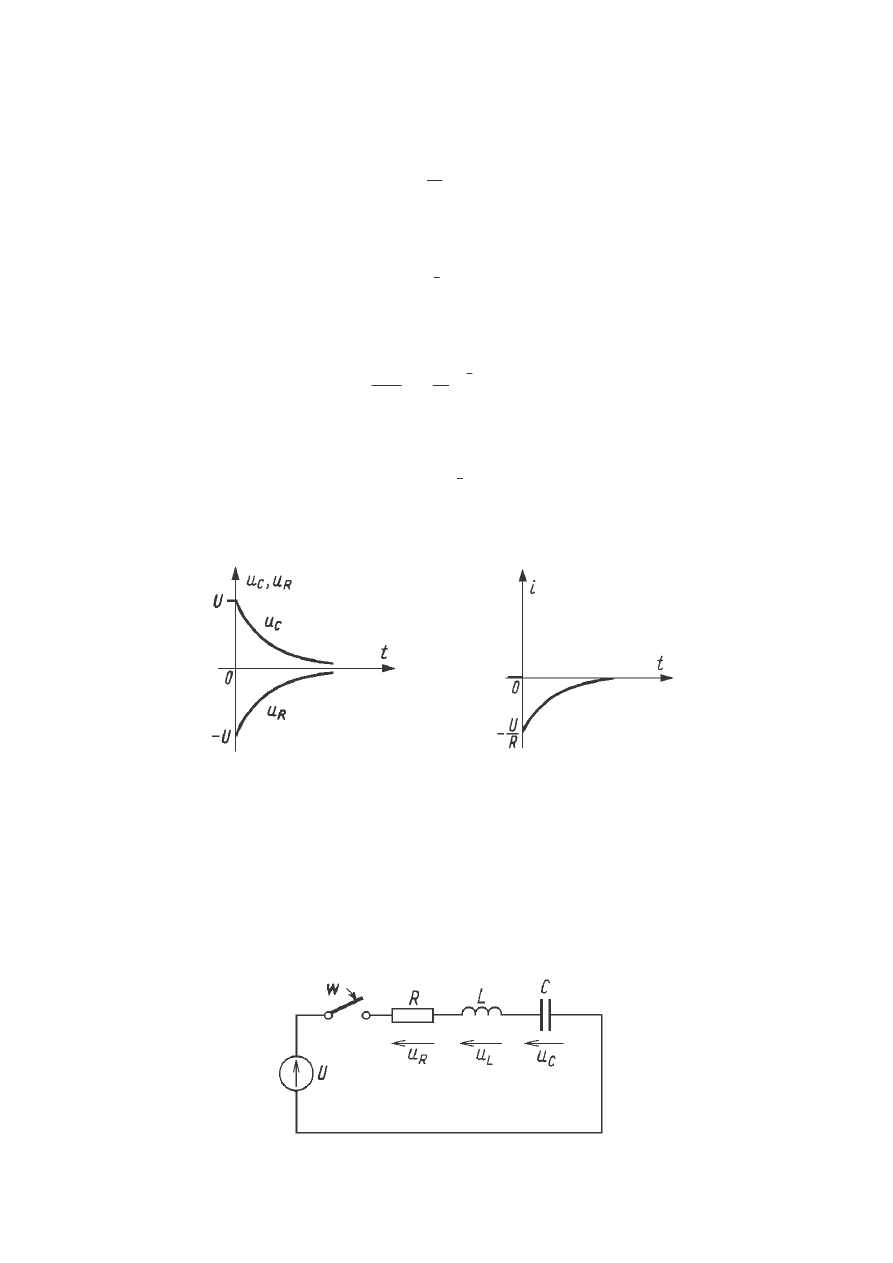
Przebiegi czasowe obliczonych wielko ci przedstawia poni szy rysunek:

Przebiegi czasowe napi i pr du w dwójniku szeregowym RC zwartym przy

niezerowym warunku pocz tkowym

Stan nieustalony w dwójniku szeregowym RLC

Dwójnik szeregowy RLC wł czono do ródła napi cia stałego U. W chwili t = 0

obwód został zamkni ty wył cznikiem W.

Stany nieustalone

13

Dwójnik szeregowy RLC wł czony na napi cie stałe

Dla obwodu musi by spełnione drugie prawo Kirchhoffa:

C

L

R

u

u

u

U

+

+

=

(32)

Podstawiaj c zale no ci dla poszczególnych napi :

C

u

dt

di

L

Ri

U

+

+

=

(33)

Po pewnych przekształceniach równanie sprowadzane jest do równania

ró niczkowego, po rozwi zaniu którego mo na wyznaczy poszczególne wielko ci
wyst puj ce w układzie.

Układ ten jest obwodem w którym nast puje ładowanie kondensatora przez cewk i

rezystancj oraz jego rozładowanie przez te elementy, gdy dwójnik ma zwarte zaciski. W
obu przypadkach nast puje przemiana energii w układzie pomi dzy jej ró nymi
postaciami oraz jej gromadzenie w polu elektrycznym i magnetycznym. W zale no ci od
warto ci parametrów poszczególnych elementów w układzie wyst puj oscylacje
amplitudy pr du i napi cia.

Je eli rezystancja

C

L

2

R

<

wówczas w układzie dominuj ce znaczenie maj

warto ci parametrów L i C, a głównym zjawiskiem w nim wyst puj cym jest wymiana
energii pomi dzy cewk i kondensatorem. Warto tłumienia wyst puj cych w układzie
oscylacji zale y od warto ci rezystancji R.

Pr d w obwodzie:

t

sin

e

L

U

i

0

t

0

ω

ω

=

α

−

(34)

Napi cie na pojemno ci:

)

t

sin(

e

LC

U

U

u

0

t

0

C

ϕ

+

ω

ω

−

=

α

−

(35)

gdzie:

L

2

R

=

α

- współczynnik tłumienia;

Stany nieustalone

14

2

2

0

LC

1

L

2

R

LC

1

α

−

=

−

=

ω

- pulsacja drga własnych (drga swobodnych);

α

ω

=

ϕ

0

tg

.

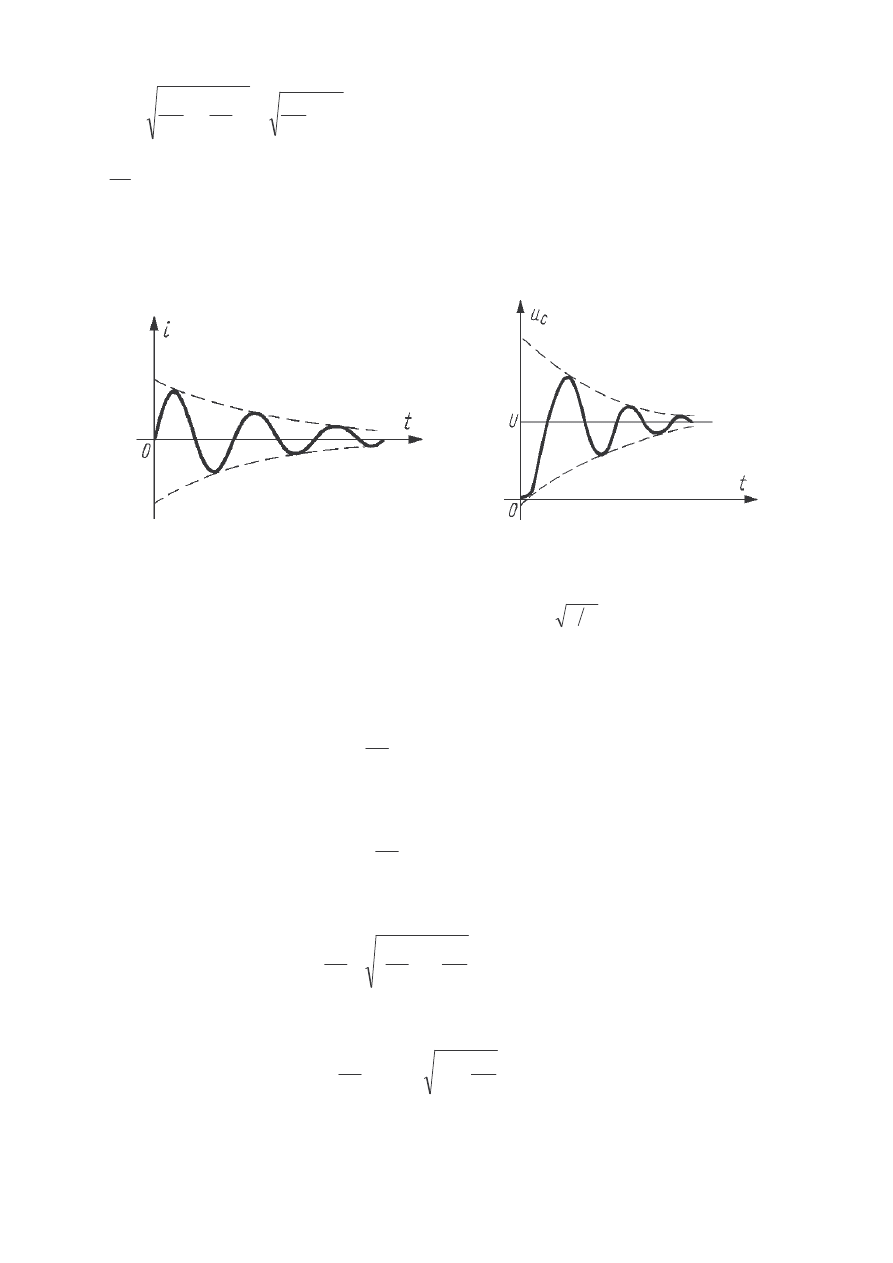
Wyst puj ce w układzie przebiegi czasowe pr du i napi cia przedstawiono na

rysunku.

Przebiegi czasowe pr du oraz napi cia na kondensatorze w układzie

szeregowym RLC przy rezystancji R mniejszej od warto ci krytycznej.

W sytuacji przeciwnej, tzn. przy rezystancji

C

L

2

R

>

dominuj ce znaczenie w

układzie ma rezystancja, natomiast przebiegi w obwodzie maj charakter aperiodyczny.

W obwodzie przepływa pr d o warto ci:

)

e

e

(

L

U

i

t

s

t

s

2

1

−

β

=

(36)

Napi cie na kondensatorze:

)

e

s

e

s

(

L

U

U

u

t

s

1

t

s

2

C

2

1

−

β

+

=

(37)

We wzorze tym:

β

±

α

−

=

−

±

−

=

LC

1

L

2

R

L

2

R

s

2

2

,

1

(38)

sk d:

L

2

R

=

α

,

LC

1

2

−

α

=

β

(39)

Wyst puj ce w układzie przebiegi czasowe przedstawione s na rysunku:

Stany nieustalone

15

Przebiegi czasowe pr du oraz napi cia w dwójniku szeregowym RLC przy

rezystancji R wi kszej od warto ci krytycznej

Reasumuj c: rezystancja wynosz ca

C

L

2

R

=

jest rezystancj krytyczn , przy

której zmianie ulega charakter zjawisk wyst puj cych w obwodzie, poni ej przebiegi s
okresowe, powy ej nieokresowe.