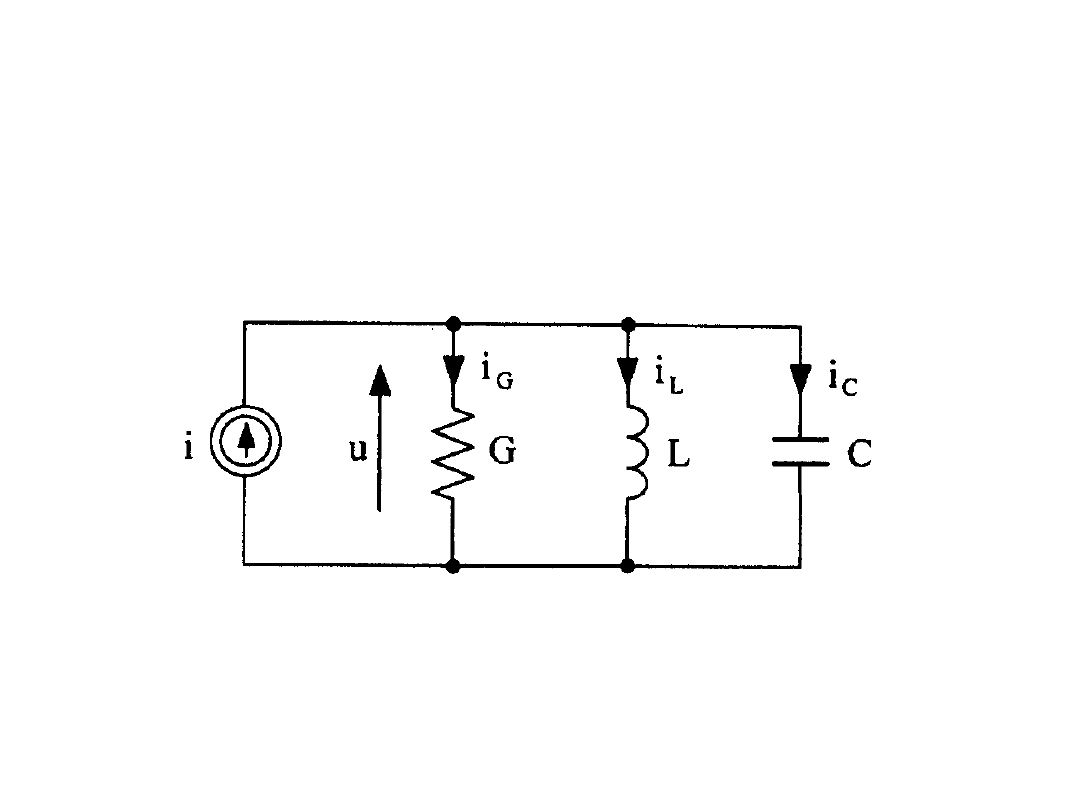
Stan nieustalony w równoległym obwodzie RLC

analiza analogiczna jak dla połączenia
szeregowego

i

i

i

i

C

L

G







t

i

GL

Gu

i

L

G

d

d





2

2

dt

i

d

LC

dt

di

L

dt

d

C

dt

du

C

i

L

L

C



















i

i

t

i

GL

t

i

LC

L

L

L







d

d

d

d

2

2

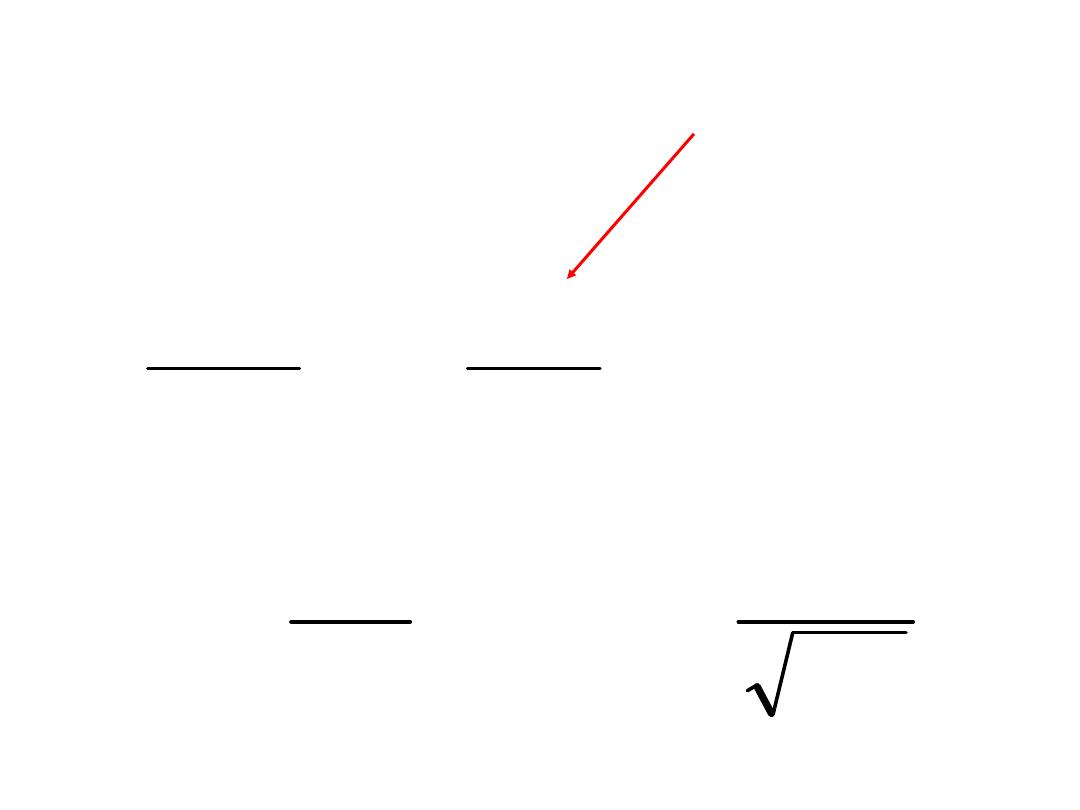
S

W

L

L

L

i

i

i





0

d

d

2

d

d

2

2

2











S

S

S

L

n

L

L

i

t

i

t

i

LC

,

C

G

n

1

2









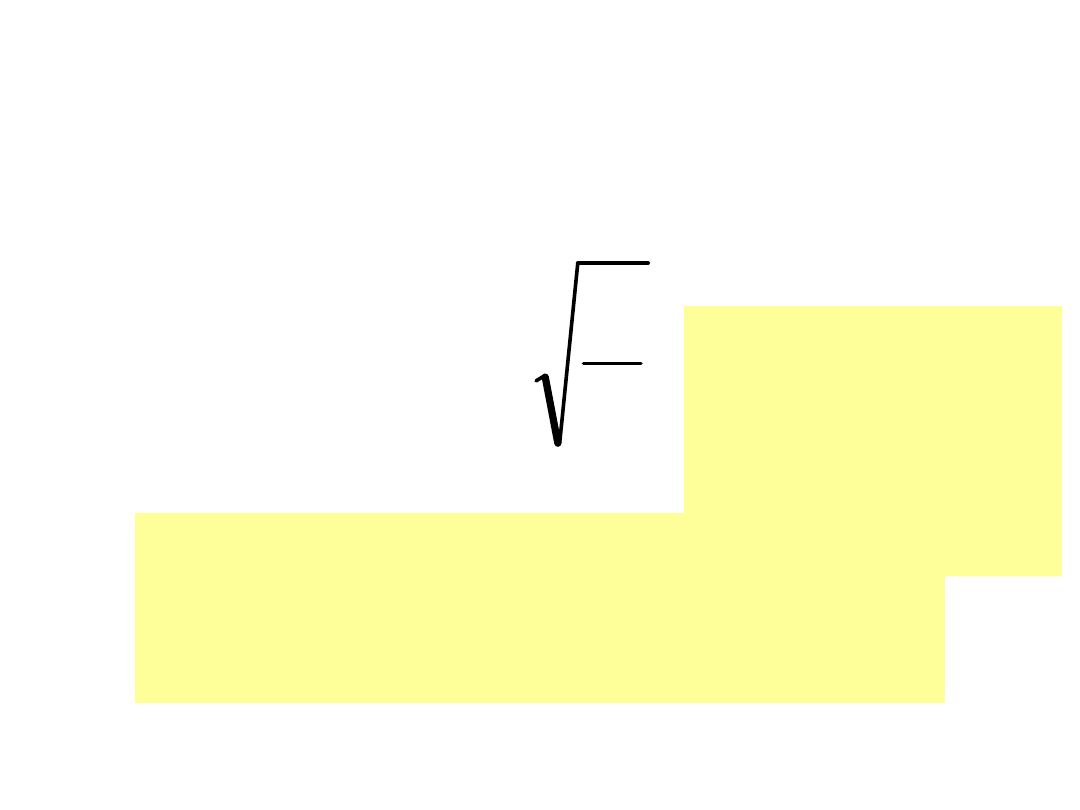
0

2

2

2











n

s

s

L

C

2

G











n

-
rozwiązanie
aperiodyczn
e

t

s

t

s

L

A

A

i

S

2

1

e

e

2

1





L

C

2

G











n

- rozwiązanie
aperiodyczne
graniczne

t

L

t

A

A

i

S

2

1

e

)

(









L

C

2

G











n

- rozwiązanie
oscylacyjne

)

(

sin

e

0













t

A

i

t

L

S

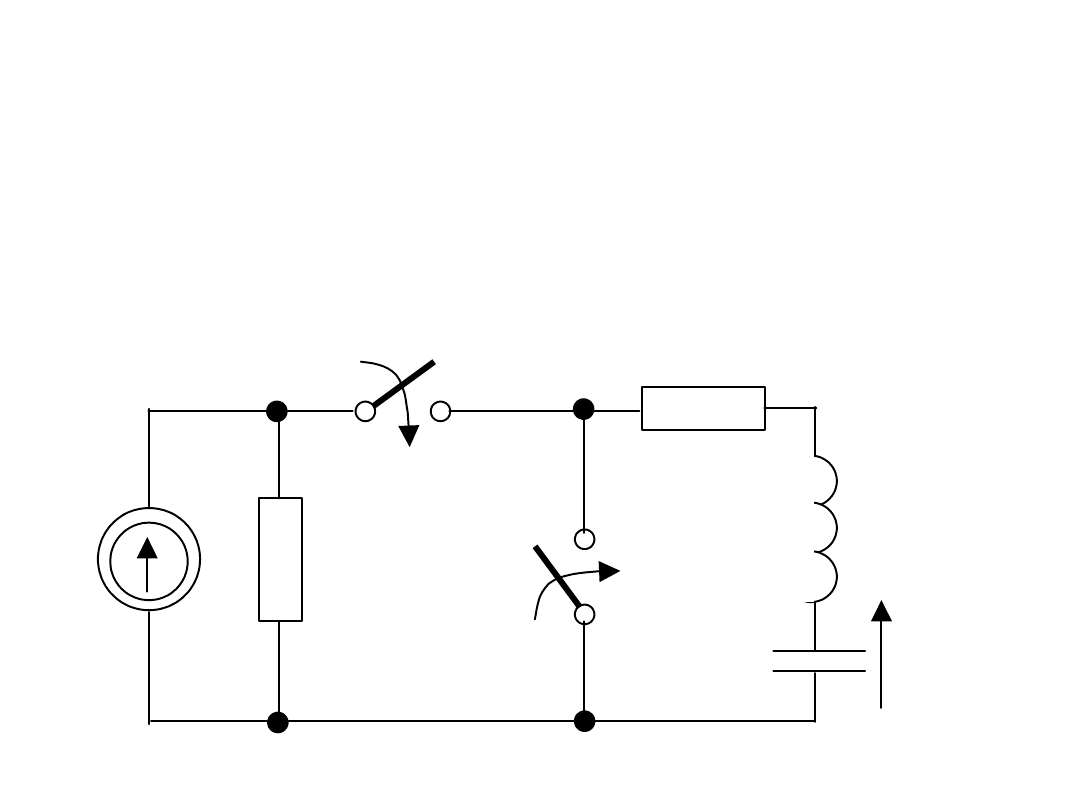
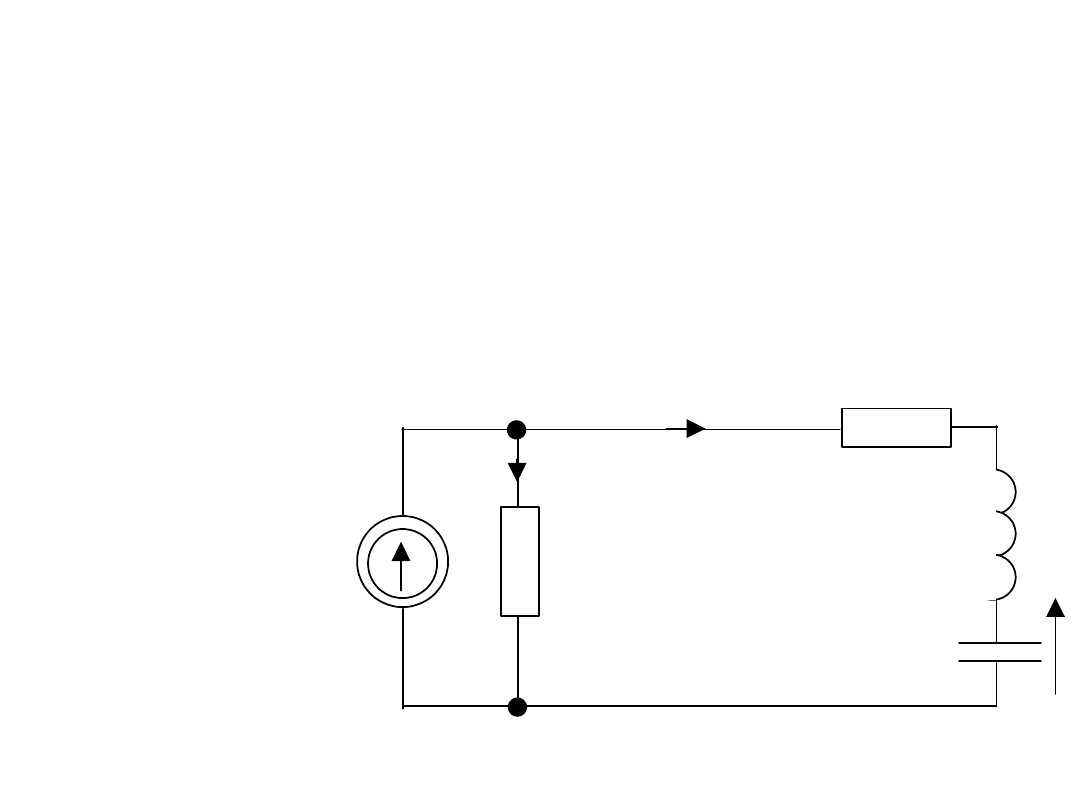
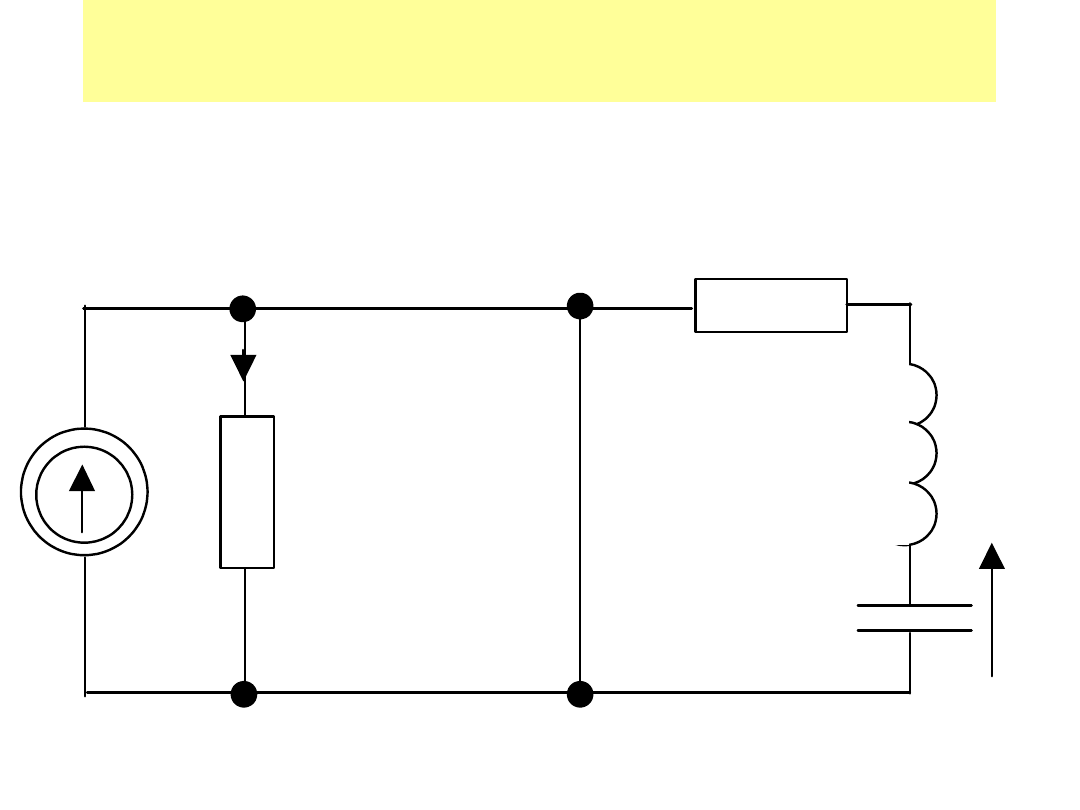
Przykład

Dla t<0 układ był w stanie ustalonym i panowały
w nim zerowe warunki początkowe.
Wyznaczyć u

C

(t) i narysować.

Dane i=10A, R=50, C=250F, L=200mH

i

R

R

L

C

w

1

w

2

t=0

t

1

=1ms

Warunki początkowe

   

   

0

0

0

0

0

0

















C

C

L

L

u

u

i

i

1

0

t

t 



i

R

R

L

C

i

2

i

1

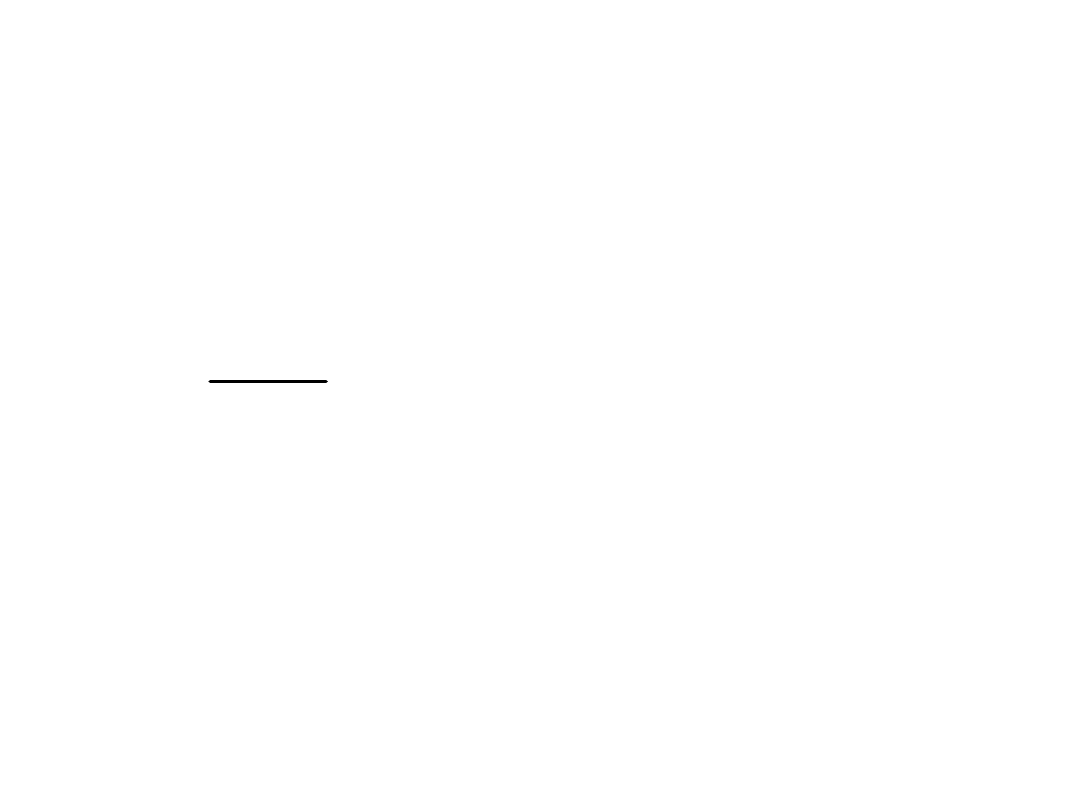
V

iR

u

i

w

w

C

L

500

50

10

0



















NPK

R

i

u

u

R

i

PPK

i

i

i

dt

du

C

i

i

i

i

C

L

C

C

c

C

C

L

2

2

1

0























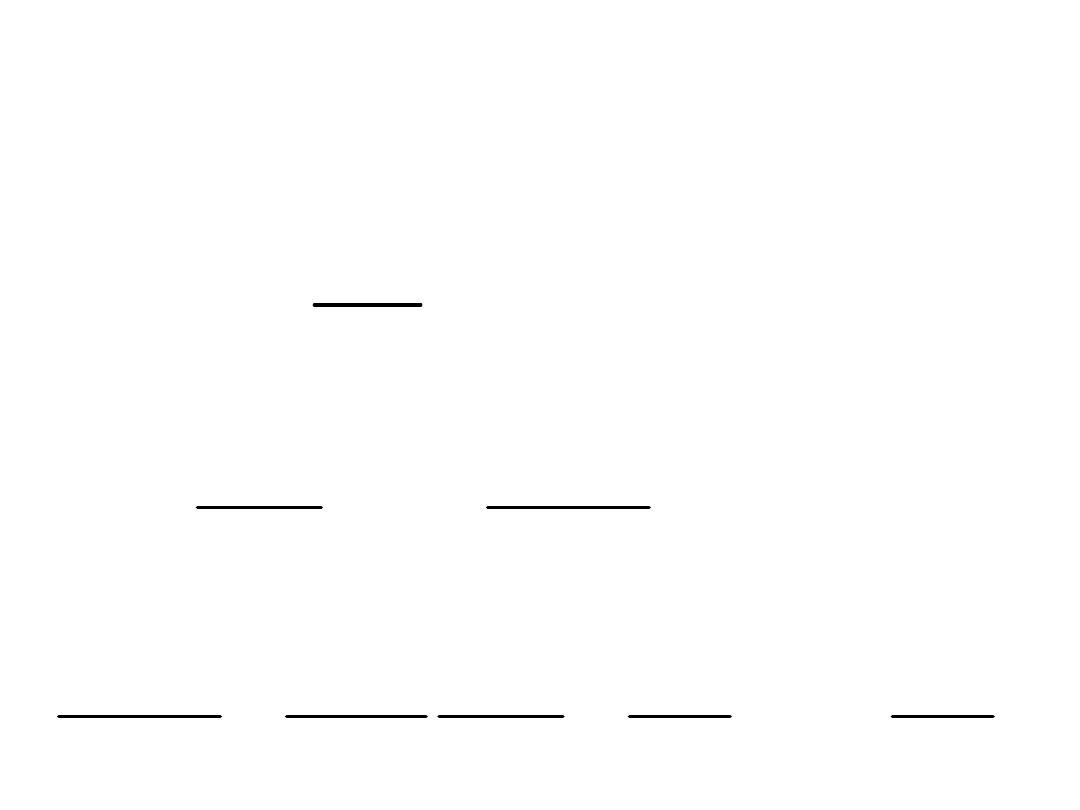
i

LC

R

u

LC

dt

du

LC

RC

dt

u

d

iR

u

dt

u

d

LC

dt

du

RC

iR

u

dt

di

L

R

i

R

i

i

u

u

R

i

i

i

i

i

i

i

C

C

C

C

C

C

C

C

C

C

C

L

C

C

C







































1

2

2

2

0

2

2

2

2

2

2

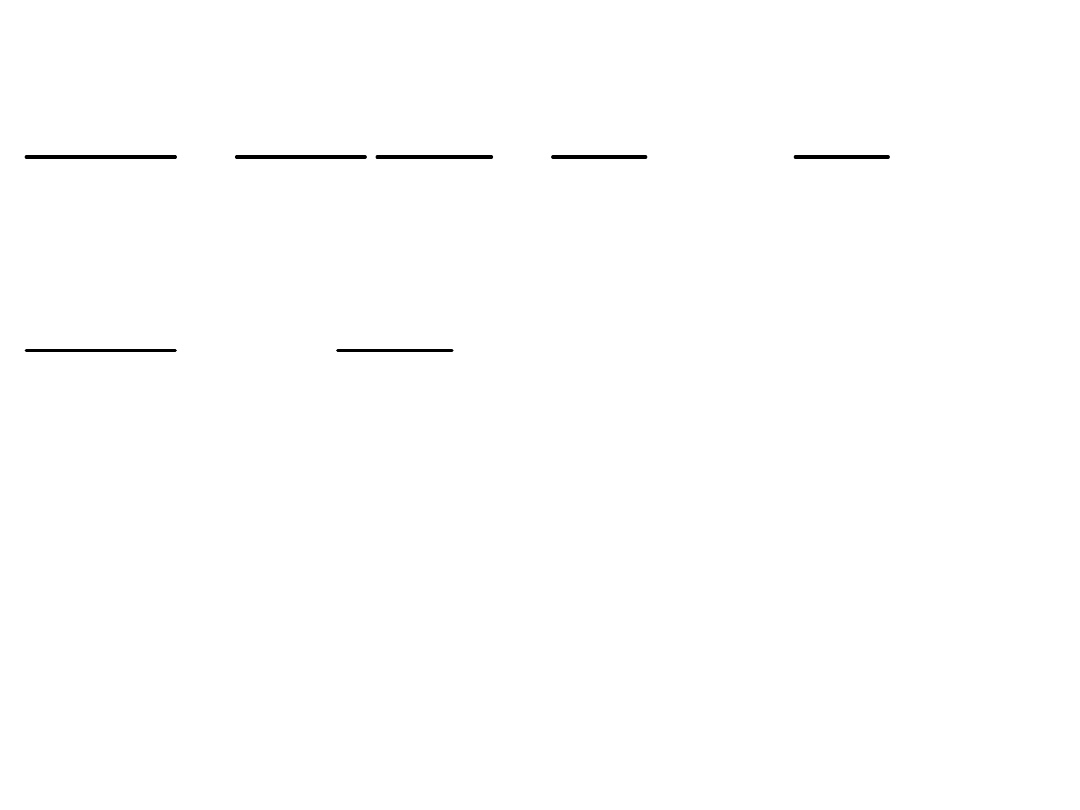
85

.

43

2

.

456

0

20000

500

10

10

20000

500

1

2

2

1

2

6

2

2

2

2































s

s

s

s

u

dt

du

dt

u

d

i

LC

R

u

LC

dt

du

LC

RC

dt

u

d

C

C

C

C

C

C

   

0

0

0

500

0

0

85

.

43

2

2

.

456

1

85

.

43

2

2

.

456

1











































t

C

t

C

L

L

t

t

C

C

C

C

t

t

C

dt

du

dt

du

C

i

i

e

A

e

A

u

u

u

u

e

A

e

A

u

s

w

s

















2

.

553

2

.

53

0

500

0

85

.

43

2

.

456

85

.

43

2

.

456

2

1

2

1

2

1

2

1

0







































A

A

A

A

A

A

A

A

dt

du

t

C

t

t

C

e

e

u

85

.

43

2

.

456

2

.

553

2

.

53

500











1

t

t 

i

R

R

L

C

i

2

0



w

C

u

warunki początkowe



 



V

e

e

t

t

u

t

t

u

C

C

25

.

4

2

.

553

2

.

53

500

3

3

10

85

.

43

10

2

.

456

1

1











































1

1

t

t

C

t

t

C

dt

du

dt

du

Ponieważ

L

C

i

dt

du

C











s

V

e

e

dt

du

t

t

C

6

.

7837

85

.

43

2

.

553

2

.

456

2

.

53

3

3

1

10

85

.

43

10

2

.

456































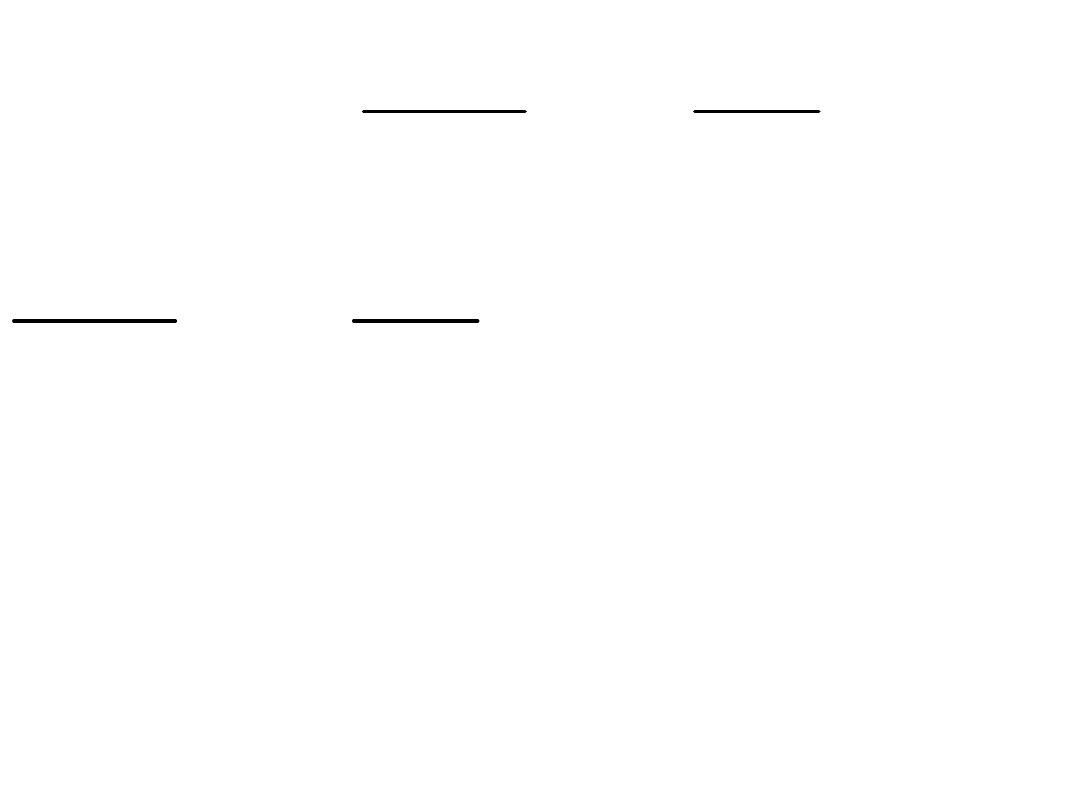
j

s

j

s

s

s

u

dt

du

dt

u

d

u

dt

du

RC

dt

u

d

LC

NPK

C

C

C

C

C

C

14

.

66

125

14

.

66

125

0

20000

250

0

20000

250

0

2

1

2

2

2

2

2































 













































































6

.

7837

cos

14

.

66

sin

125

25

.

4

sin

6

.

7837

cos

14

.

66

sin

125

25

.

4

sin

14

.

66

sin

0

1

1

1

1

125

A

A

A

A

A

dt

du

A

u

t

t

Ae

t

u

t

t

C

t

t

C

t

t

C

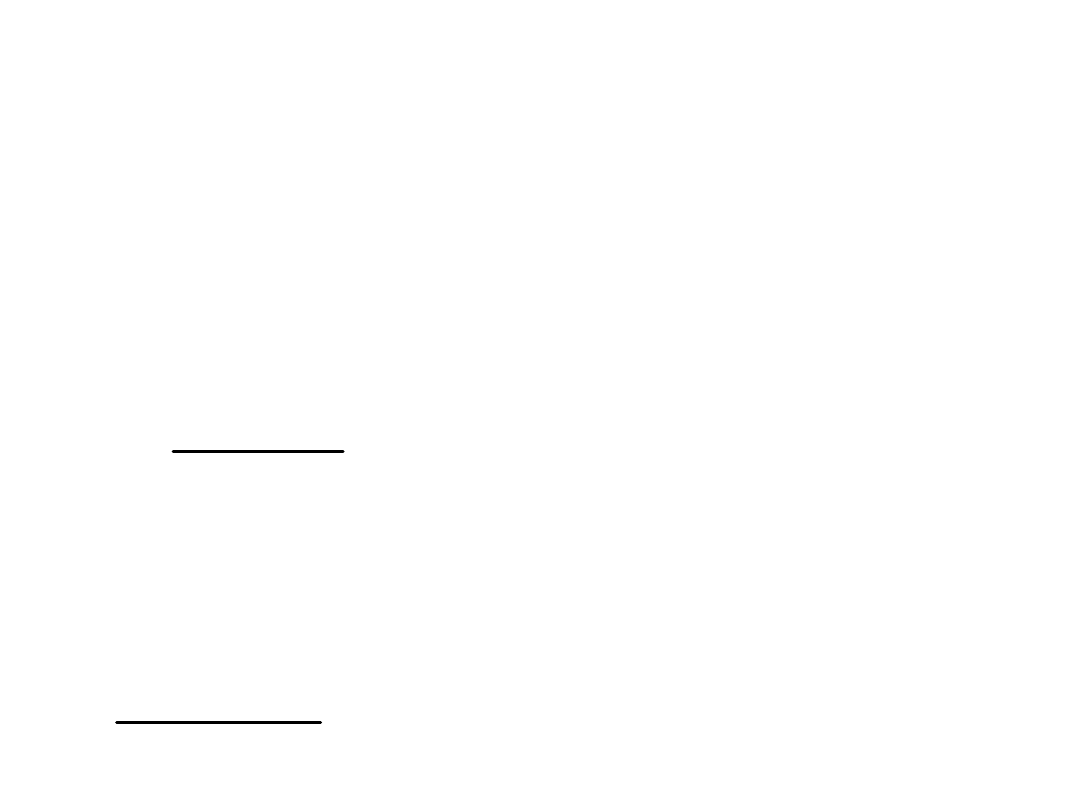
6

.

126

5

5

1

sin

25

.

4

5

5

1

03359

.

0

52

.

126

25

.

4

52

.

126

cos

25

.

4

sin

6

.

7837

cos

14

.

66

25

.

4

125

25

.

4

sin

















































A

tg

A

A

A

A

 













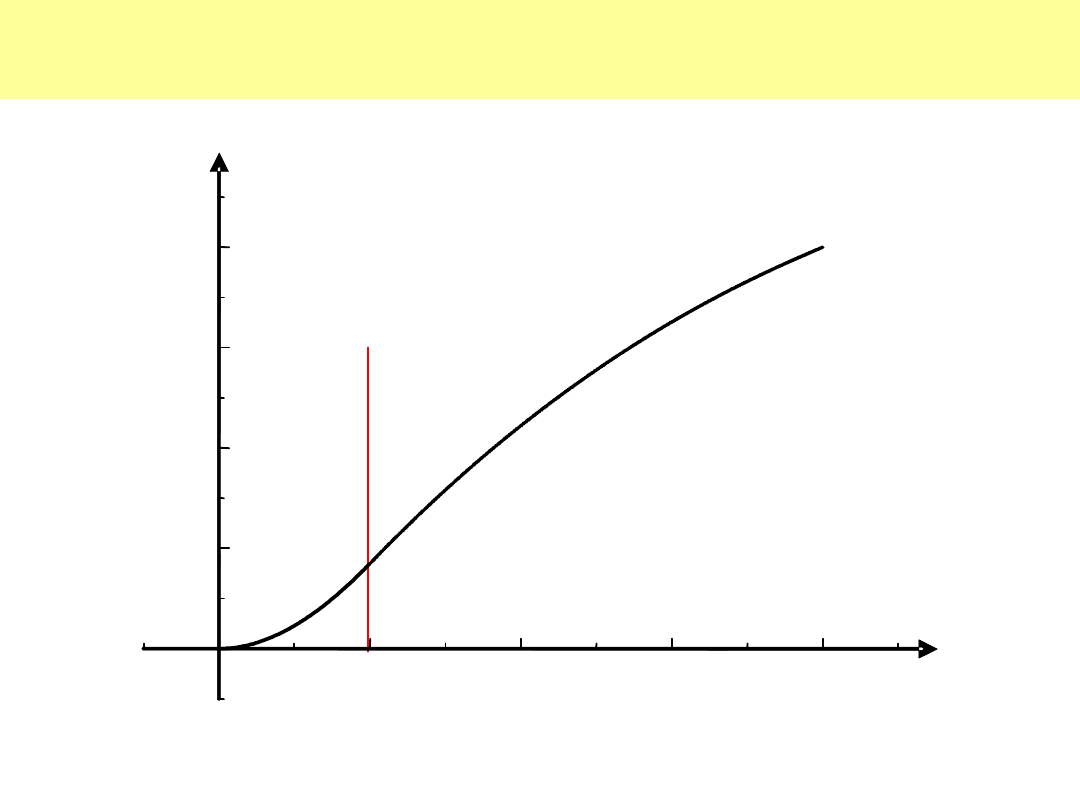
5

5

1

14

.

66

sin

6

.

126

1

125

1















t

t

e

t

u

t

t

C

0

1m

2m

3m

4m

0

5

10

15

20

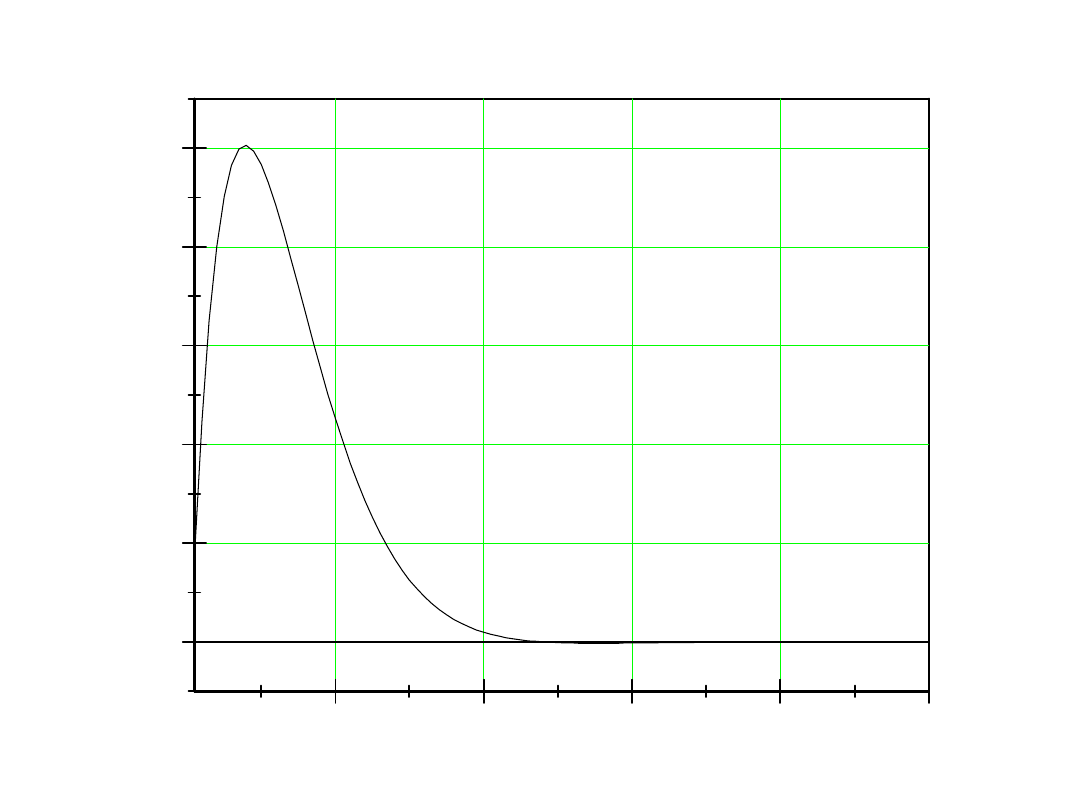
20,0m

40,0m

60,0m

80,0m

100,0m

0

5

10

15

20

25

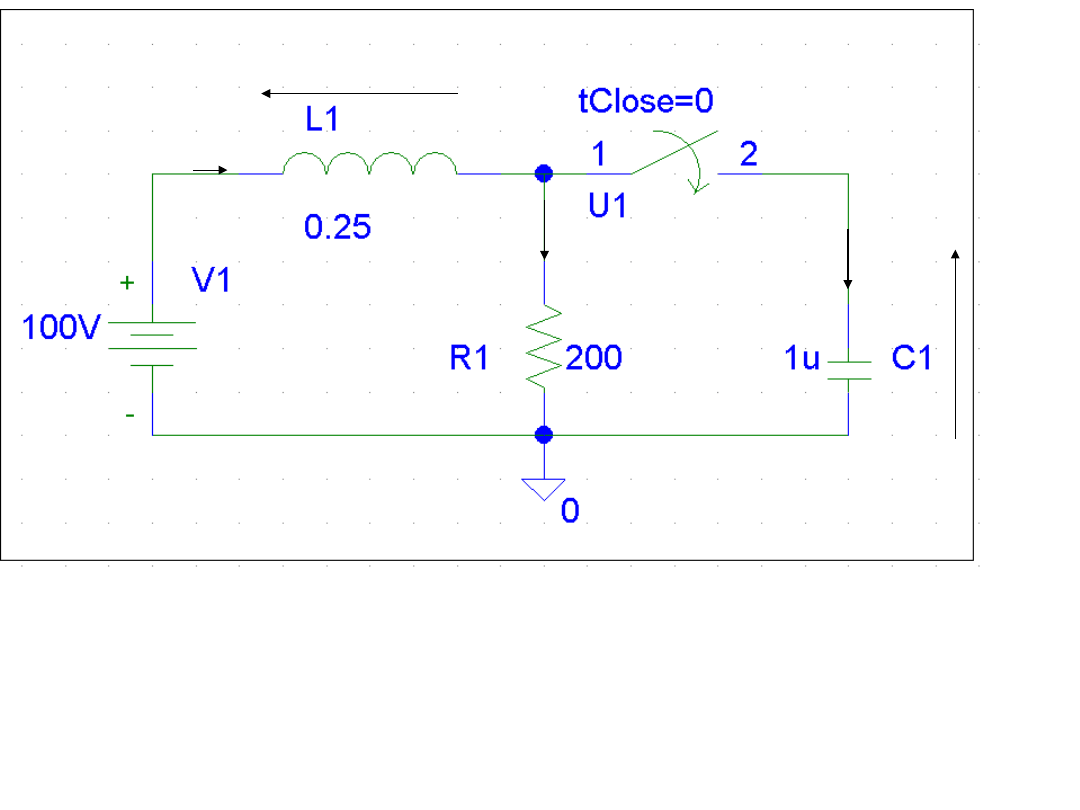
i

L

u

L

i

R

i

C

u

C

ozn. L1 – L R1 – R C1 – C V1 – E

 

V

200

0 



C

u

Warunki początkowe

   

   

V

200

0

0

A

5

0

200

100

0

0





















C

C

L

L

u

u

.

R

E

i

i

V

100

A

5

0









E

u

.

R

E

i

w

w

C

L

obliczamy składowe wymuszone po komutacji

Układamy równanie różniczkowe

L

u

L

E

dt

di

u

dt

di

L

E

R

u

i

dt

du

C

i

i

i

i

C

L

C

L

C

R

C

C

C

R

L

























0

0

0









dt

du

C

R

u

i

C

C

L

rózniczkujemy stronami

(*)

0

1

2

2









dt

u

d

C

dt

du

R

dt

di

C

C

L

L

u

L

E

dt

di

C

L





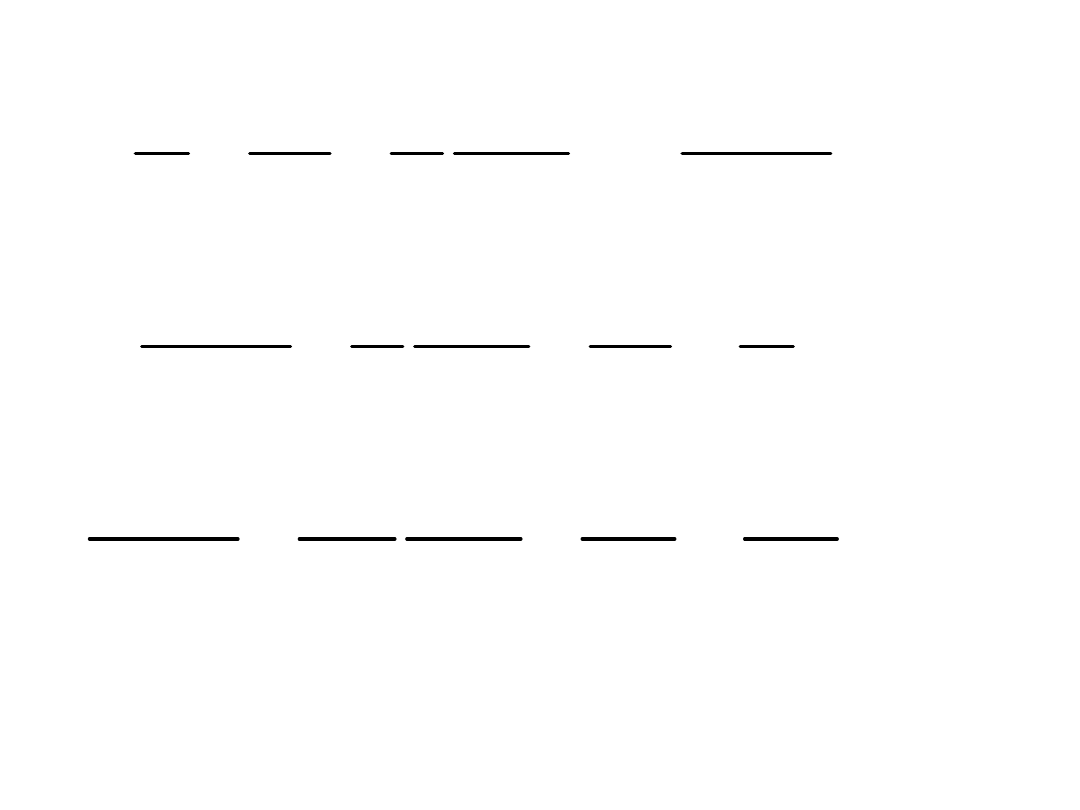
LC

E

LC

u

dt

du

RC

dt

u

d

L

E

L

u

dt

du

R

dt

u

d

C

dt

u

d

C

dt

du

R

L

u

L

E

C

C

C

C

C

C

C

C

C























1

1

0

1

2

2

2

2

2

2

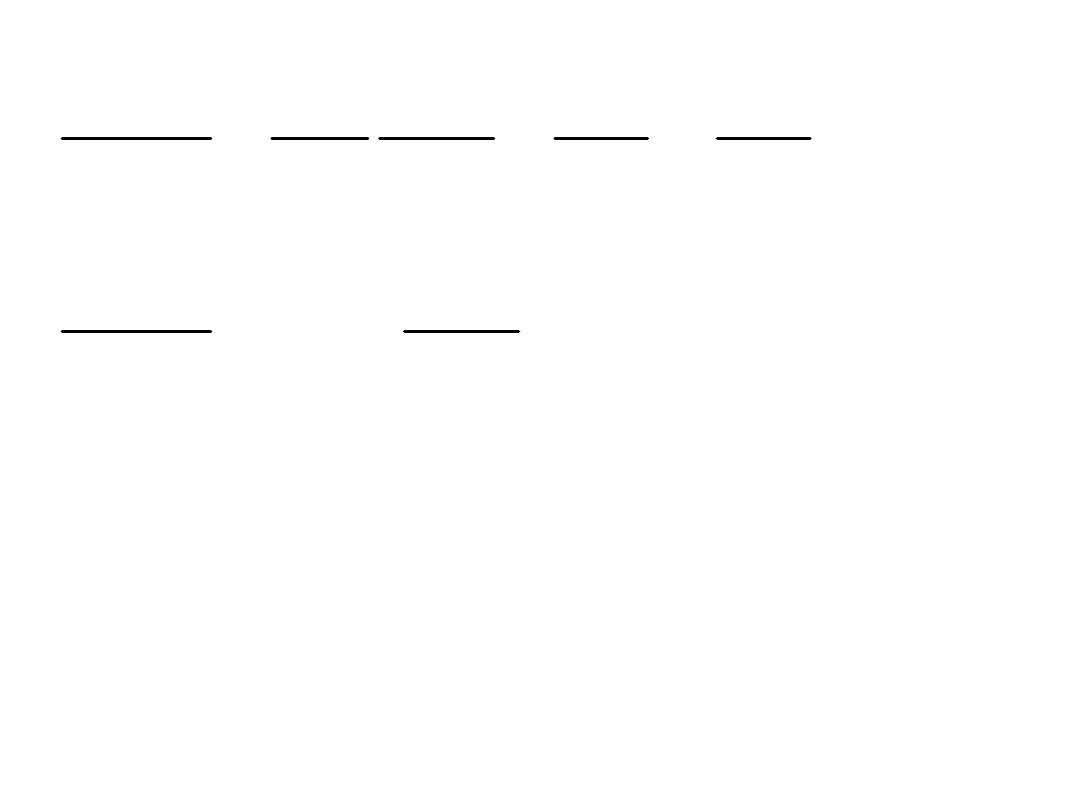
4

6

2

2

2

2

10

4

10

4

5000

1

















C

C

C

C

C

C

u

dt

du

dt

u

d

LC

E

LC

u

dt

du

RC

dt

u

d

 

 

 

t

u

t

u

t

u

S

w

C

C

C





RORN = RSRN +
RORJ

0

10

4

5000

6

2

2









S

S

S

C

C

C

u

dt

du

dt

u

d

0

10

4

5000

6

2









s

s

równanie jednorodne

równanie charakterystyczne

3000

10

9

10

4

4

5000

6

6

2



















1000

4000

2

1









s

s

przypadek aperiodyczny

t

s

t

s

C

e

A

e

A

u

s

2

1

2

1





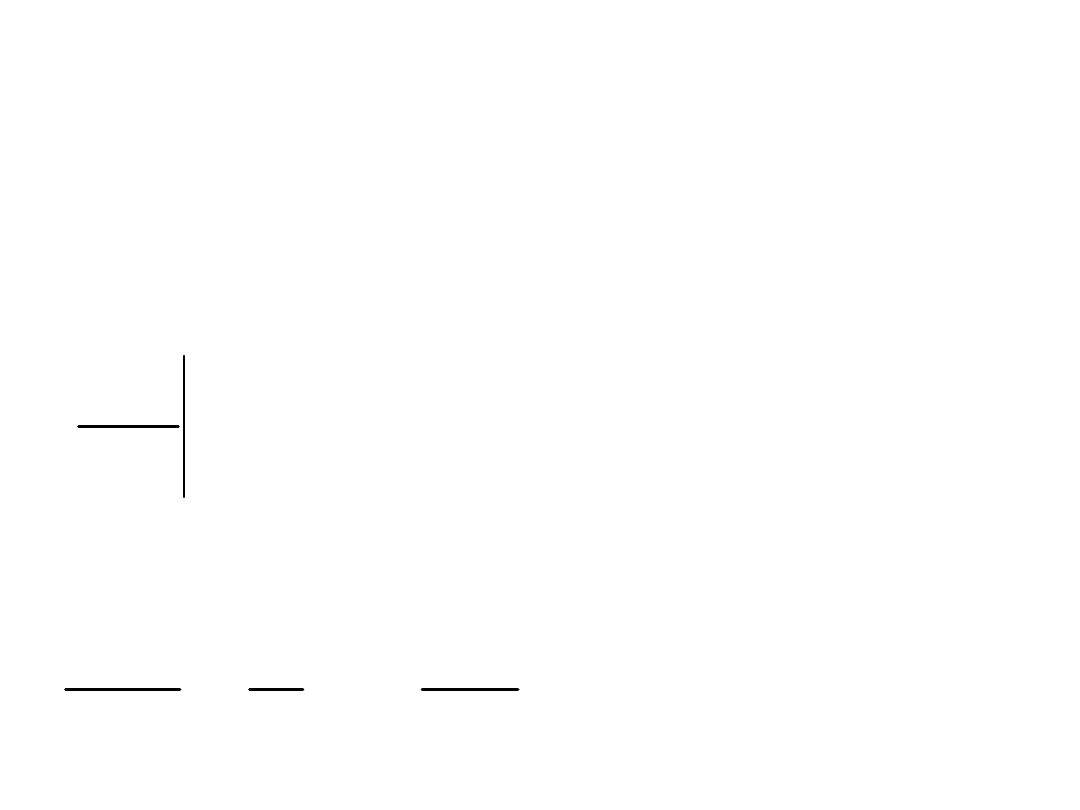
t

t

C

C

C

C

t

t

C

e

A

e

A

u

u

u

u

e

A

e

A

u

s

w

s

1000

2

4000

1

1000

2

4000

1

100























???

0







t

C

dt

du

z równania z (*) mamy

C

L

C

u

RC

i

C

dt

du

1

1





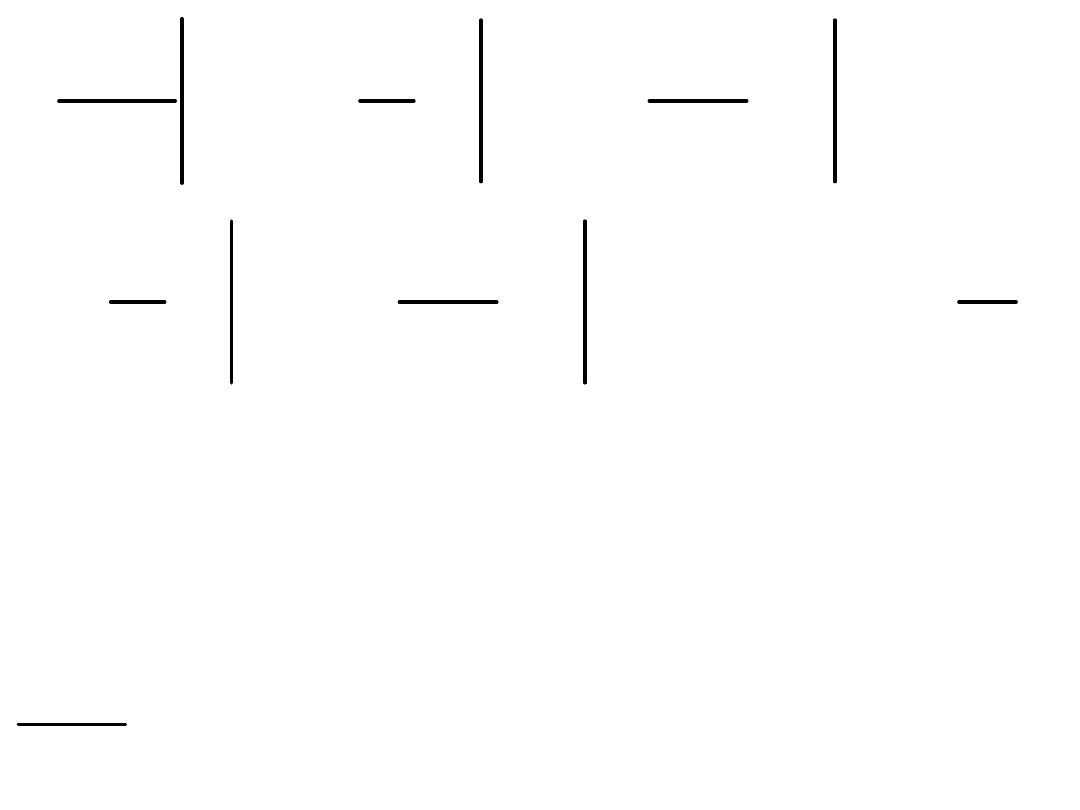
s

V

10

5

1

1

1

1

5

0

0

0

0

0





































t

C

t

L

t

C

t

L

t

C

u

RC

i

C

u

RC

i

C

dt

du

t

t

C

e

A

e

A

u

1000

2

4000

1

100











różniczkujemy po czasie

i
otrzymuje
my









t

t

C

e

A

e

A

dt

du

1000

2

4000

1

1000

4000













z układu dwóch równań wyznaczamy stałe

















3

100

3

400

200

100

500000

1000

4000

1000

4000

2

1

2

1

2

1

2

1

0









































A

A

A

A

A

A

A

A

dt

du

t

C

A zatem rozwiązanie przyjmuje postać

t

t

C

e

.

e

.

u

1000

4000

33

33

33

133

100











0,0

1,0m 2,0m 3,0m 4,0m 5,0m 6,0m 7,0m 8,0m 9,0m 10,0m

100

120

140

160

180

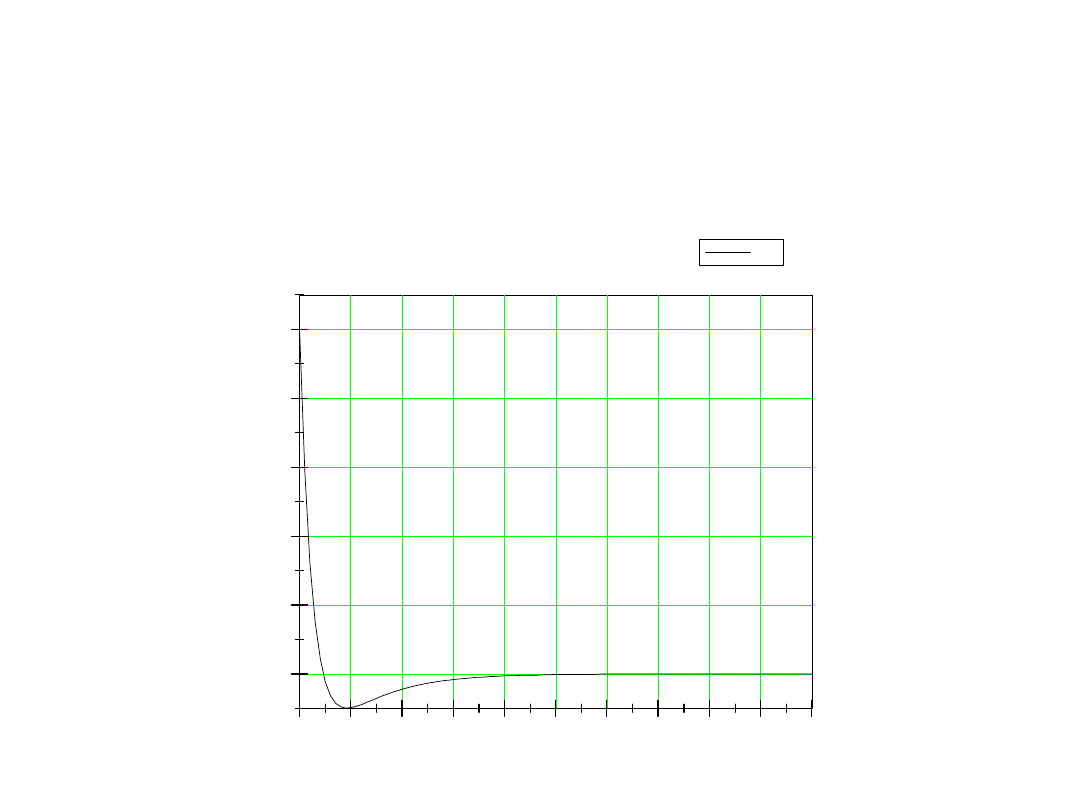
200

uc

czas

F1

W celu określenia prądu i

L

korzystamy z wcześniejszego równania

t

t

C

C

L

.

dt

du

C

R

u

i

1000

4000

e

30

4

e

30

4

5

0

















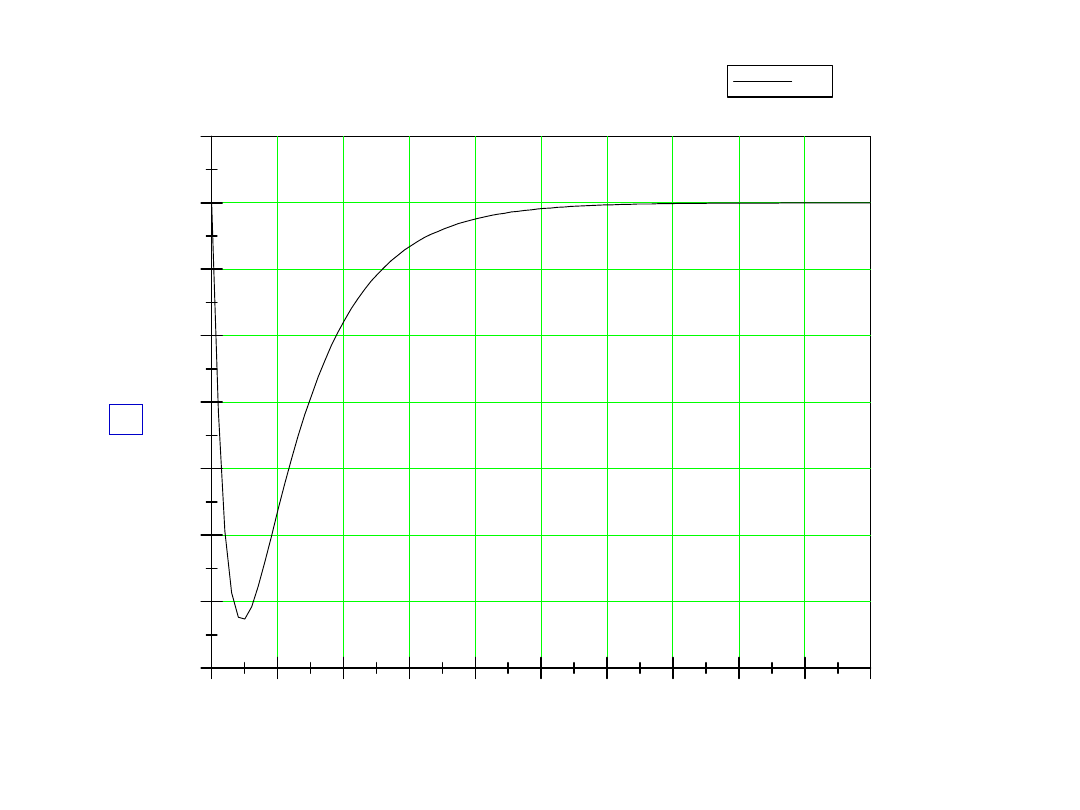
0,0

1,0m 2,0m 3,0m 4,0m 5,0m 6,0m 7,0m 8,0m 9,0m 10,0m

0,43

0,44

0,45

0,46

0,47

0,48

0,49

0,50

0,51

IL

czas

F1