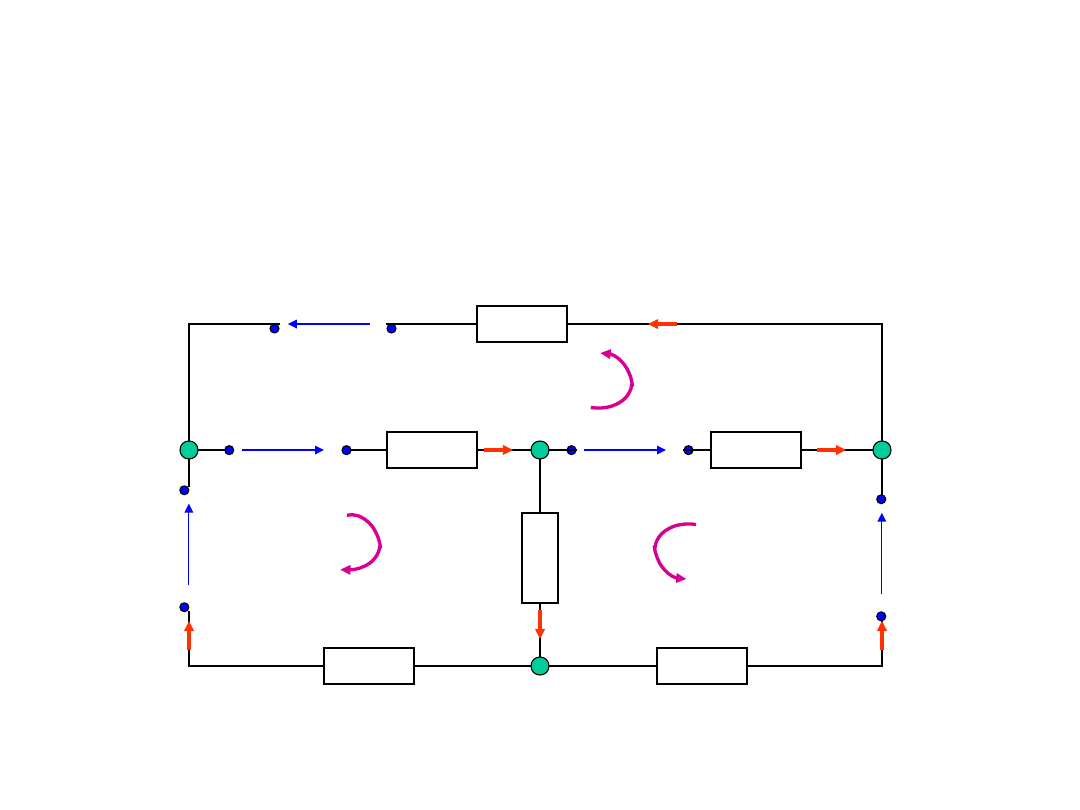
Obliczanie obwodów

elektrycznych - przykład

A

u

3

u

5

u

4

u

1

u

2

B

C

D

R

1

R

2

R

3

R

4

R

5

i

1

i

2

i

3

i

4

i

5

i

6

R

6

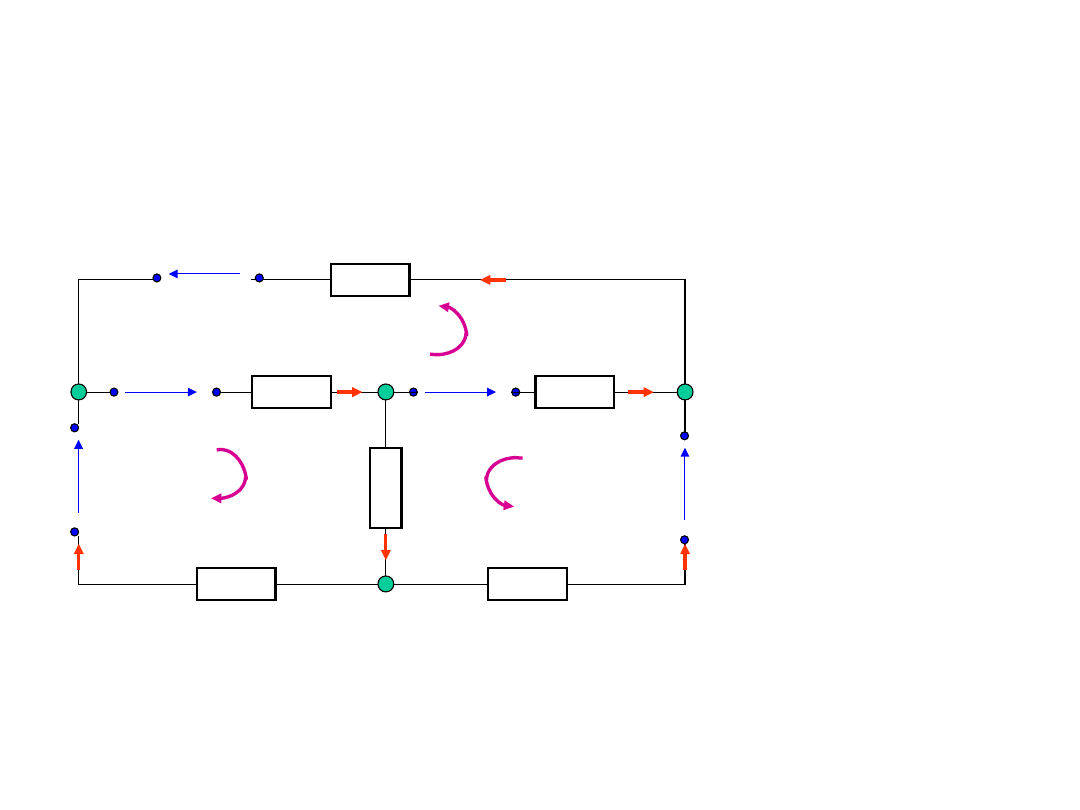
Obliczanie obwodów

elektrycznych - przykład

u

1

= 6V

u

2

= 30V

u

3

= u

4

=

10V

u

5

= 36V

A

i

1

u

3

u

5

u

4

u

1

u

2

B

C

D

R

1

R

2

R

3

R

4

R

5

i

2

i

3

i

4

i

5

i

6

R

6

R

1

= R

2

= R

3

= R

5

= 2 , R

4

= 4 , R

6

= 10



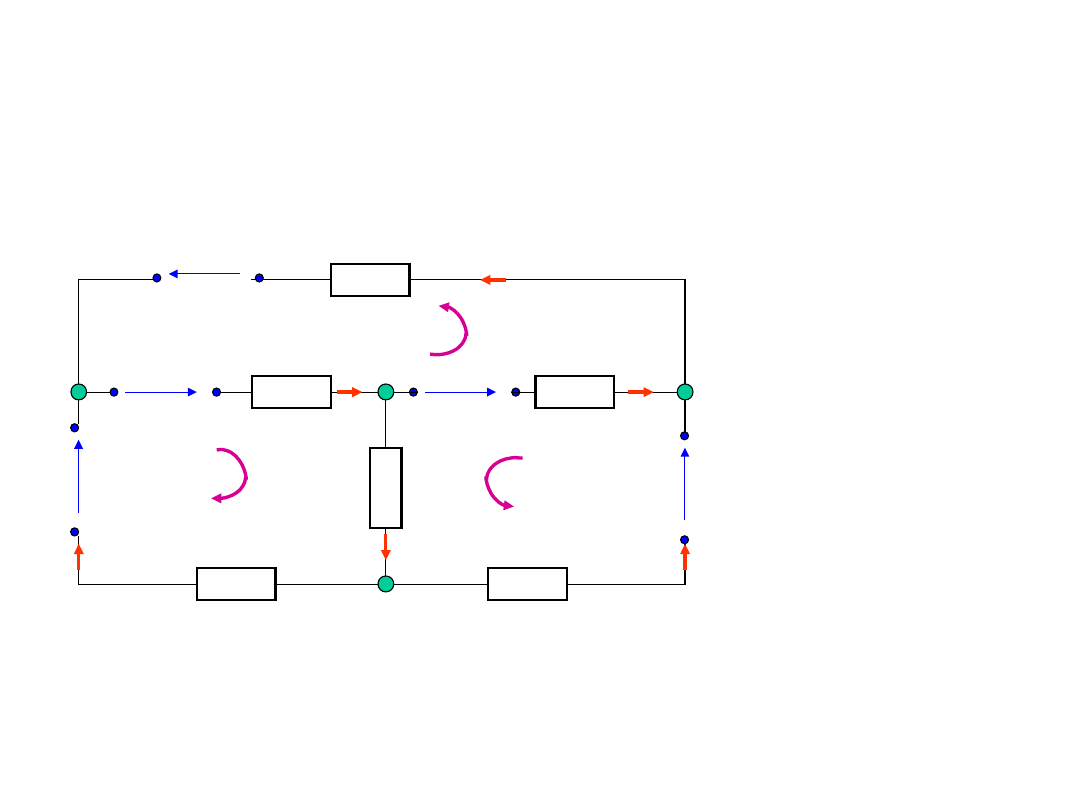
Obliczanie obwodów

elektrycznych - przykład

węzły:
 = 4

gałęzie

n = 6

A

i

1

u

3

u

5

u

4

u

1

u

2

B

C

D

R

1

R

2

R

3

R

4

R

5

i

2

i

3

i

4

i

5

i

6

R

6

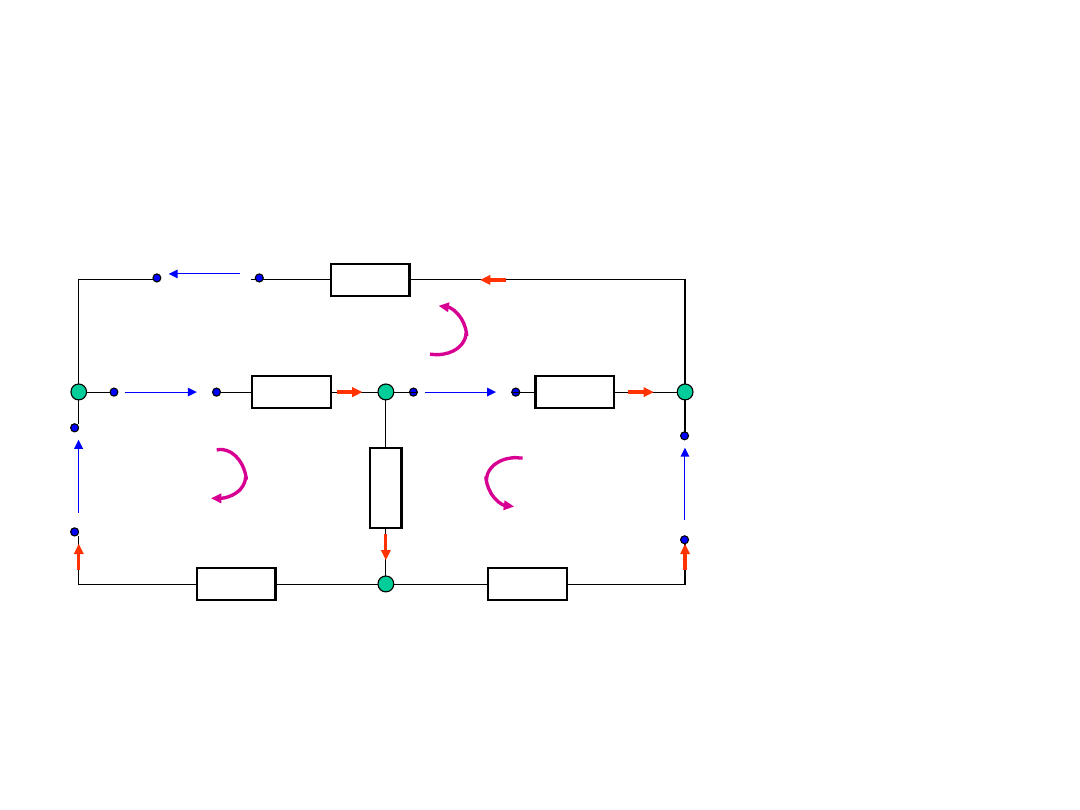
Obliczanie obwodów

elektrycznych - przykład

Liczba
równań wg
PPK:
 - 1 = 4 – 1
= 3

Liczba
równań wg
NPK:

n -  + 1 = 6

– 4 + 1 = 3

A

i

1

u

3

u

5

u

4

u

1

u

2

B

C

D

R

1

R

2

R

3

R

4

R

5

i

2

i

3

i

4

i

5

i

6

R

6

Liczba niewiadomych – 6 (prądy od

i

1

do

i

6

).

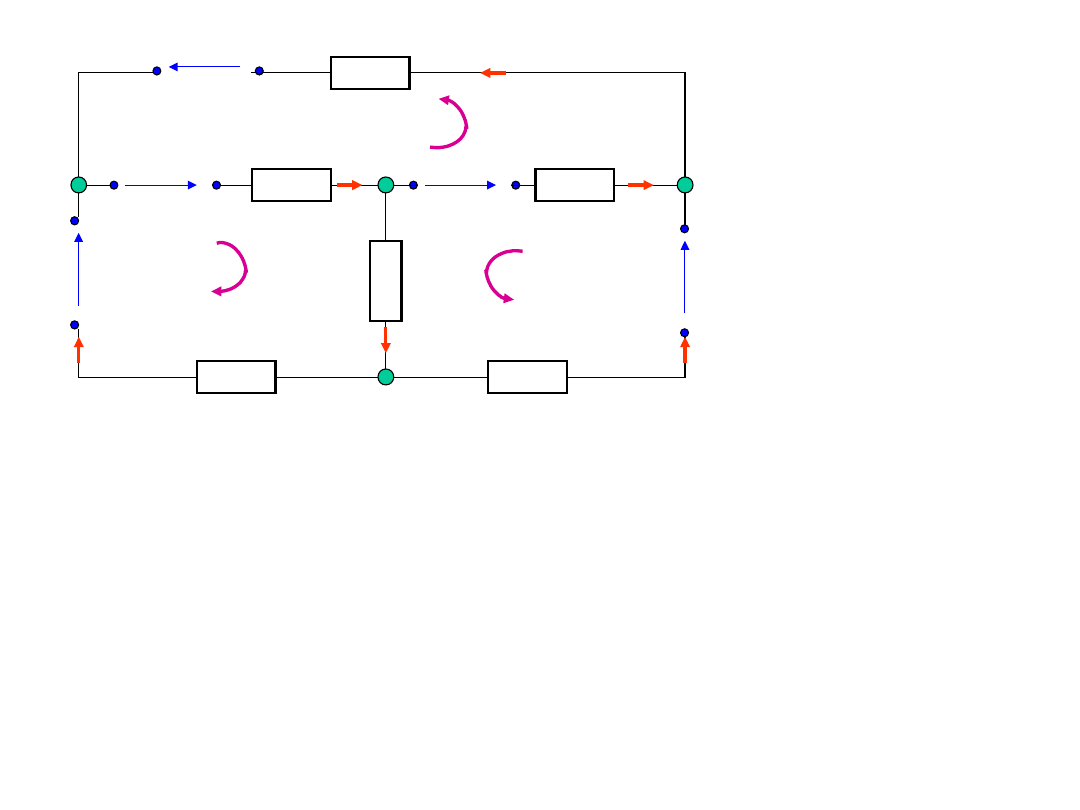
A

i

1

u

3

u

5

u

4

u

1

u

2

B

C

D

R

1

R

2

R

3

R

4

R

5

i

2

i

3

i

4

i

5

i

6

R

6

Dla węzła

A

0

5

3

1







i

i

i

Dla węzła

B

0

2

3

4







i

i

i

0

2

1

6







i

i

i

Dla węzła

C

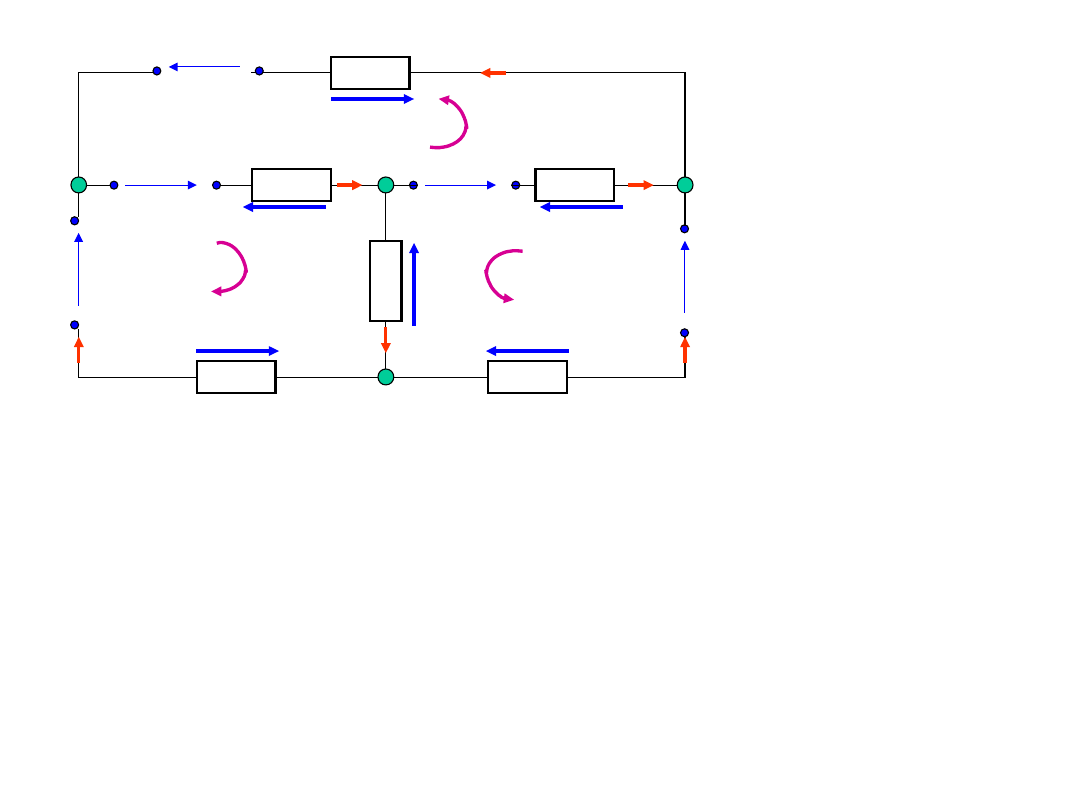
A

i

1

u

3

u

5

u

4

u

1

u

2

B

C

D

R

1

R

2

R

3

R

4

R

5

i

2

i

3

i

4

i

5

i

6

R

6

Dla pętli

ADCA

Dla pętli

BDCB

Dla pętli

ADBA

0

6

6

5

5

5

1

1

1













i

R

i

R

u

u

i

R

0

6

6

4

4

4

2

2

2













i

R

u

i

R

u

i

R

0

4

4

4

5

5

5

3

3

3















i

R

u

i

R

u

u

i

R

0

6

6

5

5

5

1

1

1













i

R

i

R

u

u

i

R

0

6

6

4

4

4

2

2

2













i

R

u

i

R

u

i

R

0

4

4

4

5

5

5

3

3

3















i

R

u

i

R

u

u

i

R

Po podstawieniu wartości:

0

10

2

36

6

2

6

5

1













i

i

i

0

10

10

4

30

2

6

4

2













i

i

i

0

4

10

2

36

10

2

4

5

3















i

i

i

czyli:

0

42

10

2

2

6

5

1











i

i

i

0

20

10

4

2

6

4

2











i

i

i

0

56

4

2

2

4

5

3











i

i

i

podstawiając:

2

1

6

3

1

5

2

3

4

i

i

i

i

i

i

i

i

i













otrzymujemy układ trzech równań z trzema
niewiadomymi:

42

2

10

14

3

2

1







i

i

i

20

4

16

10

3

2

1







i

i

i

56

8

4

2

3

2

1







i

i

i

a po jego rozwiązaniu:

A

i

A

i

A

i

10

5

2

3

2

1









pozostałe prądy:

A

i

i

i

A

i

i

i

A

i

i

i

3

5

2

8

10

2

5

5

10

2

1

6

3

1

5

2

3

4



































Przykład obliczania obwodów

Zadanie.
Spawarkę na napięcie 60V, pobierającą
prąd o natężeniu 20A, połączono
szeregowo z oporem dodatkowym i
włączono do sieci o napięciu 240V.
Obliczyć wartość oporu zapewniającego
normalną pracę spawarki.

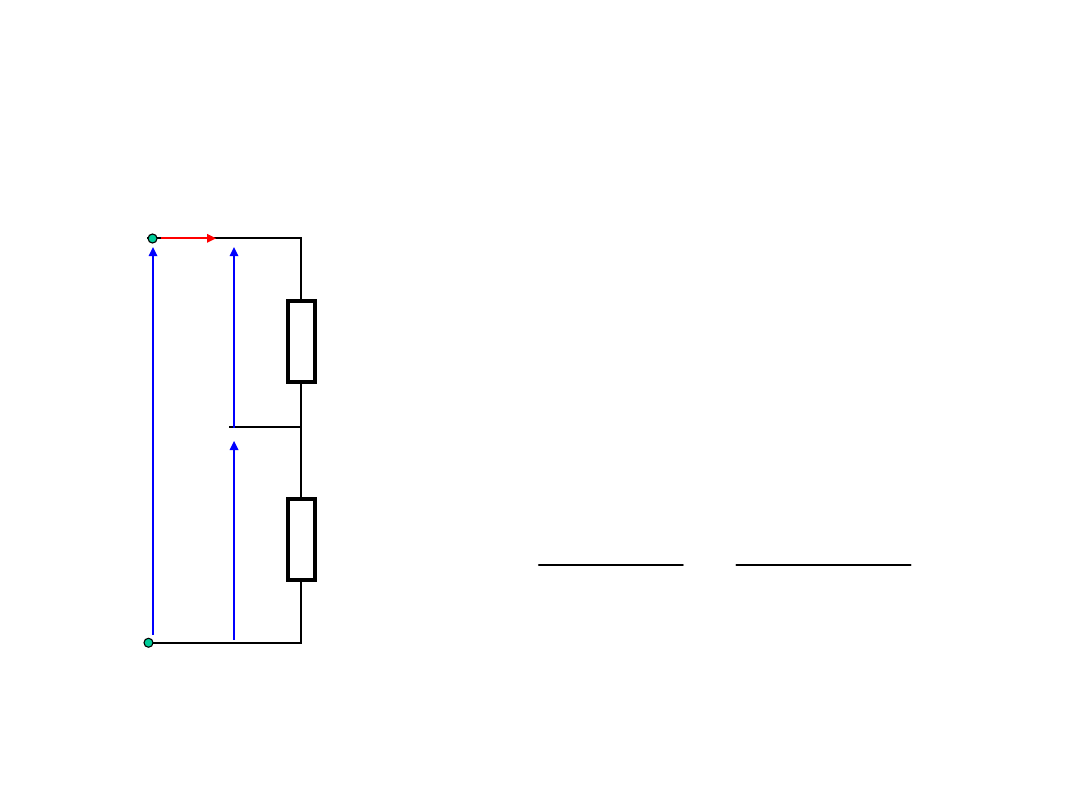
Przykład obliczania obwodów

d

s

d

s

IR

U

U

U

U





















9

20

60

240

I

U

U

R

s

d

U

U

s

R

s

R

d

I

U

d

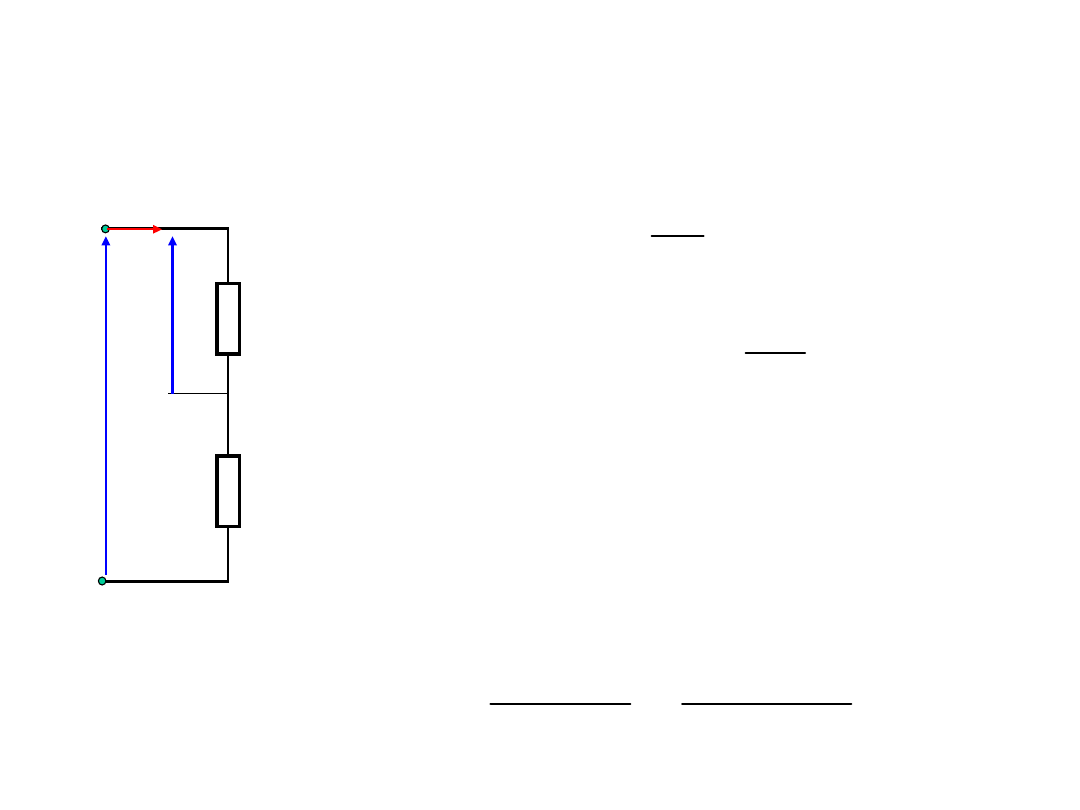
Przykład obliczania obwodów

lub
:

I

U

R

s

s



d

s

d

s

R

I

U

R

R

R









U

U

s

R

s

R

d

I

I

R

U

U

RI

U

d

s



















9

20

60

240

I

U

U

R

s

d

Praca prądu elektrycznego

Energia elektryczna prądu przepływającego

przez odbiorniki włączone w obwód zamienia

się na inne rodzaje energii użytecznej:
- na energię mechaniczną - 24% - w silnikach,
- na energię cieplną - 74,5% - w grzejnikach,

piecach oporowych,
- na światło - 1% - w lampach
- na energię chemiczną – 0,5%       

-    

Praca prądu elektrycznego

Praca wykonana przy przesunięciu ładunku q w polu

elektrycznym:





qU

V

V

q

W

B

A







Pamiętając, że:

It

q

t

q

I







Praca prądu elektrycznego

Praca wykonana przy przepływie prądu stałego o

natężeniu I przez przewodnik o oporze R w czasie t:

ItU

W 

Ponieważ zgodnie z prawem Ohma:

IR

U 

zate
m:

Rt

I

UIt

W

2





Praca prądu elektrycznego

Jednostką pracy prądu elektrycznego w układzie SI

jest

dżul.

2

2

3

2

1

1

1

1

1

1

1

1

1

1

s

kgm

s

A

m

kg

s

A

V

s

A

V

C

J

























Moc prądu elektrycznego

Moc prądu stałego, czyli stosunek pracy W do

czasu t, w którym została ona wykonana:

UI

t

UIt

t

W

P







lub:

R

I

t

Rt

I

t

W

P

2

2







Moc prądu elektrycznego

Jednostką mocy w układzie SI jest

wat

(W):

V

A

s

V

s

A

s

V

C

s

J

W

1

1

1

1

1

1

1

1

1

1

1

1

















1 wat to moc prądu o natężeniu 1A przy
napięciu 1V

.

Jednostka wielokrotna mocy -

kilowat

(kW)

W

W

kW

1000

10

1

3





Praca prądu elektrycznego

Pochodząca od jednostki wielokrotnej mocy (kW)

jednostka pracy prądu elektrycznego -

kilowatogodzina

(kWh), czyli praca, jaką

wykonuje prąd o mocy 1kW w czasie 1 godziny.

kJ

J

Ws

s

W

kWh

3600

10

3600

10

3600

60

60

10

1

3

3

3



















Praca i moc prądu elektrycznego

- przykład

Piec elektryczny jest włączony do sieci prądu
stałego o napięciu 240V i pobiera prąd o
natężeniu 11A. Obliczyć moc pieca oraz
koszt energii zużytej w ciągu doby, jeżeli
cena 1kWh energii elektrycznej wynosi 0,70
zł.

Dane: U = 240V, I = 11A, t = 24h, c =

0,70zł

Praca i moc prądu elektrycznego

- przykład

Moc prądu elektrycznego:

UI

P

Praca prądu
elektrycznego:

Pt

UIt

W





Koszt energii
elektrycznej:

cPt

cW

K





czyli
:

zł

K

kW

W

P

4

,

44

24

6

,

2

7

,

0

6

,

2

2640

11

240

















Zadanie

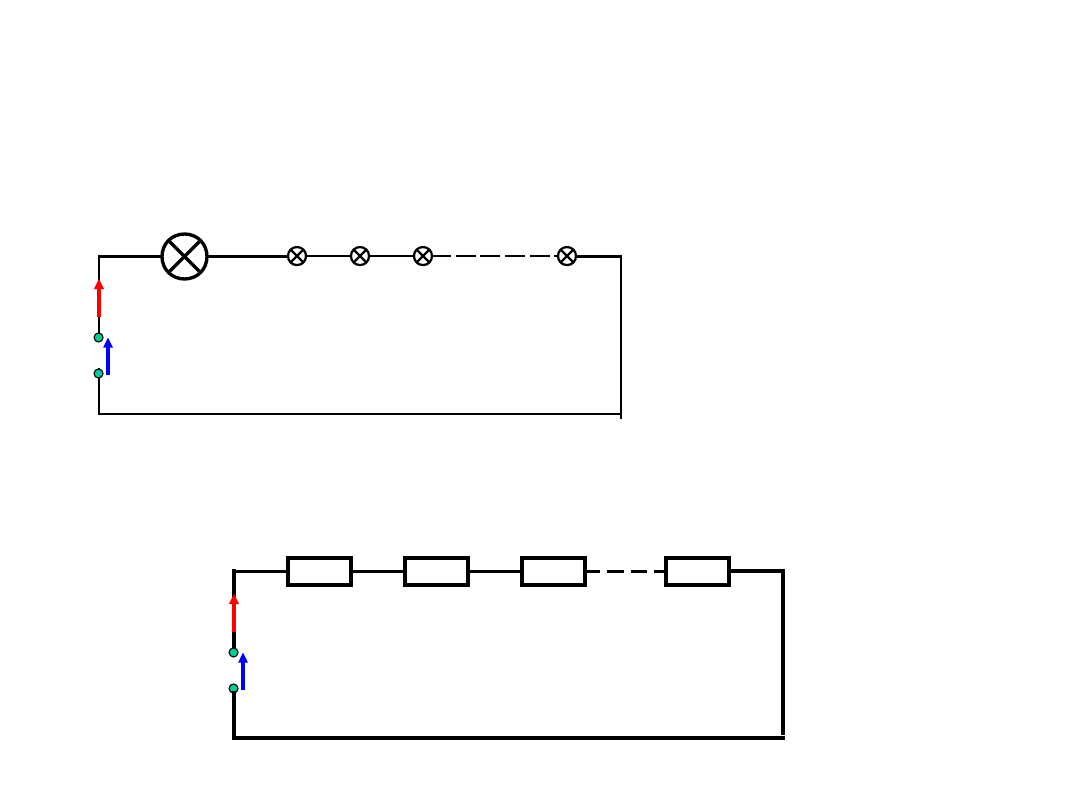
Zaprojektować instalacje oświetleniową
choinki, włączaną do sieci o napięciu
240V i złożoną z szeregowo połączonej
jednej żarówki 40W o napięciu 240V
oraz pewnej liczby żaróweczek
latarkowych o napięciu 3,8V i natężeniu
prądu 0,1A. Obliczyć niezbędną liczbę
żaróweczek.

Zadanie

I

U

Dane:

U=240V

U

1

= 240V; P

1

=

40W

U

2

= 3,8V; I

2

=

0,1A

I

U

R

1

R

2

R

2

R

2

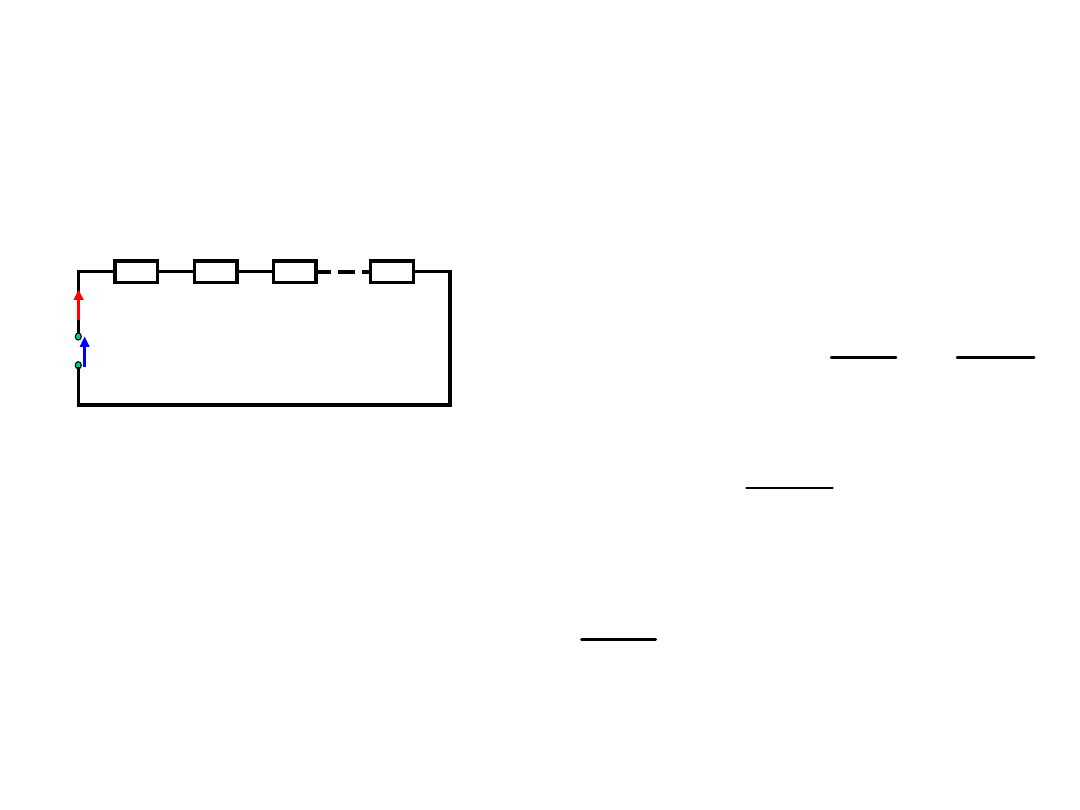
Zadanie

I

U

R

1

R

2

R

2

R

2

Dla dużej
żarówki:

1

2

1

1

1

1

1

1

1

R

U

R

U

U

I

U

P







czyli
:

1

2

1

1

P

U

R 

Dla małej
żarówki:

2

2

2

I

U

R 

Zadanie

I

U

R

1

R

2

R

2

R

2

Opór zastępczy
(równoważny) obwodu
elektrycznego:

2

1

nR

R

R





W obwodzie, pod wpływem napięcia

U

nie

może płynąć prąd większy niż:

I

= I

2

a

więc:

2

2

1

I

nR

R

U

R

U

I









Zadanie

2

1

2

1

2

2

2

2

2

1

2

1

2

2

2

1

2

U

P

U

I

U

U

n

I

U

I

P

U

I

U

n

R

I

R

I

U

n













Zadanie

3

,

25

8

,

3

40

240

1

,

0

8

,

3

240

2











n

n

26



n

Prawo Joule’a

Jeżeli przez przewodnik o oporze R płynie prąd
o natężeniu I a napięcie na końcach przewodu
wynosi U, to ilość energii elektrycznej,
zamienionej w nim na energię cieplną w czasie
t jest równoważna pracy prądu, czyli:

Rt

I

Q

UIt

Q

W

Q

2







lub:

Prawo Joule’a - przykład

Obliczyć czas i koszt zagotowania 1 litra wody

przy użyciu czajnika elektrycznego o mocy 2kW,

jeśli temperatura początkowa wody wynosi

20

0

C, a cena 1kWh energii elektrycznej 0,70zł.

Dane:
P=2000W,

V

w

= 1l = 10

-3

m

3

,

m

w

= V

w



w

= 1kg (

w

=1000kg/m

3

)



0

= 20

0

C,



wrz

= 100

0

C 

 = 100-

20=80K
c= 0,70zł/kWh

Prawo Joule’a - przykład

Ilość ciepła potrzebna do ogrzania wody:



















w

w

wrz

w

w

m

c

m

c

Q

0

gdzie c

w

– ciepło właściwe (ciepło przemiany

do ilości substancji podlegającej przemianie i
przyrostu temperatury podczas tej
przemiany)

kgK

J

c

w

4150



Prawo Joule’a - przykład

min

8

,

2

166

2000

80

1

4150

























s

W

k

kg

K

kg

J

P

m

c

t

w

w



Pt

Q

W

Q





Według prawa
Joul’e:

czyli:

Pt

m

c

w

w







Prawo Joule’a - przykład

Koszt:





gr

zł

J

K

kg

zł

K

kg

J

kWh

zł

K

kg

K

kg

J

c

m

c

P

c

m

Pc

Ptc

Wc

K

w

w

wrz

w

w

5

10

49

3600

10

176400

70

,

0

80

1

4150

3

3

0























































Przemiana energii na ciepło

Wykorzystywana – w urządzeniach
grzejnych, niepożądana – w
urządzeniach, w których występuje jako
strata energii, np. w liniach
energetycznych.
Przykład: linią energetyczną trzeba
przesłać moc 1500kW.
Linia nr 1 – o napięciu 15kV
Linia nr 2 – o napięciu 110kV

Moc przesyłana

A

I

kV

U

A

U

P

I

kV

U

UI

P

14

110

1500

110

100

15

1500

15

2

2

1

1





















Straty mocy

Straty mocy wydzielone w linii w postaci ciepła:

R

I

Q

2



Dla linii 15kV – przewód YAKY
240mm

2

– R

k

=0,125/km

Dla linii 110kV – przewód AFl
500mm

2

– R

k

=0,06 /km

Straty mocy

Straty mocy wydzielone w liniach:

l

R

I

Q

l

R

I

Q

k

k

2

2

2

2

1

2

1

1





15kV:

110kV:

100

06

,

0

14

125

,

0

100

2

2

2

2

2

1

2

1

2

1











k

k

R

I

R

I

Q

Q

Źródło energii

Rozróżniamy dwa rodzaje źródeł energii
elektrycznej:

- źródło napięcia
- źródło prądu

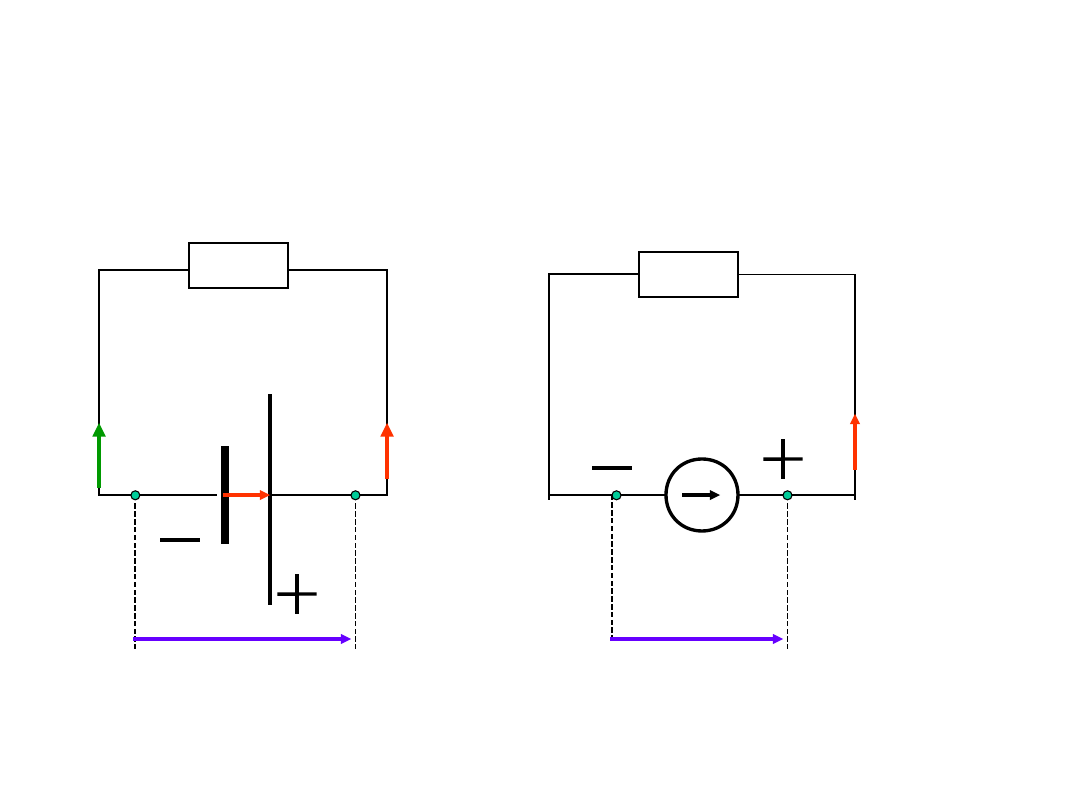
Źródło napięcia

R

E

U

I

U

I

R

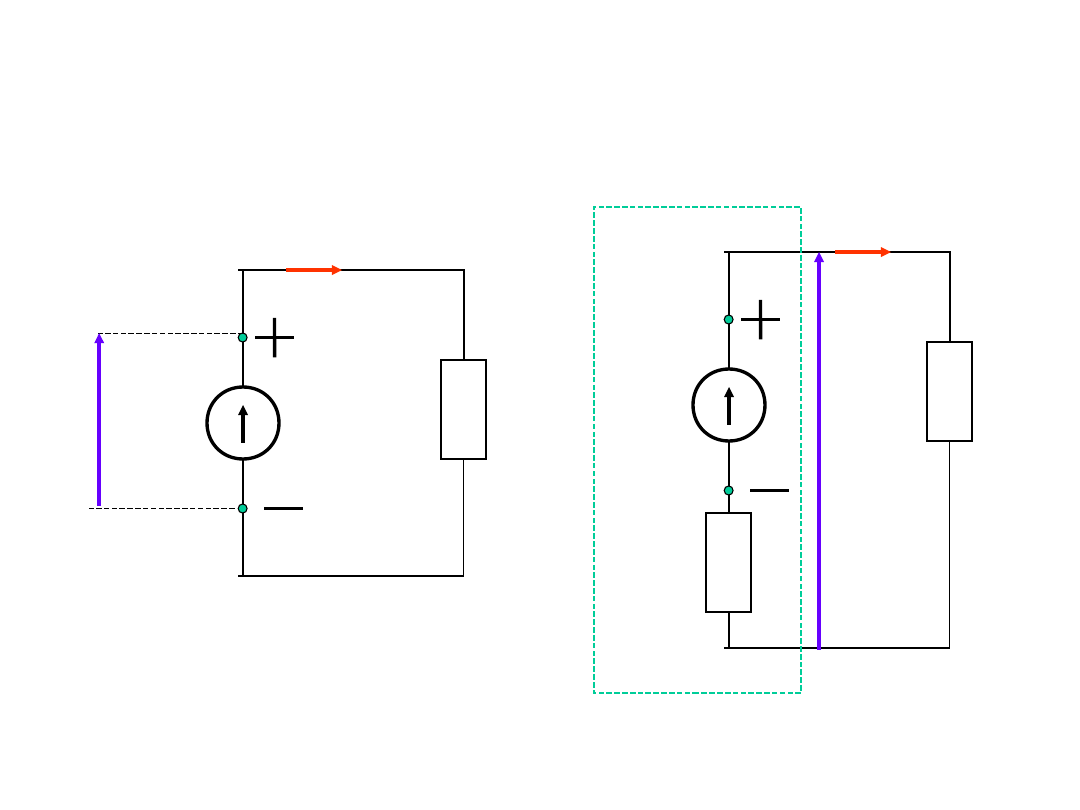
Idealne i rzeczywiste źródło

napięcia

R

E

U

I

R

E

U

I

R

w

0



w

R

0



w

R

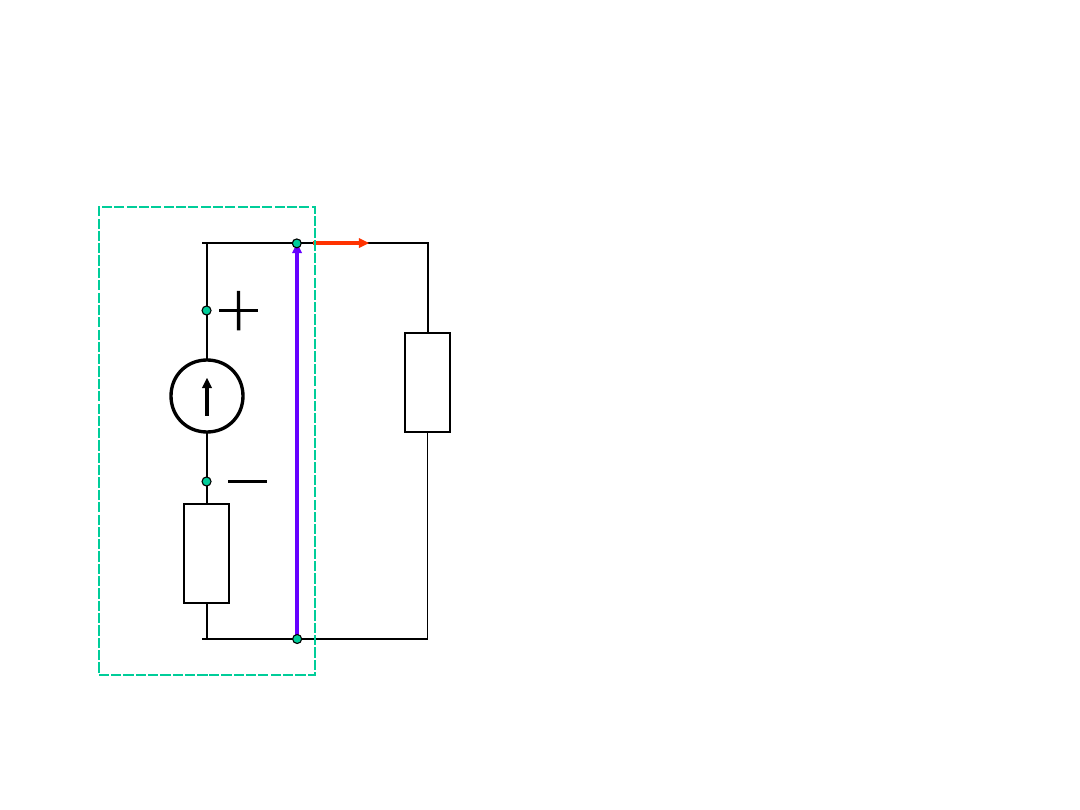
Rzeczywiste źródło napięcia

I

R

E

U

w





R

E

U

I

R

w

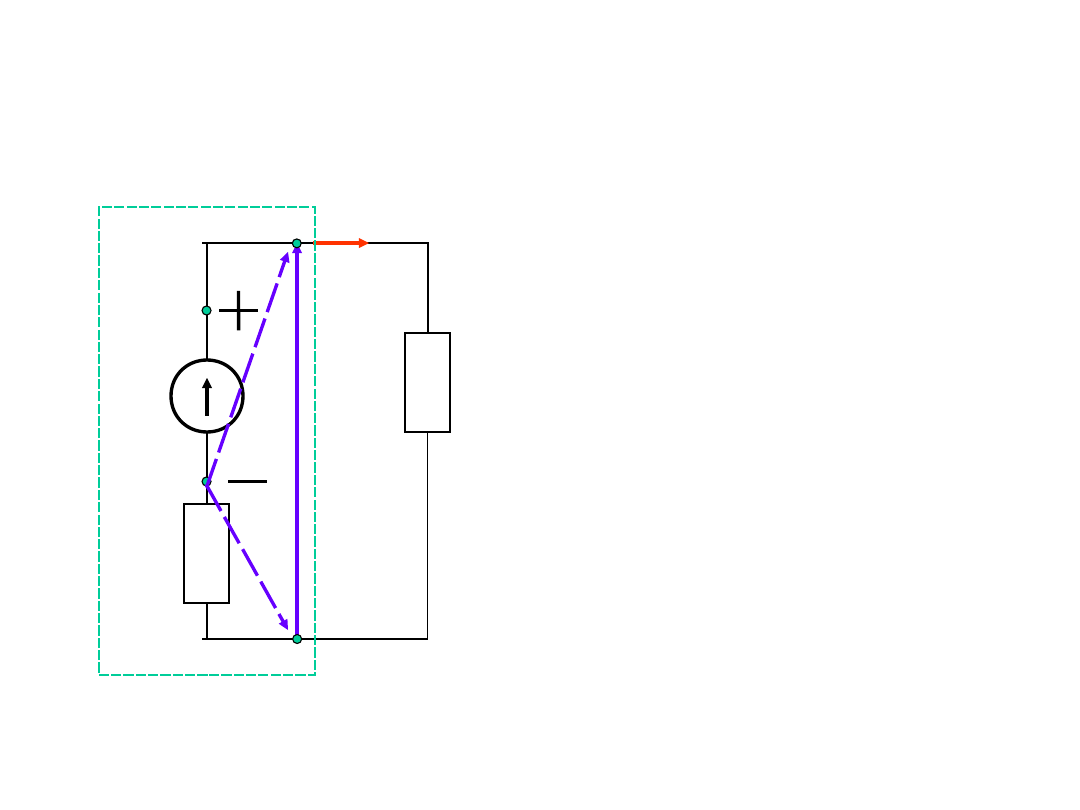
Rzeczywiste źródło napięcia





I

R

E

V

V

V

V

V

V

U

w

C

B

C

A

B

A





















R

E

U

I

R

w

A

B

C

Napięcie na zaciskach
rzeczywistego źródła jest
równe sile
elektromotorycznej źródła
tylko wówczas, gdy źródło
nie jest obciążone (I=0).

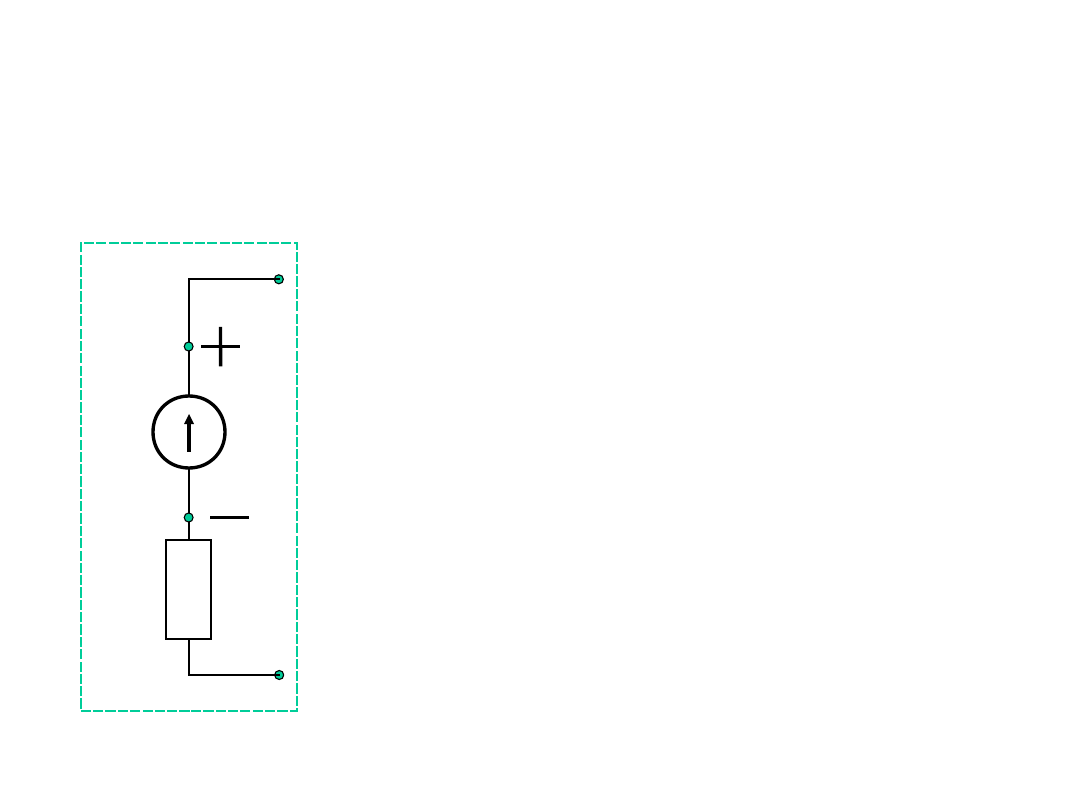
Rzeczywiste źródło napięcia

E

R

w

Źródło napięcia – źródło
energii o postaci
połączenia szeregowego
idealnego źródła napięcia
i opornika.

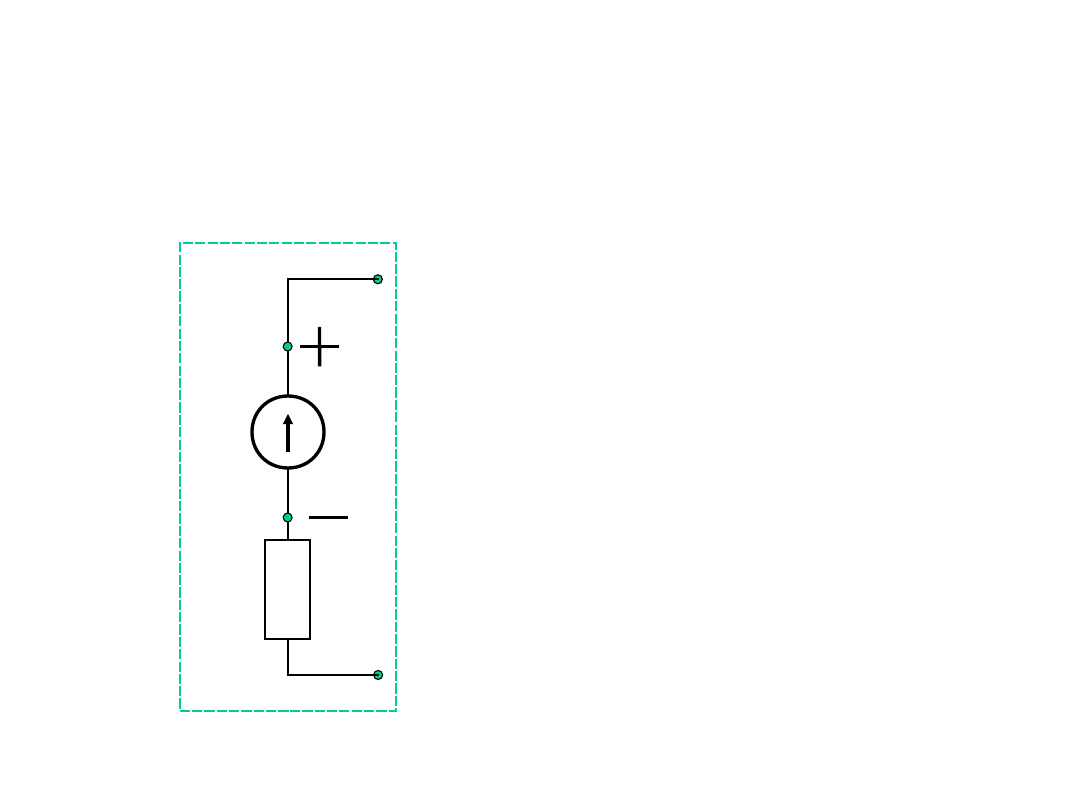
Stan jałowy źródła napięcia

E

R

w

A

B

E

U

I



0

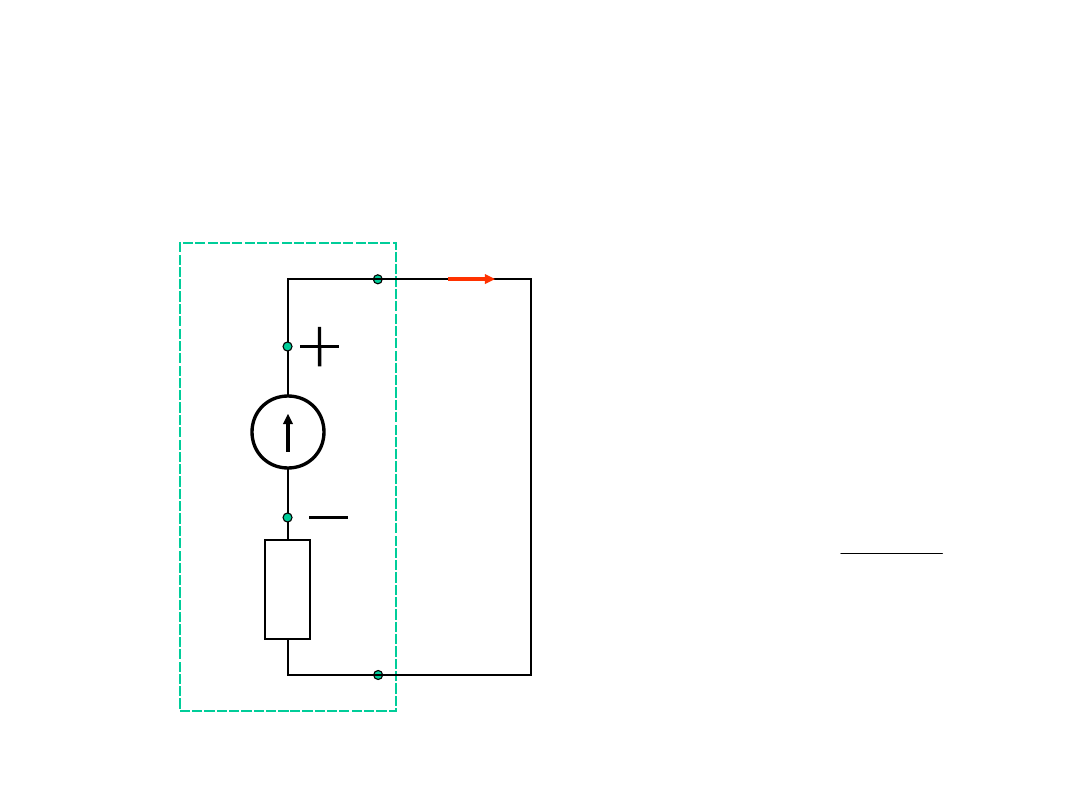
Stan zwarcia źródła napięcia

w

zw

R

E

I

U



0

E

R

w

A

B

I

zw

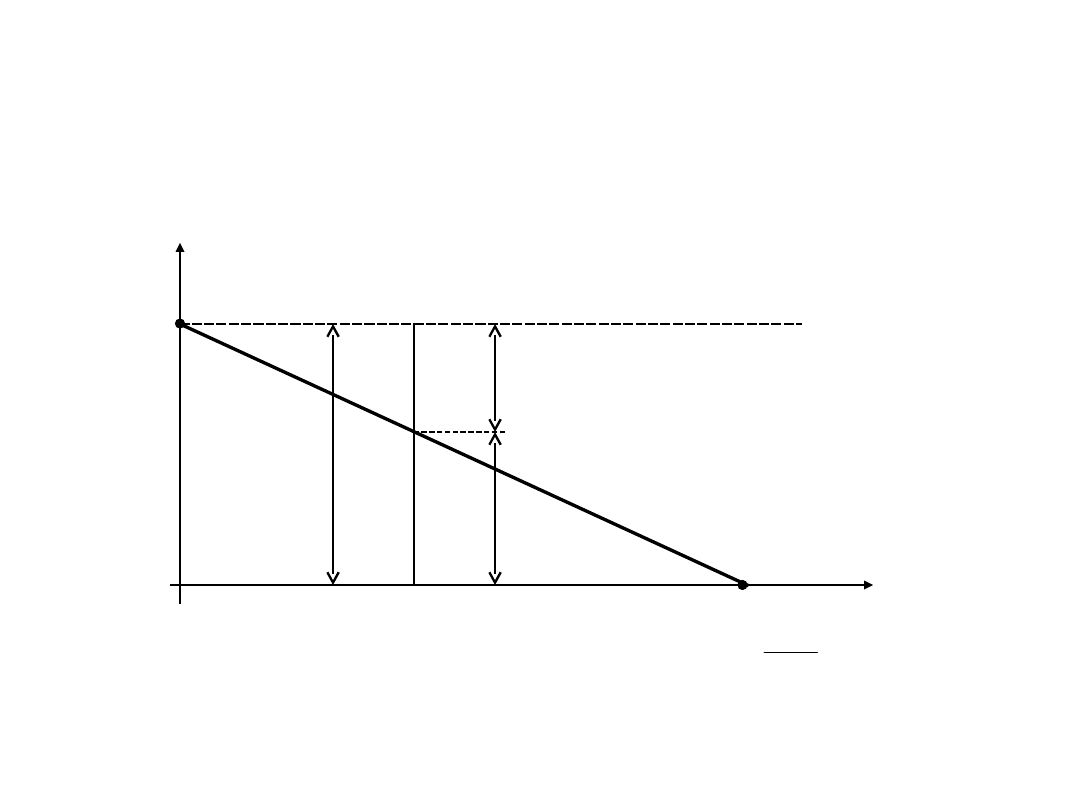
Charakterystyka źródła napięcia

0

A

B

U

I

E

R

w

I

U

w

zw

R

E

I 

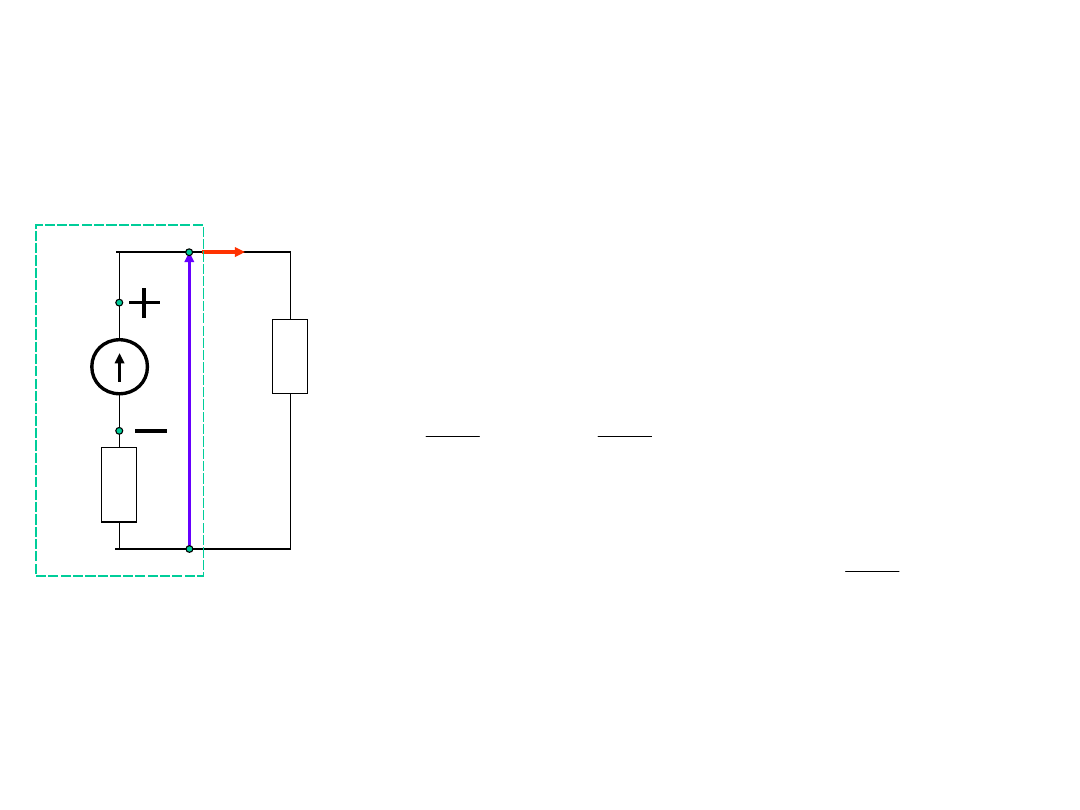
Źródło prądu

R

E

U

I

R

w

Dla źródła
napięcia:

U

I

R

I

R

R

E

w

w









)

(

w

w

R

U

I

R

E





Jeżeli
oznaczymy:

w

w

R

G

1



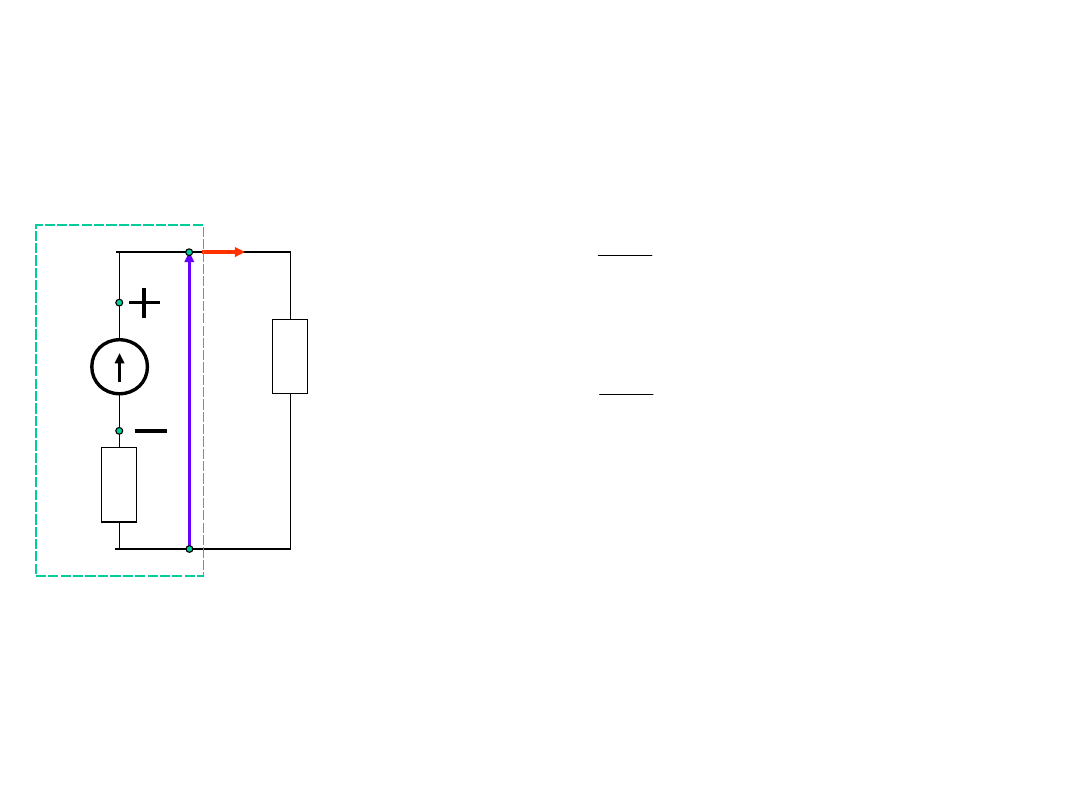
Źródło prądu

R

E

U

I

R

w

oraz:

U

G

R

U

I

E

G

R

E

I

w

w

w

w

w

g









mamy:

I

I

I

w

g





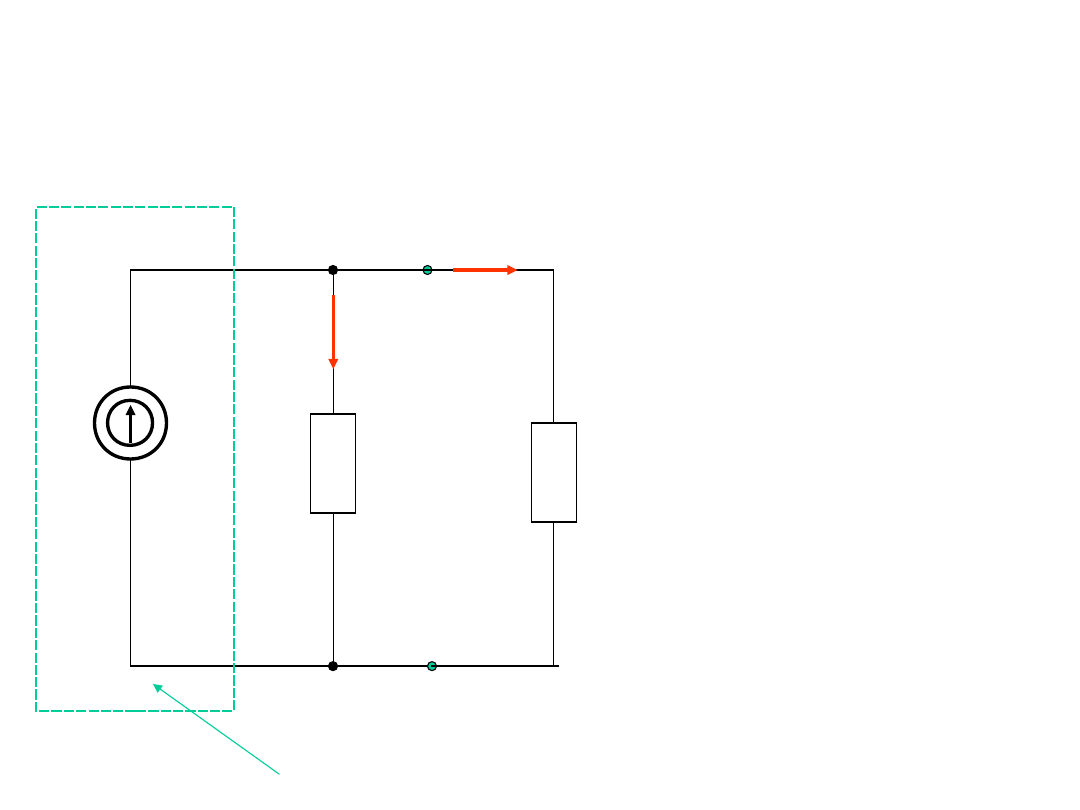
Źródło prądu

R

I

I

I

w

g





I

g

R

w

=1/

G

w

A

B

I

w

I

idealne źródło prądu

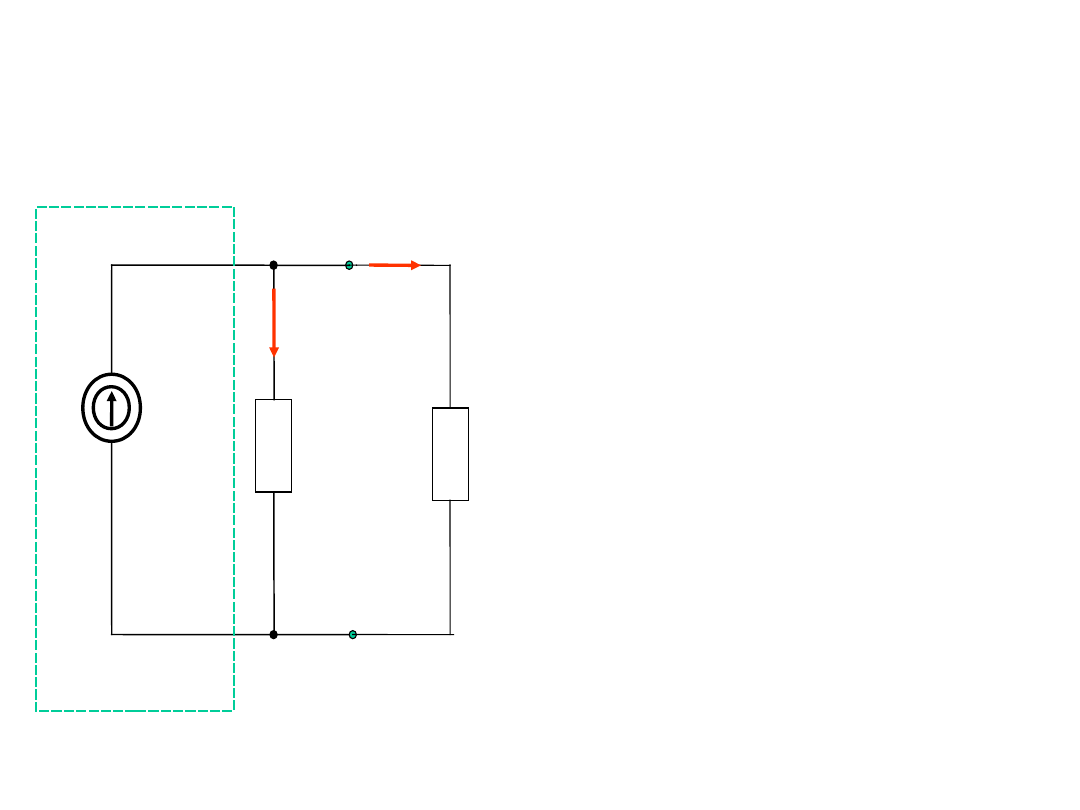
Źródło prądu

R

I

g

R

w

A

B

I

w

I

Napięcie między
punktami A i B:

U

U

G

R

I

R

w

w

w

w





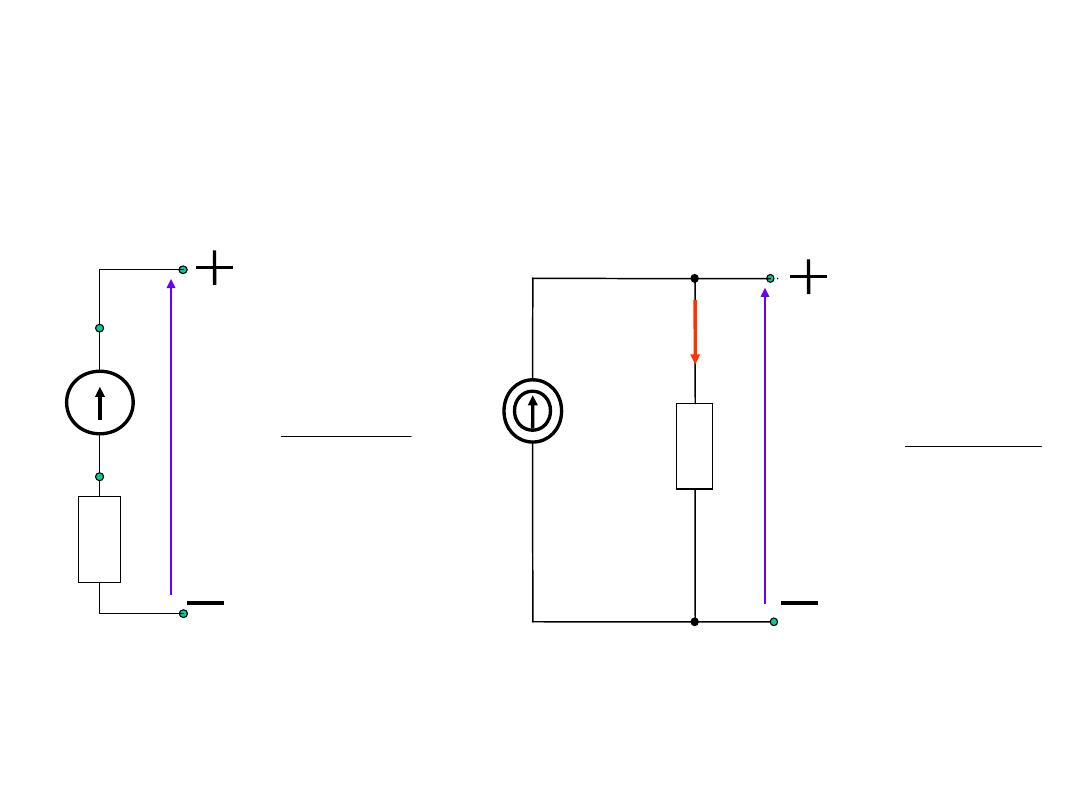
Źródło napięcia i źródło prądu

E

R

w

A

B

I

g

G

w

A

B

I

w

I

R

E

U

R

R

E

I

U

I

R

E

w

w

w













U

G

I

G

G

G

I

I

I

I

I

w

g

w

g

w

g











U

U

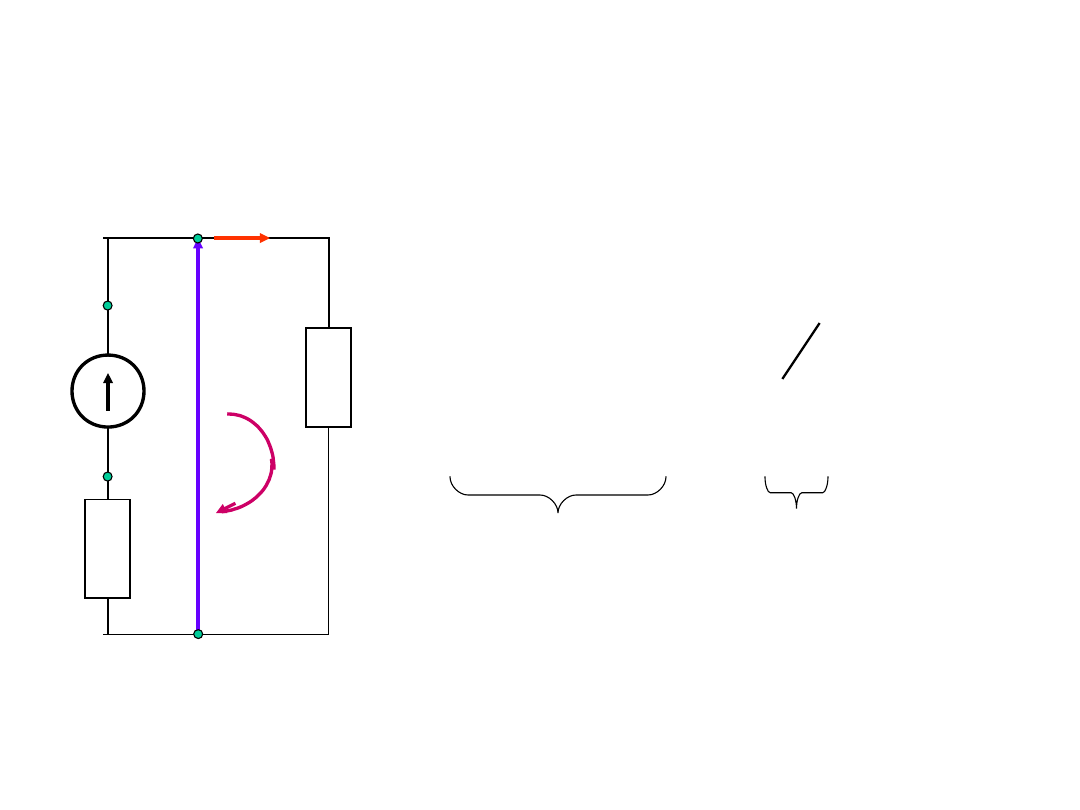
Sprawność w obwodzie

elektrycznym

R

E

U

I

R

w

Zgodnie z NPK:

EI

RI

I

R

E

RI

I

R

w

w









2

2

I



moc
pobrana
przez
obwód

moc
wytworzona
w obwodzie

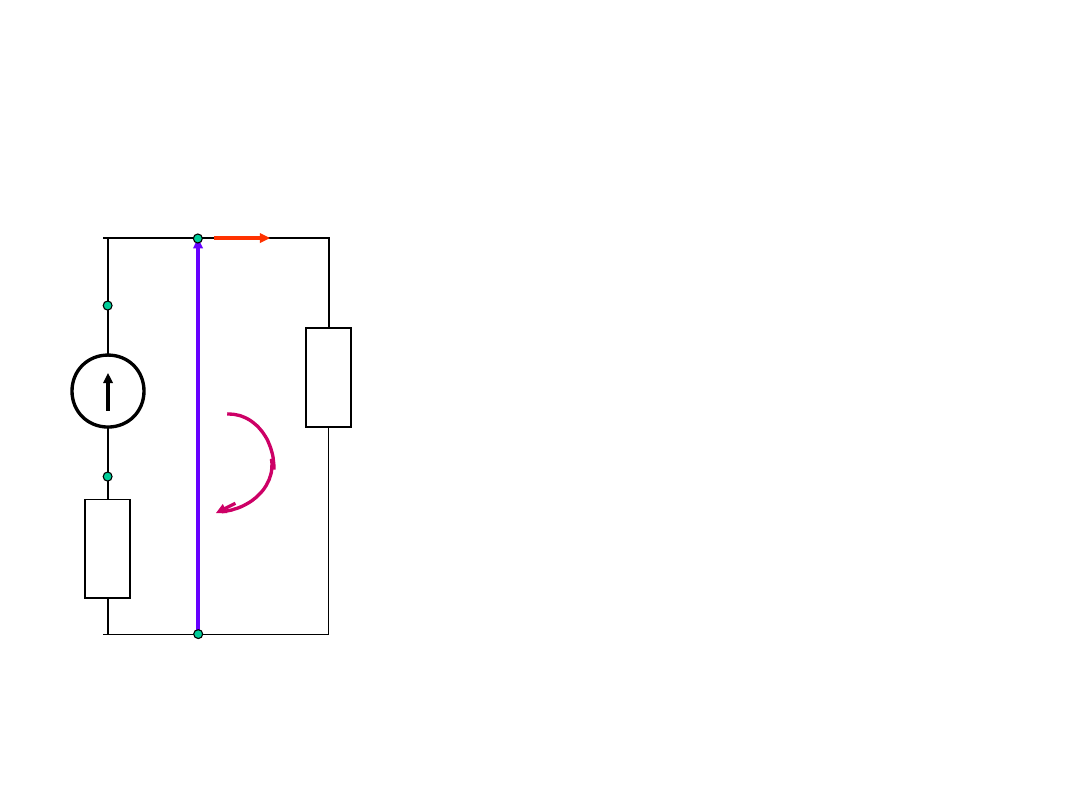
Sprawność w obwodzie

elektrycznym

R

E

U

I

R

w

2

I

R

w

- moc tracona na
oporności źródła

2

RI

- moc wykorzystana
w odbiorniku

Sprawność w obwodzie

elektrycznym

Sprawność układu elektrycznego to stosunek
mocy wykorzystanej (użytecznej) do mocy
wytworzonej, czyli:

R

R

R

RI

I

R

RI

EI

RI

w

w











2

2

2

2

2





Sprawność w obwodzie

elektrycznym

R

R

R

w







1





dla

0



w

R

W rzeczywistych źródłach:

0



w

R

wię
c

1





Dopasowanie odbiornika do

źródła

Szukamy wartości R takiej, aby moc
wykorzystana w odbiorniku była maksymalna:





2

2

2

E

R

R

R

P

R

R

E

I

RI

P

w

w











0

max





dR

dP

gdy

P

P

Dopasowanie odbiornika do

źródła































2

2

2

3

2

3

2

2

2

2

3

2

2

2

2

2

E

R

R

R

R

E

R

R

R

R

R

R

E

R

R

R

R

R

R

R

R

R

E

R

R

R

R

R

R

R

dR

dP

w

w

w

w

w

w

w

w

w

w

w

w









































Dopasowanie odbiornika do

źródła





2

2

E

R

R

R

R

dR

dP

w

w







0



dR

dP

gdy

R

R

w



Dopasowanie odbiornika do

źródła

Odbiornik jest dopasowany do źródła, gdy
pobiera z tego źródła największa moc.

Prąd płynący w odbiorniku dopasowanym
do źródła:

w

R

E

I

2



Sprawność obwodu z odbiornikiem
dopasowanym do źródła:

5

,

0











w

w

w

w

R

R

R

R

R

R



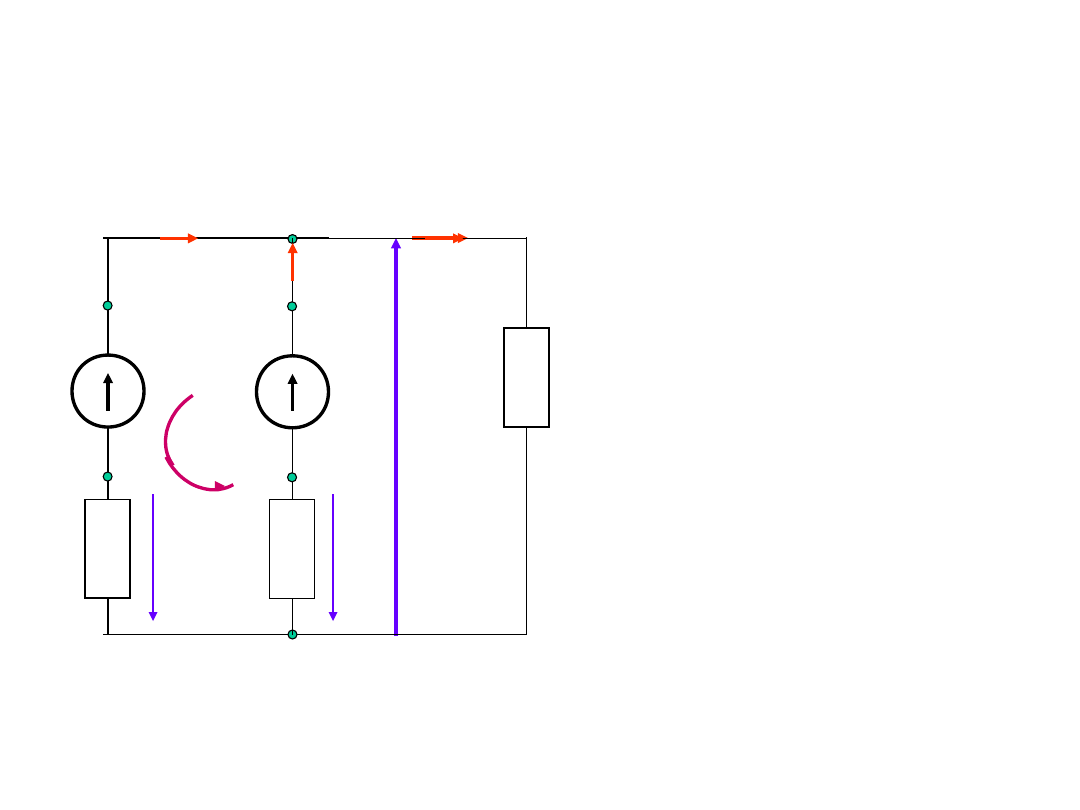
Równoległe połączenie źródeł

energii

E

1

R

w

1

U

I

E

2

R

w

2

+

+

-

-

I

2

I

1

R

Zgodnie z PPK i
NPK:

2

1

2

2

1

1

2

1

E

E

I

R

I

R

I

I

I

w

w











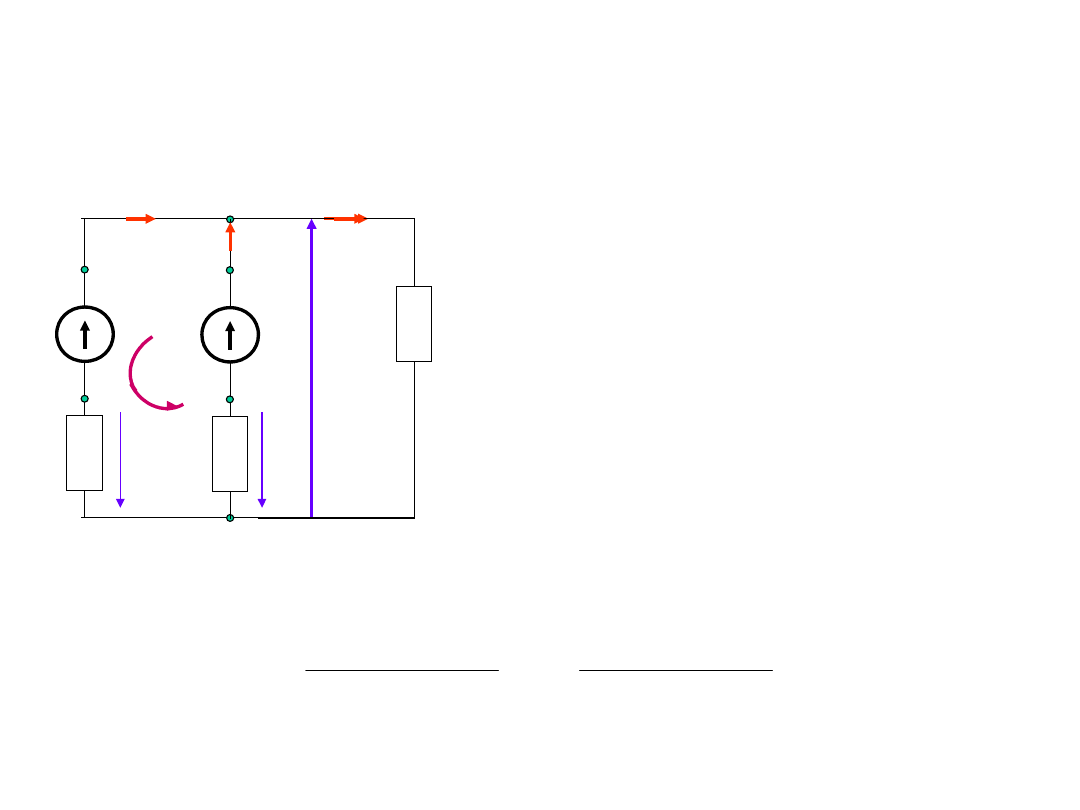
Równoległe połączenie źródeł

energii

E

1

R

w1

U

I

E

2

R

w2

+

+

-

-

I

2

I

1

R









2

1

1

2

1

2

2

1

2

1

2

1

2

1

2

2

2

1

1

2

1

E

E

I

R

R

R

I

E

E

R

R

I

I

R

E

E

I

R

I

R

I

R

I

I

I

w

w

w

w

w

w

w

w

w





























2

1

2

1

2

1

1

2

w

w

w

w

w

R

R

E

E

I

R

R

R

I











Równoległe połączenie źródeł

energii

2

1

2

1

2

1

2

2

1

2

1

2

1

1

2

1

2

1

w

w

w

w

w

w

w

w

w

w

w

w

R

R

E

E

I

R

R

R

R

R

E

E

I

R

R

R

R

R

I

I

I































Równoległe połączenie źródeł

energii

2

1

2

1

2

1

1

'

2

2

1

2

'

1

w

w

w

w

w

w

w

w

w

R

R

E

E

I

I

R

R

R

I

I

R

R

R

I















Oznaczmy:

Wówczas
:

w

w

I

I

I

I

I

I









'

1

1

'

2

2

Równoległe połączenie źródeł

energii

w

w

I

I

I

I

I

I









'

1

1

'

2

2

I

1

’ oraz I

2

’ – prądy robocze

I

w

– prąd wyrównawczy

2

1

2

1

w

w

w

R

R

E

E

I







I

w

= 0 tylko wtedy, gdy E

1

= E

2

Równoległe połączenie źródeł

energii

w

w

I

I

I

I

I

I









'

1

1

'

2

2

Gdy E

1

> E

2

wówczas I

1

> I

1

’

oraz I

2

< I

2

’

Równoległe połączenie źródeł

energii

Straty mocy w równolegle połączonych
źródłach:

1. Dla I

w

= 0

2

'

2

2

2

'

1

1

1

I

R

I

R

P

w

w





2. Dla I

w



0

2

2

2

2

1

1

2

I

R

I

R

P

w

w





Równoległe połączenie źródeł

energii

















2

2

1

1

2

2

1

2

'

2

2

2

'

1

1

2

'

2

2

2

'

1

1

2

2

2

2

1

1

2

w

w

w

w

w

w

w

w

w

w

w

w

w

w

I

R

R

P

I

R

R

I

R

I

R

I

I

R

I

I

R

I

R

I

R

P

































Równoległe połączenie źródeł

energii

Przepływ prądu wyrównawczego jest
niepożądany, ponieważ:

1. prąd wyrównawczy płynie nawet przy

odłączonym odbiorniku,

2. nierównomiernie obciążone są źródła

energii,

3. występują dodatkowe straty energii.

Aby zapobiec przepływowi prądu
wyrównawczego, równolegle należy
łączyć źródła o takich samych siłach
elektromotorycznych.