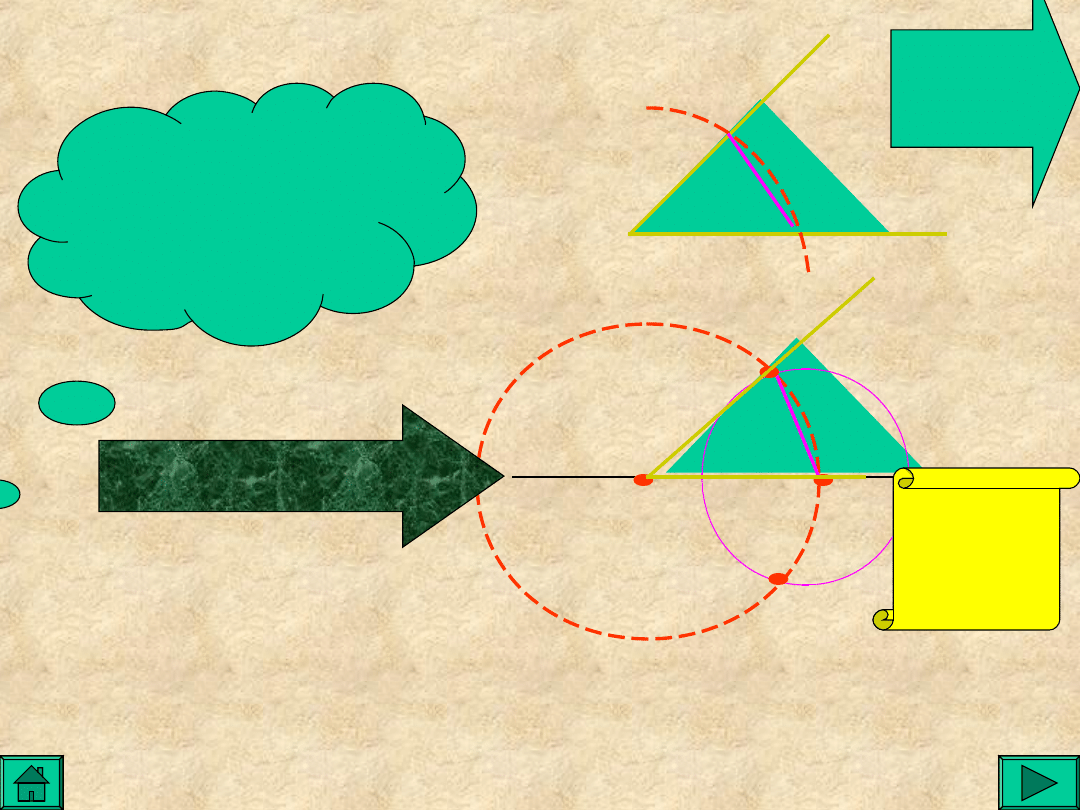


Przenoszenie

kąta



Dodawanie

kątów



Odejmowanie

kątów



Dwusieczna kąta

Przenoszenie kąta

Wykonując podane

czynności

zbudujesz kąt o

takiej samej

rozwartości.

Dany jest kąt BAC

A

Rysujemy okrąg o środku w punkcie A i A’oraz promieniu
dowolnej długości.



Kreślimy dowolną prostą k i zaznaczamy na niej

punkt A’ :

A’

B

C

Rysujemy okrąg o środku w punkcie B’ i promieniu
BC.

B’

C’

C”

Wspólne punkty obu okręgów oznaczamy C’ i
C”

Punkt A’ będzie

wierzchołkiem budowanego

kąta

Półprosta

A’B’

będzie

ramienie

m kąta.

Inne

sposoby

oznaczania

kątów

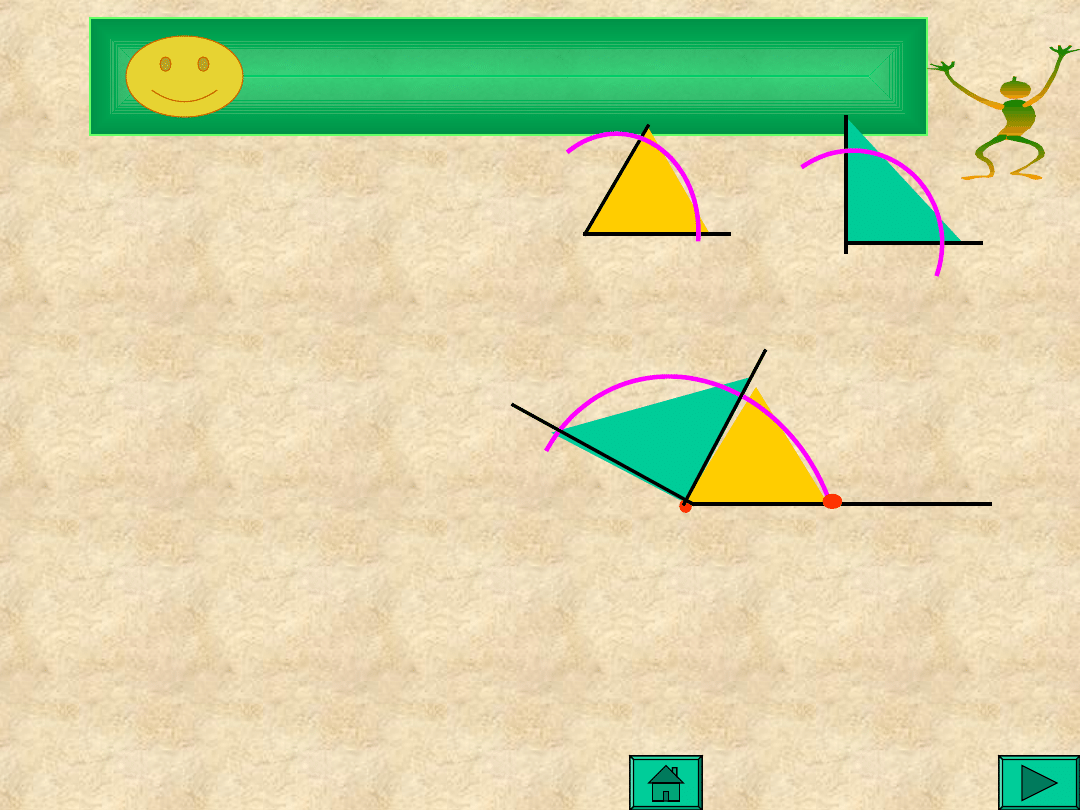
A teraz dodawanie kątów

Dane są dwa kąty AOB i

Dane są dwa kąty AOB i

CED :

CED :

A

O

B

C

E

D

Kreślimy półprostą o początku w
punkcie O’

O’

Przy półprostej O’A’ budujemy kąt równy
kątowi AOB- otrzymujemy punkt B’

B’

Przy półprostej O’B’ budujemy kąt równy kątowi
CED- otrzymujemy punkt C’

Z punktów O, E ,O’ kreślimy
łuki okręgów o tym samym
promieniu – punkt przecięcia
półprostej o początku w
punkcie O’ z okręgiem
oznaczamy A’.

C’

Kąt

C

’

O’A’ jest sumą kątów AOB i CED.

A’

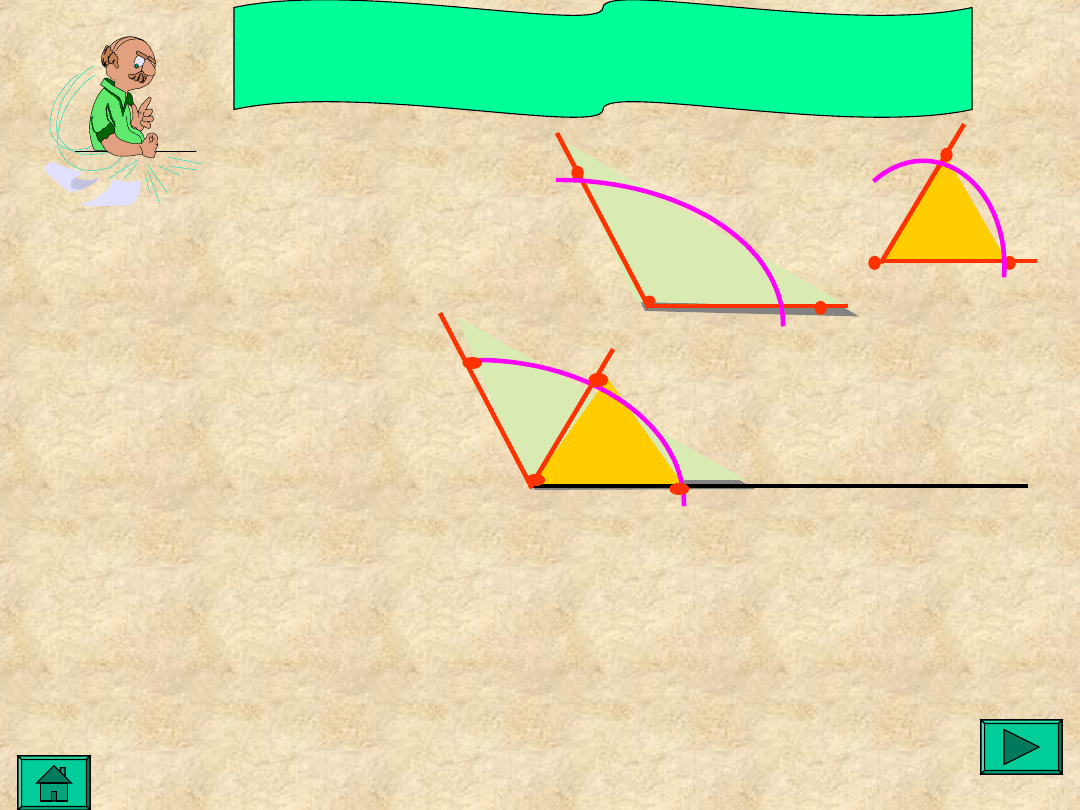
Dane są dwa kąty AOB i CED

Dane są dwa kąty AOB i CED

takie, że kąt AOB jest większy

takie, że kąt AOB jest większy

od kąta CED:

od kąta CED:

A

B

O

C

D

E

Kreślimy półprostą o początku
w punkcie O’

O’

Z punktów O, E ,O’
kreślimy łuki okręgów o
tym samym promieniu –
punkt przecięcia półprostej
o początku w punkcie O’ z
okręgiem oznaczamy A’.

A’

Przy półprostej O’A’ budujemy kąt równy kątowi AOB-
otrzymujemy punkt B’

B’

Przy półprostej O’A’ budujemy kąt równy kątowi CED-
otrzymujemy punkt C’

C’

Kąt

C

’

O’B’ jest różnicą kątów AOB

i CED.

Odejmowanie kątów

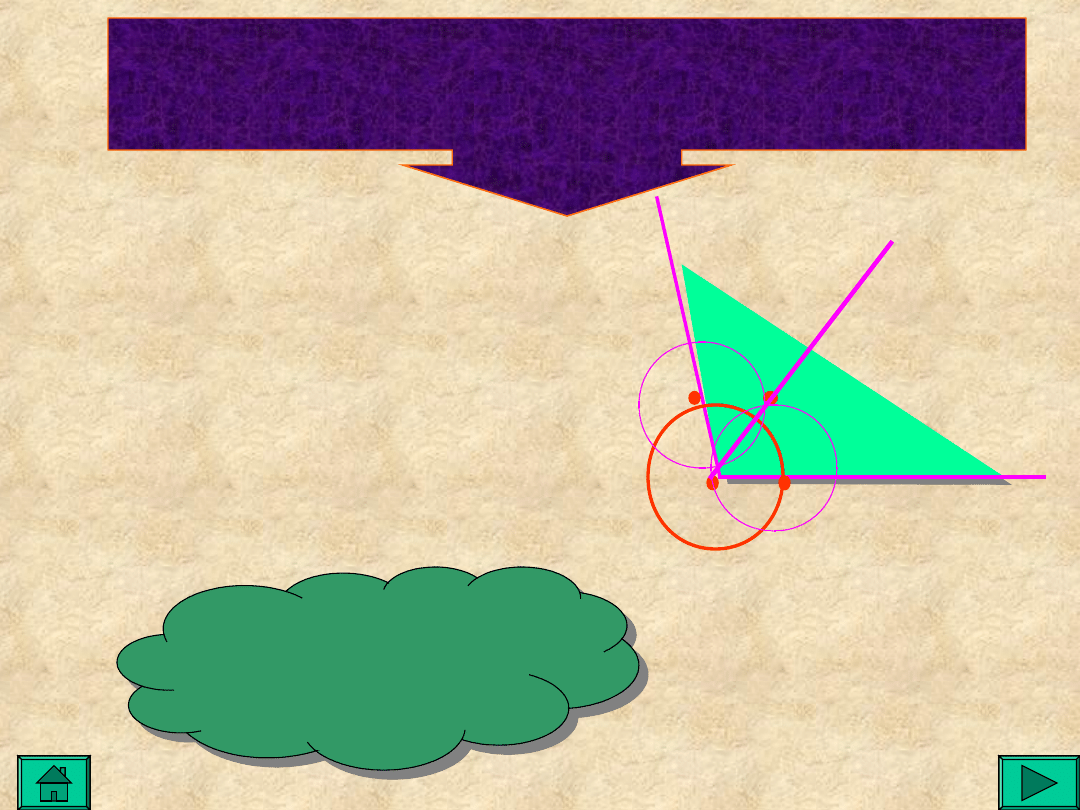
Dwusieczna kąta

Dany jest kąt o
wierzchołku A

Rysujemy okrąg o środku w
punkcie A i dowolnym
promieniu.

B

C

W punktach B i C kreślimy łuki o
promieniu większym niż połowa
odcinka BC.

A

O

Półprosta AO jest
dwusieczną kąta BAC

W matematyce często używa się liter
alfabetu greckiego. Stosujemy je głównie
do oznaczania kątów. Oto jak wygląda
alfabet grecki.