Dyfuzja w procesach

biologicznych

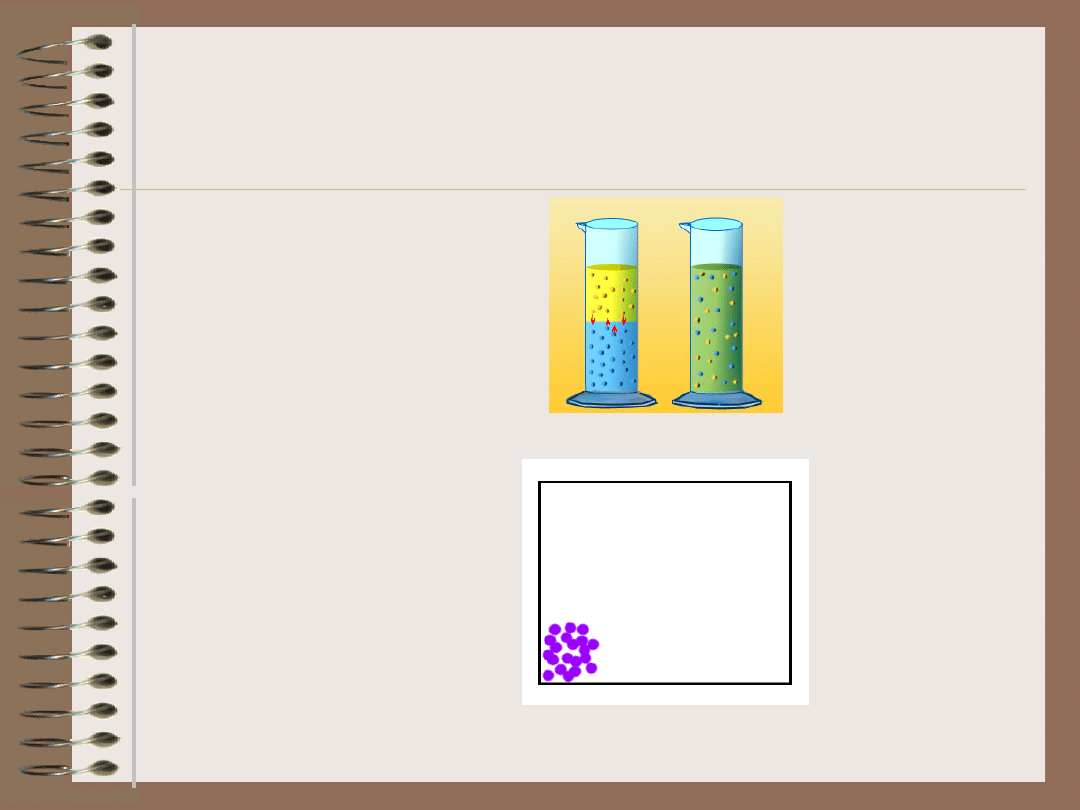
Wyróżnia się dwa rodzaje
dyfuzji:

- Chemiczną

- Populacyjną

Proces odwrotny

-KLASTERYZACJA-

- osobniki skupiają się w jednym

miejscu

Proces ten można modelować przy

użyciu automatów komórkowych.

Idea automatów komórkowych
została wprowadzona przez
Johna von Neumanna jako
uproszczony model fizyki
rzeczywistego świata.

Równanie dyfuzji substancji
chemicznej:

Model z jedną zmienną przestrzenną

Założenia:

- Substancje A i B są cieczami nie reagującymi ze sobą
- Cząsteczki cieczy przemieszczają się tylko wzdłuż rurki
-Jest to funkcja gładka

substancja A
substancja B

Zmiana stężeń obu substancji następuje

przez ich przepływ przez brzeg badanego
obszaru.

Do opisu tego przepływu stosujemy prawo,

zgodnie z którym masa substancji
przechodząca przez przekrój rurki w ciągu
krótkiego czasu δt jest proporcjonalna do
tego czasu, pochodnej oraz pola
przekroju rurki i wynosi:

∂ A

∂x

pierwszy brzeg

drugi brzeg

, gdzie D – to współczynnik proporcjonalności

Funkcja A(t,x) opisuje stężenie cieczy w zależności
od położenia w rurce x i czasu t

S- pole przekroju

t

x

x

t

A

DS

Q

x











)

,

(

t

x

x

x

t

A

DS

Q

x

x

















)

,

(

Ogólne równanie dyfuzji dla jednej zmiennej
przestrzennej:

2

2

)

,

(

)

,

(

x

x

t

A

D

t

x

t

A











Równanie opisujące dyfuzję w
przestrzeni trójwymiarowej o
współrzędnych (x, y, z )

2

2

2

2

2

2

)

,

,

,

(

)

,

,

,

(

)

,

,

,

(

z

z

y

x

t

A

y

z

y

x

t

A

x

z

y

x

t

A

A





















D > 0

Dodatniość współczynnika

dyfuzji,

oznacza, że dyfuzja jest

jednokierunkowa– zawsze

zachodzi w kierunku od większego

do mniejszego stężenia.

Ruchy Browna

TO LOSOWE PRZEMIESZCZANIE SIĘ Z

MIEJSCA NA MIEJCE

( LOSOWE RUCHY CZĄSTECZEK )

 x

 x

 x

 x

 x

 x

 x

 x

Analiza losowego ruchu osobnika wzdłuż
prostej.

Założenia:

- W chwili t cząsteczka znajduje się w odcinku [x, x +δx]
- W przedziale czasu [t, t+δt] cząsteczka przeskakuje z

prawdopodobieństwem λ

l

w lewo – do odcinka [x-δx, x]

lub w prawo z prawdopodobieństwem λ

p

do odcinka

[x+ δx, x+ 2δx]

Ilość cząsteczek w rozpatrywanym odcinku wynosi:

)

,

(

)

,

(

)

,

(

)

,

(

)

,

(

)

,

(

x

t

u

x

x

t

u

x

t

u

x

x

t

u

x

t

u

x

t

t

u

l

l

p

p































Ruchy Browna-Szereg

Taylor'a

Gdy prawdopodobieństwo skoku w lewo
lub w prawo jest jednakowe to:

...)

)

(

2

1

(

...)

)

(

2

1

(

...

)

(

2

1

2

2

2

2

2

2

2

2

2













































x

x

u

x

x

u

x

x

u

x

x

u

t

t

u

t

t

u

l

p

















2

1





l

p





...

)

(

2

1

...

)

(

2

1

2

2

2

2

2

2





















x

x

u

t

t

u

t

t

u







W równaniu przechodzimy do granicy δt 0

i δx 0 co prowadzi do powstania
równania dyfuzji:

∂u

∂ t

=

D∂

2

u

∂

2

x

DYFUZJA CIECZY A ROZPRZESTRZENIANIE

SIĘ POPULACJI - Skellam

Zaproponował model opisujący populację, która namnaża

się w sposób ciągły ze współczynnikiem rozrodczości α

i rozprzestrzeniania się na pewnym nieograniczonym

terytorium:

funkcja opisująca zagęszczenie

populacji w czasie i przestrzeni

operator Laplace'a –

przemieszczanie się osobników

w przestrzeni

współczynnik dyfuzji –

odzwierciedla mobilność

populacji – chęć osobników do

przemieszczania się

D > 0

N (t, x)

N

D

N

t

N













2

2

x

N

N











Współczynnik
rozrodczości

W układach równań REAKCJI – DYFUZJI można

otrzymać tzw.

niestabilność dyfuzyjną.

- pojawia się ona, jeśli rozwiązanie

stacjonarne stabilne w układzie bez
dyfuzji traci stabilność w układzie z dyfuzją i
zamiast niego pojawia się stabilne rozwiązanie
niejednorodne przestrzennie - wzór
przestrzenny

- Turing zauważył, że wprowadzenie dyfuzji

może zdestabilizować rozwiązanie stacjonarne
jednorodne przestrzennie.

Model melanogenezy :

- Opisuje formowanie się wzorców na skórze

ssaków -

Jest to model, w którym bierze się pod uwagę

reakcję chemiczną prowadzącą do

różnorodnego rozmieszczenia ciemnego

ubarwienia , za które odpowiada melanina.

Opisuje syntezę melaniny z substratu (tyrozyny)

w obecności enzymu ( tyrozynazy).

Równania opisujące syntezę melaniny:

-

małe stężenie składników - szybkość reakcji jest
proporcjonalna do ich stężenia. W miarę wzrostu
stężenia substratu, reakcja ulega wyhamowaniu, a w
mianowniku ułamka zaczyna dominować
składnik liniowy s. W przypadku k = 0 funkcja ta nazywa
się typu Michaelisa-Mentena

-

duże stężenie składników – dominuje wówczas czynnik
kwadratowy i reakcja dławi się samoistnie.

ϱ sa

1sks

2

s

2

STRUMIEŃ DYFUZJI:

- Opisuje go prawo A. Ficka , które mówi, że :

„Strumień cząstek jest zwrócony przeciwnie do

kierunku wzrostu gęstości i jest

proporcjonalny do gradientu gęstości.”

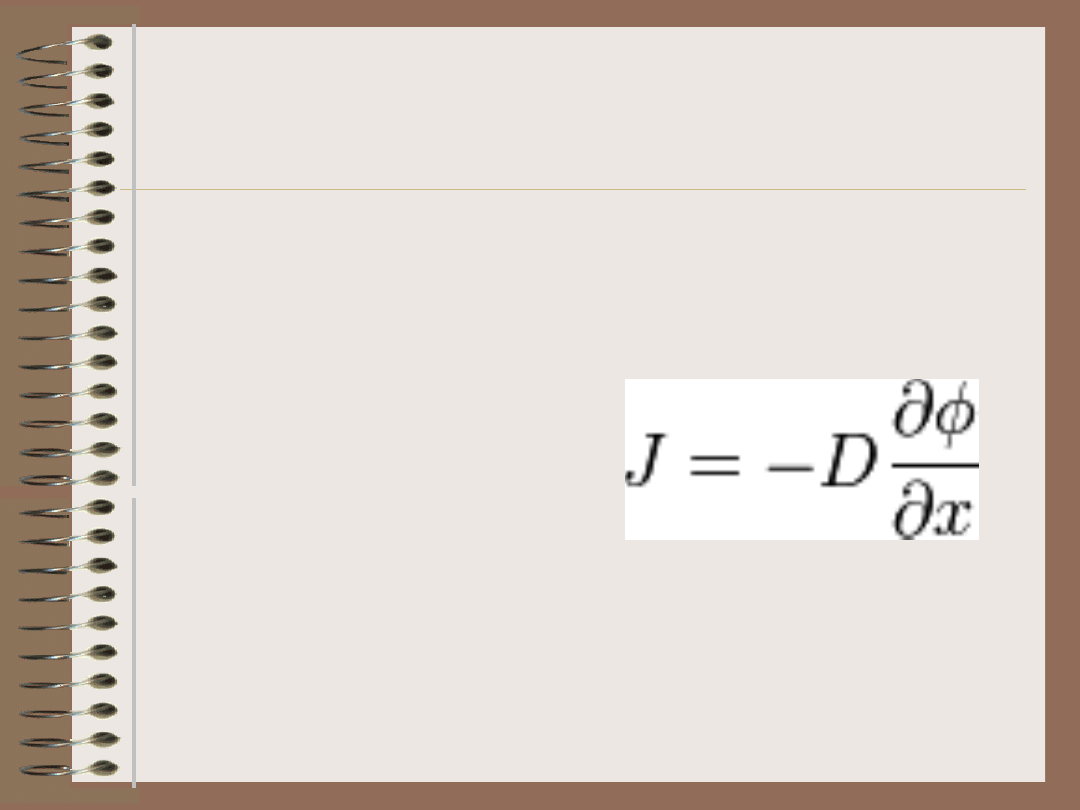
• Pierwsze prawo Ficka stosowane jest kiedy

stężenie strumienia dyfuzji objętościowej nie
zmienia się z czasem Jin = Jout.

W przestrzeni jednowymiarowej strumień
dyfuzji wynosi:

 

             

Gdzie:

-D -jest współczynnikiem proporcjonalności dyfuzji

-J jest strumieniem składnika

-φ jest stężeniem

- x jest odległością od źródła dyfundującej substancji

- Drugie prawo Ficka jest stosowane, gdy

strumień dyfuzji zmienia się lokalnie w czasie
:

- W przypadku dyfuzji w przestrzeni dwu lub

więcej wymiarowej drugie prawo Ficka
przyjmuje postać:

TEMPO DYFUZJI TLENU JEST JEDNYM

Z CZYNNIKÓW OGRANICZAJĄCYCH

ROZMIARY CIAŁA ORGANIZMÓW

WIELOKOMÓRKOWYCH, U KTÓRYCH

NIE WYSTĘPUJE UKŁAD

KRWIONOŚNY.

BIBLIOGRAFIA:

- „Matematyka w biologii”. Urszula Foryś,

Wydawnictwo Naukowo-Techniczne. Warszawa
2005

- „Matematyka dla biologów”. Dariusz Wrzosek,

Wydawnictwo Uniwersytetu Warszawskiego.
Warszawa 2008

- „Matematyka dla przyrodników i inżynierów”.

Donald A. McQuarrio. Wydawnictwo. Naukowe
PWN, Warszawa 2005