Organizacja przedmiotu i treści

kształcenia

• WYKŁAD

• Elementy termodynamiki fenomenologicznej.

Model gazu dokonałego. Równanie Van der Vaalsa.

Punkt krytyczny. I i II zasada termodynamiki.Procesy

odwracalne i nieodwracalne. Entropia. Mechanizmy

transportu energii i ciepła, przewodnictwo cieplne.

• Elektryczność i magnetyzm. Pole elektryczne.

Prawo Coulomba. Energia pola. Pojemność

elektryczna. Prąd elektryczny. Prawo Ohma i

Kirchhoffa. Elektryczne i magnetyczne właściwości

materii. Fale elektromagnetyczne, widmo fal

elektromagnetycznych.

• Elementy mechaniki kwantowej. Kwantowa natura

materii i energii. Promieniowanie ciała doskonale

czarnego. Efekt fotoelektryczny. Efekt Comptona.

Hipoteza de Broglie"a. Zasada nieoznaczoności

Heisenberga. Budowa atomu i jądra atomowego

.   

Organizacja przedmiotu i treści

kształcenia

• ĆWICZENIA AUDYTORYJNE

• Podstawy mechaniki klasycznej. Elementy

hydromechaniki. Elementy termodynamiki

fenomenoogicznej. Grawitacja.

• ĆWICZENIA LABORATORYJNE

• Cwiczenia praktyczne z zakresu mechaniki

ogólnej, ciepła i termodynamiki, elektryczności i

magnetyzmu oraz optyki w tym elementy

akustyki, model pasmowy ciał stałych, poziomy

energetyczne właściwości stanów skupienia

materii, promieniotwórczość naturalna i

sztuczna, elementy fizyki jądrowej.

Efekty kształcenia

Umiejętność wykonania pomiaru

podstawowych wielkości

fizycznych. Rozumienie

podstawowych zjawisk i procesów

fizycznych występujących w

budownictwie. Wykorzystanie

praw przyrody w technice i życiu

codziennym.

Forma zaliczenia

• Jedna ocena z całego modułu na którą

składają się:

• Ocena z jednego jednogodzinnego

kolokwium z zakresu materiału
wykładowego (30%)

• Ocena z pisemnych sprawozdań z

wykonanych ćwiczeń i ustnych
sprawdzianów z zagadnień związanych z
wykonywanymi ćwiczeniami (40%)

• Ocena z dwóch jednogodzinnych kolokwiów

z zakresu materiału ćwiczeniowego (30%).

Literatura podstawowa

• Halliday D., Resnick R., Walker J. :

Podstawy fizyki PWN, Warszawa, 2003.
     

• 1. Jaworski B. i inni : Kurs Fizyki, tom

1,2,3 PWN, Warszawa, 1984.

• 2. Massalski, M. Massalska: Fizyka dla

inżynierów tom 1 PWN Warszawa
1978.

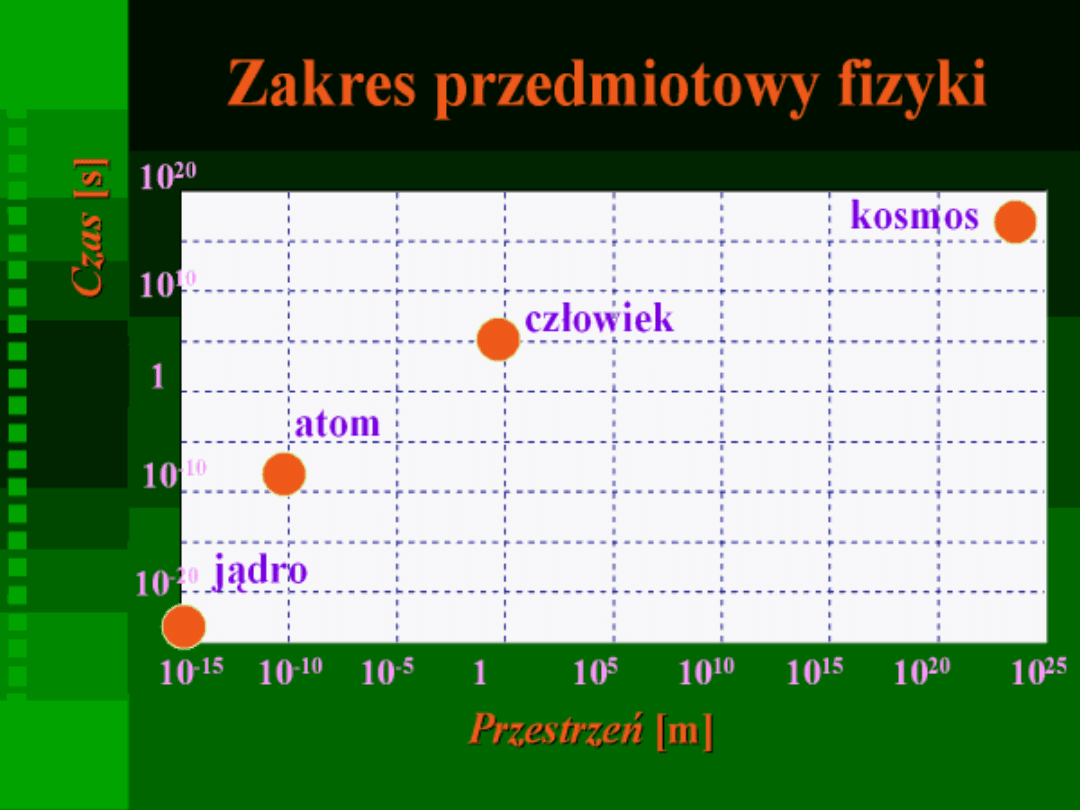
Podstawy

termodynamiki

fenomenologicznej

Podstawy

termodynamiki

fenomenologicznej

Termodynamika zajmuje się badaniem

energii i jej przemian.

Jest wiele różnych rodzajów energii.

Wszystkie one mogą stać się

przedmiotem rozważań

termodynamicznych.

Ogólnie rzecz biorąc, termodynamika
zajmuje się głównie dwoma rodzajami
energii:

ciepłem i pracą.

Podejście makroskopowe

-związki pomiędzy

wielkościami
makroskopowymi jak ciśnienie objętość temperatura,
energia wewnętrzna entropia

stanowię podstawę

termodynamiki fenomenologicznej.

Podejście mikroskopowe

-

przedstawienie wielkości
fizycznych takich jak: prędkość, masa, energia,
opisujących
atomy i cząsteczki czyli elementy tworzące
układ

stanowi podstawę mechaniki statystycznej

Uwagi:

Równoważność obu podejść

Wielkości makroskopowe –postrzegane przez zmysły
Wielkości mikroskopowe – nie są bezpośrednio postrzegane przez zmysły

Związki pomiędzy mechaniką

klasyczną a termodynamiką

Zagadnienia mechaniki klasycznej obejmują
takie pojęcia jak

siła, masa, odległość, czas

i

inne. Mechanika opiera się na II prawie
Newtona:

)

( v

m

dt

d

F









Do opisu zjawisk mechaniki stosuje się

ciało swobodne

na które działają wszystkie

siły zgodnie z II zasadą dynamiki.

System (układ) mechaniczny

jest

zdefiniowany przez współrzędne
przestrzenne i prędkość.

Oddziaływanie z otoczeniem jest opisane przez
działanie sił.

Stan układu

jest opisany przez współrzędne

przestrzenne, prędkość i jego zachowanie się.
Zmiana stanu układu z jednego do drugiego
jest opisany przez oddziaływanie z otoczeniem.
Układ mechaniczny nie zmienia swego stanu
bez działania siły zewnętrznej.

Podczas, gdy w mechanice zajmujemy się
wielkościami dynamicznymi, w termodynamice
zajmujemy się porcjami energii.

Układem w termodynamice nazywamy
wyodrębnioną ilość materii

. Materia pozostała

poza układem stanowi otoczenie a granicę
pomiędzy tymi dwoma stanami stanowi brzeg
układu.

Granice naszego układu mogą być rzeczywiste lub pozorne.

Stan układu termodynamicznego

opisany jest

przez

współrzędne termodynamiczne.

Zwykle

nie możemy na początku podać wszystkich
współrzędnych. Typowymi przykładami takich
współrzędnych są

temperatura, ciśnienie,

objętość, gęstość, energia chemiczna,ilość
substancji.

Te współrzędne zwykle nazywamy
własnościami układu.

TEMPERATURA

=

“stan ciepłoty, gorąca”

Wolno poruszające się atomy lub cząsteczki
maja niską temperaturę.

Szybko poruszające się atomy lub cząsteczki
maja wysoką temperaturę.

Rozważmy krótko niektóre z podanych
„współrzędnych”

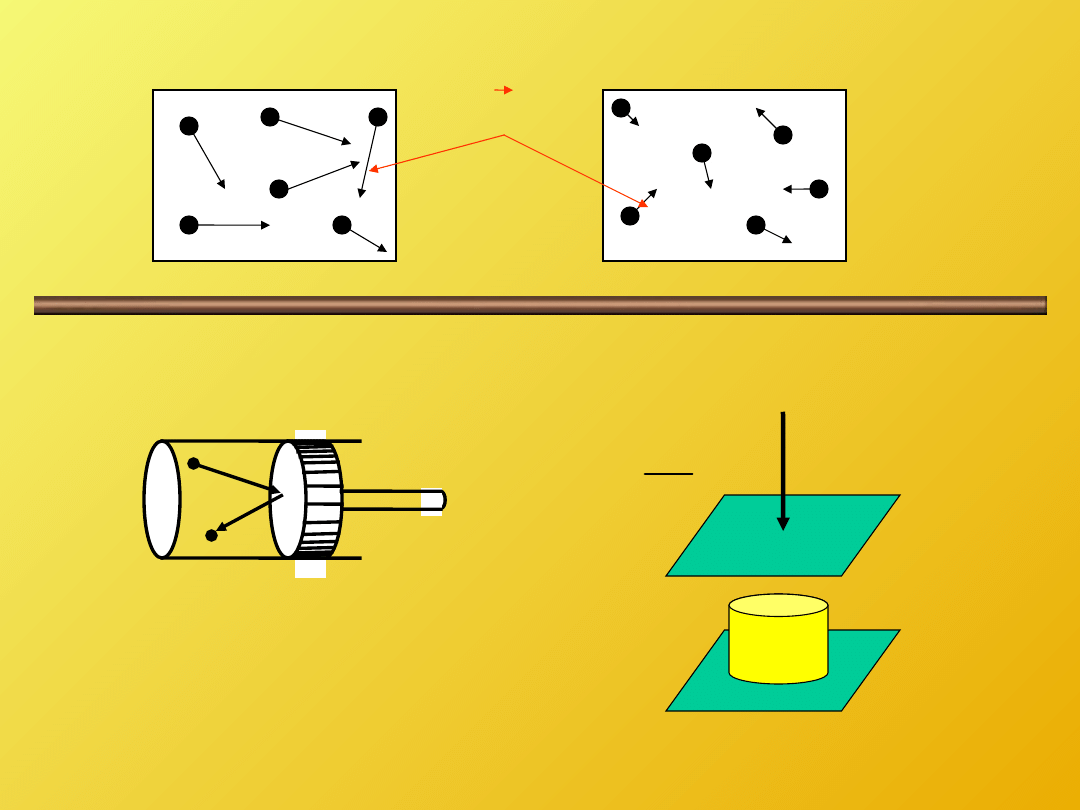
Wysoka T

Niska T

v

CIŚNIENIE

=siła działająca na

powierzchnię

zderzenie

A

F

p 

F

A

cięża
r

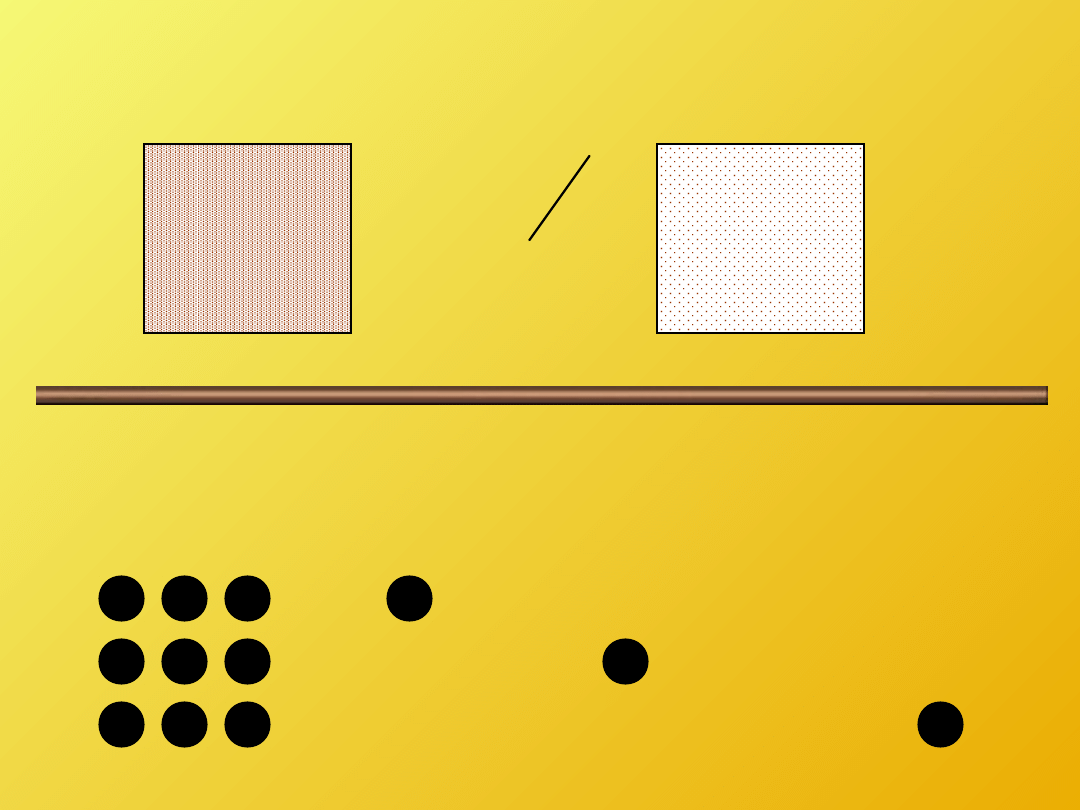
GĘSTOŚĆ

=„masa na jednostkę

objętości”

Duża
gęstość

Mała
gęstość

V

m





…

……….

………………...

1 2 3 12

144

6.022 × 10

23

tuzin

gross

ILOŚĆ SUBSTANCJI

= „ile tego jest”

Liczba
Avogad
ry

Ciało stałe

Ciecz

Gaz

Plazma

STANY SKUPIENIA

Zmiana układu termodynamicznego

polega na

zachodzeniu jakiegoś procesu przemiany.

W termodynamice interesuje nas, jakim
zmianom może podlegać układ na wskutek tych
przemian.

Jeśli chcemy opisać stan układu na każdym
etapie przemiany, musimy być w stanie
zdefiniować stan układu.

Aby to móc zrobić musimy wprowadzić

pojęcie

równowagi układu.

Układ jest w równowadze, jeśli np. jego
ciśnienie, temperatura i gęstość są
jednorodne. Definicja ta jednak nie jest pełna.

Aby móc określić współrzędne

termodynamiczne układu, musi on znajdować

się w równowadze.

Interesują nas

przemiany będące

łańcuchem stanów równowagi.

W takiej

przemianie potrafimy zdefiniować układ na
każdym etapie.

Procesy takie nazywamy

odwracalnymi

lub kwazistatycznymi.

Proces odwracalny

jest to proces który

może przebiegać w obydwie strony
nieskończenie długo bez strat.

Proces nieodwracalny

jest to taki w

którym mamy do czynienia ze stratą
energii.

Przyczynami takich strat mogą być:

Tarcie, spadki temperatury, ciśnienia i
stężenia.

Przykładem procesu nieodwracalnego jest pęknięcie
wazonu.

Temperatura, ciepło i zerowa zasada
termodynamiki

Zwykle przyjmuje się, że rozumiemy pojęcie ciepła i
temperatury. Termodynamika zajmuje się badaniami
mającymi na celu precyzyjne pojmowanie tych pojęć.
Zwykle intuicyjne pojmowanie temperatury kiedy
czegoś dotykamy wiąże się z transportem energii lub
wymianą ciepła. Można więc wywnioskować, że
pomiędzy dwoma ciałami o tej samej temperaturze
nie ma wymiany ciepła.

Równość temperatury nie pozwala nam stworzyć
bezwzględnej skali temperatur.

Pojęcie równości temperatur ujmuje tzw.

zerowa

zasada termodynamiki.

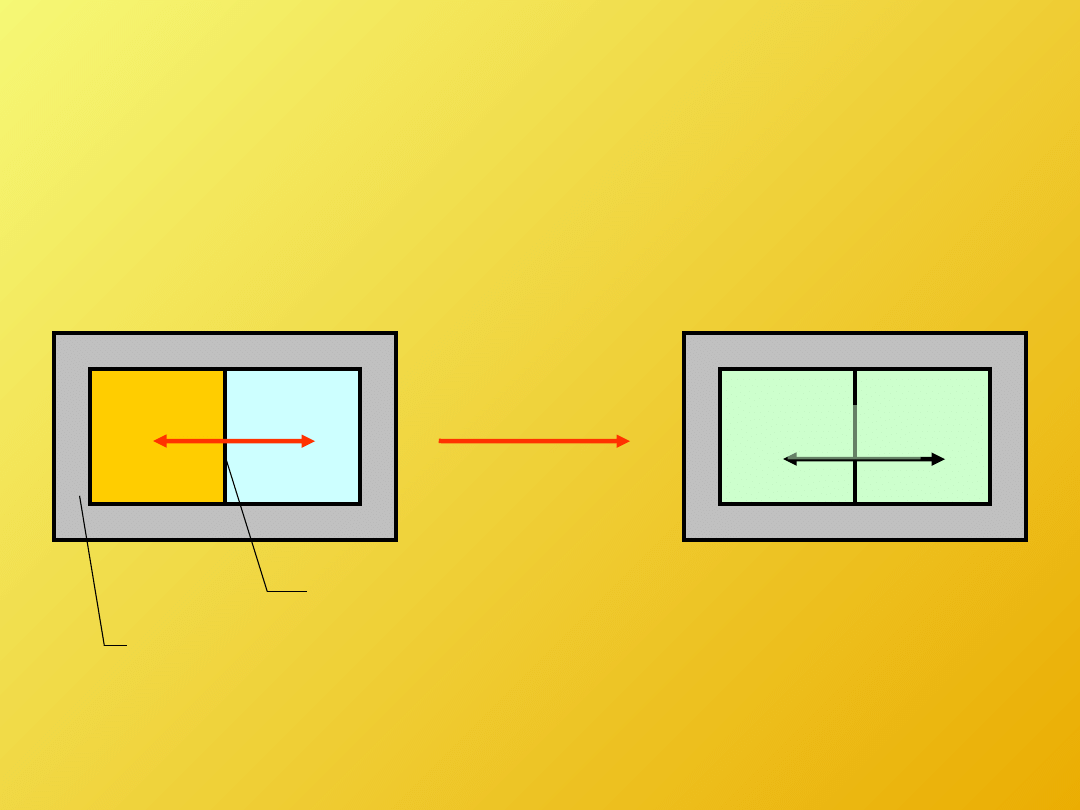
Dążenie układów do stanu

równowagi termicznej ...

A

B

ścianka
adiabatyczna

ścianka
diatermiczna

Q

A

B

Q = 0

Stan
początkowy

Stan
końcowy

Układ:

dwa dowolne podukłady A i B

rozdzielone ścianką diatermiczną i
izolowane od otoczenia ścianką
adiabatyczną

Obserwacja I:

podukłady wymieniają

między sobą energię na sposób ciepła;
szybkość tego procesu dąży do zera
podukłady A i B osiągają stan równowagi
termicznej względem siebie.

Dążenie układów do stanu

równowagi termicznej - fakty

doświadczalne ...

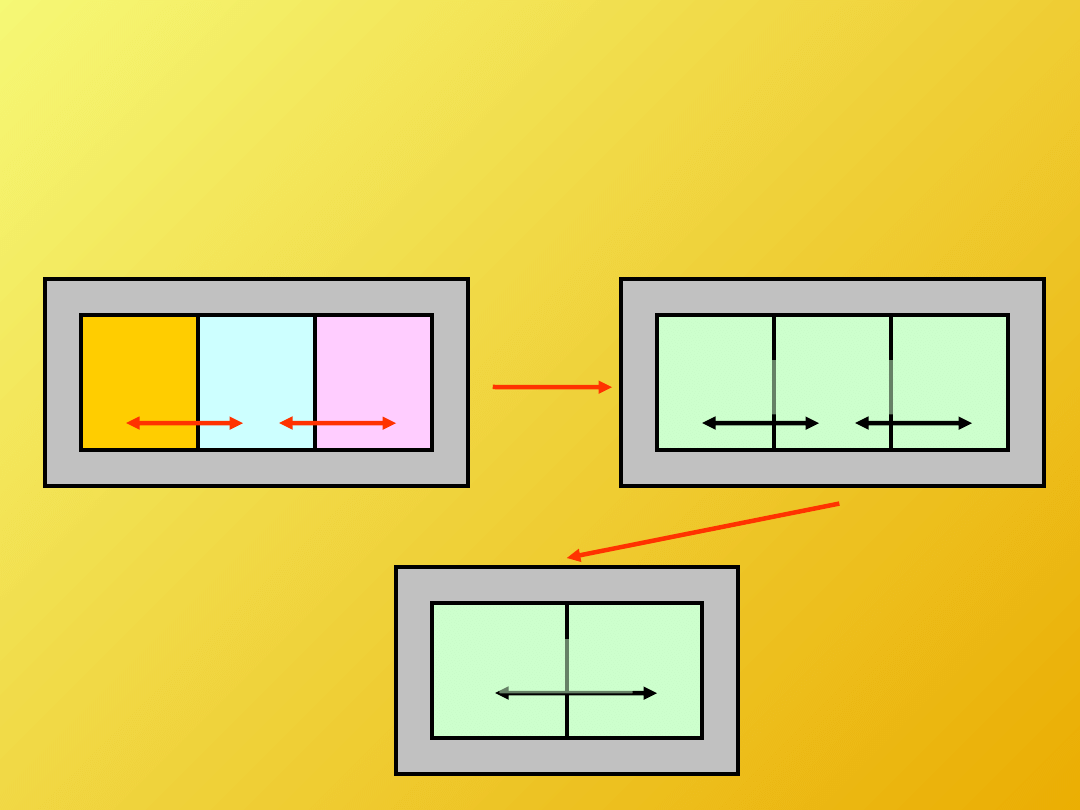
...Dążenie układów do stanu

równowagi termicznej

A

B

Q = 0

A

B

C

Q

Q

A

B

C

Q = 0Q = 0

Stan
początkowy

Stan końcowy
I

Stan
końcowy II

Układ:

trzy dowolne podukłady A, C i B

rozdzielone ściankami diatermiczymi i
izolowane od otoczenia ścianką
adiabatyczną; kontakt termiczny A - B
możliwy wyłącznie za pośrednictwem C

Obserwacja II:

podukłady wymieniają

między sobą energię na sposób ciepła;
szybkość tego procesu dąży do zera
podukłady A i C oraz B i C osiągają stan
równowagi termicznej względem siebie.

....

Dążenie układów do stanu

równowagi termicznej - fakty

doświadczalne ...

Obserwacja III:

jeżeli podukłady A i C

oraz B i C parami w stanie równowagi
termicznej, to po usunięciu podukładu
C i bezpośrednim zetknięciu
podukładów A i B przez ściankę
diatermiczną nie obserwuje się
wymiany energii na sposób ciepła
między nimi.

...Dążenie układów do stanu

równowagi termicznej - fakty

doświadczalne

Jeżeli układy A i B są w stanie
równowagi termicznej z układem C,
to są one również w stanie
równowagi termicznej względem
siebie.

E.A. Guggenheim, R. Fowler (1939)

Zerowa zasada termodynamiki

Zasady termodynamiki

(0 - 3)

-

zwięzłe uogólnienia faktów
doświadczalnych uznane za
aksjomaty; służą do definiowania
funkcji stanu oraz określania
związków między nimi i
parametrami mierzalnymi.

•Wspólną właściwość układów w stanie
równowagi termicznej nazywa się

temperaturą

. Każdemu ukła- dowi

przypisuje się intensywny parametr
stanu - temperaturę;

układy

pozostające w stanie równowa- gi
termicznej mają taką samą
temperaturę

.



Termometria - dział

termodynamiki poświęcony pomiarom
temperatur.

•Konsekwencja zerowej zasady
termodynamiki...

Termometr i pomiar
temperatury:

• Układ mający jeden stopień swobody

(temperatu- rę)



pozostałe

parametry stanu termometru są
funkcjami wyłącznie temperatury

• Wybrać łatwo i dokładnie mierzalny

parametr stanu termometru



parametr termometryczny

.

• Utworzyć skalę temperatur



określić

zależność funkcyjną między
parametrem termometrycznym i
temperaturą.

• Ustalić stan równowagi termicznej

między termo- metrem i badanym
układem, zmierzyć wartości
parametru termometrycznego i
obliczyć tempera- turę w przyjętej
skali.

t

c

=[(T)-

273.15]

o

C

t

c

– Temperatura w skali Celsjusza

T – Temperatura w skali Kelvina

t

c

=5/9[t

F

-

32]

o

C

t

c

– Temperatura w skali Celsjusza

t

F

– Temperatura w skali Fahrenheita

Skale

temperatur

Zero

absolutne

0K

-273.15

o

C -

459.67

o

F

Punkt potrójny

wody

273.1
5K

0.01

o

C

32.00

o

F

Skale temperatur Kelvina , Celsjusza, Fahrenheita

Najwyższa temperatura

:

10 lutego 2000r. europejskie laboratorium cząstek elementarnych
CERN pod Genewą wydało komunikat, że udało się zaobserwować
plazmę kwarkowo-gluonową, która była 100tys. razy gorętsza niż
wnętrze Słońca, co odpowiada temperaturze

10

12

K

i 20 razy bardziej

gęsta niż jądro atomu. Powstała na skutek eksperymentów z jądrami
ołowiu rozpędzanymi do bardzo dużych prędkości i doprowadzanych
do zderzeń. Taka sytuacja prawdopodobnie miała miejsce w dziejach
Wszechświata 12-15 miliardów lat temu, około 10 ms po Wielkim
Wybuchu.

Najniższa temperatura

:

Najniższa temperatura osiągnięta została w 1995r. na Uniwersytecie w
Boulder, Colorado (USA), kiedy fizycy Eric Cornell i Carl Wieman
wytworzyli nowy stan materii, przewidziany przez Einsteina i Bosego.
W swym eksperymencie schłodzili atomy rubidu to temperatury około

10

-8

K

i uzyskali kondensację Bosego-Einsteina (maksymalne możliwe

wygaszenie ruchów atomów). W celu schłodzenia atomów rubidu użyli
pułapki laserowej (światło lasera podczerwonego oddziaływało tylko z
poruszającymi się cząsteczkami i spowalniało je, a następnie
pułapkowało -- schłodzenie do 10

-5

K) i pułapki magnetycznej. Dalsze

schłodzenie uzyskali dzięki wyrzucaniu najbardziej energetycznych, a
więc "najcieplejszych" atomów poprzez proces podobny do
odparowania.
 

 

Ciepło

– to forma energii a nie substancja.

(Benjamin Thompson 1753-1814)

Pojemność cieplna

T

Q

C







Ilość ciepła potrzebna do ogrzania ciała o jeden stopień

Ciepło
właściwe

T

m

Q

c







Pojemność cieplna przypadająca na
jednostkę masy ciała





2

1

T

T

dT

c

Q

Ciepło

dostarczone do ciała o masie m i cieple właściwym c przy

Zmianie temperatury od T

1

do T

2

c - ciepło właściwe (jest funkcją temperatury)

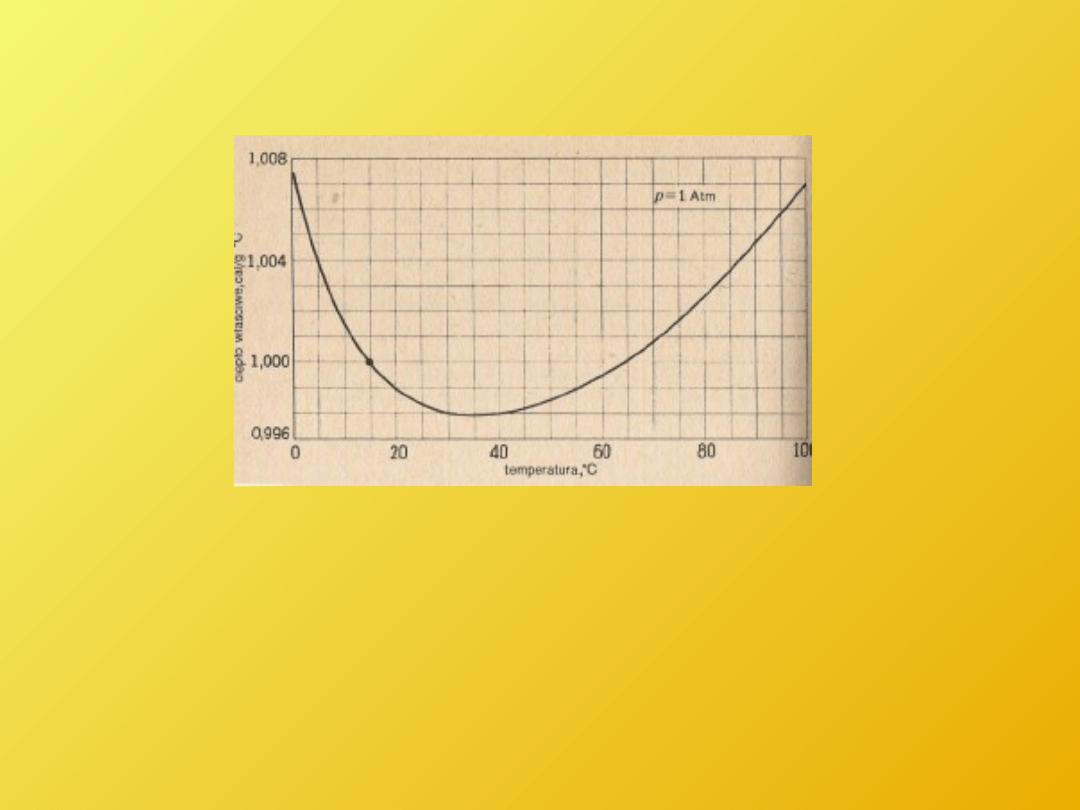
Ciepło właściwe wody w funkcji temperatury

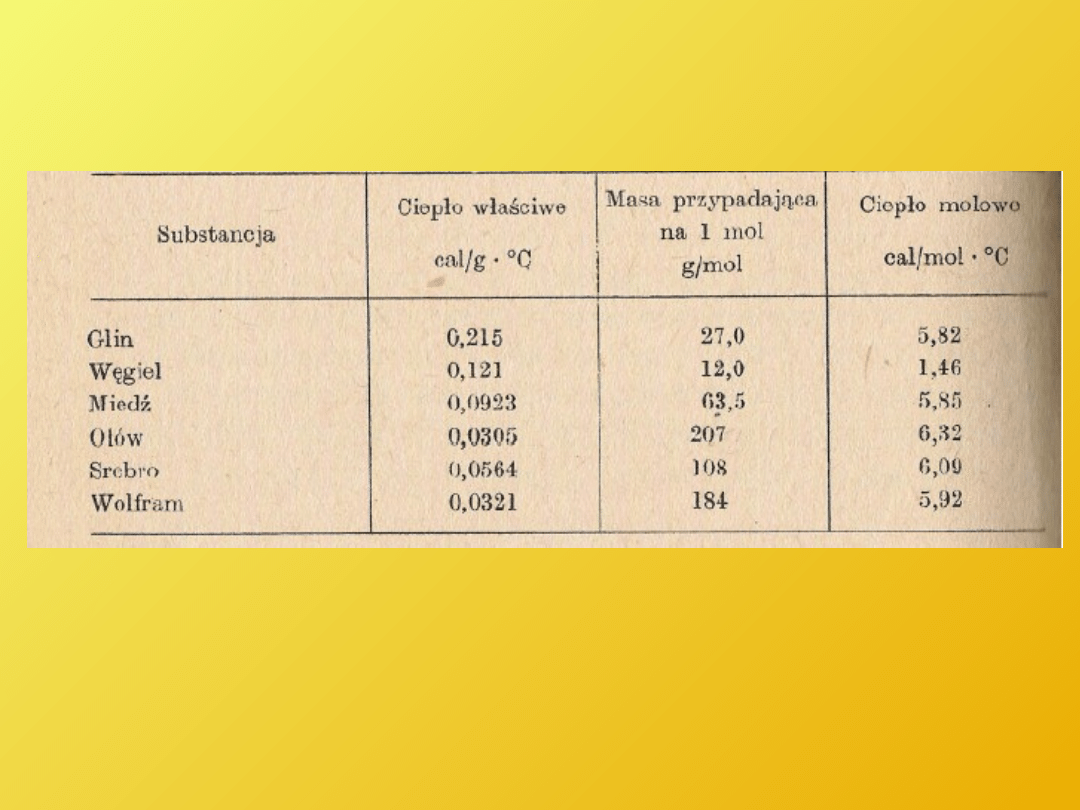
Ciepło molowe

- ilość ciepła potrzebna do ogrzania

jednego mola substancji o jeden stopień

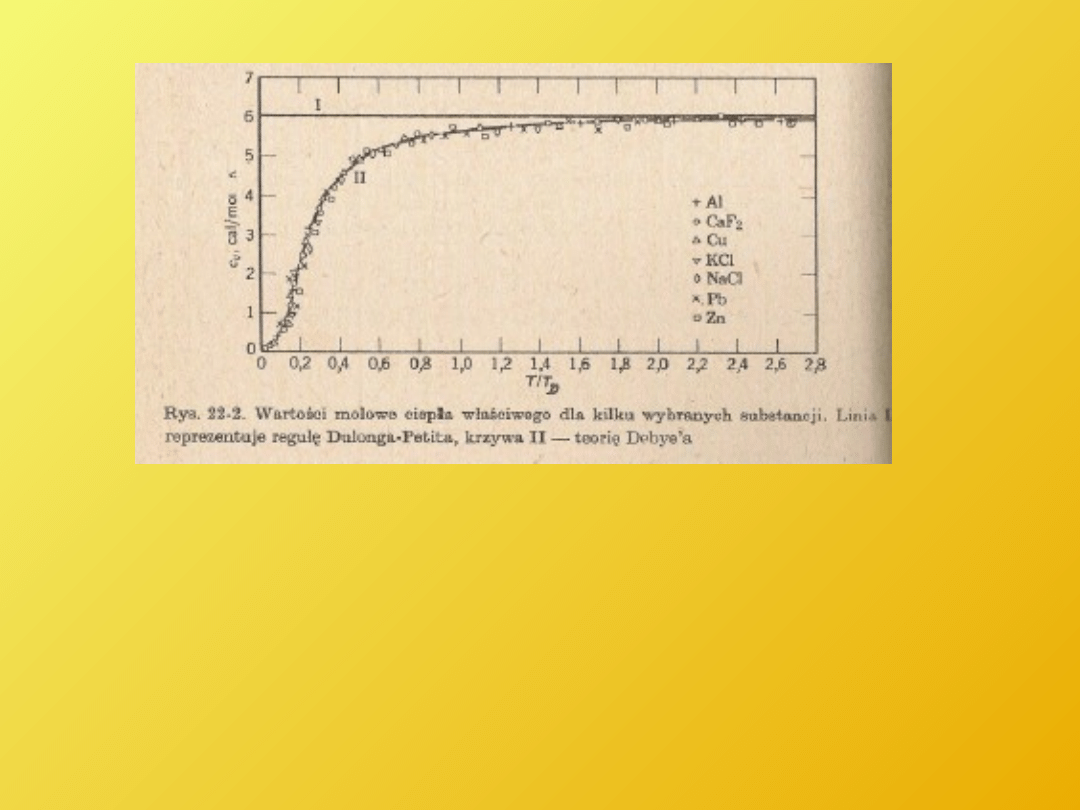
Ciepło molowe dla kilku wybranych substancji
I - reguła Dulonga Petita

(1819 r )

II – teoria Debye’a

(1912 r)

Ciepło a praca

Pierwsza zasada termodynamiki

Przykład zamiany pracy mechanicznej na ciepło

Opadający ciężarek napędza generator elektryczny ,
generator powoduje przepływ prądu przez opornik
ogrzewający wodę w której jest zanurzony.

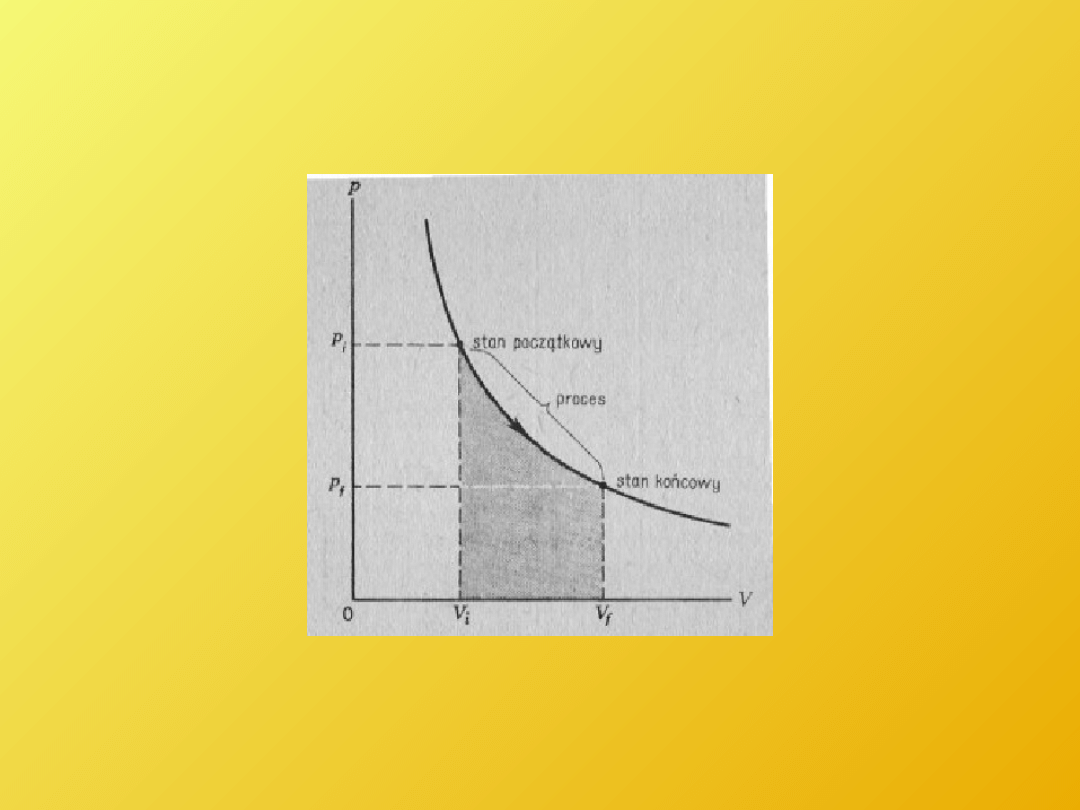
Praca wykonana przez gaz

równa jest polu powierzchni pod krzywą p, V.









2

1

V

V

pdV

dW

W

Zarówno ciepło jak i praca „zależą od obranej drogi”

Żadne z nich oddzielnie nie może samo podlegać zasadzie zachowania

Ilość ciepła tracona lub otrzymywana przez

układ

zależy nie tylko od początkowego i końcowego

stanu układu

lecz także od stanów pośrednich tj. od drogi

procesu

Stan A

Stan
B

Droga 2

Droga 3

Droga
1

3

3

2

2

1

1

W

Q

W

Q

W

Q











Różnica Q-W nie zależy od sposobu przeprowadzenia

układu ze stanu A do B

Gdy przeprowadzamy układ ze stanu początkowego do stanu końcowego

Wielkość Q-W zależy wyłącznie od stanu początkowego i końcowego

a nie zależy od drogi po jakiej dokonuje się przejście.

Istnieje więc pewna funkcja współrzędnych termodynamicznych,

której wartość końcowa minus wartość początkowa równa jest zmianie

Q-W w tym procesie.

Funkcję tę nazywamy energią wewnętrzną układu.

W

Q

U

U

U

A

B











Gdy układ podlega tylko infinitezymalnej zmianie stanu (bardzo małej)
Wtedy:

dW

dQ

dU





Pierwsza zasada termodynamiki

Każdy układ termodynamiczny w stanie równowagi

jest scharakteryzowany ustaloną wartością pewnej funkcji stanu

nazywanej energią wewnętrzną U, której zmiana dU

w różniczkowym procesie określona jest równaniem:

dW

dQ

dU





W postaci całkowej (dla całego procesu)

W

Q

U







Oznaczenia

1. Ciepło Q uważamy za dodatnie (Q0), gdy dostarczane jest z

otoczenia do układu; ciepło dostarczane z układu do otoczenia
jest ujemne (Q0),
2. Pracę W uważamy za dodatnią (W0), gdy wykonywana jest

przez układ nad otoczeniem; praca wykonywana przez
otoczenie nad układem jest ujemna (W0),

Energia wewnętrzna U

układu jest całkowitą

energią układu z wyłączeniem energii

kinetycznej układu jako całości oraz energii

potencjalnej w zewnętrznych polach.

1.     Energia wewnętrzna jest funkcją stanu
układu,

2.     Energia wewnętrzna sumy układów jest
sumą energii wewnętrznych układów
składowych oraz energii wzajemnego
oddziaływania między wszystkimi układami
sumy

3.     Energia wewnętrzna układu może się
zmieniać w wyniku wymiany pracy lub ciepła
między układem a otoczeniem

Istotą I zasady termodynamiki jest

to że istnieje

użyteczna wielkość termodynamiczna nazywana
„energią wewnętrzną” Zasada ta daje też przepis jak
określić ilościowe zmiany tej wielkości.

Istotą zerowej zasady termodynamiki jest

stwierdzenie istnienia

użytecznej wielkości termodynamicznej jaką jest temperatura.

I zasada termodynamiki

mówi o zachowaniu energii w

każdym procesie

nie odpowiada jednak na pytanie

czy określony proces może rzeczywiście
zachodzić.

Na to pytanie odpowiada II zasada termodynamiki.

Gaz doskonały – opis makroskopowy

Dla wszystkich gazów, przy dostatecznie

małych gęstościach doświadczalnie można
stwierdzić istnienie pewnych prostych związków
pomiędzy parametrami termodynamicznymi takimi
jak p, V, T.

Dla ustalonej masy gazu

const

T

pV



nR

T

pV



Gdzie R uniwersalna stała gazowa
8,314 J/mol K
n liczba moli gazu

Gaz doskonały

to gaz spełniający powyższe równanie w

dowolnych warunkach.

Gaz doskonały – opis mikroskopowy

Podejście mikroskopowe jest realizowane w oparciu o następujące założenia

1. Gaz składa się z cząsteczek, które można traktować jak punkty materialne
2. Cząsteczki poruszają się chaotycznie i podlegają zasadom dynamiki Newtona
3. Całkowita liczba cząstek jest bardzo duża
4. Cząsteczki mają objętość własną pomijalnie małą
5. Poza momentem zderzenia na cząsteczki nie działają żadne siły
6. Zderzenia są sprężyste i trwają nieskończenie krótko

Przemiany politropowe gazu doskonałego

Równaniem przemiany

nazywamy równanie stanu gazu z

nałożonym odpowiednim warunkiem przemiany

 

Przemianą politropową

jest taka przemiana , w której

pojemność cieplna gazu (ciepło molowe przemiany) jest stała
(warunek przemiany: C= const)

 Równanie przemiany politropowej (równanie politropy)

k= (C-C

p

)/(C-C

V

) = const

Wybrane przemiany politropowe:

k = 0  p = const  przemiana izobaryczna,
k = 1  pV = const  przemiana izotermiczna,
k = Cp/Cv  pV

k

=const  przemiana adiabatyczna,

k =   V = const  przemiana izochoryczna

 

const

pV 



Definicja mikroskopowa

•

Gaz składa się z cząsteczek, które traktować można jak
punkty materialne. Łączna objętość wszystkich cząsteczek gazu
jest więc pomijalna. Zależnie od rodzaju gazu, cząsteczka może
być atomem lub związana grupą atomów. Z punktu widzenia
chemii cząsteczki gazu to cząsteczki pierwiastka lub związku
chemicznego. Wszystkie one są identyczne.

•

Cząsteczki podlegają prawom mechaniki Newtona.

•

Całkowita liczba cząsteczek jest bardzo duża. Cząsteczki
poruszają się chaotycznie we wszystkich kierunkach, zderzają ze
ściankami naczynia i ze sobą nawzajem. Niezależnie od losów
poszczególnych cząsteczek, o zachowaniu gazu w skali makro
decydują średnie wartości całego zespołu.  

•

Cząsteczki zdarzają się ze sobą sprężyście, wymieniają pęd
bez strat energii.

•

Poza momentami zderzeń cząsteczki nie oddziałują ze sobą,
a czas trwania tych zderzeń jest pomijalnie mały. Zakładamy
tym samym mały - w porównaniu z rozmiarami cząsteczek - zasięg
sił oddziaływania międzycząsteczkowego. Znaczy to też że
pomiędzy zderzeniami cząsteczki poruszają się ruchem
jednostajnym prostoliniowym. 

Definicja mikroskopowa określa więc gaz doskonały jako zespół

cząsteczek o szczególnych własnościach. Podane tu elementy
definicji są punktem wyjścia kinetycznej teorii gazu.

Gaz doskonały – opis
mikroskopowy

Definicja makroskopowa
(termodynamiczna)

Za gaz doskonały uważać będziemy gaz spełniający
łącznie prawa Boyle'a-Mariotte'a, Gay-Luusaca i
Charlesa, czyli gaz dla którego w stałej temperaturze
iloczyn objętość i ciśnienie są odwrotnie
proporcjonalne, dla określonej objętości ma stały
stosunek ciśnienia do temperatury jest stały, a pod
stałym ciśnieniem - proporcjonalne są objętość i
temperatura. Łącznie możemy to zapisać jedną
zależnością:
            

Powyższy związek, definiujący gaz doskonały w ujęciu
makroskopowym dotyczy oczywiście ustalonej ilości
materii (ustalona masa, ustalona liczba cząsteczek,
ustalona liczba moli gazu)
Definicja ta określa związek pomiędzy parametrami
termodynamicznymi gazu - a więc określa gaz
doskonały poprzez jego równanie stanu.

Gaz doskonały – opis makroskopowy

Gazy doskonałe nie istnieją

. 

Model, jakim jest gaz doskonały, pozwala na proste

rachunki i sprawdza się dość dobrze w pewnych warunkach.
Jednak cierpi braki zarówno co do realizmu założeń, jak i co do
opisu zachowania się gazów. Założenia, które posłużyły do
budowy modelu gazu doskonałego w pewnych warunkach tracą
zasadność. Postulat zerowej objętości cząsteczek gazu nie daje się
obronić, podobnie jak założenie że cząsteczki nie oddziałują ze
sobą.  W efekcie model gazu doskonałego nie opisuje poprawnie
rzeczywistości. Wartości doświadczalne odbiegają od
przewidywań teorii. 
Co gorsza, poza niedociągnięciami ilościowymi, model ten ponosi
klęskę jakościową. Zawodzi całkowicie w tych warunkach, gdzie
objętości cząsteczek staje się porównywalna z objętością
zajmowana przez gaz (gdy na skutek koncentracji cząsteczek
odległości między nimi stają się porównywalne z ich rozmiarami).
Według równania Clapeyrona w temperaturze dążącej do zera
bezwzględnego objętość gazu pod stałym ciśnieniem malałaby do
zera. Mówimy tu o przejściach fazowych (skraplanie gazu w
niskich temperaturach i wysokich ciśnieniach), których to przejść
model wcale nie przewiduje.

 

Równanie Van der Waalsa

Ma ono postać

gdzie 
p jest ciśnieniem gazu,
v jest objętością molową v = V/n lub po prostu objętością
jednego mola gazu,
R to uniwersalna stała gazowa,
T jest temperaturą bezwzględną (mierzoną w kelwinach),
natomiast a i b to stałe, wyznaczane na drodze
doświadczalnej dla każdego gazu.
 
Jak widać, do  równania Clapeyrona, zapisanego przy użyciu
objętości molowej

pv = RT

wprowadzone zostały poprawki - poprawka do ciśnienia (+
a/V

2

) i poprawka do objętości (- b). 

Poprawka do ciśnienia ma odzwierciedlać przyciąganie
między cząsteczkami gazu dla większych odległości.
Poprawka do objętości to próba uwzględnienia objętości
własnej cząsteczek gazu (ściślej mówiąc - sił odpychania na
małych odległościach).
 





RT

b

v

v

a

p















 

2

Wartości stałych a i b można uzyskać dopasowując
krzywe doświadczalne lub z wartości tzw. parametrów
krytycznych gazu:

c

c

p

T

R

a

64

27

2



c

c

p

RT

b

8



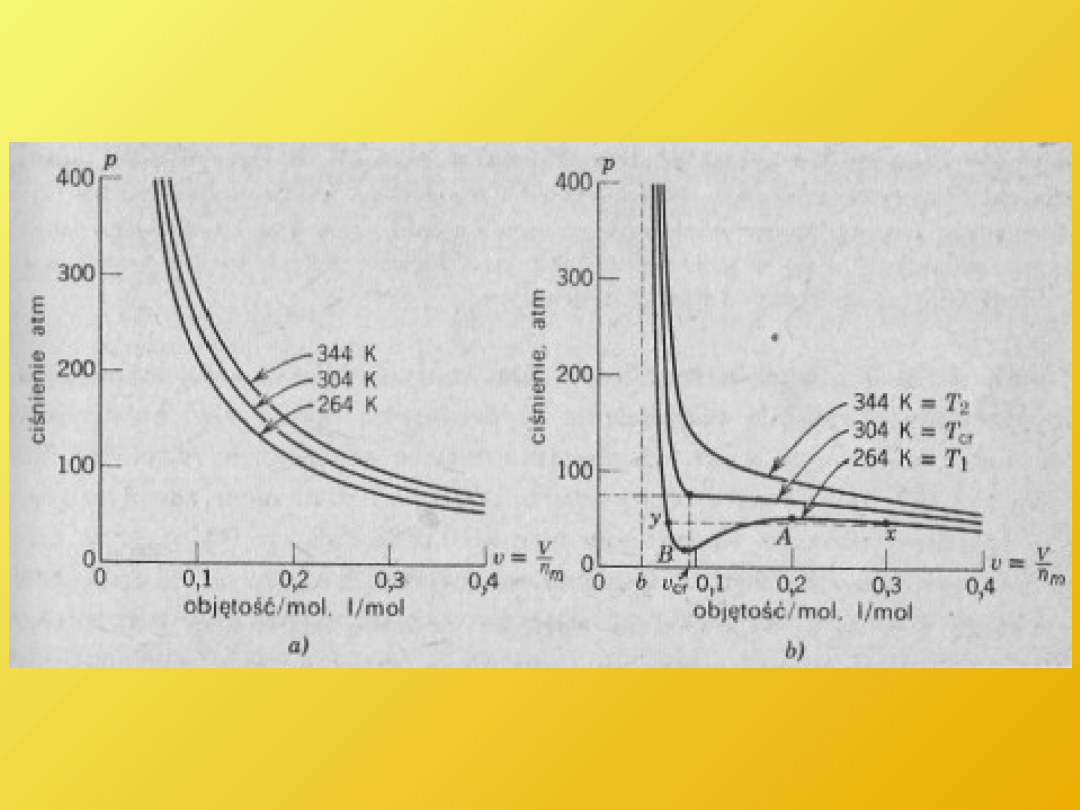
a. Izotermy gazu doskonałego

b. Izotermy gazu Van der Waalsa

Druga zasada

termodynamiki

 

Z doświadczenia wiemy, że są procesy

zgodne z zasadą zachowania energii, które nigdy
nie występują w przyrodzie. Na przykład, nigdy nie
obserwujemy, by kamień leżący na podłodze
spontanicznie się oziębił i wzniósł do sufitu,
uzyskując kosztem ciepła energię potencjalną. Nie
spodziewamy się też, by w słoneczny letni dzień
zamarzł staw, oddawszy energię wewnętrzną
otoczeniu.

Zadaniem drugiej zasady

termodynamiki jest włączyć do
termodynamiki takie fakty doświadczalne, jej
podstawą jest zdrowy rozsądek.

 

Zasada ta określa kierunek transferu i
przemiany ciepła.

Przy omawianiu I zasady termodynamiki
stwierdziliśmy, że wszystkie rodzaje energii są
równie użyteczne, żadna z nich nie jest
preferowana, tylko, że dla układu izolowanego musi
ona zostać zachowana.

Możemy jednak rozróżnić różne rodzaje energii,
np..pracę mechaniczną i energię wewnętrzną, którą
można zmienić przez pracę. Rozróżniamy również
ciepło, które definiujemy przez energię wewnętrzna
i pracę.

Z równania które mówi o zmianie energii
wewnętrznej dla

cyklu zamkniętego









0

dW

dQ

można by wyciągnąć wniosek, że dwa człony tego
równania są równoważne. II zasada termodynamiki
przyjmuje fakt, że ciepło i praca nie są równoważne
i podaje szereg relacji, które uzupełniają I zasadę w
badaniu układów termodynamicznych.

Przypomnijmy:

• Ciepło przepływa od temperatury wyższej do

temperatury niższej, a nie odwrotnie.

Czyli ciało ciepłe ochłodzi się w
kontakcie z chłodnym ciałem a nie
odwrotnie..

Pierwsze sformułowanie sprowadza się do tego, że
np. naczynie z wodą włożone do lodówki nie
zagotuje się, mimo, że z punktu widzenia zachowania
energii jest to możliwe. Przepływ ciepła odbywa się
tylko w jedną stronę, co nie jest wynikiem zasady
zachowania energii.

2.

Dwa gazy umieszczone w izolowanym naczyniu

wymieszają się jednorodnie w całym naczyniu i
nie będą w stanie

spontanicznie się rozdzielić

.

3.

Bateria rozładuje się przez opornik wydzielając

pewną ilość ciepła, przy czym proces odwrotny
jest niemożliwy.

4.

Nie jest możliwe skonstruowanie maszyny

pracującej w sposób ciągły przez pobór ciepła
z pojedynczego zbiornika i wykonującej
równoważną ilość pracy.

Przyjrzyjmy się bliżej pierwszemu i czwartemu

.

Stwierdzenie 4 mówi o niemożności zbudowania perpetuum mobile
drugiego rodzaju.

Perpetuum mobile pierwszego rodzaju byłoby urządzeniem, które
wytwarza energię bez brania pod uwagę I zasady termodynamiki.

Konkludując, możemy powiedzieć, że

II zasada

termodynamiki przyjmuje jednokierunkowy
przepływ ciepła i pewne określone typy przemiany
energii.

Będziemy chcieli sformułować II zasadę
termodynamiki przez podanie zależności
analitycznych, bazując na argumentach
makroskopowych i przyjmując czwarte
sformułowanie jako doświadczalny aksjomat.

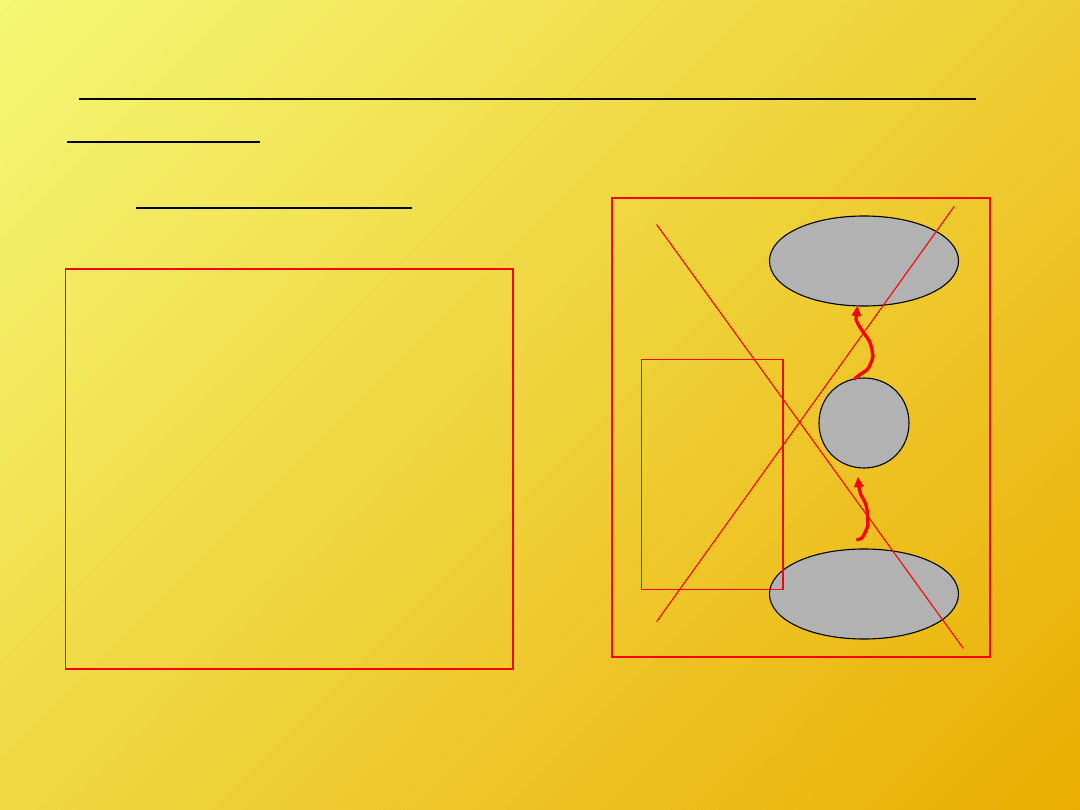
Sformułowanie Clausiusa oraz Kelvina-Plancka II
zasady

termodynamiki

T

2

T

1



Q

2

Q

1

Sformułowanie
Clausiusa:

Nie można
skonstruować
urządzenia
działającego
cyklicznie, którego
jedynym efektem
będzie transport ciepła
od ciała zimniejszego
do cieplejszego.

T

2

>

T

1

Q

1

=

Q

2

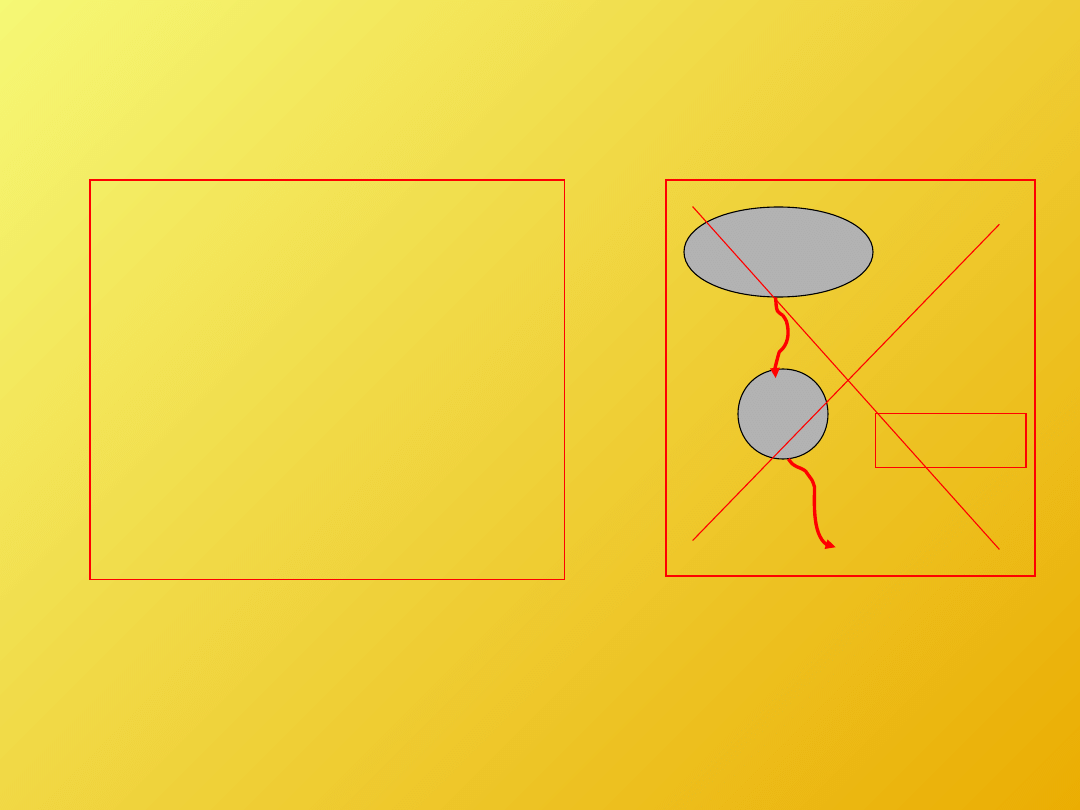
Sformułowanie Kelvina –
Plancka:

Nie można
skonstruować
urządzenia działającego
cyklicznie, którego
jedynym efektem jest
produkcja pracy i
wymiana ciepła z
pojedynczym
zbiornikiem.

T



W

Q = W

Procesy odwracalne oraz cykle

Zdefiniujmy najpierw

proces kwazistatyczny. Jest to

proces przebiegający tak wolno, że układ stale pozostaje
dowolnie blisko stanu równowagi.

Kiedy proces można nazwać odwracalnym?
Otóż jeżeli weźmiemy gaz w cylindrze, zauważymy, że
kwazistatyczne rozprężanie tego gazu związane jest z
wykonaniem pracy i oddaniem ciepła. Jeśli jesteśmy w
stanie przywrócić warunki początkowe przez dodanie
dokładnie tej samej ilości ciepła, oraz wykonanie tej
samej pracy, to gaz w cylindrze możemy sprężyć do
warunków początkowych. Można więc powiedzieć, że
proces kwasistatyczny jest procesem odwracalnym.
Inaczej mówiąc

proces odwracalny jest to taki

proces, po zajściu którego można przywrócić
warunki początkowe tylko przez narzucenie
warunku ograniczającego usuniętego na początku
procesu.

Procesem

nieodwracalnym

nazywamy proces, który nie jest

odwracalny.

Cyklem odwracalnym nazywamy ciąg
następujących po sobie procesów
odwracalnych takich, że układ w sposób
periodyczny wraca do stanu początkowego.

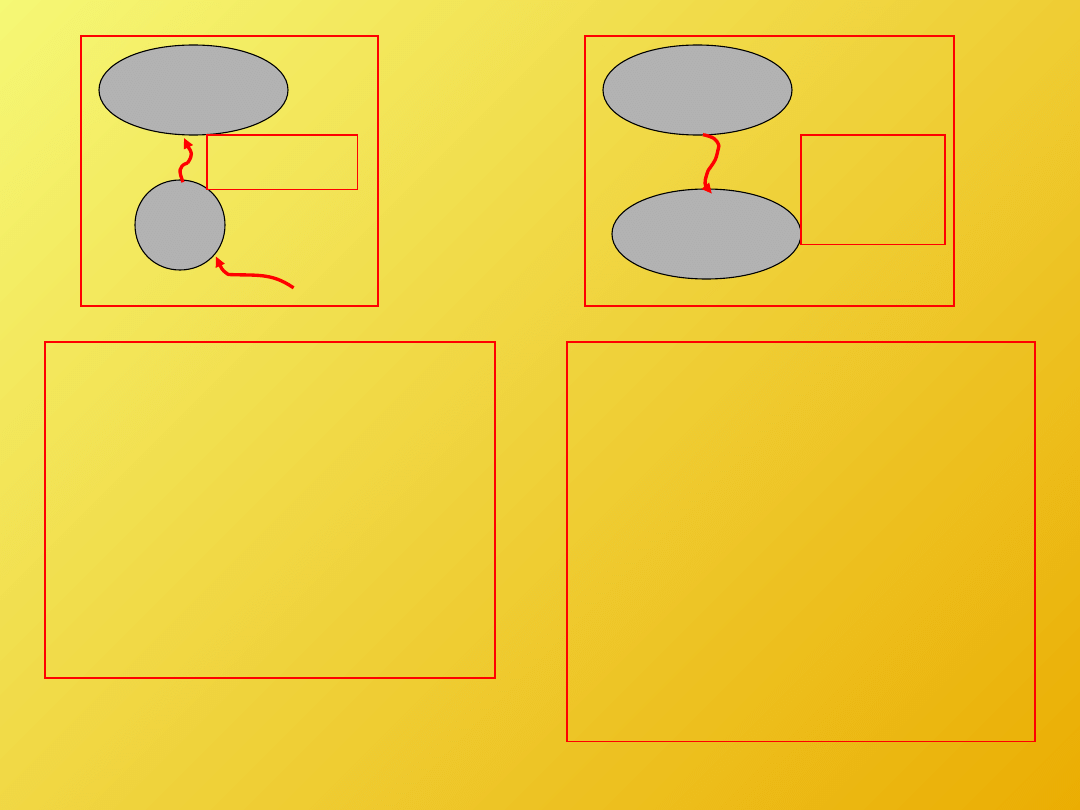
Konwersja pracy w
ciepło jest procesem
nieodwracalnym.

Sytuacja odwrotna
narusza sformułowanie
Kelvina-Plancka II
zasady termodynamiki

Transport ciepła przez
skończoną różnicę
temperatury jest
procesem
nieodwracalnym.

Sytuacja odwrotna
narusza sformułowanie
Kelvina-Plancka II
zasady termodynamiki

T



W

Q = W

T

2

T

1

Q T

2

>

T

1

Należy jeszcze zdefiniować

cykl mocy, czyli cykl

dostarczający pracę kosztem dostarczanego ciepła,

oraz

cykl chłodniczy, który kosztem dostarczanej

pracy oddaje ciepło

.

Odwracalny cykl mocy może zostać zamieniony na
odwracalny cykl chłodniczy przez odwrócenie
strumienia ciepła i pracy.

Równoważność sformułowania Clausiusa ze
sformułowaniem Kelvina-Plancka II zasady
termodynamiki możemy pokazać następująco.

Załóżmy, że jest możliwy transfer ciepła wbrew
stwierdzeniu Clausiusa, czyli bezpośrednio z
chłodnicy do zbiornika ciepła. Do tego procesu
możemy dodać odwracalny silnik taki jak na
środkowym obrazku. Wynikiem dodania takich
procesów jest powstanie silnika, który wykonuje
pracę korzystając tylko z jednego zbiornika ciepła.
A taki proces jest wykluczony przez

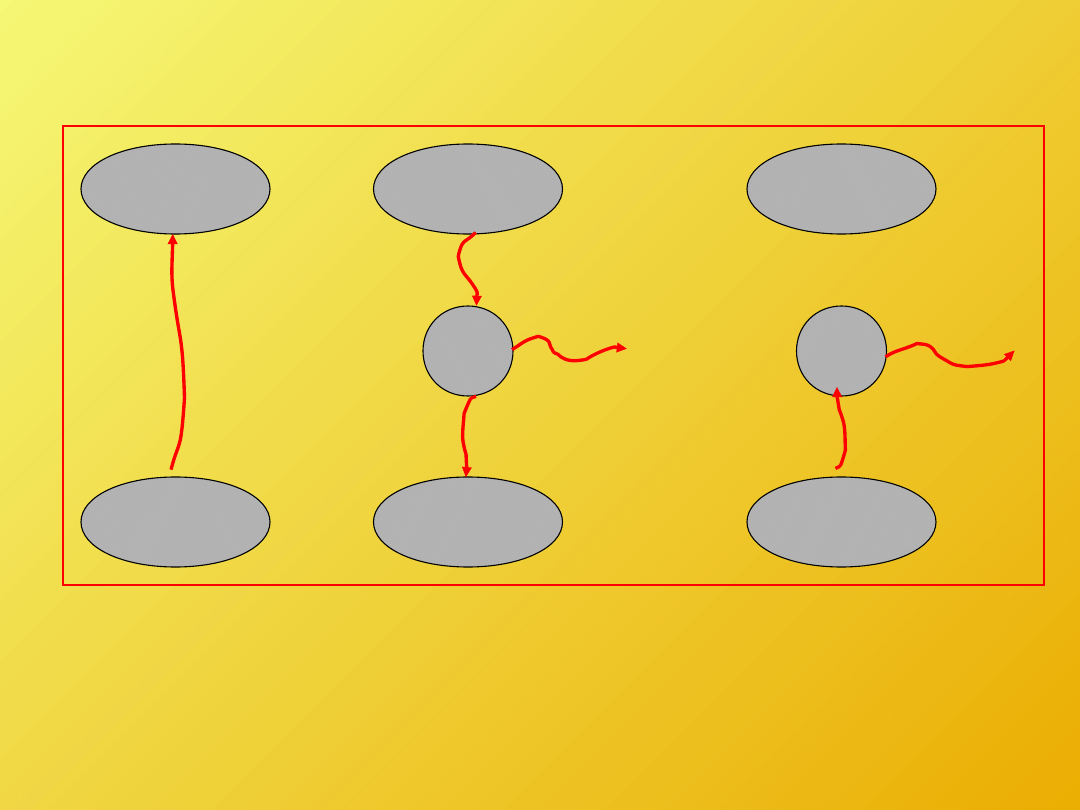
sformułowanie Kelvina-Plancka II zasady termodynamiki

T

2

T

1

Q

2

T

2

T

1



Q

2

Q

1

T

2

T

1



Q

2

-

Q

1

+

W=Q

2

-

Q

1

=

W=Q

2

-

Q

1

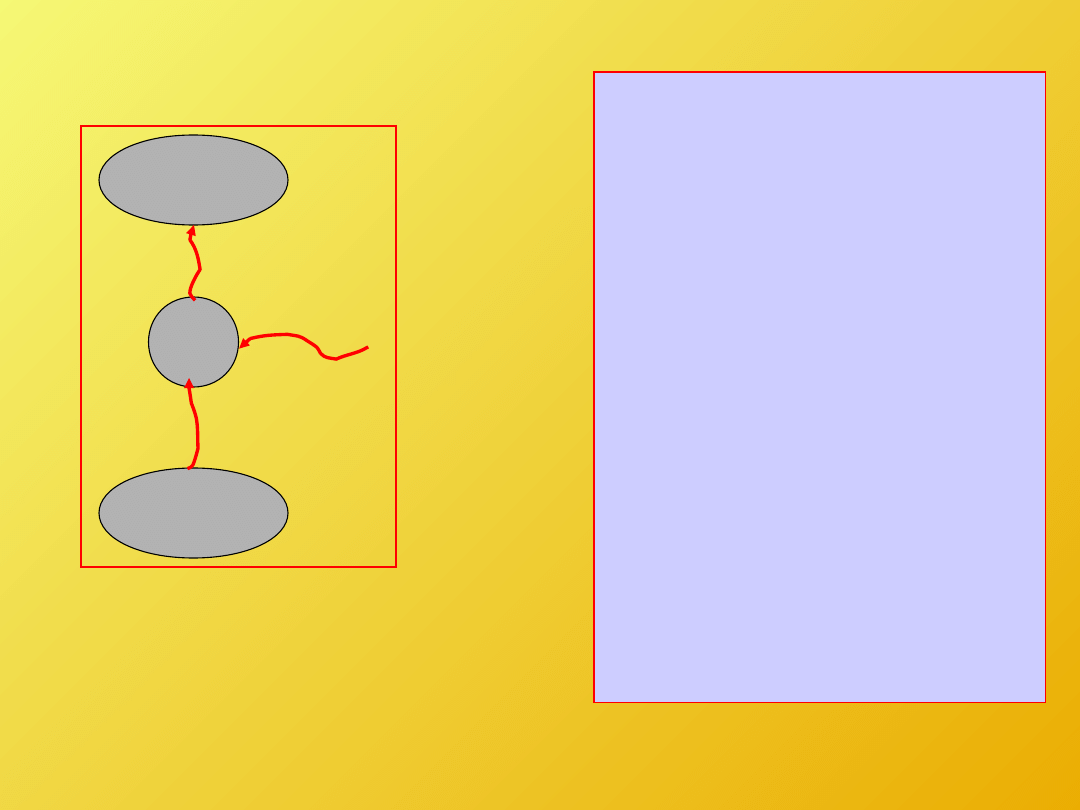
Pokazaliśmy więc, że złamanie sformułowania
Clausiusa II z.t. pociąga za sobą złamanie
sformułowania Kelvina – Plancka II z.t..

T

2

T

1



Q

1

W=Q

2

-

Q

1

Q

2

Dla kompletu
zdefiniujmy
sobie jeszcze

cykl

chłodzący

.

Jeśli chodzi o

konwencję znakową
dla ciepła i pracy

, to

mówimy:

Energia dodana do
systemu

=

Energia akumulowana
w systemie

+

Energia usunięta z
systemu

.

Wszystkie poniższe sformułowania drugiej

zasady termodynamiki są równoważne

:

 

Clausius (1850

): Nie istnieje proces

termodynamiczny, którego jedynym wynikiem
byłoby pobranie ciepła ze zbiornika
chłodniejszego i przekazanie go do zbiornika
cieplejszego (nie jest możliwe zbudowanie
idealnej maszyny chłodzącej)
 

Kelvin (1851

): Nie istnieje proces

termodynamiczny, którego jedynym wynikiem
byłoby pobranie ciepła ze zbiornika i
całkowita zamiana tego ciepła na pracę
mechaniczną.

Późniejsze od sformułowania Kelvina jest sformułowanie
podane przy pomocy pojęcia silnika termodynamicznego
 

Planck

: Nie możliwe jest zbudowanie silnika

termodynamicznego pracującego cyklicznie, który całe
pobrane ciepło zamieniałby na pracę (nie jest możliwe
zbudowanie idealnego silnika cieplnego – czyli
perpetuum mobile drugiego rodzaju).
 

Dla sprawności silnika cieplnego, z teorią których druga
zasada jest związana, oznacza to, że sprawność silników
cieplnych jest mniejsza od jedności
Druga zasada termodynamiki pozwala na zdefiniowanie
bezwzględnej skali temperatur Kelvina identycznej ze skalą
temperatury gazu doskonałego.
Pozwala ona też na wprowadzenie

użytecznej funkcji stanu

nazywanej

entropią

.

Związana jest z pojęciem procesów

odwracalnych i nieodwracalnych,z kierunkiem procesów
zachodzących samorzutnie w układach izolowanych, z
kierunkowością zjawisk w przyrodzie. Za pomocą pojęcia
entropii druga zasada termodynamiki daje się wysłowić:

Boltzmann

: Entropia układu izolowanego nie maleje.

 

 

Druga zasada termodynamiki nie jest ścisłym
prawem przyrody, ma jedynie charakter
statystyczny.

Zdarzenia sprzeczne z nią mogą w

rzeczywistości zajść, lecz są mało
prawdopodobne

. Ściślej mówiąc są tym mniej

prawdopodobne, im więcej cząstek liczy układ
termodynamiczny. II zasada termodynamiki dobrze
sprawdza się w skali makro, gorzej w skali mikro. W
zaawansowanym wykładzie mechaniki statystycznej
dowodzi się nawet, że pewne wydarzenia sprzeczne
z drugą zasadą termodynamiki z pewnością będą
miały miejsce. Jednak czas, jaki przychodzi czekać
na tego typu zajście w makroskopowym układzie,
znacznie przekracza wiek wszechświata, możemy
się więc „nie doczekać”...

Entropia

jest termodynamicznym parametrem

stanu układu. W interpretacji statystycznej, określa
ona stopień nieuporządkowania układu, albo inaczej
mówiąc, stopień jego wyjątkowości. Statystycznie
określa się ją jako:

Gdzie const jest jakąś stałą. W natomiast jest
definiowane jako liczba mikrostanów
nieodróżnialnych od naszego makrostanu. Z tego
wynika np. że wazon ma małą entropię
(nieuporządkowanie), natomiast rozbite odłamki dużą
(jest wiele możliwych realizacji rozbitego wazonu).

const

W

k

S



 ln

Z punktu widzenia przemian termodynamicznych,
entropię definiuje się jako uogólnione przemieszczenie.
Dla siły i pracy można napisać zależność:

Podobne równanie można zapostulować dla całkowitego
pochłoniętego ciepła (odpowiednik pracy z powyższego
wzoru) i jednostki napędowej (temperatura), zużytej
na ,,uogólnionej drodze'' (entropii):

Można udowodnić, że entropia jest funkcją stanu. Tzn.
nie zależy ona od drogi, po jakiej się do niej doszło.

Fds

dW

TdS

dQ

W cyklu odwracalnym wielkość Q/T jest zachowywana

Stąd wielkość Q/T nie zależy od drogi, a tylko od stanu

początkowego

i końcowego układu termodynamicznego

 

Entropia S jest funkcją stanu układu,
 S(V,T)

W procesach odwracalnych entropia jest

zachowywana

S

całkowita

= 0,

natomiast w procesach nieodwracalnych entropia
rośnie

dS

n

 dQ/T

 

Entropią układu termodynamicznego nazywamy taką
funkcję S

tego układu, której przyrost dS w procesie odwracalnym jest
równy stosunkowi przyrostu ciepła Q pobranego przez układ
do temperatury układu (termostatu)

dS = dQ/T

Na ogół w przemianach

termodynamicznych nie interesuje nas
entropia jako taka, ale jej zmiany. Sprawa jest
podobna do energii potencjalnej: poziom zerowy
jest przyjmowany umownie. W przypadku entropii
jest on zgodnie z postulatem Plancka przyjmowany
dla doskonałych kryształów na poziomie
temperatury 0 K, co umożliwia wyzerowanie stałej,
obecnej w interpretacji statystycznej. W
temperaturze 0 K istnieje bowiem zgodnie z
zasadami fizyki kwantowej tylko jeden
mikrostan (W=1).

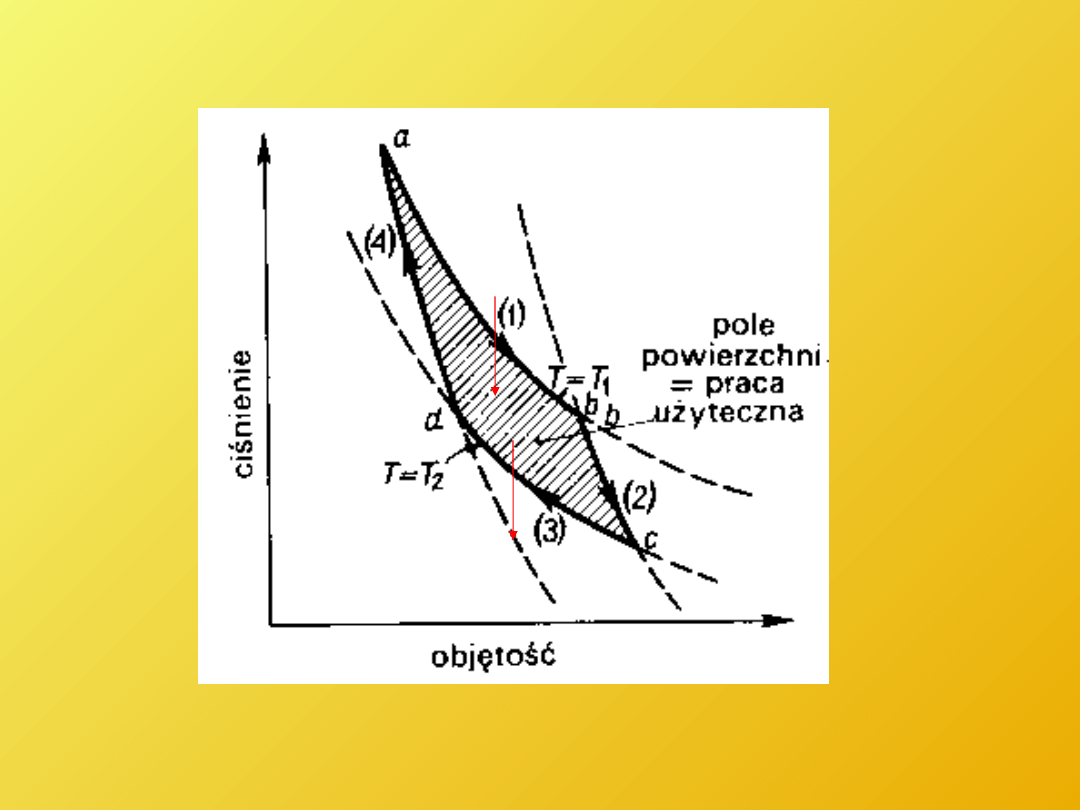
Cykl Carnota

(odwracalny

) (Nicolas Leonard Sadi Carnot 1796 - 1832)

Dla procesów kołowych odwracalnych (izotermy T

1

, T

2

, -adiabaty)

Q

1

/T

1

= Q

2

/T

2

Q

1

Q

2

W

T
 
T

1

 
 
T

2

 
 

S

1

S

2

S

 
 

Cykl Carnota (T, S)

Sprawność silnika cieplnego Carnota

 

Twierdzenie Carnota

Sprawność wszystkich odwracalnych silników

pracujących z tymi samymi termostatami jest jednakowa

 

 

 

1

1

2

1

1

2

1

Q

W

Q

Q

Q

T

T

T













Dla dowolnej maszyny cieplnej nieodwracalnej
(tj. dla cyklu nieodwracalnego) sprawność cyklu
nieodwracalnego



n

= 1 - (Q’

2

/Q

1

)  1 - (T

2

/T

1

) = 

c



n

 

o

Sprawność nieodwracalnego cyklu jest

zawsze mniejsza od sprawności cyklu

Carnota pracującego między tymi

samymi termostatami

 

W

Q

2





Sprawność w cyklu odwrotnym
Carnota

 

Sprawność układu chłodzącego

Efekty Q

2

Nakłady W

Naklady

Efekty





I zasada termodynamiki (sformułowanie
klasyczne)

Nie jest możliwe perpetuum mobile I
rodzaju

, tzn. nie można zbudować ciągle

pracującego silnika, który wykonuje większą
pracę niż pobiera energii z zewnątrz.
 

II zasada termodynamiki (sformułowanie
klasyczne)

Nie jest możliwe perpetuum mobile II
rodzaju

, tzn. nie można zbudować ciągle

pracującego silnika, który pobrane z otoczenia
ciepło zamienia całkowicie na pracę.

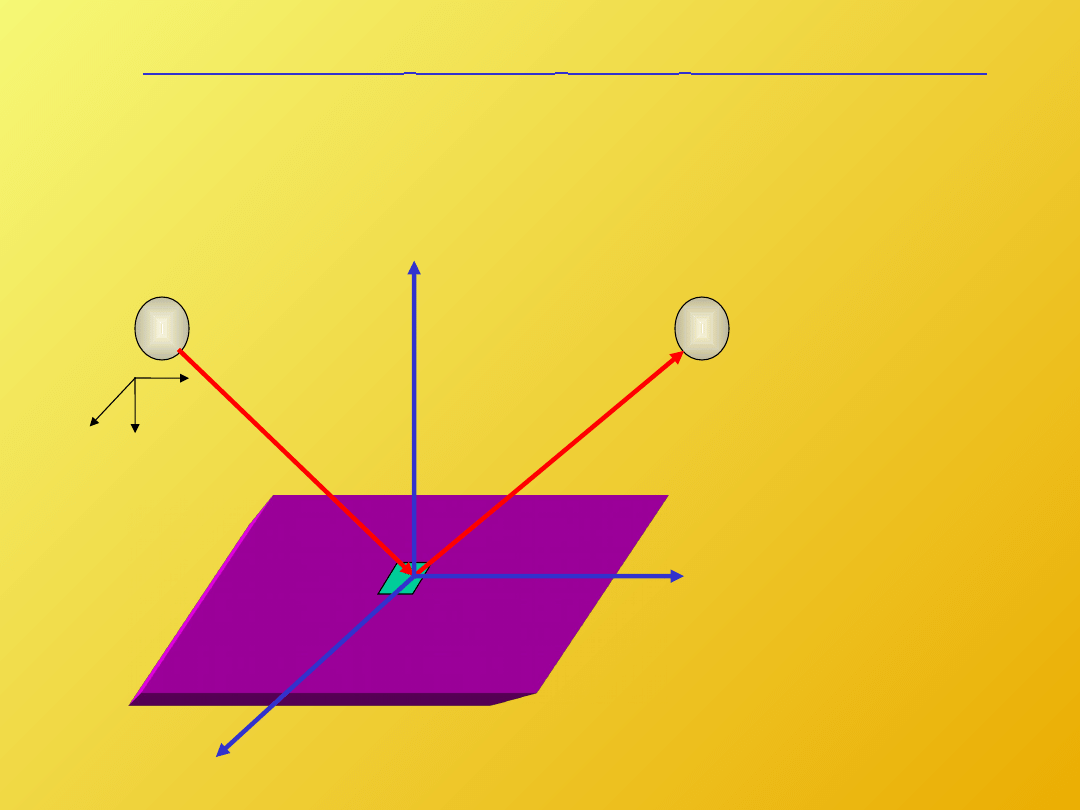
Kinetyczna teoria gazów

interpretacja

ciśnienia i temperatury

x

y

z

v

x

v

y

v

z

dA

Kinetyczna

teoria

gazu

doskonałego

Aby pokazać proste zależności pomiędzy
termodynamiką mikroskopową a makroskopową
rozważmy kinetyczną analizę

ruchu
cząsteczek
gazu.
Ciśnienie jest
zdefiniowane
jako siła
wywierana na
ściankę przez
uderzające w
nią cząsteczki.

Pęd
przekazany
ściance przez
każdą cząstkę
jest równy

:

z

cz

z

cz

z

cz

v

M

v

M

v

M

dt

F

2

)

(











(1)

Liczba molekuł uderzająca powierzchnię

dA

dana

jest przez strumień molekuł w kierunku

z

s

moleku

ł

v

dA

n

n

z

/



(2)

·

n

jest liczbą molekuł na jednostkę objętości.

Jeśli założymy przypadkowy ruch molekuł, to tylko
połowa molekuł poruszać się będzie w kierunku

–z .

z

z

v

dA

n

n

2

1





(3)

·

Z zależności pomiędzy popędem siły a zmianą pędu
znajdujemy, że całkowity pęd przekazany
powierzchni dA w czasie dt jest równy iloczynowi

dt

dA

v

n

v

M

dt

F

z

z

cz

)

2

1

(

)

2

(







Czyli ciśnienie

2

z

cz

v

n

M

p

dA

F





(4)

Wiemy,
że

2

2

2

2

z

y

x

v

v

v

v







a z przypadkowości
ruchu

wynika,
że

2

2

2

2

3

1 v

v

v

v

z

y

x







.

Otrzymu

je

my

2

3

/

1

v

M

n

p

cz



(5)

2

2

2

2

1

2

2

2

1

2

...

2

...

2

2

v

N

M

N

V

V

N

M

V

M

V

M

CZ

CZ

CZ

CZ



























gdzie

We wzorze (5)
iloczyn

V

m

M

n

cz



czyli masę na
substancji na
jednostkę
objętości.

Po wstawieniu tego do równania

(5)

otrzymujemy

wyrażenie;

2

3

1

v

m

pV

(6)

Porównując to równanie z równaniem

gazu

doskonałego

otrzymujemy:









2

2

3

2

2

3

3

1

2

2

2

v

M

kT

n

v

NM

T

k

N

v

m

T

nR

cz

cz

A







(7)

Temperatura jest miarą średniej energii
kinetycznej gazu.

nRT

pV 

Wynik ten zwany jest prawem Boyle’a

k

E

T ~

A

A

N

n

N

k

N

R







Żeby podany powyżej związek był zgodny z klasycznym,

termodynamicznym prawem gazów doskonałych, prawa strona

równania, związana z energią kinetyczną cząstki, musi zawierać

kinetyczną definicję temperatury bezwzględnej.

TEMPERATURA



Temperatura definiowana w ramach termodynamiki klasycznej

(makroskopowej), to parametr opisujący stan równowagi termodynam

i

cznej

układu.



W teorii kinetycznej zdefiniujemy temperaturę jako:

k

cz

E

k

v

M

k

T





























3

2

2

3

2

2

gdzie

jest średnią energią kinetyczną przypadającą na 1 cząsteczkę gazu.
 Współczynnik proporcjonalności w powyższej definicji zawiera wielkość

k

zwaną stałą Boltzmanna, :

K

J

k

23

10

38

,

1









Dla tak zdefiniowanej temperatury,

oba prawa gazów

doskonałych (termodynamiczne i w teorii kinetycznej) są

równoważne.

k

E

2

2

2

2

1

2

2

2

1

2

...

2

...

2

2

v

N

M

N

V

V

N

M

V

M

V

M

CZ

CZ

CZ

CZ



























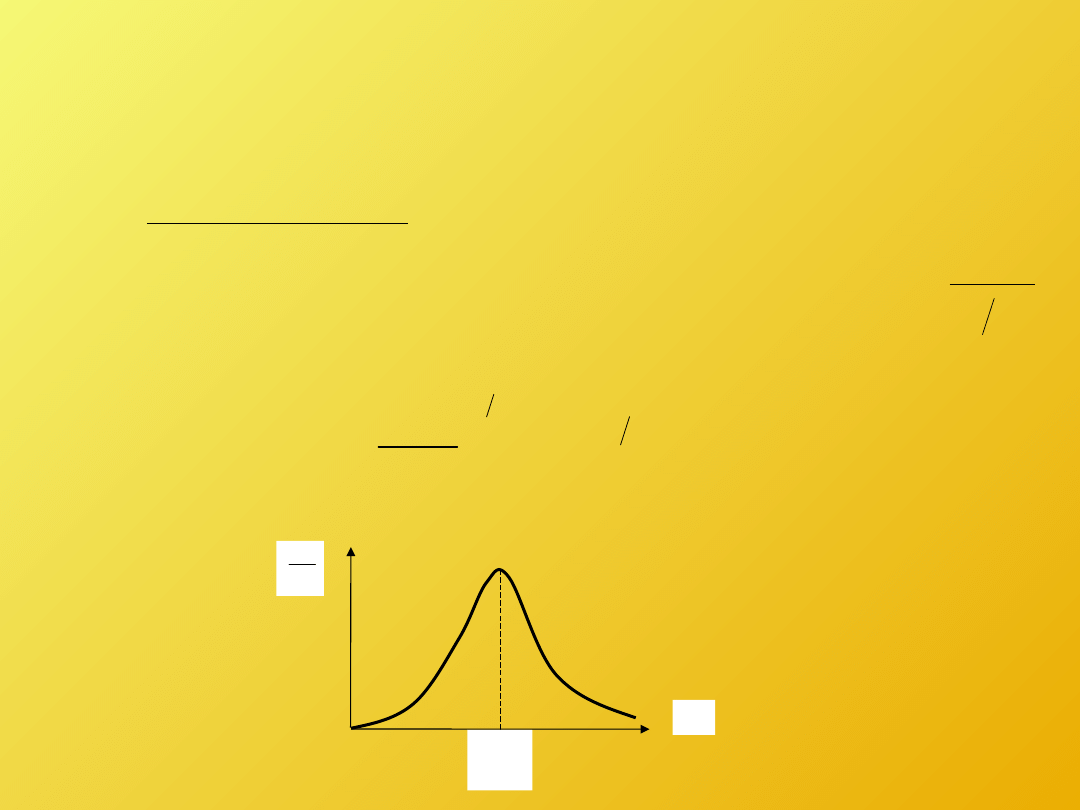
ROZKŁAD PRĘDKOŚCI CZĄSTECZEK

 Wyprowadzając podstawowe równanie kinetycznej teorii gazów

wprowadziliśmy pojęcie średniej kwadratu prędkości (średniej
prędkości kwadratowej), która charakteryzowała zbiór cząsteczek jako
całość. Problemem pozostaje wyznaczenie tej średniej, czyli znalezienie
formuły rozkładu prędkości cząsteczek gazu doskonałego

.



Maxwell rozwiązał teoretycznie to zagadnienie, podając prawo

pozwalające określić, jaka liczba cząstek

dn

z całej ilości

0

n

cząstek gazu doskonałego w jednostce objętości

V

N

n 

0

v

do

dv

v

:

dv

v

e

kT

M

n

dn

kT

v

M

cz

cz

2

2

2

3

0

2

2

4



























ma w danej temperaturze prędkości w przedziale od

v

pr

v

dv

dn

cz

pr

M

kT

v

2



T

1

T

2

T

3

ROZKŁAD MAXWELLA

Korzystając z rozkładu Maxwella można wyliczyć:

-prędkość najbardziej prawdopodobną:
z warunku:

-prędkość średnią kwadratową:

cz

kw

M

kT

v

v

3

2





-prędkość średnią:

cz

M

kT

v



8



 Wraz ze wzrostem temperatury, krzywe przedstawiające rozkład prędkości cząsteczek gazu zmieniają się:

dv

dn

v

pr

v

3

2

1

T

T

T





Maksimum krzywej przesuwa się wraz ze wzrostem temperatury w kierunku
większych prędkości – przy ogrzewaniu gazu udział cząsteczek obdarzonych małymi
prędkościami zmniejsza się.

 

0



dv

v

dn

o

n

vdv

v

n

v







0

)

(

o

n

dv

v

v

n

v







0

2

2

)

(

kw

pr

v

v

v





ŚREDNIA DROGA SWOBODNA

 Cząsteczki gazu mają skończone wymiary i stale zderzają się ze sobą (wymieniając

się energią kinetyczną i pędami, stąd rozkład prędkości Maxwella!). Pomiędzy
dwoma kolejnymi zderzeniami cząsteczki poruszają się prostoliniowo i jednostajnie
a odległość przy tym pokonywaną nazwiemy średnią długością drogi swobodnej.



.
 Korzystając z rozkładu Maxwella, można pokazać, że średnia droga swobodna

cząsteczki zależy od „wymiaru” cząsteczki

d

i liczby cząsteczek w jednostce objętości gazu

0

n

:

0

2

2

1

n

d







 Przy stałej temperaturze liczba cząsteczek w objętości gazu jest wprost

proporcjonalna do ciśnienia gazu, więc średnia droga swobodna jest odwrotnie
proporcjonalna do ciśnienia. A zatem:

const

p







6

10

5

,

6





3

10

5





5

,

0

50 5000

[cm]

10

-6

10

-4

10

-2

1

760

p

[mm

Hg]

Oddziaływania międzycząsteczkowe Energia wewnętrzna

Krótkozasięgowy charakter oddziaływania

Energia wewntrzna

Ciepło molowe

nRT

NkT

U

2

3

2

3





zależna tylko od temperatury, zakładamy brak energii potencjalnej

Ciepło które trzeba dostarczyć do jednego mola gazu, aby spowodować
jednostkową zmianę temperatury.

ndT

dU

C

v



R

ndT

nRT

d

C

v

2

3

2

3

















Zgodność tylko dla gazu jednoatomowych

STOPNIE SWOBODY CZĄSTECZEK



Liczba stopni swobody ciała to najmniejsza możliwa

liczba współrzędnych (liczba współrzędnych niezależnych), które

musimy podać, aby jednoznacznie określić położenie ciała w

przestrzeni.

 Cząsteczki gazu jednoatomowego mają trzy stopnie

swobody – ich położenie opisują trzy współrzędne, np. x,y,z

układu kartezjańskiego.

 Cząsteczki dwuatomowe mają pięć stopni swobody –

trzeba na przykład podać trzy współrzędne jednego atomu i

dwie współrzędne, określające położenie drugiego atomu

względem pierwszego (tylko dwie, bo stała odległość między

nimi da nam automatycznie trzecią współrzędną!).

 Cząsteczki, zbudowane z większej ilości atomów bądź

po prostu ciała sztywne (traktowane jako układ wielu atomów, o

nie zmieniających się odległościach między nimi), maja sześć

stopni swobody.

ZASADA EKWIPARTYCJI ENERGII

 Jednym z ważniejszych praw fizyki statystycznej jest prawo równomiernego

rozkładu energii między stopnie swobody: na każdy stopień swobody
cząsteczki średnio przypada jednakowa energia kinetyczna, równa

2

kT

(

zasada ekwipartycji energii

).

 Jeżeli cząstka jest obdarzona

i

stopniami swobody, to jej średnia energia kinetyczna:

 W przypadku gazu doskonałego jedyną energią cząstek była energia
kinetyczna. W przypadku np. ciał stałych należy

uwzględniać

również

energię potencjalną oddziaływań międzycząsteczkowych. Można
wykazać, że zasada ekwipartycji energii jest wtedy również słuszna, jeśli
tylko energia potencjalna jest funkcją kwadratów współrzędnych
cząsteczki.

.

2

kT

i

E

k



i – liczba stopni swobody
Pojedyncza cząstka

i=3

Podwójna cząsteczka

i=5

Więcej niż 2 cząstki

i=6

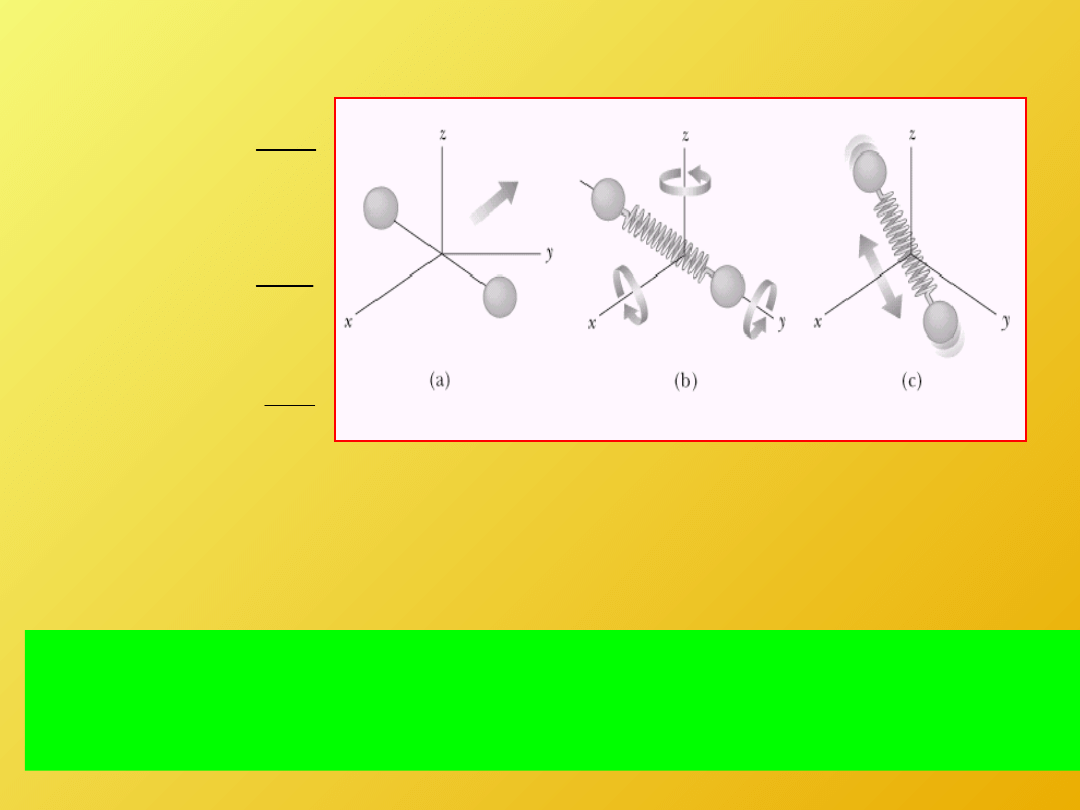
Dostępne formy ruchu dla cząstek:

-a) Ruch postępowy

-b) Ruch rotacyjny

-c) Ruch wibracyjny

2

2

mv

2

2



I

2

2

kx

Gdy liczba punktów materialnych jest bardzo duża oraz obowiązuje

mechanika Newtonowska

Powyższe formy absorpcji energii mają taką samą wartość średnią

i ta średnia wartość zależy wyłącznie od temperatury

Dostępna energia zależy wyłącznie od temperatury

i rozkłada się w równych porcjach na wszystkie

sposoby, w jakie cząsteczki mogą ją absorbować.

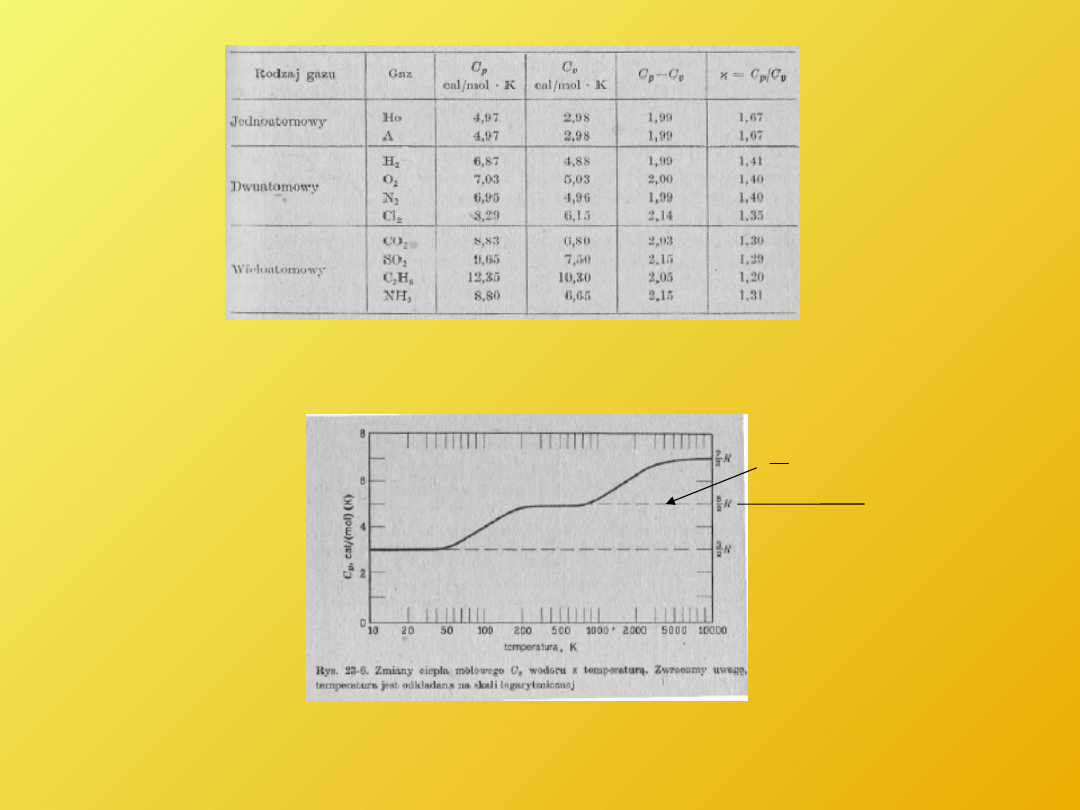
Ciepła molowe niektórych gazów wyznaczone doświadczalnie T=293K p=10

5

Pa

Ciepło molowe wodoru w funkcji temperatury (brak zgodności z mechaniką klasyczną C

v

(T))

R

2

5